Exciting of Strong Electrostatic Fields and Electromagnetic Resonators at the Plasma Boundary by a Power Electromagnetic Beam
Abstract
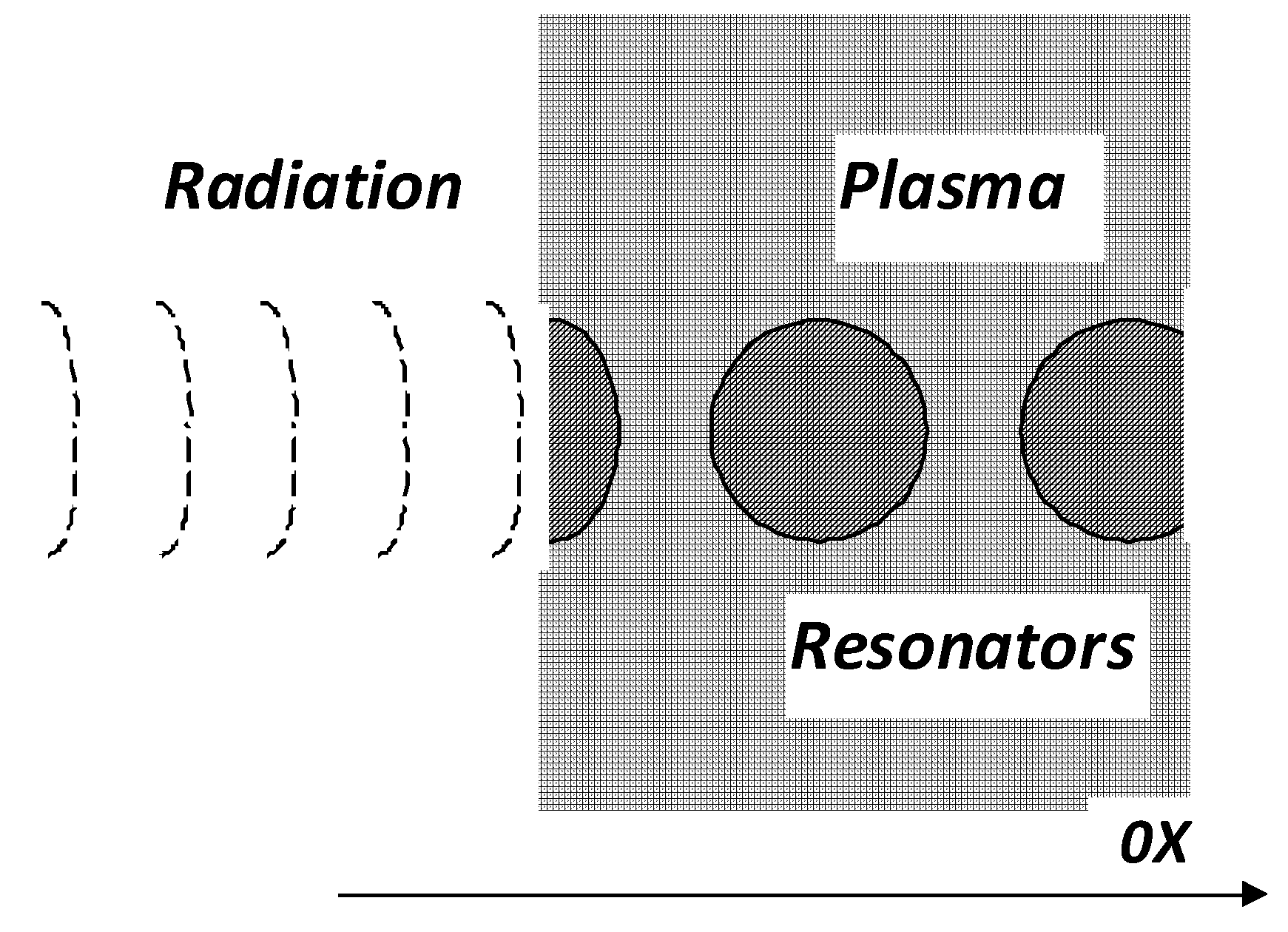
:1. Introduction
2. Basic Equations
3. Analytical and Numerical Results
3.1. Conditions for the Formation of Globe-Shaped Resonators of the Electromagnetic Field
3.2. Generation of Electrostatic Fields of Surface Charge near Plasma Space by a Beam of Electromagnetic Radiation
4. Summary and Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rosenbluth, M.N.; Liu, C.S. Excitation of plasma waves by two laser beams. Phys. Rev. Lett. 1972, 29, 701. [Google Scholar] [CrossRef]
- Gradov, O.M.; Stenflo, L. On the parametric transparency of a magnetized plasma slab. Phys. Lett. 1981, 83, 257. [Google Scholar] [CrossRef]
- Gradov, O.M.; Ramazashvili, R.R.; Stenflo, L. Parametrlc transparency of a magnetized plasma. Plasma Phys. 1982, 24, 1101. [Google Scholar] [CrossRef]
- Aliev, Y.M.; Gradov, O.M.; Kyrie, A.Y.; Čadež, V.M.; Vuković, S. Total absorption of electromagnetic radiation in a dense inhomogeneous plasma. Phys. Rev.A 1977, 15, 2120. [Google Scholar] [CrossRef]
- Forslund, D.W.; Kindel, J.M.; Lee, K.; Lindman, E.L. Absorption of laser light on self-consistent plasma-density profiles. Phys. Rev. Lett. 1976, 36, 35. [Google Scholar] [CrossRef]
- Gradov, O.M.; Larsson, J.; Lindgren, T.; Stenflo, L.; Tegeback, R.; Uddholm, P. Anomalous radiation from a nonstationary plasma. Phys. Scr. 1980, 22, 151. [Google Scholar] [CrossRef]
- Berger, J.M.; Newcomb, W.A.; Dawson, J.M.; Frieman, E.A.; Kulsrud, R.M.; Lenard, A. Heating of a confined plasma by oscillating electromagnetic fields. Phys. Fluids 1958, 1, 301. [Google Scholar] [CrossRef]
- Stratton, J.A. Electromagnetic Theory; McGraw-Hill: New York, NY, USA, 1941. [Google Scholar]
- Gradov, O.M. Self-consistent plasma boundary distortions during the interaction of a normally incident electromagnetic beam and a nonlinear surface charge. Chin. J. Phys. 2021, 72, 360–365. [Google Scholar] [CrossRef]
- Gradov, O.M. Three-dimensional surface charge nonlinear waves at a plasma boundary. Phys. Scr. 2019, 94, 125601. [Google Scholar] [CrossRef]
- Gradov, O.M. Nonlinear behavior of a surface charge on the curved plasma boundary with a moving cavity. Phys. Lett. A 2020, 384, 126566. [Google Scholar] [CrossRef]
- Yamagiva, M.; Koga, J. MeV ion generation by an ultra-intense short-pulse laser: Application to positron emitting radionuclide production. J. Phys. D Appl. Phys. 1999, 32, 2526. [Google Scholar] [CrossRef]
- Kovalev, V.F.; Bychenkov, V.Y. Analytic theory of relativistic self-focusing for a Gaussian light beam entering a plasma: Renormalization-group approach. Phys. Rev. E 2019, 99, 043201. [Google Scholar] [CrossRef] [PubMed]
- Boyer, C.N.; Destler, W.W.; Kim, H. Controlled collective field propagation for ion-acceleration using a slow-wave structure. IEEE Trans. Nucl. Sci. 1977, 24, 1625–1627. [Google Scholar] [CrossRef]
- Jeffreys, H.; Swirles, B. Methods of Mathematical Physics; Cambridge University Press: Cambridge, UK, 1956. [Google Scholar]
- Bateman, H.; Erdélyi, A. Higher Transcendental Functions; McGraw-Hill: New York, NY, USA, 1953; Volume I–II. [Google Scholar]
- Ma, J.Z.G.; Hirose, A. Parallel propagation of ion solitons in magnetic flux tubes. Phys. Scr. 2009, 79, 045502. [Google Scholar] [CrossRef]
- Brodin, G.; Stenflo, L. Large amplitude electron plasma oscillations. Phys. Lett. A 2014, 378, 1632. [Google Scholar] [CrossRef]
- Vladimirov, S.V.; Yu, M.Y.; Tsytovich, V.N. Recent advances in the theory of nonlinear surface waves. Phys. Rep. 1994, 241, 1–63. [Google Scholar] [CrossRef]
- Vladimirov, S.V.; Yu, M.Y.; Stenflo, L. Surface-wave solitons in an electronic medium. Phys. Lett. A 1993, 174, 313. [Google Scholar] [CrossRef]
- Xu, H.; Zhu, Z.; Xue, J.; Zhan, Q.; Zhou, Z.; Wang, X. Giant enhancements of high-order upconversion luminescence enabled by multiresonant hyperbolic metamaterials. Photonics Res. 2021, 9, 395. [Google Scholar] [CrossRef]
- Gu, P.; Chen, J.; Chen, S.; Yang, C.; Zhang, Z.; Du, W.; Chen, Z. Ultralarge Rabi splitting and broadband strong coupling in a spherical hyperbolic metamaterial cavity. Photonics Res. 2021, 9, 829. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gradov, O.M. Exciting of Strong Electrostatic Fields and Electromagnetic Resonators at the Plasma Boundary by a Power Electromagnetic Beam. Technologies 2022, 10, 78. https://doi.org/10.3390/technologies10040078
Gradov OM. Exciting of Strong Electrostatic Fields and Electromagnetic Resonators at the Plasma Boundary by a Power Electromagnetic Beam. Technologies. 2022; 10(4):78. https://doi.org/10.3390/technologies10040078
Chicago/Turabian StyleGradov, O. M. 2022. "Exciting of Strong Electrostatic Fields and Electromagnetic Resonators at the Plasma Boundary by a Power Electromagnetic Beam" Technologies 10, no. 4: 78. https://doi.org/10.3390/technologies10040078
APA StyleGradov, O. M. (2022). Exciting of Strong Electrostatic Fields and Electromagnetic Resonators at the Plasma Boundary by a Power Electromagnetic Beam. Technologies, 10(4), 78. https://doi.org/10.3390/technologies10040078





