Patterns Simulations Using Gibbs/MRF Auto-Poisson Models
Abstract
:1. Introduction
2. Materials and Methods
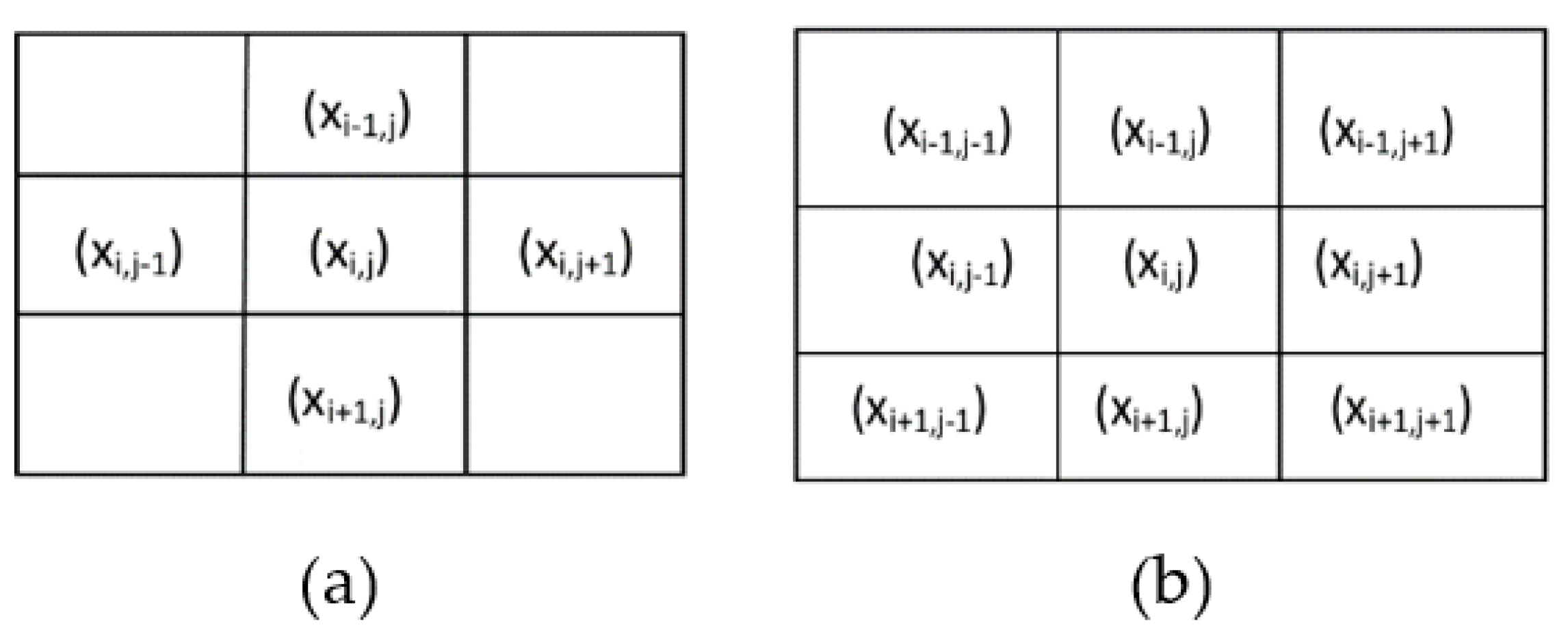
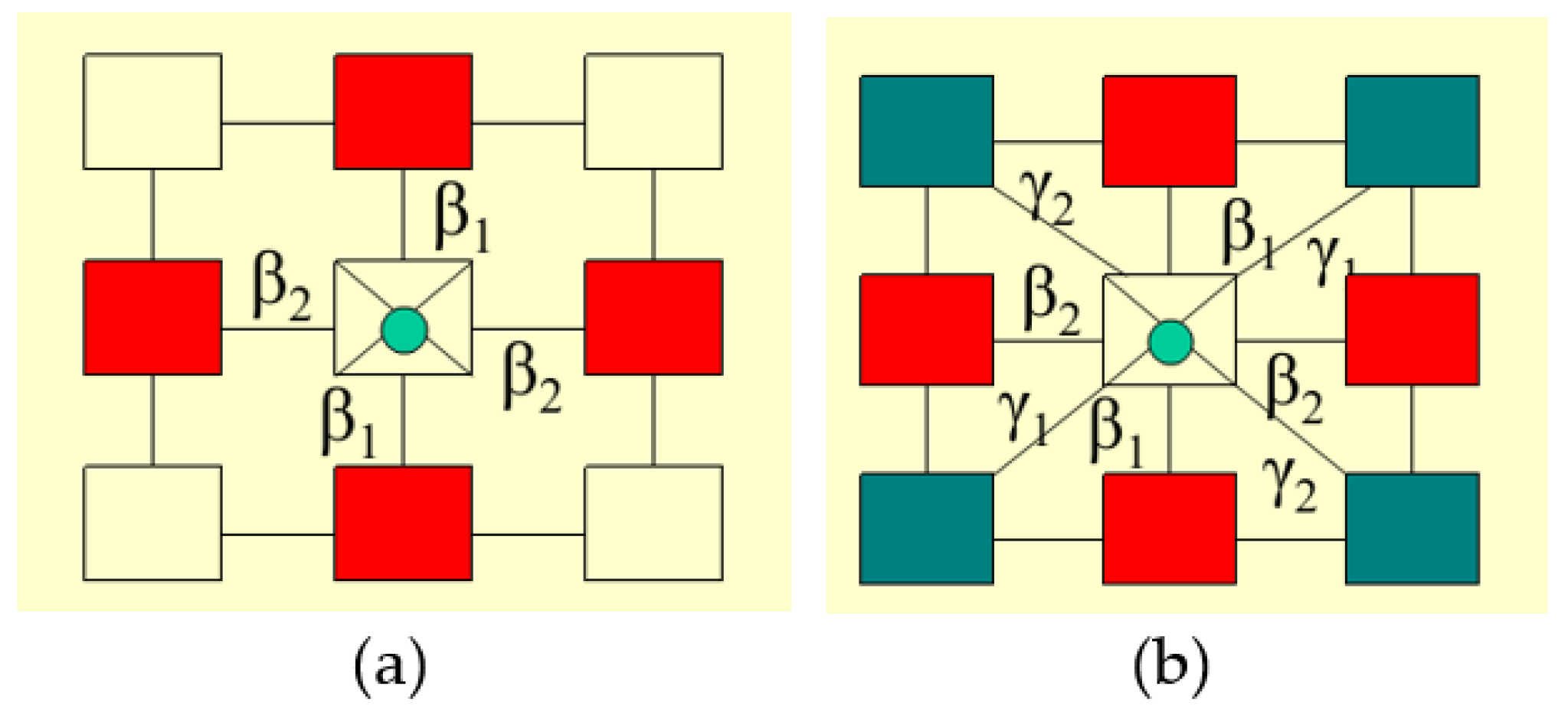
Markov Random Fields Modeling
3. Results
Simulation Process Using MCMC Method
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zimeras, S.; Matsinos, Y. Modeling Uncertainty based on spatial models in spreading diseases: Spatial Uncertainty in Spreading Diseases. Int. J. Reliab. Qual. E-Healthc. 2019, 8, 55–66. [Google Scholar]
- Aykroyd, R.G.; Zimeras, S. Inhomogeneous prior models for image reconstruction. J. Am. Stat. Assoc. 1999, 94, 934–946. [Google Scholar]
- Besag, J. Spatial interaction and the statistical analysis of lattice systems. J. R. Stat. Soc. 1974, 36, 192–236. [Google Scholar]
- Besag, J. On the statistical analysis of dirty pictures. J. R. Stat. Soc. 1986, 48, 259–302. [Google Scholar]
- Zimeras, S. Statistical Models in Medical Image Processing. Ph.D. Thesis, Leeds University, Leeds, UK, 1997. [Google Scholar]
- Zimeras, S.; Georgiakodis, F. Bayesian models for medical image biology using Monte Carlo Markov Chain techniques. Math. Comput. Modeling 2005, 42, 759–768. [Google Scholar]
- Cross, G.R.; Jain, A.K. Markov Random Field Texture Models. IEEE Trans. Pattern Anal. Mach. Intell. 1983, 5, 25–39. [Google Scholar] [CrossRef]
- Zimeras, S. Spreading Stochastic Models Under Ising/Potts Random Fields: Spreading Diseases. In Quality of Healthcare in the Aftermath of the COVID-19 Pandemic; IGI Global: Hershey, PA, USA, 2022; pp. 65–78. [Google Scholar]
- Hamersley, J.A.; Clifford, P. Markov fields on finite graphs and lattices. 1971, unpublished work.
- Kindermann, R.; Snell, J.L. Markov Random Fields and Their Applications; American Mathematical Society: Providence, RI, USA, 1980. [Google Scholar]
- Hastings, W.K. Monte Carlo simulation methods using Markov chains, and their applications. Biometrika 1970, 57, 97–109. [Google Scholar]
- Geman, S.; Geman, D. Stochastic relaxation, Gibbs distributions, and Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 1984, 6, 721–741. [Google Scholar]
- Green, P.J.; Han, X.L. Metropolis Methods, Gaussian Proposals and Antithetic Variables. In Stochastic Models, Statistical Methods, and Algorithms in Image Analysis. Lecture Notes in Statistics; Barone, P., Frigessi, A., Piccioni, M., Eds.; Springer: New York, NY, USA, 1992; Volume 74. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.; Rosenbluth, M.; Teller, A.; Teller, E. Equations of state calculations by fast computing machines. J. Chem. Physics 1953, 21, 1087–1091. [Google Scholar]
- Smith, A.F.M.; Robert, G.O. Bayesian computation via the Gibbs sampler and related Markov chain Monte Carlo methods. J. R. Stat. Soc. B 1993, 55, 3–23. [Google Scholar]
- Agaskar, A.; Lu, Y.M. Alarm: A logistic auto-regressive model for binary processes on networks. In Proceedings of the IEEE Global Conference on Signal and Information Processing, Austin, TX, USA, 3–5 December 2013; pp. 305–308. [Google Scholar]
- Kaiser, M.S.; Pazdernik, K.T.; Lock, A.B.; Nutter, F.W. Modeling the spread of plant disease using a sequence of binary random fields with absorbing states. Spat. Stat. 2014, 9, 38–50. [Google Scholar] [CrossRef]
- Shin, Y.E.; Sang, H.; Liu, D.; Ferguson, T.A.; Song, P.X.K. Autologistic network model on binary data for disease progression study. Biometrics 2019, 75, 1310–1320. [Google Scholar] [CrossRef]
- Zimeras, S.; Matsinos, Y. Spatial Uncertainty. In Recent Researches in Geography, Geology, Energy, Environment and Biomedicine; WSEAS Press: Kerkira, Greece, 2011; pp. 203–208. [Google Scholar]
- Zimeras, S.; Matsinos, Y. Modelling Spatial Medical Data. In Effective Methods for Modern Healthcare Service Quality and Evaluation; IGI Global: Hershey, PA, USA, 2016; pp. 75–89. [Google Scholar]
- Zimeras, S.; Matsinos, Y. Bayesian Spatial Uncertainty Analysis. In Energy and Environment; Recent Researches in Environmental and Geological Sciences, Proceedings of the 7th International WSEAS International Conference on Energy & Environment, Kos Island, Greece, 14–17 July 2012; WSEAS Press: Kerkira, Greece, 2012; pp. 377–385. [Google Scholar]
- Aykroyd, R.; Haigh, J.; Zimeras, S. Unexpected Spatial Patterns in Exponential Family Auto Models. Graph. Model. Image Process. 1996, 58, 452–463. [Google Scholar] [CrossRef]
- Morales-Otero, M.; Núñez-Antón, V. Comparing Bayesian Spatial Conditional Overdispersion and the Besag–York–Mollié Models: Application to Infant Mortality Rates. Mathematics 2021, 9, 282. [Google Scholar]
- Brown, J.P.; Lambert, D.M. Extending a smooth parameter model to firm location analyses: The case of natural gas establishments in the United States. J. Reg. Sci. 2016, 56, 848–867. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zimeras, S. Patterns Simulations Using Gibbs/MRF Auto-Poisson Models. Technologies 2022, 10, 69. https://doi.org/10.3390/technologies10030069
Zimeras S. Patterns Simulations Using Gibbs/MRF Auto-Poisson Models. Technologies. 2022; 10(3):69. https://doi.org/10.3390/technologies10030069
Chicago/Turabian StyleZimeras, Stelios. 2022. "Patterns Simulations Using Gibbs/MRF Auto-Poisson Models" Technologies 10, no. 3: 69. https://doi.org/10.3390/technologies10030069
APA StyleZimeras, S. (2022). Patterns Simulations Using Gibbs/MRF Auto-Poisson Models. Technologies, 10(3), 69. https://doi.org/10.3390/technologies10030069




