Abstract
Metal casting is an industrially important manufacturing process offering a superior combination of design flexibility, productivity and cost-effectiveness, but has limitations due to filling related defects. Several semisolid casting processes are available capable of casting at a range of solid fractions to overcome this. The current communication aims to review the filling front behaviour and give a new perspective to the gate design in semisolid processing compared to conventional high-pressure die-casting. It is shown that solid fraction and gate widths are critical to avoid instability and spraying.
1. Introduction
Metal casting is an industrially important manufacturing process offering a superior combination of design flexibility, productivity and cost-effectiveness [1,2]. Aluminium is a vital material offering lightweight solutions for the transportation industry and cooling solutions for the electronics and telecom industries. Using semisolid casting processes, the ability to replace heavier materials and designs with more efficient solutions has significantly increased. Many examples exist from the electronics industry [3] and automotive and truck components [3,4]. Today, several processes are available with different capabilities and characteristics, ranging from low solid fractions, such as the GISS process, to high fraction solid processing, such as the SEED process [5].
The success of these processes is often referred to as a reduction in turbulence from an increase in viscosity [6,7,8]. Very little attention has been given to fill front stability that has been a focus for improvements in gravity die casting processes [1]. Fill front stability is characterised by the Weber number or similar, but rarely used in the discussion of filling [1,2]. A possible reason for this is that the filling process in high pressure die casting (HPDC) is very violent, with high gate speed very far from what would be required for a stable front [1,2,9]. In the GISS process, a measure with the ratio of gate speed, v (m/s), over solid fraction, fs (-), was developed as a process index where values from 22 below gave a stable filling for a thin plate [10].
In reality, there are many mechanisms active in jet break up where break up can occur in many different modes, starting from laminar flow and growth of instabilities, to so-called Rayleigh break-up. In the current study, this type of break up is considered stable and does not occur within the lengths available in the die, as shown in Figure 1a [11]. It is essential to understand that spray formation in HPDC is not the same as atomisation and spraying that for a flat jet would appear as in Figure 1b, with surface tension-driven hole formation generating ligaments and droplet formation. The break-up is instead a consequence where a break-up takes place in the transition regime and turbulent regime, where the travelled distance is reduced before the gate or jet-speed reaches the actual spray regime under normal gate speed, with speed below 55 m/s [9,12,13]. Depending on the degree of filling of the cavity cross-section and cavity geometry, two scenarios are possible. For a cavity cross-section not fully filled, the break-up would have the possibility to occur in a similar fashion as the flat jet break up. For a filled cavity, there would be undulations on the surface, entraining gas and possible droplet formation similar to gravity casting. These latter two are illustrated in Figure 1c.
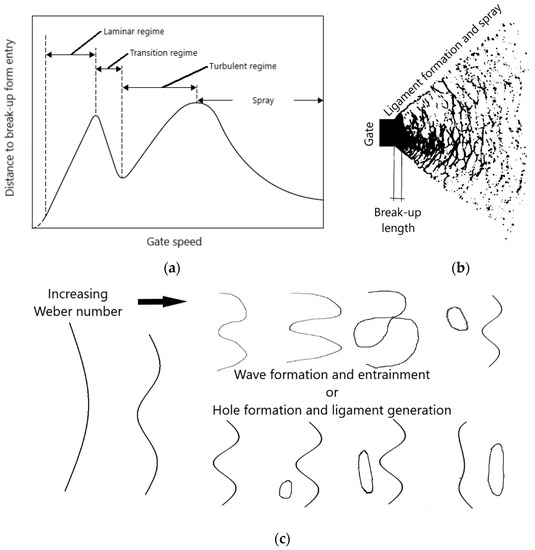
Figure 1.
Break-up illustration with (a) Schematic illustration of the travelled distance before break-up and gate speed adapted from Lefebvre and McDonnel [11]. (b) Break-up distance of flat jet with ligament formation for partially filled die cavities and (c) different instabilities with surface wave formation and entrainment for a filled fie cavity and hole formation and ligament formation for a partially filled cavity.
Saeedipour et al. [14] analysed HPDC processes and break-up and concluded that the atomisation regime reached speeds as high as 70 m/s. The first and second wind break-up was the critical regime for all the other speeds. First wind break-up corresponds to break-up in the transition regime and would be more related to folding and ligament formation for a flat jet that would enter the die cavity. Second wind break-up is related to break up in the turbulent regime and corresponds to droplet formation with beads or cold shot formation.
The current communication aims to review the filling front behaviour and give a new perspective to the gate design in HPDC, and especially SSM processing using HPDC.
2. Methodology
This communication is an a priori analysis of the fill front behaviour, taking a literature foundation in developing a theoretical framework for the analysis of fill front stability. The example used is that of rheocasting an A356 alloy. The A356 alloy is a preferred type of alloy in rheocasting, due to its large solidification range [3,4].
3. Theoretical Framework
3.1. Turbulence, Surface Stability and Fill Front Break-Up
The problems related to filling in HPDC involve all types of behaviour, ranging from a stable front to a wavy fill front and a fully developed spray and atomisation flow state [12]. Turbulence is mainly characterised by the Reynolds number, with turbulence starting as low as 2500, shown in Equation (1). The Reynolds number is the ratio of inertial forces to viscous forces within a fluid volume subjected to motion at different fluid velocities.
where ρ is density (kg/m3), v is gate speed (m/s), μ is viscosity (Pa s) and DH is the hydraulic diameter (m). The analysis takes its foundation in the fill front stability developed by Campbell [1] and by Miller [15], who worked mainly with gravity-driven processes. At low viscosity and low flow speeds, gravity matters and is characterized by the Froude number. The Froude number is a ratio of the flow inertia to the external field and is based on a speed–length ratio. The external field under the current conditions is gravity and that is only relevant for flow speed up to 0.25 m/s according to Miller [15]. At higher speeds, the surface tension phenomenon becomes important, and the stability can be assessed based on the Weber number instead, We, as in Equation (2) [11]. The Weber number is the ratio of drag forces/cohesion forces
where σ is surface tension (N/m). The absolute stability of a fill front is with We < 0.8, but a practical limit is given by We < 2 [2].
In atomisation and spray theory, there are several modes for the break-up with first and second wind break up. First wind break up is similar to the Weber number stability criterion as waves are formed, and with time in a flat jet, ligaments will form. Second wind break-up involves the formation of droplets similar to what is found as cold shots or beads. This can be analysed using the Ohnesorge number, Oh, Equation (3) [11]:
The boundaries for the first and second wind break-up are straight lines in a logarithmic plot of the Ohnesorge number versus the Reynolds adapted from Lefebvre and McDonnel [11] and Saeedipour et al. [14], as seen in Figure 2.
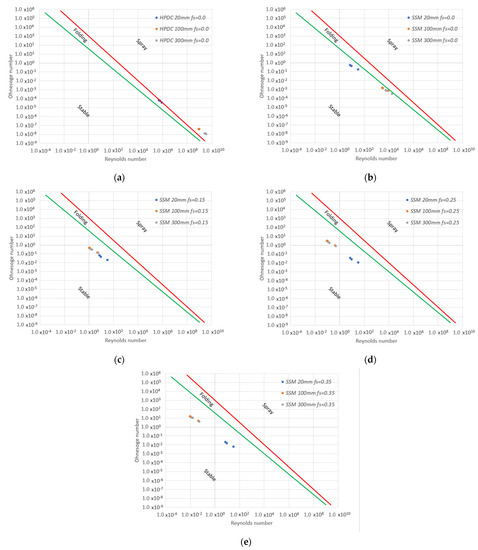
Figure 2.
Break-up analysis with the Ohnesorges number plotted against the Reynolds number for (a) HPDC conditions without solid content; (b) SSM conditions without any solid fraction; (c) SSM conditions with fs = 0.15 where practical stability based on We was found; (d) SSM conditions with fs = 0.25 where absolute stability based on We was found; (e) SSM conditions with fs = 0.35, a typical fraction used in high fraction SSM processing. The green line is first wind break-up, and the red line is second wind break-up. Blue markers are 20 mm gate width, orange markers are 100 mm gate width and grey is for 300 mm gate widths.
3.2. Surface Tension and Shear Strength Build-Up in the Mushy State
The surface tension of the aluminium melt is 0.8 Pa. The strength build-up in the two-phase region was studied by Pan et al. [16], which analysed two microstructure types based on the A356 alloy. The magnetohydrodynamically stirred material is the most similar to what is expected in SSM processing and also the slurry with the lower strength. The expression for the strengths was given by Equation (4):
Under the assumption that the internal resistance to motion in the slurry can be seen acting in the direction of the surface tension, it is possible to add this as a cohesive force of the slurry and, as such different from viscosity.
4. Discussion
4.1. Effect of a Solid Fraction Present on the Weber Number and Front Stability
Starting with the fill front stability, the Weber number is one measure [1,2], and a complementary criterion was developed by Janudom et al. [10] based on the gate speed and the solid fraction. In Table 1, typical data for casting A356, cast under different conditions, gate speed and thickness, and gate width and used in the analysis are collated. For HPDC and semisolid casting, a practical limit is to keep We < 2, but We < 0.8 results in absolute stability [1,2]. All conditions in Table 1 will result in folding or spraying for the typical HPDC conditions without a solid phase present. The conditions will be similar for the typical SSM conditions without a solid phase present as a hypothetical case as We > 2 for all cases. It should be noted that the liquid aluminium viscosity was approximated to 1 mPa s [17,18] and for the SSM, approximately to 2 Pa s [19,20].

Table 1.
Weber number (We) for different processed and conditions.
The gate speeds for RheoMetal processing (Bromma, Sweden) are significantly lower than those found in HPDC. Comparing the Weber numbers for the gate geometries analysed will give instability with folding and possibly spraying. Increasing the solid fraction gradually will reduce the Weber number since the shear strengths are added to the surface tension term. At a solid fraction fs = 0.15, the practical stability limit, based on the Weber number, is reached within the conditions investigated. The ratio v/fs had a practical maximum of approximately 22, resulting in a slightly more conservative measure than the Weber number.
Increasing the solid fraction further results in that the absolute limit, based on the Weber number, being reached from fs = 0.25 or higher and at fs = 0.35 all conditions result in absolute stability. The ratio v/fs is, in general, more conservative but does not give a critical value at a constant Weber number. This is concluded by comparing the v/fs is 23 for both fs = 0.15 with a 6 mm gate and fs = 0.35 and with a 2 mm gate but where the We = 1.30 and We = 0.26, respectively. The foundation of the v/fs is more related to turbulence and the Reynolds number Re [10].
4.2. Effect of the Solid Fraction of the Spray Behaviour
In the analysis of the folding and spraying of the SSM processed material, additional gate thicknesses and gate speed recommendations were added with an 8 mm gate with a speed of 3 m/s, 10 mm gate with 2.5 m/s and a 12 mm gate with 2 m/s. The gate widths of 20 mm, 100 mm and 300 mm were kept.
Starting with HPDC conditions, Figure 2a shows similar results as Saeedipour et al. [13] in terms of Ohnesorges number but higher Reynolds number due to a geometric difference. The results indicate similar break-up behaviour where the 20 mm gate width is on the second win break-up boundary (red line), and the wider gates of 100 and 300 mm are well into the droplet formation range. Shifting the speeds to those recommended for SSM processing (RheoMetalTM process) moves the conditions in the safe region where laminar flow Rayleigh break-up may occur. The Weber number, Table 1, for SSM with fs = 0 does not fulfil the practical of 2, not the absolute stability of 0.8. The Weber number is thus a more conservative measure.
Adding the effect of solid fraction reduced the Webers number to the practical limit at fs = 0.15 corresponding to Figure 2c. Absolute stability was reached at fs = 0.25, corresponding to Figure 2d. The levels used on many higher solid fraction SSM processes is fs = 0.35 provides absolute stability, is well inside the stable region and fulfils the v/fs condition for all geometries.
5. Conclusions
In the current paper, the effect of the solid phase on the filling conditions was analysed a priori using three different tools, (1) the Weber number for fluid dynamics and used in gravity die casting, (2) the first and second wind break-up analysis utilising Ohnesoges number and the Reynolds number and (3) the criterion developed for the GISS process with the gate speed divided by the solid fraction.
The three different measures all showed similar results, with gate speed divided by the solid fraction being the most conservative. The Weber number and thus also the Ohnesorges number were corrected for the presence of a solid fraction, resulting in a practical fill front stability level being reached for a solid fraction of 0.15.
Absolute stability based on the Weber number was reached at a solid fraction of 0.25. Not even at this high fraction could a sufficiently low value of the gate speed divided with the solid fraction be reached for all geometries. The conclusion for the v/fs ratio measure is that it will force the gate speed to very low values and likely hinder the users from choosing processing conditions of SSM processes to achieve the possible extended flow lengths possible, which is one of the benefits [5,8].
The break-up analysis utilising Ohnesorges and Reynolds numbers in the assessment of the first and second wind break-up was the most forgiving, and no solid fraction was required to obtain stability allowing for fill speed to be even higher than the recommended values for the RheoMetal process, suggesting that there is a significant margin to fill front instability. However, the diagram shows that the stable regime in the diagram is a laminar break-up regime and break-up is possible with extended flow lengths. A break-up is likely possible for large components and long flow lengths, and then the Webernumber criterion should be adhered to.
In all this analysis, it was assumed that for A356, the shear strength of the slurry was determined by Pan et al. [16], which is one uncertainty. The slurry quality, slurry structure and solid fraction are essential, and ideally, for the high solid fraction, this parameter is an essential metric for the gating design and choice of fill parameters for a good quality casting.
Author Contributions
Conceptualisation, A.E.W.J.; methodology, A.E.W.J.; formal analysis, A.E.W.J. and Q.Z.; investigation, A.E.W.J. and Q.Z.; writing—original draft preparation, A.E.W.J.; writing—review and editing, A.E.W.J., Q.Z. and S.J.; supervision, A.E.W.J. and S.J.; project administration, A.E.W.J. and S.J.; funding acquisition, A.E.W.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Vinnova under the ReCKA project (contract No. 2018-02831).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data used are contained within the paper.
Acknowledgments
The authors are indebted to Comptech AB for supporting with gate speed parameters and discussions leading to the idea behind this paper.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the study’s design, in the collection, analyses, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
References
- Campbell, J. Complete Casting Handbook Metal Casting Processes, Metallurgy, Techniques and Design, 2nd ed; Butterworth-Heinemann: Oxford, UK, 2015; ISBN 978-0-444-63509-9. [Google Scholar]
- Jarfors, A.E.W.; Seifeddine, S. Metal Casting; Springer: Berlin, Germany, 2015; ISBN 9781447146704/9781447146698. [Google Scholar]
- Jarfors, A.E.W.; Zheng, J.C.; Chen, L.; Yang, J. Recent Advances in Commercial Application of the Rheometal Process in China and Europe. Solid State Phenom. 2019, 285, 405–410. [Google Scholar] [CrossRef]
- Li, D.Q.; Zhang, F.; Midson, S.P.; Liang, X.K.; Yao, H. Recent Developments of Rheo-Diecast Components for Transportation Markets. Solid State Phenom. 2019, 285, 417–422. [Google Scholar] [CrossRef]
- Jarfors, A.E.W. A Comparison between Semisolid Casting Methods for Aluminium Alloys. Metals 2020, 10, 1368. [Google Scholar] [CrossRef]
- Atkinson, H.V. Semisolid Processing of Metallic Materials. Mater. Sci. Technol. 2010, 26, 1401–1413. [Google Scholar] [CrossRef] [Green Version]
- Jarfors, A.E.W. Pressure Different Casting. Encycl. Mater. Met. Alloys 2022, 4, 117–128. [Google Scholar] [CrossRef]
- Jarfors, A.E.W. Semisolid Casting of Metallic Parts and Structures; Elsevier Ltd.: Amsterdam, The Netherlands, 2022; Volume 4, ISBN 9780128197264. [Google Scholar]
- Street, A.C. The Diecasting Handbook; Portcullis Press Ltd.: Redhill, UK, 1977. [Google Scholar]
- Janudom, S.; Wannasin, J.; Basem, J.; Wisutmethangoon, S. Characterization of Flow Behavior of Semi-Solid Slurries Containing Low Solid Fractions in High-Pressure Die Casting. Acta Mater. 2013, 61, 6267–6275. [Google Scholar] [CrossRef]
- Lefebvre, A.H.; Mcdonell, V.G. Atomization and Sprays, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1989; ISBN 9781498736268. [Google Scholar]
- Hao, S.; Hu, B.; Pehlke, R. Atomization in High Pressure Die Casting—A Problem and a Challenge. Die Cast. Eng. 1998, 42, 42. [Google Scholar]
- Saeedipour, M.; Pirker, S.; Schneiderbauer, S. Numerical Study on Liquid Jet Breakup and Droplet-Wall Interaction in High Pressure Die Casting Process. In Proceedings of the ICLASS 2015—13th International Conference on Liquid Atomization and Spray Systems, Tainan, Taiwan, 23–27 August 2015. [Google Scholar]
- Saeedipour, M.; Schneiderbauer, S.; Pirker, S.; Bozorgi, S. Prediction of Surface Porosity Defects in High Pressure Die Casting. TMS Annu. Meet. 2015, 155–163. [Google Scholar] [CrossRef]
- Miller, R.A. Casting Solutions for Readiness, Thin Wall and High Strength Die Casting Alloys; The Ohio State University: Columbus, OH, USA, 2017; Available online: https://files.core.ac.uk/pdf/23/84591373.pdf (accessed on 26 May 2022).
- Pan, Q.Y.; Apelian, D.; Alexandrou, A.N. Yield Behavior of Commercial Al-Si Alloys in the Semisolid State. Metall. Mater. Trans. B 2004, 35, 1187–1202. [Google Scholar] [CrossRef]
- Dinsdale, A.T.; Quested, P.N. The Viscosity of Aluminium and Its Alloys—A Review of Data and Models. J. Mater. Sci. 2004, 39, 7221–7228. [Google Scholar] [CrossRef]
- Zhang, F.; Du, Y.; Liu, S.; Jie, W. Modeling of the Viscosity in the AL-Cu-Mg-Si System: Database Construction. Calphad 2015, 49, 79–86. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, H.; Fu, H.; Fonseca, J.; Yang, Y.; Du, M.; Zhang, H. Modelling Flow-Induced Microstructural Segregation in Semi-Solid Metals. Mater. Des. 2022, 213, 110364. [Google Scholar] [CrossRef]
- Das, P.; Samanta, S.K.; Dutta, P. Rheological Behavior of Al-7Si-0.3Mg Alloy at Mushy State. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2015, 46, 1302–1313. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).