Quantifying Correlation Uncertainty Risk in Credit Derivatives Pricing †
Abstract
1. Introduction
1.1. Model Risk Management
An integral part of model development is testing, in which the various components of a model and its overall functioning are evaluated to show the model is performing as intended; to demonstrate that it is accurate, robust, and stable; and to evaluate its limitations and assumptions.
Validation activities should continue on an ongoing basis after a model goes into use to track known model limitations and to identify any new ones. Validation is an important check during periods of benign economic and financial conditions, when estimates of risk and potential loss can become overly optimistic and the data at hand may not fully reflect more stressed conditions...Generally, senior management should ensure that appropriate mitigating steps are taken in light of identified model limitations, which can include adjustments to model output, restrictions on model use, reliance on other models or approaches, or other compensating controls.
You will see that not even among quants there is consensus about what model risk is.
1.2. Layout of the Paper
2. Model Risk Methodology
2.1. Previous Work
2.2. Proposed Framework
3. Two-Factor Asymptotic Model
3.1. Underlying Processes
3.2. The No-Arbitrage Conditions
3.3. Derivation of Governing PDE
4. CDS Pricing
4.1. Fixed Coupon Leg
4.2. Protection Leg
4.3. Calibration to CDS Market
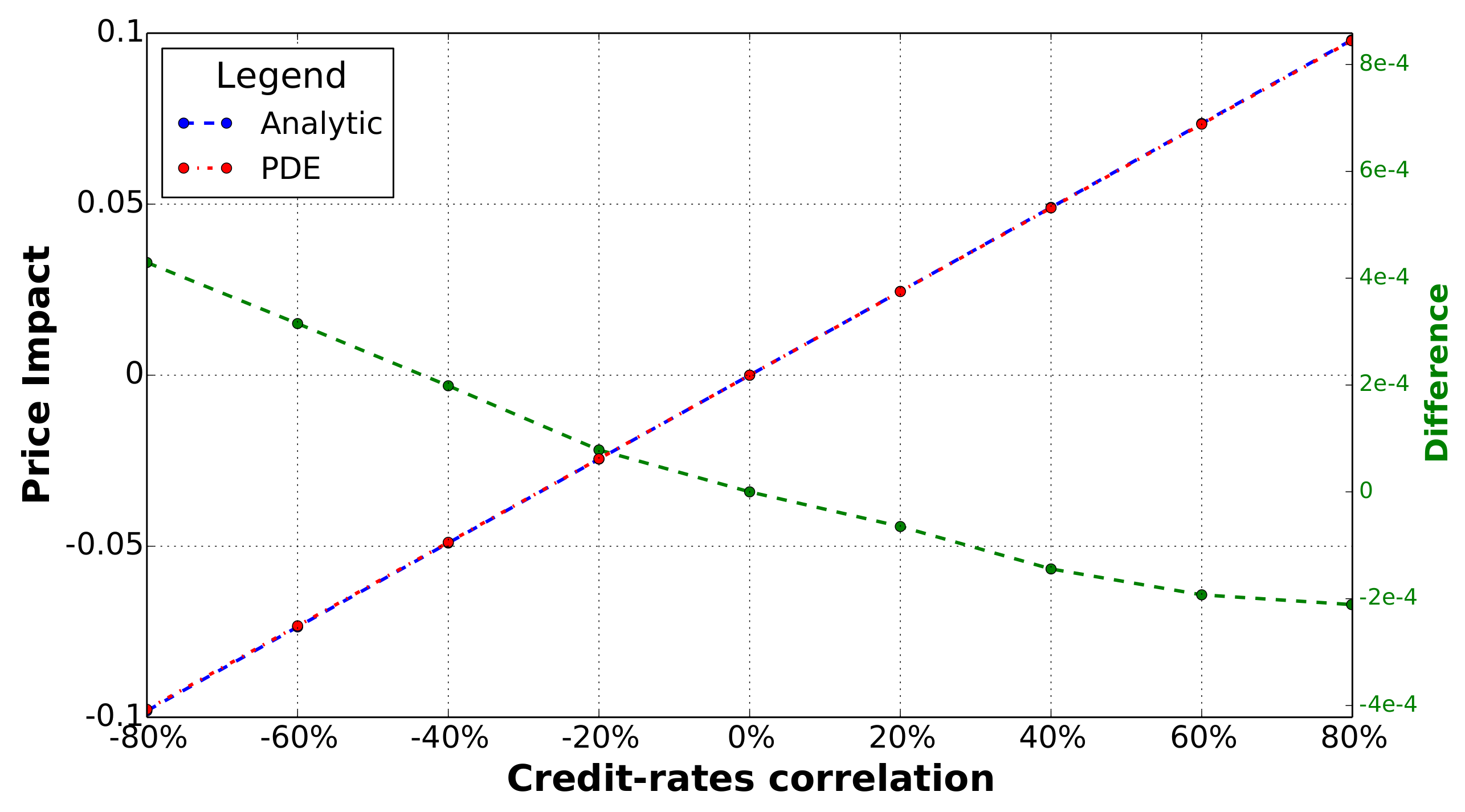
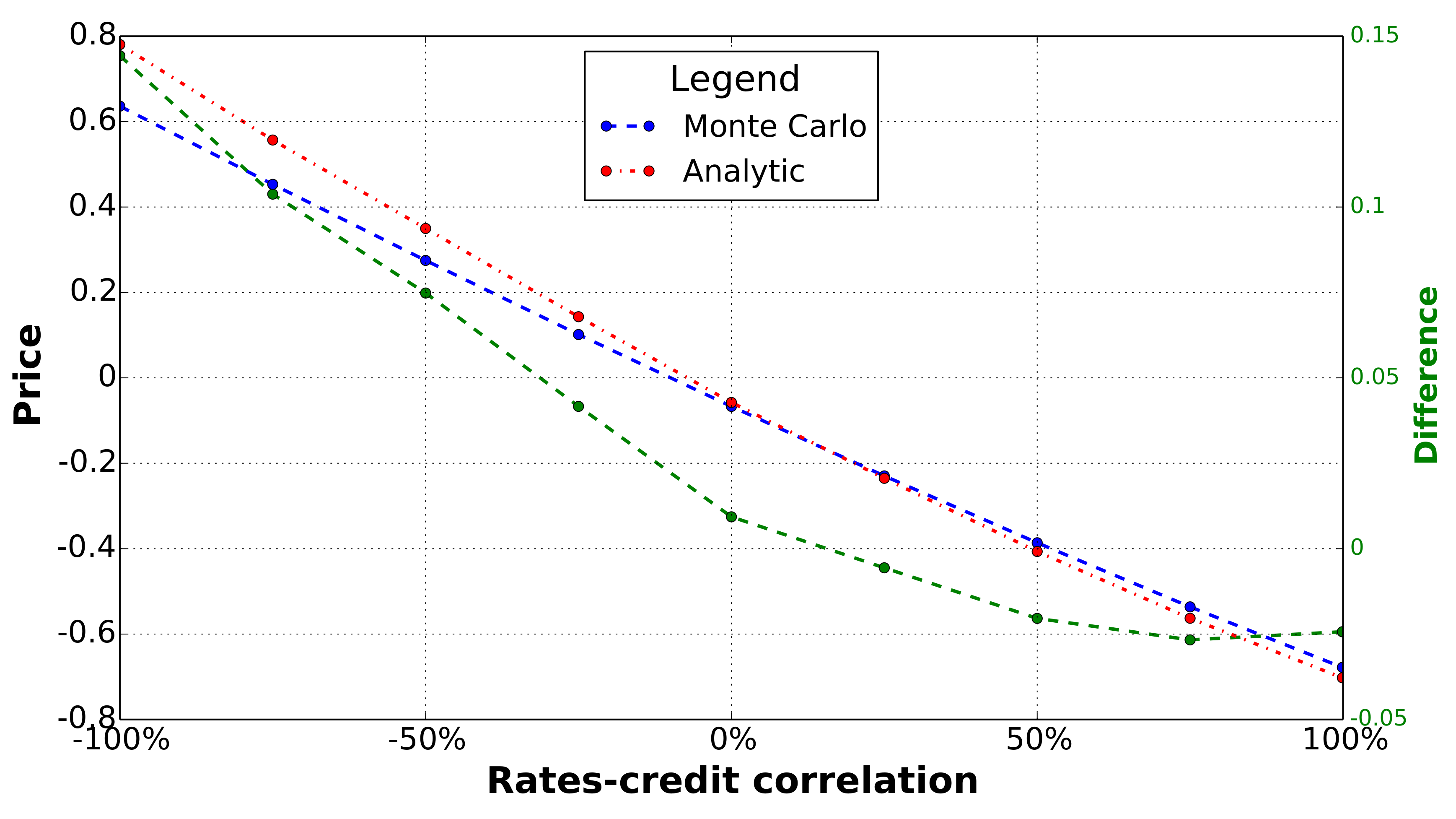
5. Calculating Correlation Risk
5.1. Interest Rate Swap Extinguisher
5.2. Contingent CDS
5.3. Capped Libor Flows
6. Conclusions
Conflicts of Interest
Appendix A. Green’s Function
Appendix A.1. Calibration
Appendix A.1.1. Pricing of Risk-Free Cash Flow
Appendix A.1.2. Pricing of Risky Cash Flow
References
- Black, Fischer, and Piotr Karasinski. 1991. Bond and Option Pricing when Short Rates are Lognormal. Financial Analysts Journal 47: 52–59. [Google Scholar] [CrossRef]
- Cont, Rama. 2004. Model Uncertainty and its Impact on the Pricing of Derivative Instruments. Finance Concepts Working Paper FC-04-02. Available online: https://ssrn.com/abstract=562721 or http://dx.doi.org/10.2139/ssrn.562721 (accessed on 30 December 2017).
- Cortina, Elsa. 2007. Modeling Defaultable Bonds with Mean-Reverting Log-Normal Spread: A Quasi Closed-Form Solution. Available online: http://www.famaf.unc.edu.ar/~torres/trabajosparapublicacion/06-finanzas_cuantitativas/06-finanzas_cuantitativas-01.pdf (accessed on 30 December 2017).
- Crespo, Ignacio, Pankaj Kumar, Peter Noteboom, and Marc Taymans. 2017. The Evolution of Model Risk Management. Risk Insights, McKinsey & Company. Available online: https://www.mckinsey.com/business-functions/risk/our-insights/the-evolution-of-model-risk-management (accessed on 30 December 2017).
- Foschi, Paolo, Stefano Pagliarani, and Andrea Pascucci. 2013. Approximations for Asian Options in Local Volatility Models. Journal of Computational and Applied Mathematics 237: 442–59. [Google Scholar] [CrossRef]
- Funahashi, Hideharu. 2015. An Analytic Approximation for European Option Prices under Stochastic Interest Rates. International Journal of Theoretical and Applied Finance 18: 1550026. [Google Scholar] [CrossRef]
- Glasserman, Paul, and Xngbo Xu. 2014. Robust risk measurement and model risk. Quantitative Finance 14: 29–58. [Google Scholar] [CrossRef]
- Hagan, Patrick, Andrew Lesniewski, and Diana Woodward. 2005. Probability Distribution in the SABR Model of Stochastic Volatility. Available online: http://www.lesniewski.us/papers/working/ProbDistrForSABR.pdf (accessed on 30 December 2017).
- Horvath, Blanka, Antoine Jacquier, and Colin Turfus. 2017. Analytic Option Prices for the Black–Karasinski Short Rate Model. Available online: https://archive.org/details/GreenFunctionForShortRateModel (accessed on 30 December 2017).
- Hull, John, and Alan White. 1990. Pricing Interest Rate Derivative Securities. The Review of Financial Studies 3: 573–92. [Google Scholar] [CrossRef]
- Jobst, Norbert, and Stavros A. Zenios. 2001. Extending Credit Risk (Pricing) Models for the Simulation of Portfolios of Interest Rate and Credit Risk Sensitive Securities. Available online: http://fic.wharton.upenn.edu/fic/papers/01/0125.pdf (accessed on 30 December 2017).
- Joshi, Aruna. 2017. Managing Risk of Financial Models: A Smart and Simple Guide for the Practitioner. North Charleston: CreateSpace Self-Publishing. 100p. [Google Scholar]
- Morini, Massimo. 2011. Understanding and Managing Model Risk: A Practical Guide for Quants, Traders and Validators. Indianapolis: Wiley Finance. 448p. [Google Scholar]
- Pagliarani, Stefano, and Andrea Pascucci. 2011. Analytical Approximation of the Transition Density in a Local Volatility Model. Available online: http://mpra.ub.uni-muenchen.de/31107/ (accessed on 30 December 2017).
- Pagliarani, Stefano, and Andrea Pascucci. 2013. Local Stochastic Volatility with Jumps: Analytical Approximations. International Journal of Theoretical and Applied Finance 16: 1350050. [Google Scholar] [CrossRef]
- Pan, Jun, and Kenneth J. Singleton. 2007. Default and Recovery Implicit in the Term Structure of Sovereign CDS Spreads. Available online: http://www.mit.edu/~junpan/sovrev.pdf (accessed on 30 December 2017).
- Schönbucher, Philipp. 1999. A Tree Implementation of a Credit Spread Model for Credit Derivatives. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=240868 (accessed on 30 December 2017).
- Turfus, Colin, and Alexander Shubert. 2017. Analytic Pricing of CoCo Bonds. International Journal of Theoretical and Applied Finance 20: 1750034. [Google Scholar] [CrossRef]
- Turfus, Colin. 2017a. Correlation Risk in CDS Pricing. Available online: https://archive.org/details/CorrelationRiskInCDSPricing (accessed on 30 December 2017).
- Turfus, Colin. 2017b. Analytic Pricing of Interest Rate Swap Insurance. Available online: https://archive.org/details/AnalyticPricingOfInterestRateSwapInsurance (accessed on 30 December 2017).
- Turfus, Colin. 2017c. Analytic Pricing of Extinguishable Libor Cap-Floor Quanto. Available online: https://archive.org/details/ExtinguishableLiborCapFloorQuanto (accessed on 30 December 2017).
- Turfus, Colin. 2017d. Analytical Solution for CVA of a Collateralised Call Option. Available online: https://archive.org/details/CallOptionCVABlackKarasinski (accessed on 30 December 2017).
- Turfus, Colin. 2017e. Analytical Pricing of Convertible Bonds’. Available online: https://archive.org/details/ConvertibleBondPricing (accessed on 30 December 2017).
- Turfus, Colin. 2018. Analytic Pricing of Quanto CDS. Available online: https://archive.org/details/QuantoCDS (accessed on 30 December 2017).
- US Federal Reserve. 2011. SR 11-7: Guidance on Model Risk Management. Available online: https://www.federalreserve.gov/supervisionreg/srletters/sr1107.htm (accessed on 30 December 2017).
| 1. | It should be mentioned that the author in his book eschews the idea that any one book should aim to be definitive. |
| 2. | For other choices of model parameter than , this will often still tend to be the case on the basis that the uncertain/unmodelled parameter will be of secondary importance; if this were not so, the consequent high degree of uncertainty introduced into pricing would compromise the utility of the pricing algorithm. |
| 3. | We shall henceforth write for simplicity as a shorthand for . |
| 4. | The errors can in addition be expected to approximate to near zero since the calibration swaps are assumed to be at the money, whence the (risky) discounting affects both legs almost equally. |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turfus, C. Quantifying Correlation Uncertainty Risk in Credit Derivatives Pricing. Int. J. Financial Stud. 2018, 6, 39. https://doi.org/10.3390/ijfs6020039
Turfus C. Quantifying Correlation Uncertainty Risk in Credit Derivatives Pricing. International Journal of Financial Studies. 2018; 6(2):39. https://doi.org/10.3390/ijfs6020039
Chicago/Turabian StyleTurfus, Colin. 2018. "Quantifying Correlation Uncertainty Risk in Credit Derivatives Pricing" International Journal of Financial Studies 6, no. 2: 39. https://doi.org/10.3390/ijfs6020039
APA StyleTurfus, C. (2018). Quantifying Correlation Uncertainty Risk in Credit Derivatives Pricing. International Journal of Financial Studies, 6(2), 39. https://doi.org/10.3390/ijfs6020039




