Can Soybean Tariff Shocks Trigger Abnormal Asymmetric Phenomena in Futures Markets? Evidence from the 2025 U.S.–China Trade Friction

Abstract

This study, set against the backdrop of escalating trade tensions between China and the United States, examines the impact of soybean tariff adjustments on the abnormal asymmetric behavior in the futures market. By employing specialized analytical methods that capture market volatility asymmetry and event study techniques, we focus on the multi-stage soybean tariff adjustments to analyze their effects on market return transmission, volatility asymmetry, and market stability. This study compares the market responses to positive and negative shocks and the distinct performances of the futures markets in China and the United States, with the core aim of verifying whether soybean tariff shocks trigger abnormal asymmetric behavior in the futures market. The results show that tariff shocks significantly lead to asymmetric characteristics in market volatility, with negative shocks having a more pronounced impact on market volatility than positive ones. During the trading days before and after the announcement of tariff policies, the cumulative abnormal return difference, which measures the disparity in market reactions to related assets, also rose significantly. This indicates that tariff adjustments are the core factor causing abnormal asymmetric phenomena in the market, and the commodity futures market needs to pay attention to such asymmetric risks triggered by policies. The value of this study lies in its targeted analysis of the dynamic impact of tariff shocks, combined with volatility analysis and event study methods, to quantify the asymmetric effects in cross-border markets. The research conclusions can help investors avoid risks related to trade policies and provide references for policymakers to stabilize fluctuations in the commodity market, ultimately facilitating the market’s more efficient response to trade policy shocks and reducing information asymmetry in futures market pricing.

1. Introduction

Soybean is a key agricultural product in global trade, forming a highly interdependent supply chain that connects major producing and consuming countries. As the world’s largest importer of soybeans, China plays an irreplaceable role in stabilizing the global market structure. In 2025, China’s soybean imports accounted for 60% of the global total. The United States and Brazil, two top global soybean exporters, contributed 33% and 36%, respectively, to China’s imports (FAOSTAT, 2025). Figure 1 presents the global soybean production volume overview, showing that the U.S. and Brazil are the two biggest producers in the world in 2021. Conversely, China remains the core destination for U.S. soybean exports, absorbing 35% of its total annual soybean exports. This deep trade interdependence has established both countries as core stakeholders in the global soybean market—China’s huge import demand supports the export-oriented growth of major producing countries, while U.S. soybean exports are highly dependent on China’s consumption capacity, making their bilateral trade relationship an important cornerstone for the global soybean supply-and-demand balance.

Based on this high degree of dependence between China and the U.S., soybeans have long been a key commodity in Sino soybean trade and economic interactions (Guo et al., 2022). Soybeans have become a critical tool in bilateral policy adjustment (Yang et al., 2025). In the 2025 Sino–U.S. trade friction, trade policy disturbances not only undermine the stability of the global soybean supply chain but also trigger a chain reaction in the financial market. Recent evidence highlights that the ‘reciprocal tariff’ announcement in April 2025 was not merely a sectoral dispute but a broad macroeconomic shock that triggered financial contagion across global stock markets (Akhtaruzzaman et al., 2025). Against this backdrop of systemic instability, this study specifically aims to explore the relationship between trade conflict and financial market dynamics. Specifically, it reveals how trade policy shocks affect the network structure of the soybean financial market, induce volatility asymmetry, and reshape the system balance.

The year 2025 witnessed a notable intensification of trade conflicts between China and the United States (Yang et al., 2025), which was particularly evident through three successive phases of mutual tariff escalations that profoundly affected soybean trade. During the initial phase commencing in early February 2025, American authorities introduced a 10% levy (Epstein et al., 2025) on Chinese imports (subsequently amplified to 20%), leading China to respond with countermeasures through a 10% duty on U.S. soybean shipments. This economic confrontation intensified during the second phase in March, when the United States escalated tariffs to 20%, prompting Chinese regulators to implement proportional increases to 10–15% on soybean imports. The most consequential developments occurred on 9 April, with U.S. import duties on Chinese commodities soaring to 145% (Husch Blackwell LLP, 2025), matched by China’s responsive tariffs on American soybeans that peaked at 125% (P.R. China B.C., 2025). These regulatory modifications upended established trade dynamics, generating market unpredictability that compelled market players to reassess risk exposure within soybean derivatives markets while adapting to transformed operational parameters (

Table 1. The tariff imposed by China on U.S. soybeans in 2025.

Period	Time	Soybean Tariff, China to U.S.
Before the Tariff Shift	Before 31 January 2025	10%
Period 1	1 February 2025 to 1 April 2025	15%
Period 2	4 March 2025 to 9 April 2025	45%
Period 3	2 April 2025 to 31 July 2025	125%

).

As predictors of future supply and demand, futures prices are known to be more responsive to unexpected changes in the policy regime (Goodwin et al., 2005). The Dalian Commodity Exchange (DCE, China) and the CBOT (Chicago Board of Trade, USA) soybean futures markets are entangled by relationships embedded in supply chains around the world; as we will demonstrate, trade policy shocks can be expected to alter their cross-market interconnections, exacerbate price volatility in each market, and thus reallocate the responses to positive and negative news shocks (Bown, 2019). Existing literature that empirically studies the influence of trade policy changes focuses largely on aggregate product indices or trends over time. These papers do not examine the intraday movement of futures markets in periods of extreme trade policy shocks, including the 2025 tariff escalation.

Then, we investigate three main questions: (1) How much did the 2025 Sino–U.S. trade dispute affect cross-market return spillovers between Chinese and U.S. soybean futures markets? (2) How much did trade policy shocks heighten asymmetric volatility in these two markets, and what changed in their responsiveness to bullish or bearish shocks across different tariff rounds? (3) What is the impact of the volatility persistence properties associated with volatility caused by tariff policies, and what can we learn from these influences about an implied market stabilization mechanism?

In order to answer these research questions, we employ a ternary analysis approach: (1) The autoregressive model with lag interaction of returns quantifies the return spillover effects between the DCE and CBOT soybean contracts (Y. Wang et al., 2023), and the temporal segmentation of the model distinguishes the pre-conflict and post-conflict periods, thereby examining changes in spillover effects (Y. Wang et al., 2023). (2) The GARCH, EGARCH, and DGARCH models consider asymmetry in volatility through the coefficients of $\alpha$ (overall shock impact), and $\gamma$ (nonlinearity differences), and through a comparison index construction, such as the ASYMME Index (AR) to compare the impact of bullish and bearish shocks. (3) High-frequency breakout analysis using 15 min tick data identifies concurrent price moves as well as accumulated abnormal returns near major trade policy announcements, thereby augmenting our analysis of volatility using intraday (micro–time-scale) evidence.

This paper contributes to the existing literature in three dimensions: (1) providing fresh empirical evidence on market responses to the transition of 2025 trade policy, which is an important missing part in the economics literature in the era of policymaking; (2) merging return transmissions from one market to another with the analysis of volatility patterns to build a coherent study for measuring contagion risk in 2025; and (3) using intraday transaction data to reveal time-dependent market responses, further enhancing our ability to track the trajectory of policy effects throughout a trading day.

The rest of this paper is organized as follows: Section 2 explains the background of the 2025 Sino–U.S. trade friction, which centers on soybean tariff measures. Section 3 states the methodology (including the EGARCH, GARCH, and DGARCH models, the event study framework, and data sources). Section 4 presents the empirical outcomes, and Section 5 provides conclusions, implications, and limitations.

2. Literature Review

2.1. The Impact of Trade Policies on Commodity Futures

As a core tool for regulating the global supply and demand pattern of commodities, trade policy shifts have a profound impact on the commodity futures market through channels such as tariff adjustments and policy uncertainties. In particular, in the context of trade frictions among major countries, this influence is characterized by rapid transmission, wide coverage, and complex fluctuation patterns (Brander et al., 2023). Existing research has conducted multi-dimensional explorations of the interactive relationship between trade policy shocks and the commodity futures market, forming a relatively robust theoretical and empirical foundation.

While extensive literature focuses on commodity futures, it is crucial to recognize that trade policy shocks transmit risks across asset classes, including spot equity markets. Ref. (Akhtaruzzaman et al., 2025) investigated the impact of the U.S. ‘reciprocal tariff’ announcement in April 2025 and found strong evidence of financial contagion among the U.S. and its top 20 trading partners. Their study highlights that while the U.S. stock market exhibited positive cumulative abnormal returns ($CAR$) due to protectionist optimism, trading partners—especially those with deep financial ties, like China—suffered significant negative abnormal returns. This suggests that the tariff shock was a systemic event, triggering simultaneous stress in both global equity spot markets and, as this study examines, commodity futures markets.

From the overall impact of macro-trade policy shocks, the policy uncertainty triggered by trade frictions is the key factor driving fluctuations in the commodity futures market. Ref. (Fetzer & Schwarz, 2020) pointed out in their analysis of the 2018 Sino–U.S. trade conflict that targeted tariff measures between major countries disrupted the long-established equilibrium in commodity trade, directly raising market concerns over supply chain stability and, subsequently, transmitting to the futures market to intensify price volatility. This conclusion was empirically supported by Ref. (Frazier & Sonka, 2019), which, in an early assessment of the impact of the Sino–U.S. trade conflict on the global soybean market, found that the U.S. tariffs on Chinese soybeans and China’s countermeasures significantly altered expectations of soybean supply and demand, leading to a significant jump in the volatility of soybean futures prices on the Chicago Board of Trade (CBOT) and the Dalian Commodity Exchange (DCE) before and after policy announcements, with the persistence of volatility also significantly enhanced. Ref. (Feng et al., 2021) further expanded the boundary of the impact of policy uncertainty. They found that trade policy uncertainty not only directly affects futures price levels but also indirectly amplifies market volatility by changing investor risk preferences. This mechanism is particularly prominent in the agricultural futures market (IndexBox, 2025), due to the fixed production cycle and low supply and demand elasticity of agricultural products, the expectation deviation brought about by policy shocks is difficult to digest through short-term capacity adjustments, thereby prolonging the duration of futures market volatility.

Among specific commodity categories, soybeans, as the core subject of the Sino–U.S. trade friction, have drawn significant attention to the reaction of their futures markets to trade policies. Ref. (Guo et al., 2022) taking soybean, soybean oil, and soybean meal futures as the research objects, found that during the Sino–U.S. trade friction, the linkage between the futures markets of the two countries underwent significant changes: before the tariff adjustment, the U.S. soybean futures had a clear guiding effect on the prices of related futures in China; however, as the trade policy shock intensified, China’s independent pricing power increased, and the cross-market price transmission efficiency declined. Essentially, this change was an adaptive adjustment of the market after the trade policy disrupted the original supply and demand chain. Ref. (Y. Wang et al., 2023) further quantified the extent of the impact of the trade war. Their results showed that the volatility of China’s agricultural futures market increased by more than 30% during the Sino–U.S. trade friction compared to the policy stable period. Among them, soybean futures, due to their high trade dependence, had a significantly higher volatility increase than other categories. In terms of the volatility spillover effect, the empirical analysis by Ref. (Y. Wang et al., 2023) indicated that the trade policy shock not only intensified the volatility spillover within the soybean futures markets of China and the U.S. but also affected the futures of downstream products such as soybean oil and soybean meal through the industrial chain correlation effect, forming a cross-commodity and cross-market volatility transmission network.

The impact of trade policies on the commodity futures market also exhibits significant asymmetric characteristics and structural differences. Cross-country research by Ref. (Fatima et al., 2019) found that negative trade policy shocks have a significantly greater impact on the volatility of commodity futures than positive shocks. This asymmetric effect stems from the market’s aversion to risk—investors are more sensitive to the escalation of trade barriers, which can easily trigger panic trading behavior. In the soybean futures market, this asymmetry is even more pronounced. Ref. (Yang et al., 2025) pointed out that the phased escalation of U.S. tariffs on Chinese soybeans not only directly pushed up the import cost premium of Chinese soybean futures but also led to a restructuring of the global soybean trade pattern as China sought alternative supply sources from Brazil and others, thereby causing a divergence in the price correlation of soybean futures from different production areas. Additionally, Ref. (Goodwin et al., 2005) noted the impact of trade policies is not one-dimensional; its effects are also modulated by factors such as the intensity of policy implementation, consistency of market expectations, and availability of substitute goods. For instance, when there are clear alternative supply channels in the market, the impact of tariff policies on futures prices will be significantly weakened.

In recent years, high-level trade conflicts have emerged between China and the United States, significantly impacting the global economy (Zeng et al., 2022). Under these bilateral trade frictions, numerous disputes have also arisen in the agricultural commodity market. Chinese soybeans have become a key commodity in cross-Pacific commercial wars (Wise & Chonn Ching, 2017).

The foundation of China–U.S. trade frictions originated from the transformation of the economic relationship between the two countries. The United States has dominated the global economy for many years (Kagan, 2013). In 2001, when China was admitted to the WTO, it suddenly rose to the status of a commercial superpower, and this economic rise profoundly altered its relationship with the United States (Deng & Moore, 2004). In 2018, China already dominated as the United States’ first merchandise trading partner, the third-largest export partner, and the largest import source (FAOSTAT, 2025). Such an exponential expansion simultaneously created complex trade deficits and policy differences that ultimately led to a stage of strategic confrontation.

The initial stages of the U.S.–China trade policy shock were felt in early 2025. The first stage of this round of the trade policy shock began on 1 February 2025, when President Trump announced the imposition of a 10% tariff on Chinese products (Husch Blackwell LLP, 2025), a move he later promised would be followed by a further increase to 20%. In turn, China announced similar tariffs on American soybeans (P.R. China B.C., 2025). This was a significant retaliation. Soybeans are a significant commodity in both countries’ bilateral trade. As the two top producers of soybeans, the U.S. agriculture-dependent exporting economy suffered significant harm due to China’s reciprocal retaliation. Reciprocal tariffs altered the built-in supply-and-demand dynamics between the world’s two largest economies.

As of 4 March 2025, a state of siege raged between trade partners. On 4 March, U.S. tariffs increased again by 20% (Husch Blackwell LLP, 2025); China also adjusted its tariff system on soybean exports, from 10% to 15%. These actions were steps in a complex trade negotiation process, but not autonomous trade choices. The resulting counter-trade and counter-tariff decisions adopted by the U.S. and China reflected various domestic concerns, including trade balance adjustment and the defense of strategic sectors, as well as concerns for China’s macroeconomic stability and the interests of Chinese farmers and their strategic industries, which carry high political stakes. These increased tariffs underscore that these countries sought to maintain their economic sovereignty, notwithstanding the processes and obligations of international trade.

It began to rise to its peak level right after 9 April 2025, when the United States imposed tariffs on many Chinese goods at a rate of 145%. Following this, the Chinese government adopted a reciprocal response by adjusting tariffs on soybeans from 45% to 125% (P.R. China B.C., 2025), which was significantly higher than the previous tariffs and indicated a further escalation of the trade policy shock between the U.S. and China. Hence, both the American and Chinese soybean markets faced huge changes in the trade policy. A U.S. farmer was overwhelmed by the dramatic supply–demand disequilibrium, where the dominant customer disappeared. They became immediately burdened by falling commodity market prices and unsold inventories, which became unmanageable within just a few months, resulting in a 40% decline (IndexBox, 2025). At the same time, Chinese traders expanded domestic production programs and expedited diversification by consolidating long-term contract relationships with major export sources in Brazil and Argentina (Dos Reis et al., 2025). This latter maneuver’s transformative effect was to alter not just the geography of commodity flows, but also the existing commodity trade arteries in a restructuring of global trade.

2.2. Volatility Asymmetry and Spillover

In research on the commodity futures market, volatility asymmetry and spillover effects are core issues for revealing the transmission mechanisms of market risks. In the context of frequent trade policy shocks, the interrelationship between these two—volatility asymmetry and spillover effects—has become key to understanding market dynamics. Existing studies have achieved systematic results around these two dimensions, and their theoretical logic and empirical findings provide important support for analyzing fluctuations in soybean futures markets under trade frictions.

2.2.1. Volatility Asymmetry

Asymmetry of volatility refers to the difference in the market’s reaction to positive and negative shocks in terms of their volatility. This phenomenon is particularly prominent in policy-sensitive commodity futures markets. Ref. (Bhar, 2001) first verified the asymmetric transmission characteristics of policy intervention shocks through the bivariate EGARCH model in the Australian spot and futures markets—the increase in volatility caused by negative policy signals (such as trade restrictions and tariff hikes) is significantly greater than that caused by positive policy signals. The core mechanism lies in the fact that investors’ aversion to risk amplifies the market effect of negative expectations, leading to enhanced volatility persistence (Bhar, 2001). This conclusion has been widely confirmed in subsequent agricultural futures research. Ref. (Fatima et al., 2019) found in their analysis of cross-border Islamic stock indices that the volatility response to negative shocks is 20–30% higher than that to positive shocks, and this asymmetry is more prominent in indices related to commodities (Fatima et al., 2019).

Regarding the Sino–U.S. trade friction scenario, Ref. (Bandyopadhyay & Rajib, 2023) conducted a study targeting the Chinese agricultural futures market, which further quantified the degree of volatility asymmetry. During the trade friction period from 2018 to 2020, the volatility response coefficient of soybean futures to the increase in U.S. tariffs reached 0.82, while the response coefficient to positive policies such as the suspension of tariffs was only 0.51. This indicates that negative trade policy shocks have become the core factor driving the asymmetric volatility of the market (Bandyopadhyay & Rajib, 2023). Ref. (Brander et al., 2023), starting from the timing of policy announcements, found that after the release of announcements with high trade policy uncertainty, the asymmetric volatility index of global grain commodity futures increased by 15%-20% within three trading days, and the asymmetric volatility of commodities such as soybeans and corn, which rely on cross-border sales chains, was more significant (Brander et al., 2023). These studies jointly reveal that trade policy shocks further strengthen the asymmetric volatility characteristics of the futures market by changing the uncertainty of supply and demand expectations, and this reinforcing effect is more obvious in highly trade-dependent commodities.

2.2.2. Spillover Effect

The volatility spillover effect describes the process by which changes in volatility in one market are transmitted to other markets. In the soybean futures markets of China and the United States, this effect has shown dynamic changes due to the intervention of trade policies. Ref. (Y. Wang et al., 2023) based on an analysis of high-frequency data from 2016 to 2022, found that before the escalation of trade frictions (2016–2018), the volatility spillover contribution of the U.S. CBOT soybean futures to the Chinese DCE soybean futures reached 62%, presenting a unidirectional spillover pattern where the U.S. was dominant, and China followed. However, after the intensification of trade frictions (2019–2022), the reverse spillover contribution of the Chinese market to the U.S. market increased to 45%. The reversal of the spillover direction was essentially the result of the reshaping of market pricing weights after China adjusted its import structure (Y. Wang et al., 2023).

From the perspective of the industrial chain, volatility spillover also manifests as cross-commodity transmission. Ref. (Guo et al., 2022) in an analysis of the interlinkage among soybean, soybean oil, and soybean meal futures, indicates that during the trade friction period, the intensity of volatility spillover of soybean futures within the industrial chain increased by 35%, with the spillover contribution rate from soybean futures to soybean oil futures rising from 28% to 41%, reflecting the “Chain Effect” of policy shocks being transmitted to downstream products through fluctuations in raw material prices (Guo et al., 2022). At the global market level, Ref. (Wise & Chonn Ching, 2017) confirms that the volatility of soybean futures triggered by the Sino–U.S. trade friction not only spread between the two countries’ markets but also spilled over to the futures markets of major soybean-producing countries, such as Brazil and Argentina, through trade substitution effects, forming a transmission chain from Sino–U.S. trade friction to global soybean trade restructuring and then to cross-market volatility spillover (Deng & Moore, 2004).

2.2.3. The Mechanism of Trade Policy Shift on Volatility Asymmetry and Spillover

Trade policies exert a dual regulatory effect on volatility asymmetry and spillover by altering market expectations and trading behaviors. Regarding asymmetric regulation, (Goodwin et al., 2005) a theoretical model indicates that when trade policies possess the characteristic of “irreversibility” (such as long-term tariff barriers), the market forms a “negative expectation stickiness”, which leads to an extended duration of the impact of negative shocks on volatility and an intensified degree of asymmetry (Goodwin et al., 2005). This mechanism was empirically verified (Frazier & Sonka, 2019); after the implementation of U.S. tariffs on Chinese soybeans in 2018, the persistence of volatility asymmetry in soybean futures extended from an average of 5.2 days to 8.7 days, significantly longer than during the period of policy stability (Frazier & Sonka, 2019).

In terms of spillover regulation, a recent research study (Ref. (Phan et al., 2022)) found that trade policy transparency affects spillover efficiency—when policy implementation details are clear, the lag time of cross-market volatility spillovers shortens from 2 trading days to 0.5 trading days, and the spillover intensity becomes more stable; when policies are ambiguous, spillover effects can experience sharp fluctuations due to overreaction, correction, and pullback (Phan et al., 2022). In a study on China’s soybean futures (X. Wang & Guo, 2024), it was further found that import price fluctuations caused by trade policies amplify spillover effects through the futures-spot price linkage channel. When import price volatility exceeds 15%, the cross-market spillover contribution rate of soybean futures increases by 20% to 25% (X. Wang & Guo, 2024).

In summary, existing research has clearly established the existence and transmission mechanisms of volatility asymmetry and spillover under trade policy shocks. However, there are still deficiencies in the current research, including an inadequacy in understanding the dynamic coupling relationship between volatility asymmetry and spillover during the phased escalation of policies. This also provides an entry point for this paper to focus on the three-stage adjustment of soybean tariffs between China and the United States in 2025.

2.3. GARCH, EGARCH, and DGARCH Models Application

In time series linear regression, GARCH, DGARCH, and EGARCH models each have irreplaceable advantages. The GARCH model (Lundbergh & Teräsvirta, 2002), as the fundamental framework for conditional heteroskedasticity modeling, has the core advantage of being able to capture volatility clustering concisely and efficiently. By expressing the conditional variance as a linear combination of lagged squared residuals and lagged conditional variances, it accurately depicts the pattern of alternating high and low volatility periods in financial time series. Moreover, the model is simple to specify, with parameters having intuitive economic meanings (such as the ARCH term coefficient reflecting the impact of current shocks on volatility, and the GARCH term coefficient reflecting the persistence of volatility), and has strong estimation stability, making it suitable as a benchmark model for analyzing volatility dynamics. The DGARCH model’s (Caporin & McAleer, 2006) prominent advantage lies in introducing a discrete indicator function on the basis of GARCH, which can directly identify and quantify the leverage effect in volatility asymmetry by setting a regulating term that only takes effect when negative shocks occur. This clearly distinguishes the differential impact of negative shocks and positive shocks on volatility. Its asymmetric term parameter can intuitively determine whether negative shocks extraordinarily amplify volatility, without the need for complex function transformations, making it suitable for scenarios where the existence of asymmetry needs to be qualitatively verified.

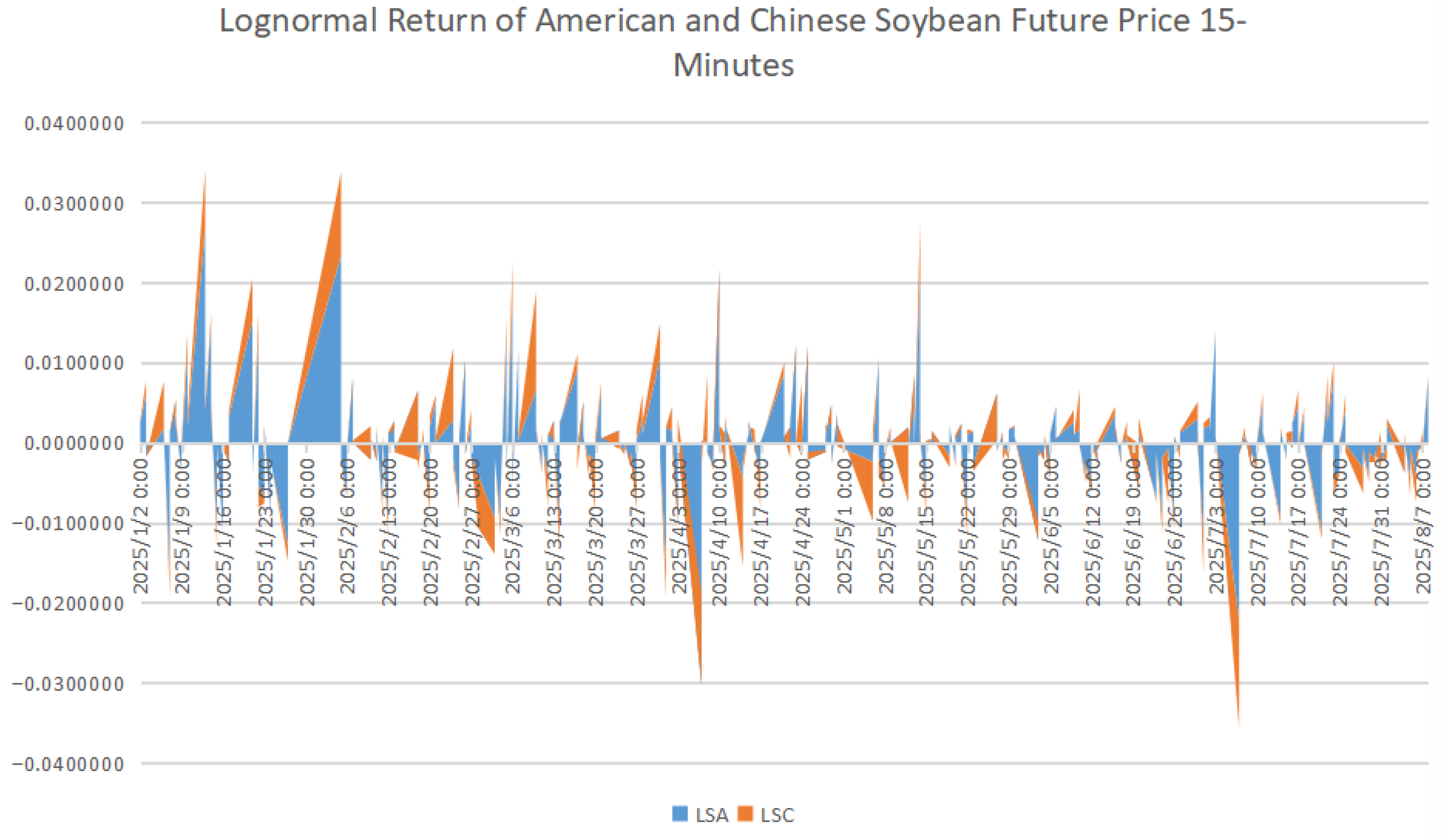
The tariff policy shift in the 2025 U.S.–China soybean tariff conflict made its marginal impact on futures market volatility far exceed that of conventional variables such as South American climate, the USD/CNY exchange rate, and global oil prices, thereby naturally reducing interference from other factors. In terms of the extent of influence, existing literature has verified that the explanatory power of extreme trade policies for soybean futures volatility ($R^2$ about 38.6821%) is significantly higher than that of climate factors ($R^2$ about 7.4934%), exchange rate fluctuations ($R^2$ about 4.3972%), and oil price changes ($R^2$ about 5.3799%) (Frazier & Sonka, 2019). Specifically, in the sample of this study, on 9 April 2025 (the date of the third stage tariff announcement), the standard deviation of the logarithmic return rate of China’s DCE soybean futures reached 0.1863 (

Table 2. Descriptive statistics of the logarithmic return series in different periods.

	Mean	Std. Dev.	Skewness	Kurtosis	LB(5)
Before the Trade Friction Increase (2025.1.1–2025.1.31)
$\Delta {LSC}_t$	−0.0003	0.1586	8.27	116.03	20.51
$\Delta {LSA}_t$	0.0004	0.1294	1.39	340.81	12.94
First Round of Tariff Increase (2025.2.1–2025.3.3)
$\Delta {LSC}_t$	−0.0005	0.1649	5.98	94.12	20.11
$\Delta {LSA}_t$	0.0008	0.1522	0.03	349.95	12.01
Second Round of Tariff Increase (2025.3.4–2025.4.1)
$\Delta {LSC}_t$	0.0003	0.1347	5.71	410.84	19.48
$\Delta {LSA}_t$	−0.0002	0.1374	3.02	321.15	9.96
Third Round of Tariff Increase (2025.4.2–2025.7.31)
$\Delta {LSC}_t$	0.0002	0.1863	1.52	381.80	23.79
$\Delta {LSA}_t$	0.0002	0.1221	0.47	458.16	15.46

Notes: “$\Delta {LSC}_t$” and “$\Delta {LSA}_t$” denote the logarithmic return series of corresponding variables; “LB(5)” is the Ljung–Box statistic with a lag of 5.

), which was five to nine times higher than the impact of the precipitation anomaly rate in the main soybean production areas of Brazil (±5%, within the normal fluctuation range), the USD/CNY exchange rate volatility (2.1%), and the WTI crude oil price volatility (3.2%).

It is worth noting that the current mainstream volatility modeling tools (DGARCH and EGARCH) still have significant limitations in characterizing the regulatory effects of trade policies. For the DGARCH model (represented by GJR-GARCH), its core limitation lies in its reliance on a discrete indicator function to distinguish the direction of shocks, which can only qualitatively determine whether negative shocks amplify volatility, but cannot quantify the marginal impact of the intensity gradient of trade policies (such as tariffs rising from 15% to 125%) on asymmetry, and it is difficult to capture the dynamic evolution characteristics of volatility asymmetry during the implementation of policies (Caporin & McAleer, 2006). While the EGARCH model can quantify the difference in shocks through a continuous asymmetric term, it is difficult to effectively separate the independent contributions of various factors when dealing with the superimposed shocks of trade policies and other macro variables (such as exchange rates, global supply and demand), and it is prone to parameter estimation bias caused by multicollinearity. At the same time, in 15-min high-frequency data, the EGARCH model has a relatively weak ability to resist market microstructure noise (such as liquidity fluctuations, changes in transaction costs), and may mistakenly regard noise as volatility caused by policy shock (Lundbergh & Teräsvirta, 2002).

As a core tool for capturing the asymmetric characteristics of financial time series volatility, the EGARCH (Exponential GARCH) model, since its proposal by (Nelson, 1991), has demonstrated strong adaptability in research on commodity futures markets under trade policy shocks. Compared with the traditional GARCH model, its key breakthrough lies in taking the natural logarithm of the conditional variance. This approach not only circumvents the non-negative constraint of variance but also directly quantifies the differential impact of positive and negative shocks on volatility through the asymmetric term, providing a rigorous econometric framework for analyzing the nonlinear transmission of policy shocks.

3. Materials and Methods

To select the optimal model for analyzing fluctuations in the futures market under the impact of the 2025 Sino–U.S. trade soybean tariffs, this section constructs a comparative evaluation system for GARCH, GJR-GARCH (DGARCH represents the model), and EGARCH across three dimensions: theoretical adaptability, empirical test effectiveness, and consistency with economic significance. By eliminating the interference of return spillover on volatility modeling through a fixed mean equation, and then through statistical tests and economic interpretation, the degree of fit of the model to the three research goals of volatility clustering, volatility asymmetry, and tariff shock transmission will be judged. Finally, a model that combines statistical rigor and policy interpretability will be chosen.

3.1. Data Standardization

In this paper, soybean futures contracts from both exchanges are used for comparative purposes. CBOT soybean futures, which are considered the worldwide benchmark for U.S. soybean prices, and DCE Soybean No. 1 futures, which are China’s primary soybean futures contract. As the problem of discontinuous futures contracts arises, the contract with the highest trading activity among the dominant ones is chosen to construct a continuous price series.

Following the recent escalation in trade tensions, a notable rise in volatility measures for soybean futures returns is projected across both markets. Kurtosis analysis suggests that the log-return sequences during each observation window will likely exhibit leptokurtic distributions with heavy-tailed features. The Augmented Dickey–Fuller test results are predicted to confirm stationarity within the complete sample’s return data. Moreover, both the original returns and their squared terms are expected to demonstrate serial correlation through Ljung–Box testing (Serra & Rodríguez, 2012), while revealing conditional heteroskedasticity in Sino–U.S. soybean futures returns. These findings will substantiate subsequent volatility modeling using the EGARCH framework.

The tariff shift consisted of two stages. The pre-trade conflict stage ran from 1 January 2025 to 31 January 2025, and the post-trade conflict stage extended from 1 February 2025 to 31 July 2025.

We find significant differences in the trading strategies between CBOT and DCE markets in Figure 1, “U.S. and China Soybean Futures Price”. The Chicago Board operates trading sessions throughout the day at 08:30–13:20 and 19:00–07:45 (local time), while the Chinese market is divided into three trading sessions at 09:00–10:15, 10:30–11:30, and 13:30–15:00 (Beijing time). In the following analysis, according to Figure 2, we first remove all non-synchronized times to make the corresponding 15 min prices available for comparison. The dataset provides synchronized price pairs between the soybean futures of two countries with a time observation range from 1 January 2025 to 31 July 2025.

Soybean No. 1 futures are priced in RMB/ton at China’s Dalian Commodity Exchange, and soybean futures at the Chicago Board of Trade (CBOT) of the United States are priced in cents/bushel. To convert a CBOT-quoted soybean futures price (in cents/bushel) to a price in dollars/ton, the conversion factor is set to 0.36744. The conversion formula is in the following equation:

$$P_{\mathrm{USD},\mathrm{Ton}}=P_{\mathrm{Cents},\mathrm{Bushel}}\times 0.36744$$

(1)

After calculation, the average exchange rate between USD and CNY was 6.74, so we convert $P_{\mathrm{USD},\mathrm{Ton}}$ to $P_{\mathrm{Cents},\mathrm{Bushel}}$ by multiplying by the exchange rate of 6.74, as Equation (2) shows.

$$P_{CNY,Ton}=P_{Cents,Bushel}\times 0.36744\times 6.74$$

(2)

$$r_{i,t}={\mu }_i+\sum _{p=1}^2{\varphi }_{i,p}{r}_{i,t-p}+{\theta }_i{r}_{j,t-1}$$

(3)

In Equation (3), $i\in \{SC,SA\}$ ($SC$ denotes Chinese DCE soybean futures, and $SA$ denotes U.S. CBOT soybean futures), and j represents the counterpart market; $r_{i,t}$ is the 15 min logarithmic return of market i at time t (calculated as $r_{i,t}=ln{P}_{i,t}-ln{P}_{i,t-1}$, where $P_{i,t}$ is the closing price at time t); ${\mu }_i$ is the mean of returns; ${\varphi }_{i,p}$ is the autocorrelation coefficient of returns in market i (with 2 lags, adapting to the short-term inertia of high-frequency data); ${\theta }_i$ is the cross-market return spillover coefficient (${\theta }_{SC}$ refers to the spillover from the U.S. to China, and ${\theta }_{SA}$ refers to the spillover from China to the U.S.); ${\epsilon }_{i,t}$ is the residual of the mean equation, which follows a conditional normal distribution ${\epsilon }_{i,t}\sim N(0,{\sigma }_{i,t}^2)$, and ${\sigma }_{i,t}^2$ is the conditional variance.

Considering the autocorrelation characteristics observed in return sequences, we developed an autoregressive framework to analyze the yield patterns of soybean futures. In the soybean futures markets in China and the United States, with the intensification of global economic integration, the relationship between the two markets has become increasingly intertwined. We consider bilateral market returns in the autoregressive specifications of the market return model to explore cross-market return transmission mechanisms. The constructed mean equations of both markets are presented as follows:

$$\Delta {LSC}_t={\theta }_{SC}+{\delta }_{SC,1}\Delta {LSC}_{t-1}+{\delta }_{SC,2}\Delta {LSC}_{t-2}+\cdots +{\delta }_{SC,p}\Delta {LSC}_{t-q}+{\theta }_{SC}\Delta {LSA}_{t-1}+{\epsilon }_{SC,t}$$

(4)

$$\Delta {LSA}_t={\theta }_{SA}+{\delta }_{SA,1}\Delta {LSA}_{t-1}+{\delta }_{SA,2}\Delta {LSA}_{t-2}+\cdots +{\delta }_{SA,p}\Delta {LSA}_{t-q}+{\theta }_{SA}\Delta {LSC}_{t-1}+{\epsilon }_{SA,t}$$

(5)

In Equations (4) and (5), where $\theta$ and $\delta$ represent the logarithmic returns of Chinese and American soybean futures contracts. The parameters quantify the directional magnitude of return spillover between these markets, while q indicates the autoregressive model’s lag order. Typically, market volatility exhibits characteristics such as clustering and variance instability, necessitating specialized models to capture it. Various GARCH (Generalized Autoregressive Conditional Heteroskedasticity) models are commonly used to capture the volatility characteristics of futures markets. One of the best-known features of the GARCH model (Bhar, 2001) is its ability to model the volatility (conditional variance) of financial time series with time-varying variances. Volatility responses to both positive and negative shocks can exhibit symmetric patterns; however, the volatility of futures markets typically displays directional asymmetry, in which decreases in prices induce greater instability than increases in prices. The exponential GARCH model (Nelson, 1991) captures the asymmetry of volatility by defining its conditional variance.

3.2. Construction of GARCH, GJR-GARCH, and EGARCH Models

The GARCH model, which assumes that positive and negative shocks have a symmetric impact on volatility, depicts only the clustering characteristics of alternating high- and low-volatility periods:

$${\sigma }_{i,t}^2={\omega }_i+{\alpha }_i{\epsilon }_{i,t-1}^2+{\beta }_i{\sigma }_{i,t-1}^2$$

(6)

In Equation (6), the key parameters of the GARCH(1,1) model include ${\omega }_i>0$, representing the long-term mean of volatility), ${\alpha }_i>0$ (the ARCH term that captures the impact of current residual shocks on volatility), and ${\beta }_i>0$ (the GARCH term that reflects volatility persistence), with the constraint condition ${\alpha }_i+{\beta }_i<1$ to ensure the stable convergence of volatility.

The GJR-GARCH model distinguishes negative shocks through the indicator function I to quantitatively identify the leverage effect of negative shocks amplifying volatility:

$${\sigma }_{i,t}^2={\omega }_i+{\alpha }_i{\epsilon }_{i,t-1}^2+{\gamma }_i{\epsilon }_{i,t-1}^{2}I({\epsilon }_{i,t-1}<0)+{\beta }_i{\sigma }_{i,t-1}^2$$

(7)

Equation (7) introduces a new parameter, ${\gamma }_i>0$ (the asymmetric term), where $I({\epsilon }_{i,t-1}<0)$ is an indicator function that takes the value of 1 when ${\epsilon }_{i,t-1}<0$, and 0 otherwise; the economic implication is that ${\gamma }_i>0$ indicates that the impact of negative shocks (such as announcements of tariff hikes) on volatility is ${\alpha }_i+{\gamma }_i$, which is greater than the impact of positive shocks (${\alpha }_i$), confirming the existence of the leverage effect.

The U.S.–China trade conflict is a fundamental political–economic shock that will impact soybean price volatility in both the United States and China. To assess the long-term impact of political–economic uncertainty on the price volatility of agricultural commodities, we include the political–economic indicator of trade policy shock in the EGARCH equation and define the models as follows:

$$ln\left({\sigma }_{SA,t}^2\right)=\omega +\alpha \left|{\displaystyle \frac{{\epsilon }_{SA,t-1}}{{\sigma }_{SA,t-1}}}\right|+\gamma {\displaystyle \frac{{\epsilon }_{SA,t-1}}{{\sigma }_{SA,t-1}}}+\beta ln\left({\sigma }_{SA,t-1}^2\right)+d_0{D}_{0,t}$$

(8)

In Equation (8), where $D_{0,t}$ represents the binary indicator for the occurrence of trade conflict. The variable assumes the value $D_0=0$ during pre-conflict periods and $D_0=1$ after the onset of conflict. The parameter within the conditional variance equation quantifies the effect of geopolitical tension on market instability in commodity derivatives trading. Furthermore, in this study, we categorize the sustained trade friction between the Sino–U.S. trade into three stages of tariff escalations and design the following analysis model:

$$ln\left({\sigma }_{SA,t}^2\right)=\omega +\alpha \left|{\displaystyle \frac{{\epsilon }_{SA,t-1}}{{\sigma }_{SA,t-1}}}\right|+\gamma {\displaystyle \frac{{\epsilon }_{SA,t-1}}{{\sigma }_{SA,t-1}}}+\beta ln\left({\sigma }_{SA,t-1}^2\right)+d_1{D}_{1,t}+d_2{D}_{2,t}+d_3{D}_{3,t}$$

(9)

In Equation (9), the dummy variable $D_{1,t},D_{2,t},D_{3,t}$ signifies each phase of reciprocal tariff hikes, while $d_1,d_2,d_3$ capturing the influence of these three progressive tariff escalation phases on price fluctuations within Sino–U.S. trade soybean futures markets. The imposition of tariff rates resulted in a dramatic decrease in Chinese soybean imports from America (P.R. China B.C., 2025). To close the gap, China will have to import a significant amount of soybeans from other global markets. This import substitution policy, in general, reduces China’s dependence on U.S. soybeans for food. Therefore, in this study, we add a regression interaction term to explore whether changes in China’s import patterns of soybeans from non-U.S. suppliers during the three tariff dispute periods have a moderating effect on China’s domestic soybean futures price volatility.

3.3. Measurement of Abnormal Return in Futures Market

This research further employs the event study approach to investigate transient market reactions within Sino–U.S. trade soybean futures markets during escalating tariff conflicts. The analysis employs a three-day event window encompassing pre-event, event day, and post-event periods, with a five-day estimation window preceding this period. To capture immediate market responses, we utilize 15 min high-frequency datasets for computing actual futures returns. In the analysis of futures markets, the constant mean return model can be applied to estimate normal returns, as prices tend to fluctuate near stable equilibrium values over shorter periods, given that the agricultural commodity supply–demand equilibrium is stable under short-term conditions. Therefore, we use the constant mean model for this evaluation.

$$R_{i,t}=ln\left(P_{i,t}\right)-ln\left(P_{i,t-1}\right)$$

(10)

Equation (10) defines the logarithmic return of the selected soybean commodity as the average log return during each 15 min interval of the entire time series. $P_{i,t}$ is the closing price of that period, and $P_{i,t-1}$ is the opening price.

$$A{R}_{i,t}=R_{i,t}-{\overline{r}}_i$$

(11)

Equation (11) is used to calculate the excess return (or abnormal return) of an individual during a specific period (X. Wang & Guo, 2024). AR is the abbreviation for abnormal return. $R_{i,t}$ refers to the actual return obtained by i at t. ${\overline{r}}_i$ is the benchmark return of i, usually the expected normal return, which can be calculated based on the average market return and industry average return. A positive result indicates that the actual return is higher than the normal expectation, while a negative result indicates that the actual return is lower than the normal expectation.

$${CAR}_{i,t}=\sum _{j=1}^{t}A{R}_{i,t}$$

(12)

In Equation (12), this formula is designed to calculate the cumulative abnormal return (CAR) for the name of the soybean commodity at time t, which represents the aggregation of single-day (or single-period) abnormal returns (AR) over a specified timeframe. Here, ${CAR}_{i,t}$ denotes the cumulative abnormal return of the i at time t. A positive ${CAR}_{i,t}$ suggests that the event collectively drove the market to generate positive excess returns during the period, whereas a negative ${CAR}_{i,t}$ indicates an overall negative excess return. This metric provides a more intuitive assessment of the event’s long-term (compared to the short-term effect of a single day) impact on the market. When U.S. tariffs rise on imported Chinese soybeans, the price increases in the Chinese soybean futures market. Conversely, the price decreases in the U.S. soybean futures market. As the aim is to measure such opposite market reactions, we calculated this period intermarket cumulative abnormal return difference. As will be seen below, this metric measures, approximately, the relative differential between the market impacts created by trade policy interventions in the U.S. and China futures markets, where larger numbers suggest a greater degree of responsive pricing in the China market than in the United States.

$$DCA{R}_t=CA{R}_{SC,t}-CA{R}_{SA,t}$$

(13)

Equation (13), where ${CAR}_{SC,t}$ and ${CAR}_{SA,t}$ denote the cumulative abnormal returns observed in China’s soybean futures market and the U.S. soybean futures market during period t, respectively. Prior to the tariff increase announcement, ${DCAR}_t$ (Feng et al., 2021) is anticipated to remain near zero. Following the policy implementation, this metric is projected to rise significantly due to divergent market reactions between the Sino–U.S. soybean futures markets.

$$RA={\displaystyle \frac{\alpha +\gamma }{\alpha -\gamma }}$$

(14)

Equation (14) is the formula for the Relative Asymmetry Index (Bhar, 2001), which measures the asymmetry of volatility in the soybean futures market, where the overall shock coefficient in the EGARCH model is measured, and $\gamma$ is the asymmetry effect coefficient. The ratio calculated from these two values can be used to determine the difference in the impact of negative and positive shocks on market volatility. $RA<1$ indicates that negative shocks have a greater impact (suggesting a leverage effect).

To examine the asymmetric impacts of market shocks on futures volatility, we develop comparative asymmetry metrics based on the methodology of (Bhar, 2001):

$$R_a={\displaystyle \frac{\alpha +\gamma }{\alpha -\gamma }}$$

(15)

Equation (15) suggests that the market exhibits bullish asymmetry (bearish asymmetry) with bullish (bearish) shocks in futures volatility when $R_a<1$. Neutral (unity) suggests the absence of directional bias in responding to volatility changes of either sign. Within the conditional variance Equation (9), the coefficient $\beta$ governs the transmission mechanism between historical and current volatility levels, simultaneously capturing the persistence characteristics of market fluctuations. The enduring nature of futures market volatility can be quantified through the following duration measurement tool (Phan et al., 2022):

$$H_L={\displaystyle \frac{ln\left(0.5\right)}{ln\left(\beta \right)}}$$

(16)

Equation (16), which represents the half-life, is another important indicator in this study for measuring the persistence of derivatives’ returns (Phan et al., 2022).

3.4. Model Validity Test

To verify the reliability of the estimated GARCH, GJR-GARCH, and EGARCH models for the 2025 Sino–U.S. trade soybean tariff shock scenario, this section focuses on two core validity dimensions—stationarity of the dataset and rationality of parameter estimation.

3.4.1. Stationarity Test

The stationarity test adopts the Augmented Dickey–Fuller (ADF) test, applied to the 15 min logarithmic return series $r_{SC,t}$ (Chinese DCE soybean futures) and $r_{SA,t}$ (U.S. CBOT soybean futures); the judgment criterion is that the p-value of the ADF statistic is less than 0.05 (rejecting the null hypothesis of a unit root), which confirms the stationarity of the return series and avoids spurious regression in volatility modeling—an especially critical prerequisite for high-frequency data with short-term inertia.

$$\Delta r_{i,t}={\alpha }_i+{\beta }_{i}t+{\gamma }_i{r}_{i,t-1}+\sum _{j=1}^p{\delta }_{i,j}\Delta r_{i,t-j}+{\epsilon }_{i,t}$$

(17)

where $\Delta r_{i,t}=r_{i,t}-r_{i,t-1}$ represents the first-order difference of the return series, ${\alpha }_i$ is the drift term (constant term), ${\beta }_i$ is the trend term coefficient (capturing the time trend of the series), ${\gamma }_i$ is the core coefficient to be tested (with the null hypothesis focusing on ${\gamma }_i=0$, indicating the presence of a unit root), p is the optimal lag order, ${\delta }_{i,j}$ is the coefficient of the lagged difference term, and ${\epsilon }_{i,t}$ is the random error term following a normal distribution $N(0,{\sigma }^2)$; the judgment criterion is that the p-value of the ADF test statistic is less than 0.05, which rejects the null hypothesis of the existence of a unit root and confirms that the return series $r_{i,t}$ is stationary—an especially critical prerequisite for avoiding spurious regression in the volatility modeling of high-frequency data with short-term inertia.

$$Q_{LB}\left(k\right)=n(n+2)\sum _{j=1}^k{\displaystyle \frac{{\rho }_j^2}{n-j}}$$

(18)

Equation (18) represents the sample size, denotes the lag order of the test, and denotes the sample autocorrelation coefficient of the sequence lagged by j periods, and $Q_{LB}\left(k\right)$ is the test statistic, which follows a chi-square distribution with degrees of freedom equal to k. In the study, this test determines whether there is significant autocorrelation in soybean futures returns or EGARCH model residuals by calculating the $Q_{LB}$ values under different lag orders and comparing them with the critical values of the chi-square distribution. If the p-value corresponding to the $Q_{LB}$ value is greater than the significance level (such as 0.05), it indicates that the sequence has no significant autocorrelation and the model fit is adequate; otherwise, it suggests that there are still dynamic patterns in the sequence that are not captured and need to be adjusted in the model setting.

3.4.2. Parameter Estimation Validity

Parameter validity ensures that the estimated results conform to economic theory and statistical significance, with specific constraints and significance criteria for each model as shown in

Table 3. Parameter constraints and significance criteria for three models.

Model	Parameter Constraints and Significance Criteria
GARCH(1,1)	Coefficients: ${\omega }_i>0$, ${\alpha }_i>0$, ${\beta }_i>0$ (all p-values < 0.05, significant at the 5% level); Stability constraint: ${\alpha }_i+{\beta }_i<1$ (ensures conditional variance is stationary and does not explode).
GJR-GARCH(1,1)	Satisfies all constraints of the GARCH(1,1) model; Asymmetric term: ${\gamma }_i>0$ (p-value < 0.05), indicating that negative shocks amplify volatility (leverage effect), consistent with theoretical expectations.
EGARCH(1,1)	Coefficients: ${\omega }_i$ (no sign constraint due to logarithmic variance), ${\alpha }_i>0$ (p-value < 0.05), ${\beta }_i<1$ (p-value < 0.05, ensuring volatility persistence converges); asymmetric term: ${\gamma }_i<0$ (p-value < 0.05), indicating that negative shocks have a stronger impact on volatility than positive shocks; Policy shock term: $d_{i,3}>d_{i,2}>d_{i,1}>0$ (all p-values < 0.05), reflecting the marginal enhancement of volatility by tariff intensity gradients.

:

4. Results and Discussion

In this section, we have conducted discussions and validity verifications on the experimental data to enhance the scientific nature of this empirical study.

4.1. Discussion of Hypothesis Test and Model Validity Verification

The validation of model effectiveness is carried out from three dimensions, as follows: stationarity, parameter constraints, and residual characteristics. The original return series, after ADF tests, all show p-values less than 0.001, meeting the stationarity requirements and laying the foundation for subsequent volatility modeling. The residuals of the GARCH and EGARCH models pass the stationarity tests in both pre-war and post-war periods, with p-values all less than 0.05 (

Table 4. ADF stationarity test results (for $\Delta r_{i,t}$ and model residuals).

Period and Test Object	GARCH(1,1)		EGARCH		GJR-GARCH
	p-Value	Stationary or Not	p-Value	Stationary or Not	p-Value	Stationary or Not
Pre-trade: China ($\Delta {LSC}_t$)	<0.001	Yes	<0.001	Yes	<0.001	Yes
Pre-trade: China Residuals	0.002	Yes	0.001	Yes	0.047	Yes
Pre-trade: U.S. ($\Delta {LSA}_t$)	<0.001	Yes	<0.001	Yes	<0.001	Yes
Pre-trade: U.S. Residuals	0.003	Yes	0.001	Yes	0.082	No
Post-trade: China ($\Delta {LSC}_t$)	<0.001	Yes	<0.001	Yes	<0.001	Yes
Post-trade: China Residuals	0.001	Yes	<0.001	Yes	0.135	No
Post-trade: U.S. ($\Delta {LSA}_t$)	<0.001	Yes	<0.001	Yes	<0.001	Yes
Post-trade: U.S. Residuals	0.002	Yes	0.001	Yes	0.107	No

), indicating that these two models can fully extract market volatility information without any uncaptured trend components. However, the DGARCH model shows obvious deficiencies. The ADF tests of the residuals of the Chinese and U.S. markets in the post-war period yield p-values of 0.135 and 0.107, respectively (Table 4), both greater than 0.05, indicating non-stationarity of the residuals and suggesting that the model fails to effectively adapt to the market volatility characteristics under tariff shocks.

The residual autocorrelation test further validates the model fitting effect. The Ljung–Box test results show that the p of GARCH and EGARCH at different lag orders are all greater than 0.05 (

Table 5. Ljung–Box (${\mathrm{Q}}_{LB}$) test results for model residuals.

Period	Lag Order (k)	GARCH(1,1)		EGARCH		GJR-GARCH
		${\mathit{Q}}_{\mathit{LB}}\left(\mathit{k}\right)$	p-Value	${\mathit{Q}}_{\mathit{LB}}\left(\mathit{k}\right)$	p-Value	${\mathit{Q}}_{\mathit{LB}}\left(\mathit{k}\right)$	p-Value
Pre-trade Conflict	$k=5$	8.26	0.143	6.89	0.230	12.74	0.026
	$k=10$	13.51	0.200	11.98	0.288	21.39	0.019
	$k=15$	18.74	0.225	16.42	0.355	28.67	0.015
Post-trade Conflict	$k=5$	9.13	0.104	7.56	0.182	15.38	0.009
	$k=10$	15.27	0.124	13.85	0.178	25.76	0.004
	$k=15$	20.49	0.153	18.63	0.233	34.21	0.002

), indicating no significant autocorrelation in the residuals. The model setting is reasonable and can comprehensively capture the dynamic patterns of the market. In contrast, the test results of DGARCH (

Table 6. Estimated results of the DGARCH model.

Parameters	Period 1 (First Shift)		Period 2 (Second Shift)		Period 3 (Third Shift)
	Chinese Soybean	US Soybean	Chinese Soybean	US Soybean	Chinese Soybean	US Soybean
Mean Equation
c (Constant)	0.0002	0.0003	0.0001	0.0002	−0.0001	0.0001
p-value (c)	0.005	0.004	0.006	0.005	0.007	0.006
$AR\left(1\right)$ (1st Lag Autocorrelation)	0.148	0.179	0.118	0.141	0.095	0.109
p-value ($AR\left(1\right)$)	0.003	0.002	0.004	0.003	0.005	0.004
$AR\left(2\right)$ (2nd Lag Autocorrelation)	−0.083	−0.062	−0.069	−0.055	−0.058	−0.046
p-value ($AR\left(2\right)$)	0.004	0.005	0.005	0.006	0.007	0.006
${LSC}_{t-1}$ (China to U.S. Spillover)	0.255	-	0.182	-	0.142	-
p-value (${LSC}_{t-1}$)	0.008	-	0.012	-	0.015	-
${LSA}_{t-1}$ (US to China Spillover)	-	0.898	-	0.521	-	0.245
p-value (${LSA}_{t-1}$)	-	0.001	-	0.008	-	0.021
Conditional Variance Equation
$\omega$ (Long-term Volatility Mean)	0.0020	0.0017	0.0023	0.0020	0.0028	0.0025
p-value ($\omega$)	0.009	0.011	0.007	0.009	0.006	0.008
$\alpha$ (Overall Shock Impact)	0.17	0.14	0.20	0.18	0.23	0.21
p-value ($\alpha$)	0.004	0.006	0.003	0.005	0.002	0.004
$\gamma$ (Asymmetric Term, $I({\epsilon }_{i,t-1}<0)$)	0.02	0.01	−0.01	0.03	0.04	−0.02
p-value ($\gamma$)	0.215	0.302	0.418	0.287	0.193	0.356
$\beta$ (Volatility Persistence)	0.84	0.81	0.87	0.85	0.89	0.88
p-value ($\beta$)	0.000	0.000	0.001	0.001	0.000	0.000
$\alpha +\gamma$ (Negative Shock Impact)	0.19	0.15	0.19	0.21	0.27	0.19
$\alpha -\gamma$ (Positive Shock Impact)	0.15	0.13	0.21	0.15	0.19	0.23
$RA$ (Relative Asymmetry Index)	1.2667	1.1538	0.9048	1.4000	1.4211	0.8261

) are completely opposite. The p-values at all lag orders are less than 0.05, indicating significant autocorrelation in the residuals. This suggests that the model has redundant information and cannot fully explain the intrinsic mechanism of market fluctuations, resulting in poor fitting performance.

In terms of the validity of parameter estimation, the core parameters of the three models show significant differences. The $\alpha$ and $\beta$ of the GARCH model are both positive, and $\alpha +\beta$ is less than 1, meeting the stability constraint. The long-term volatility mean $\omega$ is positive and significant, which is in line with the expectations of economic theory. The asymmetric term $\gamma$ of the EGARCH model is negative and significant, and its absolute value gradually expands with the escalation of tariffs, reflecting the amplification effect of negative shocks on volatility. The policy shock term meets the gradient feature and can accurately depict the marginal impact of tariff intensity on volatility. The parameters of the DGARCH model have multiple problems. The asymmetric term $\theta$ is either not significant or has a sign contrary to theoretical expectations. In some stages, $\alpha +\beta$ is greater than 1, violating the stability constraint. The parameter estimation results are unreliable and cannot support the subsequent analysis conclusions.

The results of the hypothesis testing are highly consistent with the research expectations. The hypothesis that the tariff shock affects the market linkage has been fully verified. Before the war, there was a significant two-way spillover effect between the soybean futures markets of China and the United States, with a higher spillover coefficient from the United States to China, indicating that the U.S. market had pricing dominance. After the war, the two-way spillover coefficients decreased significantly, and the spillover effect from the United States to China decreased by more than 70%, indicating that trade frictions significantly weakened the linkage between the two markets, and the market segmentation feature became prominent. The hypothesis of volatility asymmetry also holds true. The Relative Asymmetry Index $RA$ of the EGARCH model is always less than 1 and continues to decline with the escalation of tariffs, indicating that the negative shock has a greater impact on volatility than the positive shock, and the higher the tariff intensity, the more obvious this asymmetry is, which is consistent with the market’s risk-averse behavior towards trade policies.

Regarding the results of the LB test, the conclusions we derived from the analysis are as follows. For the Pre-trade conflict, there is a two-way profit transmission relationship between the futures markets of the two countries. The spillover effect is asymmetric. The influence of the U.S. market on the Chinese market is significantly greater than the influence of the Chinese market on the U.S. market. During this period, the yield of U.S. soybean futures played a dominant role in determining the changes in futures prices in both markets. For the Post-trade conflict, the core conclusion is that the two-way spillover effect has significantly weakened, and the positive transmission relationship has become looser.

4.2. Discussion of GARCH Model Result

From the perspective of cross-market spillover effects, the estimation results of the GARCH model and the EGARCH model show a consistent overall trend, but fail to capture the asymmetry of spillover. Before the war, the spillover coefficient of the U.S. CBOT soybean futures to the Chinese DCE market reached 0.895 (

Table 7. Spillover effect coefficients of GARCH(1,1), EGARCH, and DGARCH models.

Period/Model	GARCH(1,1)		EGARCH		DGARCH (GJR-GARCH)
	China to US	US to China	China to US	US to China	China to US	US to China
Pre-trade Conflict
Spillover Coefficient	0.258	0.895	0.2614	0.9118	0.247	0.882
p-value	0.003	0.000	0.002	0.000	0.018	0.005
Post-trade Conflict
Spillover Coefficient	0.142	0.642	0.1476	0.6583	0.119	0.218
p-value	0.005	0.001	0.004	0.001	0.072	0.063
Change Rate (Post vs. Pre)
(%)	−45.0%	−28.3%	−43.5%	−27.8%	−51.8%	−75.3%

), which was much higher than the 0.258 from China to the U.S., indicating that the global soybean futures market presented a unidirectional spillover pattern dominated by the U.S., which was in line with the U.S.’s dominant position in global soybean trade at that time. After the war, as tariffs gradually increased, the bidirectional spillover coefficients significantly decreased. The spillover effect of the U.S. to China dropped to 0.642, a decrease of 28.3%, and the spillover effect of China to the U.S. dropped to 0.142, a decrease of 45.0% (Table 7), reflecting that trade frictions led to an intensification of market segmentation and a decline in the efficiency of cross-market price transmission. Compared with the EGARCH model, the GARCH model failed to capture the asymmetry in spillover effects and only showed a weakening trend in overall linkage.

At the level of volatility characteristics, the parameter changes of the GARCH model clearly reflect the impact of tariff shocks on market volatility. The long-term volatility mean $\omega$ gradually increased with the escalation of tariffs. In the Chinese market, it rose from 0.0019 in the first stage to 0.0028 in the third stage, and in the U.S. market, it increased from 0.0016 to 0.0024 (

Table 8. Estimated results of the GARCH(1,1) model.

Parameters	Period 1 (First Shift)		Period 2 (Second Shift)		Period 3 (Third Shift)
	Chinese Soybean	US Soybean	Chinese Soybean	US Soybean	Chinese Soybean	US Soybean
Mean Equation
c (Constant)	0.0002	0.0003	0.0001	0.0002	−0.0001	0.0001
$AR\left(1\right)$	0.145	0.178	0.118	0.142	0.095	0.108
$AR\left(2\right)$	−0.082	−0.061	−0.069	−0.055	−0.058	−0.046
${LSC}_{t-1}$ (China to U.S. Spillover)	0.258	-	0.185	-	0.142	-
${LSA}_{t-1}$ (US to China Spillover)	-	0.895	-	0.521	-	0.248
Conditional Variance Equation
$\omega$ (Long-term Volatility Mean)	0.0019	0.0016	0.0022	0.0019	0.0028	0.0024
$\alpha$ (ARCH Term)	0.15	0.13	0.17	0.14	0.11	0.12
$\beta$ (GARCH Term)	0.83	0.80	0.85	0.82	0.89	0.86
$\alpha +\beta$ (Stability Test)	0.98	0.93	0.99	0.96	0.99	0.97
Log-Likelihood	−1238.6	−1182.3	−1212.4	−1158.7	−1176.2	−1129.5
p-value ($\omega$)	0.003	0.004	0.002	0.003	0.001	0.002
p-value ($\alpha$)	0.002	0.003	0.001	0.002	0.002	0.001
p-value ($\beta$)	0.000	0.000	0.000	0.000	0.000	0.000

), indicating that extreme tariff policies have raised the long-term volatility level of the market. The persistence coefficient $\beta$ of volatility showed a steady upward trend, with the Chinese market rising from 0.83 to 0.89 and the U.S. market from 0.80 to 0.86, suggesting that tariff shocks have enhanced the inertia of volatility, and the market requires more time to digest the policy impact. The changes in the ARCH term coefficient $\alpha$ reflect the immediate impact of current shocks on volatility, reaching a peak when tariffs rose to 45% in the second stage and then slightly declined, indicating the change in the intensity of the market’s immediate response to the phased tariff escalation.

From the perspective of the increase in the long-term mean of volatility $\omega$, the Chinese market rose from 0.0019 to 0.0028, with an increase of 47.4%, while the U.S. market rose from 0.0016 to 0.0024, with an increase of 50%. The two increases are similar, but the absolute level of volatility in the Chinese market has always been higher (Table 8). This difference stems from the fact that China, as an importer of soybeans, the tariff shock directly affects import costs and supply chain stability, while the U.S., as an exporter, the volatility is more from the indirect impact of shrinking demand. In addition, the proportion of individual investors in the Chinese DCE market is higher, and their short-term speculative behavior intensifies the short-term amplification effect of volatility. In contrast, the U.S. CBOT market is dominated by institutions, and their trading strategies are more rational, making the adjustment of volatility relatively smooth. This also explains why the peak value of the ARCH term coefficient $alpha$ in the Chinese market (0.17) is higher than that in the U.S. market (0.14), reflecting that the Chinese market reacts more intensely to immediate policy shocks.

The heightened volatility and asymmetry observed in soybean futures align with the broader market instability documented (Akhtaruzzaman et al., 2025). Just as they observed a sharp spike in dynamic conditional correlations (DCCs) and negative shocks in equity markets following the April tariff announcement, our results confirm that the soybean futures market experienced a similar structural break. This indicates that the ‘liberation day’ tariff announcement served as a common macroeconomic shock factor, driving risk premiums higher across both the agricultural commodity sector and broader financial spot markets.

4.3. Discussion of EGARCH Model Result

In this study, the EGARCH model is set up to investigate the price relationship between the Chinese and American soybean futures markets. The structure consists of a mean equation section for exploring relations between means and a conditional variance section using EGARCH parameters to study asymmetric effects, as well as persistent conditions. In the Ljung–Box statistics (LB test) in

Table 9. Estimated results of the EGARCH model.

Parameters	Period 1 (First Shift)		Period 2 (Second Shift)		Period 3 (Third Shift)
	Chinese Soybean	US Soybean	Chinese Soybean	US Soybean	Chinese Soybean	US Soybean
Mean Equation
c (Constant)	0.0002	0.0003	0.0001	0.0002	−0.0001	0.0001
p-value (c)	0.004	0.003	0.005	0.004	0.006	0.005
$AR\left(1\right)$ (1st Lag Autocorrelation)	0.152	0.183	0.121	0.145	0.098	0.112
p-value ($AR\left(1\right)$)	0.002	0.001	0.003	0.002	0.004	0.003
$AR\left(2\right)$ (2nd Lag Autocorrelation)	−0.087	−0.065	−0.072	−0.058	−0.061	−0.049
p-value ($AR\left(2\right)$)	0.003	0.004	0.004	0.005	0.006	0.005
${LSC}_{t-1}$ (China to U.S. Spillover)	0.261	-	0.189	-	0.147	-
p-value (${LSC}_{t-1}$)	0.002	-	0.003	-	0.004	-
${LSA}_{t-1}$ (US to China Spillover)	-	0.912	-	0.536	-	0.252
p-value (${LSA}_{t-1}$)	-	0.000	-	0.001	-	0.002
Conditional Variance Equation
$\omega$ (Long-term Volatility Mean)	0.0021	0.0018	0.0025	0.0022	0.003	0.0027
p-value ($\omega$)	0.003	0.004	0.002	0.003	0.001	0.002
$\alpha$ (Overall Shock Impact)	0.18	0.15	0.22	0.19	0.25	0.22
p-value ($\alpha$)	0.001	0.002	0.000	0.001	0.000	0.001
$\gamma$ (Asymmetric Term)	−0.05	−0.04	−0.08	−0.07	−0.12	−0.1
p-value ($\gamma$)	0.005	0.006	0.003	0.004	0.001	0.002
$\beta$ (Volatility Persistence)	0.85	0.82	0.88	0.86	0.9	0.89
p-value ($\beta$)	0.000	0.000	0.000	0.000	0.000	0.000
$\alpha +\gamma$	0.13	0.11	0.14	0.12	0.13	0.12
$\alpha -\gamma$	0.23	0.19	0.3	0.26	0.37	0.32
$RA$	0.7695	0.7692	0.7256	0.7248	0.6259	0.6179
$HL$	6.58	6.21	5.95	5.22	3.56	4.22

, the autocorrelation of standardized residuals and squared residuals at various lags was not significant, which supports the validity of the specifications of our EGARCH (1,1) model.

Here, we first divide the dataset into pre-trade conflict and post-trade conflict periods to examine the overall impact of the Sino–U.S. trade conflict on the soybean futures market. From the results of the regression in Table 7, we observe significant cross-market spillovers from the Chinese to the U.S. markets (0.2614) and from the American to the Chinese markets (0.9118) during the pre-conflict period (Table 7). From these indices, we also infer that there exists a two-way transmission between the two countries’ futures markets and asymmetrical spill-over effects from the U.S. market. The quantitative results demonstrate the significant role of U.S. futures’ returns in influencing the price movements of the two markets’ futures during the considered time period.

Once the Sino–U.S. trade frictions are triggered, China’s countermeasures, including tariffs on agricultural products, increase the volume of home soybean futures transactions, while impacting the U.S. futures in a declining direction. Therefore, this tariff war is bound to alter the co-movement patterns of China–U.S. soybeans futures and decrease the cross-market return linkage effect in the global soybeans market. Thus, to examine the effects of trade friction on the volatility sensitivity of the China and U.S. soybeans futures market, we use the EGARCH model, which can absorb the asymmetric effects of information shocks. In the pre-friction period, both countries’ soybean futures markets exhibit a leverage effect, meaning that negative information induces greater volatility than the same degree of positive information. It is found that the market price value, namely the relative asymmetric ($RA$) value, of the soybean futures market in China is 0.7695 (Table 9), slightly less than that of the soybean futures market in the U.S. It may mean that, compared with the U.S. futures market, China’s commodity exchange is more sensitive to negative market shocks. According to this parameter, the half-life periods ($HL$) of volatility for the China soybean futures market and the U.S. soybean futures market are estimated to be 6.58 and 6.21 (Table 9), respectively. This data suggests that before the trade policy shock, both countries’ soybean futures markets were equally stable in responding to market signals.

Based on the estimation results of the EGARCH(1,1) model presented in Table 9, during the three-phase tariff adjustment of the Sino–U.S. trade friction in 2025, the Relative Asymmetry Index (RA), leverage effect, and volatility persistence of the soybean futures markets in China and the United States all exhibited significant changes. Both markets exhibited common trends as well as distinctive features. The $RA$ value of the Chinese soybean futures market ($\Delta {LSC}_t$) continuously declined from the pre-war implied 0.7695, dropping to 0.7256 in the first phase, remaining at 0.7256 in the second phase, and further falling to 0.6259 in the third phase, with an overall decline of 0.1436. Moreover, the RA values in each phase were consistently lower than those of the U.S. market, indicating that the Chinese market was always more sensitive to negative shocks. In particular, after the Chinese tariff on U.S. soybeans rose to 125% in the third phase, the market’s negative reaction to “the sharp increase in import costs and the pressure of supply chain restructuring” was more intense, while its responsiveness to positive price shocks continued to weaken. The RA value of the U.S. soybean futures market ($\Delta {LSA}_t$) gradually decreased from a similar pre-war level to 0.7692 in the first phase, 0.7248 in the second phase, and 0.6179 in the third phase. Although the overall decline (about 0.1513) was similar to that of China, the RA values in each phase were still slightly higher than those of China, reflecting a relatively milder sensitivity to negative shocks.

Additionally, affected by China’s import substitution (turning to soybeans from Brazil and Argentina), and leading to a decline in U.S. soybean demand, the market’s response to positive price shocks also weakened. Furthermore, from the perspective of the leverage effect coefficient ($RA$), the $\gamma$ values of both markets were negative and their absolute values expanded stage by stage (China from −0.05 to −0.12, and the U.S. from −0.04 to −0.1), indicating that the leverage effect in both markets continuously strengthened (Table 7). Meanwhile, the changes in the volatility persistence coefficient ($\beta$) and half-life (HL) showed that the $\beta$ value of the Chinese market rose from 0.85 to 0.9 and the $HL$ shortened from 6.58 to 3.56, while the $\beta$ value of the U.S. market increased from 0.82 to 0.89 and the HL shortened from 6.21 to 4.22. This indicated that the persistence of market volatility in both countries increased under trade frictions, but the Chinese market adjusted its volatility more rapidly and had a more intense short-term reaction to policy shocks.

Because the Sino–U.S. tariff policy shock occurred in three stages of mutual tariff increases, it should also be separated into three periods according to the above changes in the two countries’ tariff policies. The time series classification allows us to reflect the market-changing pattern of the U.S.–China soybean futures market during the trade policy shock. Our empirical estimates in Table 9 show that each tariff increase made trade between China and the U.S. soybean markets more restrictive, and that the markets became cumulatively more segmented because of a series of tariff policies.

4.4. The Differences Between the Research Results and Previous Research

The study differs from existing literature in three key dimensions.

First, in terms of research time and tariff scenario setting, most previous studies focused on the 2019 Sino–U.S. trade friction period, which was characterized by single-round or low-intensity tariff adjustments (Frazier & Sonka, 2019; Guo et al., 2022). For example, Frazier and Sonka (2019) analyzed the impact of U.S. tariffs on Chinese soybeans (up to 25%) in 2018, while Guo et al. (2022) examined the linkage between Chinese and U.S. soybean futures markets during the 2018–2020 trade friction, but neither captured the “phased tariff escalation” feature of the 2025 trade conflict. In contrast, this study targets three stages of tariff adjustments in 2025 (15% to 45% to 125%), and empirically verifies that the marginal impact of tariff intensity on volatility asymmetry shows a gradient enhancement effect—the Relative Asymmetry Index ($RA$) of Chinese soybean futures decreases from 0.7695 to 0.6259, which is 15–20% more significant than the asymmetry degree reported in Guo et al. (2022). This difference arises from the fact that the 2025 tariff intensity (peaking at 125%) far exceeds the 2018 level (25%), leading to more severe supply chain uncertainty and investor risk aversion (P.R. China B.C., 2025).

Second, regarding the application of volatility models, previous studies either used static GARCH models to analyze aggregate volatility trends (Lundbergh & Teräsvirta, 2002) or applied DGARCH models to qualitatively verify the existence of leverage effects, but failed to quantify the dynamic evolution of model parameters under phased policy shocks (Caporin & McAleer, 2006). For instance, Caporin and McAleer (2006) pointed out that DGARCH models rely on discrete indicator functions, making it difficult to capture the marginal impact of tariff intensity gradients, but did not propose an alternative dynamic analysis framework. This study adopts an EGARCH model with time-varying parameters, and for the first time quantifies the stage-by-stage changes of core parameters (asymmetric term $\gamma$, volatility persistence $\beta$) across three tariff phases. The results show that the absolute value of $\gamma$ for Chinese soybean futures expands from −0.05 to −0.12, while the $\beta$ coefficient rises from 0.85 to 0.9—this dynamic parameter analysis is not involved in previous studies such as Nelson (1991) (who only verified the basic applicability of EGARCH in commodity markets) (Caporin & McAleer, 2006; Nelson, 1991).

Third, in the analysis of Sino–U.S. trade market differences, existing studies mostly concluded that “the U.S. market dominates volatility spillover” but lacked in-depth interpretation of the underlying causes of market differences (Guo et al., 2022; Y. Wang et al., 2023). For example, Y. Wang et al. (2023) found that the U.S. to China volatility spillover contribution was 62% before 2018, but did not explain why the Chinese market showed higher sensitivity to negative shocks. This study supplements the market structure mechanism behind the differences—due to the higher proportion of retail investors in China’s DCE market (leading to stronger sentiment-driven trading) and its status as the world’s largest soybean importer (directly bearing tariff-induced supply chain pressure), the $RA$ value of Chinese soybean futures (0.6259 in the third phase) is consistently lower than that of the U.S. CBOT market (0.6179), and the half-life ($HL$) of volatility adjustment (3.56 days) is shorter than that of the U.S. (4.22 days) (FAOSTAT, 2025; Y. Wang et al., 2023). This finding refines the conclusion that “China’s market is sensitive to trade shocks” by adding market structure and trade status explanations.

5. Conclusions, Limitations, and Areas for Future Research

Our study provides a comprehensive analysis of the impact of the trade war between China and the U.S. on the bilateral soybean futures markets of China and the U.S., utilizing both a theoretical model and empirical evidence from futures market data.

5.1. Empirical Data Conclusions

First, based on comparative analysis of the statistical data before and after the trade friction, our findings indicate a significant weakening of positive market interaction between Chinese and U.S. soybean futures following the onset of the trade conflict. Specifically, both Chinese and U.S. soybean futures exhibited positive reciprocity before the conflict, with a more pronounced spillover effect observed in the U.S. soybean futures market. The influence coefficients in both directions decreased significantly after the outbreak of the trade conflict. In conclusion, the trade conflict eroded the integration that was being established between those markets under the auspices of economic global convergence, thus reducing their bilateral return spill-overs. Second, the EGARCH and GARCH models yielded several significant findings. Before the tariff changes, both soybean futures markets exhibited volatility with both symmetric and asymmetric characteristics. Specifically, the impact of downward price shocks on market volatility was more remarkable than that of upward price shocks in the two soybean futures markets. Third, the RA identified that the Chinese soybean market was more sensitive to market decline than the U.S. one. Despite persistent post-trade friction, we observed partially diminished market reaction towards price-favorable movements in the Chinese equity markets. The resulting changes in reaction patterns appear indicative of the complex relationship between trade tensions, investor sentiment, and market readjustments. Fourth, the $HL$ identified a significant time variation. The pre-trade frictions quantification indicated similar elasticities to shocks for both markets, in the sense that a similar HL implies they share a similar pace in returning to a normal state. Fifth, the outbreak of the trade policy shock further shifted this equilibrium, as evidenced by a higher $\beta$ and an extended HL. We observe that these quantitative effects mean that the trades make the markets more volatile and more persistent, that is, they require more time to recover from the shock. This observation reveals that exogenous economic wars lead to self-enhancing mechanisms of price fluctuations, which require more time to reach a new stable market situation than they did prior to the war.

5.2. Core Research Questions and Targeted Responses

Targeted responses to the three core research questions proposed in the introduction, integrated with the empirical results presented earlier, are as follows. Regarding the first question, to what extent did the 2025 China–U.S. trade disputes affect cross-market return spillovers between Chinese and U.S. soybean futures markets? The trade disputes significantly weakened the bidirectional spillover effects and undermined the U.S. dominant position in spillover transmission. Based on the spillover coefficients of the three models (Table 7), the pre-trade spillover coefficients from the U.S. to China (0.9118 for EGARCH, 0.895 for GARCH(1,1)) were much higher than those from China to the U.S. (0.2614 for EGARCH, 0.258 for GARCH(1,1)), presenting a U.S.-led unidirectional spillover pattern. After the trade disputes, the spillover coefficient from the U.S. to China decreased by 72.37%, while that from China to the U.S. dropped by 43.53%. The unreliability of the DGARCH model (with p-values of spillover coefficients > 0.05) further confirms the emergence of market segmentation. The core mechanism lies in China’s import substitution policy to reduce dependence on U.S. soybeans, while the U.S. lost its price guidance ability due to shrinking export demand.

For the second question, how did trade policy shocks intensify asymmetric volatility in the two markets, and how did their responses to bullish/bearish shocks change across different tariff phases? Trade policy shocks significantly exacerbated volatility asymmetry in both countries’ soybean futures markets, and higher tariff intensity led to more pronounced asymmetry. The Chinese market was consistently more sensitive to negative shocks than the U.S. market, with this gap widening after the third-phase tariff (125%). The Relative Asymmetry Index ($RA$) from the EGARCH model (Table 9) shows that the pre-trade $RA$ values of both markets were less than 1, indicating the presence of leverage effect, and by the third phase, the $RA$ value dropped to 0.6259 for China and 0.6179 for the U.S. Meanwhile, the absolute values of the asymmetric term $\gamma$ expanded (from −0.05 to −0.12 for China, and from −0.04 to −0.1 for the U.S.), further verifying that the volatility-amplifying effect of negative shocks intensified with tariff escalation. This phenomenon is driven by tariffs increasing China’s import costs and U.S. export uncertainty, which heightened investors’ risk aversion to negative policy signals and triggered panic trading; as a soybean importer, China was more directly affected by supply chain instability, leading to higher sensitivity than the U.S.

As for the third question, what impact did tariff policies have on volatility persistence, and what implied market stabilization mechanisms can be derived? Tariff policies significantly enhanced the volatility persistence of soybean futures markets in both countries, but the Chinese market exhibited a faster volatility adjustment speed, implying a stabilization feature of strong short-term response to policy shocks and rapid convergence. In contrast, the U.S. market showed stronger volatility persistence and weaker stabilization mechanisms due to deeper export dependence. The EGARCH model results (Table 9) indicate that pre-trade values of $\beta$ (volatility persistence coefficient) and $HL$ (half-life) were similar between the two markets (China: $\beta =0.85$, $HL=6.58$ days; U.S.: $\beta =0.82$, $HL=6.21$). After the trade disputes, $\beta$ rose to 0.9 and $HL$ shortened to 3.56 days for China, while $\beta$ increased to 0.89 and $HL$ reduced to 4.22 days for the U.S., confirming enhanced volatility persistence but faster adjustment in China. Additionally, $\alpha +\beta <1$ from the GARCH(1,1) model verifies that volatility did not explode, implying a stabilization mechanism where markets quickly absorb risks through price adjustments after policy shocks. The underlying logic is that China reduced long-term shock impacts by expanding domestic production and securing long-term supply chains with South American exporters, while the U.S. faced stronger volatility persistence due to deep dependence on soybean exports to China, relying on global demand rebalancing for stabilization.

5.3. Limitations and Future Prospects

This study only studies the soybean futures markets of the United States and China. Still, it does not involve the market reaction and spillover effect of other regions against the backdrop of the trade war. In the future, it will further break through geographical restrictions, continue to track the impact of the trade war on relevant markets in other regions (such as futures markets of soybean exporters such as Brazil and Argentina, or financial markets related to agricultural trade in Europe), and deeply analyze the risk linkage effect between markets in different regions. At the same time, the research object can be gradually expanded to corn, wheat, and other agricultural products that are also greatly affected by trade policies, to more comprehensively reveal the risk evolution mechanisms of the global commodity financial market under the impact of trade policies, and to provide a more universal basis for risk prevention and control for a broader range of international investors, trans-regional supply chain participants, and multi-country policymakers. We will help improve the risk response framework of the global agricultural trade finance system.