Liquidity Drivers in Illiquid Markets: Evidence from Simulation Environments with Heterogeneous Agents
Abstract
1. Introduction
2. Motivation and Research Question
3. Literature Review
3.1. Markets for Non-Bankable Assets
3.2. Zero-Learning-Agent Models
3.3. Liquidity Dynamics in Illiquid Markets
3.4. Tokenized and Alternative Asset Markets
3.5. Synthesis and Contribution
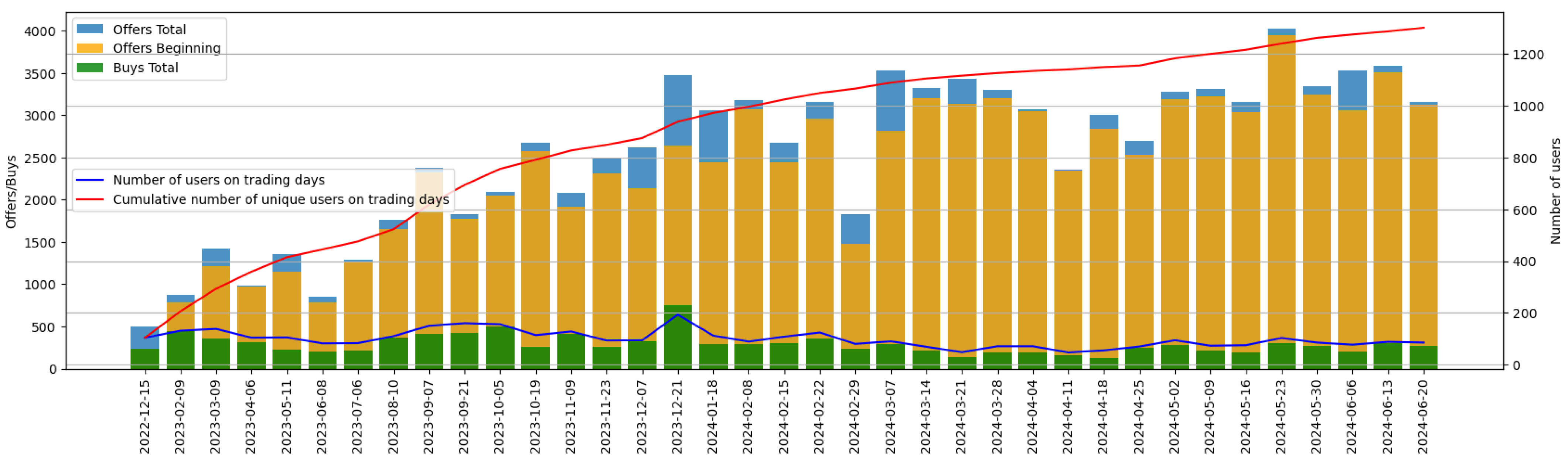
4. Market Setup and Data
- Market organization: The secondary market for trading shares opens at least once per month.1 Sellers may list shares for sale between 09:00 and 21:00 on designated trading days; buyers may make purchases only between 18:00 and 21:00 on those same days. Because buyers cannot place buy orders directly but can only accept existing sell offers, the market operates as an offer book driven by sellers. Any sell offers that remain unmatched are automatically deleted at the end of each trading day.
- Trading rules: Sell offers must be priced between 75% and 110% of the asset’s monthly updated reference valuation provided by the platform, ensuring that buyers are protected from offers that deviate substantially from current values. Sellers incur a two percent exit fee when a transaction completes on the secondary market; buyers pay no fees for successful trades.
- Order matching and market dynamics: Sell offers are processed in the sequence they arrive, ordered first by price and then by listing timestamp. Buyers are served in the order of arrival. The system allows both exact matches and partial matches between buy and sell orders.
- Interactive trading interface: Sellers may modify or withdraw their offers at any time. Buyers view offers in real time and make purchase decisions based on prevailing market conditions.
- Pure Buyer (PB): Agents of this type purchase solely in the secondary market; the empirical dataset contains 727 such agents.
- Pure Seller (PS): Agents of this type sell exclusively in the secondary market after initially acquiring assets on the primary market; the empirical dataset contains 413 such agents.
- Buyer Seller (BS): Agents of this type both purchase and sell in the secondary market; the empirical dataset contains 225 such agents.
5. Materials and Methods
5.1. Methodology
5.2. Implementation
5.2.1. Agents
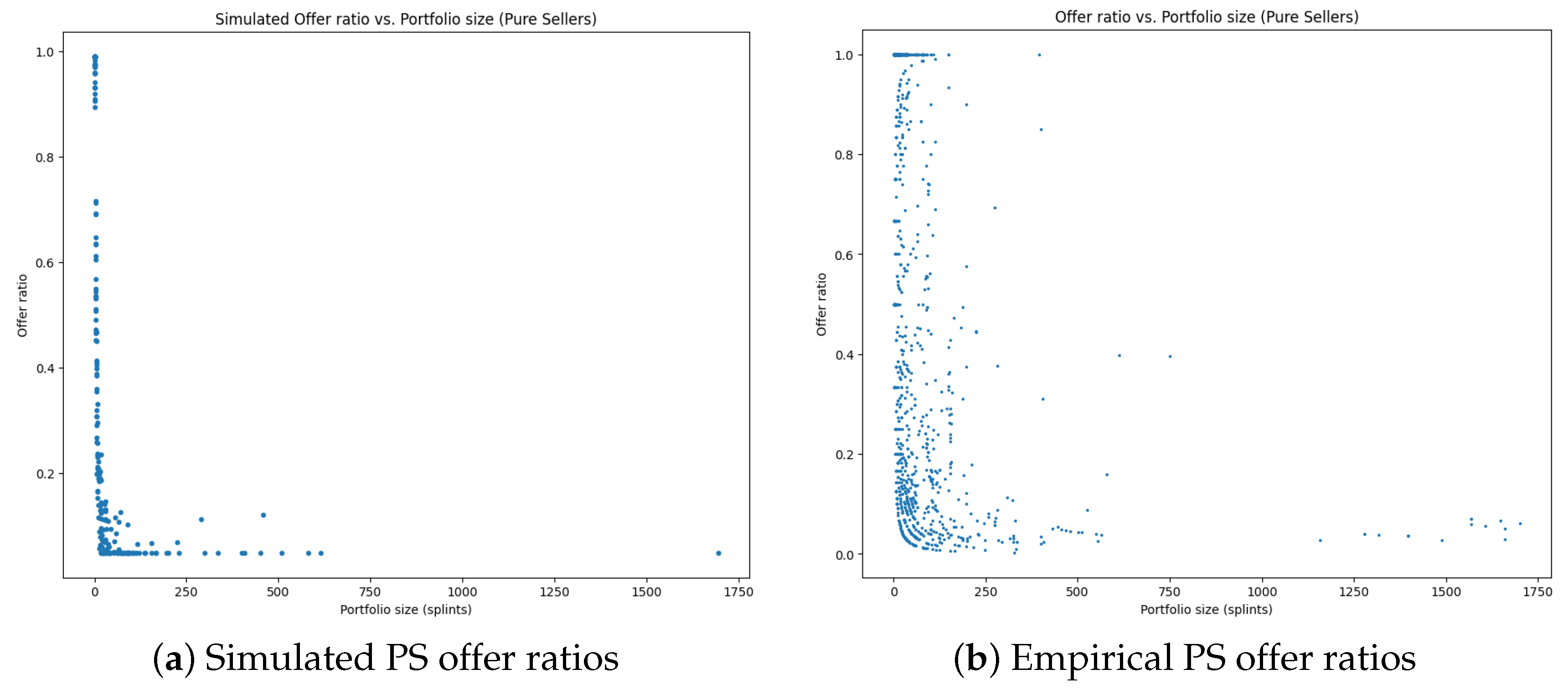
Pure Seller
- represents the median number of assets held by all Pure Seller agents;
- is the number of assets of the individual agent i;
- is a Gaussian noise term with and .
Pure Buyer
Buyer Seller
- represents the median number of assets held by all Buyer Seller agents;
- is the number of assets of the individual agent i;
- is a Gaussian noise term with with .
5.3. Process
5.4. Initialization
5.5. Synthetic Data Generation and Analysis
5.5.1. Univariate Sampling
- Y is the simulated liquidity ratio;
- is the parameter of interest.
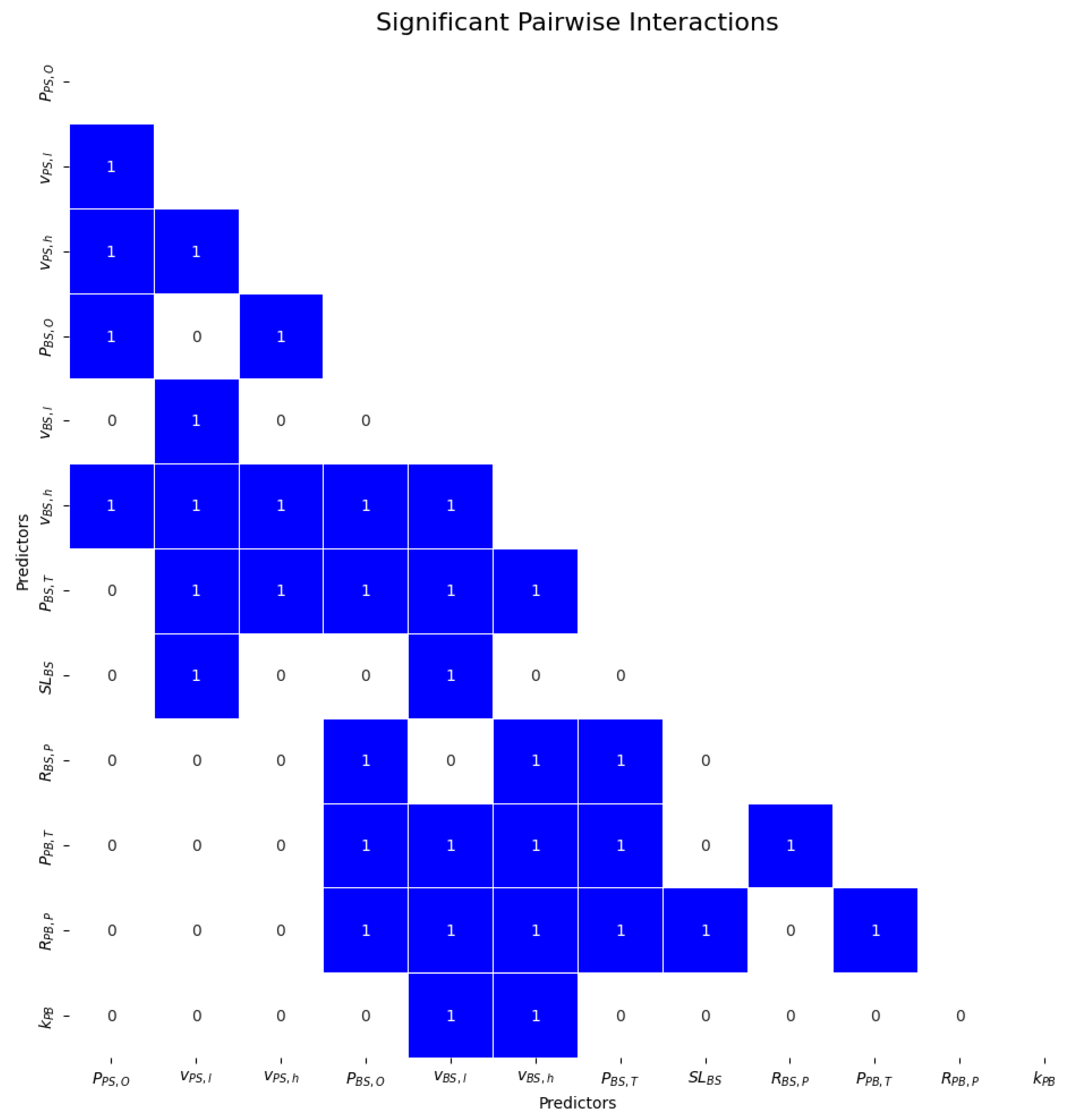
5.5.2. Multivariate Sampling
- Y is the simulated liquidity ratio;
- denotes the independent variable i, corresponding to one of the total m parameters of interest.
6. Results
6.1. Replication of Empirical Distribution
6.2. Single Linear Regression
6.3. Multiple Linear Regression
7. Discussion
7.1. Limitations
7.2. Extensions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABM | Agent-based model |
| DLT | Distributed ledger technology |
| ZI | Zero-intelligence models |
| OTC | Over-the-counter |
| PB | Pure Buyer |
| PS | Pure Seller |
| BS | Buyer Seller |
| KS | Kolmogorov–Smirnov test |
| MWU | Mann–Whitney U test |
| ECDF | Cumulative distribution function |
| 1 | Note that the platform adjusted its trading schedule from a four-week cycle to a biweekly window and then to a weekly schedule over the course of the observation period. |
| 2 | During the preparation of this manuscript, the authors used ChatGPT (OpenAI, GPT-4, 14 March 2023 release) to assist in proofreading and improving the linguistic quality of the text. Additionally, GitHub Copilot (OpenAI Codex-based, 29 June 2022 general availability release) was employed to enhance the quality and structure of the simulation code used in the agent-based model. The authors have reviewed and edited all outputs and take full responsibility for the content of this publication. |
| 3 | A corresponding dynamic is observed and described in Fluri et al. (2024). |
References
- Amihud, Y., Mendelson, H., & Pedersen, L. H. (2006). Liquidity and asset prices. Foundations and Trends in Finance, 1(4), 269–364. [Google Scholar] [CrossRef]
- Anufriev, M., Arifovic, J., Ledyard, J., & Panchenko, V. (2013). Efficiency of continuous double auctions under individual evolutionary learning with full or limited information. Journal of Evolutionary Economics, 23, 539–573. [Google Scholar] [CrossRef]
- Arifovic, J. (1996). The behavior of the exchange rate in the genetic algorithm and experimental economies. Journal of Political Economy, 104(3), 510–541. [Google Scholar] [CrossRef]
- Arthur, W. B., Holland, J. H., LeBaron, B., Palmer, R., & Tayler, P. (2018). Asset pricing under endogenous expectations in an artificial stock market. In W. B. Arthur, S. N. Durlauf, & D. A. Lane (Eds.), The economy as an evolving complex system ii (pp. 15–44). CRC Press. [Google Scholar] [CrossRef]
- Barclay, M. J., & Hendershott, T. (2003). Price discovery and trading after hours. The Review of Financial Studies, 16(4), 1041–1073. [Google Scholar] [CrossRef]
- Bardoscia, M., Carro, A., Hinterschweiger, M., Napoletano, M., Popoyan, L., Roventini, A., & Uluc, A. (2025). The impact of prudential regulation on the UK housing market and economy: Insights from an agent-based model. Journal of Economic Behavior & Organization, 229, 106839. [Google Scholar] [CrossRef]
- Bouchaud, J.-P. (2008). Economics needs a scientific revolution. Nature, 455(7217), 1181. [Google Scholar] [CrossRef]
- Chen, S.-H., & Yeh, C.-H. (2001). Evolving traders and the business school with genetic programming: A new architecture of the agent-based artificial stock market. Journal of Economic Dynamics and Control, 25(3–4), 363–393. [Google Scholar] [CrossRef]
- Fluri, L., Yilmaz, A., Bieri, D., Ankenbrand, T., & Perucca, A. (2024). Simulating liquidity: Agent-based modeling of illiquid markets for fractional ownership. arXiv, arXiv:2411.13381. [Google Scholar] [CrossRef]
- Fosco, C., & Mengel, F. (2011). Cooperation through imitation and exclusion in networks. Journal of Economic Dynamics and Control, 35(5), 641–658. [Google Scholar] [CrossRef]
- Gode, D. K., & Sunder, S. (1993). Allocative efficiency of markets with zero-intelligence traders: Market as a partial substitute for individual rationality. Journal of Political Economy, 101(1), 119–137. [Google Scholar] [CrossRef]
- Harris, L. (2002). Trading and exchanges: Market microstructure for practitioners. Oxford University Press. [Google Scholar] [CrossRef]
- Keynes, J. M. (1936). The general theory of employment, interest and money. Palgrave Macmillan. [Google Scholar] [CrossRef]
- Kopp, A., Westphal, R., & Sornette, D. (2022). Agent-based model generating stylized facts of fixed income markets. Journal of Economic Interaction and Coordination, 17, 947–992. [Google Scholar] [CrossRef]
- LeBaron, B. (2000). Agent-based computational finance: Suggested readings and early research. Journal of Economic Dynamics and Control, 24(5–7), 679–702. [Google Scholar] [CrossRef]
- LeBaron, B. (2001). A builder’s guide to agent-based financial markets. Quantitative Finance, 1(2), 254. [Google Scholar] [CrossRef]
- Muth, J. F. (1961). Rational expectations and the theory of price movements. Econometrica, 29, 315–335. [Google Scholar] [CrossRef]
- Palmer, R. G., Arthur, W. B., Holland, J. H., LeBaron, B., & Tayler, P. (1994). Artificial economic life: A simple model of a stockmarket. Physica D: Nonlinear Phenomena, 75(1–3), 264–274. [Google Scholar] [CrossRef]
- Seo, Y., Altiner, Z., Lee, S., Moon, I.-C., & Yun, T.-S. (2025). Finance and market concentration using agent-based modeling: Evidence from South Korea. Journal of Artificial Societies and Social Simulation, 28(3), 5. [Google Scholar] [CrossRef]
- Sornette, D. (2009). Why stock markets crash: Critical events in complex financial systems. Princeton University Press. [Google Scholar] [CrossRef]
- Tesfatsion, L., & Judd, K. L. (2006). Handbook of computational economics: Agent-based computational economics. Elsevier. [Google Scholar]
- Tirole, J. (2011). Illiquidity and all its friends. Journal of Economic Literature, 49(2), 287–325. [Google Scholar] [CrossRef]
- Yang, X., Zhang, J., Ye, Q., & Chang, V. (2025). Leveraging asymmetric price limits for financial stability in industrial applications: An agent-based model. Computers in Industry, 164, 104197. [Google Scholar] [CrossRef]



| Parameter | Variable | Value in Model |
|---|---|---|
| PS Offer Probability | 0.114 | |
| PS Price Range | ||
| PB Trading Probability | 0.092 | |
| PB Purchase Ratio | 0.566 | |
| PB Decision Steepness | 2 | |
| BS Offer Probability | 0.278 | |
| BS Price Range | ||
| BS Trading Probability | 0.104 | |
| BS Purchase Ratio | 0.485 | |
| BS Search Length | 5 | |
| Price Range Market |
| Parameter | Variable | Value Range |
|---|---|---|
| PS Offer Probability | ||
| PS Price Range | ||
| PB Trading Probability | ||
| PB Purchase Ratio | ||
| PB Decision Steepness | ||
| BS Offer Probability | ||
| BS Price Range | ||
| BS Trading Probability | ||
| BS Purchase Ratio | ||
| BS Search Length |
| Source | Mean | Median | Std | Skew | Kurtosis |
|---|---|---|---|---|---|
| Empirical | 0.1449 | 0.0974 | 0.1088 | 1.8363 | 3.2647 |
| ABM | 0.1297 | 0.1125 | 0.1159 | 1.3395 | 1.6730 |
| Test | Statistic | p-Value |
|---|---|---|
| Kolmogorov–Smirnov | 0.216 | 0.135 |
| Mann–Whitney U | 1914.0 | 0.758 |
| Variable | Coef | Std Err | t | p > |t| | [0.025 | 0.975] |
|---|---|---|---|---|---|---|
| −0.358 | 0.010 | −37.236 | 0.000 | −0.377 | −0.339 | |
| 0.048 | 0.005 | 9.917 | 0.000 | 0.038 | 0.057 | |
| 0.086 | 0.005 | 18.192 | 0.000 | 0.076 | 0.095 | |
| 0.793 | 0.012 | 66.327 | 0.000 | 0.770 | 0.817 | |
| 0.131 | 0.005 | 28.400 | 0.000 | 0.122 | 0.140 | |
| −0.001 | 0.001 | −0.819 | 0.413 | −0.002 | 0.001 | |
| −0.746 | 0.009 | −79.012 | 0.000 | −0.764 | −0.727 | |
| 0.125 | 0.005 | 24.331 | 0.000 | 0.115 | 0.135 | |
| 0.236 | 0.004 | 52.431 | 0.000 | 0.227 | 0.245 | |
| 1.298 | 0.011 | 122.838 | 0.000 | 1.278 | 1.319 | |
| 0.229 | 0.005 | 48.225 | 0.000 | 0.219 | 0.238 | |
| 0.001 | 0.000 | 4.905 | 0.000 | 0.001 | 0.002 |
| Dep. Variable: | Liquidity Ratio | R-squared: | 0.743 | |||
| Model: | OLS | Adj. R-squared: | 0.743 | |||
| Method: | Least Squares | F-statistic: | 1696 | |||
| No. Observations: | 10,000 | Prob (F-statistic): | <0.001 | |||
| Df Residuals: | 9987 | Log-Likelihood: | −4853 | |||
| Df Model: | 12 | AIC: | 9733 | |||
| Covariance Type: | HC3 | BIC: | 9827 | |||
| Durbin–Watson: | 2.000 | |||||
| Coef. | Std. Err | z | p > |z| | [0.025 | 0.975] | |
| −1.761 | 0.004 | −447.140 | 0.000 | −1.768 | −1.753 | |
| −0.082 | 0.004 | −20.484 | 0.000 | −0.090 | −0.074 | |
| 0.049 | 0.004 | 11.767 | 0.000 | 0.039 | 0.055 | |
| 0.060 | 0.004 | 14.863 | 0.000 | 0.052 | 0.067 | |
| 0.184 | 0.004 | 43.873 | 0.000 | 0.176 | 0.193 | |
| 0.061 | 0.004 | 15.163 | 0.000 | 0.053 | 0.069 | |
| −0.017 | 0.004 | −4.339 | 0.000 | −0.025 | −0.009 | |
| −0.374 | 0.004 | −90.585 | 0.000 | −0.382 | −0.366 | |
| 0.020 | 0.004 | 4.922 | 0.000 | 0.012 | 0.027 | |
| 0.156 | 0.004 | 37.563 | 0.000 | 0.148 | 0.164 | |
| 0.472 | 0.005 | 86.900 | 0.000 | 0.461 | 0.482 | |
| 0.148 | 0.004 | 36.922 | 0.000 | 0.140 | 0.156 | |
| 0.027 | 0.004 | 6.727 | 0.000 | 0.019 | 0.035 | |
| Dep. Variable: | Liquidity Ratio | R-squared: | 0.808 | |||
| Model: | OLS | Adj. R-squared: | 0.807 | |||
| Method: | Least Squares | F-statistic: | 715 | |||
| No. Observations: | 10,000 | Prob (F-statistic): | <0.001 | |||
| Df Residuals: | 9953 | Log-Likelihood: | −3402 | |||
| Df Model: | 46 | AIC: | 6899 | |||
| Covariance Type: | HC3 | BIC: | 7238 | |||
| Durbin–Watson: | 2.005 | |||||
| Coef. | Std. Err | t | p > |t| | [0.025 | 0.975] | |
| −1.763 | 0.003 | −513.331 | 0.000 | −1.770 | −1.757 | |
| −0.081 | 0.004 | −22.961 | 0.000 | −0.087 | −0.074 | |
| 0.048 | 0.003 | 13.856 | 0.000 | 0.041 | 0.055 | |
| 0.061 | 0.003 | 17.622 | 0.000 | 0.054 | 0.068 | |
| 0.181 | 0.004 | 50.743 | 0.000 | 0.174 | 0.188 | |
| 0.060 | 0.003 | 17.114 | 0.000 | 0.053 | 0.067 | |
| −0.018 | 0.003 | −5.208 | 0.000 | −0.024 | −0.011 | |
| −0.375 | 0.004 | −104.297 | 0.000 | −0.382 | −0.368 | |
| 0.018 | 0.003 | 5.047 | 0.000 | 0.011 | 0.024 | |
| 0.155 | 0.004 | 44.027 | 0.000 | 0.148 | 0.162 | |
| 0.477 | 0.004 | 110.708 | 0.000 | 0.468 | 0.485 | |
| 0.146 | 0.003 | 42.130 | 0.000 | 0.139 | 0.153 | |
| 0.029 | 0.004 | 8.366 | 0.000 | 0.022 | 0.036 | |
| 0.022 | 0.004 | 6.241 | 0.000 | 0.015 | 0.029 | |
| 0.026 | 0.003 | 7.586 | 0.000 | 0.020 | 0.033 | |
| 0.028 | 0.004 | 7.578 | 0.000 | 0.020 | 0.035 | |
| −0.021 | 0.004 | −5.889 | 0.000 | −0.028 | −0.014 | |
| −0.009 | 0.004 | −2.501 | 0.012 | −0.016 | −0.002 | |
| −0.009 | 0.004 | −2.451 | 0.014 | −0.016 | −0.002 | |
| −0.022 | 0.004 | −6.184 | 0.000 | −0.029 | −0.015 | |
| −0.014 | 0.004 | −3.370 | 0.001 | −0.023 | −0.006 | |
| 0.016 | 0.004 | 4.337 | 0.000 | 0.009 | 0.023 | |
| −0.011 | 0.004 | −2.968 | 0.003 | −0.018 | −0.004 | |
| −0.028 | 0.004 | −7.709 | 0.000 | −0.035 | −0.021 | |
| −0.024 | 0.004 | −5.304 | 0.000 | −0.032 | −0.015 | |
| 0.018 | 0.004 | 4.800 | 0.000 | 0.010 | 0.025 | |
| 0.018 | 0.004 | 4.019 | 0.000 | 0.009 | 0.027 | |
| 0.016 | 0.004 | 4.235 | 0.000 | 0.009 | 0.024 | |
| −0.010 | 0.004 | −2.729 | 0.006 | −0.017 | −0.003 | |
| 0.007 | 0.004 | 1.987 | 0.047 | 9.97 × 10−5 | 0.015 | |
| 0.029 | 0.004 | 8.072 | 0.000 | 0.022 | 0.036 | |
| −0.043 | 0.004 | −9.549 | 0.000 | −0.052 | −0.034 | |
| −0.014 | 0.004 | −3.950 | 0.000 | −0.021 | −0.007 | |
| 0.044 | 0.003 | 12.518 | 0.000 | 0.037 | 0.050 | |
| 0.009 | 0.004 | 2.542 | 0.011 | 0.002 | 0.016 | |
| −0.009 | 0.003 | −2.587 | 0.010 | −0.015 | −0.002 | |
| −0.113 | 0.004 | −25.947 | 0.000 | −0.122 | −0.105 | |
| −0.034 | 0.004 | −9.547 | 0.000 | −0.040 | −0.027 | |
| 0.062 | 0.004 | 17.241 | 0.000 | 0.055 | 0.069 | |
| 0.029 | 0.004 | 7.975 | 0.000 | 0.022 | 0.036 | |
| 0.012 | 0.003 | 3.406 | 0.001 | 0.005 | 0.019 | |
| 0.024 | 0.004 | 5.450 | 0.000 | 0.015 | 0.032 | |
| −0.083 | 0.004 | −18.767 | 0.000 | −0.092 | −0.075 | |
| −0.026 | 0.004 | −5.778 | 0.000 | −0.034 | −0.017 | |
| 0.008 | 0.004 | 2.130 | 0.033 | 0.001 | 0.015 | |
| −0.017 | 0.004 | −4.744 | 0.000 | −0.024 | −0.010 | |
| 0.023 | 0.003 | 6.528 | 0.000 | 0.016 | 0.030 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fluri, L.; Yilmaz, A.E.; Bieri, D.; Ankenbrand, T.; Perucca, A. Liquidity Drivers in Illiquid Markets: Evidence from Simulation Environments with Heterogeneous Agents. Int. J. Financial Stud. 2025, 13, 145. https://doi.org/10.3390/ijfs13030145
Fluri L, Yilmaz AE, Bieri D, Ankenbrand T, Perucca A. Liquidity Drivers in Illiquid Markets: Evidence from Simulation Environments with Heterogeneous Agents. International Journal of Financial Studies. 2025; 13(3):145. https://doi.org/10.3390/ijfs13030145
Chicago/Turabian StyleFluri, Lars, Ahmet Ege Yilmaz, Denis Bieri, Thomas Ankenbrand, and Aurelio Perucca. 2025. "Liquidity Drivers in Illiquid Markets: Evidence from Simulation Environments with Heterogeneous Agents" International Journal of Financial Studies 13, no. 3: 145. https://doi.org/10.3390/ijfs13030145
APA StyleFluri, L., Yilmaz, A. E., Bieri, D., Ankenbrand, T., & Perucca, A. (2025). Liquidity Drivers in Illiquid Markets: Evidence from Simulation Environments with Heterogeneous Agents. International Journal of Financial Studies, 13(3), 145. https://doi.org/10.3390/ijfs13030145






