Spot Volatility Measurement Using a Change-Point Duration Model in the High-Frequency Market
Abstract
1. Introduction
2. Model
2.1. Spot Volatility Measurement via Price Duration
2.2. The Change-Point Price Duration Model
2.3. Comparison with Other Models
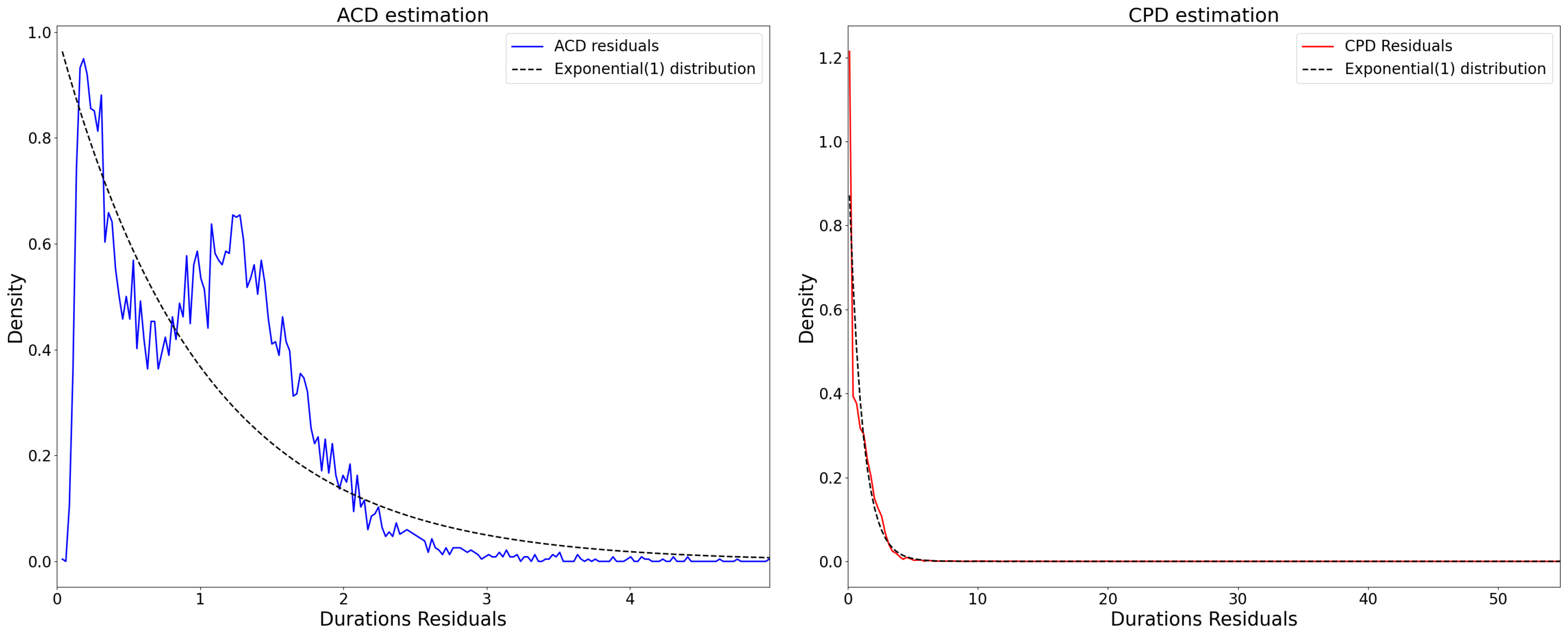
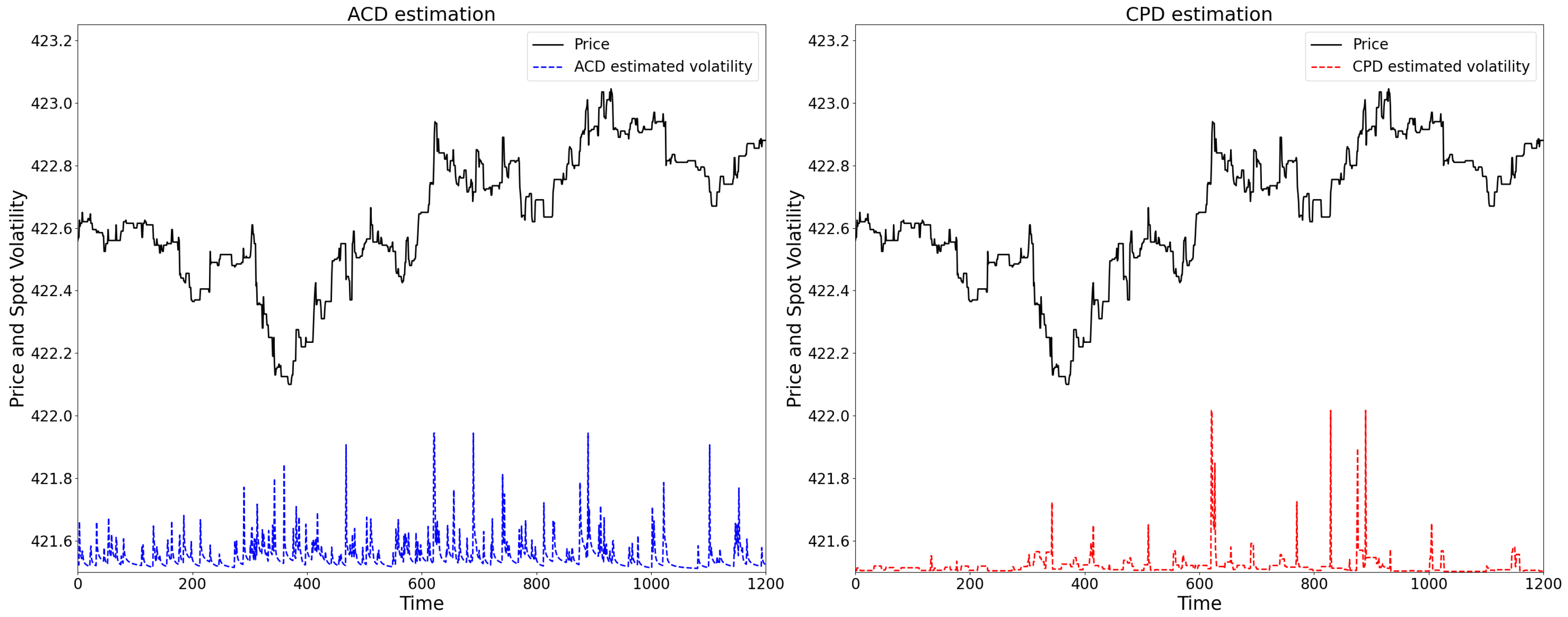
2.3.1. Compare with ACD Model
2.3.2. Compare with Nonparametric Duration-Based Estimator
2.3.3. Compare with Candlestick-Based Estimator
3. Model Estimation and Simulation
3.1. Estimation Algorithm
- E-step: Compute the expected complete log-likelihood , given current parameter values. This involves evaluating the posterior change-point probability and the distribution of intensity using forward–backward filtering (See Appendix A).As the prior distribution is a Gamma distribution, which is a conjugate prior for the exponential distribution, the posterior distribution of is also a Gamma distribution. Hence, the posterior distribution of intensity is as follows:where and represent the change-point probability that the last changing point occurs at i and the next changing point occurs at . The calculation steps of this posterior change-point probability is introduced in Appendix B.
- M-step: Maximize the expected log-likelihood with respect to , , and p. The update for p has a closed form:indicates there is a changing point at the -th price-change event, i.e., , and represents the probability of a changing point at the -th price-change event, given the observed data and old parameters.Posterior mean estimates of are then computed aswhere are obtained by solving the likelihood equations numerically. The computation of and is described in Appendix A and Appendix B.
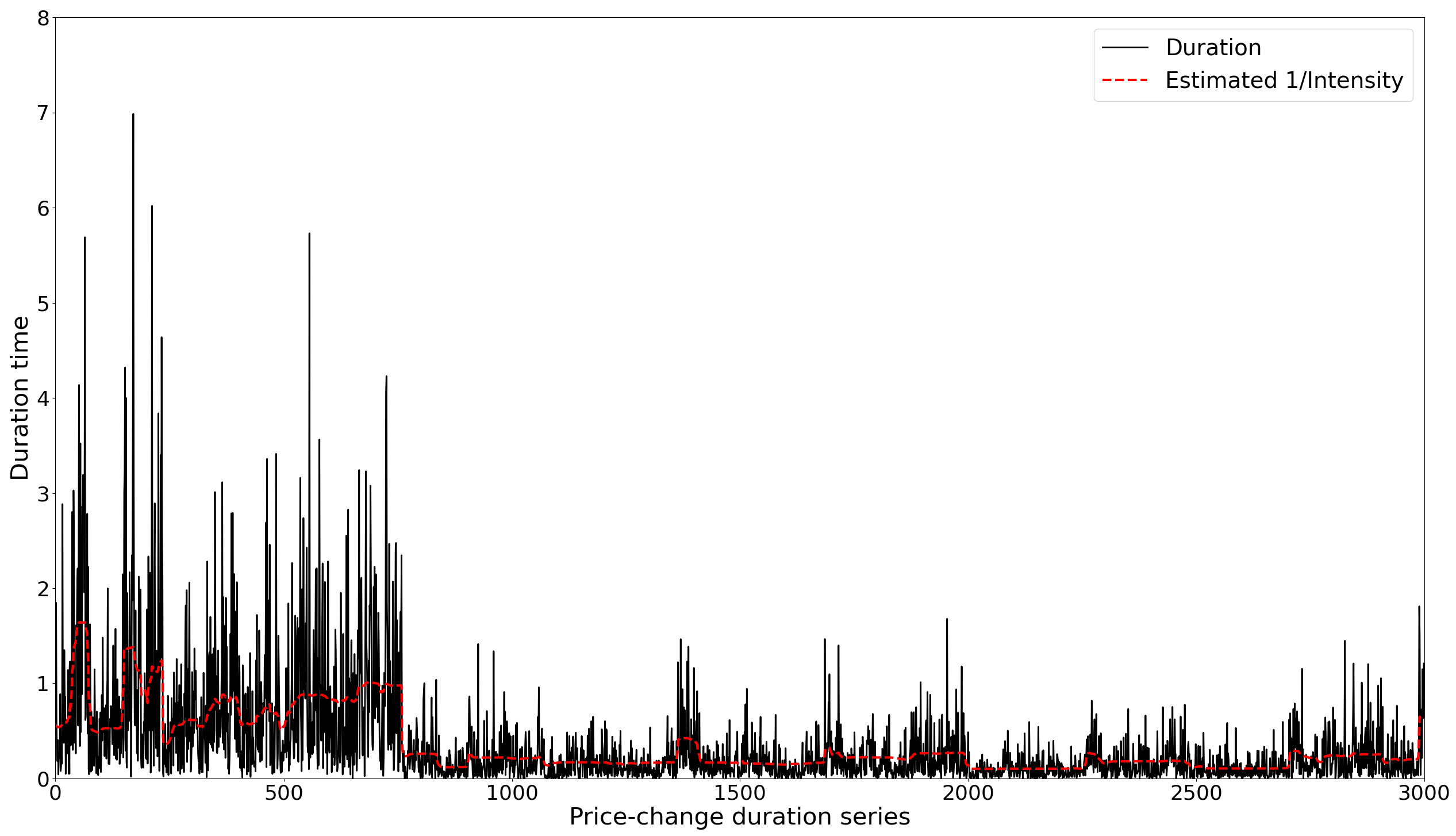
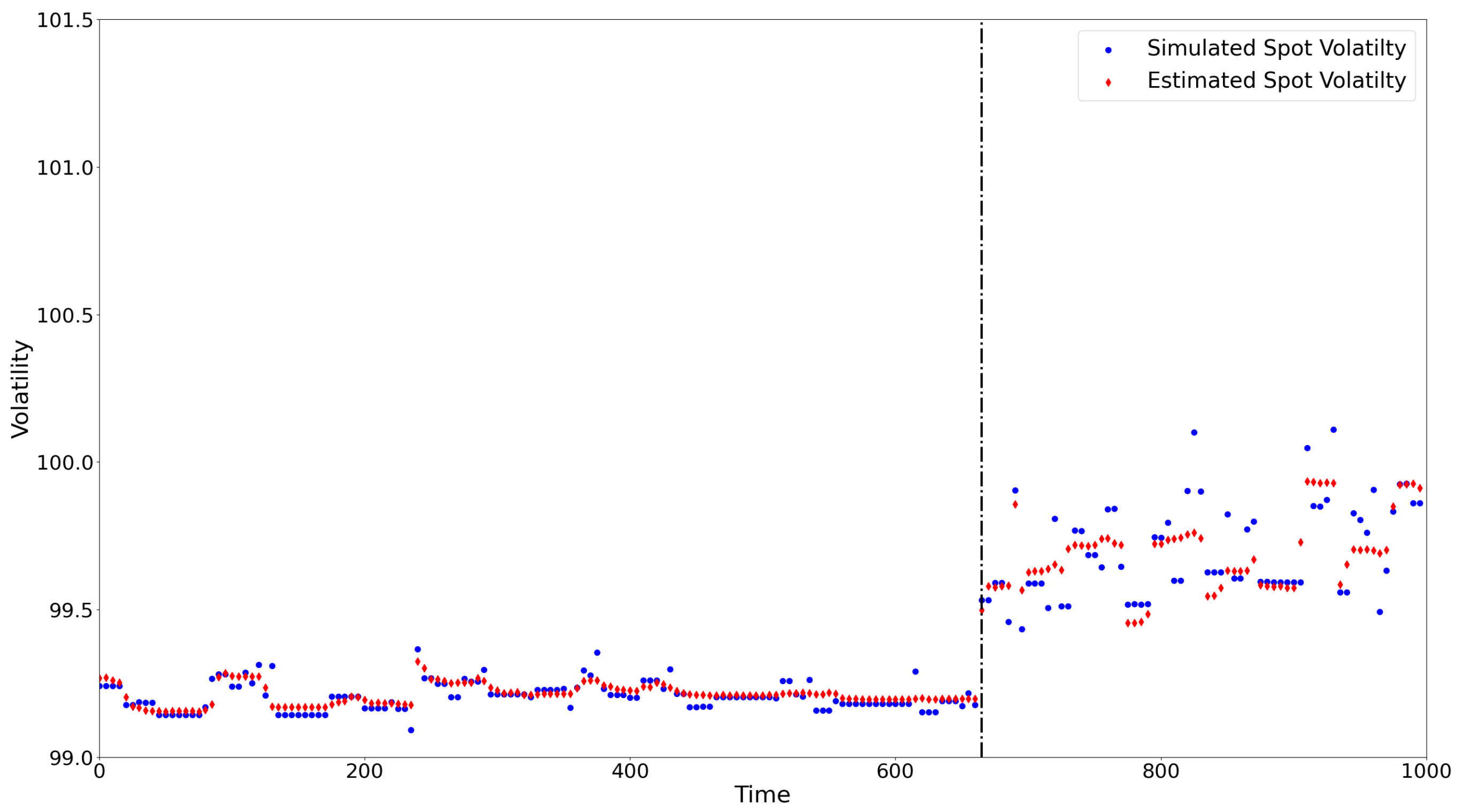
3.2. Simulation Study
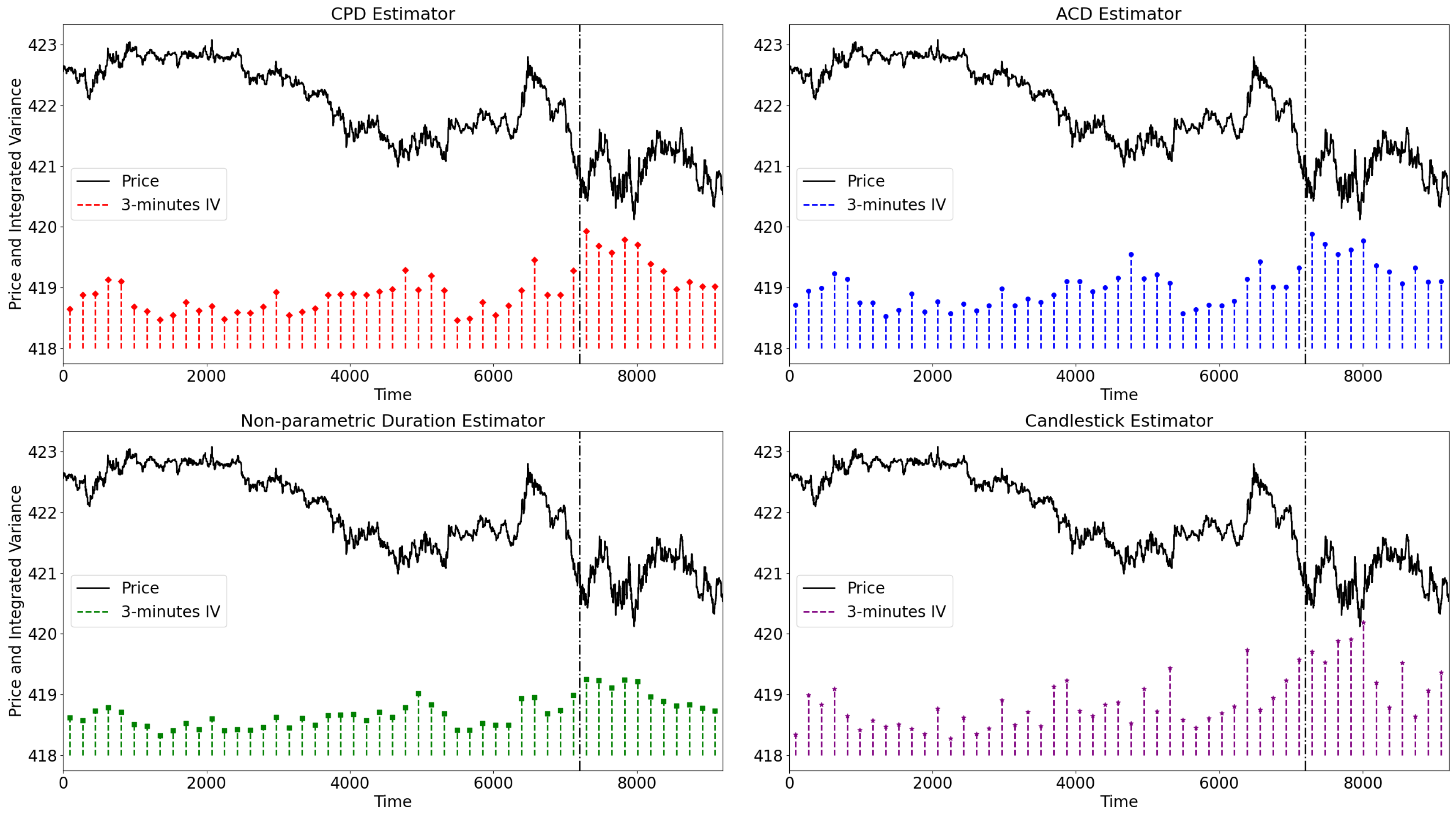
4. Real Data Analysis
4.1. Data Environment
4.2. Spot Volatility Measurement
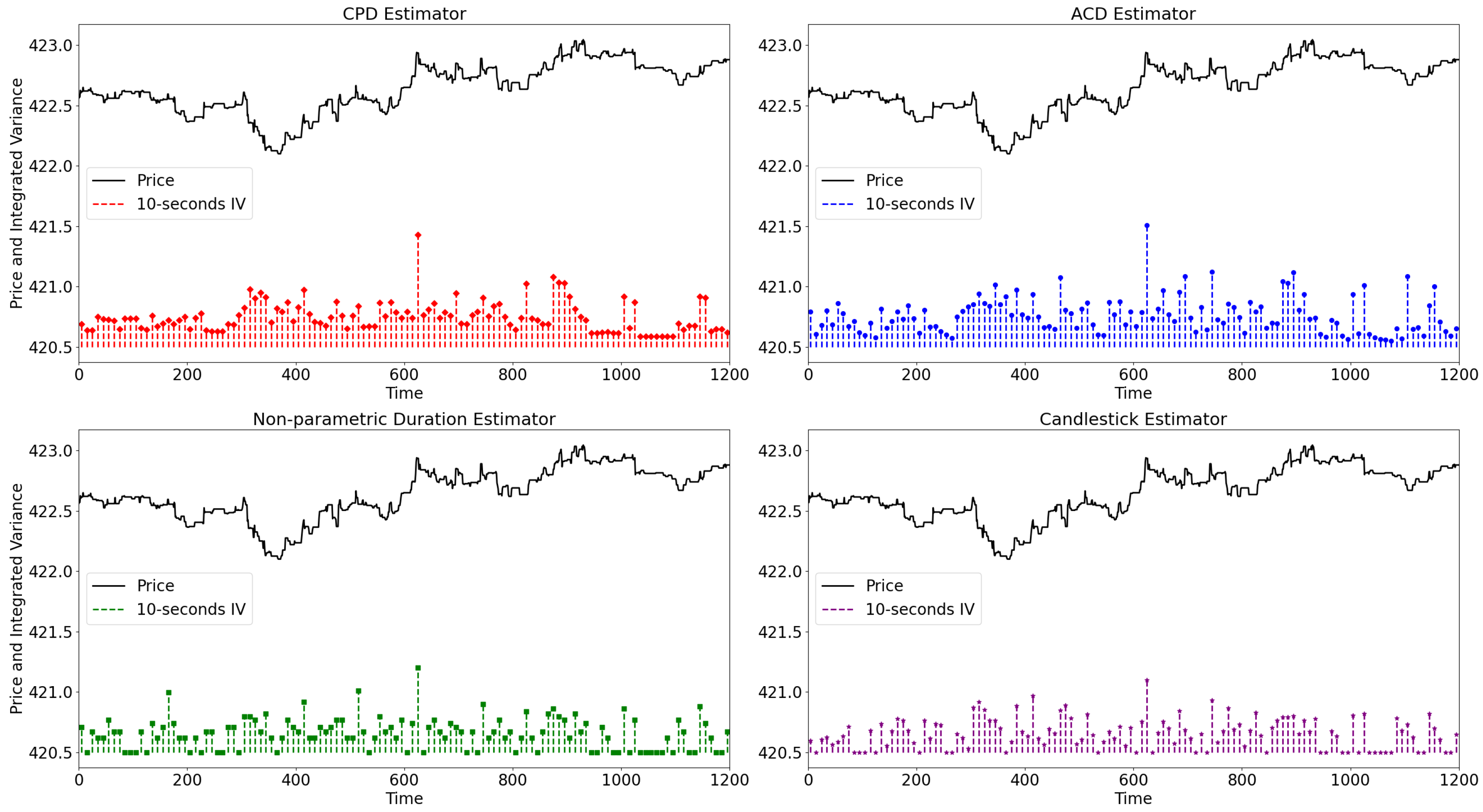
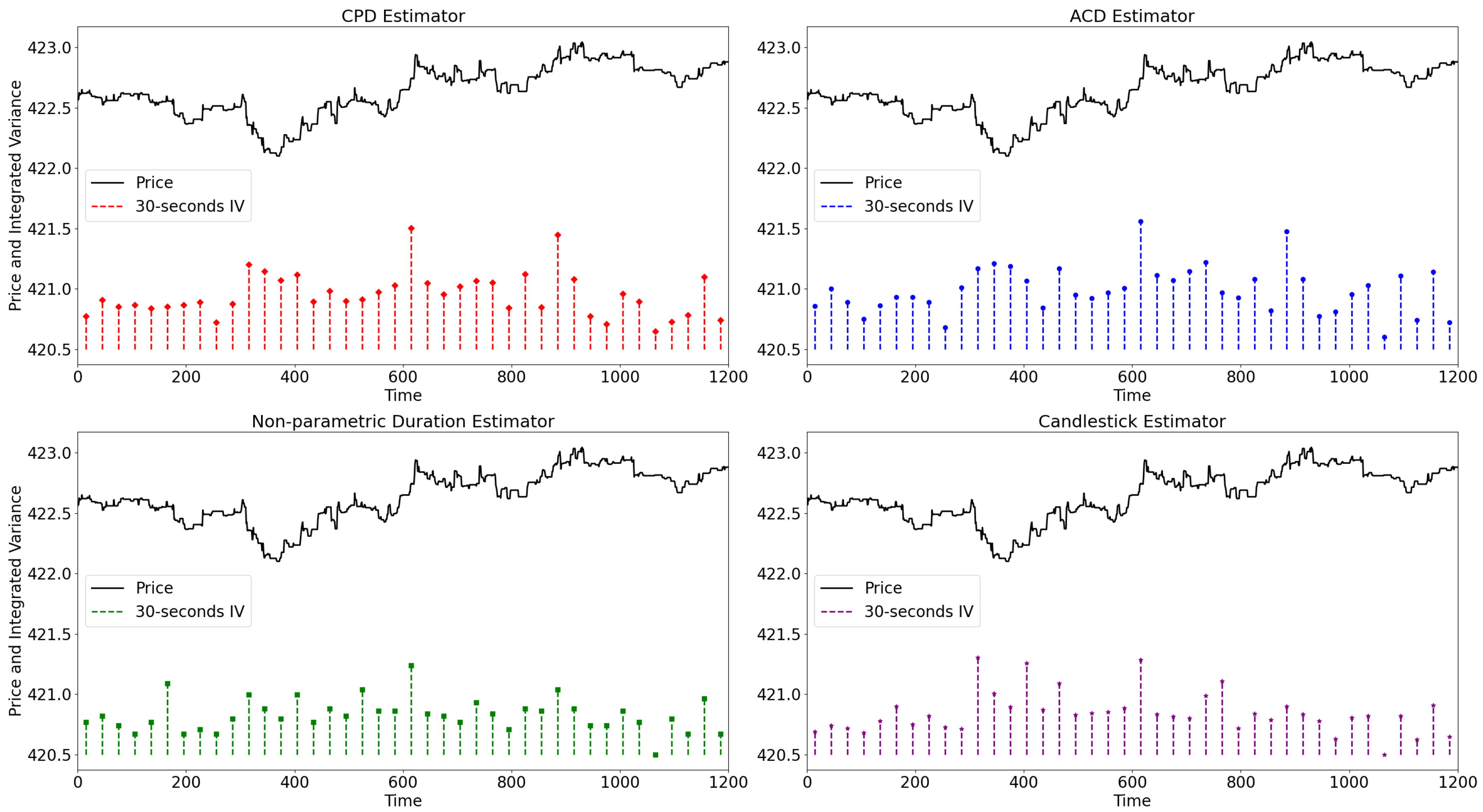
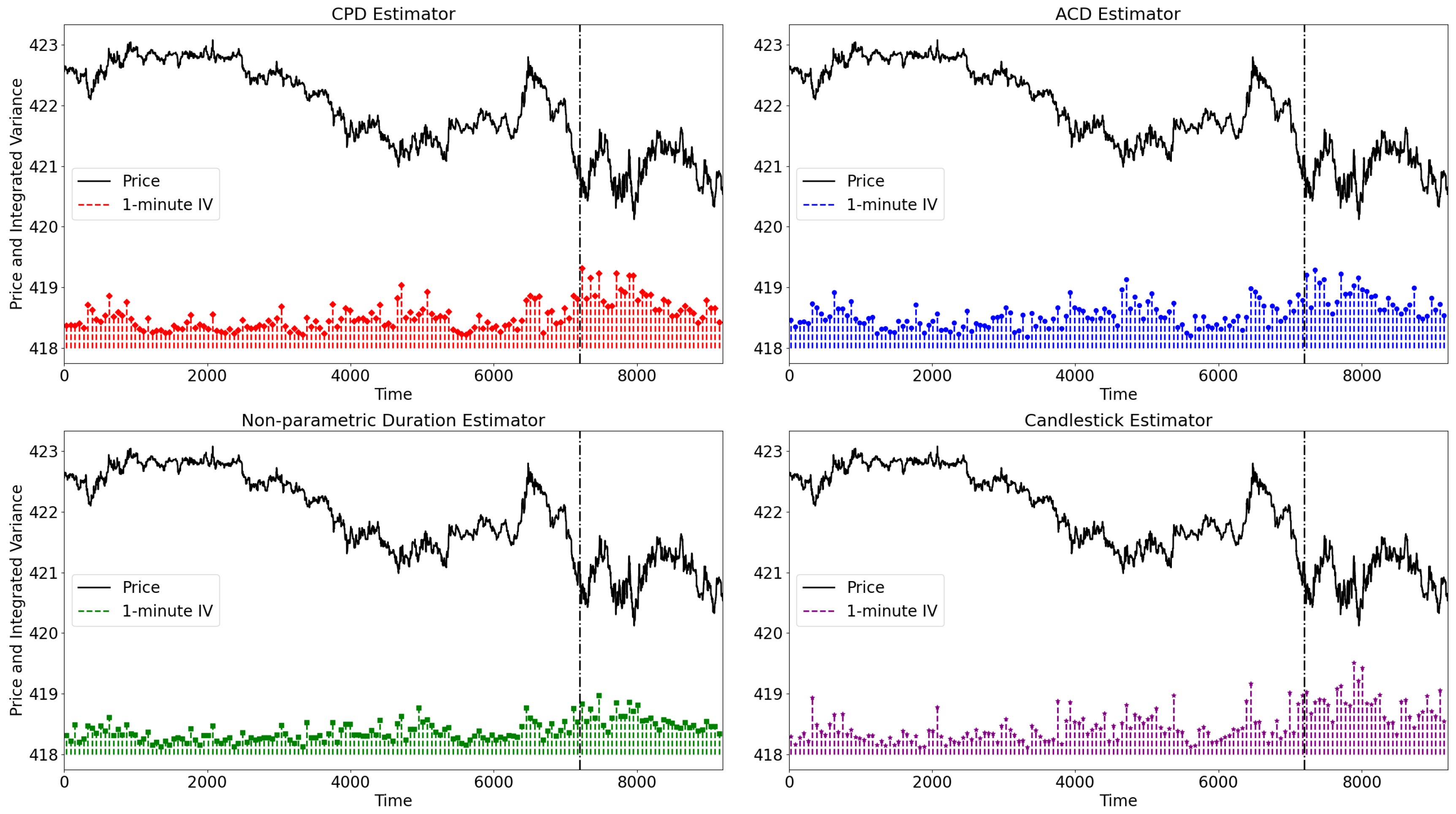
4.3. Integrated Variance Measurement
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Supplementary EM Steps
Appendix A.1. Expected Likelihood
Maximization and the Update of Parameters
Appendix B. The Posterior Distribution of λt in EM
Appendix B.1. Forward–Backward Filter
- Forward Filter
- Backward Filter
- Combination (Forward–Backward Algorithm)
Appendix B.2. Calculation Steps of the Posterior Intensity Distribution
- The conditional densities are Gamma distributions, i.e., .
- The next thing is to calculate . By the foward–backward filter part, we can derive that , andwhere is defined as
- The normalizing constants are obtained in closed form due to conjugacy:
- The forward probabilities and backward probabilities are computed recursively, which in turn yield and hence the posterior .
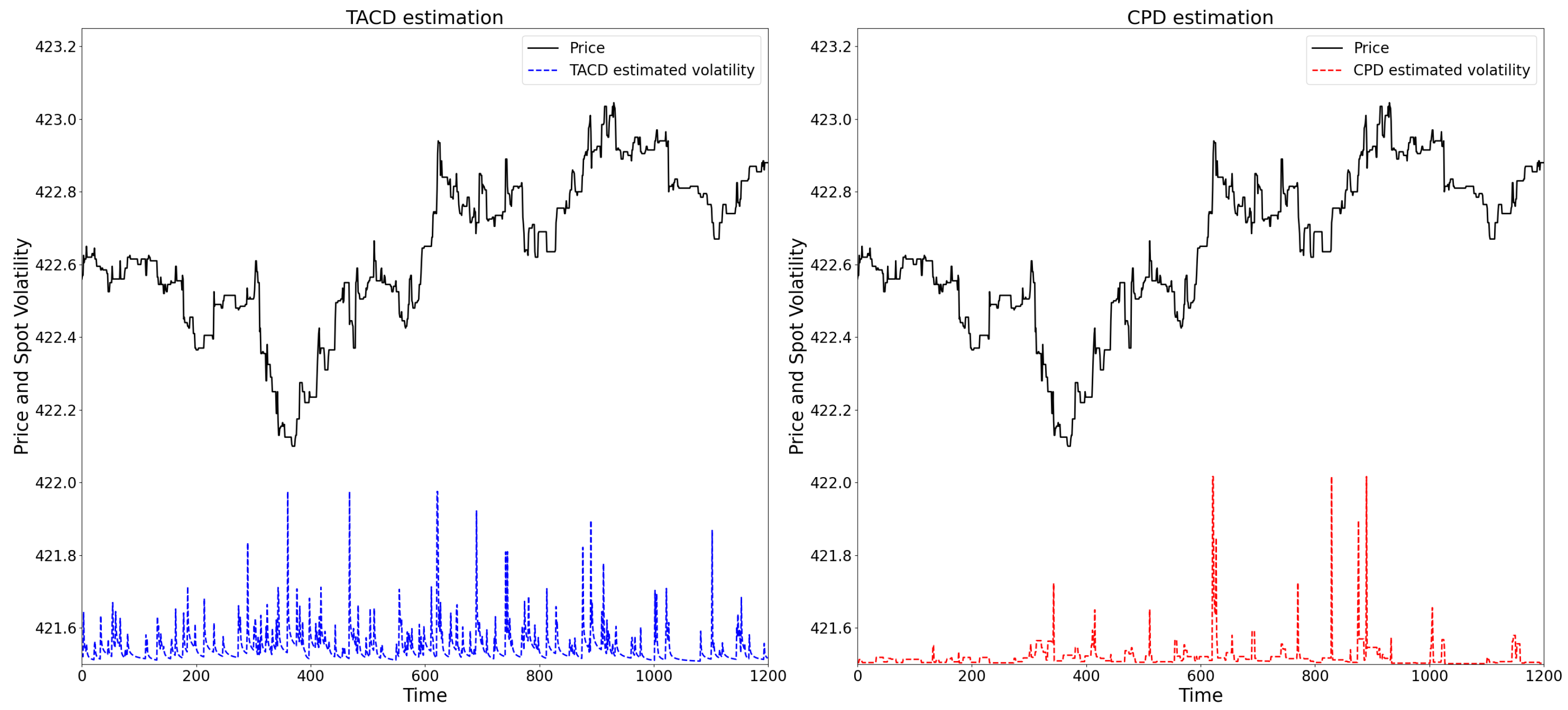
Appendix C. Comparison with TACD Model


| 1 | These approaches build on earlier work by Gallant et al. (1999) and Alizadeh et al. (2002), who introduced range-based volatility estimators for modeling and forecasting time-varying volatility. |
| 2 | Boston Marathon bombing occured on 15 April 2013. https://en.wikipedia.org/wiki/Boston_Marathon_bombing (accessed on 8 July 2025). |
References
- Admati, A. R., & Pfleiderer, P. (1988). A theory of intraday patterns: Volume and price variability. The Review of Financial Studies, 1(1), 3–40. [Google Scholar] [CrossRef]
- Alizadeh, S., Brandt, M. W., & Diebold, F. X. (2002). Range-based estimation of stochastic volatility models. The Journal of Finance, 57(3), 1047–1091. [Google Scholar]
- Andersen, T. G., & Bollerslev, T. (1998). Answering the skeptics: Yes, standard volatility models do provide accurate forecasts. International Economic Review, 39(4), 885–905. [Google Scholar] [CrossRef]
- Andersen, T. G., Bollerslev, T., Diebold, F. X., & Labys, P. (2003). Modeling and forecasting realized volatility. Econometrica, 71(2), 579–625. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O. E., & Shephard, N. (2002). Econometric analysis of realized volatility and its use in estimating stochastic volatility models. Journal of the Royal Statistical Society Series B: Statistical Methodology, 64(2), 253–280. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O. E., & Shephard, N. (2004). Power and bipower variation with stochastic volatility and jumps. Journal of Financial Econometrics, 2(1), 1–37. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O. E., & Shiryaev, A. N. (2015). Change of time and change of measure. World Scientific Publishing Company. [Google Scholar]
- Bauwens, L., & Giot, P. (2000). The logarithmic ACD model: An application to the bid-ask quote process of three NYSE stocks. Annales d’Economie et de Statistique, 60, 117–149. [Google Scholar]
- Bollerslev, T., Li, J., & Li, Q. (2024). Optimal nonparametric range-based volatility estimation. Journal of Econometrics, 238(1), 105548. [Google Scholar] [CrossRef]
- Box, G. E., & Tiao, G. C. (1975). Intervention analysis with applications to economic and environmental problems. Journal of the American Statistical association, 70(349), 70–79. [Google Scholar]
- Cho, D. C., & Frees, E. W. (1988). Estimating the volatility of discrete stock prices. The Journal of Finance, 43(2), 451–466. [Google Scholar] [CrossRef]
- Daley, D. J., & Vere-Jones, D. (2003). An introduction to the theory of point processes: Volume I: Elementary theory and methods. Springer. [Google Scholar]
- Easley, D., Engle, R. F., O’Hara, M., & Wu, L. (2008). Time-varying arrival rates of informed and uninformed trades. Journal of Financial Econometrics, 6(2), 171–207. [Google Scholar] [CrossRef]
- Easley, D., Hvidkjaer, S., & O’hara, M. (2002). Is information risk a determinant of asset returns? The Journal of Finance, 57(5), 2185–2221. [Google Scholar] [CrossRef]
- Easley, D., & O’hara, M. (1992). Time and the process of security price adjustment. The Journal of Finance, 47(2), 577–605. [Google Scholar] [CrossRef]
- Engle, R. F., & Russell, J. R. (1998). Autoregressive conditional duration: A new model for irregularly spaced transaction data. Econometrica, 66(5), 1127–1162. [Google Scholar] [CrossRef]
- Gallant, A. R., Hsu, C.-T., & Tauchen, G. (1999). Using daily range data to calibrate volatility diffusions and extract the forward integrated variance. Review of Economics and Statistics, 81(4), 617–631. [Google Scholar] [CrossRef]
- Gerhard, F., & Hautsch, N. (2002). Volatility estimation on the basis of price intensities. Journal of Empirical Finance, 9(1), 57–89. [Google Scholar] [CrossRef]
- Glosten, L. R., & Milgrom, P. R. (1985). Bid, ask and transaction prices in a specialist market with heterogeneously informed traders. Journal of Financial Economics, 14(1), 71–100. [Google Scholar] [CrossRef]
- Hautsch, N. (2011). Econometrics of financial high-frequency data. Springer Science & Business Media. [Google Scholar]
- Hong, S. Y., Nolte, I., Taylor, S. J., & Zhao, X. (2023). Volatility estimation and forecasts based on price durations. Journal of Financial Econometrics, 21(1), 106–144. [Google Scholar] [CrossRef]
- Hujer, R., Vuletic, S., & Kokot, S. (2002). The markov switching acd model (Tech. Rep.). Working paper series: Finance & Accounting. Johann Wolfgang Goethe-Universität Frankfurt am Main, Fachbereich Wirtschaftswissenschaften. [Google Scholar]
- Lai, T. L., Liu, H., & Xing, H. (2005). Autoregressive models with piecewise constant volatility and regression parameters. Statistica Sinica, 15(2), 279–301. [Google Scholar]
- Li, J., Wang, D., & Zhang, Q. (2024). Reading the candlesticks: An OK estimator for volatility. Review of Economics and Statistics, 106(4), 1114–1128. [Google Scholar] [CrossRef]
- Li, Z., & Xing, H. (2022). High-frequency quote volatility measurement using a change-point intensity model. Mathematics, 10(4), 634. [Google Scholar] [CrossRef]
- Tse, Y.-K., & Yang, T. T. (2012). Estimation of high-frequency volatility: An autoregressive conditional duration approach. Journal of Business & Economic Statistics, 30(4), 533–545. [Google Scholar] [CrossRef]
- Zhang, M. Y., Russell, J. R., & Tsay, R. S. (2001). A nonlinear autoregressive conditional duration model with applications to financial transaction data. Journal of Econometrics, 104(1), 179–207. [Google Scholar] [CrossRef]



| Panel A: Message File | |||||||
| Time (s) | Event Type | Order ID | Size | Price | Direction | ||
| 34,209.630122 | 1 | 10962867 | 100 | 426.79 | −1 | ||
| 34,209.630453 | 4 | 10962867 | 44 | 426.79 | −1 | ||
| 34,209.630561 | 4 | 10962867 | 56 | 426.79 | −1 | ||
| 34,209.630623 | 1 | 10962881 | 100 | 426.69 | 1 | ||
| 34,209.633680 | 1 | 10962942 | 100 | 426.79 | −1 | ||
| Panel B: Order Book File | |||||||
| Ask Price 1 | Ask Size 1 | Bid Price 1 | Bid Size 1 | Ask Price 2 | Ask Size 2 | Bid Price 2 | Bid Size 2 |
| 426.79 | 100 | 426.67 | 100 | 426.80 | 100 | 426.62 | 12 |
| 426.79 | 56 | 426.67 | 100 | 426.80 | 100 | 426.62 | 12 |
| 426.80 | 100 | 426.67 | 100 | 426.95 | 100 | 426.62 | 12 |
| 426.80 | 100 | 426.69 | 100 | 426.95 | 100 | 426.67 | 100 |
| 426.79 | 100 | 426.69 | 100 | 426.80 | 100 | 426.67 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Xing, H.; Wang, Y. Spot Volatility Measurement Using a Change-Point Duration Model in the High-Frequency Market. Int. J. Financial Stud. 2025, 13, 186. https://doi.org/10.3390/ijfs13040186
Li Z, Xing H, Wang Y. Spot Volatility Measurement Using a Change-Point Duration Model in the High-Frequency Market. International Journal of Financial Studies. 2025; 13(4):186. https://doi.org/10.3390/ijfs13040186
Chicago/Turabian StyleLi, Zhicheng, Haipeng Xing, and Yan Wang. 2025. "Spot Volatility Measurement Using a Change-Point Duration Model in the High-Frequency Market" International Journal of Financial Studies 13, no. 4: 186. https://doi.org/10.3390/ijfs13040186
APA StyleLi, Z., Xing, H., & Wang, Y. (2025). Spot Volatility Measurement Using a Change-Point Duration Model in the High-Frequency Market. International Journal of Financial Studies, 13(4), 186. https://doi.org/10.3390/ijfs13040186






