A Component Expected Shortfall Approach to Systemic Risk: An Application in the South African Financial Industry

Abstract

The accelerated growth and interconnectedness of financial institutions and movement towards products and activities outside the regulatory purview have been met with huge concerns. South Africa is one of the emerging economies that this conundrum has beset. Any potential instability in the financial sector likely poses insurmountable consequences and unprecedented government intervention, especially given that the country currently has no deposit insurance scheme. Although it is easy to justify the channels through which banks contribute to destabilising financial markets, it remains a controversial issue for insurers and other non-banking institutions. This study aims to empirically quantify the contribution of banks and insurers to aggregate the systemic risk of their respective industries by employing the component expected shortfall (CES). The CES is a robust quantitative systemic risk measure that allows for a comprehensive assessment of systemic risk by considering the contributions of individual financial components. Our findings demonstrate that the rankings from the CES framework are closely aligned with the regulatory D-SIB surcharges of the banking entities included in the study. The close alignment of both approaches is primarily due to the consideration of the size of an institution, amongst other factors.

1. Introduction

Financial services play a pivotal role in fostering sustained economic growth and development, with the banking sector standing out as a critical component. Denis and Negotei (2018) contend that, in the aftermath of the global financial crisis of 2007–2009, the banking sector emerged as the most fragile and contagion-prone sector in all free-market economies. Consequently, governments often find themselves compelled to support faltering financial institutions to shield the broader economy (Brunnermeier and Cheridito 2019). Understandably, the banking system and the broader financial sector are susceptible to generating risks that can rapidly affect other sectors of the economy. Since the onset of the global financial crisis, efforts have been made to address this issue within the macro-prudential policy framework.

One noteworthy concept that has gained prominence in the realm of macro-prudential policy is that of systemically important financial institutions (SIFI). However, despite ongoing endeavours to pinpoint these SIFIs, consensus on the definition of systemic risk remains elusive. The absence of a shared definition of systemic risk has tangible consequences, exemplified by the diverse range of techniques developed to quantify it empirically. Drawing lessons from the global financial crisis, many countries, including South Africa, have implemented sweeping regulatory changes under the banner of macro-prudential policy. South Africa introduced the Twin Peaks system to continually enhance the regulatory framework (Financial Services Board 2018). While much attention has been focused on domestic systemically important banks, the insurance sector also raises important questions regarding financial stability. Unlike the banking industry, justifying the insurance sector’s contribution to systemic risk is less straightforward, as many characteristics, such as bank runs, contagion, and externalities, are not commonly found in insurers’ balance sheets.

Nevertheless, as indicated by the International Association of Insurance Supervisors (IAIS 2019) and several studies (Eling and Pankoke 2014; Cummins and Weiss 2013; Kaserer and Klein 2019), traditional insurance activities are generally not considered a source of systemic risk. However, insurers engaged in non-traditional activities present a distinct case. The Financial Stability Board (FSB) and IAIS have devised frameworks for identifying systemically important insurers, emphasising interconnectedness and non-traditional insurance activities. In South Africa, regulators are working on a framework for managing systemic risk effectively. Several studies have been conducted in the country to contribute to this complex task (Foggitt et al. 2017; Manguzvane and Mwamba 2019; Chatterjee and Sing 2021). While limited literature exists on quantifying systemic risk within the insurance sector, existing studies have employed systemic risk measures that cannot be aggregated to determine overall systemic risk in a specific financial industry.

This paper seeks to contribute to the empirical discourse on identifying systemically important financial institutions. While central banks’ use of the Basel Committee on Bank Supervision’s (BCBS) indicator-based approach is a valuable addition to macroprudential policy objectives, it may not be readily adaptable to reflect changing economic conditions. Consequently, this study’s primary objective is to quantify the systemic risk contributions of banks and insurers to their respective industries in a manner that allows for quick adjustments in response to evolving economic circumstances. We achieve this by employing the component expected shortfall (CES) technique of Banulescu and Dumitrescu (2015), which synthesises the too-big-to-fail and too-interconnected-to-fail theorems. While the MES heavily emphasises interconnectedness but disregards firm size, and the SRISK relies on data constancy assumptions by mixing high-frequency and low-frequency data, the CES accounts for the firm size and relies solely on market-based data without making data-related assumptions. We apply the CES methodology to a set of banks and insurers to identify the most systemically risky entities, enabling us to pinpoint contributions to systemic risk at specific times. Our findings reveal a close alignment between the rankings from the CES framework and the regulatory Domestic Systematically Important Banks (D-SIB) surcharge imposed on the banking entities included in our study. One key policy implication arising from our findings is that most systemic risk is concentrated within a limited number of institutions. Thus, imposing stricter regulations on these select entities has the potential to enhance overall financial system stability. The remainder of this study is organised as follows: Section 2 reviews the existing literature on systemic risk; Section 3 presents the methodology employed; Section 4 describes the data used and presents the empirical results; and finally, Section 5 provides the conclusion and policy recommendations.

2. Literature Review

2.1. Theoretical Framework

Systemic risk is a significant concept in finance, economics, and risk management. The definition of systemic risk is still debatable as academics and policymakers grapple with its heterogeneous nature. To understand systemic risk, it is essential to explore its conceptual framework. Even though systemic risk existed before the global financial crisis, the extent of its negative consequences has prompted academics to explore its nature and ways to mitigate it. Several studies on systemic risk place importance on the wide scope of its features. Dow (2000) explains that moral hazard is the most common feature of systemic risk.

Systemic risk could be caused by financial institutions that engage in excessively risky activities chasing short-term profits, leading to an inability to respond to drastic changes in the macroeconomy. Bisias et al. (2012) conclude that when defining systemic risk, emphasis is placed on aspects such as imbalances, the loss of confidence, common exposures, adverse effects on the general economy, information asymmetry, loopback effects, asset bubbles, contagion, and negative externalities. According to Eijffinger (2012), regardless of the definition used to explain systemic risk, the concept is basically about the malfunction of one or multiple parts of the system that eventually cause harm to the whole system. In this study, we adopt this approach to examine system risk empirically. Systemic risk varies considerably and factors in an extensive range of characteristics (Smaga 2014). Smaga (2014) further explains that the source of systemic risk need not just be a financial institution but could be a financial instrument, the financial market, or the whole system. This means that the financial system could act as both the source and the channel through which systemic risk is transmitted. According to Allen and Carletti (2013), there are four types of systemic risks: “(i) panics—banking crises due to multiple equilibria; (ii) banking crises due to asset price falls; (iii) contagion; and (iv) foreign exchange mismatches in the banking system.”

Moreover, systemic risk can be broken down into two dimensions: cross-sectional and time. The cross-sectional dimension entails the distribution of systemic risk across the whole financial system at a particular point in time, whereas the time dimension shows how systemic risk builds up over time; this could include the collective behaviour of financial institutions and feedback effects.

2.2. Empirical Literature

The literature is awash with studies that attempt to quantify systemic risk in the financial sector. Some researchers have focused on employing market-based measures of systemic risk. Tobias and Brunnermeier (2016) apply the Conditional Value at Risk (CoVaR) methodology to quantify systemic risk in the US financial system. The CoVaR model has since been updated by several studies, such as Girardi and Ergün (2013), who use GARCH models rather than quantile regression. Reboredo and Ugolini (2015) apply the Copula-based CoVaR to measure system risk in the Spanish banking sector. Employing similar data as in Tobias and Brunnermeier (2016), Acharya et al. (2012) develop the marginal expected shortfall to measure systemic risk. Coleman et al. (2018) examine the contribution of Canadian banks and insurers to systemic risk through the application of Brownlees and Engle’s (2017) SRSIK measure. Naeem et al. (2022) apply a non-linear process in the form of artificial neural networks to model systemic risk for 10 industries in the US and show that the manufacturing sector is the biggest contributor to systemic risk. Kyoud et al. (2023) adjust the original CoVaR using quantile regression neural networks to quantify systemic risk in Morocco’s banking sector. Their findings show a significant increase in systemic risk during the COVID-19 pandemic. While the CoVaR of Tobias and Brunnermeier (2016) is based on quantile regression, Rahman et al. (2022) extend it using copulas at different frequencies and show that banks contribute more to systemic risk than other financial institutions.

In light of the multivariate nature of systemic risk, the literature has also devoted considerable attention to techniques based on the structural properties of financial systems, such as network analysis. The network approach employed in analysing financial systems is based on the rapid integration of financial markets. Several studies have taken the network approach to modelling systemic risk to identify risk spillover channels. Baumöhl et al. (2022) propose a new measure to quantify systemic risk through cross-quantilogram and network analysis. These authors can identify the banking sector’s large transmitters and receivers of risk. Wang et al. (2022) construct a dynamic tail risk approach to quantify systemic risk contributions by stock markets and show that the measure is robust to changing economic conditions. Similarly, Zhang et al. (2021) combine copulas and graph theory to assess systemic risk contributions in China. Their model can analyse systemic risk in both a static and dynamic manner. Several other studies have used the network approach (see Hasse 2022; Billio et al. 2012). Chen et al. (2014) quantify system risk in the banking and insurance industries by applying distress insurance premiums (DIP) created by Huang et al. (2009). They supplement the DIP with Granger causality tests and find that distressed banks significantly negatively affect insurers. Our work is closest to that of Chen et al. (2014). The authors quantify the systemic risk contribution of banks and insurers to system risk using the distress insurance premium. Our study adopts a different technique from that of Chen et al. (2014) in the form of the component expected shortfall. The DIP quantifies the premium borrowers should pay to reimburse investors for the amplified credit risk related to their possibility of defaulting. The CES analyses the additional risk to the system associated with a particular firm. It measures the potential losses conditional on substantial market distress. The CES can be easily implemented for regulatory assessment monitoring and mitigating systemic risk in the financial system.

3. Methodology

This section presents the CES, the methodology used in identifying domestic systemically important banks and insurers in this study. Let $X_{i,t}$ represent the return of institution $i$ and $X_{m,t}$ the return of the entire market (bank or insurance) at time $t$. Since Value at Risk (VaR) is not a coherent risk measure, the expected shortfall (ES) of the market, which is used to measure the risk of the market, is given by:

$${ES}_{m,t}=E_{t-1}\left(X_{m,t}\right|X_{m,t}\le Z_t)$$

(1)

where $Z_t$ is a predefined threshold, such as the VaR.

The return of the market can be defined as a value-weighted average of the individual institutions and is given by

$$X_{m,t}={\sum }_{i=1}^n{w}_i{X}_{i,t}$$

(2)

where $w_i$ is institution i’s relative market capitalisation. Equation (1) can also be rewritten to take into account Equation (2) as follows:

$${ES}_{m,t}=E_{t-1}\left({\sum }_{i=1}^n{w}_i{X}_{i,t}|X_{m,t}\le Z_t\right)={\sum }_{i=1}^n{w}_{i,t}{E}_{t-1}\left(X_{i,t}\right|X_{m,t}\le Z_t)$$

(3)

One commonly used technique to measure systemic risk is the marginal expected shortfall (MES). The MES relates to the derivative of the market’s ES with respect to the institution $i$’s relative market capitalisation by the equation:

$${MES}_{i,t}=\frac{\partial {ES}_{m,t}}{\partial w_i}=E_{t-1}(X_{i,t}|X_{m,t}\le Z_t)$$

(4)

The MES measures the expected return of institution $i$ given that the return of the market has crossed the threshold $Z_t$.

In this study, we go beyond the MES by adopting the CES of Banulescu and Dumitrescu (2015). The CES represents the portion of aggregate risk (ES) that is due to the i^th institution and is obtained as follows:

$${CES}_{i,t}=\frac{\partial {ES}_{m,t}}{\partial w_i}=w_{i,t}{E}_{t-1}(X_{i,t}|X_{m,t}\le Z_t)=w_{i,t}{MES}_{i,t}$$

(5)

The ${CES}_{i,t}$ measures the contribution of institution $i$ to the aggregate risk at time $t,$ with institutions that have a larger ${CES}_{i,t}$ contributing more to systemic risk.

While we cannot aggregate the MES of different institutions, that is not the case with the CES. We can add the CES of different institutions at a point in time and obtain the aggregate risk of the system. Thus, it is also possible to determine the proportion of risk that can be attributed to individual institutions. The percentage CES is obtained as follows:

$${CES}_{i,t}=\frac{C{ES}_{i,t}}{{ES}_{m,t}}\times 100$$

(6)

Brownlees and Engle (2012) extended the MES of Acharya et al. (2012) using a bivariate GARCH model for the return of institution $i$ and the market. Letting $X_t={\left(X_{i,t},X_{m,t}\right)}^{\mathrm{T}}$, the bivariate model can be represented as follows as follows:

$$X_t=H_t^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{\epsilon }_t$$

(7)

where ${\epsilon }_t$ is the vector of independent and identically distributed shocks. $H_t$ is the dynamic conditional covariance matrix denoted as follows:

$$H_t=\left[\begin{array}{cc}{\sigma }_{m,t}^2& {\sigma }_{m,t}{\sigma }_{i,t}{\rho }_{i,t}\\ {\sigma }_{m,t}{\sigma }_{i,t}{\rho }_{i,t}& {\sigma }_{i,t}^2\end{array}\right]$$

(8)

where ${\sigma }_{m,t}^2$ and ${\sigma }_{i,t}^2$ are the conditional standard deviations for the system and the institution, respectively, and ${\rho }_{i,t}$ is the time-varying conditional correlation. The returns of the institution and the system can also be rewritten as follows:

$$\begin{gathered} X_{i,t}={\mu }_{i,t}+{\sigma }_{i,t}⨀{\epsilon }_{i,t} \\ {X}_{m,t}={\mu }_{m,t}+{\sigma }_{i,t}{\rho }_{i,t}{\epsilon }_{i,t}+{\sigma }_{m,t}+\sqrt{1}-{\rho }_i^2{\eta }_{m,t} \end{gathered}$$

(9)

The conditional volatilities are estimated using the GJR-GARCH model, and the conditional correlation is modelled using a diagonal conditional correlation GARCH. The CES can then be defined as follows:

$$CES={w_{i,t}E}_{t-1}({\sigma }_{i,t}{\rho }_{i,t}{\epsilon }_{i,t}+{\sigma }_{m,t}+\sqrt{1}-{\rho }_i^2{\eta }_{m,t}|{\sigma }_{m,t}{\epsilon }_{m,t}\le Z_t)$$

(10)

Equation (6) can be further simplified as follows:

$$MES={w_{i,t}\sigma }_{i,t}{\rho }_{i,t}{E}_{t-1}{(\epsilon }_{m,t}|{\epsilon }_{m,t}\le k_t+{\sigma }_{i,t}+\sqrt{1}-{\rho }_i^2)$$

(11)

where $k_t=\frac{C_t}{{\sigma }_{m,t}}$.

4. Results

This section will initially describe the dataset included in this study and present the empirical results and analysis of the application of the CES methodology to a sample of institutions in the South African financial system.

4.1. Data

Daily data is used in the iterative application of the CES methodology on a sample of two financial services industries, namely the banking and insurance industries. The panel dataset includes share prices and market capitalisation data from a sample of six banking institutions and eight insurance companies (six life and two non-life), as listed in

Table 1. List of institutions and respective sectors.

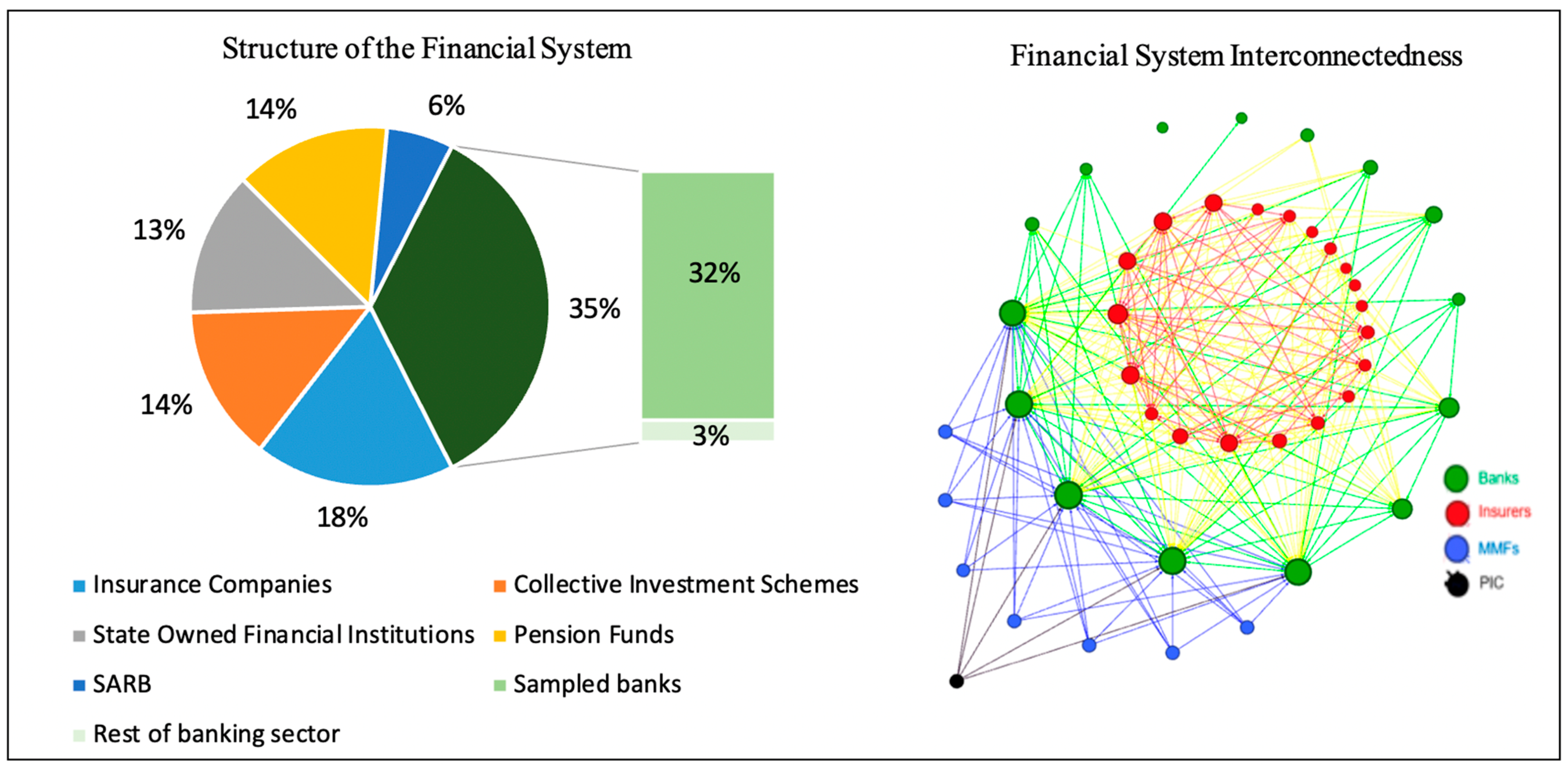
Banks	Insurance
	Life	Non-LIFE
Absa Limited (ABG)	Old Mutual Limited (OML)	Santam Limited (SNT)
Capitec Bank Limited (CPI)	Discovery Limited (DSY)	Conduit Capital (CND)
FirstRand Limited (FSR)	Sanlam Limited (SLM)
Investec Limited (INL)	Momentum Metropolitan Holdings Limited (MTM)
Nedbank Limited (NED)	Liberty Holdings Limited (LBH)
Standard Bank Group Limited (SBK)	Clientele Limited (CLI)

() iNet McGregor BFA tickers.

below.

The daily data extracted from both iNet McGregor BFA and Thomson Reuters include 4793 daily observations for each institution spanning over 19 years from February 2002 to April 2021, including several peaks and troughs of the South African economy and the stock market.

The structure of South Africa’s financial system is both sizable and complex, with banks and insurance companies comprising a large proportion of the financial system, as illustrated in Figure 1. According to the International Monetary Fund (IMF 2022), the size of banks’ balance sheets approximates more than twice the size of South Africa’s GDP, and most of the assets are held by a small number of banking institutions1. Similarly, the insurance industry’s assets exhibit a high level of concentration.

Descriptive Statistics

The share prices are transformed into daily logarithmic returns for each firm in the panel dataset.

Table 2. Descriptive statistics of financial institutions’ returns.

	Mean	Standard Deviation	Minimum	Maximum	Skewness	Kurtosis	Observation
Banks
ABG	0.03	2.03	−16.89	16.96	−0.05	5.75	4793
CPI	0.14	2.64	−32.74	48.95	1.17	42.89	4793
FSR	0.04	2.05	−16.06	12.91	−0.18	4.05	4793
INL	0.01	2.29	−54.56	16.76	−2.89	5.56	4793
NED	0.00	2.07	−17.17	12.81	−0.17	5.56	4793
SBK	0.03	1.97	−14.55	11.70	−0.06	3.61	4793
Insurers
OML	0.01	2.11	−17.61	14.65	−0.15	6.54	4793
DSY	0.06	1.90	−16.37	16.40	−0.24	7.82	4793
SLM	0.04	1.90	−15.39	11.87	−0.34	3.88	4793
MTM	0.02	1.94	−19.13	12.20	−0.29	6.18	4793
LBH	0.00	1.81	−16.22	22.43	0.16	12.43	4793
CLI	0.01	2.64	−28.77	24.78	−0.44	17.18	3232
SNT	0.04	1.67	−20.97	11.81	−0.34	10.44	4793
CND	0.02	7.82	−138.63	142.71	0.01	84.42	4793

Source: authors’ own computation.

below displays the various moments of the daily returns of all the individual institutions included in the study over the sample period. The descriptive statistics across both industries conform to the stylised facts of high-frequency financial time series data. The daily returns are small, averaging close to zero. The daily minimum returns cluster around the three periods, mainly 2008, 2015, and 2020. Due to these extreme returns, daily asset returns are not normally distributed; they are heavy-tailed and non-symmetric. This is evident in many institutions’ excess kurtosis and negatively skewed returns.

4.2. Empirical Results

The primary objective of the study is to accurately identify the riskiest and domestic systemically important banks (D-SIB) and insurance (D-SII) institutions in the South African financial system by quantifying and ranking the institutions according to their contribution to the overall risk of their respective industries according to the CES methodology. The study focuses on three specific periods that coincide with peak market distress, namely: October 2008 (the Global Financial Crisis), December 2015 (the dismissal of the then Minister of Finance in South Africa), and March 2020 (onset of the COVID-19 pandemic). Following Salim and Daly (2021), the empirical results of the CES model are then benchmarked against existing D-SIB capital requirements imposed on designated financial institutions by the financial sector regulator.

The high-frequency nature of the CES and CES% metric allows for the identification of key contributors to systemic risk on a timely basis. Figure 2 presents the time series of the CES and CES% estimates for all banks considered in the study over the sample period. Leading up to the GFC, the CES values of South African banks were already trending above average, with values spiking in 2006 and 2007, indicating elevated levels of systemic risk. During the systemic event of 2008, the CES spiked even higher due to contagion on South African banks’ equity returns from the collapse in equity prices of financial institutions in advanced economies. From 2012 to 2015, the CES decreased and was at its lowest levels. In late 2015, the banks’ CES rose sharply due to the stock market fallout from the removal of the South African Minister of Finance. Systemic risk in the South African banking sector peaked in early 2020, at the onset of the COVID-19 pandemic, with South African banks’ equity returns experiencing extreme volatility.

Interestingly, an apparent distinction between the three tiers of contributors to systemic risk in the banking industry is noted. The first tier is Standard Bank and FirstRand; the second includes Absa and Nedbank; lastly, Capitec and Investec. The tiers observed are attributable to the market capitalisation dynamics in the South African banking industry.

A similar trend in peaks and troughs of CES estimates is observed for the insurance industry in Figure 3. Systemic risk in the insurance industry is mainly attributable to the life insurance constituents, primarily Old Mutual and Sanlam, with Discovery gaining prominence in the latter years. Old Mutual had a volatile and elevated CES in the early years relative to other crisis periods. Moreover, contrary to their insurance industry peers, Old Mutual registered its peak CES estimate in the 2008 GFC period. This is perhaps due to the entity’s international exposure experiencing difficulties during this period.

Table 3. Micro- vs. macroprudential rankings of banking institutions.

October 2008				December 2015				March 2020
Rank	CES	Rank	VaR	Rank	CES	Rank	VaR	Rank	CES	Rank	VaR
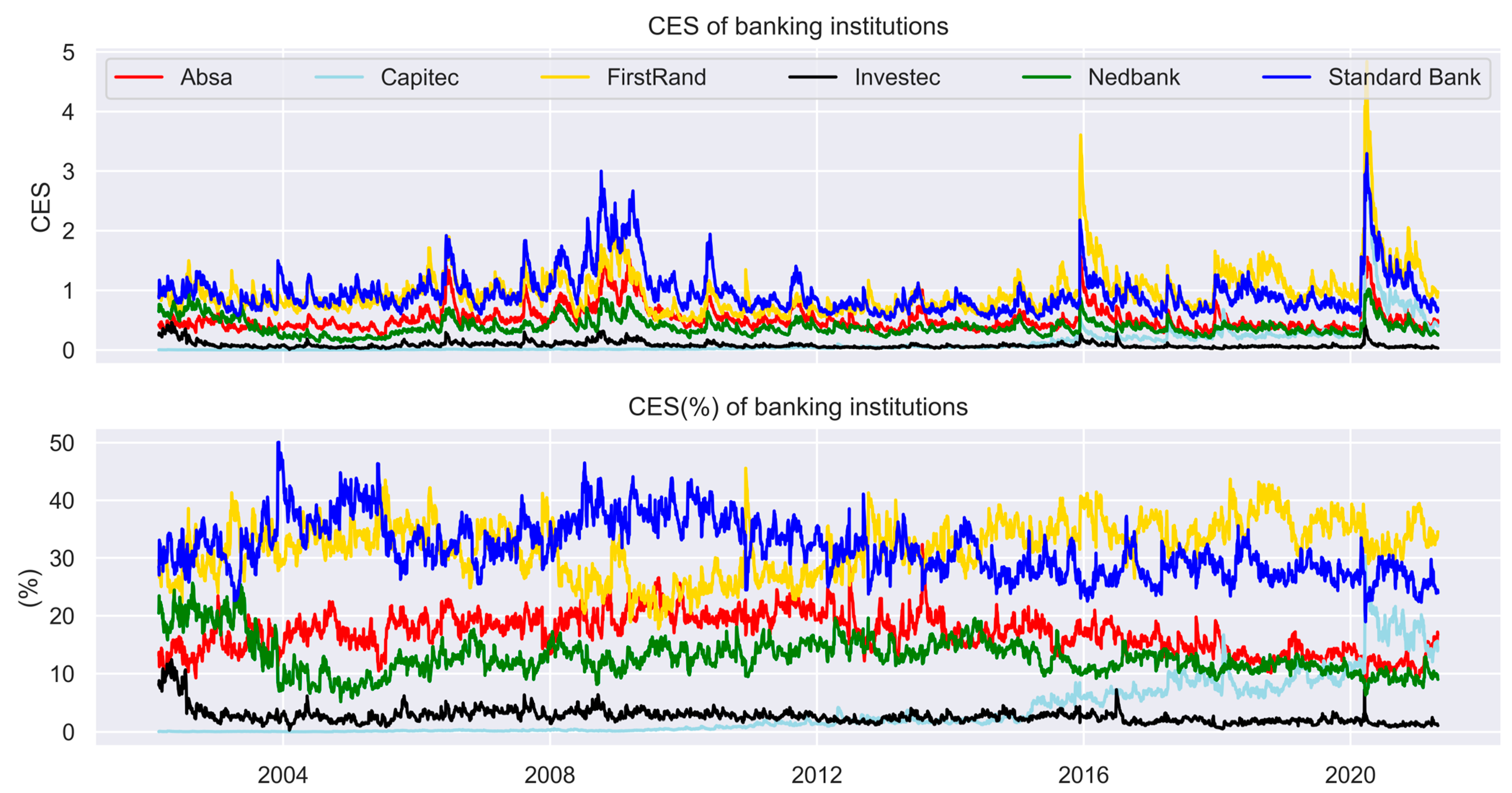
SBK	2.55 (39.7)	INL	8.06	FSR	2.21 (37.1)	FSR	6.07	FSR	2.89 (34.9)	INL	17.29
FSR	1.53 (23.8)	SBK	6.63	SBK	1.45 (25.8)	ABG	5.53	SBK	2.08 (26.3)	CPI	10.23
ABG	1.29 (20.0)	NED	6.28	ABG	1.00 (17.5)	SBK	5.42	CPI	1.68 (16.7)	NED	7.90
NED	0.79 (12.2)	ABG	6.09	NED	0.58 (10.2)	CPI	5.39	ABG	0.89 (11.1)	FSR	7.51
INL	0.26 (4.1)	FSR	5.81	CPI	0.53 (6.4)	INL	5.15	NED	0.63 (8.0)	ABG	7.45
CPI	0.01 (0.2)	CPI	4.07	INL	0.17 (3.1)	NED	4.26	INL	0.25 (2.9)	SBK	7.40

Source: authors’ own computation.

tabulates each bank’s CES and VaR estimates during selected crisis periods. The banks are ranked according to their monthly average contribution to the total systemic risk of the industry in periods of heightened market distress. This ranking is then compared to the VaR estimates and corresponding ranking.

The CES rankings differ during various periods of market distress. However, Standard Bank and FirstRand consistently feature in the top position, albeit in a different order. The two entities collectively contributed over 60% of the cumulative loss of the industry during periods of severe market distress. The rankings and identification of these two banks are consistent with several similar studies (Foggitt et al. 2017; Manguzvane and Mwamba 2019; Chatterjee and Sing 2021). Ranking stability is the key point the regulator uses to measure the SIB magnitude in the whole system (Salim and Daly 2021). Notably, Capitec’s systemic importance has increased in each sub-period, rising from being the least contributor during the 2008 Global Financial Crisis to the third-largest contributor to the industry’s aggregate loss by 2020. This captures major transformations for the bank, including acquiring a mercantile bank in 2019/2020. Contrasting the ranking of systemically important institutions from a macroprudential to a microprudential angle, Investec recorded the highest VaR estimates for two of the three periods of market turmoil. Similarly, Chatterjee and Sing (2021) find that relatively smaller banks in South Africa have a higher VaR.

In 2011, the BCBS issued the standard for the regulator’s assessment of global systemically important banks (BCBS 2013). The rationale for adopting additional policy measures for G-SIBs is based on the “negative externalities” (i.e., bankruptcies, unemployment, economic crises, and output losses) created by SIBs that current regulatory policies do not adequately address (BCBS 2013). The BCBS extended the framework to include guidelines for identifying domestic systemically important banks (D-SIBs). The local financial regulator, the South African Reserve Bank (SARB), largely adopted the D-SIB framework based on quantitative indicators such as asset size, connectivity, and substitutability, global activity, and complexity as a proxy of systemic importance (see Appendix A and Appendix B). The six banks included in this study are currently designated as SIFIs by the SARB and are classified as D-SIBs by the Prudential Authority (PA), which face a capital surcharge of between 0.5 and 0.25 percent set by the regulatory authority (Hesse and Miyajima 2022). The SARB issued Directive 4 on 27 August 2020, which requires banks to publicly disclose their D-SIB capital add-on in line with the Capital framework for South Africa based on the Basel III framework. The disclosure of the D-SIB capital add-on allows for comparing the size of D-SIB capital and the outcomes of the CES approach, as presented in

Table 4. Banking institutions: D-SIB capital add-on and CES, 2021.

Banks	D-SIB Capital Add-On Held in CET1 (%) *	CES **
Standard Bank	1.0	0.78 (25.08)
FirstRand	0.8	1.09 (34.77)
Capitec	0.5	0.5 (15.70)
Absa	0.5	0.41 (13.26)
Nedbank	0.5	0.31 (9.83)
Investec	0.25	0.04 (1.36)

In parentheses is the CES percentage; * 2021 Quarter 1 Pillar 3 disclosures; ** CES average for 2021. Source: authors’ own computation.

. Overall, the rankings from the CES framework are closely aligned with the regulatory D-SIB surcharges of the banking entities included in the study. The close alignment of both approaches is primarily due to the consideration of the size of an institution, amongst other factors. Differences may occur because the indicator approach is based on low-frequency and backward-looking accounting data as opposed to the high-frequency market-based approach offered by the CES. The outcomes of the benchmarking exercise and appreciation of disparities between approaches further reinforce the notion that market-based systemic risk measures can be utilised as complements to existing micro- and macroprudential toolkits.

Table 5. Micro- vs. macroprudential rankings of insurance institutions.

October 2008				December 2015				March 2020
	CES	Rank	VaR	Rank	CES	Rank	VaR	Rank	CES	Rank	VaR
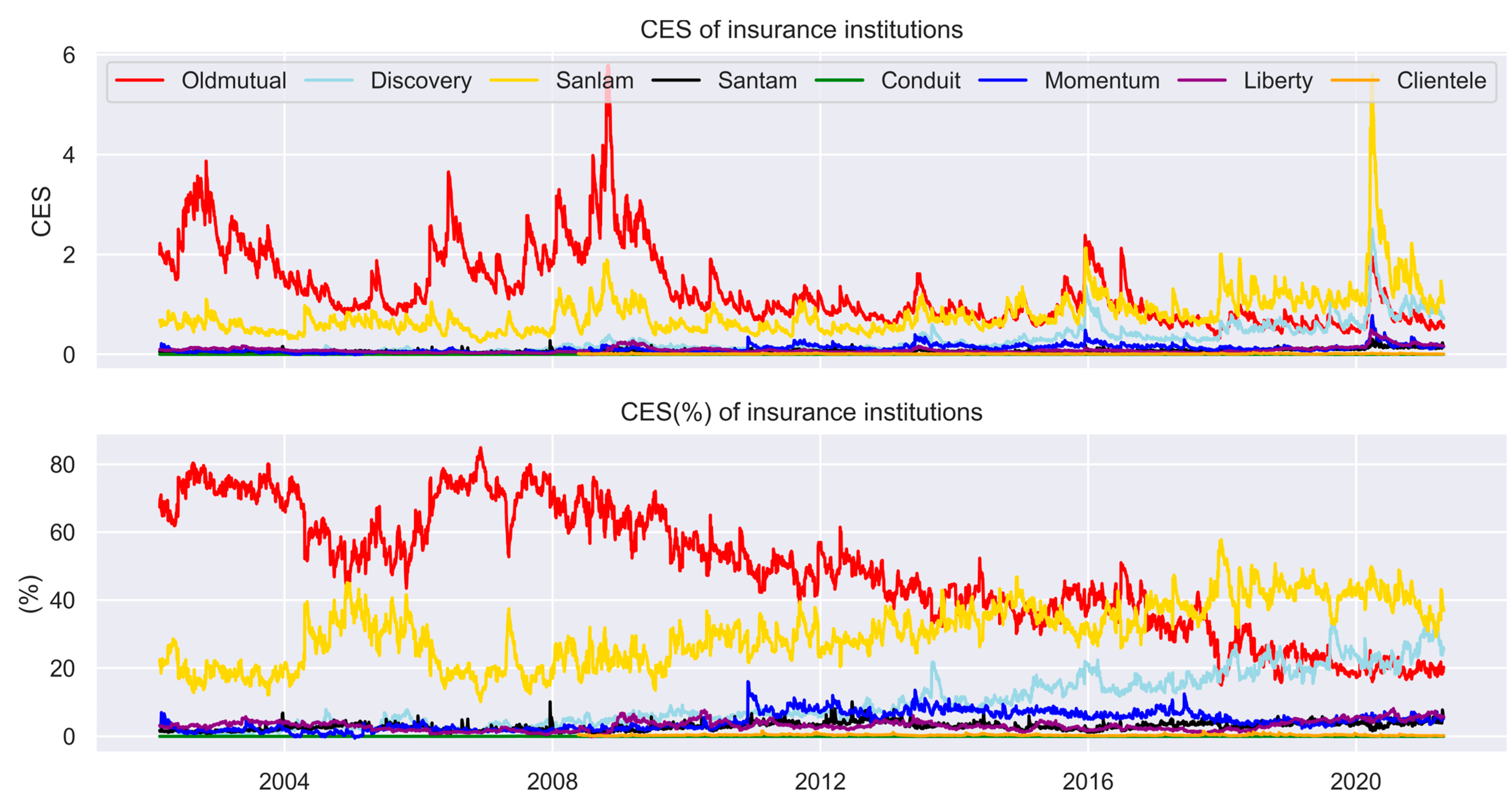
OML	4.45 (65.7)	OML	9.51	OML	1.73 (38.1)	DSY	5.84	SLM	3.32 (45.8)	CND	21.76
SLM	1.67 (25.1)	CND	8.20	SLM	1.49 (32.1)	SLM	5.76	DSY	1.52 (21.0)	DSY	9.54
DSY	0.29 (4.4)	SLM	6.45	DSY	0.94 (19.8)	CND	5.60	OML	1.39 (19.7)	SLM	7.49
MTM	0.16 (2.4)	MTM	5.18	MTM	0.28 (5.9)	MTM	4.54	MTM	0.41 (5.6)	OLM	6.78
SNT	0.11 (1.6)	LBH	4.91	SNT	0.09 (2.0)	OLM	3.87	LBH	0.33 (4.8)	LBH	5.40
LBH	0.05 (0.8)	DSY	4.76	LBH	0.09 (2.0)	LBH	3.74	SNT	0.19 (2.8)	MTM	5.38
CLI	0.01 (0.2)	CLI	4.71	CLI	0.01 (0.2)	SNT	3.56	CLI	0.02 (0.3)	CLI	5.13
CND	0.00 (0)	SNT	3.49	CND	0.00 (0.1)	CLI	3.55	CND	0.00 (0.0)	SNT	3.30

Source: Authors’ own computation.

presents the monthly average of the CES and VaR estimates of the insurance entities. The estimates are used to rank and identify the riskiest insurer in isolation, in contrast with the ranking and identification of the systemic important insurer that poses and contributes the largest to the total loss of the insurance sector during the identified sub-periods. The contrast of metrics is aligned with the evolved approach of the IAIS in assessing and mitigating systemic risk in the insurance sector, which recognises that systemic risk may arise not only from the distress or disorderly failure of individual insurers but also from the collective exposures of insurers at a sector-wide level (IAIS 2019).

According to the CES estimates, the rankings remained the same in the first two sub-periods of market distress, with Old Mutual and Sanlam identified as the most systemically important insurers in the South African insurance industry. However, during the peak of the market turmoil in 2020, the CES rankings were reordered and indicated that Sanlam, followed by Discovery and Old Mutual, were the systemically important insurers. The rankings largely align with Muteba Mwamba and Angaman (2021), who also identify Sanlam and Discovery as the systemically riskiest insurers in South Africa. The reordering of systemic important insurers coincides with the decline in the size of the market capitalisation of Old Mutual after the implementation of a managed separation strategy in 2018, which is captured in the CES percentage.

In 2020, the SARB published proposed guidelines for identifying systemically important insurers in South Africa. The identification guidelines utilise quantitative indicators, including size, interconnectedness, substitutability, and complexity. However, since the publication, there has yet to be public disclosure of the identification and designation of systemically important insurers in South Africa. Based on the CES’s performance in identifying and ranking D-SIBs and reinforcing market-based systemic risk measures in macroprudential toolkits, the CES pre-emptively identified Sanlam, Discovery, and Old Mutual as domestic systemically important insurers (DSIIs). Identifying D-SIBs and D-SIIs ensures the enforcement of enhanced regulatory measures aimed at minimising the likelihood of failure of these institutions and ensuring effective resolution without burdening local taxpayers (SARB 2020).

5. Conclusions

The increased growth and interconnectedness of financial institutions and the move away from regulated products and activities have raised enormous concerns. This paper seeks to accurately identify and rank the domestic systemically important banks (D-SIB) and insurance (D-SII) institutions in the South African financial system. This is conducted by applying the component expected shortfall approach to quantifying a financial industry’s systemic risk and each financial institution’s contributions to the overall risk of their respective industries. The analysis uses high-frequency and publicly available data from the major commercial banks and the main insurance firms in South Africa from February 2002 through April 2021. The results are encapsulated in several key points. The measure captures global and local systemic events and provides an accurate and timely ranking of institutions according to their riskiness during these periods. In the banking industry, we identify three contributors to systemic risk: the first group includes Standard Bank and FirstRand; the second group has Absa and Nedbank; and the last group comprises Capitec and Investec. Our results also reveal an interesting pattern, showing that as banks’ assets and customer base have grown, their systemic importance has increased rapidly. Overall, the rankings for banks from the CES framework closely align with the regulatory D-SIB surcharge of the banking entities included in the study. The close alignment of both approaches is primarily due to the consideration of the size of an institution, amongst other factors. Due to their size, life insurers are predominant contributors to the sector’s systemic risk. According to the CES approach, Sanlam, Discovery, and Old Mutual are identified as potential designations of DSIIs.

The CES has proved to be an effective measure of systemic risk in the South African financial industries and ensures robust and timely identification and rankings of DSIBs and DSIIs. This approach provides regulators and policymakers with a dynamic and complementary tool for improving their monitoring of systemic risk and applying appropriate and timely mitigation policies for systemic risk, which ultimately safeguards the financial system and the real economy. Further work on this study should consider the application of the CES methodology to a collective and comprehensive list of financial institutions. Furthermore, a possible modification of the application of CES methodology with the introduction of GAS copula, which are able to account for the differences in the distribution of the data.