Improving Returns on Strategy Decisions through Integration of Neural Networks for the Valuation of Asset Pricing: The Case of Taiwanese Stock
Abstract
1. Introduction
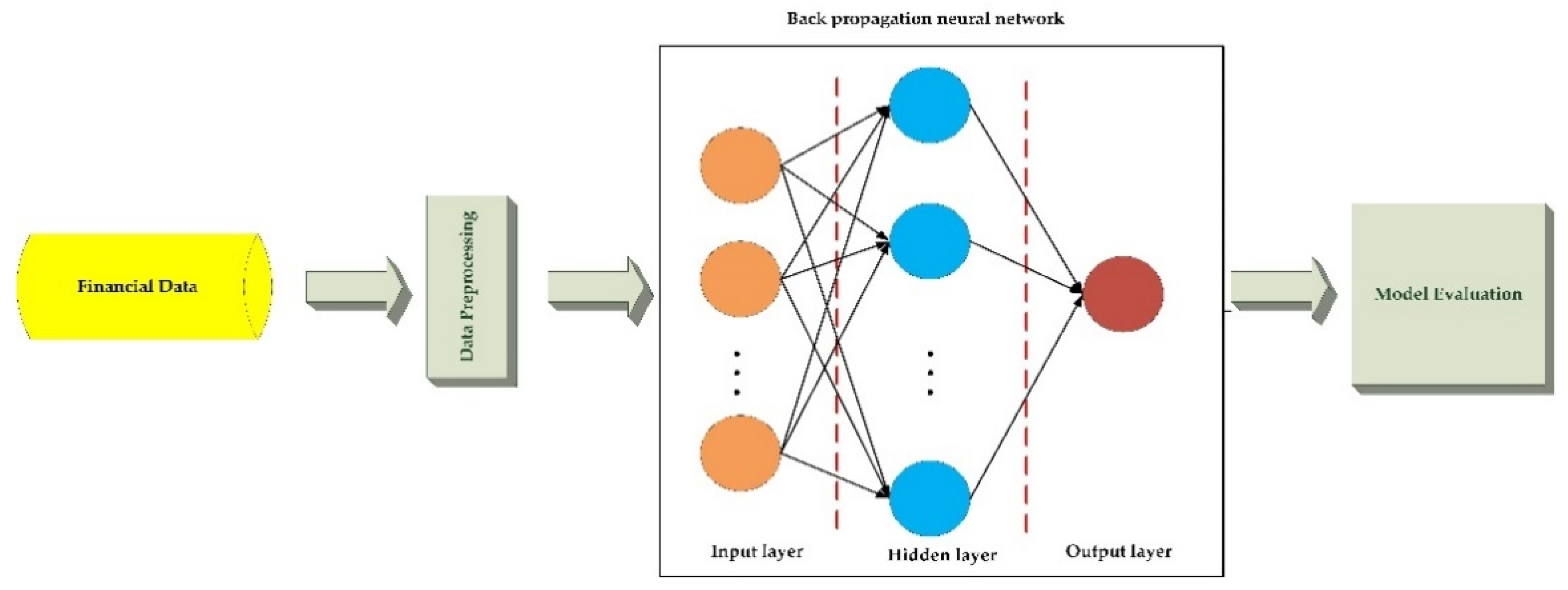
2. Neural-Network Estimation and Evaluation Model
2.1. Neural Network
2.2. Evaluation Model
3. Data and Results
3.1. Descriptive Statistics
3.2. BPNN Forecasting and Estimation
4. Evaluation, Analysis, and Discussion
4.1. Evaluation and Calculation of Discounted Cash Flow
4.2. Evaluation Results and Judgement
4.3. Sensitivity Analysis
4.4. Further Discussion and a Robust Test
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Acharya, Viral V., and Lasse Heje Pedersen. 2005. Asset pricing with liquidity risk. Journal of Financial Economics 77: 375–410. [Google Scholar] [CrossRef]
- Ahmed, Shamima, Muneer M. Alshater, Anis El Ammari, and Helmi Hammami. 2022. Artificial intelligence and machine learning in finance: A bibliometric review. Research in International Business and Finance 61: 101646. [Google Scholar] [CrossRef]
- Bekaert, Geert, Eric Engstrom, and Yuhang Xing. 2009. Risk, uncertainty, and asset prices. Journal of Financial Economics 91: 59–82. [Google Scholar] [CrossRef]
- Bollen, Johan, Huina Mao, and Xiaojun Zeng. 2011. Twitter mood predicts the stock market. Journal of Computational Science 2: 1–8. [Google Scholar] [CrossRef]
- Brownlee, Jason. 2018. Better Deep Learning: Train Faster, Reduce Overfitting, and Make Better Predictions. San Francisco: Machine Learning Mastery. [Google Scholar]
- Campbell, John Y., and Tuomo Vuolteenaho. 2004. Bad beta, good beta. American Economic Review 94: 1249–75. [Google Scholar] [CrossRef]
- Carhart, Mark M. 1997. On persistence in mutual fund performance. The Journal of Finance 52: 57–82. [Google Scholar] [CrossRef]
- Chan, Louis K.C., and Josef Lakonishok. 2004. Value and growth investing: Review and update. Financial Analysts Journal 60: 71–86. [Google Scholar] [CrossRef]
- Chang, Pei-Chann, and Chen-Hao Liu. 2008. A TSK type fuzzy rule based system for stock price prediction. Expert Systems with Applications 34: 135–44. [Google Scholar] [CrossRef]
- Chang, Tsung-Sheng. 2011. A comparative study of artificial neural networks, and decision trees for digital game content stocks price prediction. Expert Systems with Applications 38: 14846–51. [Google Scholar] [CrossRef]
- Chen, Mu-Yen. 2011. Predicting corporate financial distress based on integration of decision tree classification and logistic regression. Expert Systems with Applications 38: 11261–72. [Google Scholar] [CrossRef]
- Chen, Wun-Hua, Jen-Ying Shih, and Soushan Wu. 2006. Comparison of support-vector machines and back propagation neural networks in forecasting the six major Asian stock markets. International Journal of Electronic Finance 1: 49–67. [Google Scholar] [CrossRef]
- Da, Zhi, Joseph Engelberg, and Pengjie Gao. 2011. In search of attention. The Journal of Finance 66: 1461–99. [Google Scholar] [CrossRef]
- Desai, Shrinivas D., Shantala Giraddi, Prashant Narayankar, Neha R. Pudakalakatti, and Shreya Sulegaon. 2019. Back-propagation neural network versus logistic regression in heart disease classification. Advanced Computing and Communication Technologies 702: 133–44. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1995. Size and book-to-market factors in earnings and returns. The Journal of Finance 50: 131–55. [Google Scholar] [CrossRef]
- Goodell, John W., Satish Kumar, Weng Marc Lim, and Debidutta Pattnaik. 2021. Artificial intelligence and machine learning in finance: Identifying foundations, themes, and research clusters from bibliometric analysis. Journal of Behavioral and Experimental Finance 32: 100577. [Google Scholar] [CrossRef]
- Hadavandi, Esmaeil, Hassan Shavandi, and Arash Ghanbari. 2010. Integration of genetic fuzzy systems and artificial neural networks for stock price forecasting. Knowledge-Based Systems 23: 800–8. [Google Scholar] [CrossRef]
- Hecht-Nielsen, Robert. 1992. Theory of the backpropagation neural network. In Neural Networks for Perception. Cambridge: Academic Press, pp. 65–93. [Google Scholar] [CrossRef]
- Hirshleifer, David, Sonya S. Lim, and Siew Hong Teoh. 2011. Limited investor attention and stock market misreactions to accounting information. The Review of Asset Pricing Studies 1: 35–73. [Google Scholar] [CrossRef]
- Huang, Chenn-Jung, Dian-Xiu Yang, and Yi-Ta Chuang. 2008. Application of wrapper approach and composite classifier to the stock trend prediction. Expert Systems with Applications 34: 2870–78. [Google Scholar] [CrossRef]
- Huang, Wei, Kin Keung Lai, Yoshiteru Nakamori, and Shouyang Wang. 2004. Forecasting foreign exchange rates with artificial neural networks: A review. International Journal of Information Technology & Decision Making 3: 145–65. [Google Scholar] [CrossRef]
- Jiang, Jingchao, Guobiao Hu, Xiao Li, Xun Xu, Pai Zheng, and Jonathan Stringer. 2019. Analysis and prediction of printable bridge length in fused deposition modelling based on back propagation neural network. Virtual and Physical Prototyping 14: 253–66. [Google Scholar] [CrossRef]
- Kahneman, Daniel, and Amos Tversky. 1979. Prospect Theory: An Analysis of Decision under Risk. Econometrica 47: 263–91. [Google Scholar] [CrossRef]
- Kara, Yakup, Melek Acar Boyacioglu, and Ömer Kaan Baykan. 2011. Predicting direction of stock price index movement using artificial neural networks and support vector machines: The sample of the Istanbul Stock Exchange. Expert Systems with Applications 38: 5311–19. [Google Scholar] [CrossRef]
- Khan, Zabir Haider, Tasnim Sharmin Alin, and Md Akter Hussain. 2011. Price prediction of share market using artificial neural network (ANN). International Journal of Computer Applications 22: 42–47. [Google Scholar] [CrossRef]
- Kim, Kyoung-jae. 2003. Financial time series forecasting using support vector machines. Neurocomputing 55: 307–19. [Google Scholar] [CrossRef]
- Kim, Kyoung-jae. 2006. Artificial neural networks with evolutionary instance selection for financial forecasting. Expert Systems with Applications 30: 519–26. [Google Scholar] [CrossRef]
- Kim, Kyoung-jae, and Won Boo Lee. 2004. Stock market prediction using artificial neural networks with optimal feature transformation. Neural Computing & Applications 13: 255–60. [Google Scholar]
- Kohara, Kazuhiro, Tsutomu Ishikawa, Yoshimi Fukuhara, and Yokihiro Nakamura. 1997. Stock price prediction using prior knowledge and neural networks. Intelligent Systems in Accounting, Finance & Management 6: 11–22. [Google Scholar] [CrossRef]
- Königstorfer, Florian, and Stefan Thalmann. 2020. Applications of Artificial Intelligence in commercial banks—A research agenda for behavioral finance. Journal of Behavioral and Experimental Finance 27: 100352. [Google Scholar] [CrossRef]
- Lai, Robert K., Chin-Yuan Fan, Wei-Hsiu Huang, and Pei-Chann Chang. 2009. Evolving and clustering fuzzy decision tree for financial time series data forecasting. Expert Systems with Applications 36: 3761–73. [Google Scholar] [CrossRef]
- Lee, Ming-Chi. 2009. Using support vector machine with a hybrid feature selection method to the stock trend prediction. Expert Systems with Applications 36: 10896–904. [Google Scholar] [CrossRef]
- Liang, Yaru, Qiguang Li, Peisong Chen, Lingqing Xu, and Jiehua Li. 2019. Comparative study of back propagation artificial neural networks and logistic regression model in predicting poor prognosis after acute ischemic stroke. Open Medicine 14: 324–30. [Google Scholar] [CrossRef] [PubMed]
- Mhlanga, David. 2020. Industry 4.0 in finance: The impact of artificial intelligence (AI) on digital financial inclusion. International Journal of Financial Studies 8: 45. [Google Scholar] [CrossRef]
- Nair, Binoy B., V. P. Mohandas, and N. R. Sakthivel. 2010. A decision tree-rough set hybrid system for stock market trend prediction. International Journal of Computer Applications 6: 1–6. [Google Scholar] [CrossRef]
- Ou, Jane A., and Stephen H. Penman. 1989. Financial statement analysis and the prediction of stock returns. Journal of Accounting and Economics 11: 295–329. [Google Scholar] [CrossRef]
- Patel, Jigar, Sahil Shah, Priyank Thakkar, and K. Kotecha. 2015. Predicting stock and stock price index movement using trend deterministic data preparation and machine learning techniques. Expert Systems with Applications 42: 259–68. [Google Scholar] [CrossRef]
- Pavlidis, Nicos G., Dimitris K. Tasoulis, Vassilis P. Plagianakos, Costas Siriopoulos, and Michael N. Vrahatis. 2005. Computational Intelligence Methods for Financial Forecasting. Proceedings of the International Conference of Computational Methods in Sciences and Engineering, Lecture Series on Computer and Computational Sciences 4: 1416–19. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.403.4736&rep=rep1&type=pdf (accessed on 3 October 2022).
- Pavlidis, Nicos G., Vassilis P. Plagianakos, Dimitris K. Tasoulis, and Michael N. Vrahatis. 2006. Financial forecasting through unsupervised clustering and neural networks. Operational Research 6: 103–27. [Google Scholar] [CrossRef]
- Petrozziello, Alessio, Luigi Troiano, Angela Serra, Ivan Jordanov, Giuseppe Storti, Roberto Tagliaferri, and Michele La Rocca. 2022. Deep learning for volatility forecasting in asset management. Soft Computing 26: 8553–74. [Google Scholar] [CrossRef]
- Qadan, Mahmoud, and Maram Jacob. 2022. The value premium and investors’ appetite for risk. International Review of Economics & Finance 82: 194–219. [Google Scholar] [CrossRef]
- Refenes, Apostolos Nikolaos, and M. Azema-Barac. 1994. Neural network applications in financial asset management. Neural Computing & Applications 2: 13–39. [Google Scholar] [CrossRef]
- Ren, Na, Mehdi Zargham, and Sanaz Rahimi. 2006. A decision tree-based classification approach to rule extraction for security analysis. International Journal of Information Technology & Decision Making 5: 227–40. [Google Scholar] [CrossRef]
- Ross, Stephen A. 1976. The arbitrage theory of capital asset pricing. Journal of Economic Theory 13: 341–60. [Google Scholar] [CrossRef]
- Sharpe, William F. 1964. Capital asset prices: A theory of market equilibrium under conditions of risk. The Journal of Finance 19: 425–42. [Google Scholar] [CrossRef]
- Sun, Jie, Hui Li, Qing-Hua Huang, and Kai-Yu He. 2014. Predicting financial distress and corporate failure: A review from the state-of-the-art definitions, modeling, sampling, and featuring approaches. Knowledge-Based Systems 57: 41–56. [Google Scholar] [CrossRef]
- Tealab, Ahmed. 2018. Time series forecasting using artificial neural networks methodologies: A systematic review. Future Computing and Informatics Journal 3: 334–40. [Google Scholar] [CrossRef]
- Ticknor, Jonathan L. 2013. A Bayesian regularized artificial neural network for stock market forecasting. Expert Systems with Applications 40: 5501–6. [Google Scholar] [CrossRef]
- Tsai, Chih-Fong, Yuah-Chiao Lin, David C. Yen, and Yan-Min Chen. 2011. Predicting stock returns by classifier ensembles. Applied Soft Computing 11: 2452–59. [Google Scholar] [CrossRef]
- Vozlyublennaia, Nadia. 2014. Investor attention, index performance, and return predictability. Journal of Banking & Finance 41: 17–35. [Google Scholar] [CrossRef]
- Wang, Jar-Long, and Shu-Hui Chan. 2006. Stock market trading rule discovery using two-layer bias decision tree. Expert Systems with Applications 30: 605–11. [Google Scholar] [CrossRef]
- Wang, Jian-Zhou, Ju-Jie Wang, Zhe-George Zhang, and Shu-Po Guo. 2011. Forecasting stock indices with back propagation neural network. Expert Systems with Applications 38: 14346–55. [Google Scholar] [CrossRef]
- Wang, Runzhou, and Hong-Yan Bi. 2022. A predictive model for Chinese children with developmental dyslexia—Based on a genetic algorithm optimized back-propagation neural network. Expert Systems with Applications 187: 115949. [Google Scholar] [CrossRef]
- Wang, Yih-Farn. 2002. Predicting stock price using fuzzy grey prediction system. Expert Systems with Applications 22: 33–38. [Google Scholar] [CrossRef]
- Wong, Bo K., and Yakup Selvi. 1998. Neural network applications in finance: A review and analysis of literature (1990–1996). Information & Management 34: 129–39. [Google Scholar] [CrossRef]
- Wong, Bo K., Thomas A. Bodnovich, and Yakup Selvi. 1997. Neural network applications in business: A review and analysis of the literature (1988–1995). Decision Support Systems 19: 301–20. [Google Scholar] [CrossRef]
- Yan, Jianzhuo, Zongbao Xu, Yongchuan Yu, Hongxia Xu, and Kaili Gao. 2019. Application of a hybrid optimized BP network model to estimate water quality parameters of Beihai Lake in Beijing. Applied Sciences 9: 1863. [Google Scholar] [CrossRef]
- Yao, Xin. 1993. A review of evolutionary artificial neural networks. International Journal of Intelligent Systems 8: 539–67. [Google Scholar] [CrossRef]


| Mean | Max. | Min. | S. Dev. | Skew. | Kur. | JB | Obs. | |
|---|---|---|---|---|---|---|---|---|
| Panel A: Index | ||||||||
| Share prices | 2119.69 | 5830.00 | 418.89 | 1533.47 | 0.77 | 2.52 | 9.03 | 84 |
| Rm | 2.76 | 30.90 | −29.15 | 10.63 | −0.09 | 3.66 | 1.64 | 84 |
| SVI | 35.69 | 100.00 | 7.00 | 22.93 | 0.89 | 2.77 | 11.34 | 84 |
| Panel B: Profitability | ||||||||
| Gross profit margin | 0.53 | 0.71 | 0.38 | 0.11 | 0.13 | 1.73 | 1.96 | 28 |
| NOPAT margin | 0.38 | 0.49 | 0.22 | 0.07 | −0.64 | 2.47 | 2.23 | 28 |
| Growth of profit before tax | 0.39 | 1.25 | −0.23 | 0.43 | 0.26 | 2.10 | 1.28 | 28 |
| Return on total assets | 0.17 | 0.35 | 0.04 | 0.09 | 0.24 | 1.87 | 1.75 | 28 |
| Return on assets | 0.17 | 0.35 | 0.04 | 0.09 | 0.24 | 1.87 | 1.75 | 28 |
| Return on equity | 0.22 | 0.46 | 0.05 | 0.12 | 0.21 | 1.97 | 1.44 | 28 |
| Operating margin | 44.92 | 61.87 | 29.20 | 10.55 | 0.05 | 1.65 | 2.14 | 28 |
| Panel C: Debt-Paying Ability | ||||||||
| Current ratio | 310.88 | 458.86 | 194.49 | 58.06 | 0.39 | 3.04 | 0.73 | 28 |
| Quick ratio | 284.22 | 416.36 | 177.50 | 57.42 | 0.41 | 2.53 | 1.03 | 28 |
| Operating cash-flow ratio | 0.75 | 1.43 | 0.29 | 0.37 | 0.56 | 1.95 | 2.75 | 28 |
| Current debt/debt | 0.99 | 1.00 | 0.98 | 0.00 | −1.65 | 6.74 | 29.01 | 28 |
| Equity/assets | 0.76 | 0.85 | 0.64 | 0.04 | −0.79 | 4.08 | 4.27 | 28 |
| Debt/equity | 0.31 | 0.57 | 0.18 | 0.08 | 1.24 | 5.36 | 13.66 | 28 |
| Panel D: Operating Capacity | ||||||||
| Inventory turnover | 5.58 | 7.90 | 3.41 | 1.21 | 0.32 | 2.48 | 0.78 | 28 |
| Accounts payable turnover | 4.01 | 4.86 | 3.28 | 0.47 | −0.07 | 1.96 | 1.28 | 28 |
| Assets turnover | 0.65 | 0.92 | 0.39 | 0.14 | −0.18 | 2.05 | 1.21 | 28 |
| Sell expense/sales | 0.09 | 0.10 | 0.07 | 0.01 | −0.43 | 2.24 | 1.54 | 28 |
| Admin expense/sales | 0.02 | 0.03 | 0.02 | 0.00 | 0.25 | 3.02 | 0.29 | 28 |
| Term | Hidden Layers | Network Architecture | Learning Rate | Inertia Factor | MSE in Training | MSE in Testing |
|---|---|---|---|---|---|---|
| Panel A: SVI for four-quarter | ||||||
| 1 | 3 | 19-7-3 | 0.1 | 0.01 | 0.0842 | 0.0030 |
| 2 | 3 | 19-6-3 | 0.3 | 0.4 | 0.0794 | 0.0028 |
| 3 | 3 | 19-4-1 | 0.2 | 0.05 | 0.0752 | 0.0026 |
| 4 | 3 | 19-6-3 | 0.3 | 0.3 | 0.0590 | 0.0021 |
| 5 | 3 | 19-6-3 * | 0.2 | 0.1 | 0.0528 | 0.0018 |
| Panel B: SVI for eight-quarter | ||||||
| 1 | 3 | 19-6-3 | 0.3 | 0.5 | 0.0865 | 0.0030 |
| 2 | 3 | 19-6-3 | 0.2 | 0.05 | 0.0750 | 0.0026 |
| 3 | 3 | 19-6-3 | 0.2 | 0.1 | 0.0509 | 0.0018 |
| 4 | 3 | 19-7-4 | 0.3 | 0.4 | 0.0460 | 0.0016 |
| 5 | 3 | 19-4-3 * | 0.2 | 0.04 | 0.0414 | 0.0014 |
| Panel C: Ri (stock return) for four-quarter | ||||||
| 1 | 3 | 19-6-5 | 0.3 | 0.1 | 0.4676 | 0.0167 |
| 2 | 3 | 19-10-5 | 0.2 | 0.2 | 0.3967 | 0.0141 |
| 3 | 3 | 19-10-5 | 0.2 | 0.1 | 0.2771 | 0.0098 |
| 4 | 3 | 19-9-3 | 0.2 | 0.3 | 0.2655 | 0.0094 |
| 5 | 3 | 19-9-3 * | 0.2 | 0.2 | 0.2327 * | 0.0083 |
| Panel D: Ri (stock return) for eight-quarter | ||||||
| 1 | 4 | 19-7-3 | 0.05 | 0.1 | 0.3586 | 0.0128 |
| 2 | 3 | 19-5-4 | 0.2 | 0.2 | 0.2427 | 0.0086 |
| 3 | 3 | 19-9-3 | 0.2 | 0.3 | 0.2352 | 0.0084 |
| 4 | 3 | 19-5-4 | 0.2 | 0.3 | 0.1987 | 0.0070 |
| 5 | 3 | 19-7-3 * | 0.1 | 0.05 | 0.1304 | 0.0046 |
| Panel E: Ri (revenue growth rate) for four-quarter | ||||||
| 1 | 3 | 19-4-1 | 0.02 | 0.03 | 0.0347 | 0.0347 |
| 2 | 3 | 19-4-1 | 0.03 | 0.02 | 0.0219 | 0.0007 |
| 3 | 3 | 19-4-1 * | 0.02 | 0.01 | 0.0168 * | 0.0006 |
| Panel F: Ri (revenue growth rate) for eight-quarter | ||||||
| 1 | 3 | 19-4-1 | 0.02 | 0.03 | 0.0347 | 0.0347 |
| 2 | 3 | 19-4-1 | 0.03 | 0.02 | 0.0219 | 0.0007 |
| 3 | 3 | 19-4-1 * | 0.02 | 0.01 | 0.0168 * | 0.0006 |
| Variable | Reg. (r2) | Slope | Intercept |
|---|---|---|---|
| SVI for four-quarter | 0.9901 | 1.0400 * | −0.0483 |
| SVI for eight-quarter | 0.9779 | 0.9458 * | 0.0452 |
| Ri (Stock return) for four-quarter | 0.8987 | 0.9937 * | 0.0701 |
| Ri (Stock return) for eight-quarter | 0.9039 | 0.8876 * | 0.0701 |
| Ri (Revenue growth rate) for four-quarter | 0.9893 | 0.9904 * | −0.0029 |
| Ri (Revenue growth rate) for eight-quarter | 0.9958 | 0.9904 * | 0.0198 |
| Periods | SVI | Stock Return | Revenue Growth Rate |
|---|---|---|---|
| 2018.03 | 0.3529 | −0.1932 | 0.0568 |
| 2018.06 | 0.3657 | −0.2363 | 0.0854 |
| 2018.09 | 0.3471 | −0.1933 | 0.2158 |
| 2018.12 | 0.3660 | −0.0967 | −0.0639 |
| 2019.03 | 0.5866 | 0.3357 | 0.1291 |
| 2019.06 | 0.7028 | 0.2220 | 0.1208 |
| 2019.09 | 0.7171 | 0.1996 | 0.06185 |
| 2019.12 | 0.7254 | 0.7996 | −0.2763 |
| Indicator | FY11 | FY12 | FY13 | FY14 | FY15 | FY16 | FY17 |
|---|---|---|---|---|---|---|---|
| Panel A: DCF Valuation Assumptions | |||||||
| Risk-free rate (%) | 1.36 | 1.36 | 1.36 | 1.36 | 1.21 | 1.04 | 1.04 |
| Market risk premium (%) | −20.46 | 11.21 | 15.36 | 10.42 | −8.29 | 13.03% | 18.96 |
| Beta | 1.43 | 1.35 | 1.55 | 1.42 | 1.68 | 1.91 | 1.76 |
| Debt/value of capital (%) | 20.47 | 26.05 | 21.15 | 24.33 | 24.53 | 20.84 | 20.28 |
| Cost of debt (%) | 0.03 | 0.02 | 0.03 | 3.85% | 0.00 | 0.00 | 0.00 |
| Years of growth (%) | 94.44 | 4.37 | −20.29 | 119.44 | 134.69 | −30.27 | 36.49 |
| Years of growth (%) | 28.54 | 7.29 | 72.29 | 102.27 | 24.27 | −5.89 | 14.26 |
| Panel B: Key DCF Drivers | |||||||
| Sales growth (%) | 29.41 | 25.57 | 36.67 | 66.99 | 21.96 | −13.45 | 9.88 |
| EBIT margin (%) | 36.52 | 33.93 | 41.92 | 50.14 | 52.19 | 58.43 | 60.16 |
| NOPAT margin (%) | 74.74 | 69.93 | 82.96 | 83.16 | 74.54 | 53.08 | 47.87 |
| Net fixed assets turns (%) | 4.19 | 4.57 | 8.54 | 8.36 | 5.39 | 5.61 | 4.81 |
| Net WC turns (%) | 2.41 | 3.5 | 2.43 | 2.33 | 1.91 | 2.01 | 1.68 |
| ROIC (%) | 20.87 | 17.88 | 24.89 | 31.84 | 28.76 | 23.42 | 22.41 |
| EPS | 38.57 | 41.3 | 71.81 | 144.34 | 179.93 | 169.32 | 193.49 |
| Periods | Real Price | Pred. Price | Pred. Gaps | Judgement |
|---|---|---|---|---|
| 2018.03 | 3237.65 | 2159.456 | −0.3330 | Underestimated |
| 2018.06 | 4339.42 | 2769.627 | −0.3618 | Underestimated |
| 2018.09 | 3571.21 | 2970.950 | −0.1680 | Underestimated |
| 2018.12 | 3158.58 | 3823.144 | 0.2104 | Overestimated |
| 2019.03 | 4519.28 | 4383.435 | −0.0301 | Underestimated |
| 2019.06 | 3787.35 | 4617.363 | 0.2192 | Overestimated |
| 2019.09 | 4450.00 | 4835.738 | 0.0866 | Overestimated |
| 2019.12 | 4995.00 | 5176.731 | 0.0363 | Overestimated |
| Periods | Daily | Pred. Gaps | Monthly | Pred. Gaps | Rolling (Daily) | Pred. Gaps |
|---|---|---|---|---|---|---|
| 2018.03 | 3675.56 | −0.412 ***↓ | 3559.81 | −0.393 ***↓ | 3675.56 | −0.412 ***↓ |
| 2018.06 | 3825.74 | −0.276 ***↓ | 3888.40 | −0.288 ***↓ | 3751.93 | −0.262 ***↓ |
| 2018.09 | 4540.51 | −0.346 ***↓ | 4390.31 | −0.323 ***↓ | 4029.23 | −0.263 ***↓ |
| 2018.12 | 3273.68 | 0.168 ***↑ | 3253.55 | 0.175 ***↑ | 3830.40 | −0.002 ↓ |
| 2019.03 | 3980.65 | 0.101 ***↑ | 4172.15 | 0.051 ↑ | 3857.36 | 0.136 ***↑ |
| 2019.06 | 4106.97 | 0.124 ***↑ | 4019.86 | 0.149 *↑ | 3899.42 | 0.184 ***↑ |
| 2019.09 | 4012.00 | 0.205 ***↑ | 4171.81 | 0.159 ***↑ | 3916.11 | 0.235 ***↑ |
| 2019.12 | 4577.90 | 0.131 ***↑ | 4633.33 | 0.117 ***↑ | 4000.36 | 0.294 ***↑ |
| Periods | Beta Top_10% | Pred. Gaps | Rolling Top_10% | Pred. Gaps | Beta Last_10% | Pred. Gaps | Rolling Last_10% | Pred. Gaps |
|---|---|---|---|---|---|---|---|---|
| 2018.03 | 3571.09 | −0.395 ***↓ | 3571.09 | −0.395 ***↓ | 3958.63 | −0.454 ***↓ | 3958.63 | −0.454 ***↓ |
| 2018.06 | 3202.45 | −0.135 ***↓ | 3372.59 | −0.179 ***↓ | 4303.99 | −0.357 ***↓ | 4147.01 | −0.332 ***↓ |
| 2018.09 | 4953.13 | −0.400 ***↓ | 3925.78 | −0.243 ***↓ | 3734.14 | −0.204 ***↓ | 4001.29 | −0.258 ***↓ |
| 2018.12 | 3182.44 | 0.201 ***↑ | 3733.06 | 0.024 ↑ | 3338.70 | 0.145 ***↑ | 3828.44 | −0.001 ↓ |
| 2019.03 | 4266.30 | 0.027 ↑ | 3830.01 | 0.144 ***↑ | 3195.91 | 0.372 ***↑ | 3715.49 | 0.180 ***↑ |
| 2019.06 | 4548.75 | 0.015 ↑ | 3955.79 | 0.167 ***↑ | 3608.06 | 0.280 ***↑ | 3696.53 | 0.249 ***↑ |
| 2019.09 | 4111.43 | 0.176 ***↑ | 3978.97 | 0.215 ***↑ | 4116.47 | 0.175 ***↑ | 3759.52 | 0.286 ***↑ |
| 2019.12 | 4373.57 | 0.184 ***↑ | 4030.12 | 0.285 ***↑ | 4936.67 | 0.049 ***↑ | 3913.06 | 0.323 ***↑ |
| Types | Higher Risk-Taking Levels | Lower Risk-Taking Levels | ||||
|---|---|---|---|---|---|---|
| Beta+1% | Beta+5% | Beta+10% | Beta-1% | Beta-5% | Beta-10% | |
| Panel A: Using Revenue Growth with BPNN | ||||||
| G_1% | 1.161 * | 1.138 * | 1.110 * | 1.173 * | 1.198 * | 1.231 * |
| G_5% | 1.186 * | 1.162 * | 1.134 * | 1.198 * | 1.224 * | 1.258 * |
| G_10% | 1.218 * | 1.193 * | 1.164 * | 1.230 * | 1.257 * | 1.292 * |
| WACC_1% | 1.158 * | 1.146 * | 1.131 * | 1.165 * | 1.178 * | 1.196 * |
| WACC_5% | 1.059 * | 1.049 * | 1.036 * | 1.065 * | 1.077 * | 1.092 * |
| WACC_10% | 0.955 | 0.946 | 0.935 | 0.960 | 0.970 | 0.983 |
| Panel B: Using Stock’s Return with BPNN | ||||||
| G_1% | 0.924 | 0.905 | 0.882 | 0.933 | 0.954 | 0.981 |
| G_5% | 0.949 | 0.929 | 0.906 | 0.959 | 0.980 | 1.008 * |
| G_10% | 0.980 | 0.960 | 0.936 | 0.991 | 1.013 * | 1.042 * |
| WACC_1% | 0.920 | 0.910 | 0.897 | 0.925 | 0.937 | 0.952 |
| WACC_5% | 0.843 | 0.834 | 0.823 | 0.848 | 0.858 | 0.871 |
| WACC_10% | 0.762 | 0.754 | 0.745 | 0.766 | 0.775 | 0.786 |
| Panel C: Using SVI with BPNN | ||||||
| G_1% | 0.920 | 0.903 | 0.883 | 0.928 | 0.946 | 0.970 |
| G_5% | 0.945 | 0.927 | 0.907 | 0.954 | 0.972 | 0.997 |
| G_10% | 0.976 | 0.958 | 0.937 | 0.986 | 1.005 * | 1.031 * |
| WACC_1% | 0.916 | 0.907 | 0.897 | 0.920 | 0.930 | 0.943 |
| WACC_5% | 0.843 | 0.836 | 0.827 | 0.847 | 0.856 | 0.867 |
| WACC_10% | 0.767 | 0.760 | 0.753 | 0.770 | 0.778 | 0.787 |
| Panel D: A Summary | ||||||
| Mean | 0.971 | 0.957 | 0.939 | 0.979 | 0.995 | 1.016 * |
| S.D. | 0.136 | 0.132 | 0.127 | 0.139 | 0.143 | 0.150 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-C.; Kuo, S.-M.; Liu, Y.; Wu, Z.; Zhang, F. Improving Returns on Strategy Decisions through Integration of Neural Networks for the Valuation of Asset Pricing: The Case of Taiwanese Stock. Int. J. Financial Stud. 2022, 10, 99. https://doi.org/10.3390/ijfs10040099
Chen Y-C, Kuo S-M, Liu Y, Wu Z, Zhang F. Improving Returns on Strategy Decisions through Integration of Neural Networks for the Valuation of Asset Pricing: The Case of Taiwanese Stock. International Journal of Financial Studies. 2022; 10(4):99. https://doi.org/10.3390/ijfs10040099
Chicago/Turabian StyleChen, Yi-Chang, Shih-Ming Kuo, Yonglin Liu, Zeqiong Wu, and Fang Zhang. 2022. "Improving Returns on Strategy Decisions through Integration of Neural Networks for the Valuation of Asset Pricing: The Case of Taiwanese Stock" International Journal of Financial Studies 10, no. 4: 99. https://doi.org/10.3390/ijfs10040099
APA StyleChen, Y.-C., Kuo, S.-M., Liu, Y., Wu, Z., & Zhang, F. (2022). Improving Returns on Strategy Decisions through Integration of Neural Networks for the Valuation of Asset Pricing: The Case of Taiwanese Stock. International Journal of Financial Studies, 10(4), 99. https://doi.org/10.3390/ijfs10040099







