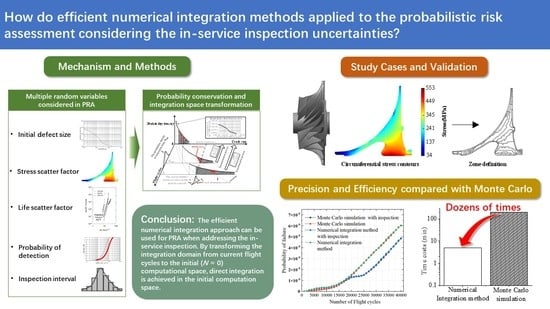
Efficient Numerical Integration Algorithm of Probabilistic Risk Assessment for Aero-Engine Rotors Considering In-Service Inspection Uncertainties
Abstract
1. Introduction
- (1)
- Monte Carlo simulation methods considering in-service inspection
- (2)
- Numerical integration methods without considering in-service inspection
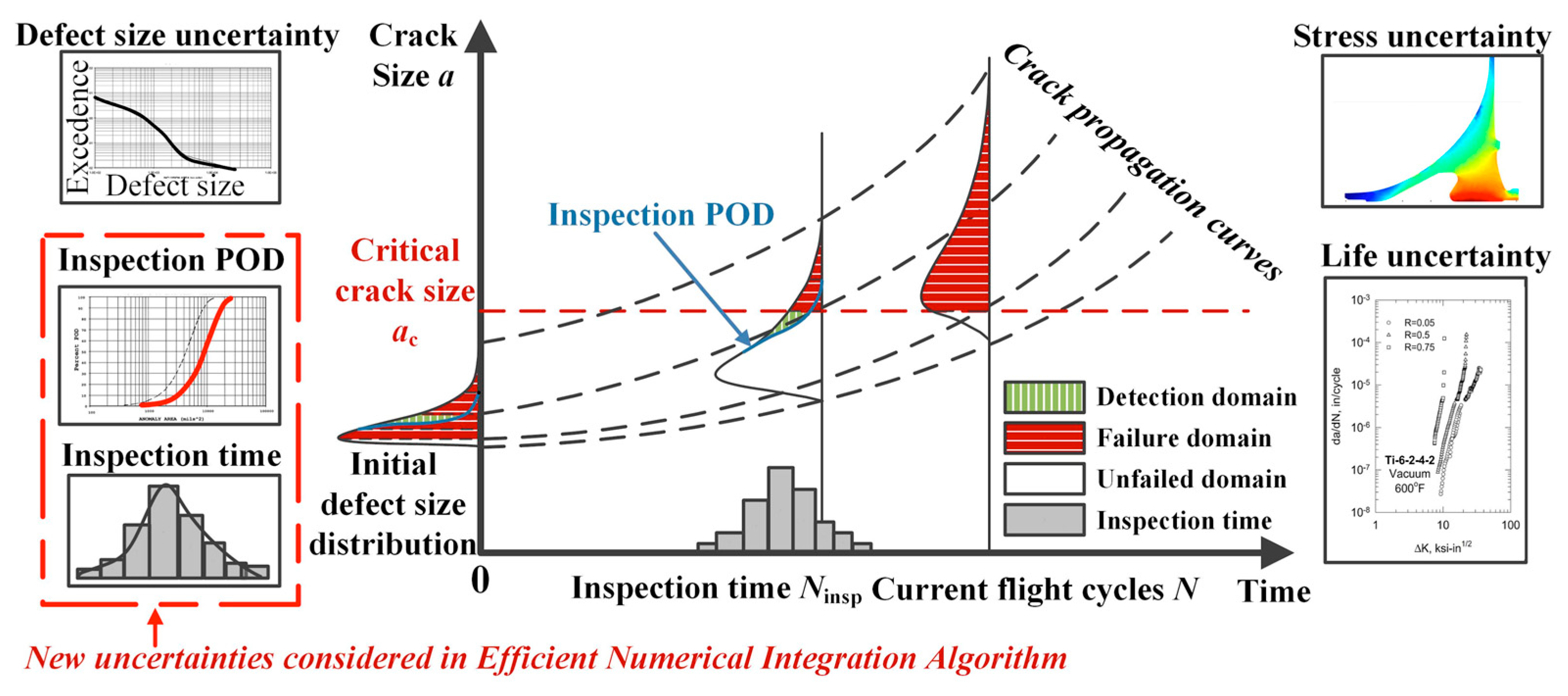
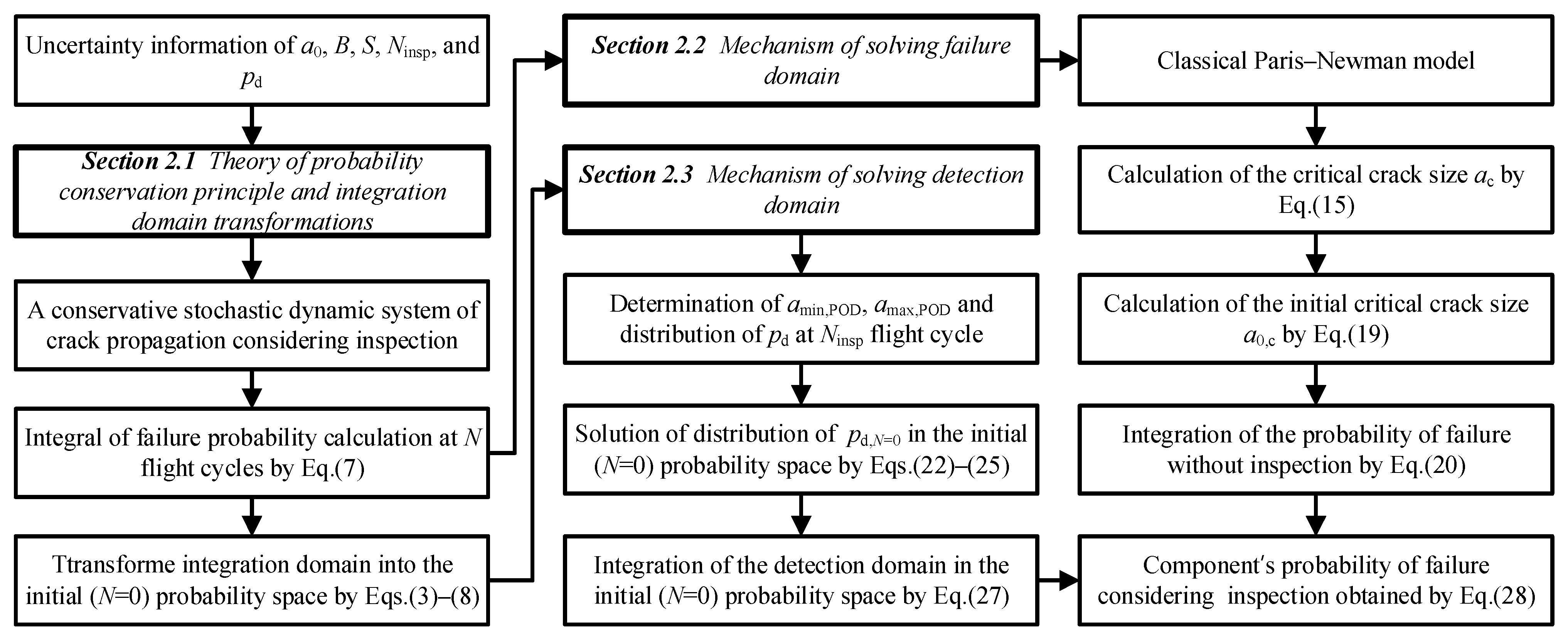
2. Efficient Numerical Integration Algorithm for Risk Assessment Considering In-Service Inspection
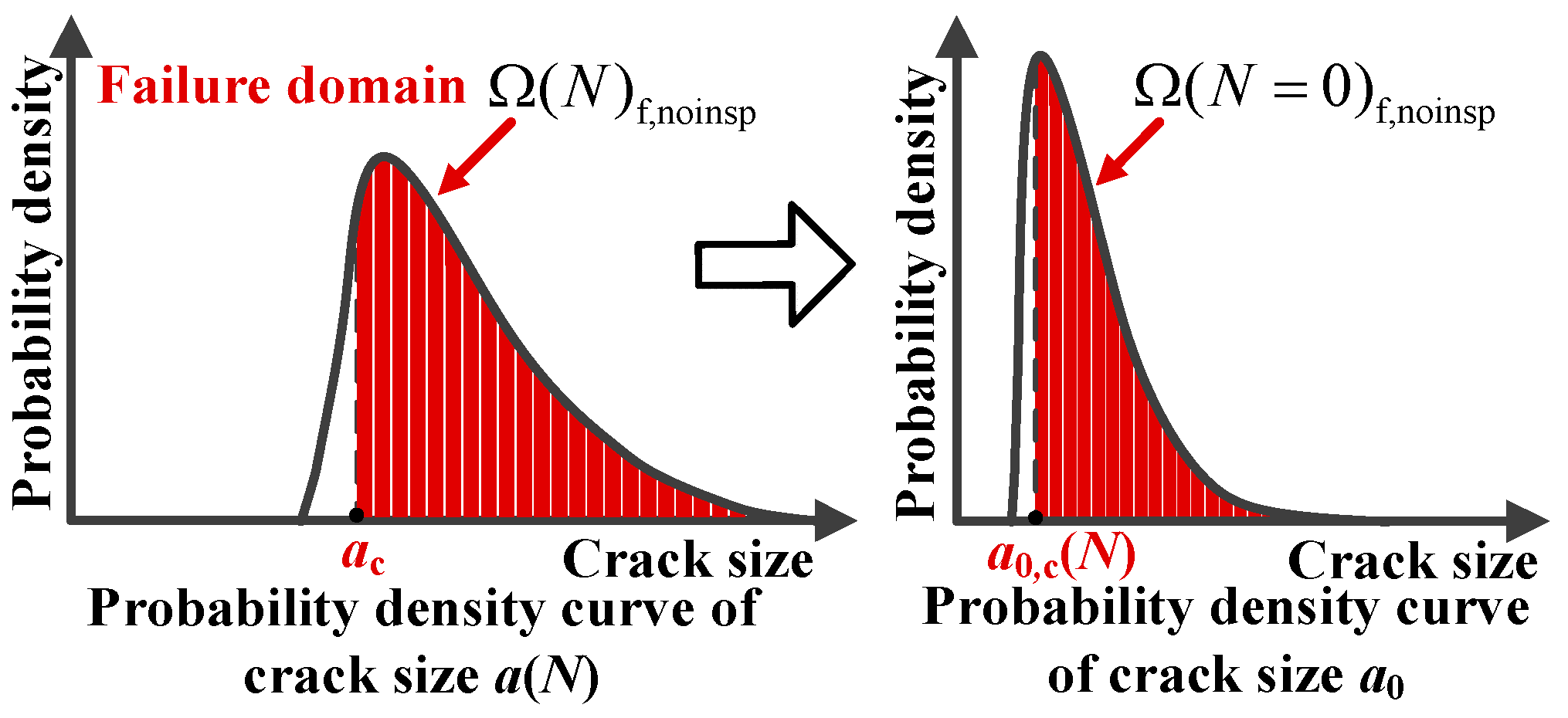
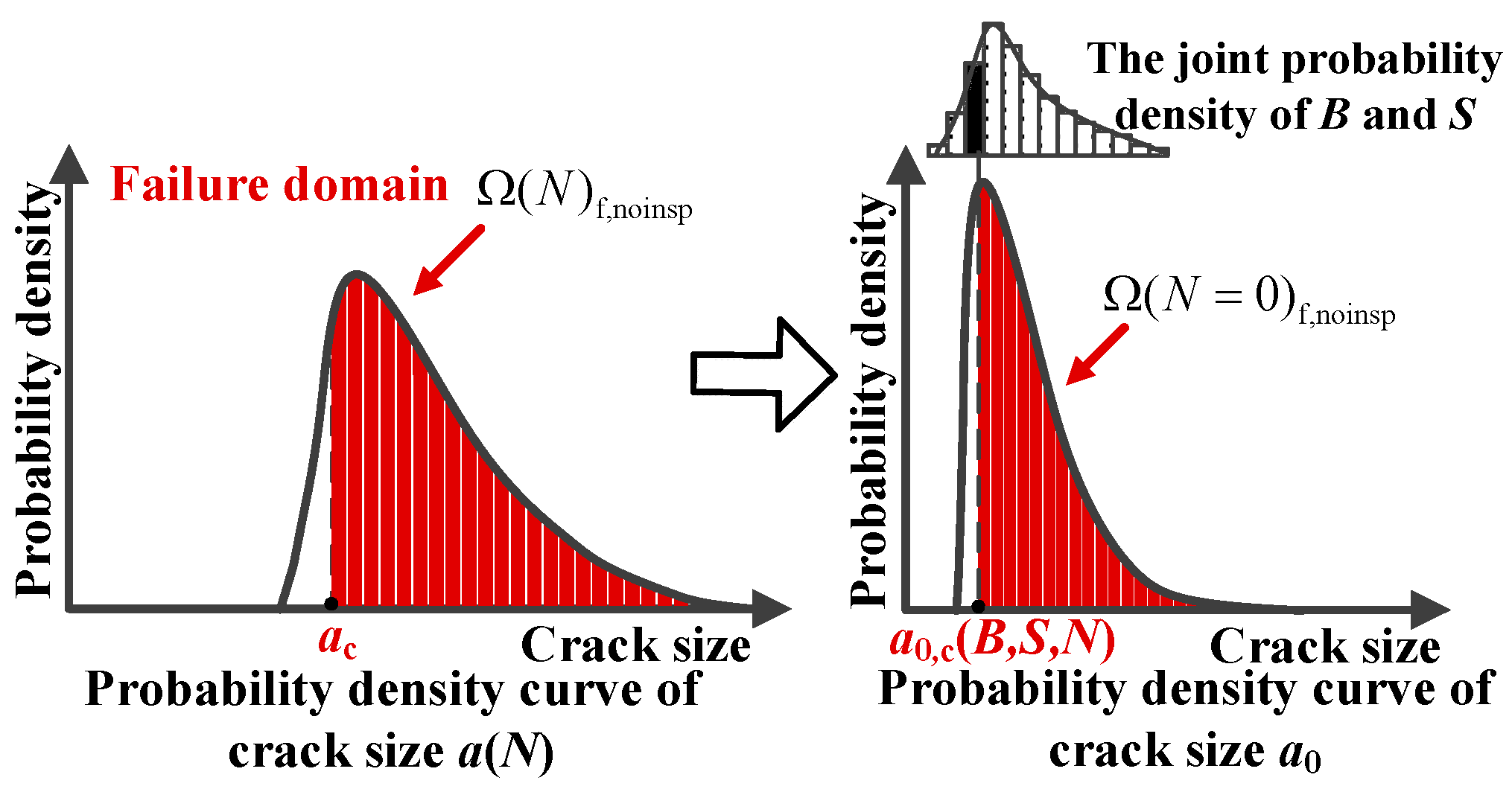
2.1. Probability Conservation Principle and Integration Domain Transformations
2.2. Mechanism of Solving Failure Domain Using the Numerical Integration Algorithm
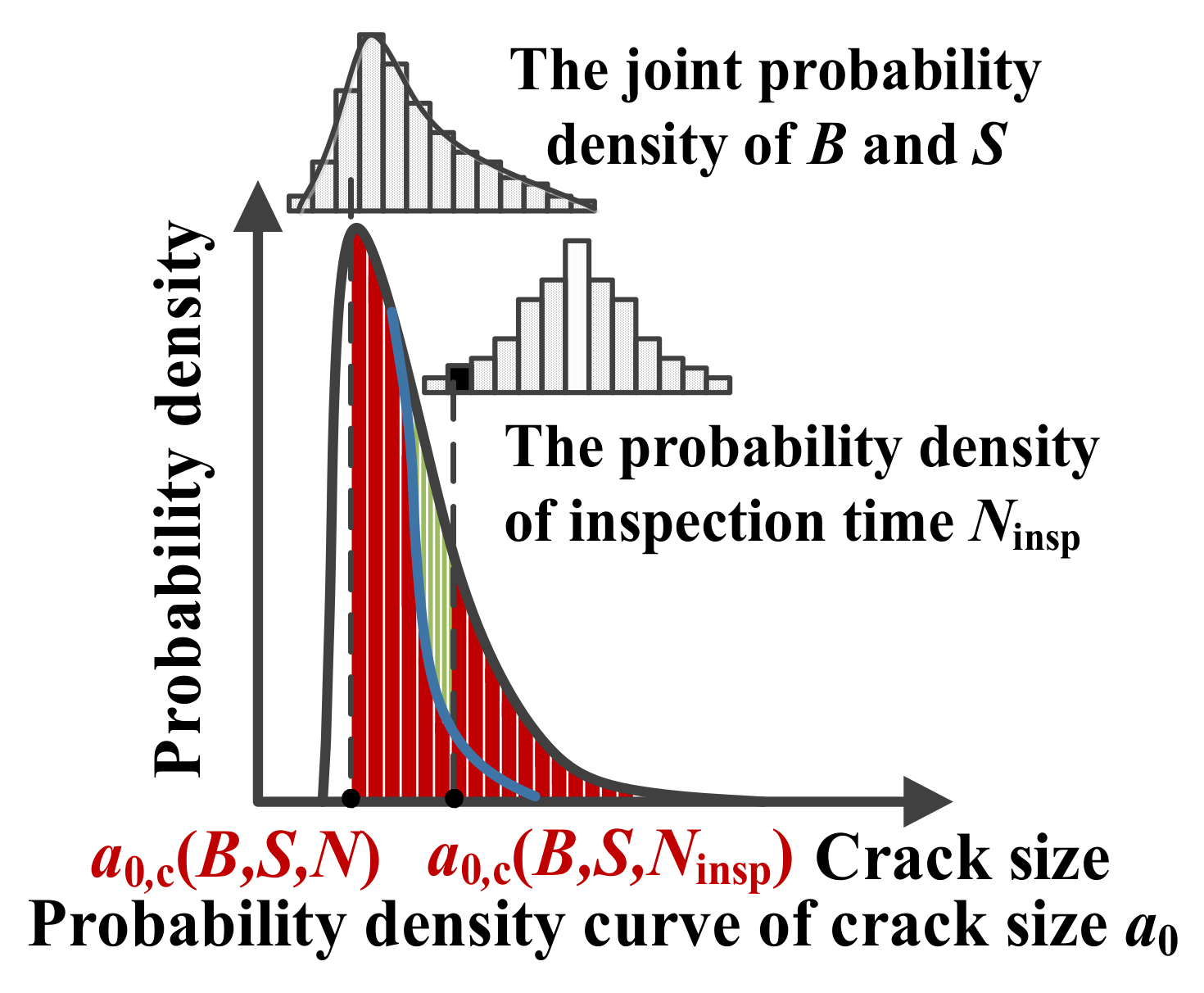
2.3. Mechanism of Solving the Detection Domain Using the Numerical Integration Algorithm
3. Results and Discussion
3.1. Computational Model and Inputs
- (1)
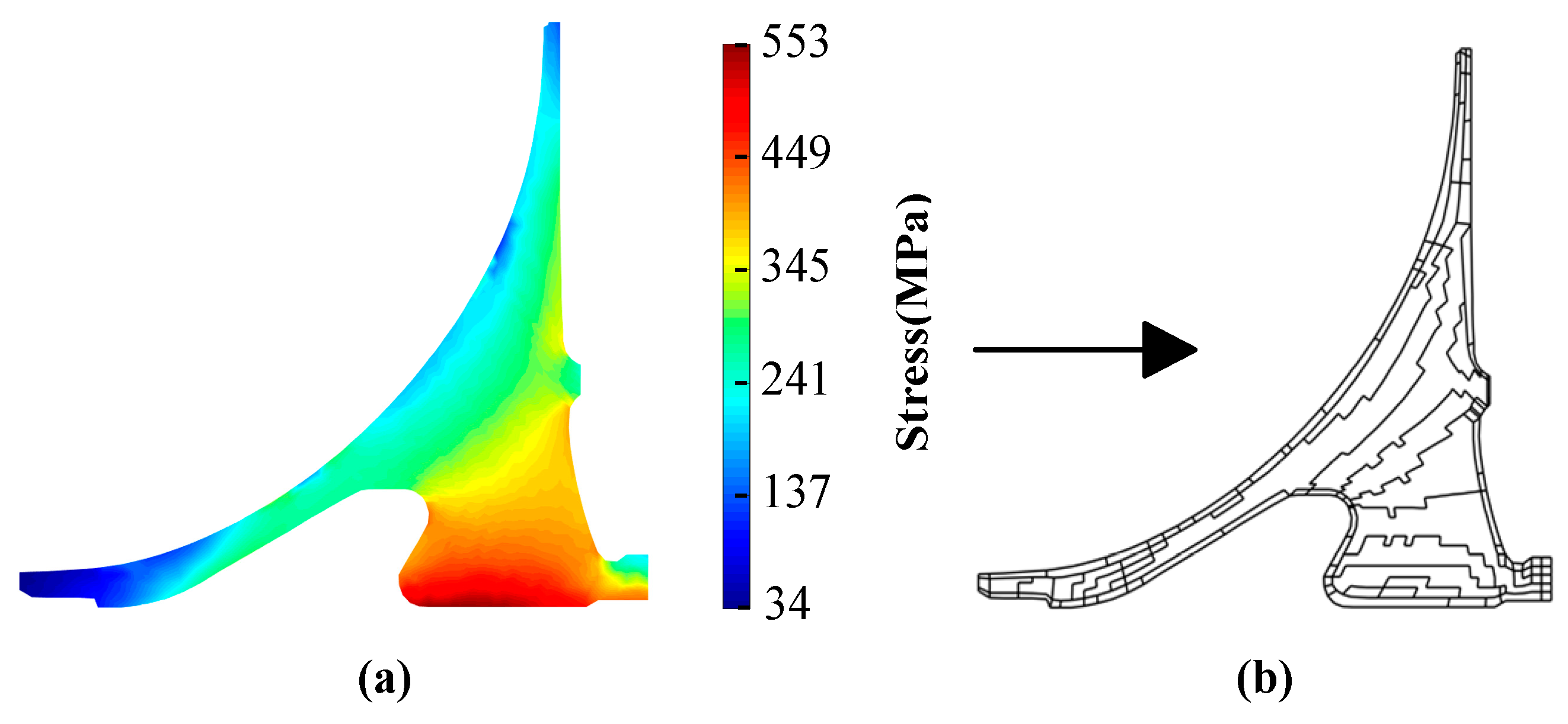
- Geometry, boundary conditions, and material properties
- (2)
- Stress distribution and zone definition
- (3)
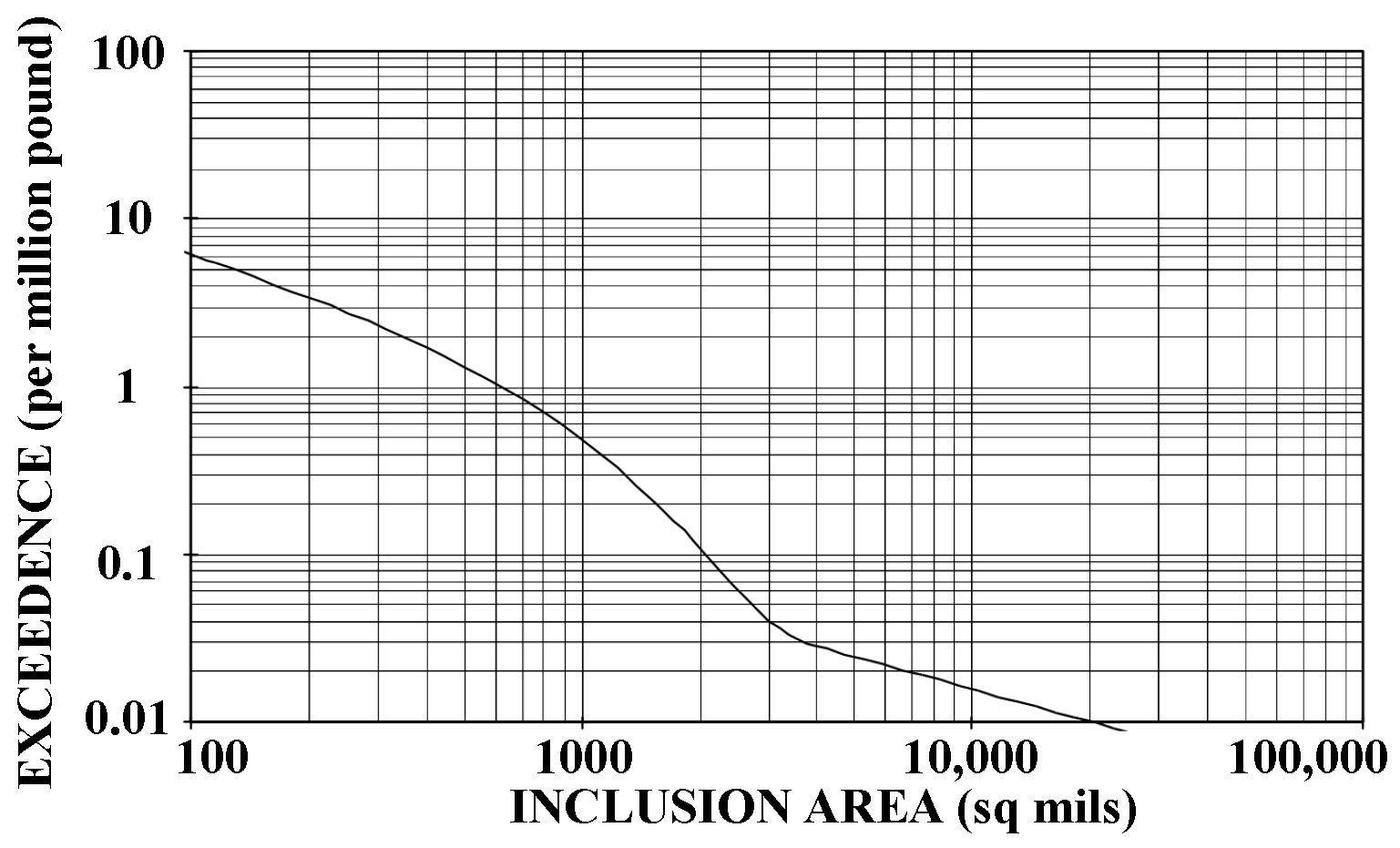
- Defect material anomaly distribution (determining the initial defect size of material)
- (4)
- Life scatter factor and stress scatter factor
- (5)
- Inspection POD and Inspection interval
- (6)
- Design service life
3.2. Computation Results and Discussion
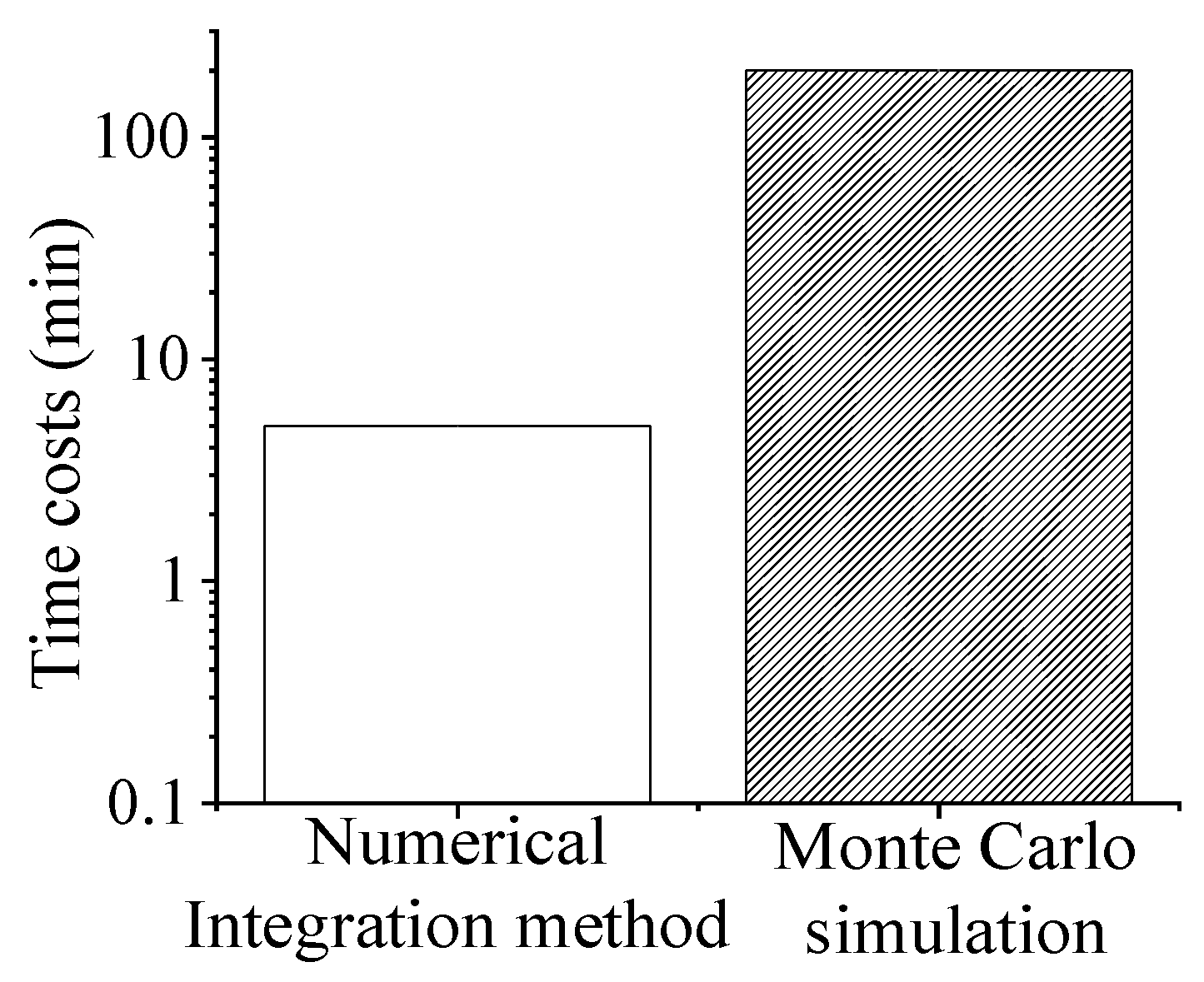
- (1)
- Comparison of the computational costs
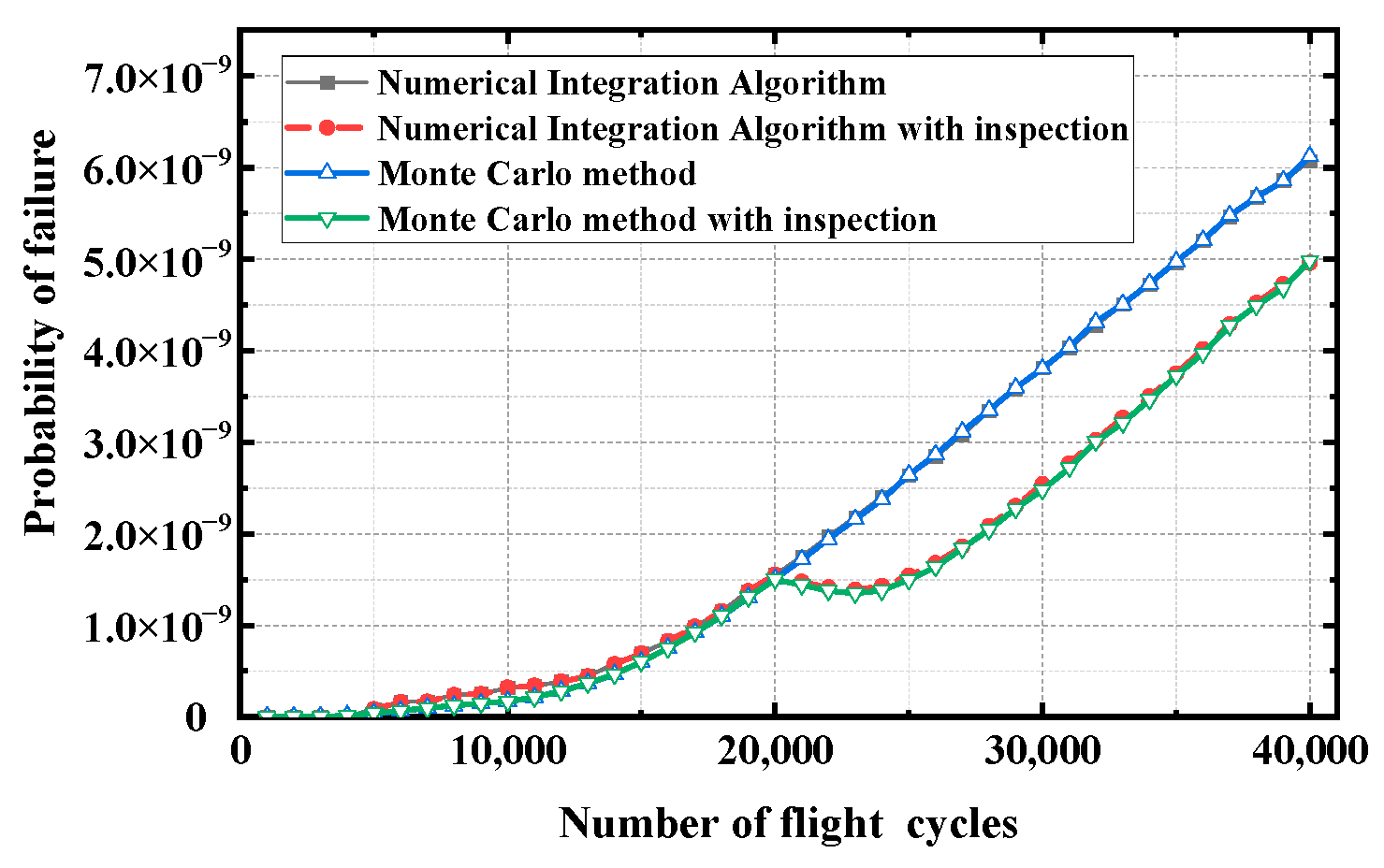
- (2)
- Comparison of the computational precision
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | Crack size (m) |
| a0 | Radius of the initial inclusion (m) |
| a0,C | Initial critical crack size (m) |
| ac | Critical crack size (m) |
| a0,min,POD | Initial crack size corresponding to the minimum detection crack size (m) |
| a0,max,POD | Initial crack size corresponding to the maximum detection crack size (m) |
| B | Stress scatter factor |
| C | Paris fatigue crack growth constants |
| CGF(·) | Crack growth function (m) |
| f | Probability density function |
| K | Stress intensity factor () |
| ΔK | Stress intensity factor range () |
| Kc | Material fracture toughness () |
| n | Paris fatigue crack growth index |
| N | Number of cycles (flight cycle) |
| Ninsp | Inspection time (flight cycle) |
| POF(N) | Probability of failure at N flight cycles |
| pd(a) | Inspection probability of detection |
| Q | Geometrical stress intensity correction factor |
| S | Life scatter factor |
| σma | Maximum equivalent stress (MPa) |
| Ω(N)f | Failure domain at current flight cycles |
| Ω(N)d | Detection domain |
| pd,N=0 (a0) | Mapping of the probability of detection curve at the initial time |
| Ω(N)f,noinsp | Failure domain without inspection |
| PRA | probabilistic risk assessment |
| POD | probability of detection |
| NDI | non-destructive inspection |
References
- Mcclung, R.C.; Lee, Y.D.; Enright, M.P.; Liang, W. New Methods for Automated Fatigue Crack Growth and Reliability Analysis. In ASME Turbo Expo 2012: Turbine Technical Conference and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2012. [Google Scholar]
- Chamis, C.C. Damage Tolerance and Reliability of Turbine Engine Components: National Aeronautics and Space Administration; Glenn Research Center: Cleveland, OH, USA, 1999. [Google Scholar]
- Lin, K.Y.; Styuart, A.V. Probabilistic approach to damage tolerance design of aircraft composite structures. J. Aircr. 2007, 44, 1309–1317. [Google Scholar] [CrossRef]
- Wu, Y.T.; Enright, M.P.; Millwater, H.R. Probabilistic methods for design assessment of reliability with inspection. AIAA J. 2002, 40, 937–946. [Google Scholar] [CrossRef]
- Federal Aviation Administration. Advisory Circular 33.70-1. Guidance Material for Aircraft Engine-Life-Limited Parts Requirements; U.S. Department of Transportation, FAA: Washington, DC, USA, 2009.
- Federal Aviation Administration. Advisory Circular 33.70-2. Damage Tolerance of Hole Features in High-Energy Turbine Engine Rotors; U.S. Department of Transportation, FAA: Washington, DC, USA, 2009.
- Federal Aviation Administration. Advisory Circular 33.14-1. Damage Tolerance for High Energy Turbine Engine Rotors; U.S. Department of Transportation, FAA: Washington, DC, USA, 2001.
- Abdessalem, A.B.; El-Hami, A. A probabilistic approach for optimising hydroformed structures using local surrogate models to control failures. Int. J. Mech. Sci. 2015, 96–97, 143–162. [Google Scholar] [CrossRef]
- Enright, M.P.; Hudak, S.J.; McClung, R.C.; Millwater, H.R. Application of Probabilistic Fracture Mechanics to Prognosis of Aircraft Engine Components. AIAA J. 2006, 44, 311–316. [Google Scholar] [CrossRef][Green Version]
- Huyse, L.; Enright, M.P. Efficient conditional failure analysis: Application to an aircraft engine component. Struct. Infrastruct. Eng. 2006, 2, 221–230. [Google Scholar] [CrossRef]
- Enright, M.P.; McClung, R.C.; Sobotka, J.C.; Irving, G.; Joe, G. Influences of non-destructive inspection simulation on fracture risk assessment of additively manufactured turbine engine components. Turbo Expo: Power for Land, Sea, and Air. Am. Soc. Mech. Eng. 2018, 51135, V07AT32A013. [Google Scholar]
- Gorelik, M. Additive manufacturing in the context of structural integrity. Int. J. Fatigue 2017, 94, 168–177. [Google Scholar] [CrossRef]
- Enright, M.P.; Millwater, H.R.; Huyse, L. Adaptive Optimal Sampling Methodology for Reliability Prediction of Series Systems. AIAA J. 2006, 44, 523–528. [Google Scholar] [CrossRef][Green Version]
- Millwater, H.R.; Enright, M.P.; Fitch, S.H.K. Convergent Zone-Refinement Method for Risk Assessment of Gas Turbine Disks Subject to Low-Frequency Metallurgical Defects. ASME J. Eng. Gas Turbines Power 2006, 129, 827–835. [Google Scholar] [CrossRef][Green Version]
- Wu, Y.T. Computational methods for efficient structural reliability and reliability sensitivity analysis. AIAA J. 1994, 32, 1717–1723. [Google Scholar] [CrossRef]
- Kibria, A.; Castillo−Villar, K.K.; Millwater, H.R. Minimizing the discrepancy between simulated and historical failures in turbine engines: A simulation-based optimization method. Math. Probl. Eng. 2015, 2015, 813565. [Google Scholar] [CrossRef]
- Yang, L.; Ding, S.T.; Wang, Z.Y.; Li, G. Efficient probabilistic risk assessment for aeroengine turbine disks using probability density evolution. AIAA J. 2017, 55, 2755–2761. [Google Scholar] [CrossRef]
- Liu, J.B.; Ding, S.T.; Li, G. Influence of Random Variable Dimension on the Fast Numerical Integration Method of Aero Engine Rotor Disk Failure Risk Analysis. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 84669. [Google Scholar]
- Kozin, F. On the Probability Densities of the Output of Some Random Systems. J. Appl. Mech. 1961, 28, 161–164. [Google Scholar] [CrossRef]
- Christian, A.; Kadau, K. Numerically efficient modified Runge–Kutta solver for fatigue crack growth analysis. Eng. Fract. Mech. 2016, 161, 55–62. [Google Scholar]
- L’Ecuyer, P.; Simard, R.; Chen, E.J.; Kelton, W.D. An Object-Oriented Random-Number Package with Many Long Streams and Substreams. Oper. Res. 2002, 50, 1073–1075. [Google Scholar] [CrossRef]
- Enright, M.P.; Huyse, L. Methodology for Probabilistic Life Prediction of Multiple-Anomaly Materials. AIAA J. 2006, 44, 787–793. [Google Scholar] [CrossRef]
- Pan, X.; Ding, S.; Zhang, W.; Liu, T.; Wang, L.; Wang, L. Probabilistic Risk Assessment in Space Launches Using Bayesian Network with Fuzzy Method. Aerospace 2022, 9, 311. [Google Scholar] [CrossRef]
- Xu, T.; Ding, S.; Zhou, H.; Li, G. Machine learning-based efficient stress intensity factor calculation for aeroengine disk probabilistic risk assessment under polynomial stress fields. Fatigue Fract. Eng. Mater. Struct. 2021, 45, 451–465. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.B. Advances in the research on probability density evolution equations of stochastic dynamical systems. Adv. Mech. 2010, 40, 170–188. [Google Scholar]
- Li, J.; Chen, J.B. The principle of preservation of probability and the generalized density evolution equation. Struct. Saf. 2008, 30, 65–77. [Google Scholar] [CrossRef]
- Sub-Team to the Aerospace Industries Association Rotor Integrity Sub-Committee. The development of anomaly distributions for aircraft engine titanium disk alloys. In Proceedings of the 38th Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 7–10 April 1997. Paper No: AIAA 97-1068. [Google Scholar]
- Newman, J.C.; Raju, I.S. Stress-intensity factor equations for cracks in three-dimensional finite bodies. In Fracture Mechanics: Fourteenth Symposium—Volume I: Theory and Analysis; ASTM International: West Conshohocken, PA, USA, 1983; pp. 238–265. [Google Scholar]
- Glinka, G.; Shen, G. Universal features of weight functions for cracks in mode I. Eng. Fract. Mech. 1991, 40, 1135–1146. [Google Scholar] [CrossRef]
- Zhou, H.M.; Ding, S.T.; Guo, L. Universal weight function method on the probabilistic surface damage tolerance assessment of aeroengine rotors. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 84669, p. V014T14A028. [Google Scholar]
- Wang, L.; Wang, X.; Su, H.; Lin., G. Reliability estimation of fatigue crack growth prediction via limited measured data. Int. J. Mech. Sci. 2017, 121, 44–57. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A critical analysis of crack propagation laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Wehling, P.; LaBudde, R.A.; Brunelle, S.L.; Nelson, M.T. Probability of detection (POD) as a statistical model for the validation of qualitative methods. J. AOAC Int. 2011, 94, 335–347. [Google Scholar] [CrossRef]
- Ding, S.T.; Wang, Z.Y.; Qiu, T.; Zhang, G.; Li, G. Probabilistic failure risk assessment for aeroengine disks considering a transient process. Aerosp. Sci. Technol. 2018, 78, 696–707. [Google Scholar] [CrossRef]
- Enright, M.P.; McFarland, J.; McClung, R.; Wu, W.T.; Shankar, R. Probabilistic Integration of Material Process Modeling and Fracture Risk Assessment Using Gaussian Process Models. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, MA, USA, 8–11 April 2013. [Google Scholar]




| Boundary Conditions | Value |
|---|---|
| Disk rotation speed | 35,000 rev/min |
| Traffic | 6.825 × 10−5 kg/s |
| Inlet temperature | 288.15 K |
| Outlet temperature | 445.83 K |
| Outlet pressure | 383 kPa |
| Parameters | Value |
|---|---|
| Density | 4450 kg/m3 |
| Young’s modulus | 120,000 MPa |
| Poisson’s ratio | 0.361 |
| da/dN | )3.87 m/cycle |
| Fracture toughness | |
| Yield strength | 834 MPa |
| Calculation Method | Probability of Failure at 40,000 Flight Cycles | Relative Error |
|---|---|---|
| Monte Carlo simulation with inspection | 4.8741197 × 10−9 | - |
| Monte Carlo simulation without inspection | 6.0264085 × 10−9 | - |
| Numerical integration with inspection | 4.8309859 × 10−9 | 0.8% |
| Numerical integration without inspection | 6.0202465 × 10−9 | 0.1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Liu, J.; Zhou, H.; Zuo, L.; Ding, S. Efficient Numerical Integration Algorithm of Probabilistic Risk Assessment for Aero-Engine Rotors Considering In-Service Inspection Uncertainties. Aerospace 2022, 9, 525. https://doi.org/10.3390/aerospace9090525
Li G, Liu J, Zhou H, Zuo L, Ding S. Efficient Numerical Integration Algorithm of Probabilistic Risk Assessment for Aero-Engine Rotors Considering In-Service Inspection Uncertainties. Aerospace. 2022; 9(9):525. https://doi.org/10.3390/aerospace9090525
Chicago/Turabian StyleLi, Guo, Junbo Liu, Huimin Zhou, Liangliang Zuo, and Shuiting Ding. 2022. "Efficient Numerical Integration Algorithm of Probabilistic Risk Assessment for Aero-Engine Rotors Considering In-Service Inspection Uncertainties" Aerospace 9, no. 9: 525. https://doi.org/10.3390/aerospace9090525
APA StyleLi, G., Liu, J., Zhou, H., Zuo, L., & Ding, S. (2022). Efficient Numerical Integration Algorithm of Probabilistic Risk Assessment for Aero-Engine Rotors Considering In-Service Inspection Uncertainties. Aerospace, 9(9), 525. https://doi.org/10.3390/aerospace9090525