A Global ArUco-Based Lidar Navigation System for UAV Navigation in GNSS-Denied Environments
Abstract
:1. Introduction
- ✶
- The factor graph structure of the Lidar navigation system based on global ArUco is constructed, which can fuse the sensor data globally. The accuracy and robustness of the navigation system can be significantly improved by combining the processing method proposed in this paper when the Lidar motion solution is degraded.
- ✶
- A global ArUco factor is constructed, which can update confidence accurately according to sampling. This factor participates in the optimization as a priori of the state in the factor graph, which ensures that the navigation system can work in the geodetic coordinate system fixed with the actual scene and corrects the error of the navigation system according to the actual scene. Compared with traditional vision, it improves the accuracy of the navigation system and reduces the use of computing resources, and enhances real-time performance.
- ✶
- A loopback determination method based on global ArUco is constructed, making loopback detection more accurate and efficient.
- ✶
- The navigation system described in this paper is tested using the UAV platform in the dry coal shed of thermal power plants, one of the practical application scenarios, and compared with other Lidar algorithms.
2. Related Work
3. ArUco-Based Lidar Navigation System for UAVs in GNSS-Denial Environment
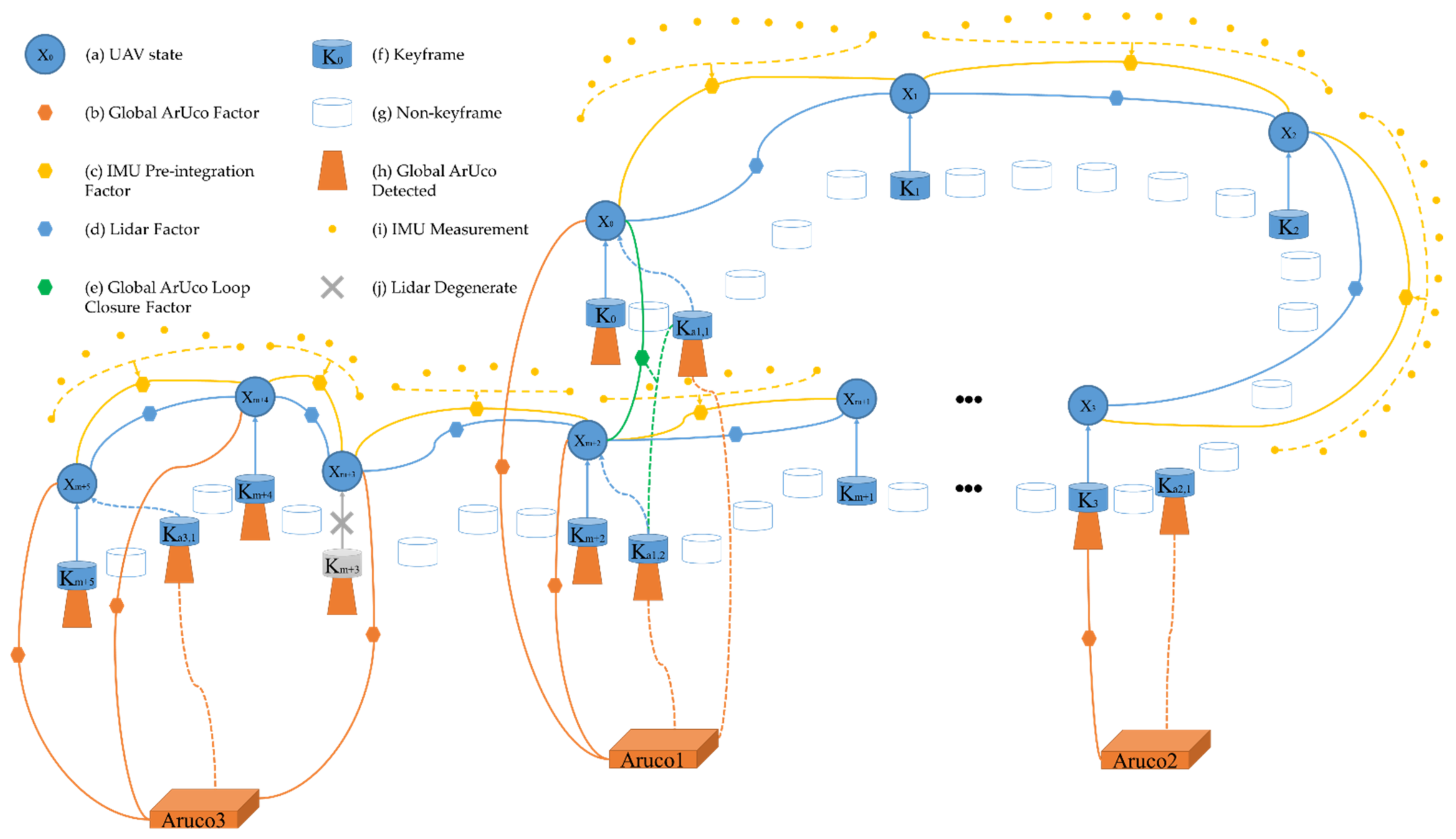
3.1. System Overview
3.2. Global ArUco Factor
3.3. IMU Pre-Integration Factor
3.4. Lidar Factor
3.5. Global ArUco Loop Closure Factor
4. Experiment
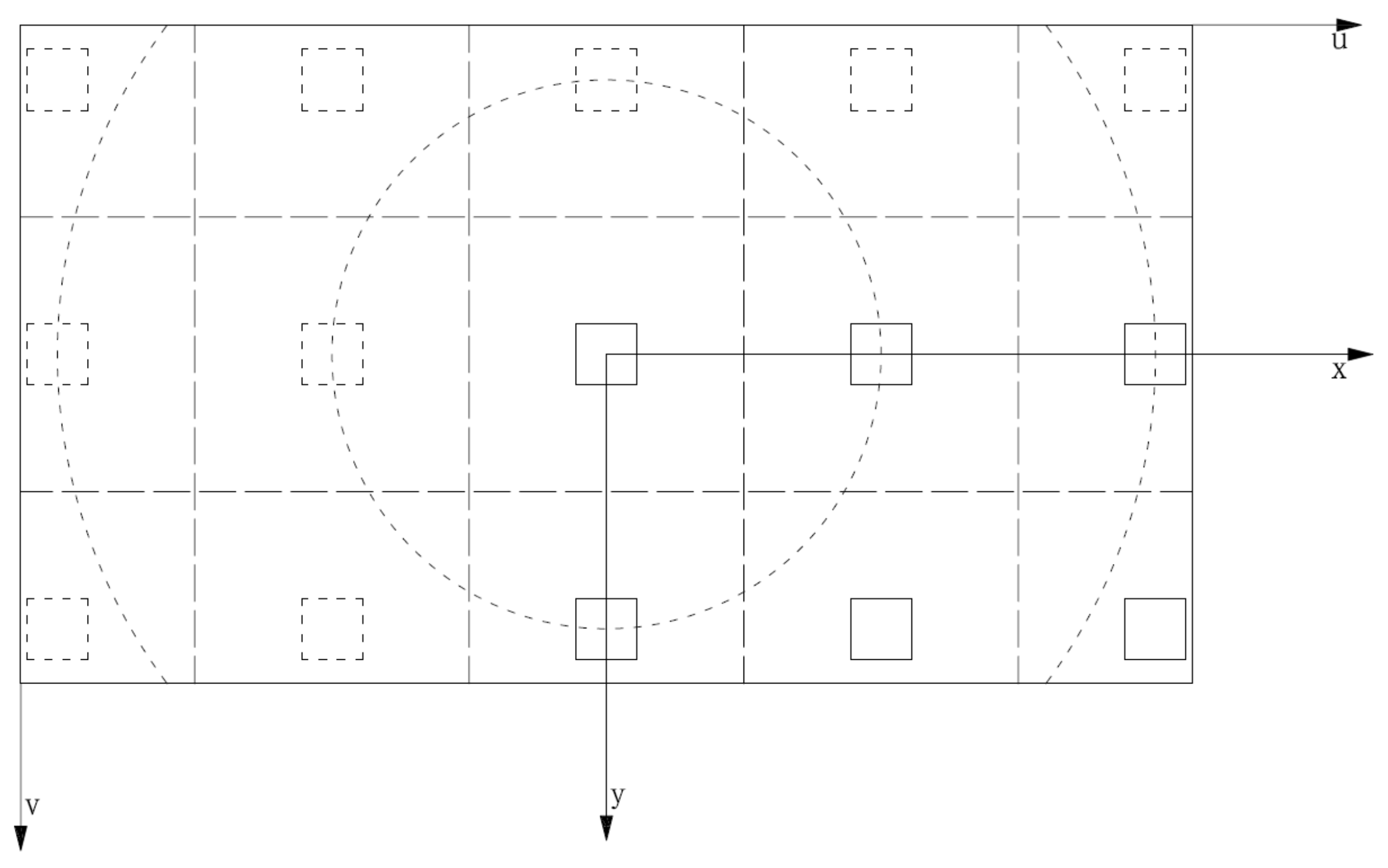
4.1. The Calibration of Global ArUco Dynamic Measurement Noise Covariance
4.2. The Tests of the Navigation System in the Working Condition
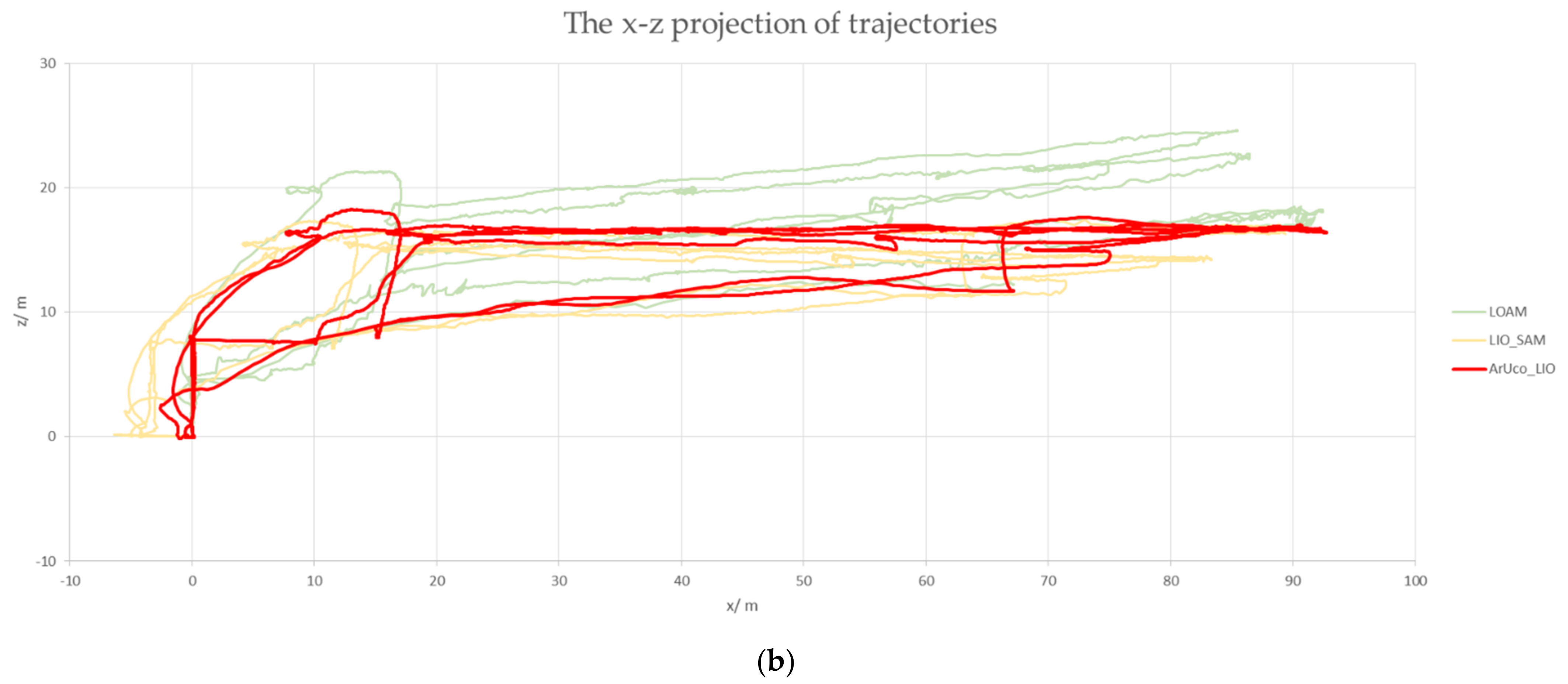
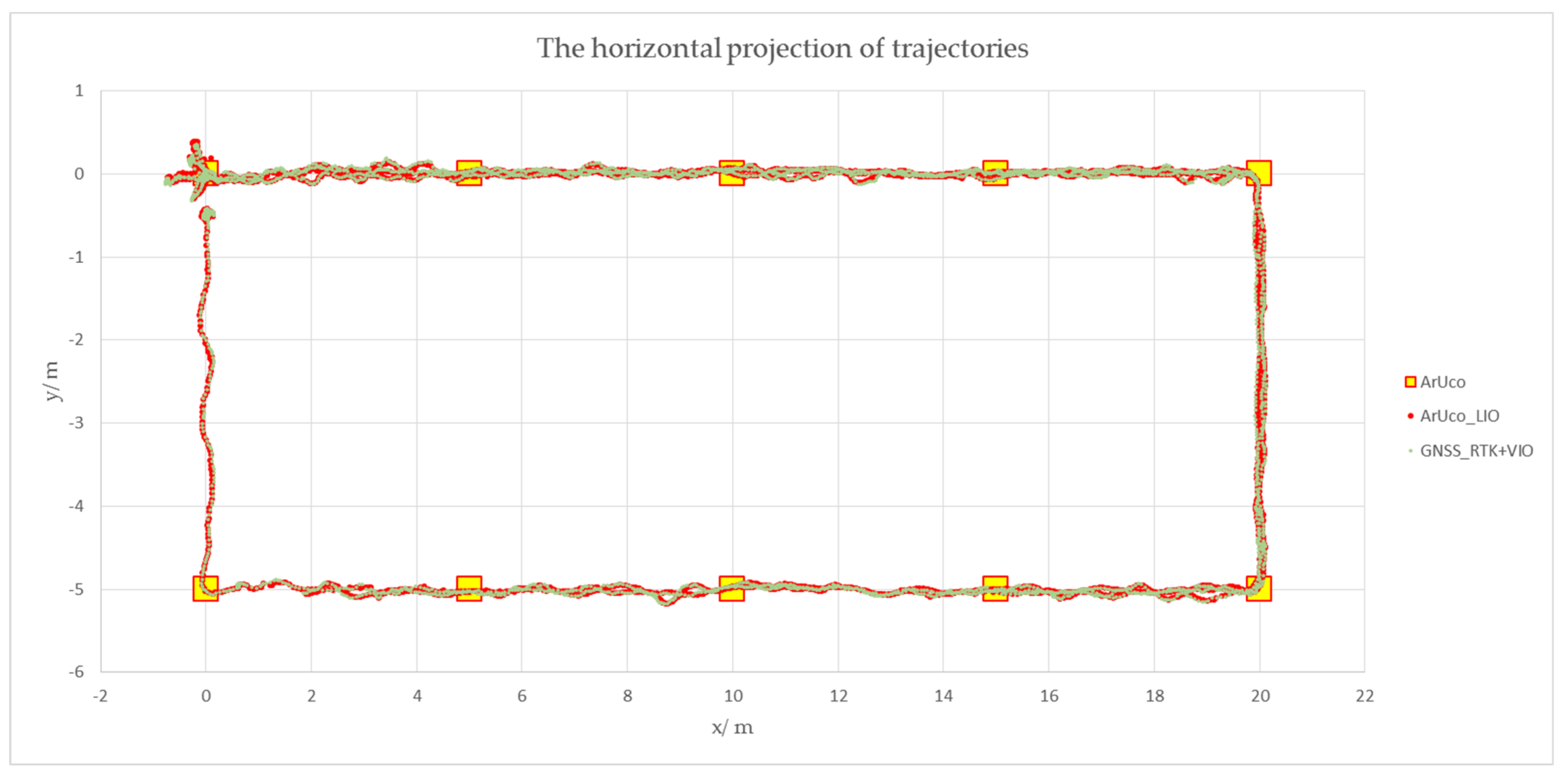
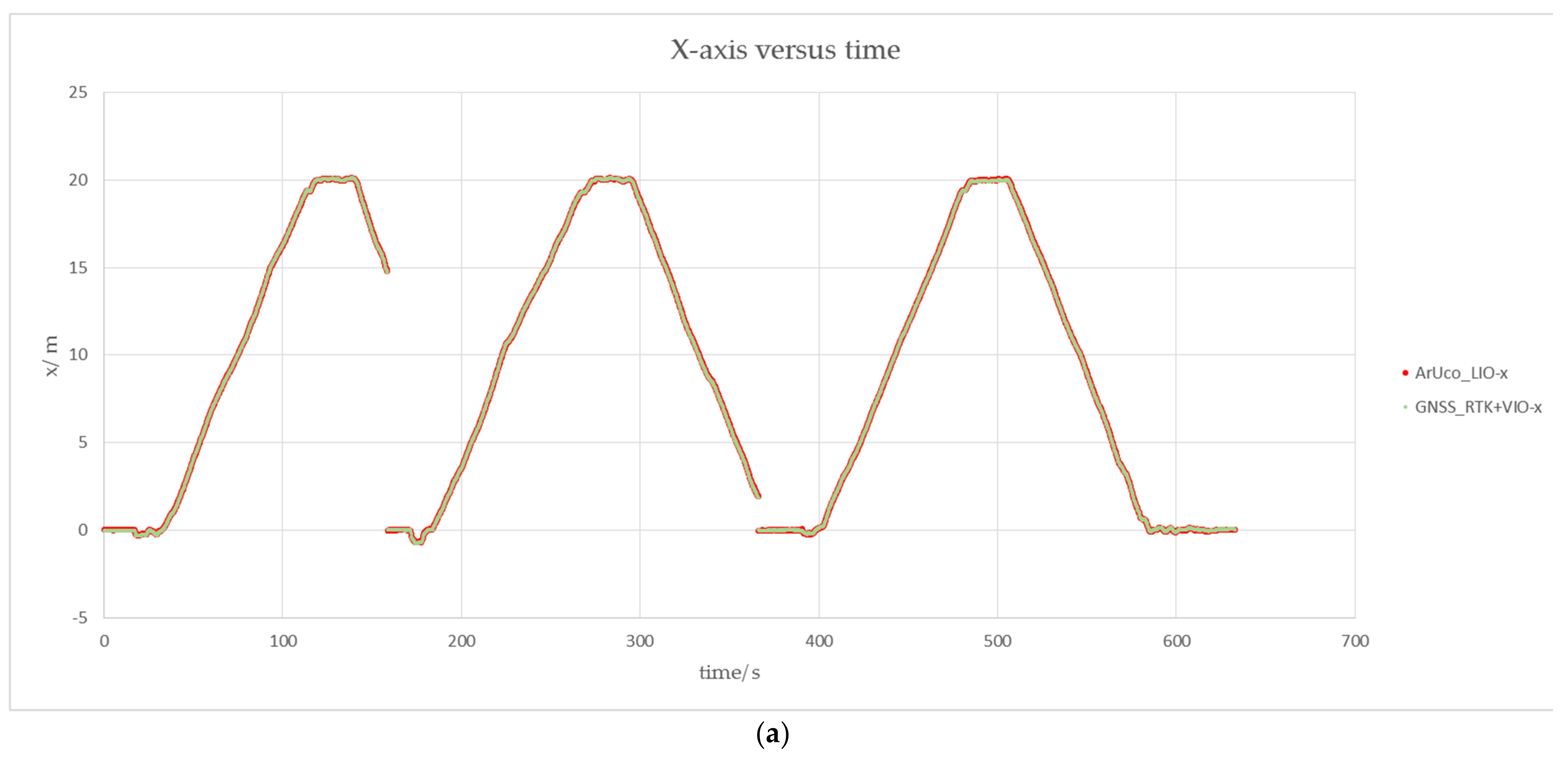
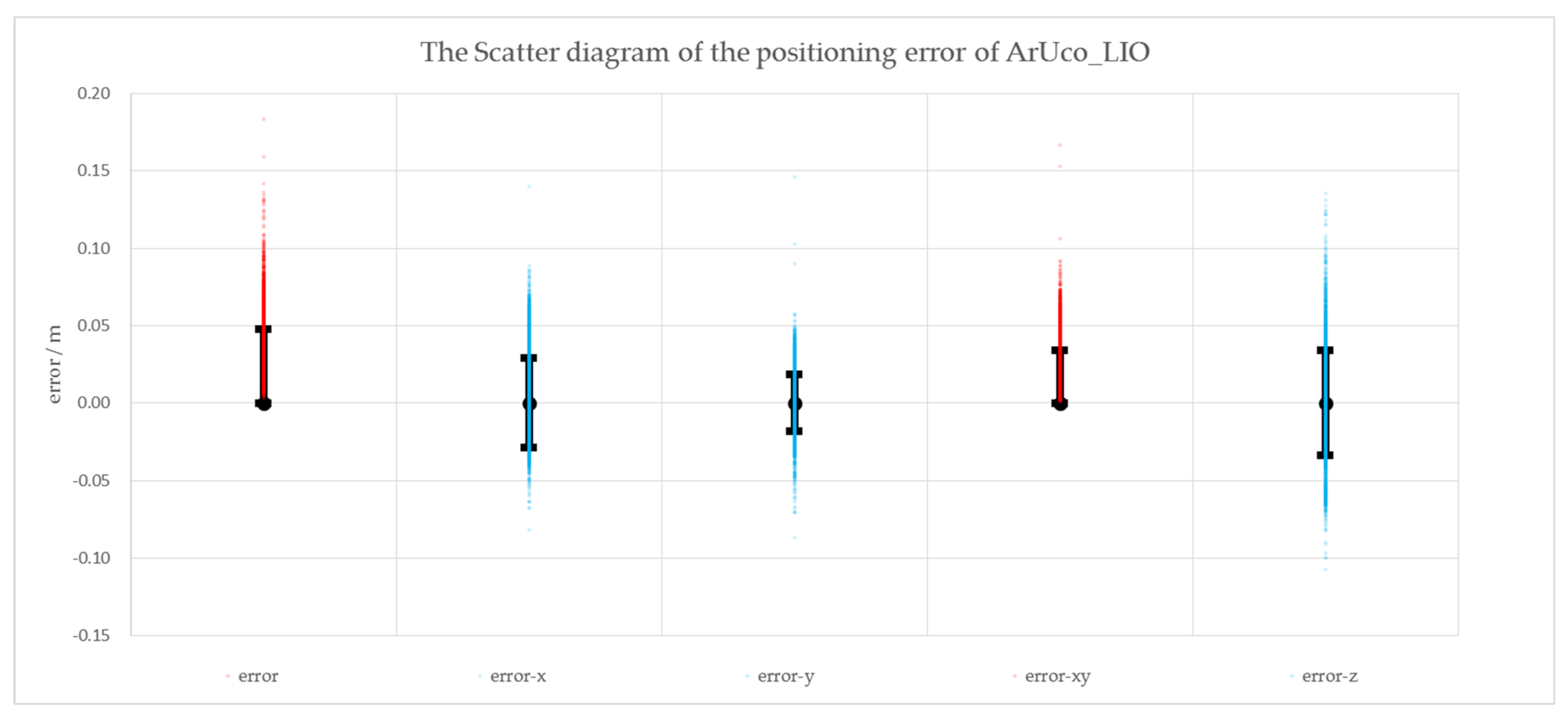
4.3. The Experiment on the Navigation System Accuracy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Dalamagkidis, K.; Valavanis, K.P.; Piegl, L.A. Current Status and Future Perspectives for Unmanned Aircraft System Operations in the US. J. Intell. Robot. Syst. 2008, 52, 313–329. [Google Scholar] [CrossRef]
- Cui, L. Research on the Key Technologies of MEMS-SINS/GPS Integration Navigation System. Ph.D. Thesis, Chinese Academy of Sciences, Changchun, China, 2014. [Google Scholar]
- Zhou, J.; Kang, Y.; Liu, W. Applications and Development Analysis of Unmanned Aerial Vehicle (UAV) Navigation Technology. J. CAEIT 2015, 10, 274–277, 286. [Google Scholar]
- Yu, H.; Niu, Y.; Wang, X. Stages of development of Unmanned Aerial Vehicles. Natl. Def. Technol. 2021, 42, 18–24. [Google Scholar]
- Wu, Y.; Wang, X.; Yang, L.; Cao, P. Autonomous Integrity Monitoring of Tightly Coupled GNSS/INS Navigation System. Acta Geod. Et Cartogr. Sin. 2014, 43, 786–795. [Google Scholar]
- Sun, G. Research on Inertial Integrated Navigation Technology for Low-Cost Mini Unmanned Aerial Vehicle. Ph.D. Thesis, Nanjing University of Science and Technology, Nanjing, China, 2014. [Google Scholar]
- Nasrollahi, M.; Bolourian, N.; Zhu, Z.; Hammad, A. Designing Lidar-equipped UAV Platform for Structural Inspection. In Proceedings of the 34th International Symposium on Automation and Robotics in Construction, Taipei, Taiwan, 28 June–1 July 2018. [Google Scholar]
- Rydell, J.; Tulldahl, M.; Bilock, E.; Axelsson, L.; Köhler, P. Autonomous UAV-based Forest Mapping Below the Canopy. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Portland, OR, USA, 20–23 April 2020. [Google Scholar]
- Ding, Z.; Zhang, Y. Research on the influence of coal mine dust concentration on UWB ranging precision. Ind. Mine Autom. 2021, 11, 1–4. [Google Scholar]
- Mur-Artal, R.; Tardos, J.D. Visual-Inertial Monocular SLAM with Map Reuse. IEEE Robot. Autom. Lett. 2017, 2, 796–803. [Google Scholar] [CrossRef]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-time. In Proceedings of the Robotics: Science and Systems, Berkeley, CA, USA, 12−16 July 2014. [Google Scholar]
- Shan, T.; Englot, B. LeGO-LOAM: Lightweight and Ground-Optimized Lidar Odometry and Mapping on Variable Terrain. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Madrid, Spain, 1–5 October 2018. [Google Scholar]
- Xu, W.; Zhang, F. FAST-LIO: A Fast, Robust Lidar-Inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter. IEEE Robot. Autom. Lett. 2020, 6, 3317–3324. [Google Scholar] [CrossRef]
- Zhao, S.; Fang, Z.; Li, H.; Scherer, S. A Robust Laser-Inertial Odometry and Mapping Method for Large-Scale Highway Environments. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Macau, China, 3–8 November 2019. [Google Scholar]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. LIO-SAM: Tightly-coupled Lidar Inertial Odometry via Smoothing and Mapping. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 24 October 2020–24 January 2021. [Google Scholar]
- Shan, T.; Englot, B.; Ratti, C.; Rus, D. LVI-SAM: Tightly-Coupled Lidar-Visual-Inertial Odometry via Smoothing and Mapping. In Proceedings of the IEEE International Conference on Robotics and Automation, Xi’an, China, 30 May–5 June 2021. [Google Scholar]
- Garrido-Jurado, S.; Muñoz-Salinas, R.; Madrid-Cuevas, F.J.; Marín-Jiménez, M.J. Automatic generation and detection of highly reliable fiducial markers under occlusion. Pattern Recognit. 2014, 47, 2280–2292. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, Y.; He, X.; Zhang, S.; Ye, C.; Feng, T.; Xiong, L. Visual Semantic Landmark-Based Robust Mapping and Localization for Autonomous Indoor Parking. Sensors 2019, 19, 161. [Google Scholar] [CrossRef] [PubMed]
- Lv, J.; Xu, J.; Hu, K.; Hu, K.; Liu, Y.; Zuo, X. Targetless Calibration of Lidar-IMU System Based on Continuous-time Batch Estimation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 25–29 October 2020. [Google Scholar]
- Frank, D.; Michael, K. Factor Graphs for Robot Perception. Found. Trends Robot. 2017, 6, 1–139. [Google Scholar]
- Kaess, M.; Johannsson, H.; Roberts, R.; Ila, V.; Leonard, J.J.; Dellaert, F. iSAM2: Incremental smoothing and mapping using the Bayes tree. Int. J. Robot. Res. 2011, 31, 216–235. [Google Scholar] [CrossRef]
- ArUco Marker Detection. Available online: https://docs.opencv.org/4.x/d9/d6a/group__ArUco.html (accessed on 12 August 2021).
- Forster, C.; Carlone, L.; Dellaert, F.; Scaramuzza, D. On-Manifold Pre-integration for Real-Time Visual—Inertial Odometry. IEEE Trans. Robot. 2017, 33, 1–21. [Google Scholar] [CrossRef]
- Bai, W.; Li, G.; Han, L. Correction Algorithm of LIDAR Data for Mobile Robots. In Proceedings of the International Conference on Intelligent Robotics and Applications, Wuhan, China, 15–18 August 2017; pp. 101–110. [Google Scholar]
- Ji, Z.; Kaess, M.; Singh, S. On degeneracy of optimization-based state estimation problems. In Proceedings of the IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 16–21 May 2016. [Google Scholar]











| X | 1 | 2 | 3 | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y | |||||||||||||||||||||
| 1 | 4.8 × 10−8 | 1.8 × 10−7 | 1.7 × 10−6 | ||||||||||||||||||
| 2.3 × 10−7 | 4.9 × 10−8 | 5.9 × 10−8 | |||||||||||||||||||
| 3.9 × 10−5 | 5.7 × 10−6 | 1.3 × 10−5 | |||||||||||||||||||
| 5.5 × 10−3 | 6.4 × 10−4 | 1.6 × 10−3 | |||||||||||||||||||
| 7.7 × 10−3 | 2.5 × 10−3 | 2.7 × 10−3 | |||||||||||||||||||
| 5.2 × 10−5 | 3.3 × 10−5 | 5.8 × 10−5 | |||||||||||||||||||
| 2 | 7.8 × 10−8 | 7.4 × 10−7 | 5.2 × 10−6 | ||||||||||||||||||
| 1.0 × 10−6 | 9.3 × 10−7 | 1.6 × 10−6 | |||||||||||||||||||
| 2.9 × 10−5 | 2.4 × 10−5 | 4.6 × 10−5 | |||||||||||||||||||
| 1.8 × 10−3 | 8.8 × 10−4 | 2.6 × 10−4 | |||||||||||||||||||
| 2.5 × 10−2 | 2.6 × 10−2 | 2.6 × 10−2 | |||||||||||||||||||
| 9.3 × 10−4 | 1.1 × 10−3 | 1.8 × 10−3 | |||||||||||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, Z.; Lin, D.; Jin, R.; Lv, J.; Zheng, Z. A Global ArUco-Based Lidar Navigation System for UAV Navigation in GNSS-Denied Environments. Aerospace 2022, 9, 456. https://doi.org/10.3390/aerospace9080456
Qiu Z, Lin D, Jin R, Lv J, Zheng Z. A Global ArUco-Based Lidar Navigation System for UAV Navigation in GNSS-Denied Environments. Aerospace. 2022; 9(8):456. https://doi.org/10.3390/aerospace9080456
Chicago/Turabian StyleQiu, Ziyi, Defu Lin, Ren Jin, Junning Lv, and Zhangxiong Zheng. 2022. "A Global ArUco-Based Lidar Navigation System for UAV Navigation in GNSS-Denied Environments" Aerospace 9, no. 8: 456. https://doi.org/10.3390/aerospace9080456
APA StyleQiu, Z., Lin, D., Jin, R., Lv, J., & Zheng, Z. (2022). A Global ArUco-Based Lidar Navigation System for UAV Navigation in GNSS-Denied Environments. Aerospace, 9(8), 456. https://doi.org/10.3390/aerospace9080456






