A Hybrid Game Strategy for the Pursuit of Out-of-Control Spacecraft under Incomplete-Information

Abstract

This paper investigates the pursuit problem of out-of-control spacecraft under incomplete-information, and provides new ideas for the disposal of dangerous spacecraft with obstacle avoidance capability. Throughout the pursuit process, the maneuver strategy of the out-of-control spacecraft is unknown, and its possibly unconventional and irregular maneuvers may endanger the safe operation of any other spacecraft on orbit. Based on the differential game theory, complete information game strategy pairs are derived. Then, considering that the control information of the target is unavailable to the pursuer, the target’s maneuver is regarded as the disturbance item. The incomplete information game strategy is derived from the unilateral optimal cost function. Furthermore, the disturbance estimator is designed to identify the missing information of the target. The optimal hybrid game strategy is proposed as an approach to compensate the target maneuver strategy. Simulation study has been conducted and the results have validated that the missing information can be effectively estimated using the estimator. The designed hybrid game strategy can achieve rapid approach, while saving fuel consumption for on-orbit service.

1. Introduction

With the increasing frequency of commercial activities since the 1960s, spacecraft numbers continue to grow rapidly. Unavoidably, there has also been an increase in the spacecraft with launch and on-orbit operation failure [1]. Once spacecrafts, with autonomous maneuvering and decision-making capabilities, are out of control, their potential unconventional and irregular maneuvers endanger the safe operation of spacecraft on orbit, and the losses would be difficult to estimate. Therefore, in the research of on-orbit service in recent years, the safe approach and processing of out-of-control spacecraft have been paid more attention. In general, the disposal of satellites can be completed by analyzing the orbital data towards its end of mission, if it carries de-orbiting devices. However, once a satellite is out of control, its disposal has to be on-orbit processed by an active debris removal spacecraft.

In this paper, an approach method for a class of uncontrolled satellites with space situation awareness is studied. Such satellites have the ability to avoid obstacles and can make autonomous decisions to keep on-orbit service spacecraft away. Since the target can automatically perceive space information and make unconventional maneuver strategies, a bilateral optimal strategy, which considers target irregular maneuvers, based on game theory, is more suitable than the traditional unilateral optimal control strategy [2]. In addition, the out-of-control satellite has unknown maneuvers. Consequently, the pursuer cannot obtain the complete information of the target through traditional means, such as two-line elements (TLE), which leads to the problem of incomplete information game. Therefore, it is of great significance to study the pursuit game problem of the out-of-control spacecraft with obstacle avoidance capability under incomplete information. We explored the problem of space rendezvous and approach of out-of-control spacecraft within the problem of game without considering non -peaceful purpose.

There have been many studies on the two-side game, where the target has maneuverability, and most of these are based on differential game theory and applied in the military field [3]. Ye [4] derived vector guidance for satellite proximate interception. The formula for calculating the intercept time was given, by which the interception with the desired miss distance could be achieved. Stupik [5] derived the optimal thrust angle for the satellite game, based on the Hill-Clohessy-Wilshire (HCW) equation. The particle swarm optimization was used to obtain an open-loop solution, while closed-loop control strategy was given by interpolating and extrapolating a series of trajectories. For the game with complex dynamics of the two players, the problem evolved into the two-point boundary value problem (TPBVP) with coupled nonlinear equations, which is difficult to solve. Aiming at this problem, authors in Refs. [6,7,8] used the genetic algorithm to approximately calculate initial value of the adjoint state so that, then, the exact value could be calculated by nonlinear programming. In Ref. [9], the thrust configurations of the two players were assumed to be different. Then the pursuit–evasion game was transferred into a TPBVP with four unknowns and four nonlinear equations. Based on the indirect method, a numerical algorithm for solving the TPBVP was proposed. Gutman [10] derived the missile vector guidance laws in the polar coordinate and in the spherical coordinate, respectively. Furthermore, a quadratic equation on time-to-go was proposed to determine the terminal intercept time, and the bifurcation of this equation was discussed in Refs. [11,12]. With this method, the shortest intercept time could be calculated and rapid interception could be achieved.

Game theory also provides a suitable frame to study the sophisticated optimal decision and control problems, where the performance index function of each player depends on the control strategies of itself and all other players. In Ref. [13], the two-side game was considered first and the target strategy could be optimized based on the attacking missile strategy. In addition, the author analyzed the game with three players. The target evasion strategy and the defender pursuit strategy were derived cooperatively. Simulations indicated that the defender could intercept the attacking missile using the cooperative strategy. Perelman [14] considered the three-player game and derived a closed-loop game strategy based on continuous dynamics and discrete dynamics, respectively. Then, the guidance gains and the condition of the saddle-point existence were analyzed under the different game cases. Simulations showed that the pursuer could be attacked by the defender, and the target was used as a bait to lure the pursuer. Literature [15] proposed a differential game method to stabilize a combined spacecraft composed of multiple microsatellites and a failed spacecraft, in which each microsatellite could independently calculate its own control strategy. Numerical simulations verified the effectiveness of the differential game method in the attitude takeover control of the failed spacecraft.

These literatures mentioned above were the application of complete information game strategy under idealized conditions. This paper will focus on the safe approach of uncontrolled spacecraft with continuous and dynamic obstacle avoidance ability under incomplete information. In a practical pursuit process, some players have private information, and others should consider this fact when forming expectations of these players’ behaviors. The pursuer may not obtain game information completely due to lost contact and component damage of the target. Aiming at the incomplete information problem, Ref. [16] considered the evasion defense problem for a given interceptor strategy. For the target and the defender, the optimal strategy of single-direction communication and the game strategy of two-direction communication were derived, respectively. Refs. [17,18] investigated the incomplete-information and imperfect-information situations based on double integral dynamics. The missing information was treated as the extended state, and then the observer was applied to estimate the information. Satak [19,20] used series extension to approximate the unknown game value function, which played a key role in strategy derivation, and the series coefficients were updated by the observable target information. In Refs. [21,22], authors used the multiple mode adaptive estimator to identify the unknown guidance law of the pursuer. Several filters matched to possible guidance laws were applied to obtain estimated posterior probability. By fusing guidance laws in probability, the target strategy and the defender strategy could be derived. Wang [23] proposed a method to degenerate the game into a strong tracking problem. The extended Kalman Filter was used to obtain relative state of the target, the observability was analyzed under different measurement methods, based on linear quadratic differential game theory. Similar to the optimization object considered in this paper, one of the goals of our paper is to approach the target with minimal fuel consumption.

We should consider not only the completeness and symmetry of the information during the dynamic game scenario, but also the potential unconventional and irregular changes of the target maneuver strategies. The pursuer can adopt hybrid game strategies to cope with the capricious changes of the target maneuver strategy effectively. Hafer [24] considered the scenario where the spacecraft needed a hybrid strategy to avoid obstacles and evade another spacecraft. By comparing game value and obstacle value, the spacecraft would switch its strategy to balance the two missions. Turesky [25] derived evasion strategy for hybrid pursuit dynamics. If the switch information was available to the target, the evasion strategy could be given as a bang-bang form, which relied on the switch function and the zero-effort miss (ZEM). On the other hand, the matrix game was formulated for the incomplete-information scenario. Through the Nash equilibrium, the mixed saddle-point solution could be given, which guaranteed the low bound of ZEM. Shinar [26,27] considered the pursuit-evasion game with hybrid pursuer dynamics and evader dynamics. On this basis, the corresponding opponent’s strategies were derived and the capture zone was constructed.

In summary, in the current research methods of the game problem in aerospace, the theory of differential game accounts for the majority [28,29,30]. Although there is much research on pursuit–evasion, most of the discussions are about a situation in which the pursuer can obtain complete information of the target. However, due to lost contact of the target or the failure of its components, the target information is not completely available to the pursuer in practice, which makes the pursuit not achievable. Moreover, in Refs. [17,22], although the authors consider the incomplete-information situation, the player dynamics are simplified, which is not consistent with the actual scenario of spacecraft pursuit. All in all, the formation of the game relationship requires conflict of interests between spacecrafts. A large amount of literatures have studied the application of differential game in the field of target interception. However, this paper focuses on its application in the field of on-orbit services. Thus, this paper applies differential game theory to space rendezvous and the approach of runaway spacecraft, regardless of its non-peaceful uses. We assume that the pursuer can change its maneuver strategies during the game process, and that the target knows the maneuver strategies that the pursuer may take, that is, the target has complete information during the game process, but does not know the actual game strategy taken by the pursuer. In this scenario, we propose the optimal hybrid game strategy in pursuit of the out-of-control spacecraft using its incomplete information. The designed hybrid game strategy can achieve a rapid approach while saving fuel consumption. This approach strategy, based on game theory, can also deal with failed targets with dynamic avoidance capability in the future constellation.

This paper is organized as follows: the relative dynamics model is first established in Section 2, the complete information game strategy pairs and the game strategies under incomplete information are subsequently derived in Section 3. The target missing information is estimated by the disturbance estimator and the corresponding optimal hybrid strategy is then presented in Section 4. Simulation study has been conducted to verify the proposed hybrid game strategy and evaluate the satellite safe approach performance in Section 5. Lastly, conclusions are presented in Section 6.

2. Relative Dynamics Model

For the spacecraft terminal approach, we can establish a moving orbital coordinate to derive the relative dynamics for the pursuer [4]. As shown in Figure 1, we can establish a satellite near the pursuer as the reference satellite O₁, with P as a pursuer. A non-inertial orbital coordinate frame O₁xyz, known as the local vertical local horizon (LVLH) coordinate [31] can be established by setting the center of the reference satellite as the origin. The O₁x axis is directed from the Earth’s center to the reference satellite. The O₁z axis is orientated to the direction of the orbital angular momentum of the reference satellite, and the O₁y axis completes the right-hand rule.

Let ${\mathit{r}}_1$, ${\mathit{r}}_2$ be the positions of the reference satellite and the pursuer in the earth inertial coordinate frame OXYZ. Then, the dynamics of the two satellites can be given as

$$\begin{array}{l}{\ddot{\mathit{r}}}_1=-\frac{\mu }{{\mathit{r}}_1^3}{\mathit{r}}_1\\ {\ddot{\mathit{r}}}_2=-\frac{\mu }{{\mathit{r}}_2^3}{\mathit{r}}_2+\mathit{f}\end{array}$$

(1)

where μ is the earth gravitational constant, $\mathit{f}$ is the thrust acceleration of the pursuer.

Defining the relative position between the pursuer and the reference satellite as $\delta \mathit{r}={\mathit{r}}_2-{\mathit{r}}_1$ and differentiating it, we can obtain the dynamic of the pursuer as

$$\delta \ddot{\mathit{r}}={\ddot{\mathit{r}}}_2-{\ddot{\mathit{r}}}_1=-\frac{\mu }{{\mathit{r}}_2^3}{\mathit{r}}_2+\frac{\mu }{{\mathit{r}}_1^3}{\mathit{r}}_1+\mathit{f}$$

(2)

Since the orbital coordinate rotates with the motion of the reference satellite, the relative position derivatives can be derived from the vector differentiation relations as follows:

$$\begin{array}{l}\delta \dot{\mathit{r}}=\delta {\mathit{r}}^{\prime }+\omega \times \delta \mathit{r}\\ \delta \ddot{\mathit{r}}=\delta {\mathit{r}}^{″}+2\omega \times \delta {\mathit{r}}^{\prime }+\dot{\omega }\times \delta \mathit{r}+\omega \times \left(\omega \times \delta \mathit{r}\right)\end{array}$$

(3)

where $\delta {\mathit{r}}^{\prime }$, $\delta {\mathit{r}}^{″}$ are the first and the second derivatives of $\delta \mathit{r}$ in orbital coordinate, and ω represents the angular velocity of the orbital coordinate frame.

Therefore, the dynamic of the pursuer in the orbital coordinate frame can be rewritten as:

$$\delta {\mathit{r}}^{″}=-2\omega \times \delta {\mathit{r}}^{\prime }-\dot{\omega }\times \delta \mathit{r}-\omega \times \left(\omega \times \delta \mathit{r}\right)-\frac{\mu }{{\mathit{r}}^3}{\mathit{r}}_P+\frac{\mu }{{\mathit{r}}^3}{\mathit{r}}_O+\mathit{f}$$

(4)

Under the assumption that the reference satellite moves along a circular orbit and the relative distance between the pursuer and the reference satellite is far less than the geocentric distance of the reference satellite, namely, $\delta \mathit{r}\ll \mathit{r}$.

$$\begin{array}{l}\omega ={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^{\mathrm{T}}\omega \\ \dot{\omega }={\left[\begin{array}{ccc}0& 0& 0\end{array}\right]}^{\mathrm{T}}\end{array}$$

(5)

The dynamic of the pursuer in the LVLH coordinate can be simplified to the Clohessy-Wiltshire (CW) equations as:

$$\begin{array}{l}\ddot{x}-2\omega \dot{y}-3{\omega }^{2}x=u_x\\ \ddot{y}+2\omega \dot{x}=u_y\\ \ddot{z}+{\omega }^{2}z=u_z\end{array}$$

(6)

where $x$, $y$, $z$ are position components of the pursuer in the LVLH coordinate, and $u_x$, $u_y$, $u_z$ represent the three-axis thrust accelerations of the pursuer.

Defining the state variable $\mathit{X}={\left[\begin{array}{cccccc}x& y& z& \dot{x}& \dot{y}& \dot{z}\end{array}\right]}^{\mathrm{T}}$, and the control acceleration variable $\mathit{U}={\left[\begin{array}{ccc}{u}_x& u_y& u_z\end{array}\right]}^{\mathrm{T}}$, we can rewrite Equation (6) in the state space form as:

$$\dot{\mathit{X}}=\mathit{A}\mathit{X}+\mathit{B}\mathit{U}$$

(7)

with the matrices:

$$\mathit{A}=\left[\begin{array}{cccccc}0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\\ 3{\omega }^2& 0& 0& 0& 2\omega & 0\\ 0& 0& 0& -2\omega & 0& 0\\ 0& 0& -{\omega }^2& 0& 0& 0\end{array}\right], \mathrm{and} \mathit{B}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$

We select another satellite as our target $E$. For the terminal approach, the pursuer $P$ is close to the target $E$ in position. As the formula deduces, a satellite near them is chosen as the reference satellite to establish the LVLH frame. Thus, the relative dynamics for the two players in the LVLH coordinate are as follows:

$$\begin{array}{l}{\dot{\mathit{X}}}_P=\mathit{A}{\mathit{X}}_P+\mathit{B}{\mathit{U}}_P\\ {\dot{\mathit{X}}}_E=\mathit{A}{\mathit{X}}_E+\mathit{B}{\mathit{U}}_E\end{array}$$

(8)

where ${\mathit{X}}_i\left(i=P,E\right)$ denotes the state of the pursuer $P$ or the target $E$ in the orbital coordinate, respectively. ${\mathit{U}}_i\left(i=P,E\right)$ denotes the thrust accelerations of the pursuer $P$ and the target $E$, and satisfies the magnitude constraint, namely, $\Vert {\mathit{U}}_i\Vert <{\rho }_i\left(i=P,E\right)$.

We define the relative state between the pursuer and the target as ${\mathit{X}}_{\mathit{PE}}={\mathit{X}}_P-{\mathit{X}}_E$.

By differentiating the state equation and combining with Equation (8), the relative dynamics can be written as:

$${\dot{\mathit{X}}}_{\mathit{PE}}=\mathit{A}{\mathit{X}}_{\mathit{PE}}+\mathit{B}{\mathit{U}}_P+\mathit{C}{\mathit{U}}_E$$

(9)

where $\mathit{C}=-\mathit{B}$.

3. Game Strategies under Incomplete Information

From Ref. [4], the necessary condition for successful interception is that the thrust magnitude of the pursuer is higher than that of the target. When the target thrust is higher than the pursuer, the target will successfully escape. In practical application, due to private information or sensor constraints, the pursuit–evasion game information may not be completely known to the pursuer. Therefore, based on the complete information game strategy pairs, this section studies the pursuit game strategies under incomplete information. The proposed norm-based game strategy can achieve fast approach, while the linear quadratic game strategy can save fuel consumption.

3.1. Norm-Based Game Strategy

The goal of the pursuer is to compete with the target in terms of terminal approach distance. In the norm-based game strategy, it is sufficient to consider only the relative displacements between the pursuer and the target. In order to facilitate later analysis, we define the terminal zero effort misse (ZEM) between the pursuer and the target as ${\mathit{Z}}_{\mathit{PE}}(t)$.

Thus, the norm-based strategy with ignoring fuel optimization is derived.

$${\mathit{Z}}_{\mathit{PE}}(t)=\mathit{D}\mathsf{\Phi }\left(t_f,t\right){\mathit{X}}_{\mathit{PE}}$$

(10)

where $\mathit{D}=\left[\begin{array}{cc}{\mathit{I}}_3& {\mathit{0}}_3\end{array}\right]$ with ${\mathit{I}}_3\in R^{3\times 3}$, $t_f$ is the terminal time of the interception. $\mathsf{\Phi }\left(t_f,t\right)$ is the state-transition matrix of the system (9), with its explicit form being given in [4], and satisfies:

$$\dot{\mathsf{\Phi }}(t_f,t)=-\mathsf{\Phi }(t_f,t)\mathit{A}$$

(11)

Differentiating Equation (10) and using Equations (9) and (11) yield:

$$\begin{array}{cc}{\dot{\mathit{Z}}}_{\mathit{PE}}(t)& =\mathit{D}\left(\dot{\mathsf{\Phi }}\left(t_f,t\right){\mathit{X}}_{\mathit{PE}}+\mathsf{\Phi }\left(t_f,t\right){\dot{\mathit{X}}}_{\mathit{PE}}\right)\hfill \\ & =\mathit{D}\left(\mathsf{\Phi }\left(t_f,t\right)\mathit{B}{\mathit{U}}_P-\mathsf{\Phi }\left(t_f,t\right)\mathit{B}{\mathit{U}}_E\right)\hfill \\ & ={\mathit{B}}_P{\mathit{U}}_P-{\mathit{B}}_E{\mathit{U}}_E\hfill \end{array}$$

(12)

where ${\mathit{B}}_P={\mathit{B}}_E=\mathit{D}\mathsf{\Phi }\left(t_f,t\right)\mathit{B}={\mathsf{\Phi }}_{12}\left(t_f,t\right)$.

Throughout the pursuit-evasion game process, the pursuer expects the target to enter one of the pursuit zones in a limited time, while the target tries to avoid it by increasing the distance with maximum thrust. Therefore, we define the cost function $J$ as:

$$\underset{{\mathit{U}}_P}{\min }\underset{{\mathit{U}}_E}{\max }J=\Vert {\mathit{Z}}_{\mathit{PE}}\left(t_f\right)\Vert$$

(13)

Define the cost function along a solution as:

$$\tilde{J}=\Vert {\mathit{Z}}_{\mathit{PE}}\left(t\right)\Vert$$

(14)

Differentiating it and combining with Equation (12), we have:

$$\frac{\mathrm{d}}{\mathrm{d}t}\Vert {\mathit{Z}}_{\mathit{PE}}\left(t\right)\Vert =\frac{{\mathit{Z}}_{\mathit{PE}}^{\mathrm{T}}\left(t\right)}{\Vert {\mathit{Z}}_{\mathit{PE}}\left(t\right)\Vert }{\dot{\mathit{Z}}}_{\mathit{PE}}(t)=\frac{{\mathit{Z}}_{\mathit{PE}}^{\mathrm{T}}\left(t\right)}{\Vert {\mathit{Z}}_{\mathit{PE}}\left(t\right)\Vert }\left({\mathit{B}}_P{\mathit{U}}_P-{\mathit{B}}_E{\mathit{U}}_E\right)$$

(15)

Since the pursuer $P$ has the intention to minimize $J$, the strategy ${\mathit{U}}_P$ satisfies $\frac{\mathrm{d}\tilde{J}}{\mathrm{d}t}<0$. Therefore, the control strategy of the pursuer $P$ with the maximal magnitude constraint can be derived as:

$${\mathit{U}}_P=-{\rho }_P\frac{{\left(\frac{{\mathit{Z}}_{\mathit{PE}}^{\mathrm{T}}\left(t\right)}{\Vert {\mathit{Z}}_{\mathit{PE}}\left(t\right)\Vert }{\mathit{B}}_P\right)}^{\mathrm{T}}}{\Vert \frac{{\mathit{Z}}_{\mathit{PE}}^{\mathrm{T}}\left(t\right)}{\Vert {\mathit{Z}}_{\mathit{PE}}\left(t\right)\Vert }{\mathit{B}}_P\Vert }=-{\rho }_P\frac{{\mathit{B}}_P^{\mathrm{T}}{\mathit{Z}}_{\mathit{PE}}\left(t\right)}{\Vert {\mathit{B}}_P^{\mathrm{T}}{\mathit{Z}}_{\mathit{PE}}\left(t\right)\Vert }$$

(16)

On the contrary, the target $E$ tries its effort to maximize $J$ and its strategy ${\mathit{U}}_E$ satisfies $\frac{\mathrm{d}\tilde{J}}{\mathrm{d}t}>0$. Therefore, the control strategy of the target $E$ with the maximal magnitude constraint can be derived as:

$${\mathit{U}}_E=-{\rho }_E{\left(\frac{\frac{{\mathit{Z}}_{\mathit{PE}}^{\mathrm{T}}\left(t\right)}{\Vert {\mathit{Z}}_{\mathit{PE}}\left(t\right)\Vert }{\mathit{B}}_E}{\Vert \frac{{\mathit{Z}}_{\mathit{PE}}^{\mathrm{T}}\left(t\right)}{\Vert {\mathit{Z}}_{\mathit{PE}}\left(t\right)\Vert }{\mathit{B}}_E\Vert }\right)}^{\mathrm{T}}=-{\rho }_E\frac{{\mathit{B}}_E^{\mathrm{T}}{\mathit{Z}}_{\mathit{PE}}\left(t\right)}{\Vert {\mathit{B}}_E^{\mathrm{T}}{\mathit{Z}}_{\mathit{PE}}\left(t\right)\Vert }$$

(17)

For the norm-based strategy, the cost function only takes into account the relative position between the pursuer and the target, that is, the pursuer uses its strategy instead of the target strategy. Thus, the absence of the target strategy information has no impact on the norm-based strategy.

3.2. Linear Quadratic Game Strategy

First, we make an assumption that both players can obtain the complete information of the game in the zero-sum equilibrium game. The pursuer has the goal to pursuit the target with minimal cost, while the target increases the distance with the pursuer with minimal cost. Thus, we define the linear quadratic cost function as follows:

$$\underset{{\mathit{U}}_P}{\min }\underset{{\mathit{U}}_E}{\max }J=\frac{1}{2}{\mathit{X}}_{\mathit{PE}}^{\mathrm{T}}\left(t_f\right)\mathit{S}{\mathit{X}}_{\mathit{PE}}\left(t_f\right)+\frac{1}{2}{\displaystyle {\int }_{t_0}^{t_f}\left({\mathit{X}}_{\mathit{PE}}^{\mathrm{T}}\mathit{Q}{\mathit{X}}_{\mathit{PE}}+{\mathit{U}}_P^{\mathrm{T}}{\mathit{R}}_P{\mathit{U}}_P-{\mathit{U}}_E^{\mathrm{T}}{\mathit{R}}_E{\mathit{U}}_E\right)dt}$$

(18)

where $\mathit{S}>0$, ${\mathit{R}}_P>0$ and ${\mathit{R}}_E>0$ are all symmetric positive definite cost matrices, and $\mathit{Q}\ge 0$ is symmetric positive semidefinite cost matrix, $t_f$ is the terminal time of the game.

Different from the norm-based game strategy, the cost function of the linear quadratic game strategy takes into account fuel consumption. If both sides in the game have complete information about the opponent, the game is zero-sum and associates with a saddle-point strategy pair.

To derive the saddle-point strategy pair, a Hamiltonian function is introduced as:

$$H={\mathsf{\lambda }}^T\left(\mathit{A}{\mathit{X}}_{\mathit{PE}}+\mathit{B}{\mathit{U}}_P-\mathit{B}{\mathit{U}}_E\right)+\frac{1}{2}\left({\mathit{X}}_{\mathit{PE}}^{\mathrm{T}}\mathit{Q}{\mathit{X}}_{\mathit{PE}}+{\mathit{U}}_P^{\mathrm{T}}{\mathit{R}}_P{\mathit{U}}_P-{\mathit{U}}_E^{\mathrm{T}}{\mathit{R}}_E{\mathit{U}}_E\right)$$

(19)

where $\mathsf{\lambda }$ is the adjoint variable.

Thus, the game saddle-point strategy pair is obtained as:

$$\begin{array}{l}{\mathit{U}}_P=-{\mathit{R}}_P^{-1}{\mathit{B}}^{\mathrm{T}}\mathit{P}{\mathit{X}}_{\mathit{PE}}\\ {\mathit{U}}_E={\mathit{R}}_E^{-1}{\mathit{C}}^{\mathrm{T}}\mathit{P}{\mathit{X}}_{\mathit{PE}}\end{array}$$

(20)

where $\mathit{P}$ can be determined by:

$$\dot{\mathit{P}}+{\mathit{A}}^{\mathrm{T}}\mathit{P}+\mathit{P}\mathit{A}-\mathit{P}\left(\mathit{B}{\mathit{R}}_P^{-1}{\mathit{B}}^{\mathrm{T}}-\mathit{B}{\mathit{R}}_E^{-1}{\mathit{B}}^{\mathrm{T}}\right)\mathit{P}+\mathit{Q}=0$$

(21)

with $\mathit{P}$ satisfies the terminal condition:

$$\mathit{P}\left(t_f\right)=\mathit{S}$$

(22)

Next, to derive the target strategy under incomplete information. The pursuit information may not be completely known to the pursuer in practice, which causes the strategies derived in Equation (20) not be applicable. Thus, the approach strategy under incomplete information is studied, and we make an assumption as follows:

Assumption 1.

The pursuer can obtain the target state information, instead of the target maneuver information. On the contrary, the target can perceive the complete information of the whole game.

Under this assumption, the pursuer considers the target strategy to be ${\mathit{U}}_E=0$, and the relative dynamics can be written as:

$${\dot{\mathit{X}}}_{\mathit{PE}}=\mathit{A}{\mathit{X}}_{\mathit{PE}}+\mathit{B}{\mathit{U}}_P$$

(23)

Thus, the pursuit strategy can be derived by minimizing the one-side cost function

$$\underset{{\mathit{U}}_P}{\min }J=\frac{1}{2}{\mathit{X}}_{\mathit{PE}}^{\mathrm{T}}\left(t_f\right)\mathit{S}{\mathit{X}}_{\mathit{PE}}\left(t_f\right)+\frac{1}{2}{\displaystyle {\int }_{t_0}^{t_f}\left({\mathit{X}}_{\mathit{PE}}^{\mathrm{T}}\mathit{Q}{\mathit{X}}_{\mathit{PE}}+{\mathit{U}}_P^{\mathrm{T}}{\mathit{R}}_P{\mathit{U}}_P\right)dt}$$

(24)

where $\mathit{S}$, $\mathit{Q}$ and ${\mathit{R}}_P$ are identical to that in Equation (18).

The Hamiltonian function is defined as:

$$H={\mathsf{\lambda }}^T\left(\mathit{A}{\mathit{X}}_{\mathit{PE}}+\mathit{B}{\mathit{U}}_P\right)+\frac{1}{2}\left({\mathit{X}}_{\mathit{PE}}^{\mathrm{T}}\mathit{Q}{\mathit{X}}_{\mathit{PE}}+{\mathit{U}}_P^{\mathrm{T}}{\mathit{R}}_P{\mathit{U}}_P\right)$$

(25)

$$\mathit{\Phi }=\frac{1}{2}{\mathit{X}}_{\mathit{PE}}^{\mathrm{T}}\left(t_f\right)\mathit{S}{\mathit{X}}_{\mathit{PE}}\left(t_f\right)$$

(26)

From the optimal control condition $\frac{\partial H}{\partial {\mathit{U}}_P}=0$, we have

$${\mathit{U}}_P=-{\mathit{R}}_P^{-1}{\mathit{B}}^{\mathrm{T}}\mathsf{\lambda }$$

(27)

The necessary condition for the optimal saddle-point solution includes the adjoint equation $\dot{\mathsf{\lambda }}=-\frac{\partial H}{\partial {\mathit{X}}_{\mathit{PE}}}$, namely:

$$\dot{\mathsf{\lambda }}=-\left({\mathit{A}}^T\mathsf{\lambda }+\mathit{Q}{\mathit{X}}_{\mathit{PE}}\right)$$

(28)

in conjunction with the boundary condition:

$$\mathsf{\lambda }\left(t_f\right)=\frac{\partial \mathsf{\Phi }}{\partial {\mathit{X}}_{\mathit{PE}}\left(t_f\right)}=\mathit{S}{\mathit{X}}_{\mathit{PE}}\left(t_f\right)$$

(29)

Assuming the adjoint variable and the relative state also satisfy the linear relationship as follows:

$$\mathsf{\lambda }={\mathit{P}}_p{\mathit{X}}_{\mathit{PE}}$$

(30)

where ${\mathit{P}}_p$ is also a symmetric positive definite matrix, namely, ${\mathit{P}}_p>0,{\mathit{P}}_P^T={\mathit{P}}_p$. Then, the assumption given in Equation (30) is valid.

Differentiating Equation (30) and combing with Equations (23), (27) and (28), we can obtain the Ricatti equation as follows:

$${\dot{\mathit{P}}}_p+{\mathit{A}}^T{\mathit{P}}_p+{\mathit{P}}_p\mathit{A}-{\mathit{P}}_p\mathit{B}{\mathit{R}}_P^{-1}{\mathit{B}}^{\mathrm{T}}{\mathit{P}}_p+\mathit{Q}=0$$

(31)

From the boundary condition in Equation (29), ${\mathit{P}}_p$ also satisfies the terminal condition:

$${\mathit{P}}_P\left(t_f\right)=\mathit{S}$$

(32)

Thus, the one-side pursuit strategy is determined by Equations (27) and (30)–(32), namely:

$${\mathit{U}}_P=-{\mathit{R}}_P^{-1}{\mathit{B}}^{\mathrm{T}}{\mathit{P}}_p{\mathit{X}}_{\mathit{PE}}$$

(33)

For the target, the target knows the maneuver strategy that the pursuer may take, that is, the target has the complete information about the game process, but does not know the actual strategy taken by the pursuer after estimating the incomplete information. Therefore, the target’s game strategy can be optimized by considering the pursuer’s game strategy to obtain better avoidance performance.

Thus, with the pursuer using strategy (33), the relative dynamics can be rewritten as:

$$\begin{array}{c}{\dot{\mathit{X}}}_{\mathit{PE}}=\mathit{A}{\mathit{X}}_{\mathit{PE}}-\mathit{B}{\mathit{R}}_P^{-1}{\mathit{B}}^{\mathrm{T}}{\mathit{P}}_p{\mathit{X}}_{\mathit{PE}}+\mathit{C}{\mathit{U}}_E\\ ={\mathit{A}}_c{\mathit{X}}_{\mathit{PE}}+\mathit{C}{\mathit{U}}_E\end{array}$$

(34)

where ${\mathit{A}}_c$ is a time-varying matrix and defined as ${\mathit{A}}_c=\mathit{A}-\mathit{B}{\mathit{R}}_P^{-1}{\mathit{B}}^{\mathrm{T}}\mathit{P}$.

The target one-side optimization cost function is defined as:

$$\underset{{\mathit{U}}_E}{\max }J=\frac{1}{2}{\mathit{X}}_{\mathit{PE}}^{\mathrm{T}}\left(t_f\right)\mathit{S}{\mathit{X}}_{\mathit{PE}}\left(t_f\right)+\frac{1}{2}{\displaystyle {\int }_{t_0}^{t_f}\left({\mathit{X}}_{\mathit{PE}}^{\mathrm{T}}\mathit{Q}{\mathit{X}}_{\mathit{PE}}-{\mathit{U}}_E^{\mathrm{T}}{\mathit{R}}_E{\mathit{U}}_E\right)dt}$$

(35)

where $\mathit{S}$, $\mathit{Q}$, ${\mathit{R}}_E$ are identical to Equation(18).

Similar to the derivation of the pursuer strategy, the optimal strategy of the target is given as:

$${\mathit{U}}_E=-{\mathit{R}}_E^{-1}{\mathit{B}}^{\mathrm{T}}{\mathit{P}}_E{\mathit{X}}_{\mathit{PE}}$$

(36)

where ${\mathit{P}}_E$ is symmetric positive definite, and satisfies:

$${\dot{\mathit{P}}}_E+{\mathit{A}}_c^T{\mathit{P}}_E+{\mathit{P}}_E{\mathit{A}}_c+{\mathit{P}}_E\mathit{C}{\mathit{R}}_E^{-1}{\mathit{C}}^{\mathrm{T}}{\mathit{P}}_E+\mathit{Q}=0$$

(37)

with the terminal condition:

$${\mathit{P}}_E\left(t_f\right)=\mathit{S}$$

(38)

4. Optimal Hybrid Game Strategies

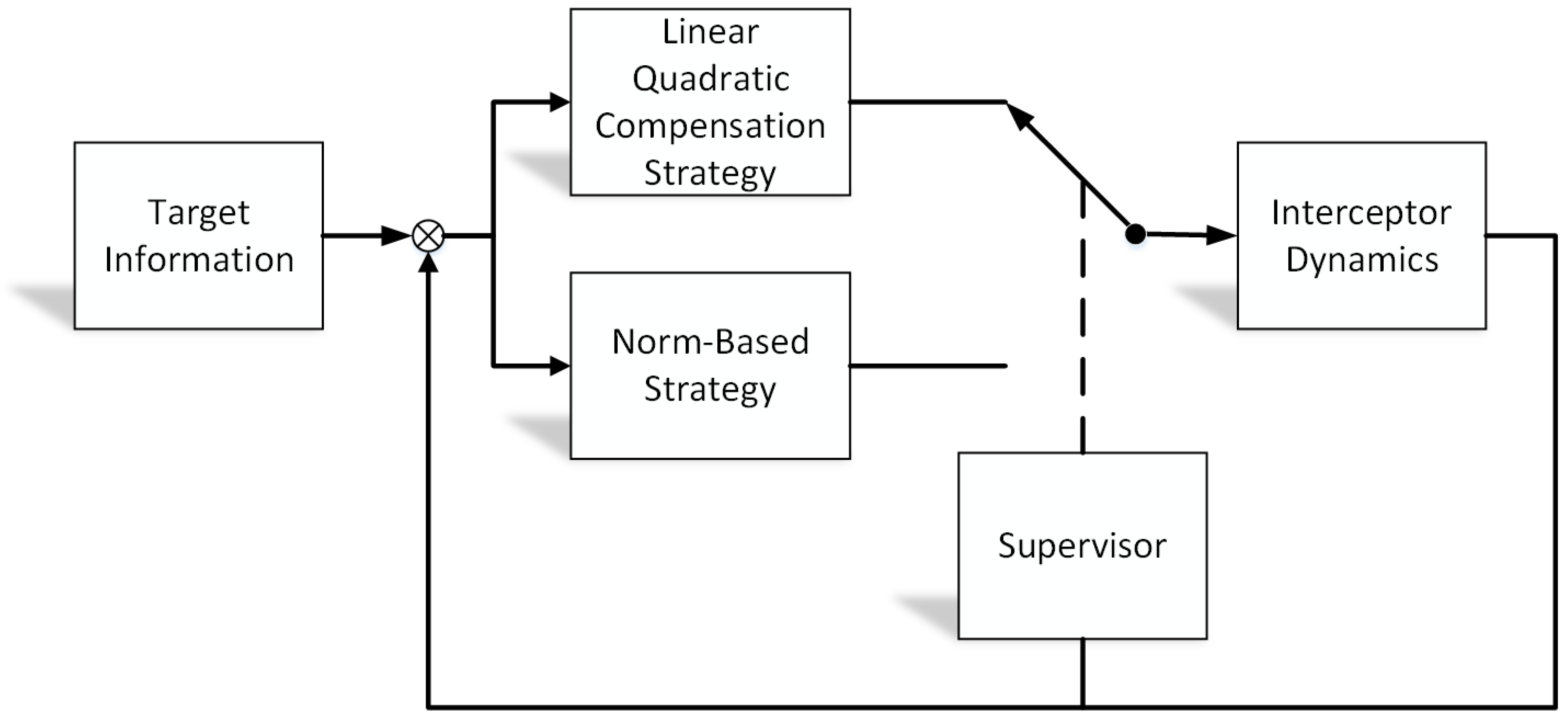
For the norm-based strategy, the interception can be guaranteed, as long as the thrust amplitude is greater than the target. Nevertheless, the fuel consumption term is not optimized, which leads to an increase in fuel consumption. On the other hand, the linear quadratic strategy can reduce fuel consumption, although the pursuit may not be realized because of the target’s strong maneuverability or the changeable maneuvering law. Thus, the hybrid game strategy, combining the linear quadratic compensation strategy with the norm-based strategy, is proposed to guarantee the approach and reduce fuel consumption. The proposed hybrid game strategy has the inherent ability to combine multiple game algorithms under a single coherent framework as shown in Figure 2. The designed hybrid game strategy can achieve rapid approach and save fuel consumption, even under the condition that the target can perceive complete information of the pursuer and obtain better evasion performance in the game strategy.

To model the system dynamics in hybrid framework, the hybrid systems state is defined as:

$$\mathit{x}=\left[\begin{array}{c}\mathit{X}\\ q\\ \tau \end{array}\right]$$

(39)

where $q$ is the game control logic variable and $\tau$ is the timer variable. The value of $q$ specifies which game strategy is currently being used, with $q\in \left\{1,2\right\}$, where $q=1$ represents the linear quadratic compensation strategy, and $q=2$ represents the norm-based strategy. The property of $q$ introduces discrete dynamics into the system. For this problem, the hybrid system $H$ is defined as:

$$H=\left(C,\mathit{F},D,\mathit{G}\right)$$

(40)

where $\mathit{F}$ is the flow map, $\mathit{G}$ is the jump map, $C$ is the flow set, and $D$ is the jump set. That is, $C$ is defined as the set of the state of $\mathit{x}$ in which the system will follow the continuous time dynamics defined by $\mathit{F}$. Similarly, $D$ and $\mathit{G}$ are defined for the discrete dynamics.

The definition of the continuous dynamics of the flow map $\mathit{F}$ follows:

$$\mathit{F}=\left[\begin{array}{c}\mathit{A}{\mathit{X}}_{PE}+\mathit{B}{\mathit{U}}_P-\mathit{B}{\mathit{U}}_E\\ 0\\ 1\end{array}\right]$$

(41)

The definition of the discrete dynamics of the flow map $\mathit{G}$ follows:

$$\mathit{G}=\left[\begin{array}{c}\mathit{A}{\mathit{X}}_{PE}\\ 3-q\\ 0\end{array}\right]$$

(42)

The flow set $C$ and the jump set $D$ are defined later. For the norm-based strategy, the strategy is given in Equation (16).

For the linear quadratic strategy, the disturbance observer is designed to estimate the unavailable target maneuver information, and the compensation strategy is derived. To simplify the analysis later, an assumption is given as follows:

Assumption 2.

The target perceives the pursuer maneuver strategy with incomplete information, namely, Equation (33), rather than knows that the pursuer uses the disturbance estimator.

To apply the disturbance estimator, defining the minus of the target strategy as the disturbance $\mathit{d}$, namely, $\mathit{d}=-{\mathit{U}}_E$, and combing with $\mathit{C}=-\mathit{B}$, the relative dynamics can be written as:

$${\dot{\mathit{X}}}_{\mathit{PE}}=\mathit{A}{\mathit{X}}_{\mathit{PE}}+\mathit{B}{\mathit{U}}_P+\mathit{B}\mathit{d}$$

(43)

Decomposing the relative state as ${\mathit{X}}_{\mathit{PE}}={\left[\begin{array}{cc}{\mathit{x}}_1& {\mathit{x}}_2\end{array}\right]}^{\mathrm{T}}$, we can obtain the relative dynamics on ${\mathit{x}}_2$

$${\dot{\mathit{x}}}_2={\mathit{A}}_{21}{\mathit{x}}_1+{\mathit{A}}_{22}{\mathit{x}}_2+{\mathit{U}}_P+\mathit{d}$$

(44)

with ${\mathit{A}}_{21}=\left[\begin{array}{ccc}3{\omega }^2& 0& 0\\ 0& 0& 0\\ 0& 0& -{\omega }^2\end{array}\right]$, ${\mathit{A}}_{22}=\left[\begin{array}{ccc}0& 2\omega & 0\\ -2\omega & 0& 0\\ 0& 0& 0\end{array}\right]$.

Thus, we design the disturbance estimator as follows:

$$\begin{array}{l}\hat{\mathit{d}}=\mathit{z}+\mathit{p}\left({\mathit{X}}_{\mathit{PE}}\right)\\ \dot{\mathit{z}}=-\mathit{L}\left({\mathit{X}}_{\mathit{PE}}\right)\left[\hat{\mathit{d}}+a_{21}{\mathit{x}}_1+a_{22}{\mathit{x}}_2+{\mathit{U}}_P\right]\end{array}$$

(45)

with the disturbance observer gain $\mathit{L}\left({\mathit{X}}_{\mathit{PE}}\right)$ being positive definite, and the $\mathit{p}\left({\mathit{X}}_{\mathit{PE}}\right)$ satisfying $\mathit{L}\left({\mathit{X}}_{\mathit{PE}}\right)=\raisebox{1ex}{$\partial \mathit{p}\left({\mathit{X}}_{\mathit{PE}}\right)$}\!\left/ \!\raisebox{-1ex}{$\partial {\mathit{X}}_{\mathit{PE}}$}\right.$. $\hat{\mathit{d}}$ is the estimated value of using to compensate the target strategy, $\mathit{z}$ is the internal additional variable of the system.

Thus, we define the estimation error of the system (45) as $\tilde{\mathit{d}}=-\left(\hat{\mathit{d}}+{\mathit{U}}_E\right)$.

If the disturbance defined in this paper $\mathit{d}$ is continuous and satisfies $\Vert \dot{\mathit{d}}\Vert \le \mathit{\delta }$, then, according to the input-to-state stable (ISS) criterion, the estimation error $\tilde{\mathit{d}}$ is uniformly ultimately bounded, as known from Ref. [32].

For the well estimation, the pursuer applies a strategy combining an interception term with a compensation term. Thus, the pursuer’s strategy can be given as:

$${\mathit{U}}_P=-{\mathit{R}}_P^{-1}{\mathit{B}}^T{\mathit{P}}_P{\mathit{X}}_{PE}-\hat{\mathit{d}}$$

(46)

where ${\mathit{P}}_p$ satisfies the Ricatti differential equation as follows:

$${\dot{\mathit{P}}}_p+{\mathit{A}}^T{\mathit{P}}_p+{\mathit{P}}_p\mathit{A}-{\mathit{P}}_p\mathit{B}{\mathit{R}}_p^{-1}{\mathit{B}}^{\mathrm{T}}{\mathit{P}}_p+\mathit{Q}=0$$

(47)

with ${\mathit{P}}_P\left(t_f\right)=\mathit{S}$.

Remark 1.

To derive the approach strategy above, we make an assumption that the target does not know the estimated value of the pursuer. If a rational target knows the estimated value, it may use the strategy as follows:

$${\mathit{U}}_E=-{\mathit{R}}_E^{-1}{\mathit{B}}^{\mathrm{T}}{\mathit{P}}_E{\mathit{X}}_{\mathit{PE}}-\hat{\mathit{d}}$$

(48)

In this case, substituting the pursuer strategy and the target strategy into Equation (9), the estimation can be offset and the relative dynamics can be rewritten as:

$$\begin{array}{cc}{\dot{\mathit{X}}}_{\mathit{PE}}& =\mathit{A}{\mathit{X}}_{\mathit{PE}}+\mathit{B}\left(-{\mathit{R}}_P^{-1}{\mathit{B}}^T{\mathit{P}}_P\mathit{X}-\hat{\mathit{d}}\right)-\mathit{C}\left(-{\mathit{R}}_E^{-1}{\mathit{B}}^{\mathrm{T}}{\mathit{P}}_E{\mathit{X}}_{\mathit{PE}}-\hat{\mathit{d}}\right)\hfill \\ & =\mathit{A}{\mathit{X}}_{\mathit{PE}}-\mathit{B}{\mathit{R}}_P^{-1}{\mathit{B}}^T{\mathit{P}}_P\mathit{X}+\mathit{C}{\mathit{R}}_E^{-1}{\mathit{B}}^{\mathrm{T}}{\mathit{P}}_E{\mathit{X}}_{\mathit{PE}}\hfill \end{array}$$

(49)

For the incomplete information game, substituting Equations (33) and (36) into Equation (9) yields an equation which is identical to Equation (49). Therefore, the case where the target knows the estimated value of the pursuer is not discussed.

If the target strategy changes slowly, the disturbance observer achieves a well estimation performance. Nevertheless, the target may adjust its strategy fast to avoid being intercepted in practice. In this case, the estimation error is large and the effective estimation cannot be achieved, and, as a result, the pursuer is still unavailable to the game information. In this case, the pursuer applies the norm-based strategy. From Ref. [4], we know that if the pursuer applies the norm-based strategy, the approach can be guaranteed as long as the thrust magnitude of the pursuer is larger than that of the target. Thus, the pursuer uses this strategy if the estimation error is large. To obtain the switch logic, and evaluate the strategy estimation performance, an auxiliary system is defined as:

$${\dot{\mathit{X}}}_{PE}=\mathit{A}{\mathit{X}}_{PE}+\mathit{B}{\mathit{U}}_P-\mathit{B}\mathit{d}$$

(50)

Defining state error $\tilde{\mathit{X}}=\mathit{X}-\hat{\mathit{d}}$, subtracting the actual system yields:

$$\begin{array}{cc}\dot{\tilde{\mathit{X}}}& =\dot{\mathit{X}}-\dot{\hat{\mathit{X}}}\hfill \\ & =\left(\mathit{A}{\mathit{X}}_{PE}+\mathit{B}{\mathit{U}}_P-\mathit{B}{\mathit{U}}_E\right)-\left(\mathit{A}{\mathit{X}}_{PE}+\mathit{B}{\mathit{U}}_P+\mathit{B}\mathit{d}\right)\hfill \\ & =\mathit{A}\tilde{\mathit{X}}+\mathit{B}\tilde{\mathit{d}}\hfill \end{array}$$

(51)

Integrating Equation (51), we have:

$$\tilde{\mathit{X}}=\mathsf{\Phi }\left(t-t_0\right){\tilde{\mathit{X}}}_0+{\displaystyle {\int }_{t_0}^t\mathsf{\Phi }\left(t-\tau \right)\mathit{B}\tilde{\mathit{d}}\mathit{d}\tau }$$

(52)

Choosing the initial state of the auxiliary system as the same one of the actual system, we have ${\tilde{\mathit{X}}}_0=0$. Thus,

$$\tilde{\mathit{X}}={\displaystyle {\int }_{t_0}^t\mathsf{\Phi }\left(t-\tau \right)\mathit{B}\tilde{\mathit{d}}\mathit{d}\tau }$$

(53)

Therefore, the estimation error $\tilde{\mathit{d}}$ can be substituted by $\tilde{\mathit{X}}$. Predesign an estimation error bound as:

$$\overline{\tilde{\mathit{X}}}=\mathsf{\epsilon }$$

(54)

If $\tilde{\mathit{X}}<\overline{\tilde{\mathit{X}}}$, a well estimation is obtained and the linear quadratic compensation strategy is implemented. On the other hand, if $\tilde{\mathit{X}}\ge \overline{\tilde{\mathit{X}}}$, the norm-based strategy is used. Thus, the flow set $C$ and the jump set $D$ are defined as:

$$\begin{array}{l}C=C_1\cup C_2\\ D=D_1\cup D_2\end{array}$$

(55)

with

$$\begin{array}{l}{C}_1=\{\tilde{\mathit{X}}:\tilde{\mathit{X}}<\overline{\tilde{\mathit{X}}},q=1\}\\ C_2=\left\{\tilde{\mathit{X}}:\tilde{\mathit{X}}\ge \overline{\tilde{\mathit{X}}},q=2\right\}\end{array}$$

(56)

and

$$\begin{array}{l}{D}_1=\left\{\tilde{\mathit{X}}:\tilde{\mathit{X}}\ge \overline{\tilde{\mathit{X}}},q=1\right\}\\ D_2=\left\{\tilde{\mathit{X}}:\tilde{\mathit{X}}<\overline{\tilde{\mathit{X}}},q=2\right\}\end{array}$$

(57)

Remark 2.

If the error bound$\overline{\tilde{\mathit{X}}}=\mathsf{\epsilon }$is large, the pursuer may always use the linear quadratic strategy. On the other hand, the pursuer always uses the norm-based strategy with a small error bound.

5. Simulation Analysis

To demonstrate the performance of the hybrid strategy under different information scenarios, several simulations were carried out. We assumed that the pursuer and the target moved around the geocentric orbit (GEO). Thus, a satellite near them was chosen as the reference satellite that moved along the GEO. We knew that the orbital angular velocity was $\omega =7.2722\times {10}^{-5}\mathrm{rad}/\mathrm{s}$. The initial positions of the pursuer and the target were [1.5; 0.5; 0] km, [0; 0; 0] km. The initial velocities they had were [0; 0; 0] km/s, [−0.05; 0; 0.01] km/s, respectively. The parameters in cost function were chosen as:

$$\mathit{Q}=\left[\begin{array}{cc}\mathit{I}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right], \mathit{S}=\left[\begin{array}{cc}\mathit{I}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right], {\mathit{R}}_{\mathit{P}}=1\times {10}^6{\mathit{I}}_{\mathbf{3}}, {\mathit{R}}_{\mathit{E}}=1.5\times {10}^6{\mathit{I}}_{\mathbf{3}}$$

The maximal thrust of the pursuer was ${\rho }_P=10 {\mathrm{m}/\mathrm{s}}^2$. The maximal thrust of the target was ${\rho }_E=8 {\mathrm{m}/\mathrm{s}}^2$. The gain of the disturbance estimator was chosen as $\mathit{L}={\mathit{I}}_3$.

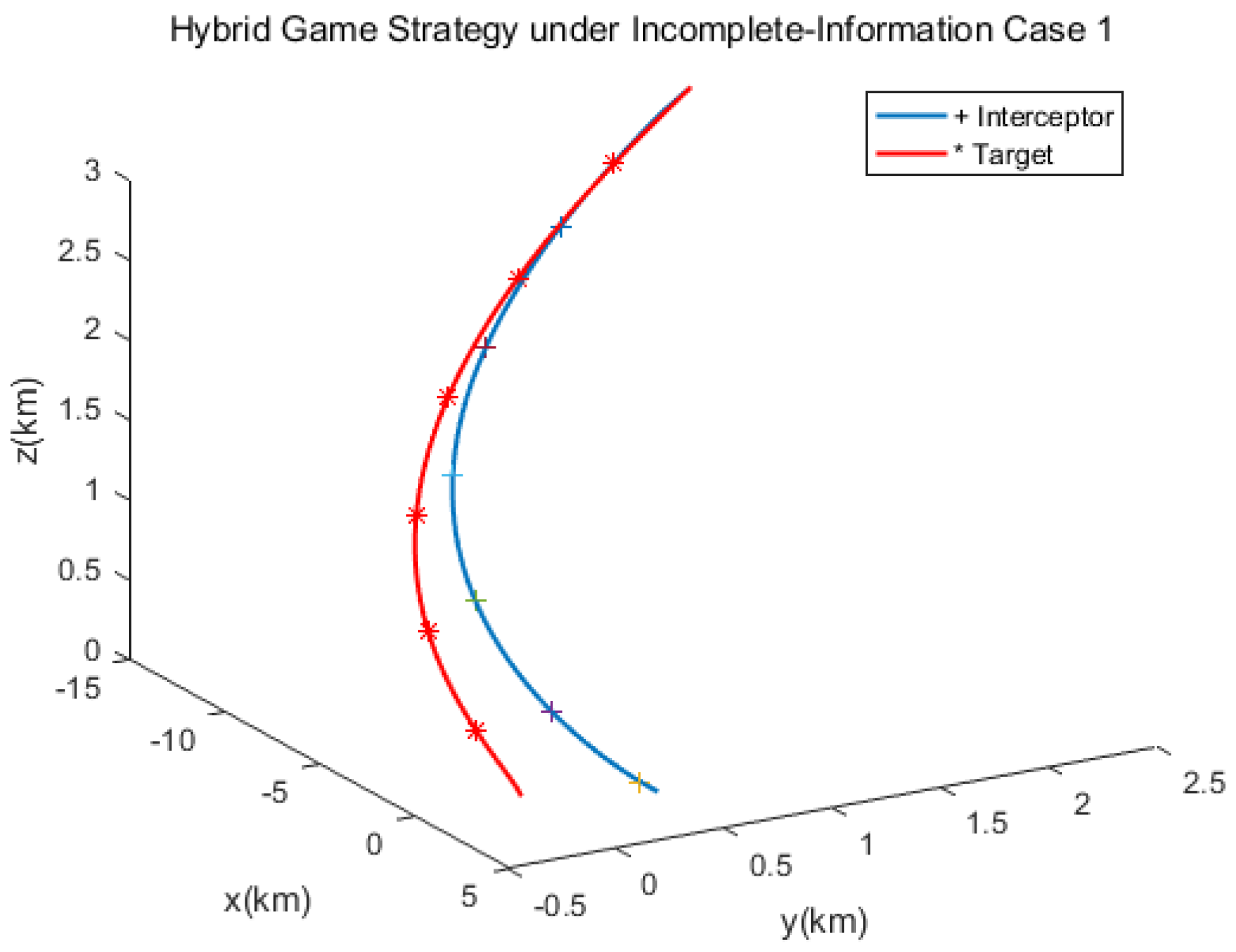
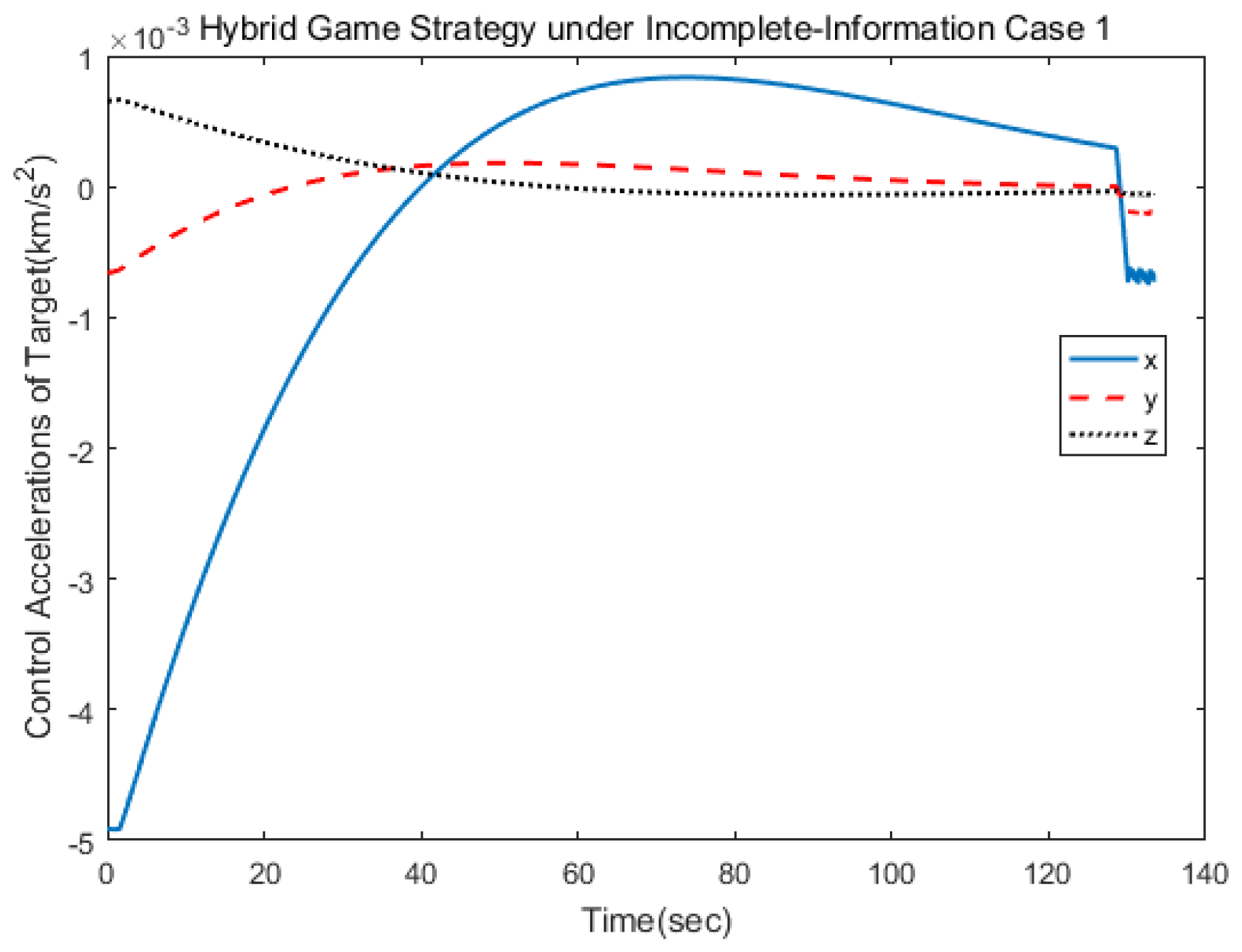
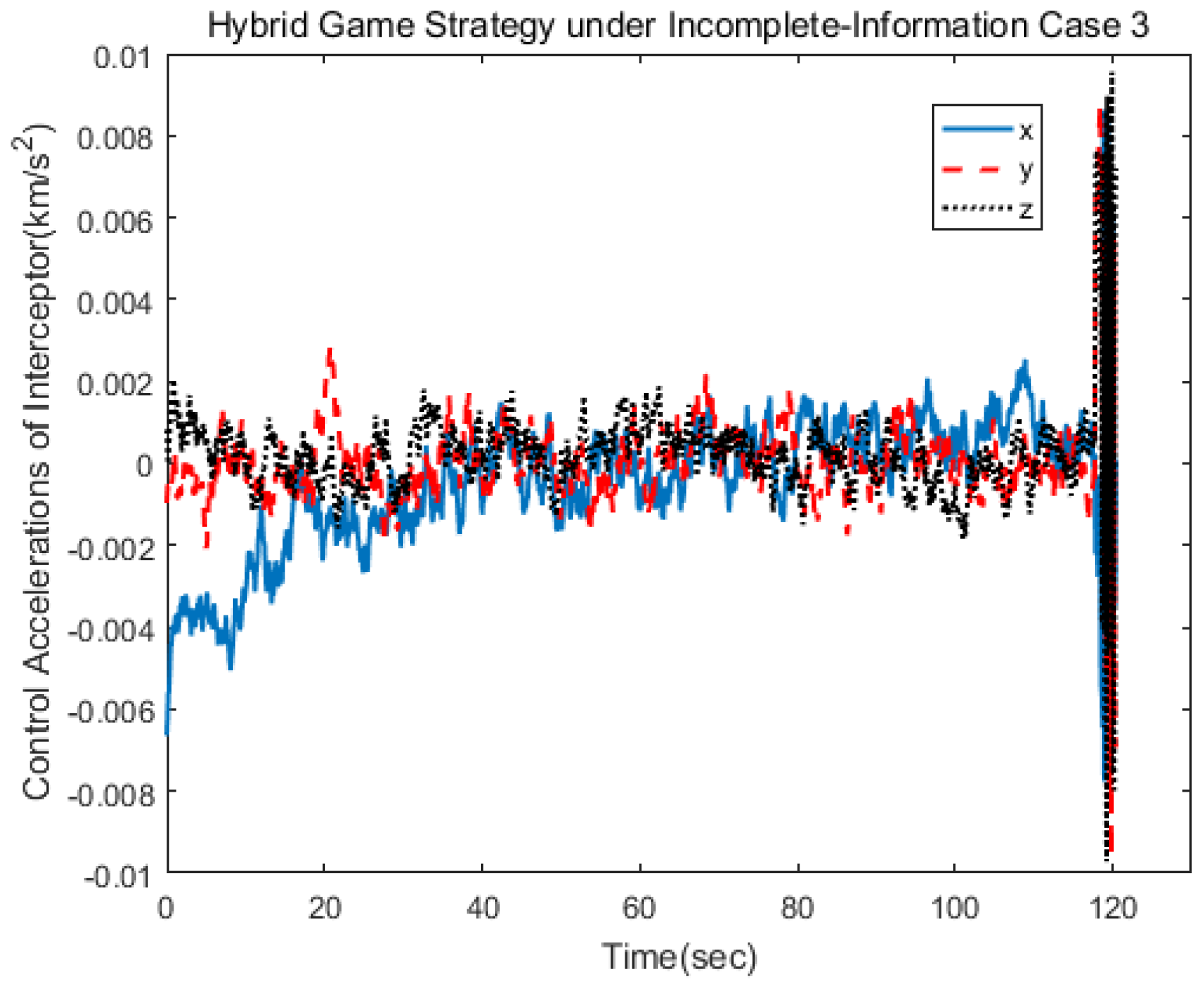
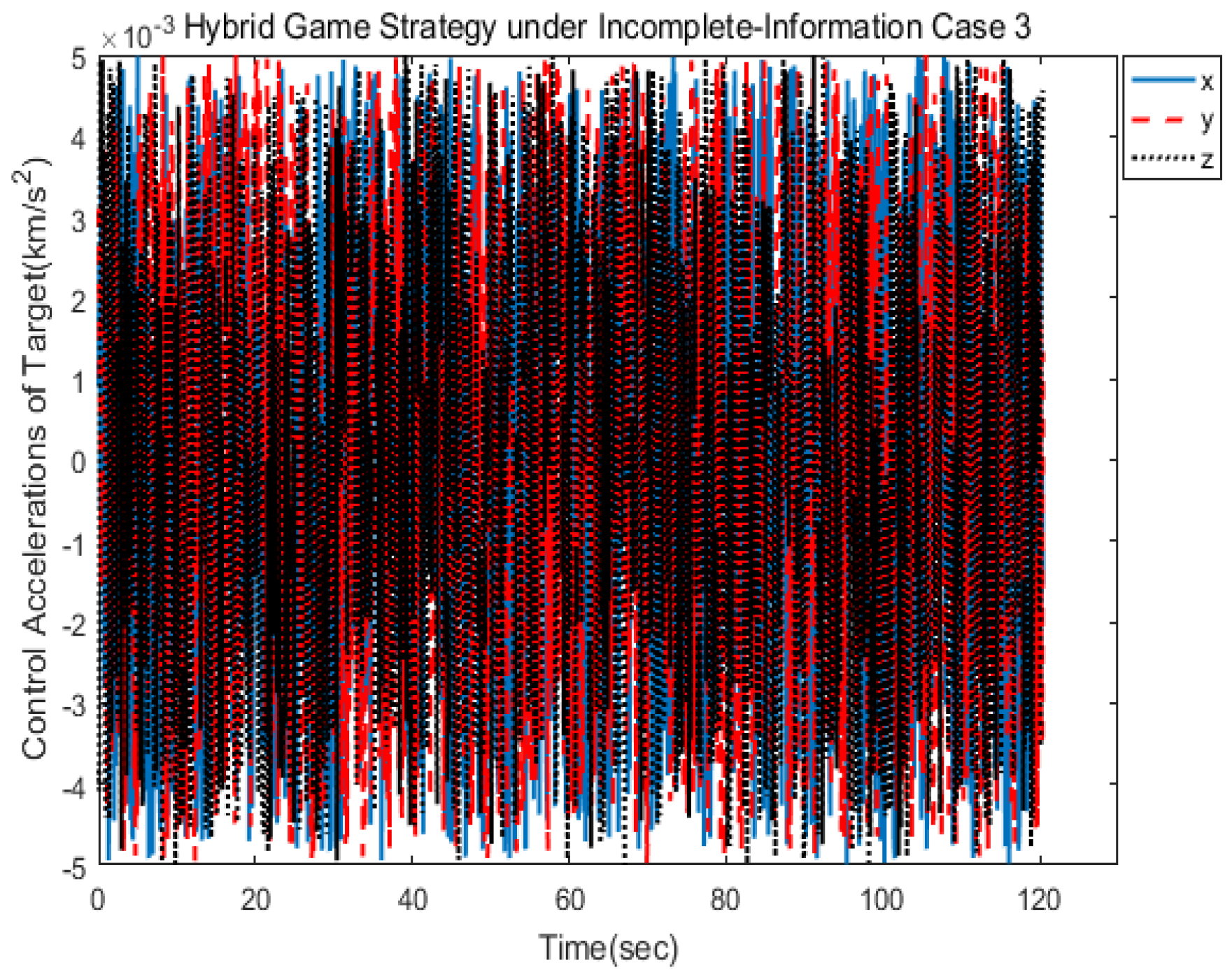
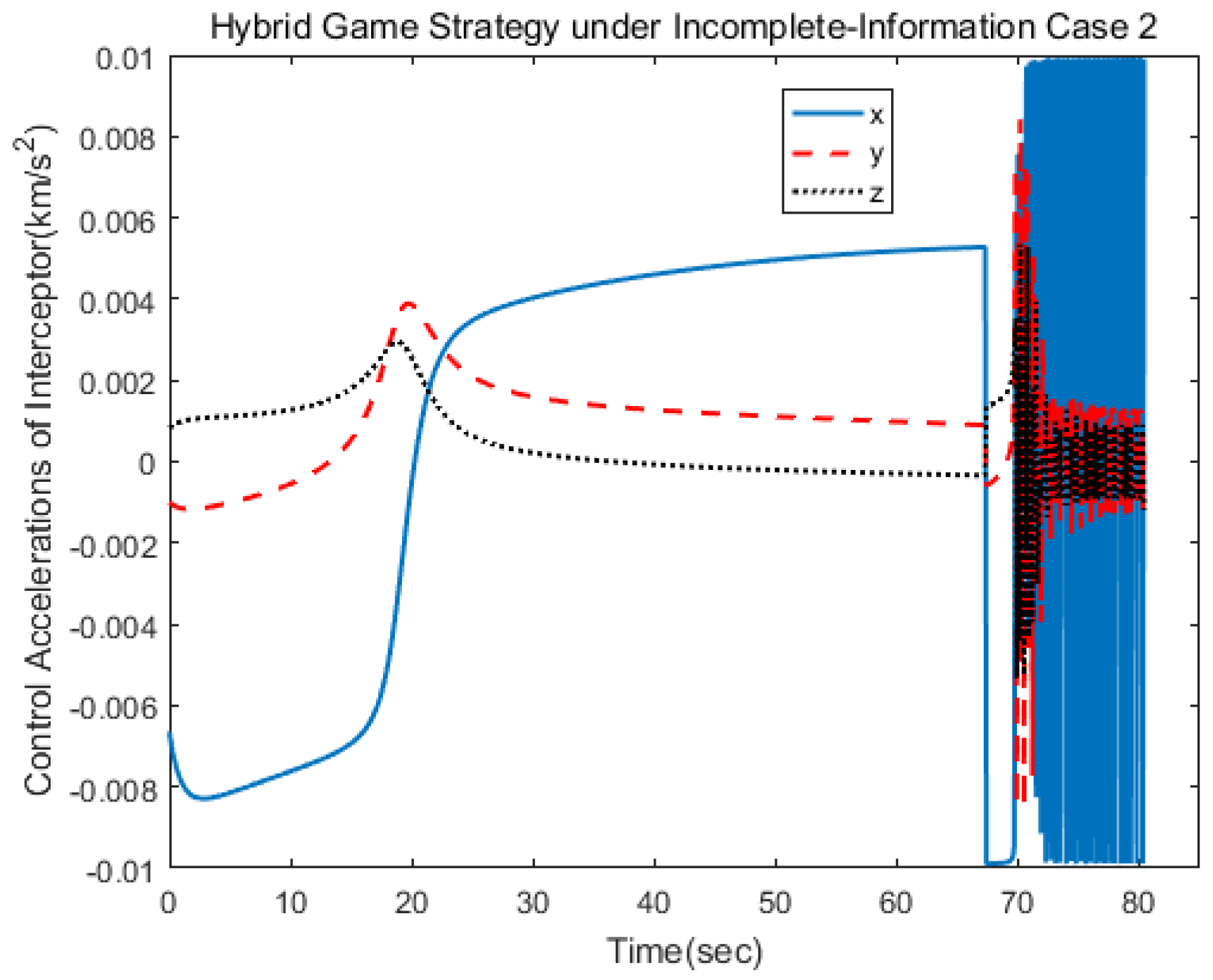
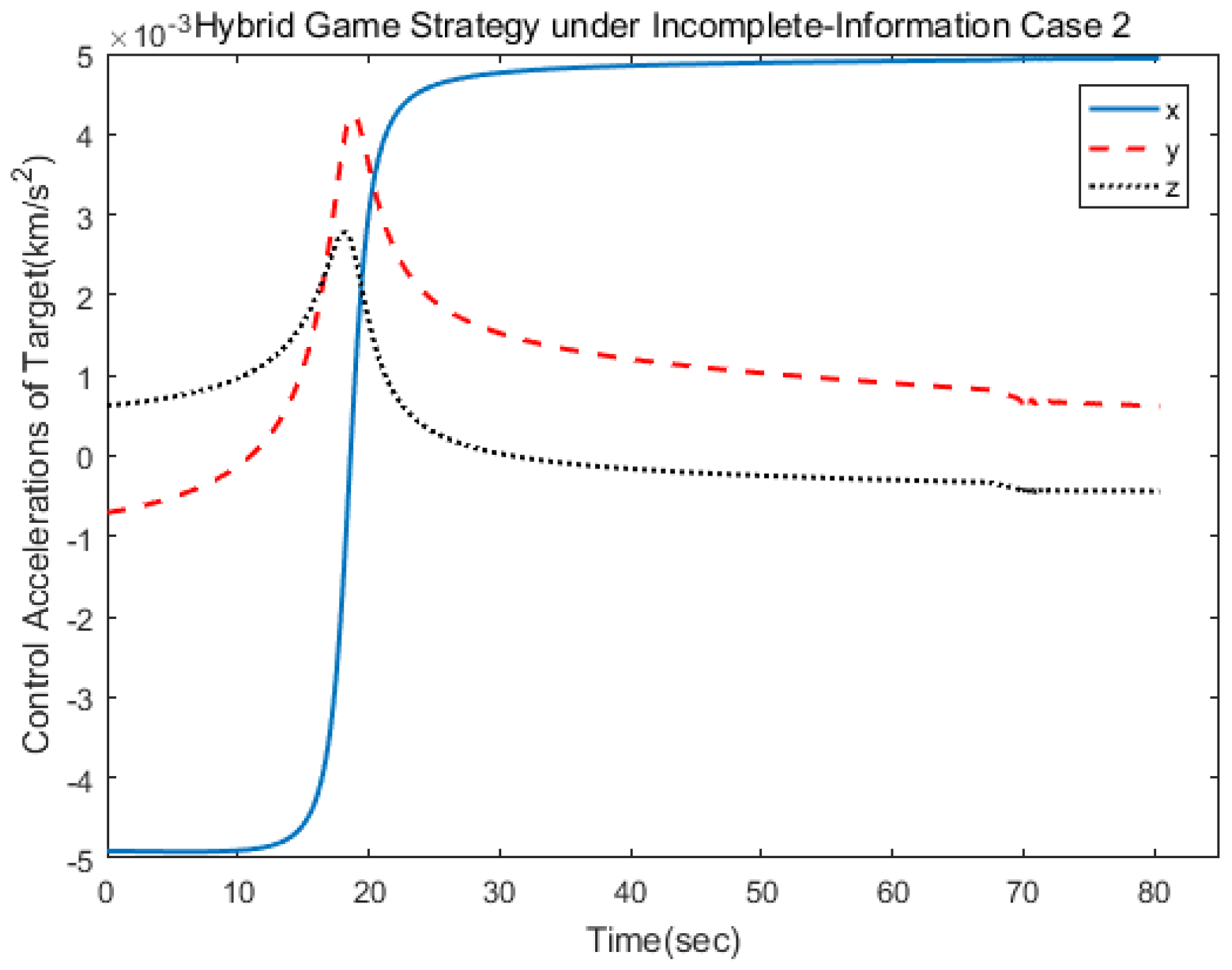
In the first scenario, the target applied the linear quadratic strategy. Figure 3 gives the trajectories of the pursuer and the target, and Figure 4 shows the relative distance between them, from which we can find that the target was approached in 134 s. Figure 5 and Figure 6 show the three-axis thrust accelerations of the spacecrafts. It can be seen that the acceleration of the pursuer was larger than that of the target, and their accelerations varied slowly.

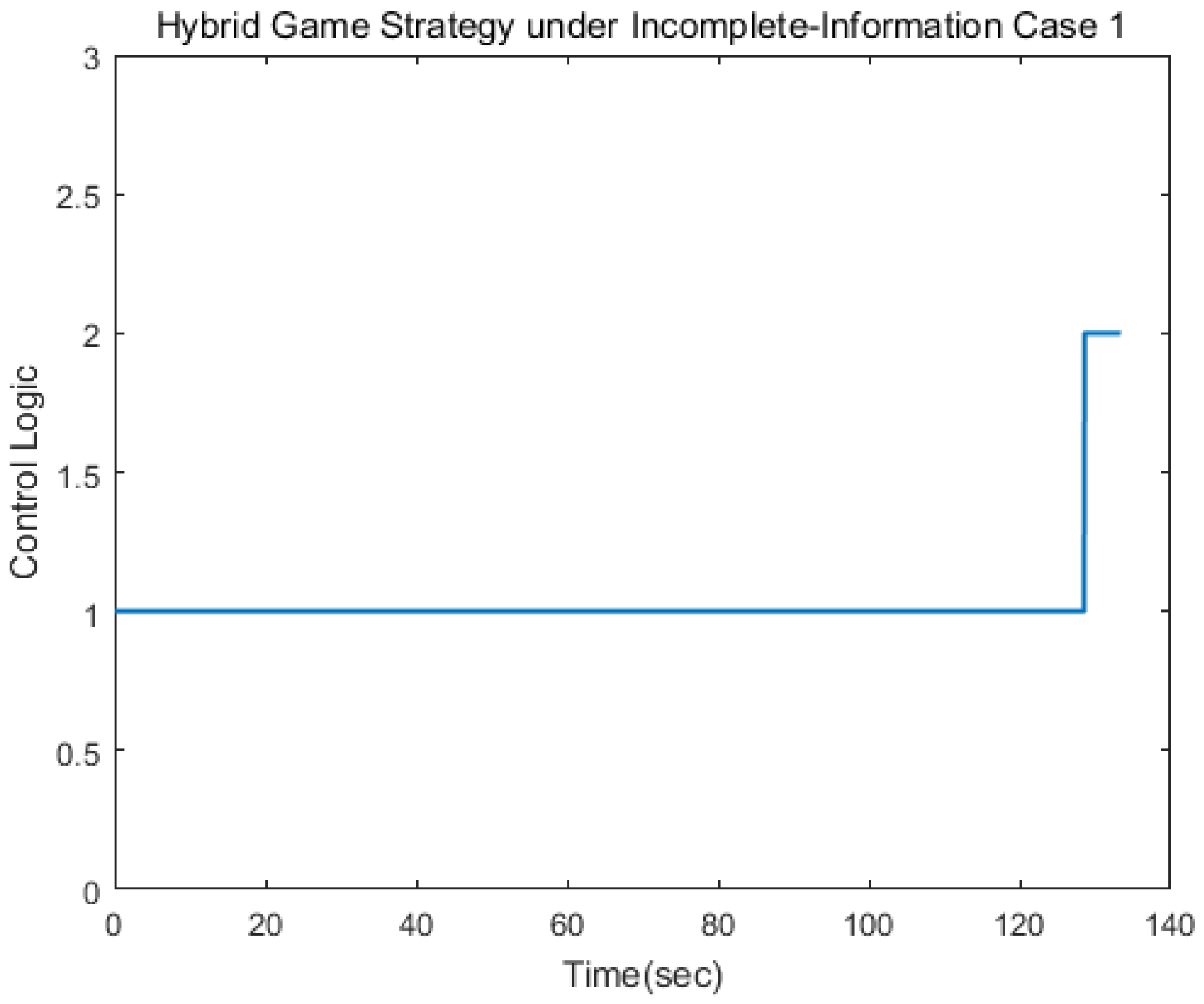
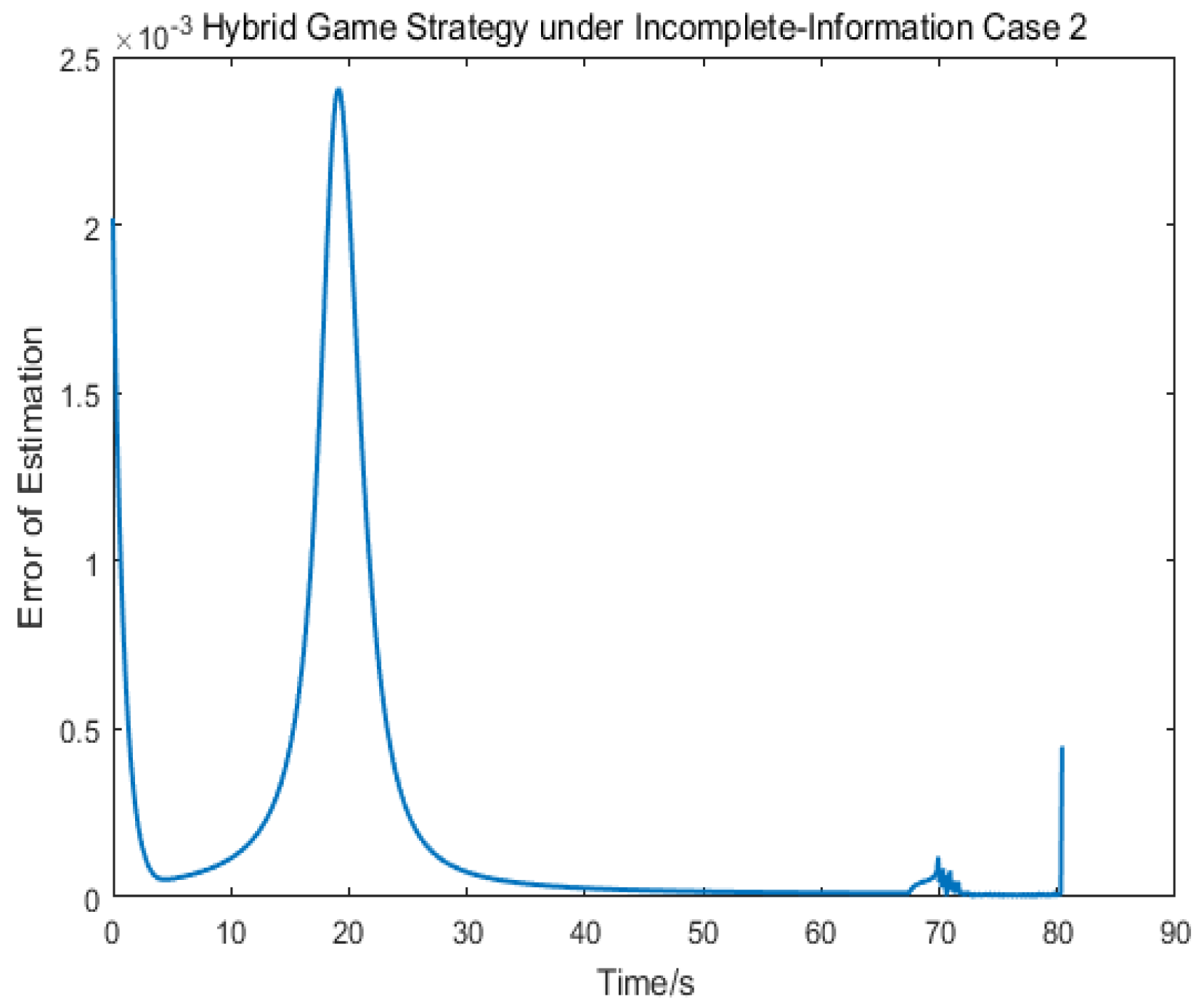
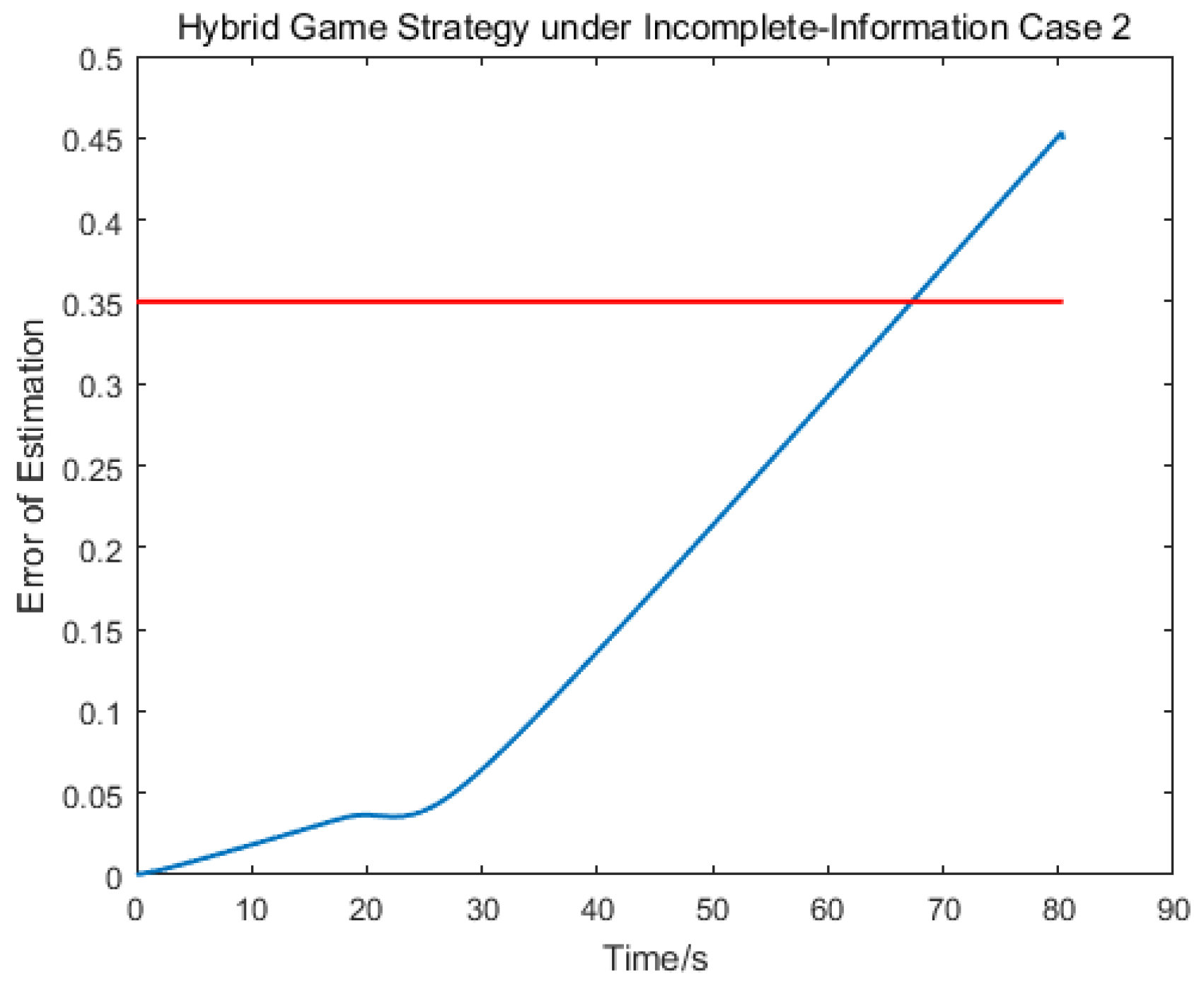
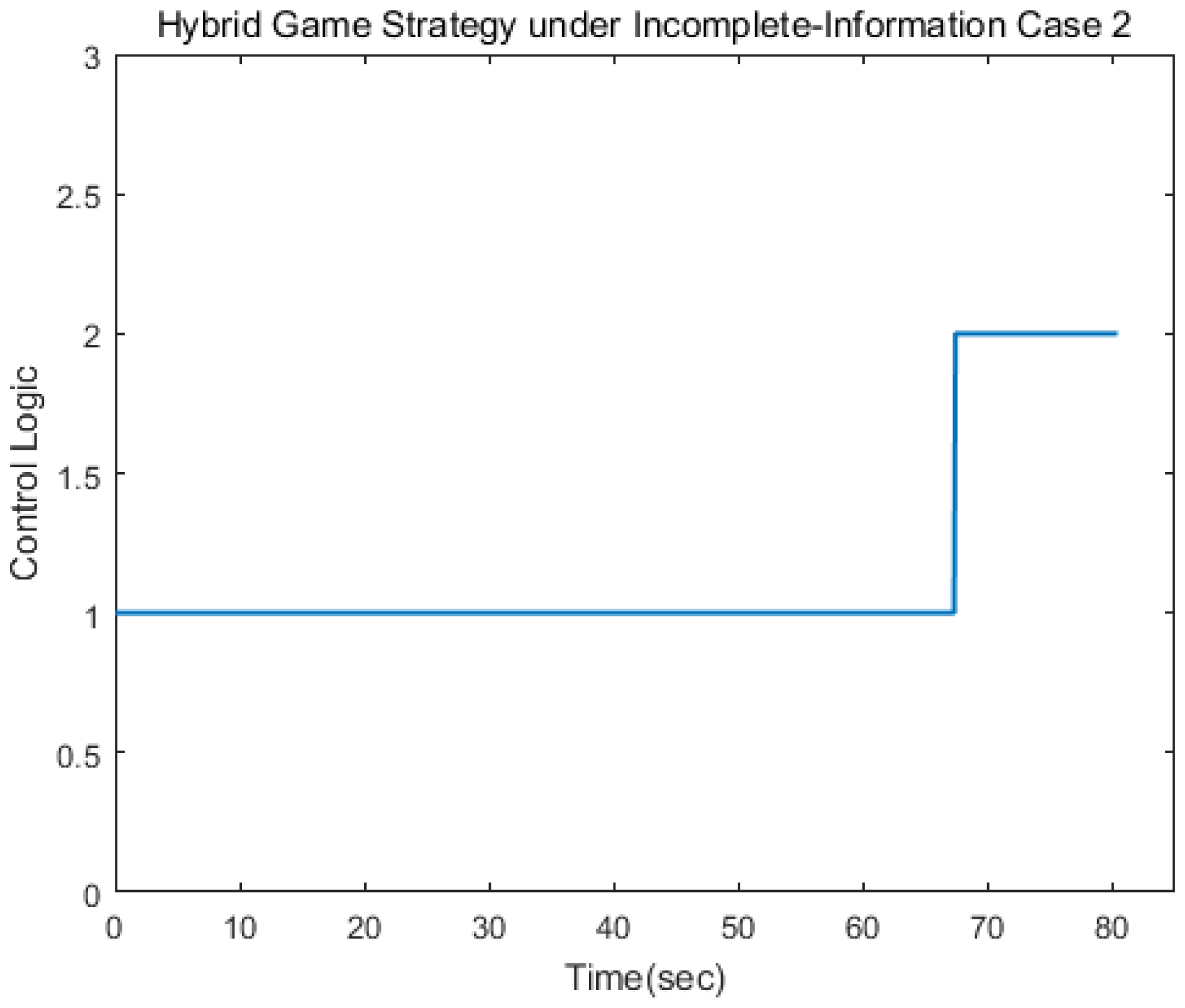
Figure 7, Figure 8 and Figure 9 depict the control logic and error of estimation, from which we knew that the pursuer used the linear quadratic compensation strategy, and, then, used the norm-based strategy after 128 s. Via the hybrid strategy, the approach could be achieved.

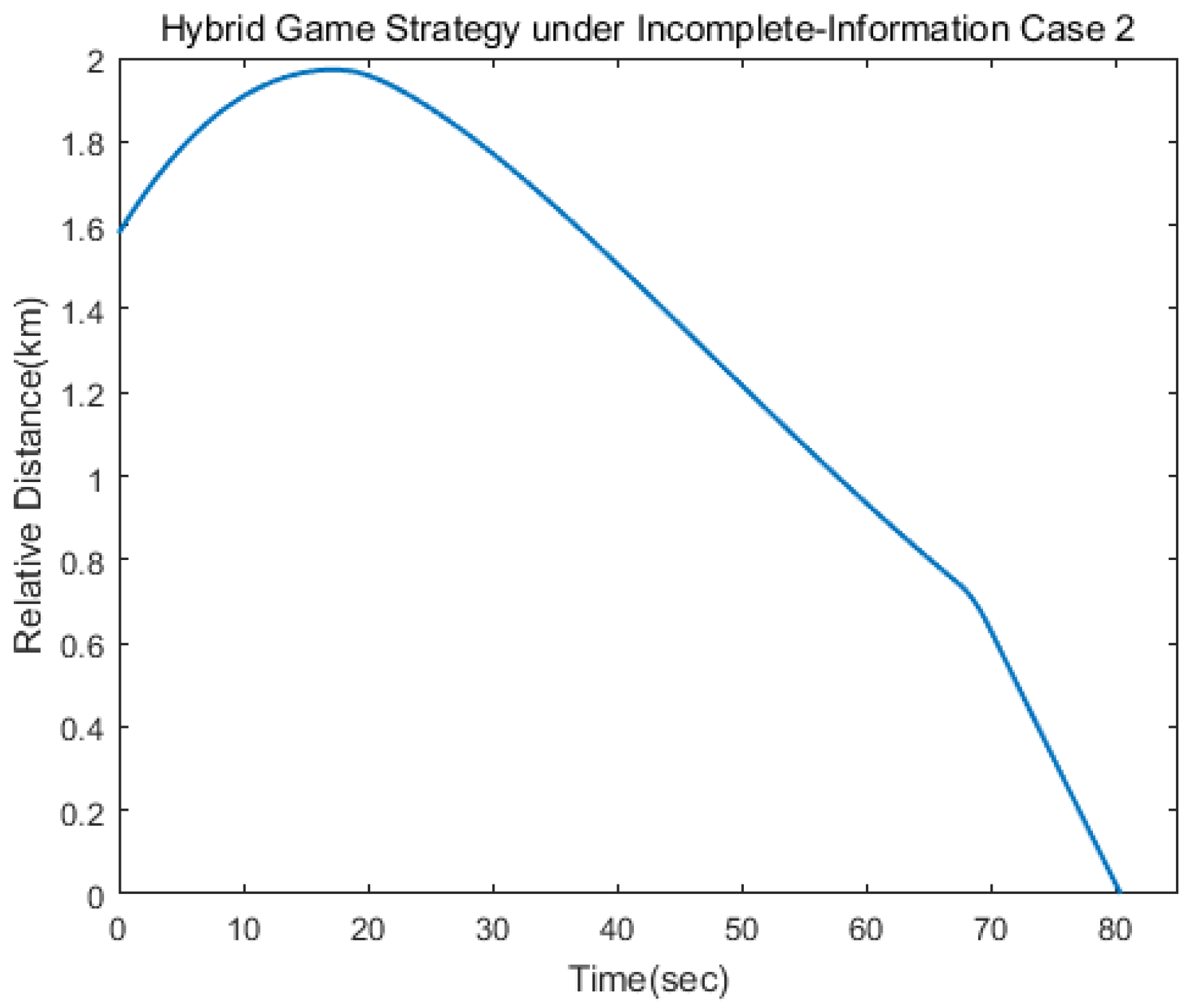
The second scenario was that the target used the norm-based strategy. Simulation results are shown as Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16. Different from the first case, the target adopted the strategy of ignoring fuel consumption, and so the limit value of change hybrid strategy would be reached faster. The control logic changed from 1 to 2 at 68 s, which indicated that the pursuer applied the linear quadratic strategy within 70 s and, then, applied the norm-based strategy. The results show that the approach could be achieved in 81 s.

Finally, to demonstrate the effectiveness of the disturbance estimator to the target strategy, we supposed the target employed random strategy, which is a non-optimal and irregular strategy. This situation simulated a real-world scenario for handling dangerously out-of-control spacecraft. The strategy is given as:

$${\mathit{U}}_E={\rho }_E\frac{\mathrm{randn}\left(3\right)}{\Vert \mathrm{randn}\left(3\right)\Vert }$$

(58)

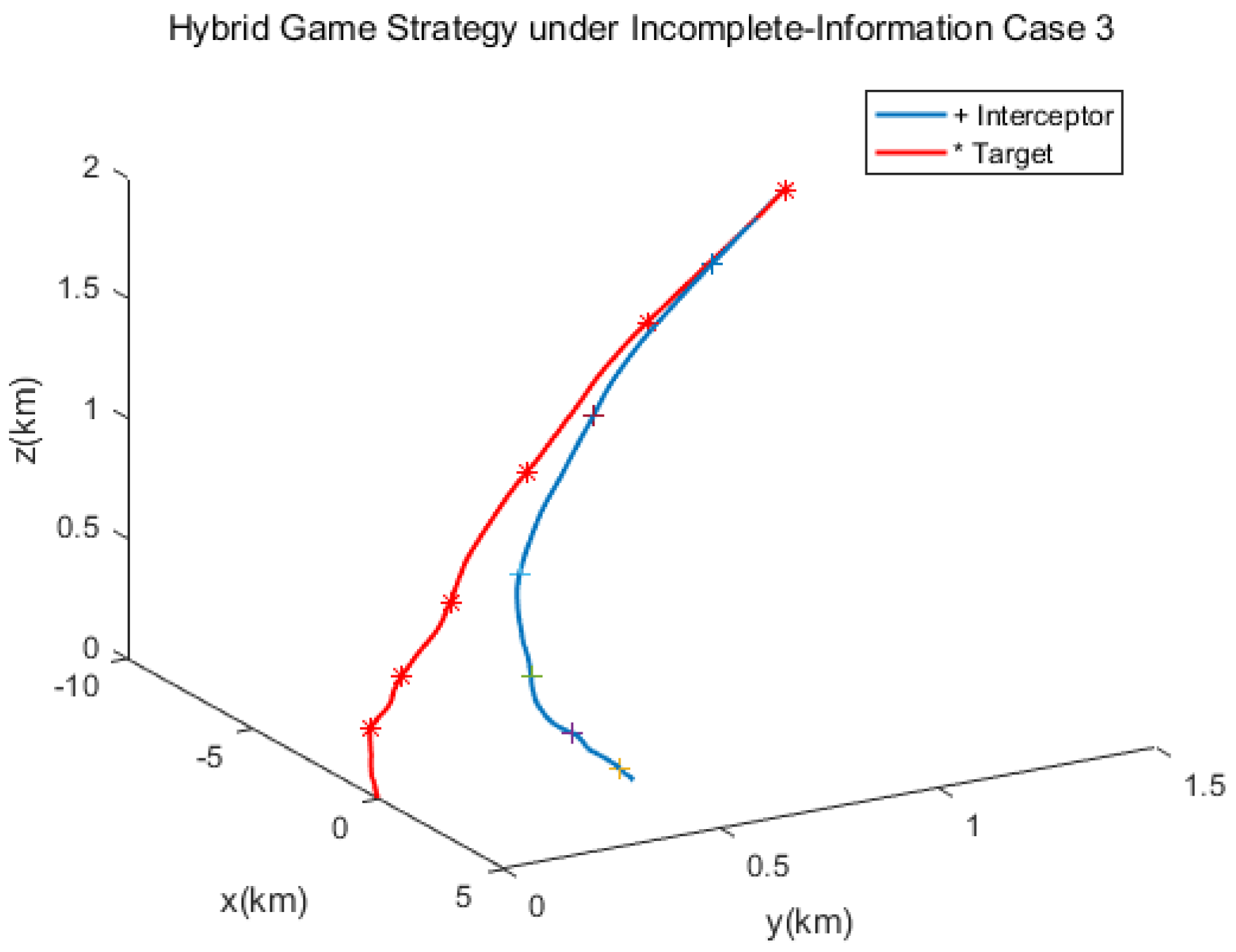
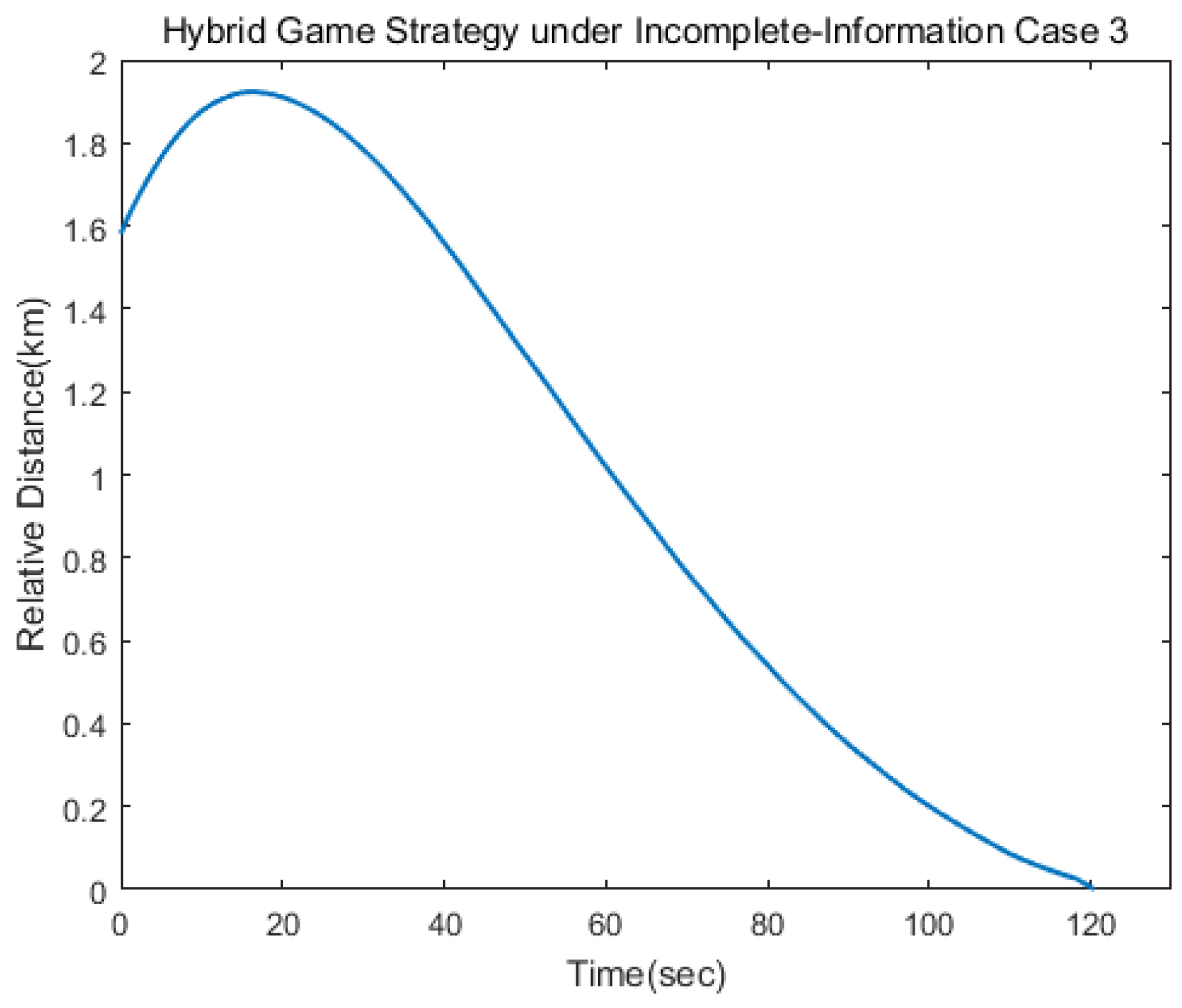
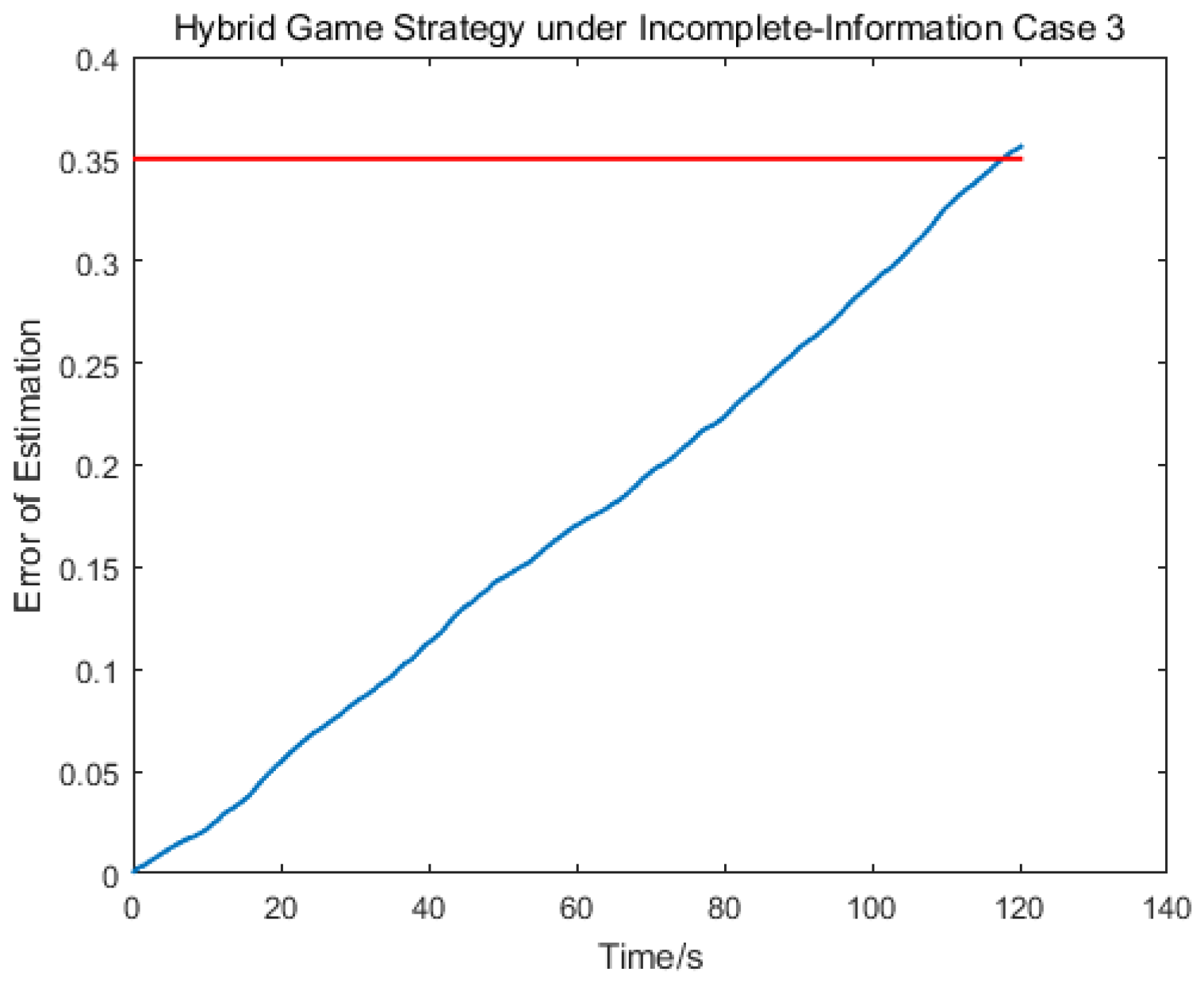
The spacecraft trajectory of hybrid game strategy is shown in Figure 17, from which we can find that the target maneuvered irregularly in the whole process. The following Figure 18 shows the relative distance between the pursuer and the target. After 120 s, the target spacecraft was approached. As can be seen from Figure 19 and Figure 20, if there was no hybrid strategy in the situation of incomplete information, approach could not be realized, so the estimation of target strategy was very meaningful. 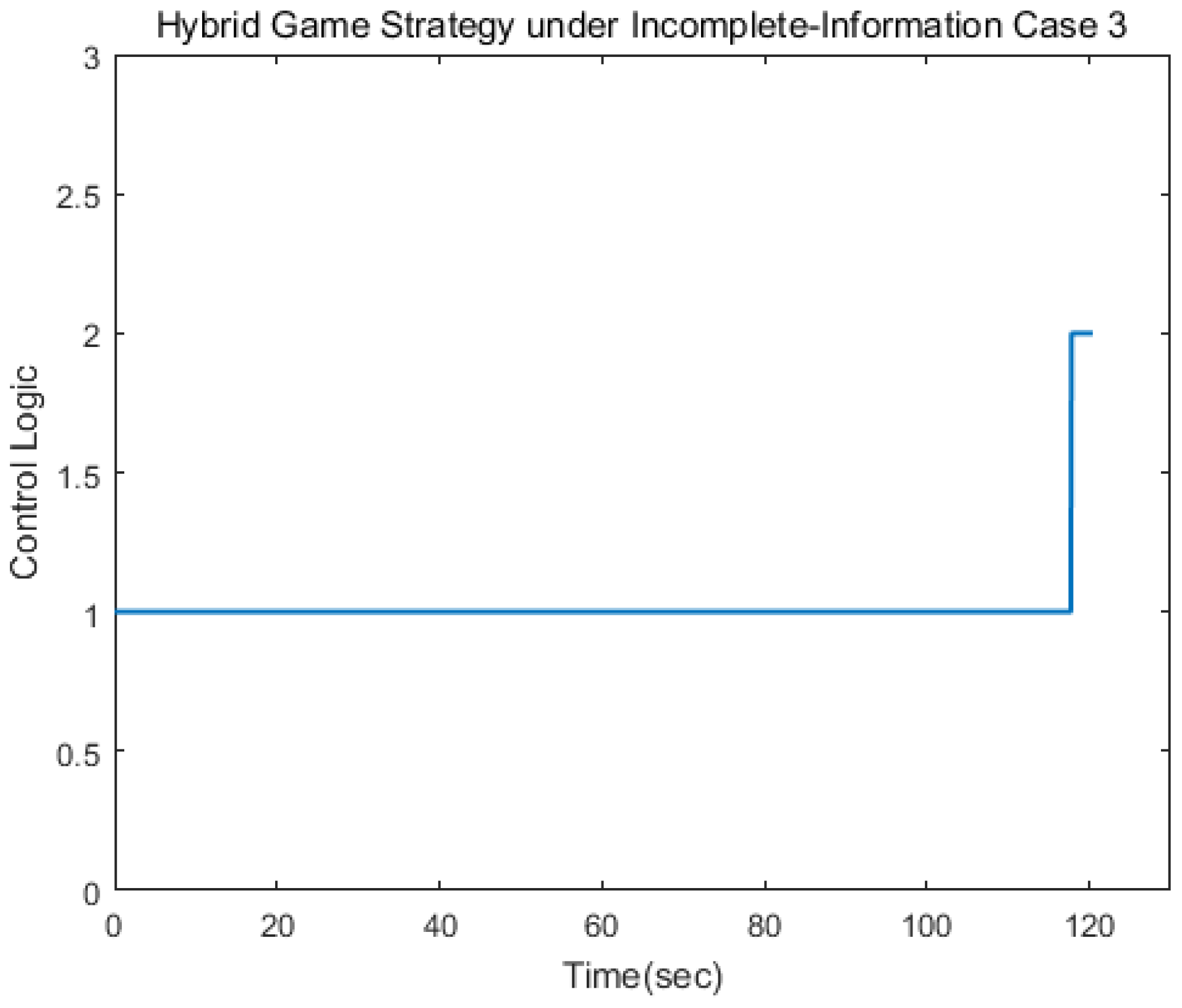As can be seen from Figure 21, since the maneuvering strategy of the out-of-control target was random and disordered, the error estimated oscillation constantly to match the true value of the target control strategy. In this scenario, the pursuer took the disturbance observer to estimate the target control matrix information, and then established the hybrid game strategy and completed the change of control logic after 117 s as shown in Figure 22 and Figure 23.

When the pursuer took the estimation behavior, the bilateral game problem turned into a unilateral optimization problem, so the pursuer could get better approaching effect by adopting the corresponding strategy. The proposed hybrid game strategy could intercept a dangerous spacecraft which is out of control in a finite time, which shows the effectiveness of information estimation in incomplete information game. Nevertheless, it was noted that when the target’s maneuver varied slowly, the disturbance estimator showed the well estimation performance. However, if the target’s maneuver was performed randomly, which meant at a fast-changing rate, the estimation performance would be degraded, which would also affect the pursuit performance.

From

Table 1. Comparison of Fuel Consumption.

	Norm-Based Strategy	Hybrid Strategy
Case 1	0.0037	0.0015
Case 2		0.0035
Case 3		0.0007

on the comparison of fuel consumption, it was observed that the designed hybrid game strategy could achieve rapid approach, while saving fuel consumption in different scenarios. Compared with the traditional unilateral optimal control strategy, considering the complex situation of pursuit–evasion of spacecrafts with the ability of perceiving information, the application of hybrid game strategy had more advantages.

6. Conclusions

This paper investigated the hybrid game strategies of an out-of-control spacecraft with incomplete-information. Firstly, the impact of hybrid game strategy on both sides was analyzed, and the complete-information intercept game switching strategy was derived from differential game theory. Furthermore, the asymmetric-information situation, where the target information was not available to the pursuer, was discussed. The incomplete-information game strategy and information-estimation strategy were derived, respectively. The method of interference estimator is proposed to improve the estimation performance, and, embedded in hybrid game strategy, is consideration of both interception effectiveness and fuel consumption in estimating unknown target maneuver information. Finally, simulations were performed to assess the effectiveness and pursuit performance.

Compared with traditional unilateral optimal control strategy, the complex situation of the out-of-control spacecraft with the ability of sensing space information was considered. The simulation verified the effectiveness of the hybrid game strategy under different information scenarios. Simulation results showed that if the out-of-control target’s maneuver was unknown to the pursuer, the difficulty of approach would increase. Using the proposed disturbance estimator, the target information could be estimated effectively and the control logic could be changed quickly to minimize fuel consumption while quickly approaching the target, which indicated the effectiveness of the proposed scheme in this paper. Therefore, the proposed hybrid game strategy can be applied in practical pursuit scenarios for dangerous spacecraft disposal missions with incomplete-information. In the future, the authors will focus on stochastic-game problems for complex dynamics of the out-of-control spacecraft.