Analysis of Numerical Methods for Droplet Impingement Characteristics under Aircraft Icing Conditions

Abstract

The investigation of super-cooled droplet impingement characteristics is the most important step for aircraft icing and anti-icing/de-icing analyses. The Lagrangian method and the Eulerian method are widely used to compute the droplet motion and collection efficiency, and the two methods are considered to obtain almost the same results for surface impingement characteristics under icing conditions. The models and implementation approaches of the two methods were established in this work, and the simulations of droplet motion were carried out for a NACA 0012 airfoil, a 2D section of an A320 head, a multi-element airfoil, and an icing wind tunnel. The collection efficiencies of the NACA 0012 airfoil obtained by the present Lagrangian and Eulerian methods show good agreement with the results in the literature, validating the established methods. The droplet impingement characteristics of the two methods are consistent for the aircraft surfaces without upstream trajectory deflections. However, when the droplet motion is deflected by the frontal body before hitting the rear surfaces, the results obtained by the two methods are different whether the droplet trajectories intersect or not, which subverts the traditional opinion that the Lagrangian and Eulerian methods would obtain the same result of the droplet impingement characteristics. The reason is studied in detail according to the droplet motion results in the icing wind tunnel. The findings of this work are helpful for the accuracy of aircraft icing and anti-icing/de-icing simulations, and useful for the development of airworthiness certification.

1. Introduction

Super-cooled liquid water droplets in clouds impact aircraft components [1], leading to ice accretion on the windward surfaces and threatening flight safety [2]. Ice protection systems should be adopted to prevent or control ice accretions as required by airworthiness regulations [3]. The first and most important step to investigate an aircraft’s icing process [4] or design an ice protection system [5] is the calculation of water droplet impingement characteristics: Droplet impingement ranges and mass flux of the impinged droplets [6]. Those characteristics are usually expressed in terms of the collection efficiency, which is the ratio of the mass flux of the water droplets impinging on the surface to that at the free stream [7]. In fact, the movement and impact process of the super-cooled water droplets in the air is a typical fluid-particle two-phase flow problem, and there are two main methods for its solution: The Lagrangian method and the Eulerian method [8].

The Lagrangian method is a traditional and classical approach for the motion and trajectory predictions of particles and has been widely applied for droplet impingement characteristics under icing conditions. It tracks the droplets’ trajectories in the airflow to obtain the impingement limits and collection efficiency distributions on aircraft surfaces. The Lagrangian method has been used in various aircraft icing codes such as LEWICE [9] and ONERA [10], and it performs well for different aircraft geometries according to the comparison against the icing wind tunnel data [11,12]. On the other hand, the Eulerian method treats the water droplets as a continuous phase corresponding to the airflow and solves the continuity and momentum equations of the droplet phase for the fields of the droplet volume fraction and velocity components [13]. It has been adopted by FENSAP-ICE [14] because it can be easily implemented for complex geometries [6]. The Eulerian method has been applied for the droplet impingement characteristics of 3D wings, rotor blades, engine components, and so on [15].

Solution process comparison of the Lagrangian and Eulerian methods shows that the former is more intuitive and easier to solve for the components with 2D or geometrically simple surfaces. In addition, the Lagrangian method can aptly describe the deformation, breakup, splashing, and bouncing of water droplets, thus it is very suitable for simulations under super-cooled large droplet (SLD) conditions [16]. However, the computational expensiveness of tracking a large number of particles reduces its usefulness in dealing with 3D or complex geometries, especially when the seeding locations of particles are not known [17]. Some new strategies have been studied for the robust and efficient implementation of the Lagrangian method [6]. On the other hand, the Eulerian method directly solves the water droplet motion for the entire fluid domain and can obtain the impingement characteristics of all the component surfaces at once [18]. Therefore, it is usually selected in the cases of 3D surfaces or components with complex shapes, and it has also been extended to ice crystal conditions [13]. However, the droplet-governing equations of the Eulerian method are highly nonlinear, and the local singularity of the droplet concentration would cause numerical instability [17]. Numerical diffusion [17] or artificial viscosity [14] has been added to eliminate those droplet oscillations and ensure convergence. Other improved solution approaches were also developed to reduce the modeling effort and overall calculation time of the Eulerian method [8]. Generally, both Lagrangian and Eulerian methods have been widely used in the aircraft icing community [19,20,21], and they still attract much attention for droplet impingement characteristics under aircraft icing conditions, but the Eulerian method is relatively popular with more and more applications [14].

As for the droplet impingement results, many comparisons have been made between Lagrangian and Eulerian methods for different components and surfaces, and their results of local water collection efficiency always match very well [7,14,15,16,17]. Therefore, although the two methods solve droplet motion differently, they are generally considered equivalent for the prediction of water droplet impingement characteristics. In addition, their results are both accepted by airworthiness certification departments, which means the choice between the two methods mainly comes down to personal habits and the difficulty of the method’s implementation, along with the parallel performance and computational efficiency. However, different results were found between Lagrangian and Eulerian methods for the rear surfaces of multi-element airfoils [18,22]. The reason was considered to be the different ways of dealing with the droplet motion after being deflected by the upstream flow around frontal elements. The Lagrangian method could capture the crossings of the droplet trajectories under the effects of the disturbed flow around frontal surfaces, while the Eulerian method could not simulate the droplet crossings, leading to deviations in the downstream droplet motion and impingement characteristics [18]. Additionally, in simulations of the granular flows such as those in the circulating fluidized bed, it was also found that the Eulerian method failed to predict the particle trajectory crossing effect, with the phenomenon of ‘delta shocks’ [23], while the crossing of the two dilute jets of particles could be captured under the Lagrangian framework, also indicating the difference of the two methods and the limitations of the Eulerian method [24,25]. Therefore, the two methods should be further analyzed in the calculations of the droplet impingement characteristics in various conditions for the difference and their causes.

To summarize, Lagrangian and Eulerian methods have been widely used in the prediction of droplet impingement characteristics under aircraft icing conditions, and they were considered to obtain almost the same impingement results. However, a discrepancy has been found in some icing simulations and granular flow calculations. The object of this paper is to compare the two methods regarding the impingement characteristics of different surfaces and analyze the causes of the differences in applicability. In the following section, the models of the Lagrangian and Eulerian methods are presented with their equations to obtain the collection efficiency. Those two methods are validated with NACA 0012 airfoil in Section 3.1. Then, a 2D section of an A320 head and multi-element airfoil are used to investigate the upstream effects and study the differences in the droplet motion and impingement characteristics. Finally, the causes are analyzed with the solutions of the droplet motion in an icing wind tunnel.

2. Numerical Simulation Methods

Following the fact that the volume fraction of super-cooled water droplets in clouds is very low (approximately 10⁻⁶) with a small diameter (around 20 μm) [26], the air-droplet two-phase flow around aircraft components is usually considered to be coupled one way, i.e., the airflow field affects water droplets’ movement via aerodynamic drag but is independent of the droplet motion [8]. Therefore, airflow is solved independently by Reynolds Averaged Navier–Stokes equations (RANS) with the Spalart–Allmaras turbulence model. In this paper, the airflow field is obtained by the commercial CFD software ANSYS FLUENT—19.1 [27], and the Lagrangian and Eulerian methods are both implemented with FLUENT UDFs (user-defined functions) on the basis of the same airflow solutions.

2.1. Lagrangian Method

The following assumptions are made for the droplet motion and impingement characteristics under aircraft icing conditions [6,17]: (1) Droplets remain spherical with no deformation, breaking, or splashing; (2) droplets do not affect each other without collision and coalescence; (3) the only force acting on the droplets is due to the aerodynamic drag, and all the other forces, including gravity, are negligible. Those assumptions are also adopted in other icing codes such as LEWICE [9] and FENSAP-ICE [15]. Then, the motion of the water droplet in the airflow field is determined by Newton’s second law, and the governing equation in the Lagrangian frame is [18]:

$$\frac{\mathrm{d}\mathit{u}}{\mathrm{d}t}=K({\mathit{u}}_a-\mathit{u})$$

(1)

where u is the droplet velocity vector, t is the time, μ_a is the air velocity vector, and K is the air-droplet exchange coefficient, given as [6]:

$$K=\frac{18{\mu }_a}{\rho d_p^2}\frac{C_D\mathrm{Re}}{24}$$

(2)

where μ_a is the air viscosity, ρ is the droplet density, d_p is the droplet diameter, C_D is the drag coefficient of the spherical droplet [26], and Re is the relative Reynolds number given as:

$$\mathrm{Re}=\frac{{\rho }_a|{\mathit{u}}_a-\mathit{u}|d_p}{{\mu }_a}$$

(3)

where ρ_a is the air density.

When a water droplet is released far away from aircraft components, the droplet and the air around it would have the same velocity as the freestream value. Then, the droplet trajectory can be obtained in the airflow field via the integration of Equation (1), and in this work, the classical Runge–Kutta method is used for the ordinary differential equation. The calculation of the droplet trajectory is carried out by the discrete phase model (DPM) of FLUENT software. The solution of the trajectory would end on the wall surface with a trap boundary condition or leave the computing domain with an escape condition. Based on the trajectories starting at different locations, the droplet impingement positions on the aircraft are determined and the collection efficiency is evaluated. Based on the definition of the collection efficiency mentioned in the Introduction, the local collection efficiency, β, is described as the ratio of the surface and the far-field water fluxes per unit of area in the Lagrangian frame [6]. To consider the crossing effects of the droplet trajectories, the value of the control volume (CV) i on the surface is calculated by [16,18]:

$${\beta }_i=\frac{\mathrm{d}{y}_i}{\mathrm{d}{s}_i}=\frac{N\Delta y}{\mathrm{d}{s}_i}$$

(4)

where ds_i is the total separation between the trajectories at the impact on the surface, dy_i is the total separation between the trajectories in the CV in the freestream, N is the total number of droplets collected in the CV, and Δy is the initial length between neighboring droplets in the airflow field [16]. The details of the model and the solution process for the Lagrangian method can be found in our previous work [18].

2.2. Eulerian Method

According to the same assumptions as those described in Section 2.1, the governing equations for water droplets in the Eulerian frame can be derived from the Lagrange equation, and are written as [17,26]:

$$\frac{\partial (\rho \alpha )}{\partial t}+\nabla \cdot (\rho \alpha \mathit{u})=0$$

(5)

$$\frac{\partial (\rho \alpha \mathit{u})}{\partial t}+\nabla \cdot (\rho \alpha \mathit{u}\mathit{u})=\rho \alpha K({\mathit{u}}_a-\mathit{u})$$

(6)

where α is the droplet volume fraction and other parameters are the same as those in the Lagrange frame.

It can be seen from the equations that there is no diffusion term to respond to the locally high gradient of the droplet volume fraction, and singularity in the droplet concentration may occur with an exceedingly large value in some areas [17]. A numerical diffusion term, as shown in our previous work of Reference [26], is adopted to avoid this problem, and Equation (5) becomes:

$$\frac{\partial (\rho \alpha )}{\partial t}+\nabla \cdot (\rho \alpha \mathit{u})=\Gamma {\nabla }^2(\rho \alpha )$$

(7)

where Γ is the numerical diffusion coefficient, and its value should be large enough in the abnormal areas to smooth out the singularity of the Eulerian method and small enough in the normal regions without affecting the solution accuracy [17,26].

In icing conditions, the water droplet can be considered a steady flow in the Eulerian frame, and then the first terms of the governing equations are eliminated. In addition, the droplet velocity in the far-field boundary is the same as the air value, and the droplets impinging the surface would be absorbed. Then, the Eulerian equations are solved with the help of the user-defined scalar (UDS) transport equations in FLUENT software [27]. The settings of the numerical diffusion coefficient and the solution process of the Eulerian method can be found in detail in previous work [26]. Based on the droplet flow field, the local collection efficiency β_i in the Eulerian frame can be calculated by:

$$\frac{\partial (\rho \alpha )}{\partial t}+\nabla \cdot (\rho \alpha \mathit{u})=\Gamma {\nabla }^2(\rho \alpha )$$

(8)

where u_i is the droplet velocity in the impingement CV, n_i is the unit normal vector at the CV surface, u_∞ is the freestream velocity, and α_i and α_∞ are the droplet volume fraction on the CV surface and in the freestream, respectively.

3. Results and Discussions

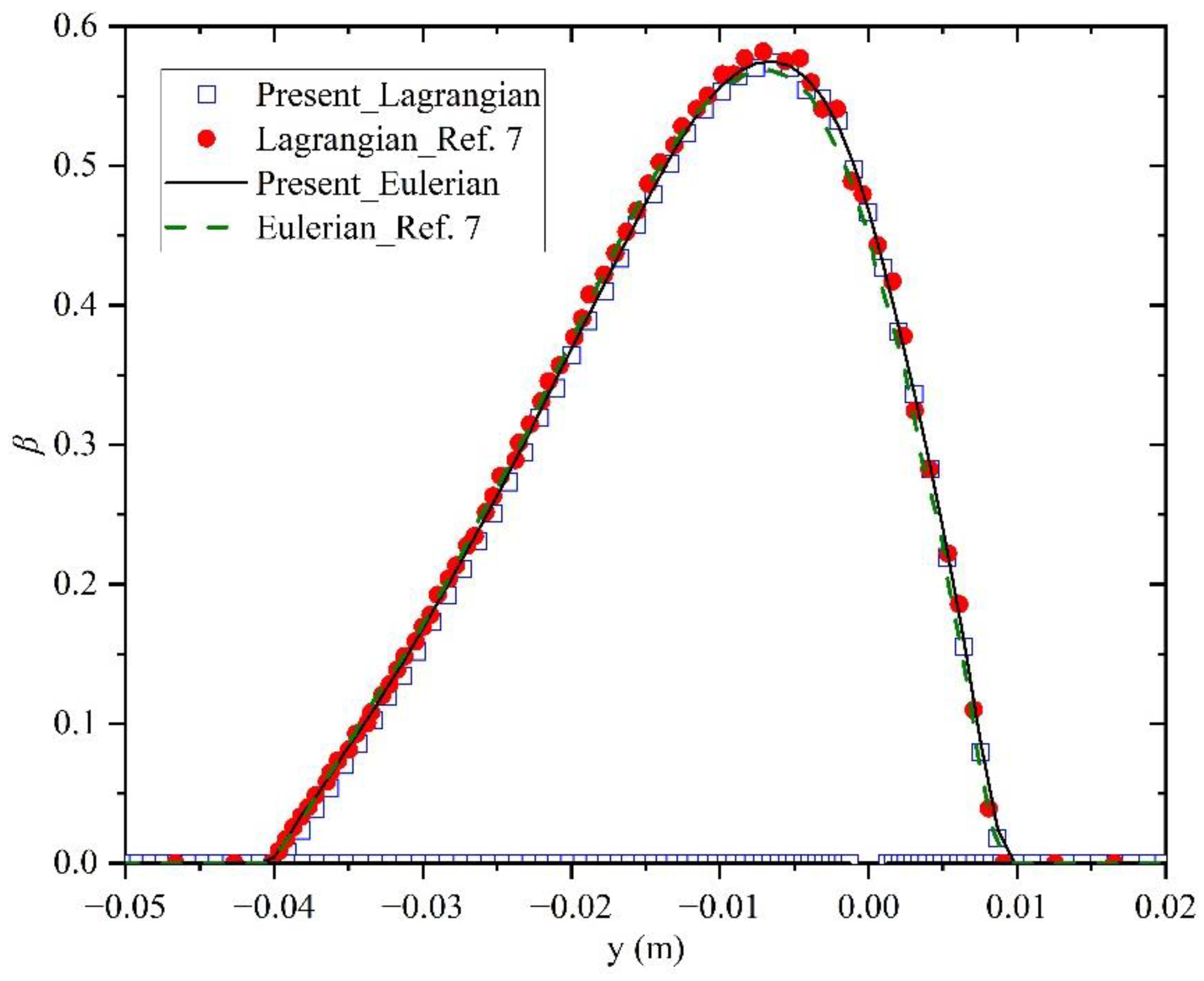
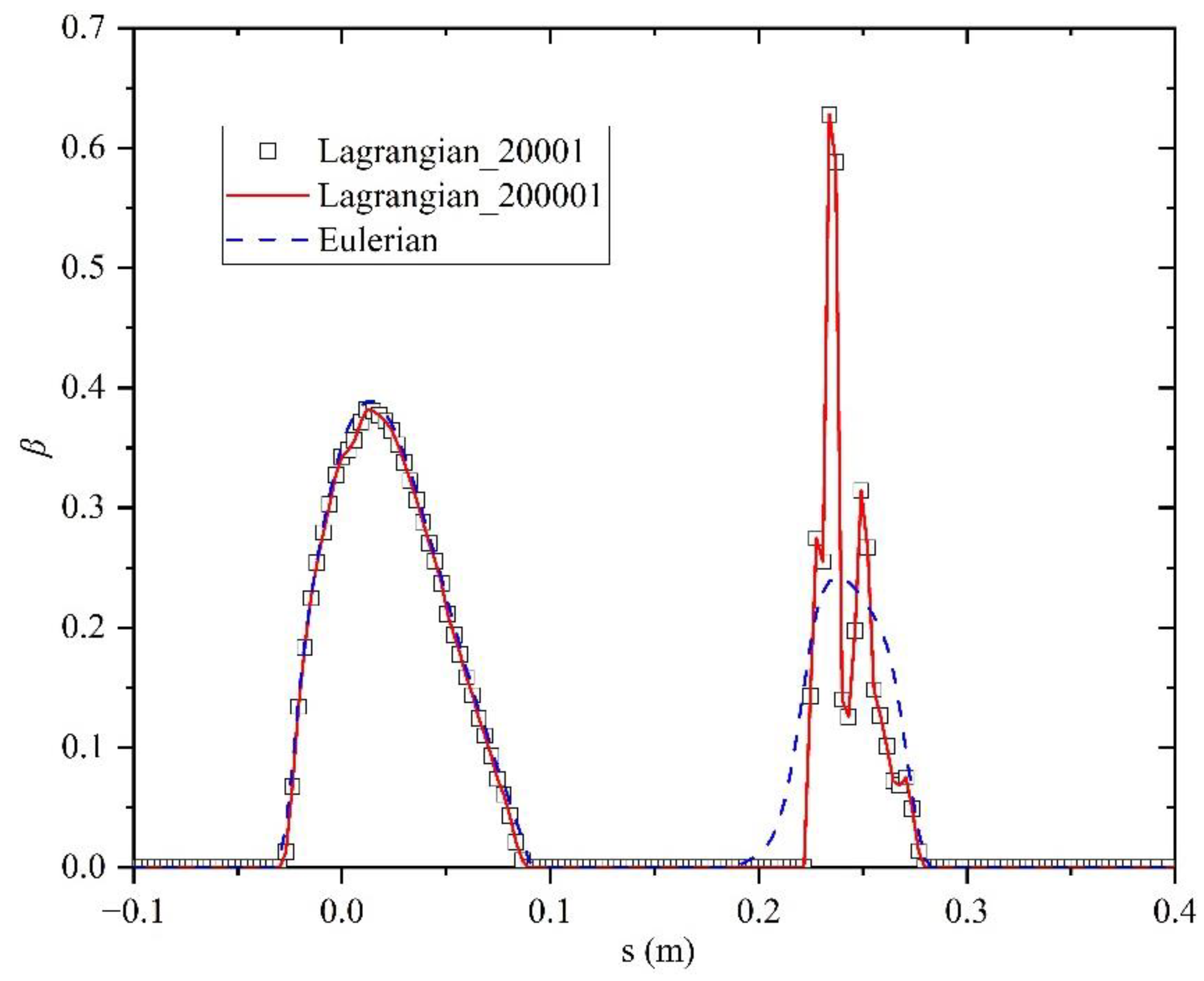
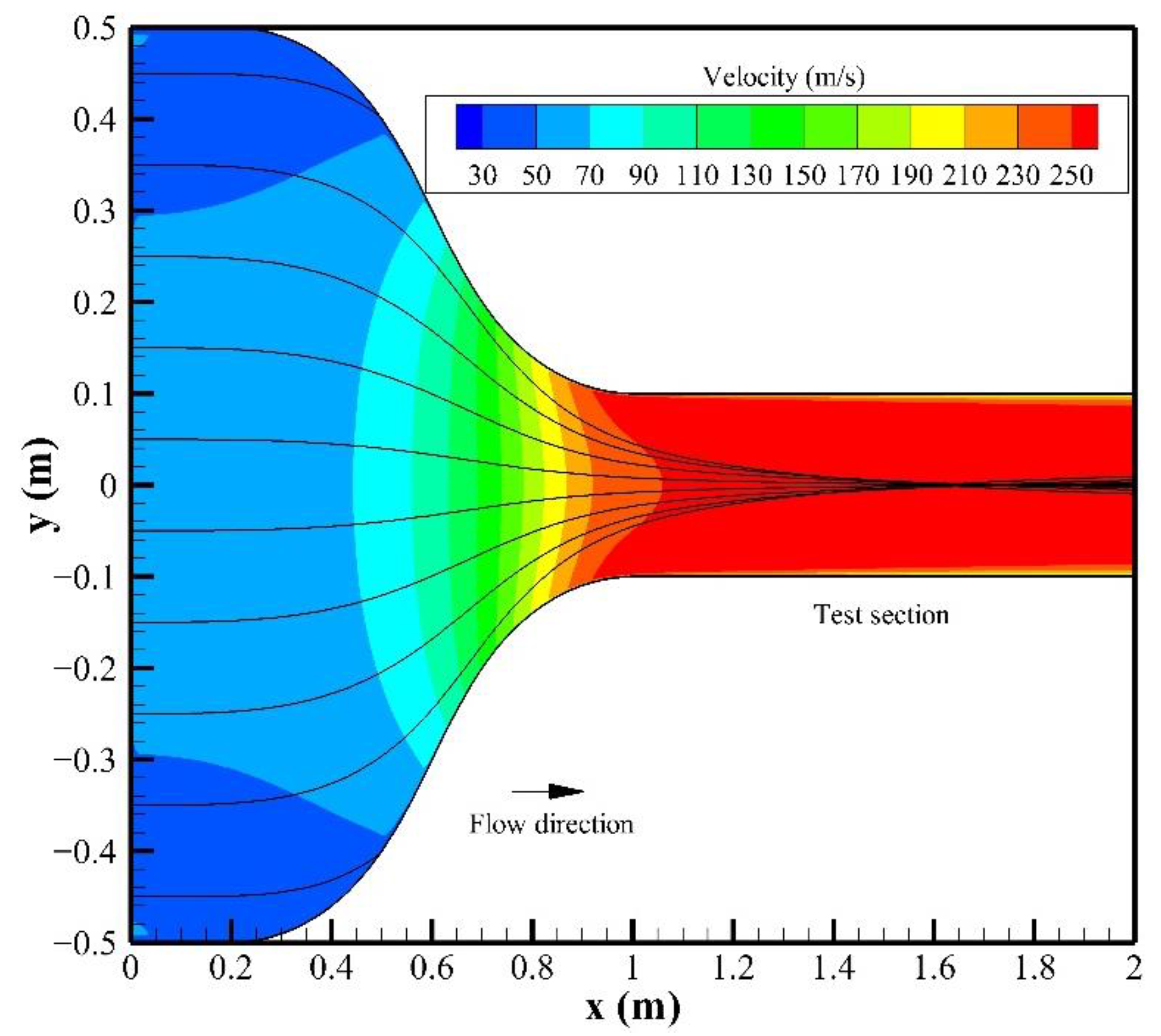
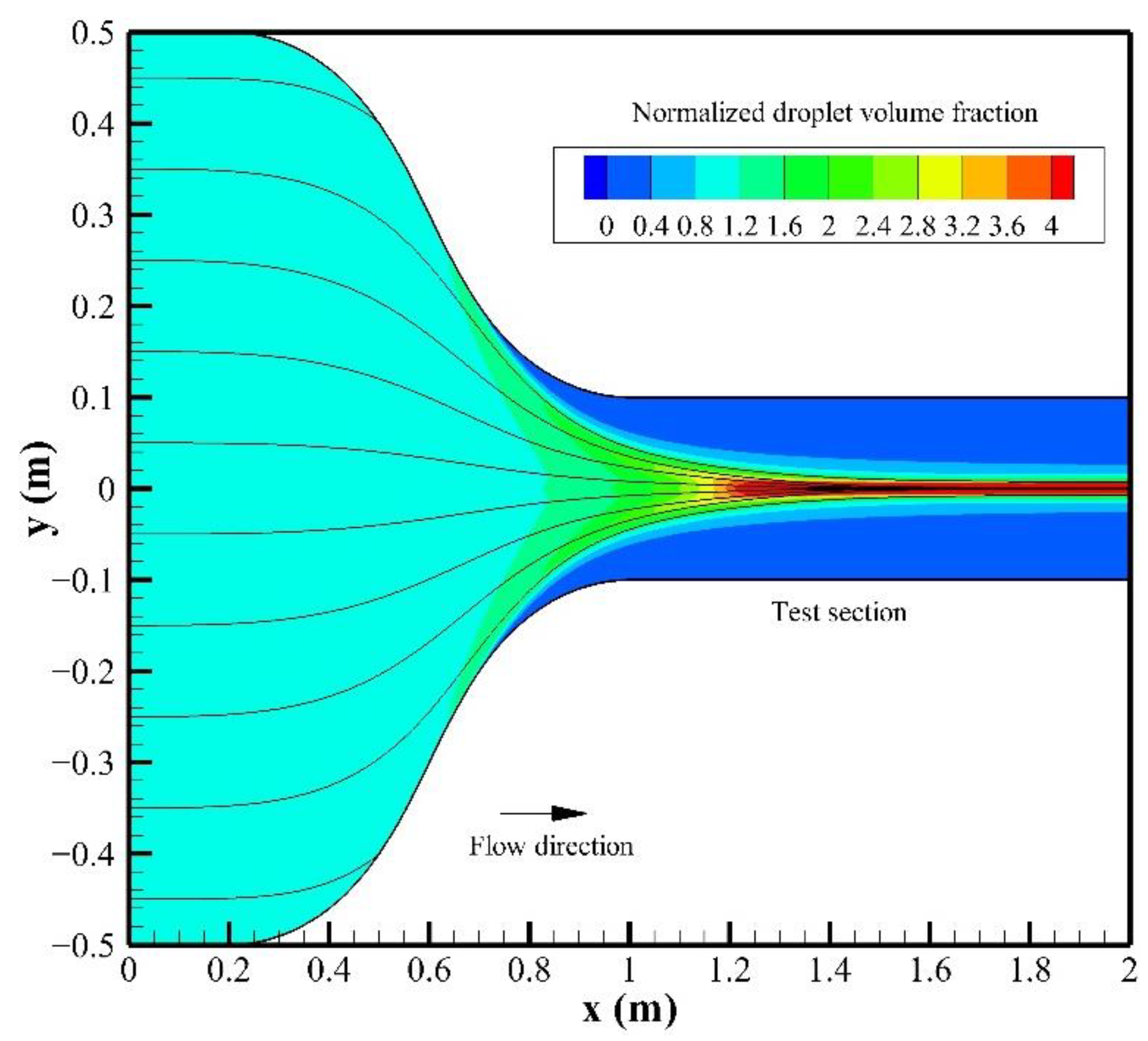
3.1. Method Validation

To verify the established Lagrangian and Eulerian methods for the droplet impingement characteristics under icing conditions, the local collection efficiency of a NACA 0012 airfoil with a unit chord is compared to the results in Reference [7]. The freestream Mach number of the validation case is 0.4 at the angle of attack of 5°. The ambient temperature is 300 K, and the inlet pressure is 1 atm, whereas the diameter of the water droplets is 16 μm.

Figure 1 shows the contour of air velocity around the NACA 0012 airfoil, along with the droplet trajectories obtained by the Lagrangian method. Due to the positive angle of attack, water droplets are more likely to hit the lower airfoil surface, and the lower droplet impingement limit is located behind the upper one in the x direction. Additionally, the air velocity changes sharply around the upper surface, so that water droplet trajectories deviate more greatly from the air streamline there. As for the droplets that bypass the wall, their trajectories concentrate around the airfoil outside the water-shaded region (also called the shadow region, meaning no droplets reach there), since the droplets closer to the surface are affected more sharply with stronger deflections by the airflow change. As shown in Figure 1, overlaps and crossings of the droplet trajectories occur at the upper trajectory’s concentrated zone after droplets are deflected, and those crossing phenomena can also be found in the literature, such as in Reference [6], Reference [12], and Reference [28].

Figure 2 presents the contour of the droplet volume fraction normalized with respect to its freestream value, and the water droplet streamlines calculated by the Eulerian method are also illustrated in the figure. There is a shadow region behind the airfoil, whose droplet volume fraction approaches zero. In other words, there are no water droplets in this region. The upper part of the shadow region is much larger than the lower one as a result of the positive angle of attack. As for the droplet streamlines, some end at the airfoil surface, and others pass around it with dense areas outside the shadow region, which is the same as the droplet trajectories obtained by the Lagrangian method. However, the streamlines obtained by the Eulerian method would never intersect due to the nature of the fluid flow fields. Since streamlines and traces always coincide in a steady flow in the Eulerian frame, the droplet traces or trajectories are different in the Lagrangian and Eulerian methods, which might lead to the deviation of the droplet movement and the impingement characteristics.

Figure 3 compares the collection efficiencies of the two methods with those in Reference [7], and good agreement is found between them, which validates the present Lagrangian and Eulerian methods. The collection efficiency reaches its maximum at the stagnation point on the lower surface and declines to zero when it moves backward. In addition, the result obtained by the Lagrangian method matches that of the Eulerian one well, both in the present work and in the reference, illustrating the equivalence of the two methods for the droplet impingement characteristics under icing conditions. It is also indicated that the deviation of the droplet trajectories predicted by the two methods has a slight effect on the local collection efficiency in this condition, because the droplet deflections and concentrations are caused by the airfoil surface itself and the trajectory deviation is located behind the impingement region. Additional verification test cases of the two methods can be found in our previous work, in Reference [18] and Reference [26]. It seems that the Lagrangian and Eulerian methods are substituted for each other to solve the droplet impingement characteristics under icing conditions.

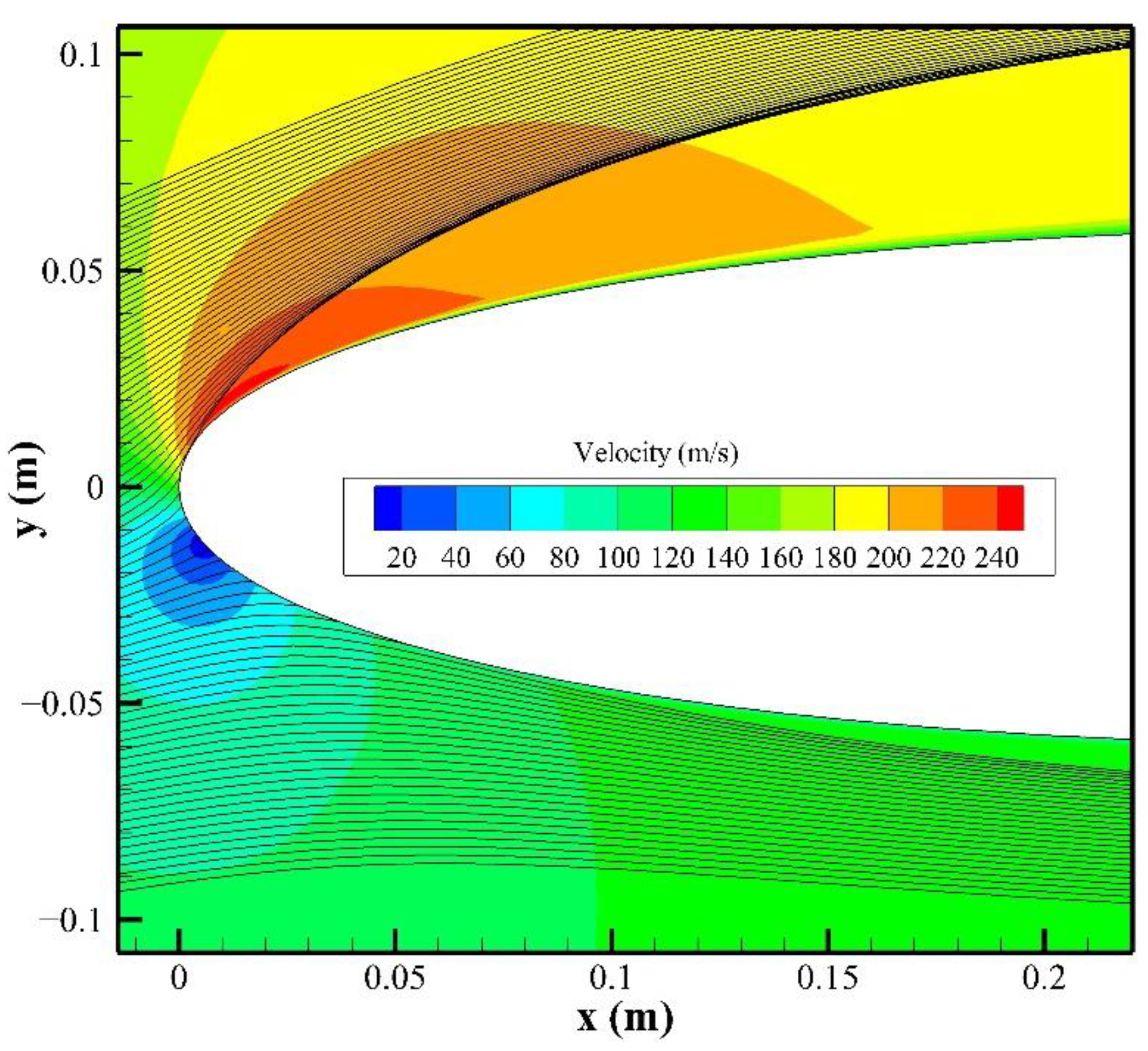
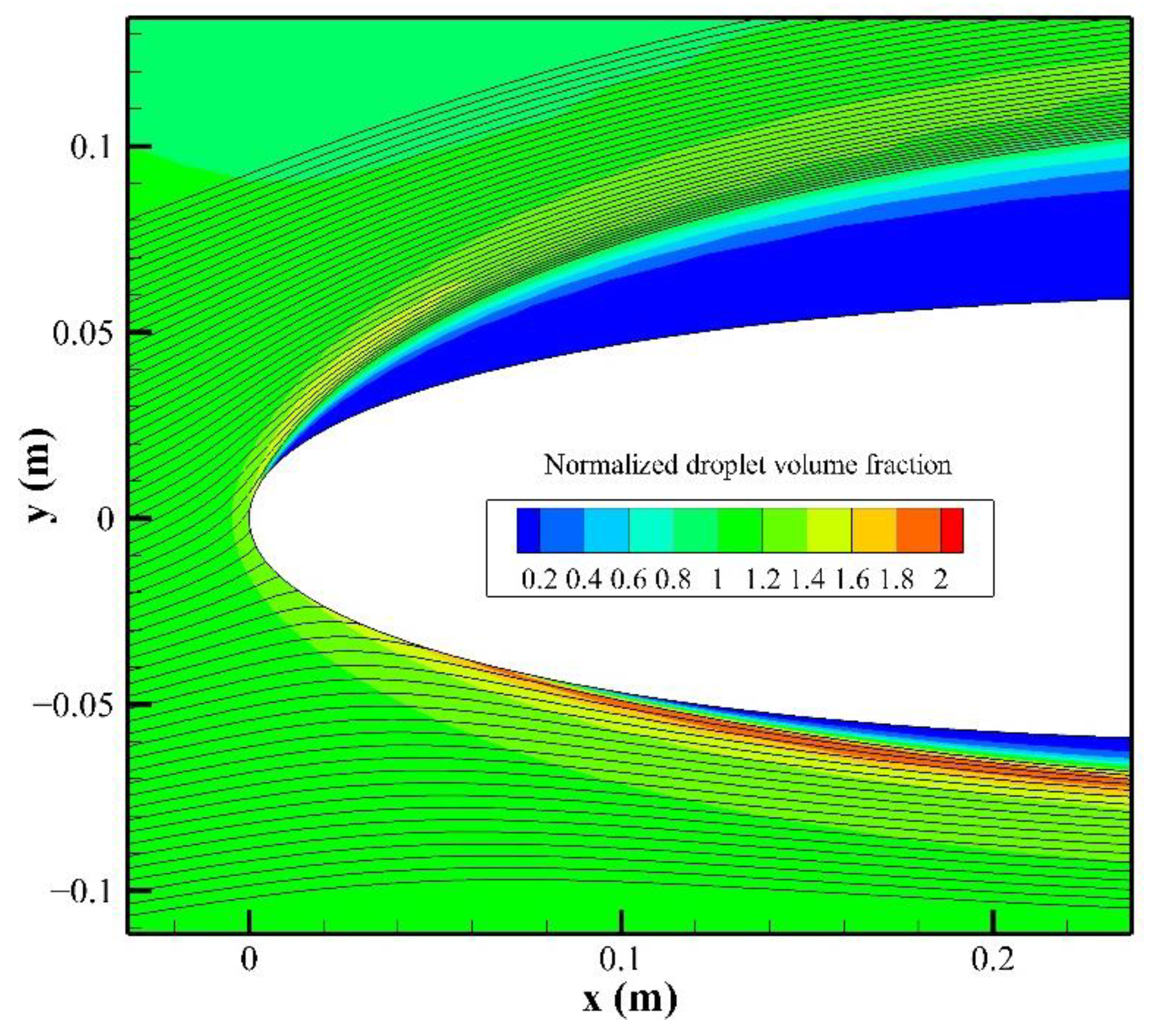
3.2. Comparison with an Aircraft Head

To study the effects of the droplet deflections, especially the trajectory crossings, a 2D section of the symmetry plane for the A320 head is investigated by the two methods. The size of the geometric model is reduced by 10 times to increase the collection efficiency for better viewing and comparison, and this large collection efficiency can also be achieved by increasing the air speed. In this case, the far-field Mach number is 0.4 at an angle of attack of 0°, and the inlet pressure is 1 atm with the ambient temperature of 300 K. A droplet diameter of 20 μm is used for the droplet motion calculations in the Lagrangian and Eulerian methods.

Droplet trajectories obtained by the Lagrangian method are shown in Figure 4, along with the velocity field around the front part of the aircraft head. There are two low-velocity zones: Around the stagnation point and near the connection point of the nose and the windshield. Some droplets could impinge on the nose surface directly, while others would bypass the nose and hit the rear windshield due to the effect of airflow around the headwall. Thus, two impingement regions exist in this condition. In addition, it can be seen that the water droplet trajectories overlap and cross each other in front of the windshield because the droplet deflection is more severe at the position closer to the surface, which is similar to the phenomenon in Figure 1. Since those trajectories’ deflections and crossings occur in front of the windshield surface, some droplets can impact the same location, and some trajectories of the adjacent droplets may end at points far away, leading to a complicated distribution of the impingement characteristics on the windshield surface [18].

On the other hand, Figure 5 illustrates the water droplet streamlines, which are also the droplet traces in a steady flow, on the contour of the normalized droplet volume fraction calculated by the Eulerian method. It can be seen that the upper shadow region is divided into two separate parts by the windshield. According to the trace lines, the water droplets can impact the nose and windshield surfaces. The contour and streamlines both indicate that there are also two impingement regions in the Eulerian method. However, different from the droplet trajectories obtained by the Lagrangian method, the Eulerian droplet traces downstream of the nose change relatively parallel without any crossings, resulting in a smooth distribution of the impingement characteristics on the windshield surface.

The comparison of the local collection efficiency between the two methods is plotted in Figure 6, where the surface distance s = 0 is the leading edge and the curve distance on the upper surface is positive. To check the independence of the number of tracked particles in the Lagrangian method, the values of 20,001 and 200,001 are used for the droplet release points, and it can be found that 20,001 particles are enough for the collection efficiency. It can be seen that there are two separate impingement regions on the resulting curve. The results of the Lagrangian and Eulerian methods show good agreement on the nose surface, but much difference is found at the rear windshield. On the windshield surface, an oscillatory characteristic is found in the Lagrangian curve due to the upstream deflections and crossings of the droplet trajectories. Denser trajectories cause a higher collection efficiency, and the sudden dip results from the sparse droplet impact, as shown in Figure 4. On the other hand, the Eulerian collection efficiency is smoother with a smaller impingement range as a result of the numerical diffusion term, which can be inferred from the smooth streamlines in Figure 5. Thus, it is indicated that the deviation of the droplet motion and trajectories obtained by the two methods would affect the droplet impingement characteristics of downstream rear surfaces. Since the Eulerian method cannot capture the crossings of the droplet trajectories due to its nature of single-value velocity in a control volume, the result of the Lagrangian method seems to be more reasonable in theory under this circumstance [18].

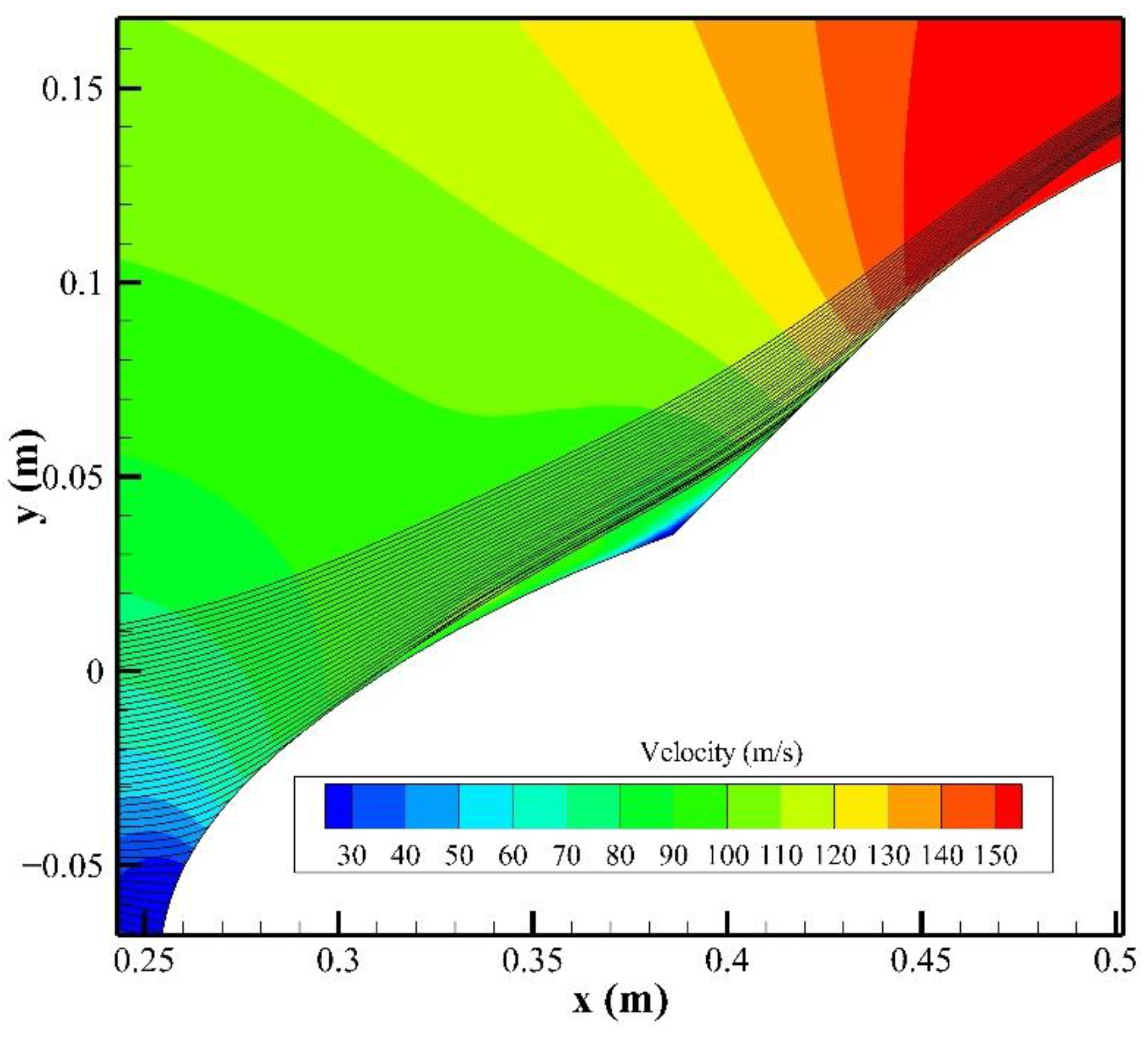
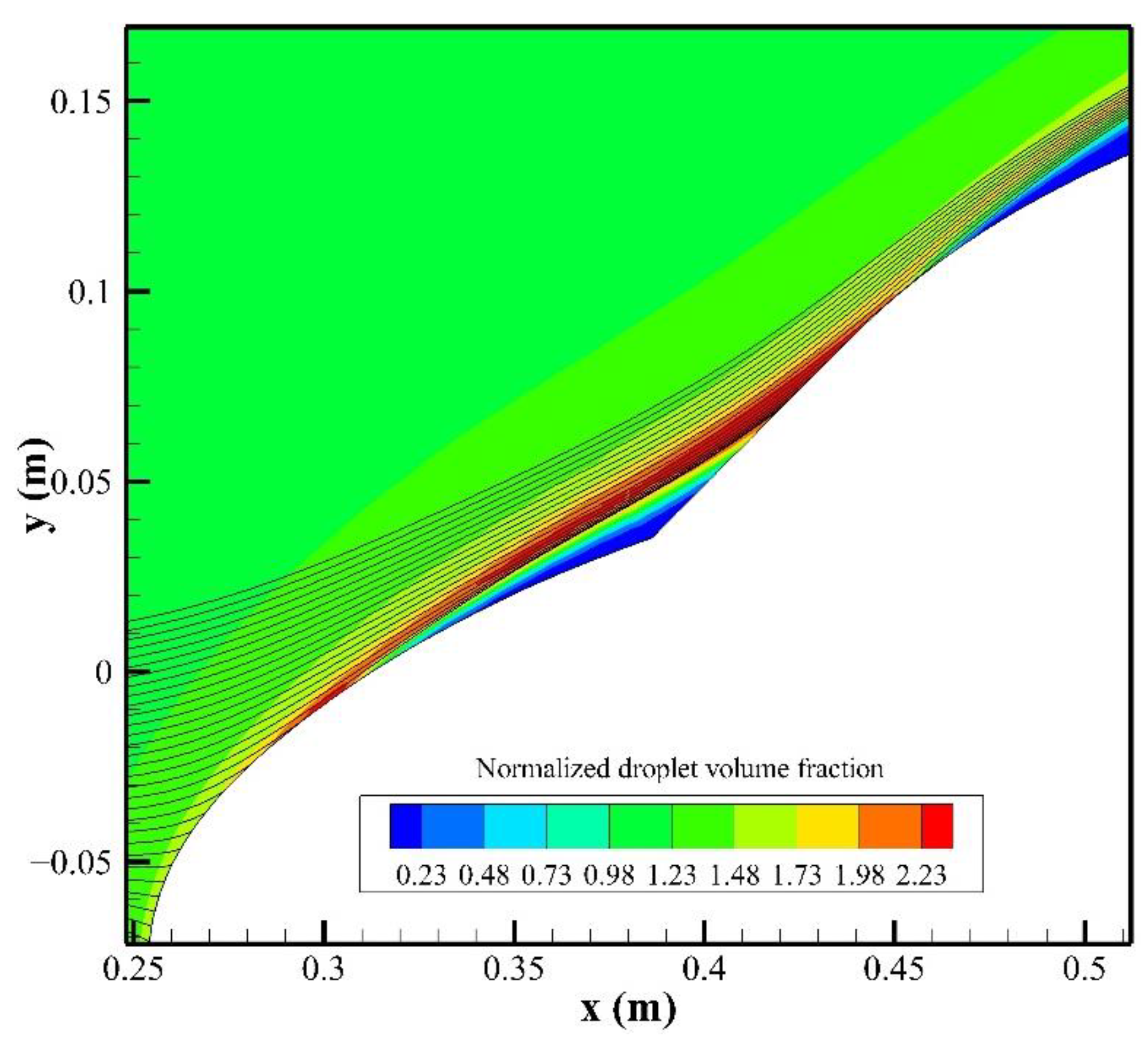
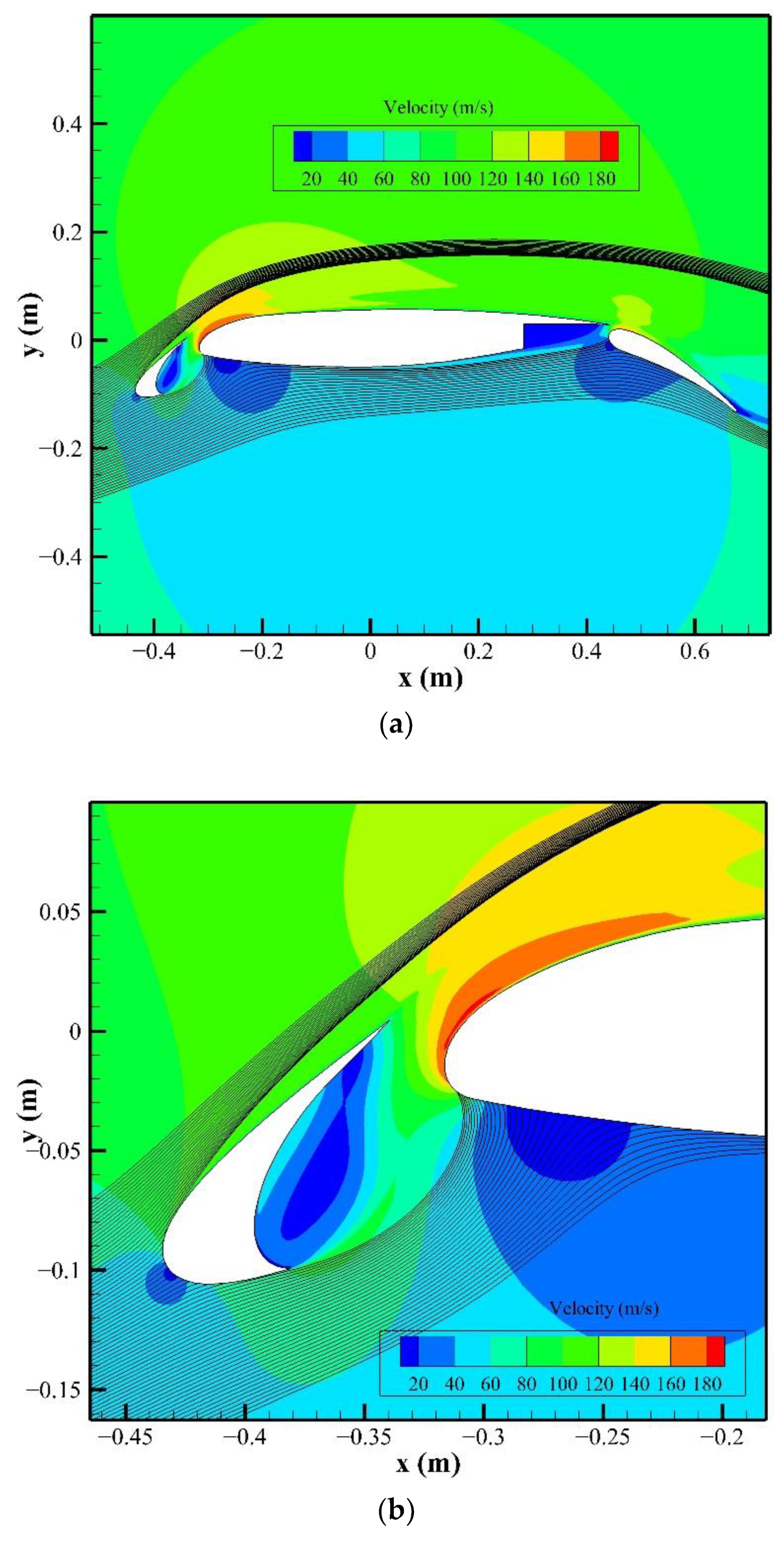
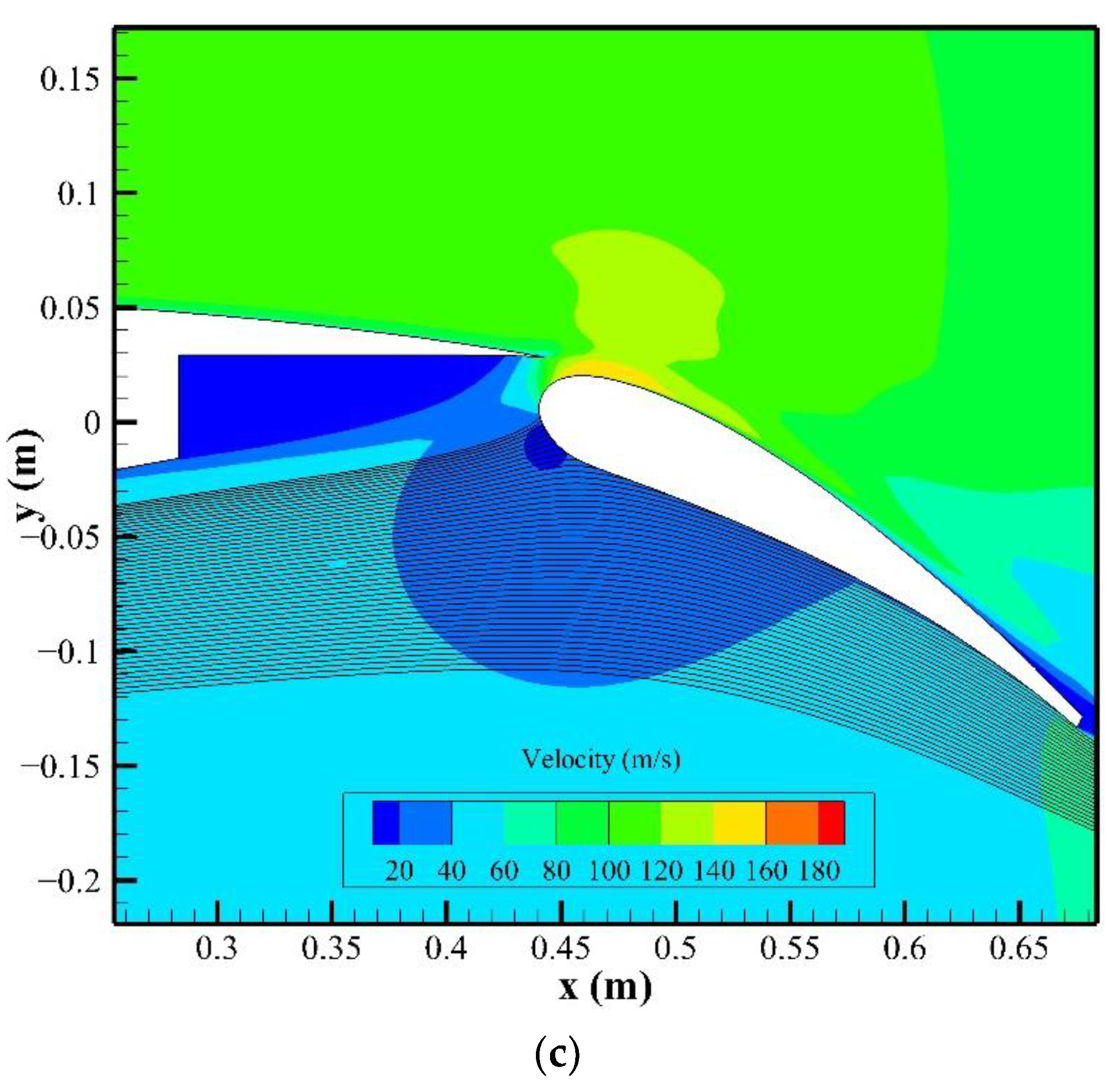
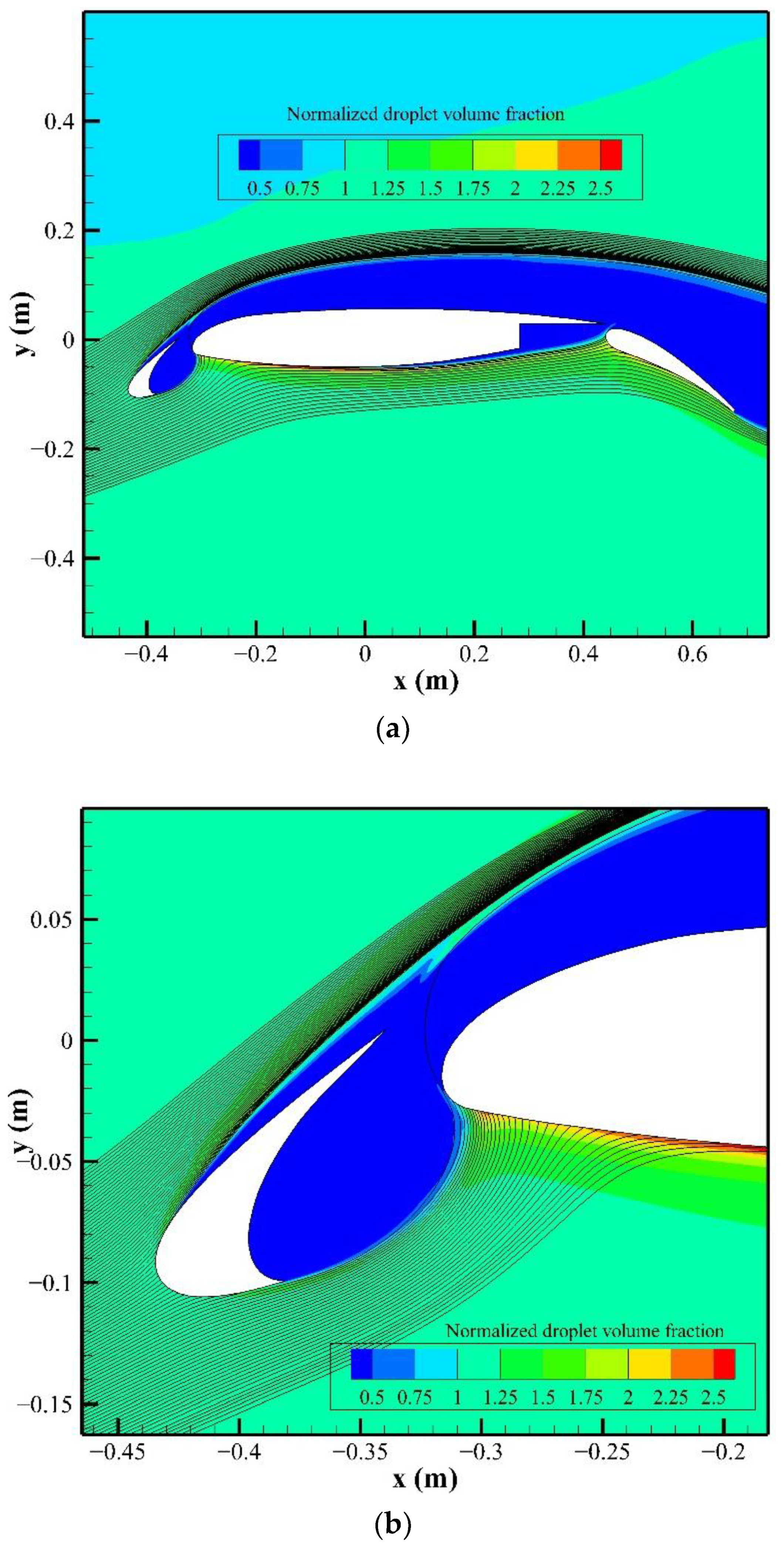
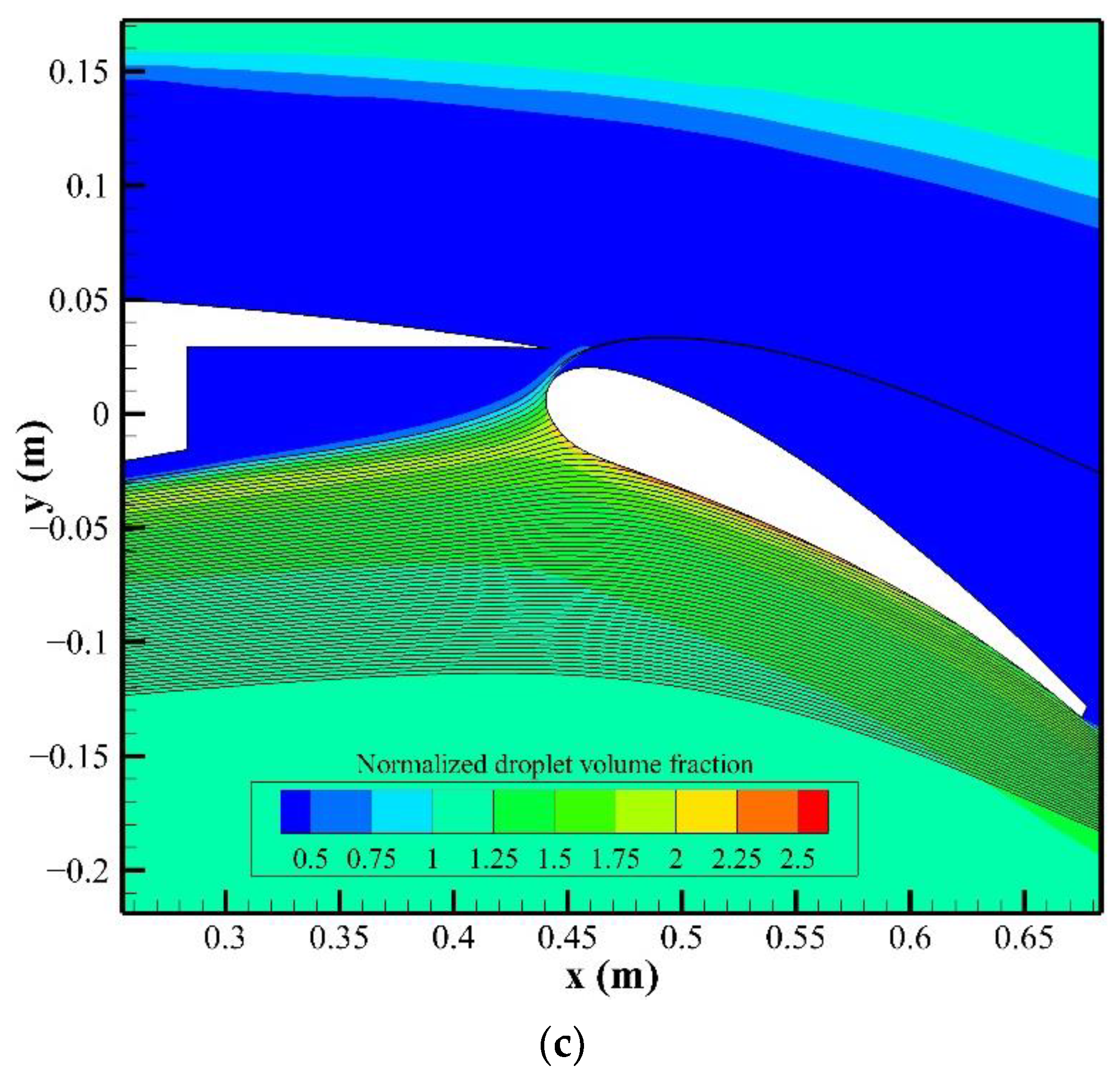
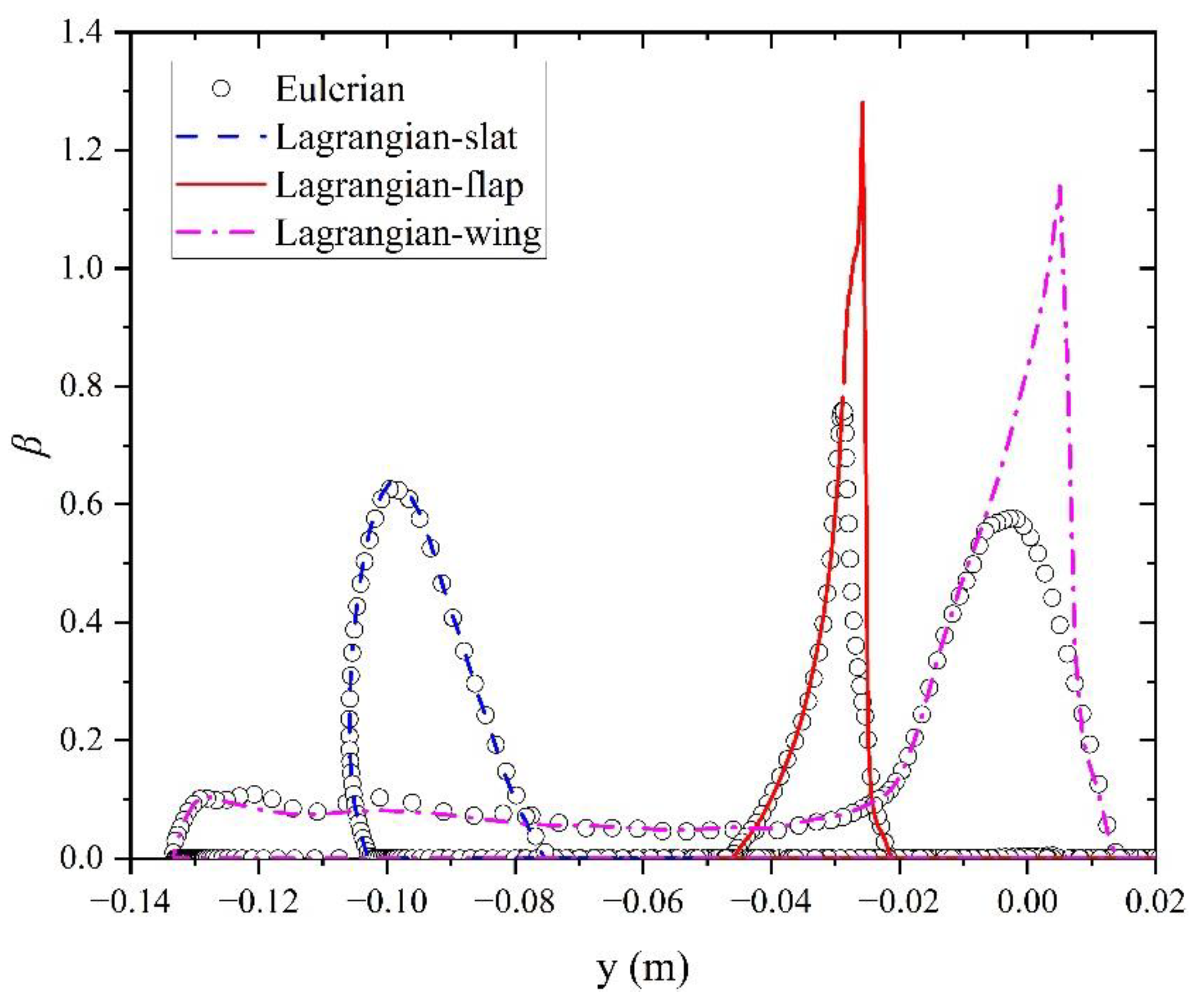
3.3. Comparison with a Multi-Element Airfoil

To further analyze the effects of the trajectory deviation obtained by the Lagrangian and Eulerian methods, a multi-element airfoil is chosen for the droplet impingement simulation, in which the droplets are deflected but without the effects of the trajectories’ crossing on the downstream impingement characteristics. The airfoil consists of a slat ahead, the main wing, and a rear flap, as shown in Figure 7. The freestream velocity is at the Mach number of 0.23 with an AOA of 4°, and the ambient temperature is 278 K with a pressure of 95,630 Pa. The droplet diameter is 21 μm, and the droplet release location in the Lagrangian method is far ahead of the slat, where the droplets have the same velocity as the freestream air.

Figure 7 shows the Lagrangian droplet trajectories on the contour of the air velocity around the multi-element airfoil. The stagnation point of each element is located on the lower surface as a result of a positive angle of attack, but the point of the main wing is further behind the leading edge since the slat ahead blocks the airflow to produce a certain degree of occlusion. Accordingly, water droplets hit the regions around the stagnation points, and every element collects the droplets. When the droplets bypass the slat, their trajectories concentrate. The trajectories overlap, and crossings are found in the upper concentrated zone, but they do not affect the impingement characteristics of the rear surfaces, as shown in Figure 7b. On the other hand, the droplets below the slat are also deflected, but their trajectories do not intersect in the lower concentrated zone before impacting the main wing. These phenomena are similar to those in Figure 1 and might be due to the positive angle of attack. As the droplets move further backward, their trajectories change more and more, in parallel, due to the long chord and smooth profile of the main wing, but the effect of the droplet deflections with dense droplet trajectories can also be found close to the main wing in front of the flap, as illustrated in Figure 7c.

Figure 8 is the contour of the normalized droplet volume fraction and the water droplet streamlines obtained by the Eulerian method. The shadow regions are formed behind the slat, main wing, and flap due to the inertia of the water droplets, and the leading edge of the main wing is located within the shadow region where there are few droplets present. Outside the shadow regions, there are droplet concentration-enhanced zones where the droplet volume fraction is larger than that in the free stream. It can be seen that those zones play an important role in the droplet impingement characteristics of the main wing surface. As demonstrated by the streamlines, the droplets impinge on all three elements of the airfoil, but when they bypass the airfoil surfaces, no overlaps or crossings of the trace lines are observed. In addition, the distance between two droplet streamlines is larger with a looser density than that obtained by the Lagrangian method, leading to the differences in the collection efficiency on the flap.

The results of the collection efficiency solved by the Lagrangian and Eulerian methods are compared with each other for the slat, main wing, and flap of the multi-element airfoil, as presented in Figure 9. Before the droplets hit the slat, there is no frontal component to affect their movements, and the droplet impingement regions and characteristics of the two methods are consistent. Deviations of the curves are found on the rear main wing and flap surfaces. Larger maximum collection efficiency is predicted for the main wing and flap by the Lagrangian method, and the Eulerian result is smoother than the Lagrangian distribution around the stagnation points due to numerical diffusion. It can be seen that the two methods would obtain almost the same collection efficiency on the surface without upstream deflections and obtain different results for the rear components after the droplets are deflected, which is the same as the situation of the A320 head. Since there is no trajectory crossing effect on the rear surfaces, in this case, the resulting deviation between the Lagrangian and Eulerian methods might be attributed to the different methods of dealing with the droplet motion after being deflected, and the crossings of the droplet trajectories may only be a typical appearance of the differences. The reason will be analyzed in detail in the next part.

3.4. Analyses and Discussions

To investigate the differences in the prediction of the droplet motion using the Lagrangian and Eulerian methods after being deflected by the upstream component, numerical simulations are carried out for a 2D section of an icing wind tunnel. The geometric model is shown in Figure 10, and the length of the entire computational domain is 2 m with the airflow from left to right. A constant air velocity is given to the inlet of the wind tunnel at x = 0 m, and the water droplets are uniformly distributed there with the same velocity of 50 m/s to the air value. The inlet air is set as an incompressible fluid, and the droplet diameter is 50 μm. The right outlet is at a constant pressure of 1 atm.

The Lagrangian droplet trajectories are presented in Figure 10 with the contour of air velocity inside the icing wind tunnel. The air first flows parallel to the wind tunnel inlet, and then changes its direction with the tunnel wall. The velocity increases continuously in the contraction section, and the value is basically stable in the test section with a slight change. Accordingly, the inlet water droplets move together with the airflow, and their motions are deflected in the contraction section. With the shrinking of the wind tunnel wall, a y-directional velocity pointing to the center line of the tunnel is formed. Due to the inertia, some of the water droplets hit the inner wall and are absorbed by the surface. For the droplets that bypass the wall, the velocity component in the y direction would not disappear because the airflow changes slowly along the wind tunnel wall without flow separation, and the y-directional velocity away from the center line is generated in the contraction and test sections. Therefore, the droplet trajectories become closer and close and are concentrated in the test section. Since the droplets do not affect each other without collision and coalescence, as described in the model assumptions in Section 2.1, their trajectories would cross over, and the distances between the droplets become larger again after the intersections.

Figure 11 shows the contour of the normalized droplet volume fraction, along with the streamlines of the water droplets obtained by the Eulerian method. Due to the droplet inertia and the deflection of the airflow in the contraction section, shadow regions appear near the wind tunnel wall in the test section. The water droplets that do not hit the wall gather to form a droplet concentration-enhanced zone toward the center of the wind tunnel, and the droplet volume fraction reaches a maximum at the centerline in the test section. The streamlines of the water droplets change direction in the contraction section with the variation of the airflow, and the distances between the streamlines gradually decrease. The droplet motion directions gradually become parallel to the center line in the test section, but there is no crossing phenomenon of the droplet streamlines.

The water droplet motions of the two methods are then compared. The Lagrangian method tracks the movement of each water droplet to obtain its trajectory, and the crossings of the droplet trajectories are captured in the test section due to the y-directional velocity generated in the contraction section. The density of the trajectories is very large near the crossover position and gradually decreases after the intersection, indicating that the maximum water droplet volume fraction appears at the trajectories’ crossing location. The centerline of the wind tunnel can be regarded as a reflection condition for the droplet trajectories in the Lagrangian method since the droplets bounce back there. In contrast, the Eulerian method solves for the droplet velocity and droplet volume fraction in each cell in the computational domain and obtains the droplet flow field and streamlines. The streamlines are the droplet trajectories in the steady flow, and they would never intersect each other due to the nature of the Eulerian velocity being a single-value function in a cell or a control volume. The droplet velocity component in the y direction gradually decreases after appearing in the contraction section and drops to zero at the centerline of the wind tunnel since the Eulerian velocity would have only one component parallel to the symmetric line there. Meanwhile, the droplet streamlines gradually approach each other in the test section, and the distances between them continue decreasing without crossings. Therefore, the water droplet volume fraction is larger at the centerline, and the value near the centerline will continue increasing without separations as the water droplets move backward, showing the phenomenon of ‘delta shocks’, similar to that described for the Eulerian result in Reference [23].

In general, the Lagrangian and Eulerian methods predict different droplet volume fractions and velocity distributions after the droplets are deflected. The Lagrangian method can track the crossing phenomenon of the droplet trajectories in the test section, while the Eulerian method cannot predict it. Furthermore, the deviation begins in the contraction section after the droplet motion deflection because the y-directional velocity is treated and solved differently in the two methods. Therefore, when the droplets are deflected by the frontal components, the Lagrangian and Eulerian methods would predict different results of the downstream droplet motion and rear impingement characteristics, whether the droplet trajectories intersect or not. The Eulerian result suggests that the droplets would collide and coalesce instead of crossing, which conflicts with the no-coalesce assumption, indicating this method is less reliable than the Lagrangian one.

4. Conclusions

The Lagrangian method and the Eulerian method are developed and compared for the droplet impingement calculation under aircraft icing conditions. A test case of a NACA 0012 airfoil is used to validate the two methods, the cases of a 2D section of an A320 head and a multi-element airfoil are tested to compare them, and an icing wind tunnel is used to analyze the differences between the Lagrangian and Eulerian methods. The present droplet impingement characteristics of the NACA 0012 airfoil agree with those in the literature, validating the established Lagrangian and Eulerian methods. The two methods achieve almost the same collection efficiencies for the frontal surfaces, indicating the equivalence of the Lagrangian and Eulerian methods for droplet impingement characteristics without upstream droplet deflections. However, when the droplet trajectories are deflected by the frontal body, the downstream droplet motion and the impingement characteristics of the rear surfaces are predicted differently by the two methods whether the trajectories intersect or not, showing the deviation of the Lagrangian and Eulerian methods. The Lagrangian method can capture the droplet deflections and the trajectory crossings, while the Eulerian results conflict with the model assumption of no droplet collision or coalescence, demonstrating the applicability of the two methods.