Looking into the Crystal Ball—How Automated Fast-Time Simulation Can Support Probabilistic Airport Management Decisions
Abstract
:1. Introduction
2. Existing Work
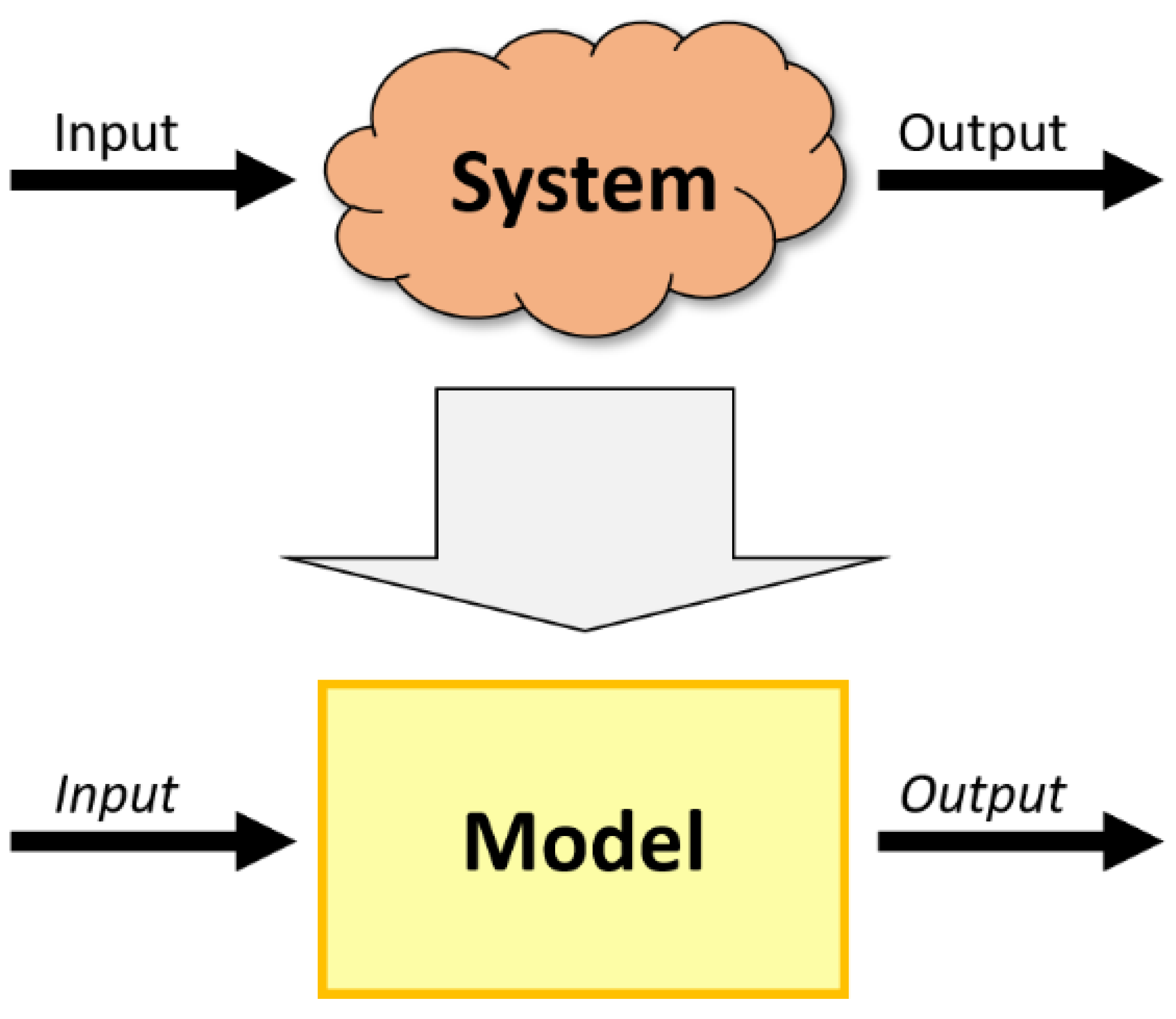
2.1. Airport Model Categories
2.2. Existing Airport Model Implementations
2.3. Former Approaches
3. Method
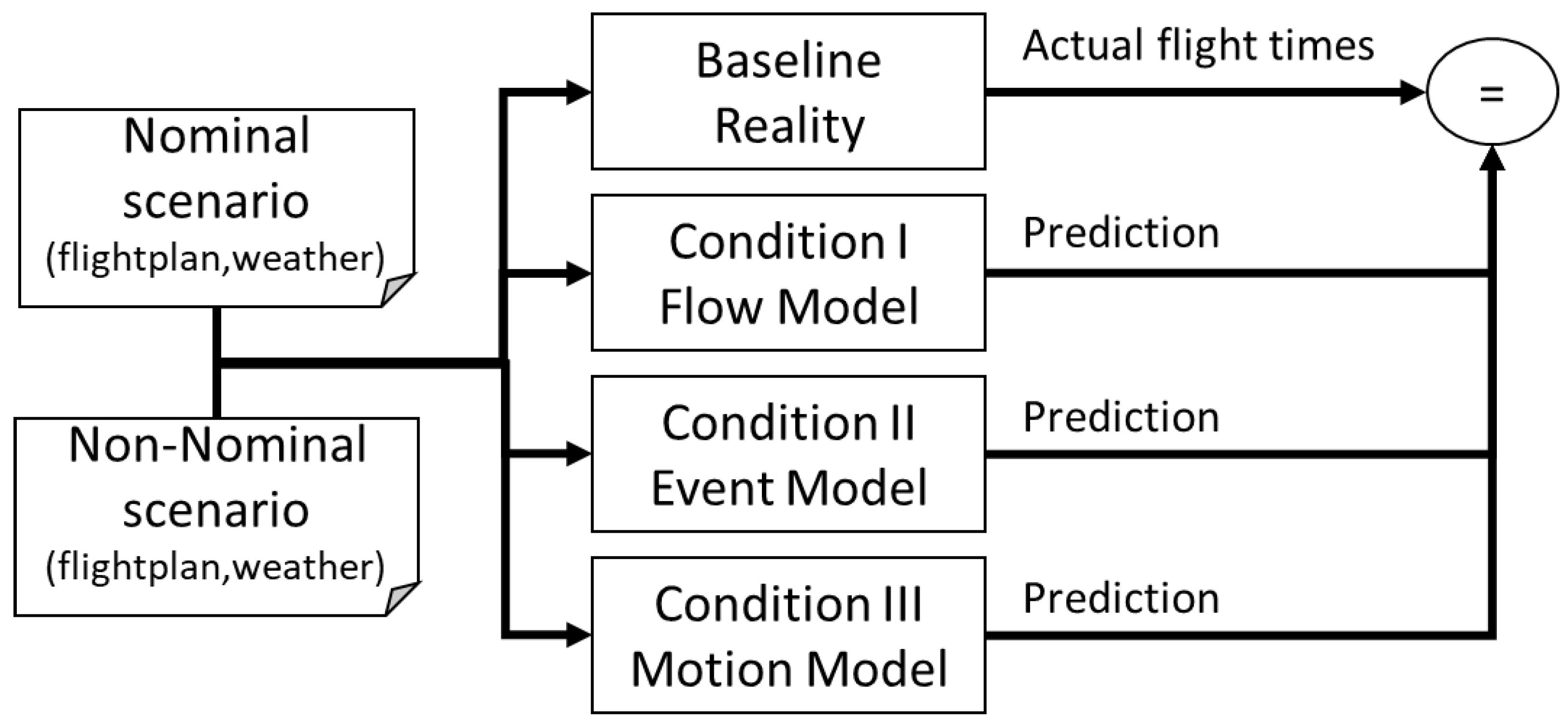
3.1. Validation Design
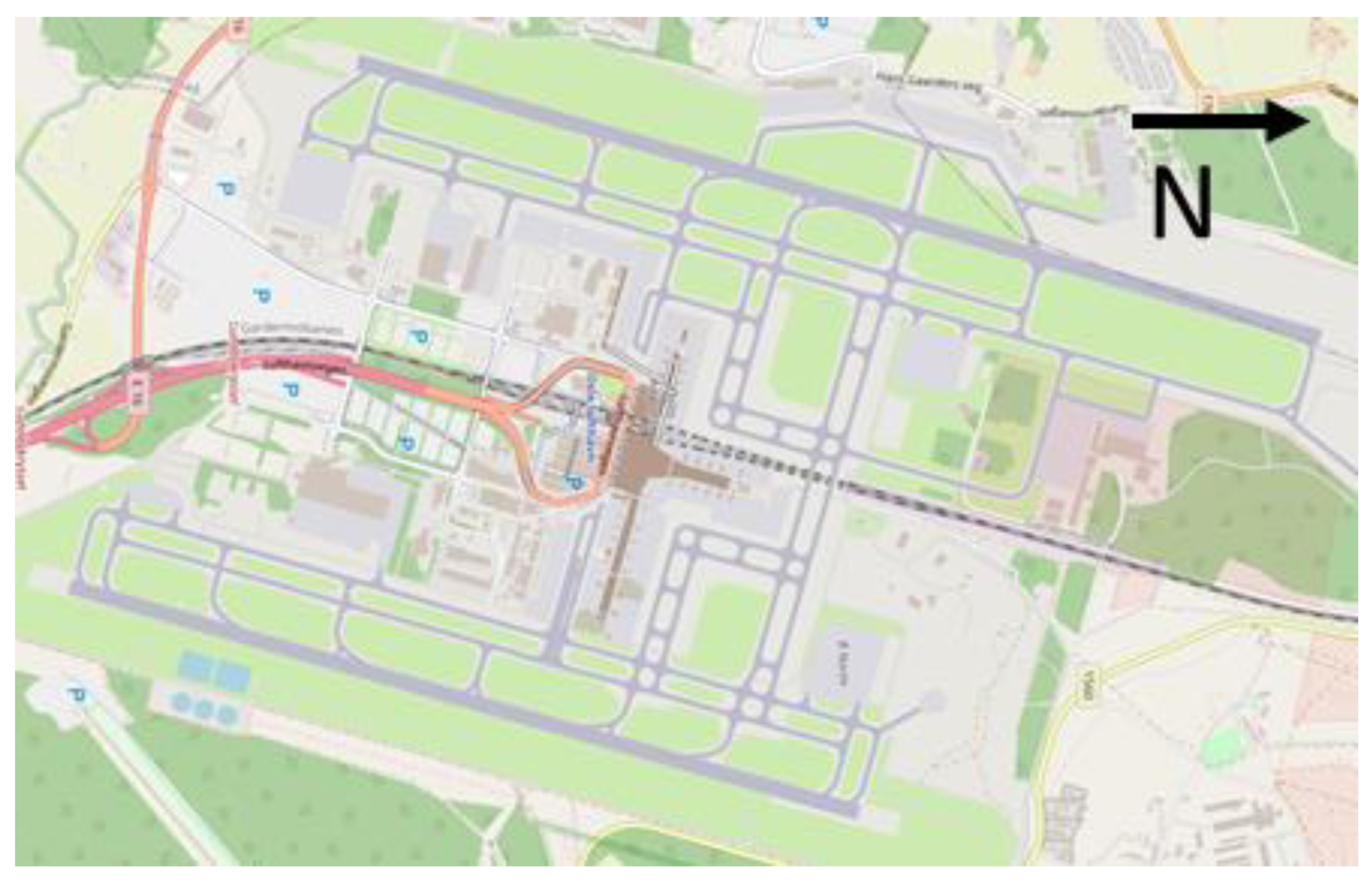
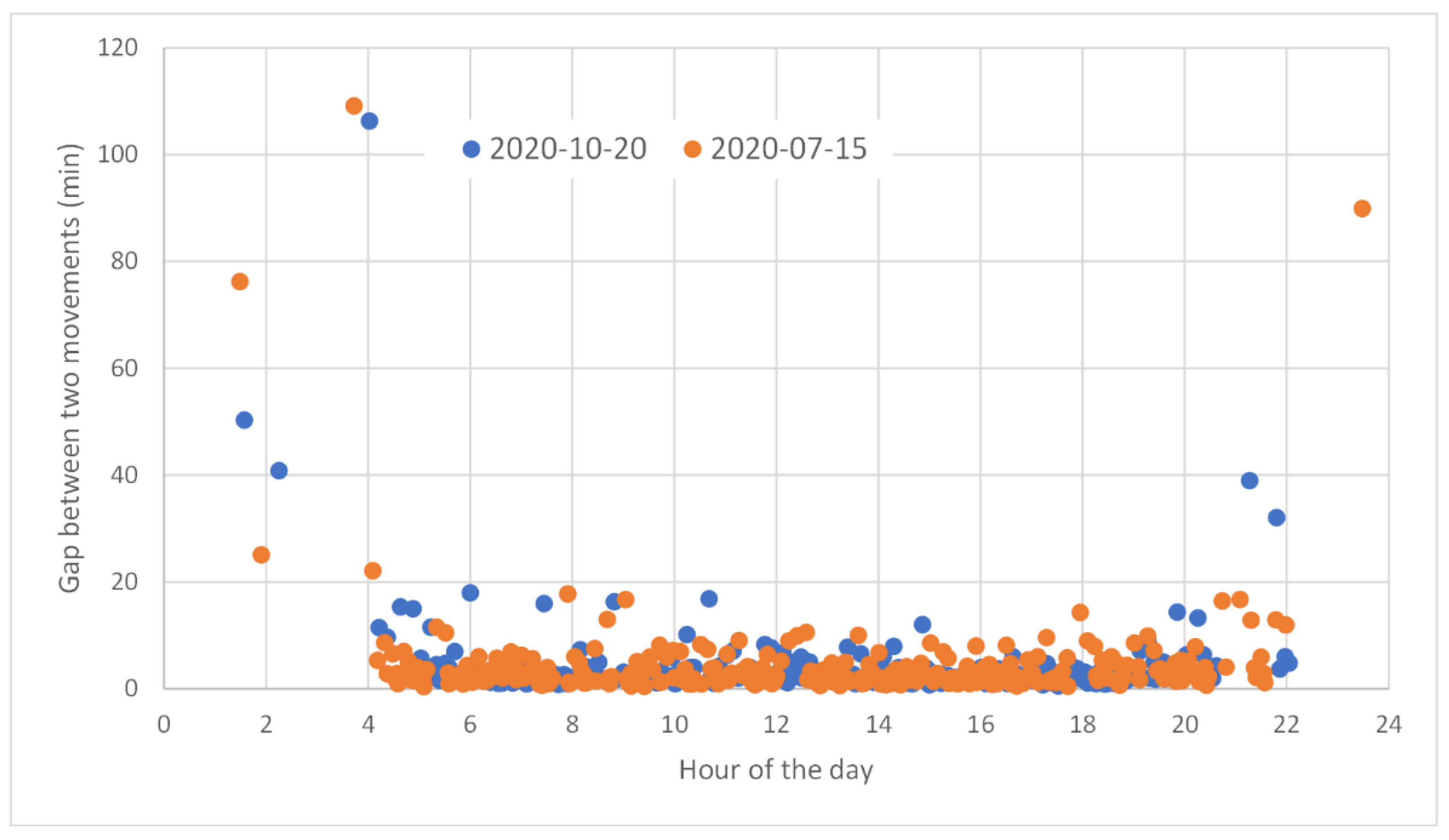
3.2. Scenario Selection and Analysis
3.2.1. Nominal Scenario
3.2.2. Non-Nominal Scenario
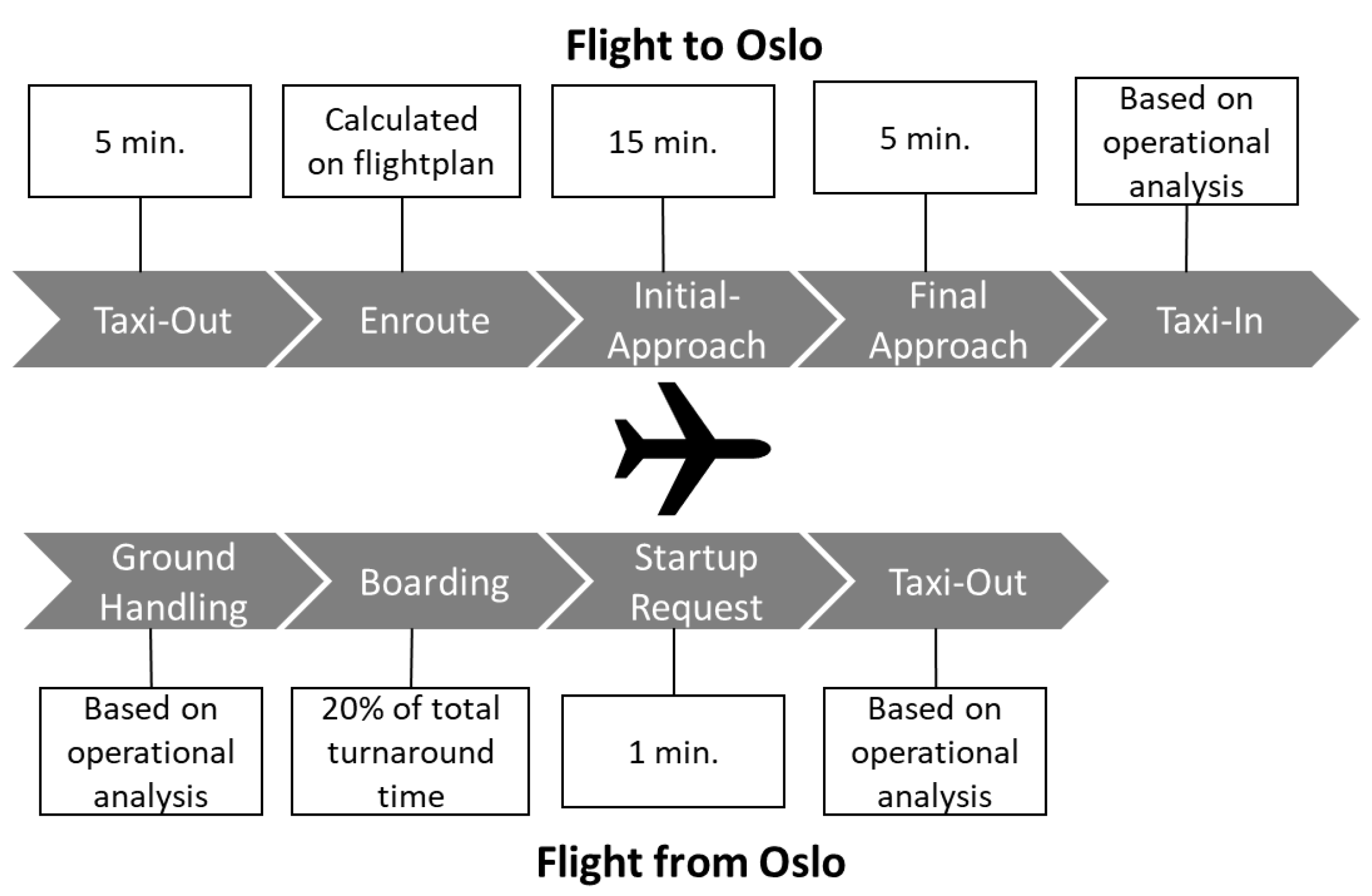
3.3. Simulation Configuration
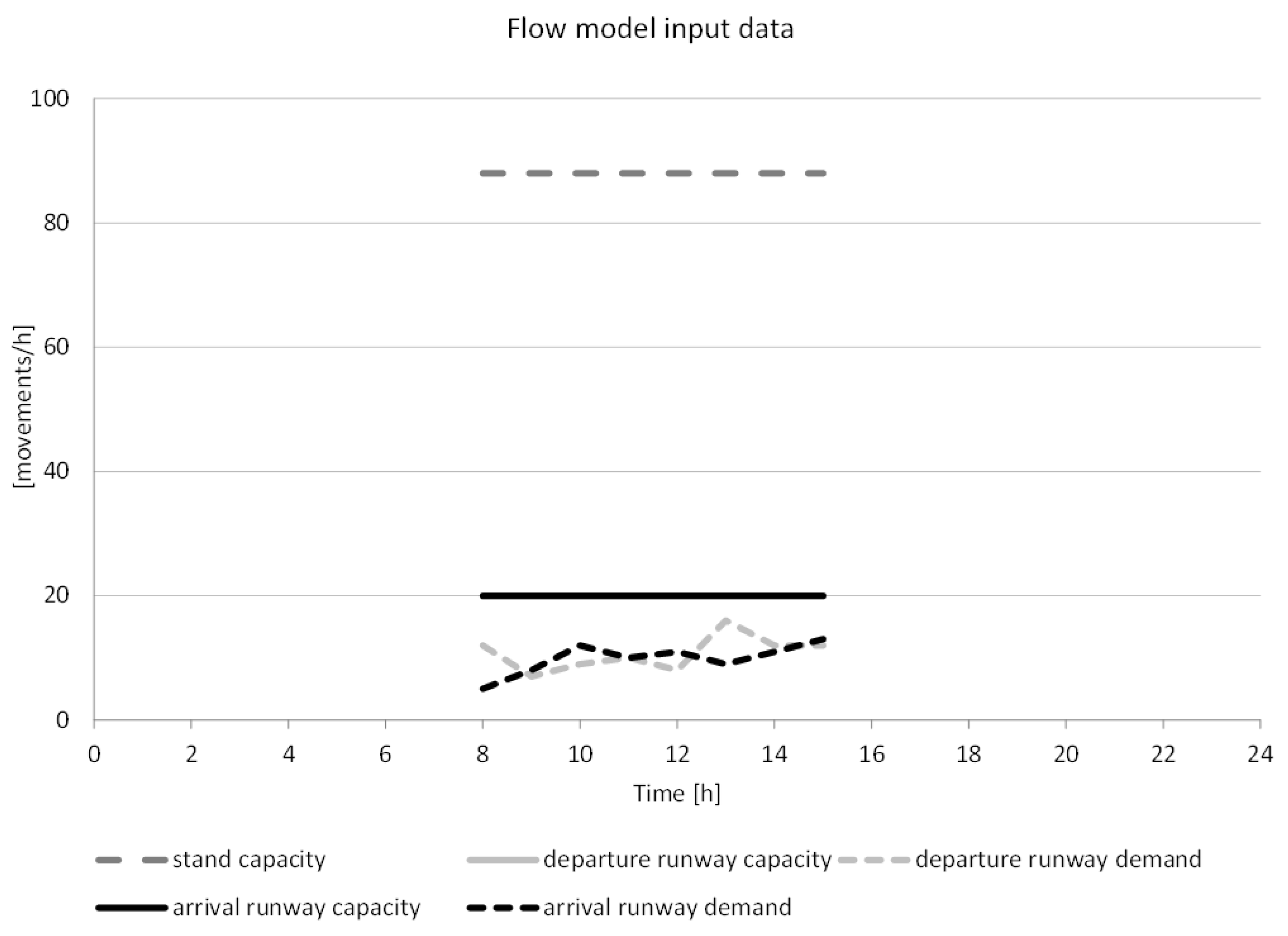
3.3.1. Flow Model
3.3.2. Event Model
3.3.3. Motion Model
3.4. Evaluation Criteria
4. Results
4.1. KPI 1—Number of Delayed Flights
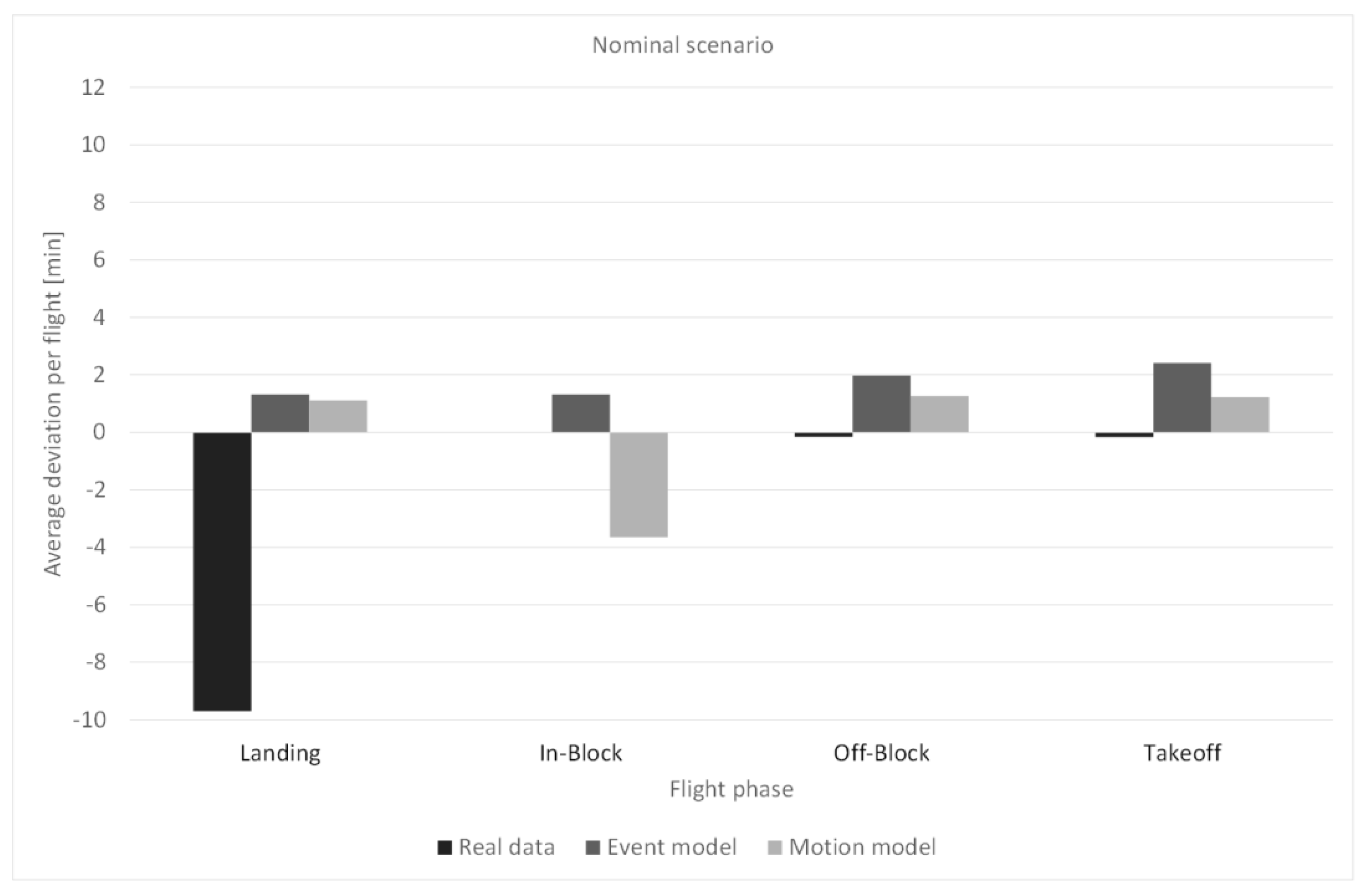
4.2. KPI 2—Average Deviation per Flight
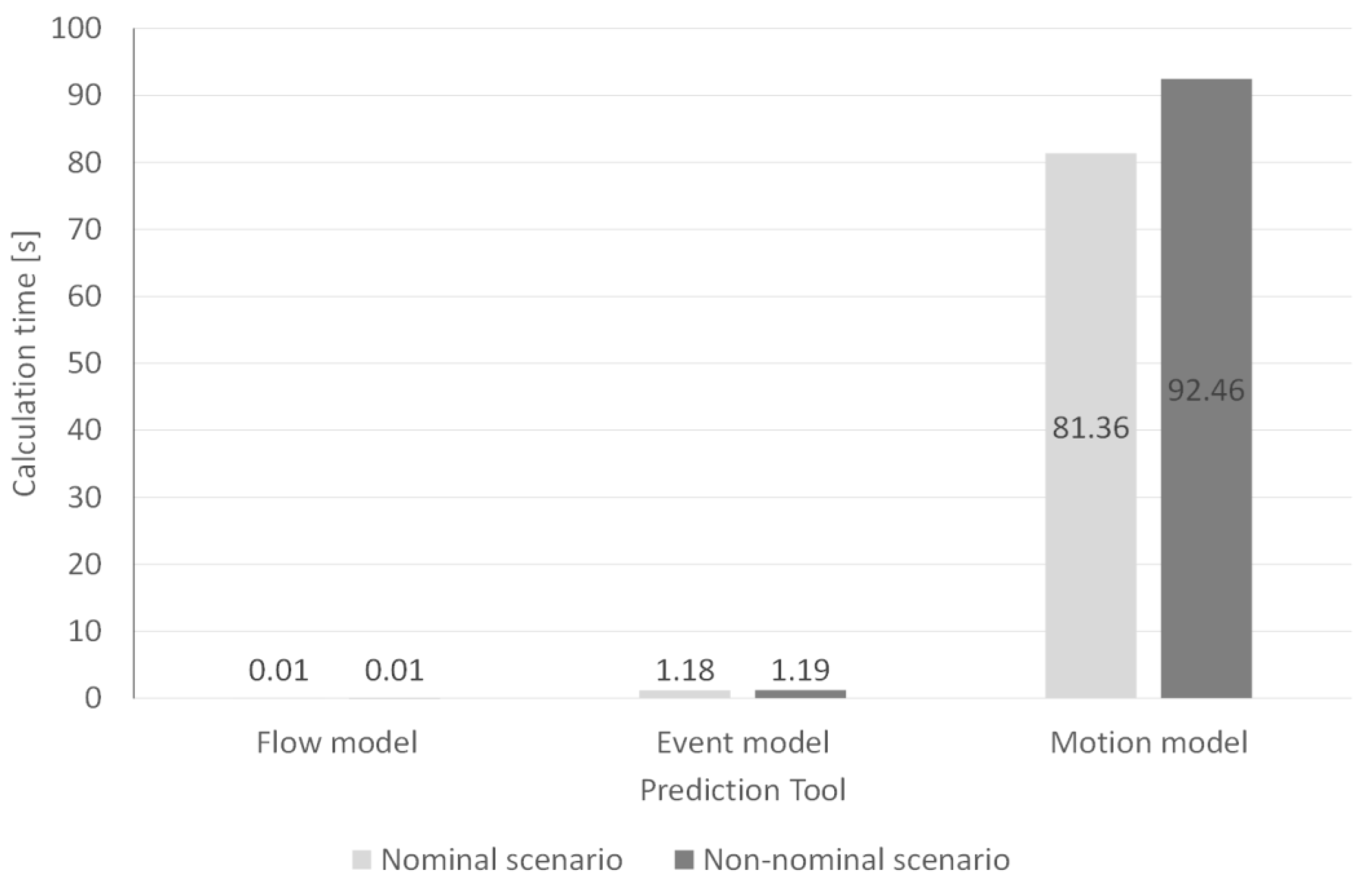
4.3. KPI 3—Calculation Time
5. Discussion
5.1. KPIs
5.2. Summary
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gill, E. Winter at Oslo Airport, Gardermoen (OSL). Int. Aiport Rev. 2008, 12, 33–37. [Google Scholar]
- Our Service for Airlines, Airports and Ground Control. Available online: https://www.dwd.de/EN/specialusers/aviation/cg_airport/airport_node.html (accessed on 25 February 2022).
- Suikat, R.; Schier, S.; Günther, Y.; Carstengerdes, N.; Piekert, F.; Lorenz, S. What-If Analysis in Total Airport Management. In Advances in Intelligent Systems and Computing; Springer: San Diego, CA, USA, 2020; pp. 517–523. [Google Scholar]
- Günther, Y.; Inard, A.; Werther, B.; Bonnier, M.; Spies, G.; Marsden, A.; Temme, M.; Böhme, D.; Lane, R.; Niederstrasser, H. Total Airport Management: Operational Concept & Logical Architecture; DLR: Braunschweig, Germany; Eurocontrol: Brussels, Belgium, 2006. [Google Scholar]
- Dow, C.; Histon, J. An Air Traffic Control Simulation Fidelity Definition and Categorization System; SAGE Publications: Los Angeles, CA, USA, 2014; pp. 92–96. [Google Scholar]
- Fishwick, P.A. Heterogeneous decomposition and inter-level coupling for combined modeling. In Proceedings of the 1991 Winter Simulation Conference, Phoenix, AZ, USA, 8–11 December 1991; pp. 1120–1128. [Google Scholar]
- Spies, G.; Piekert, F.; Marsden, A.; Suikat, R.; Meier, C.; Eriksen, P. Operational Concept for an Airport Operations Center to Enable Total Airport Management. In Proceedings of the 26th International Congress of the Aeronautical Sciences, Anchorage, AK, USA, 14–19 September 2008. [Google Scholar]
- Scharnweber, A.; Schier, S. A Unified Flight Phase and Event Model for the Analysis of Heterogeneous ATM Simulations. CEAS Aeronaut. J. 2011, 2, 171–183. [Google Scholar] [CrossRef]
- Eurocontrol. Airport CDM Implementation Manual; Eurocontrol Airport CDM Team: Brussels, Belgium, 2017. [Google Scholar]
- Schier, S.; Timmermann, F.; Pett, T. Airport Management in the Box—A Human-in-the-Loop Simulation for ACDM and Airport Management. In Proceedings of the Deutscher Luft- und Raumfahrt Kongress, Braunschweig, Germany, 13 September 2016. [Google Scholar]
- Schier, S.; Günther, Y.; Lorenz, S.; Suikat, R.; Piekert, F. Ein Flug Durch Raum Und Zeit—Entwurf Und Evaluation Einer Simulationsdynamik Für Das Flughafenmanagement. In Proceedings of the Simulation technischer Systeme inklusive der Grundlagen und Methoden in Modellbildung und Simulation, Ulm, Germany, 9 March 2017; pp. 75–80. [Google Scholar]
- AirTOP Airport and Airspace Modeling (Brochure). Available online: https://airtopsoft.com/overview/ (accessed on 1 August 2021).
- Timar, S.; Peters, M.; Davis, P.; Smith, P.; Lapis, M.B.; Wilson, I.; van Tulder, P. A What-If Analysis Tool for Planning Airport Traffic. In Proceedings of the 2017 IEEE/AIAA 36th Digital Avionics Systems Conference (DASC), St. Petersburg, FL, USA, 17–21 September 2017. [Google Scholar]
- Zografos, K.G.; Madas, M.A.; Salouras, Y. A Decision Support System for Total Airport Operations Management and Planning. J. Adv. Transp. 2013, 47, 170–189. [Google Scholar] [CrossRef]
- Günther, Y.; Pick, A.; Kern, S.; Lorenz, S.; Gerz, T.; Keis, F.; Köhler, M. Improved Airport Operations Planning by Using Tailored Forecasts of Severe Weather. In Proceedings of the Conferences in Air Transport & Operations, Brunswick, Germany, 23 July 2015. [Google Scholar]
- Günes, M. Verification and Validation of Simulation Models. Available online: https://www.mi.fu-berlin.de/inf/groups/ag-tech/teaching/2012_SS/L_19540_Modeling_and_Performance_Analysis_with_Simulation/10.pdf (accessed on 15 March 2022).
- Schier, S. Entwurf Und Evaluation Einer Kollaborativen, Simulationsbasierten Lernumgebung für das Flughafenmanagement. Ph.D. Dissertation, Fern Universität Hagen, Hagen, Germany, 2021. [Google Scholar]
- Piekert, F.; Carstengerdes, N.; Suikat, R. Dealing with Adverse Weather Conditions by Enhanced Collaborative Decision Making in a TAM APOC. In Proceedings of the ENRI International Workshop on ATM/CNS, Tokyo, Japan, 30 October 2019. [Google Scholar]
- OpenStreetMap. OSM History Dump© OpenStreetMap Contributors. Available online: https://planet.openstreetmap.org/planet/full-history/ (accessed on 25 February 2022).
- Carreras-Maide, J.; Lordan, O.; Sallan, J.M. Cost Savings from Trajectory Deviations in the European Air Space. J. Air Transp. Manag. 2020, 88, 101887. [Google Scholar] [CrossRef]
- Lichoń, D. Analysis of General Aviation Domestic Air Traffic Structure in Controlled Airspace of Poland with Refer to Sesar 2020, PJ.06-02 Project Solution. J. KONES 2017, 24, 173–180. [Google Scholar] [CrossRef]
- Bae, S.; Shin, H.-S.; Lee, C.-H.; Tsourdos, A. A New Multiple Flights Routing and Scheduling Algorithm in Terminal Manoeuvring Area. In Proceedings of the 2018 IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018; pp. 1–9. [Google Scholar]
- Wandelt, S.; Sun, X.; Gollnick, V. SO6C: Compressed Trajectories in Air Traffic Management. Air Traffic Control Q. 2014, 2, 157–178. [Google Scholar] [CrossRef]
- Office of the Federal Coordinator for Meteorological Services and Supporting Research. Federal Meteorological Handbook No. 1: Surface Weather Observations and Reports; U.S. Department Of Commerce: Washington, DC, USA, 2019.
- Aeronautical Information Publication Norway. Available online: https://avinor.no/en/ais/aipnorway/ (accessed on 6 May 2021).
- Oslo Gardermoen OSL/ENGM Airport Information. Available online: https://ext.eurocontrol.int/airport_corner_public/ENGM (accessed on 12 August 2021).
- Association of European Airlines. Recommendations for De-Icing/Anti-Icing of Aircraft on the Ground; Association of European Airlines: Brussels, Belgium, 2008. [Google Scholar]
- International Civil Aviation Organization. Manual of Aircraft Ground De-Icing/Anti-Icing Operations; International Civil Aviation Organization: Montréal, QC, Canada, 2018. [Google Scholar]
- Flughafen Köln/Bonn GmbH. Aircraft De-Icing Manual 2019/2020; Flughafen Köln/Bonn GmbH: Cologne, Germany, 2019. [Google Scholar]
- The Elephant Beta-15. Available online: https://vestergaardcompany.com/product/aircraft-deicing/the-elephant-beta-15/ (accessed on 5 October 2021).
- International Civil Aviation Organization. Procedures for Air Navigation Services (PANS)—Air Traffic Management (Doc 4444); International Civil Aviation Organization: Montréal, QC, Canada, 2016. [Google Scholar]
- Eurocontrol. User Manual for the Base of Aircraft Data (BADA) Revision 3.15; EUROCONTROL Experimental Centre: Brétigny-sur-Orge, France, 2019. [Google Scholar]
- Endsley, M.R. Measurement of Situation Awareness in Dynamic Systems. Hum. Factors 1995, 37, 65–84. [Google Scholar] [CrossRef]
- Eurocontrol. Performance Review Report Covering the Calendar Year 2018 (PRR 2018); Eurocontrol: Brussels, Belgium, 2019. [Google Scholar]
- Papenfuß, A.; Carstengerdes, N.; Schier, S.; Günther, Y. What to Say When: Guidelines for Decision Making. An evaluation of a concept for cooperation in an APOC. In Proceedings of the 12th USA/Europe Air Traffic Management Research and Development Seminar (ATM2017), Seattle, WA, USA, 26–30 June 2017. [Google Scholar]
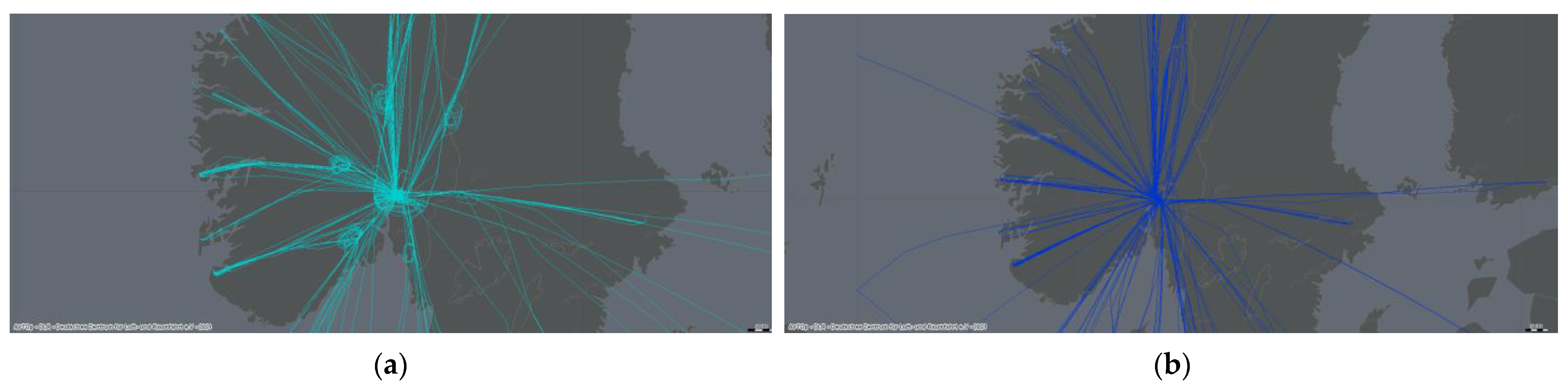

| Flights (Simulation Objects) | |||
|---|---|---|---|
| Discrete | Continuous | ||
| Time | discrete | Flow model | Event model |
| continuous | State model | Motion model | |
| Airbus A300 | Airbus 310 | Airbus A320 | Airbus A330/340 | Airbus A380 | Boeing 736/7/8 | Boeing 747-8 | Boeing 777ER |
|---|---|---|---|---|---|---|---|
| 363 l | 370 l | 230 l | 580 l | 1130 l | 230 l | 875 l | 705 l |
| Airbus A300 | Airbus 310 | Airbus A320 | Airbus A330/340 | Airbus A380 | Boeing 736/7/8 | Boeing 747-8 | Boeing 777ER | |
|---|---|---|---|---|---|---|---|---|
| Code letter | D | D | C | E | F | C | F | E |
| Min | 1.5 | 1.5 | 1 | 2.4 | 4.7 | 1 | 3.6 | 2.9 |
| Max | 18.2 | 18.5 | 11.5 | 29 | 56.5 | 11.5 | 43.8 | 35.3 |
| Mean | 9.85 | 10 | 6.25 | 15.7 | 30.6 | 6.25 | 23.7 | 19.1 |
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 5 | 5.5 | 6.25 | 10 | 19.1 | 30.6 |
| Real Data | Flow Model | Event Model | Motion Model | |
|---|---|---|---|---|
| Landing | 2 | 0 | 2 | 0 |
| In-Block | not determinable | 0 | 2 | 0 |
| Off-Block | 1 | 0 | 7 | 6 |
| Takeoff | 1 | 0 | 7 | 6 |
| Real Data | Flow Model | Event Model | Motion Model | |
|---|---|---|---|---|
| Landing | 37 | 0 | 18 | 16 |
| In-Block | not determinable | 2 | 18 | 14 |
| Off-Block | 44 | 0 | 9 | 13 |
| Takeoff | 48 | 56 | 26 | 38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pohling, O.; Schier-Morgenthal, S.; Lorenz, S. Looking into the Crystal Ball—How Automated Fast-Time Simulation Can Support Probabilistic Airport Management Decisions. Aerospace 2022, 9, 389. https://doi.org/10.3390/aerospace9070389
Pohling O, Schier-Morgenthal S, Lorenz S. Looking into the Crystal Ball—How Automated Fast-Time Simulation Can Support Probabilistic Airport Management Decisions. Aerospace. 2022; 9(7):389. https://doi.org/10.3390/aerospace9070389
Chicago/Turabian StylePohling, Oliver, Sebastian Schier-Morgenthal, and Sandro Lorenz. 2022. "Looking into the Crystal Ball—How Automated Fast-Time Simulation Can Support Probabilistic Airport Management Decisions" Aerospace 9, no. 7: 389. https://doi.org/10.3390/aerospace9070389
APA StylePohling, O., Schier-Morgenthal, S., & Lorenz, S. (2022). Looking into the Crystal Ball—How Automated Fast-Time Simulation Can Support Probabilistic Airport Management Decisions. Aerospace, 9(7), 389. https://doi.org/10.3390/aerospace9070389







