An Innovative Pose Determination Algorithm for Planetary Rover Onboard Visual Odometry
Abstract
:1. Introduction
2. Methods
- Problem formulation—constructing the optimization with respect to δθi, enhanced by the Huber robust kernel;
- Initial estimation—roughly solving the PLD criterion by DLT to create a virtual ICS, which is close to the CCS;
- Alignment—aligning the ICS with the CCS under the small rotation assumption for the algorithm not to be trapped in periodic local minimums of δθi;
- Refinement—finally obtaining the rover pose with the global minimum of δθi.
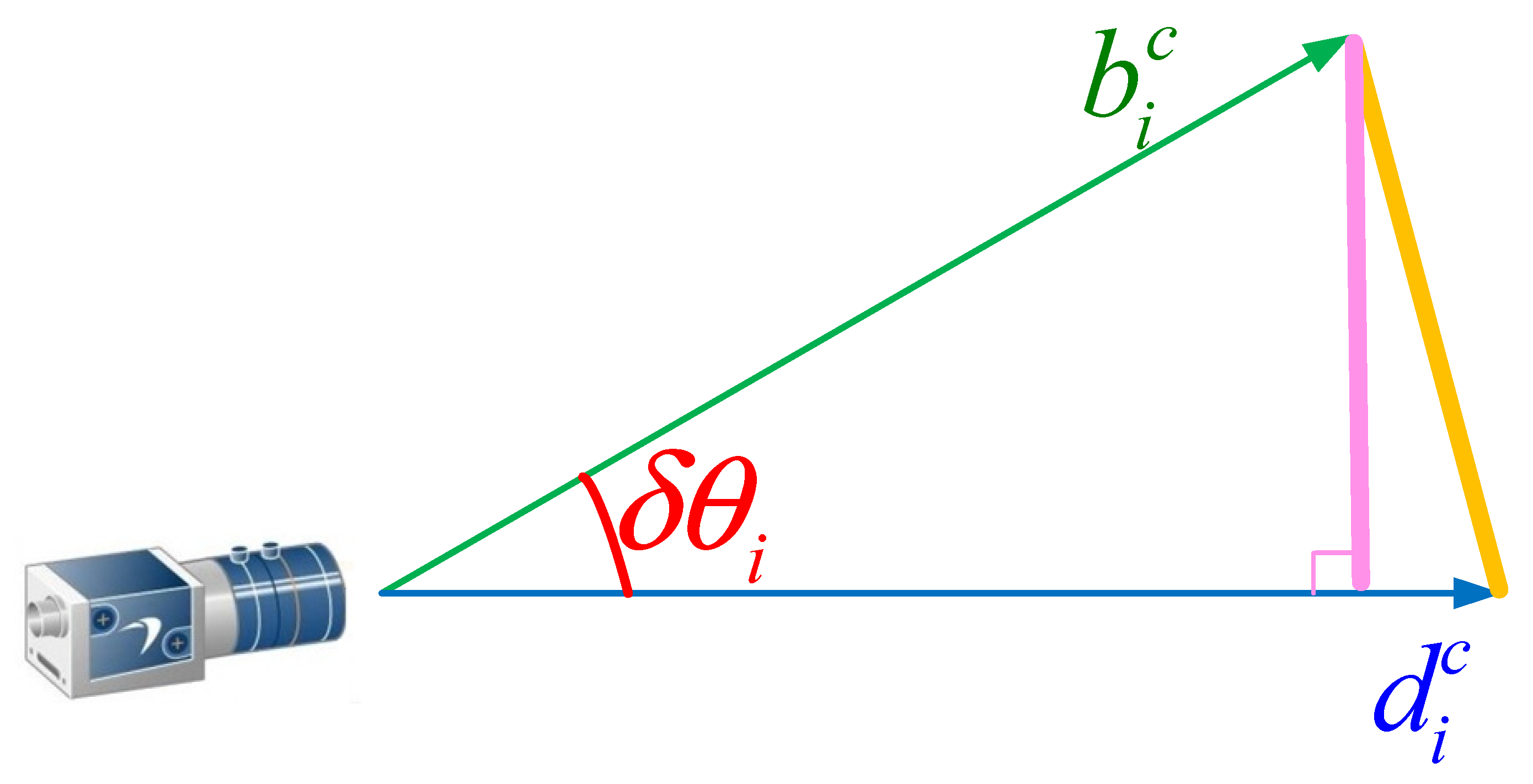
2.1. Problem Formulation
2.2. Initial Estimation
2.3. Alignment
2.4. Refinement
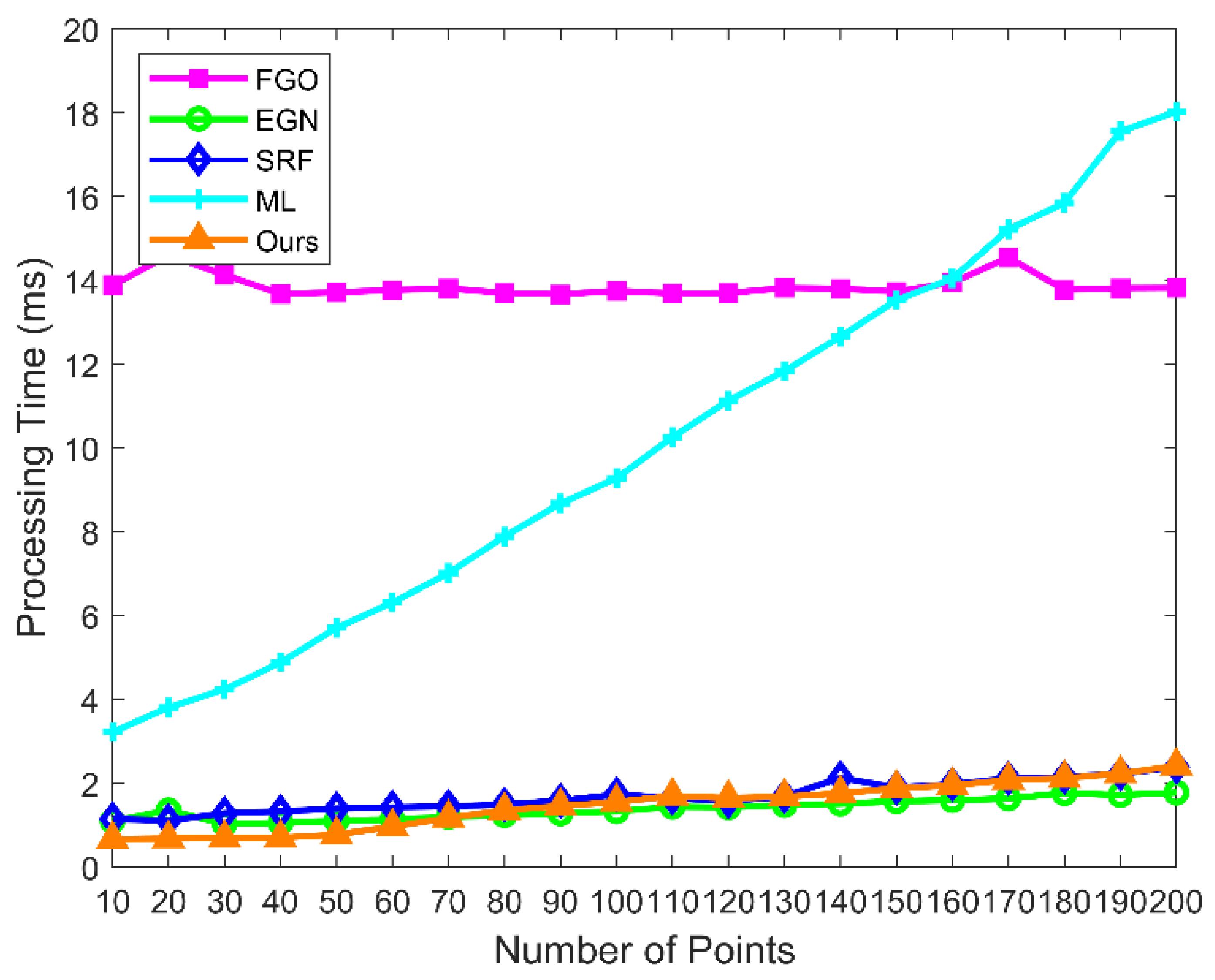
3. Implementations and Results
- The fast, general, and optimal algorithm (FGO) using the ATPC criterion [8];
- The efficient Gauss–Newton algorithm (EGN) using the PPD criterion [11];
- The simple, robust, and fast algorithm (SRF) using the PLD criterion [9];
- The maximum likelihood algorithm (ML) using the angle-based criterion [21].
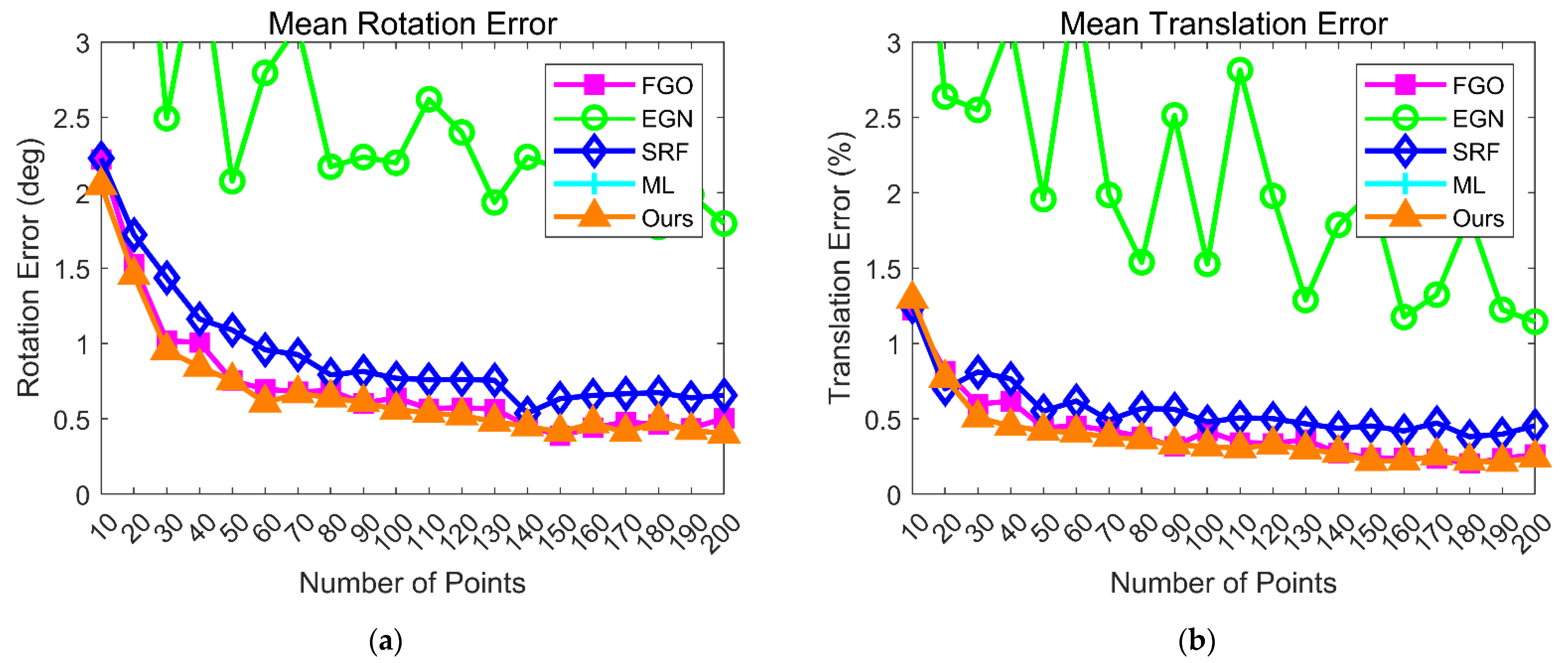
3.1. Synthetic Simulations
3.1.1. Simulations in Known Environments
- Planar configuration, with and . For example, the reference points are randomly distributed in the range of ;
- Ordinary configuration, with and . For example, the reference points are randomly distributed in the range of ;
- Quasi-singular configuration, with and . For example, the reference points are randomly distributed in the range of .
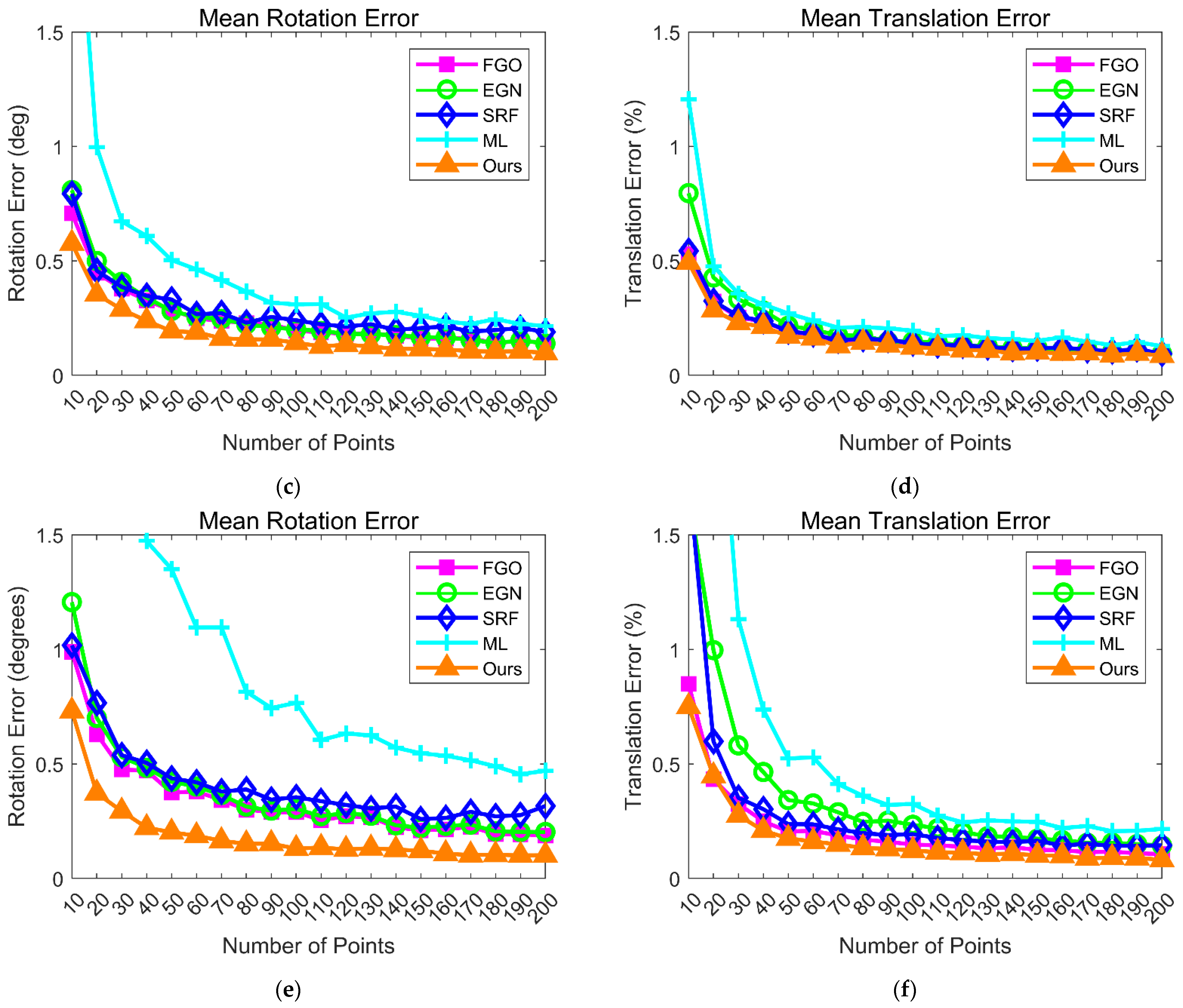
3.1.2. Simulations in Unknown Environments
- The reference points are randomly distributed in the range of , where r is the distance ratio. r is varied from 1 to 12;
- The reference points are randomly distributed in the range of , where o is the distance off center. o is varied from 0 to 10;
- The reference points are randomly distributed in the range of , where q is the tangent of the field of view (FOV). q is varied from 2 to 12.
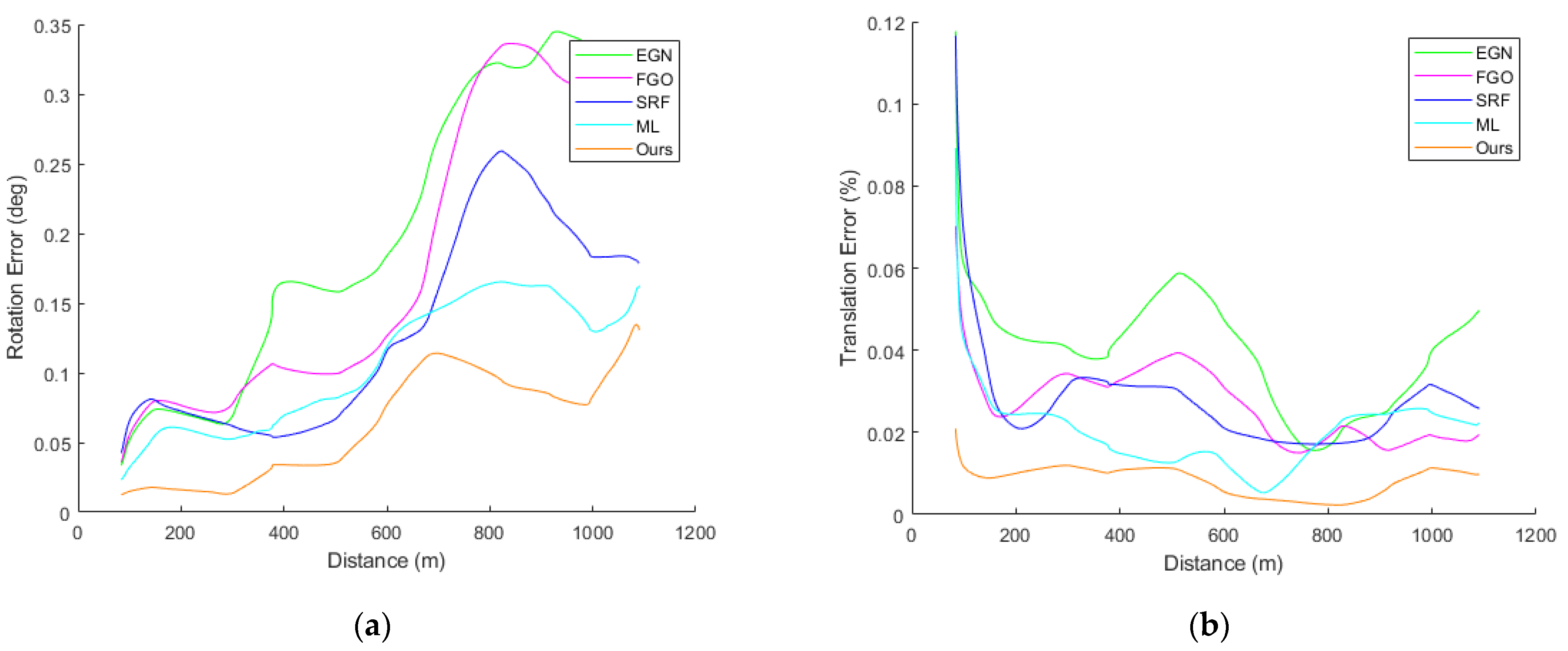
3.2. Real Experiments
3.2.1. Experiments in Known Environments
3.2.2. Experiments in Unknown Environments
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Algorithm A1: The Proposed Pose Determination Algorithm | |||
| the projection directions of reference points in the CCS | |||
| the positions of reference points in the WCS | |||
| Output:R the rotation matrix of the rover t the translation vector of the rover | |||
| 1 | is parameterized as 9 free variables) | ||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | is parameterized as small rotation) | ||
| 8 | |||
| 9 | |||
| 10 | |||
| 11 | are parameterized as Lie algebra) | ||
| 12 | do | ||
| 13 | |||
| 14 | |||
| 15 | |||
| 16 | |||
| 17 | |||
| 18 | end for | ||
| 19 | |||
References
- Andolfo, S.; Petricca, F.; Genova, A. Rovers Localization by using 3D-to-3D and 3D-to-2D Visual Odometry. In Proceedings of the IEEE 8th International Workshop on Metrology for AeroSpace, Naples, Italy, 23–25 June 2021. [Google Scholar]
- Chiodini, S.; Giubilato, R.; Pertile, M.; Salvioli, F.; Bussi, D.; Barrera, M.; Franceschetti, P.; Debei, S. Viewpoint Selection for Rover Relative Pose Estimation Driven by Minimal Uncertainty Criteria. IEEE Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, S.; Sima, B.; Wen, B.; Peng, S.; Jia, Y. A precise visual localisation method for the Chinese Chang’e-4 Yutu-2 rover. Photogramm. Rec. 2020, 35, 10–39. [Google Scholar] [CrossRef]
- Maki, J.N.; Gruel, D.; McKinney, C.; Ravine, M.A.; Morales, M.; Lee, D.; Willson, R.; Copley-Woods, D.; Valvo, M.; Goodsall, T.; et al. The Mars 2020 Engineering Cameras and Microphone on the Perseverance Rover: A Next-Generation Imaging System for Mars Exploration. Space Sci. Rev. 2020, 216, 1–48. [Google Scholar] [CrossRef] [PubMed]
- Winter, M.; Barcaly, C.; Pereira, V.; Lancaster, R.; Caceres, M.; Mcmanamon, K.; Nye, B.; Silva, N.; Lachat, D.; Campana, M. ExoMars Rover Vehicle: Detailed Description of the GNC System. In Proceedings of the 13th Symposium on Advanced Space Technologies in Robotics and Automation, Noordwijk, The Netherlands, 11–13 May 2015. [Google Scholar]
- Shao, W.; Cao, L.; Guo, W.; Xie, J.; Gu, T. Visual navigation algorithm based on line geomorphic feature matching for Mars landing. Acta Astronaut. 2020, 173, 383–391. [Google Scholar] [CrossRef]
- Haralick, R.M.; Lee, C.N.; Ottenburg, K.; Nölle, M. Analysis and Solutions of The Three Point Perspective Pose Estimation Problem. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Maui, HI, USA, 3–6 June 1991. [Google Scholar]
- Li, S.; Xu, C.; Xie, M. A Robust O(n) Solution to the Perspective-n-Point Problem. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1444–1450. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Xu, G.; Cheng, Y.; Yu, Q. A simple, robust and fast method for the perspective-n-point Problem. Pattern Recognit. Lett. 2018, 108, 31–37. [Google Scholar] [CrossRef]
- Garro, V.; Crosilla, F.; Fusiello, A. Solving the PnP Problem with Anisotropic Orthogonal Procrustes Analysis. In Proceedings of the 2nd International Conference on 3D Imaging, Modeling, Processing, Visualization & Transmission, Zurich, Switzerland, 13–15 October 2012. [Google Scholar]
- Moreno-Noguer, F.; Lepetit, V.; Fua, P. Accurate Non-Iterative O(n) Solution to PnP Problem. In Proceedings of the IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–21 October 2007. [Google Scholar]
- Ferraz, L.; Binefa, X.; Moreno-Noguer, F. Very Fast Solution to the PnP Problem with Algebraic Outlier Rejection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, IN, USA, 23–28 June 2014. [Google Scholar]
- Ferraz, L.; Binefa, X.; Moreno-Noguer, F. Leveraging Feature Uncertainty in the PnP Problem. In Proceedings of the British Machine Vision Conference, Nottingham, UK, 1–5 September 2014. [Google Scholar]
- Zheng, Y.; Kuang, Y.; Sugimoto, S.; Astrom, K.; Okutomi, M. Revisiting the PnP Problem: A Fast, General and Optimal Solution. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013. [Google Scholar]
- Yu, Q.; Xu, G.; Zhang, L.; Shi, J. A consistently fast and accurate algorithm for estimating camera pose from point correspondences. Measurement 2021, 172, 108914. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2003; pp. 146–157. [Google Scholar]
- Martinez, G. Field tests on flat ground of an intensity-difference based monocular visual odometry algorithm for planetary rovers. In Proceedings of the 15th IAPR International Conference on Machine Vision Applications, Nagoya, Japan, 8–12 May 2017. [Google Scholar]
- Li, H.; Chen, L.; Li, F. An Efficient Dense Stereo Matching Method for Planetary Rover. IEEE Access 2019, 7, 48551–48564. [Google Scholar] [CrossRef]
- Corke, P.; Strelow, D.; Singh, S. Omnidirectional visual odometry for a planetary rover. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Sendai, Japan, 28 September–2 October 2004. [Google Scholar]
- Hesch, J.A.; Roumeliotis, S.I. A Direct Least-Squares (DLS) method for PnP. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Urban, S.; Leitloff, J.; Hinz, S. MLPnP-a real-time maximum likelihood solution to the perspective-n-point problem. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Prague, Czech, 12–19 July 2016. [Google Scholar]
- Yang, K.; Fang, W.; Zhao, Y.; Deng, N. Iteratively Reweighted Midpoint Method for Fast Multiple View Triangulation. IEEE Robot. Autom. Lett. 2019, 4, 708–715. [Google Scholar] [CrossRef]
- Takeshi, F.; Ramaseshan, K.; Yuji, N.; Yusaku, Y.; Yuka, Y. Shifted Cholesky QR for Computing the QR Factorization of Ill-Conditioned Matrices. SIAM J. Sci. Comput. 2020, 42, 477–503. [Google Scholar]
- Mangelson, J.G.; Ghaffari, M.; Vasudevan, R.; Eustice, R.M. Characterizing the Uncertainty of Jointly Distributed Poses in the Lie Algebra. IEEE Trans. Robot. 2020, 36, 1371–1388. [Google Scholar] [CrossRef]
- Zhao, Y.; Vela, P.A. Good Feature Matching: Toward Accurate, Robust VO/VSLAM with Low Latency. IEEE Trans. Robot. 2020, 36, 657–675. [Google Scholar] [CrossRef] [Green Version]
- Zhou, B.; Luo, S.; Zhang, S. Pre-Weighted Midpoint Algorithm for Efficient Multiple-View Triangulation. IEEE Robot. Autom. Lett. 2021, 6, 7839–7845. [Google Scholar]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Urtasun, R. Are We Ready for Autonomous Driving? The KITTI Vision Benchmark Suite. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012. [Google Scholar]





| Algorithm | FGO | EGN | SRF | ML | Ours |
|---|---|---|---|---|---|
| Reprojection Error (pixel) | 1.634 | 5.420 | 1.642 | 3.476 | 1.604 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, B.; Luo, S.; Zhang, S. An Innovative Pose Determination Algorithm for Planetary Rover Onboard Visual Odometry. Aerospace 2022, 9, 391. https://doi.org/10.3390/aerospace9070391
Zhou B, Luo S, Zhang S. An Innovative Pose Determination Algorithm for Planetary Rover Onboard Visual Odometry. Aerospace. 2022; 9(7):391. https://doi.org/10.3390/aerospace9070391
Chicago/Turabian StyleZhou, Botian, Sha Luo, and Shijie Zhang. 2022. "An Innovative Pose Determination Algorithm for Planetary Rover Onboard Visual Odometry" Aerospace 9, no. 7: 391. https://doi.org/10.3390/aerospace9070391
APA StyleZhou, B., Luo, S., & Zhang, S. (2022). An Innovative Pose Determination Algorithm for Planetary Rover Onboard Visual Odometry. Aerospace, 9(7), 391. https://doi.org/10.3390/aerospace9070391







