A Survey of Precision Formation Relative State Measurement Technology for Distributed Spacecraft
Abstract
1. Introduction
2. Research Status of the Precision Formation of Distributed Spacecraft Project
2.1. TechSat-21
2.2. Darwin
2.3. PRISMA
2.4. XEUS
2.5. LISA
2.6. GRACE and GRACE Follow-On
2.7. CanX-4/CanX-5
2.8. Proba-3
2.9. TerraSAR-X, TanDEM-X
2.10. Gemini
2.11. CANYVAL-X
2.12. TianQin
2.13. TaiJi
2.14. IRASSI
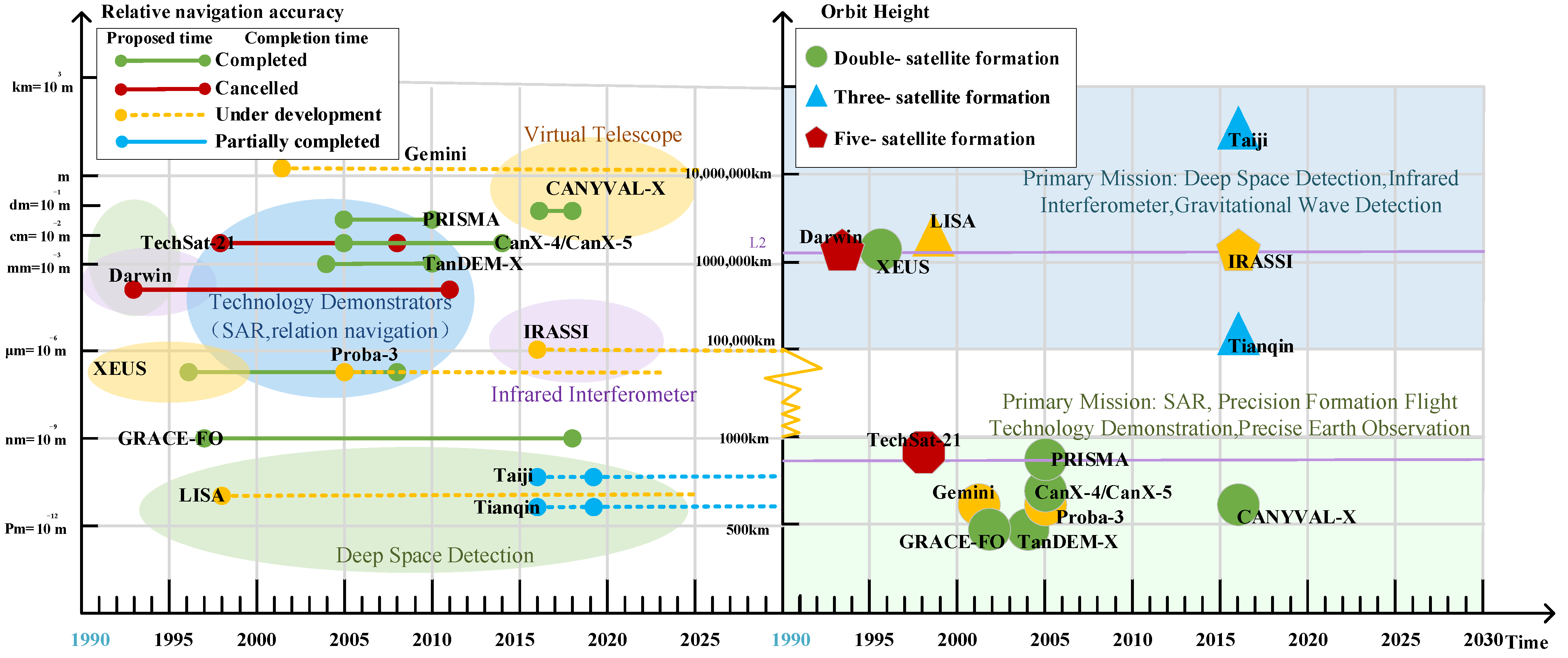
2.15. Trend Analysis of the Distributed Precise Spacecraft Formation Flying Project
3. Analysis of the Characteristics of Relative State Measurement Technology
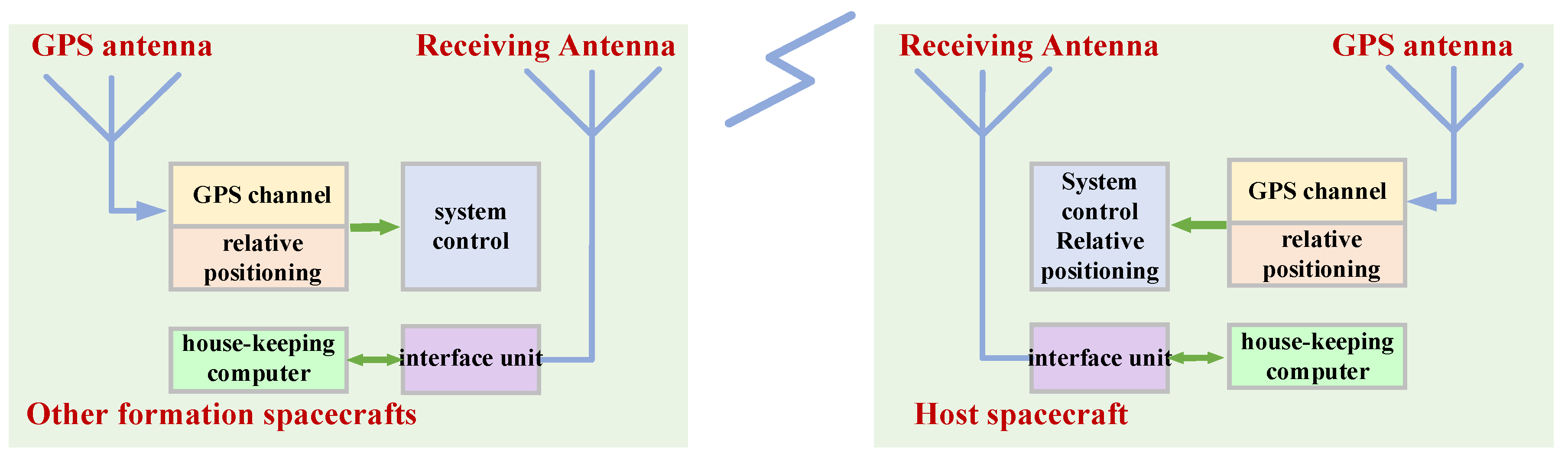
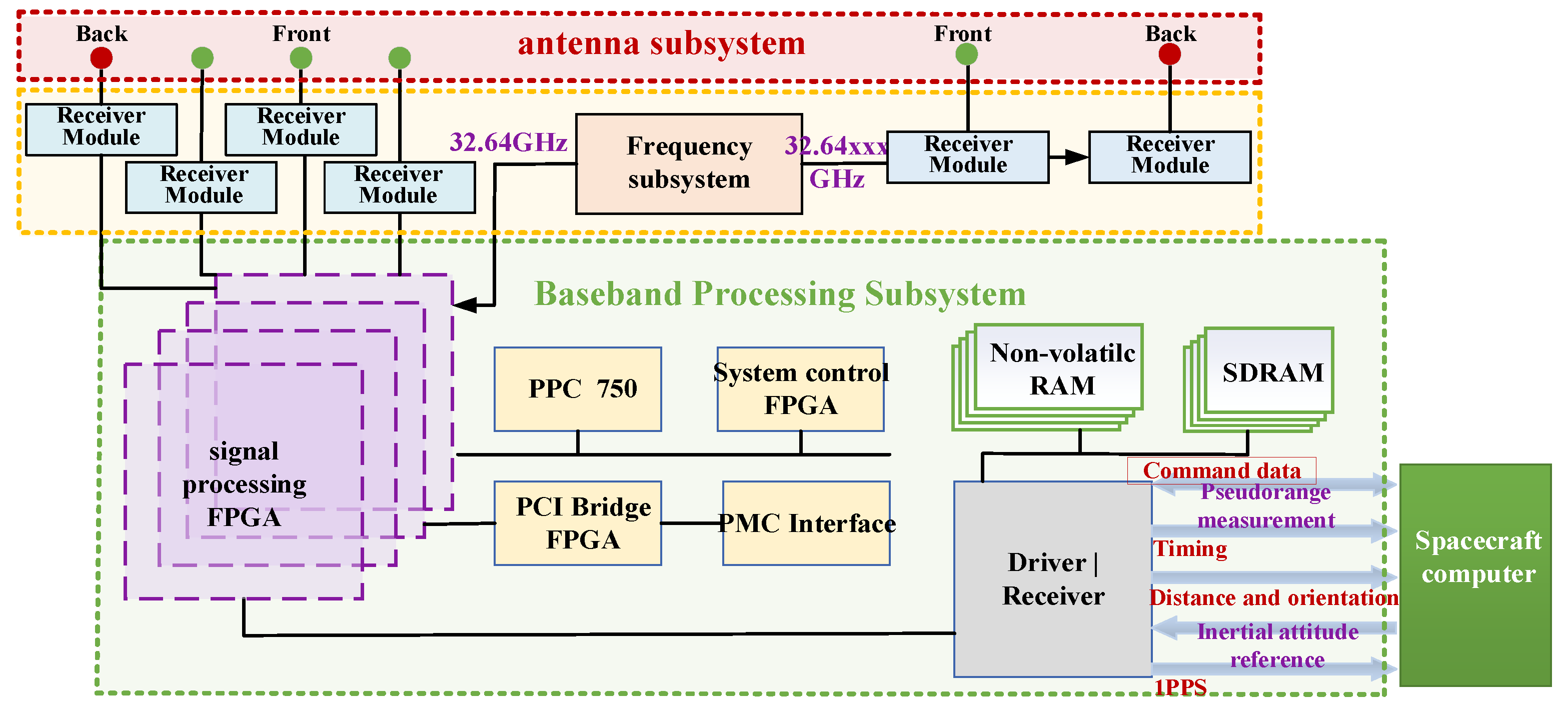
3.1. GNSS (Global Navigation System) Signal Relative Measurement Technology
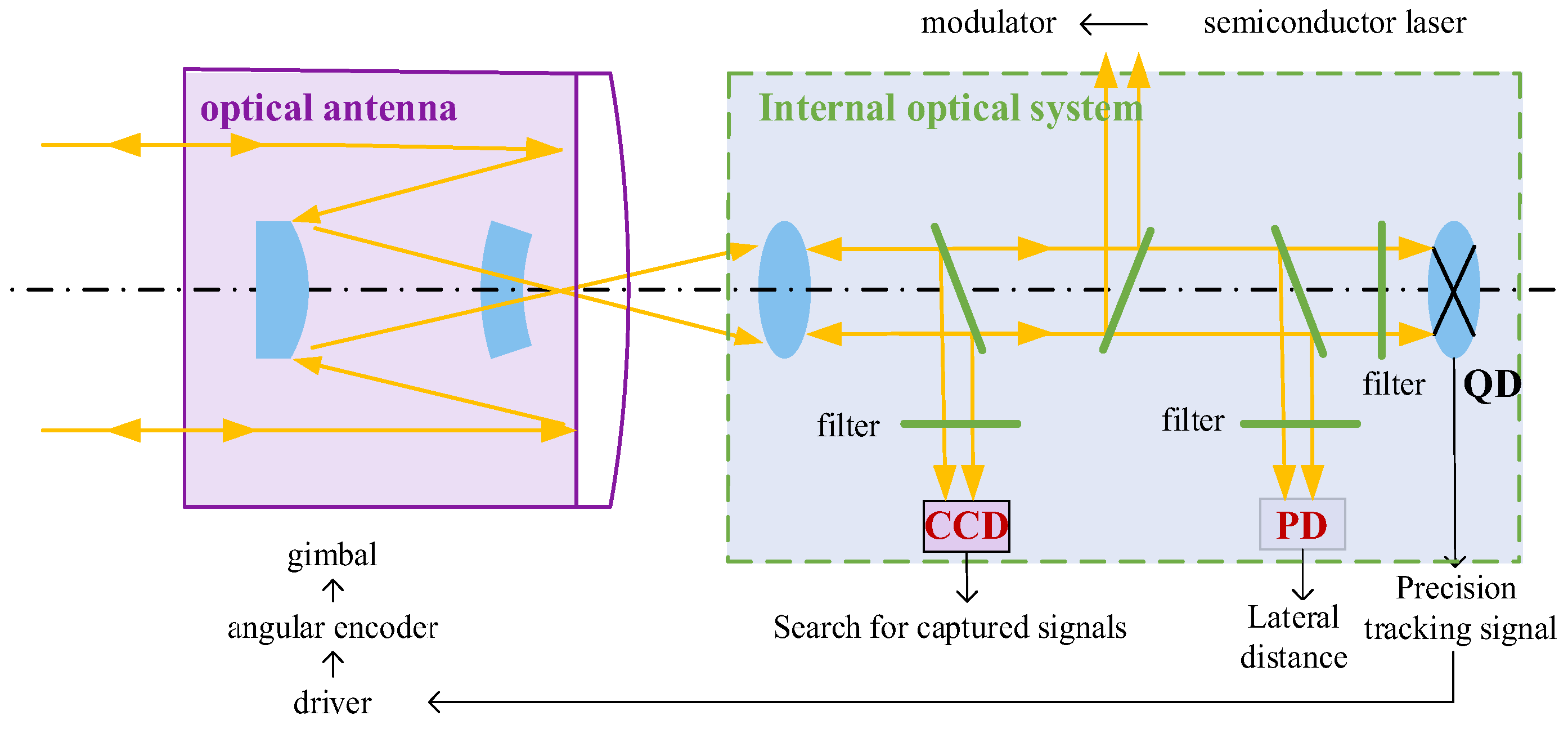
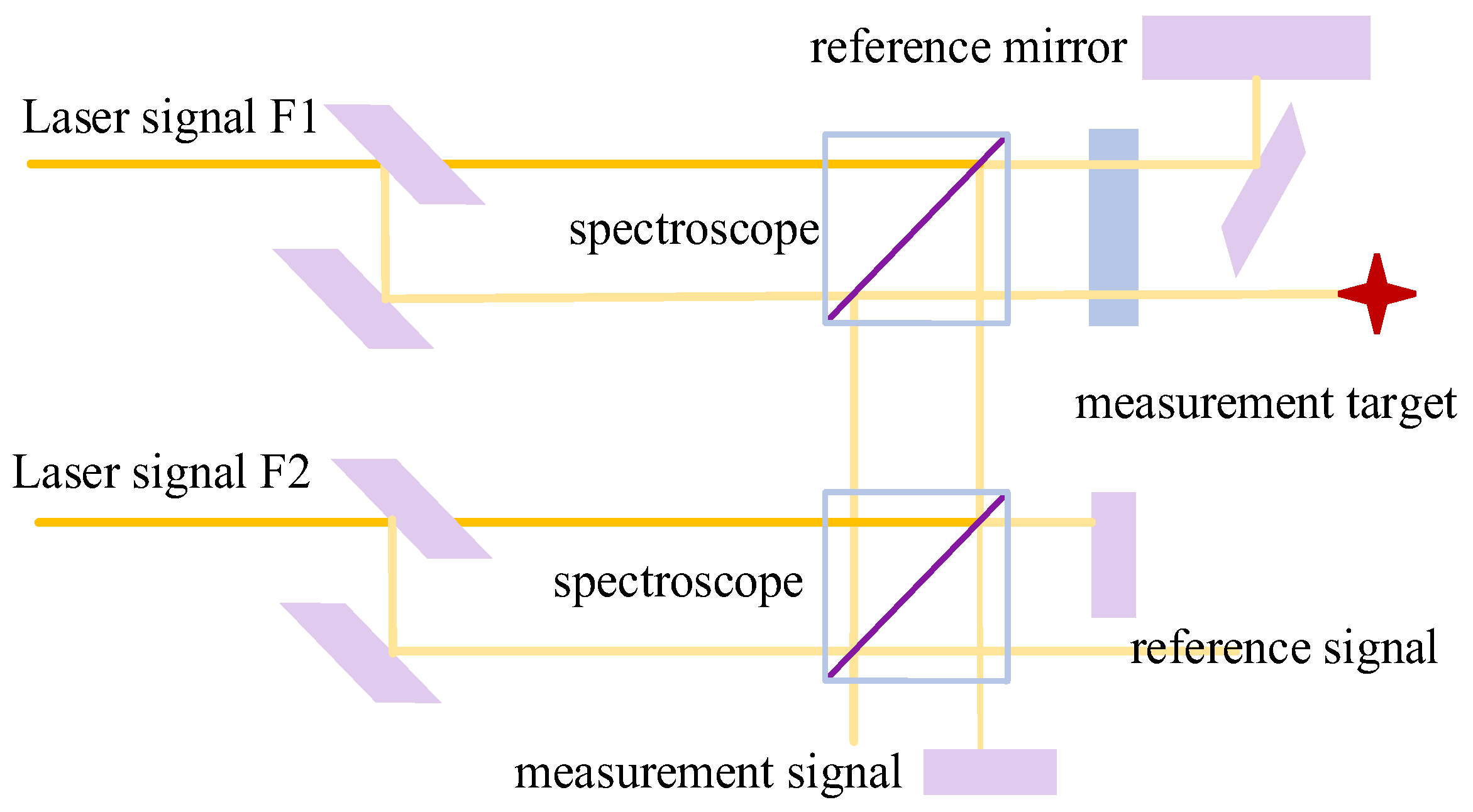
3.2. Laser Measurement Technology
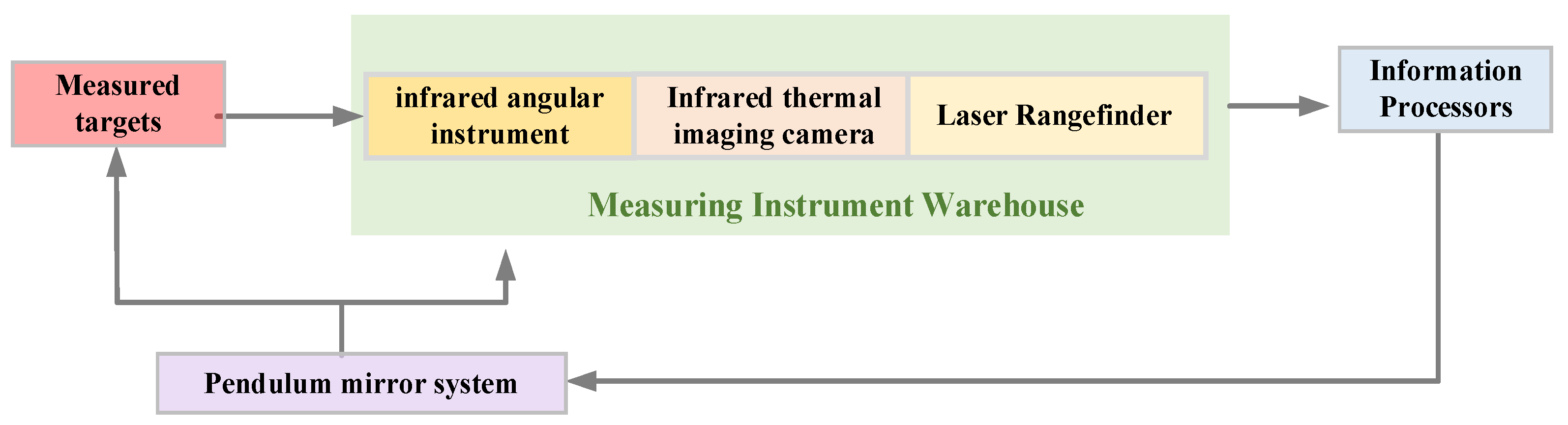
3.3. Infrared Measurement Technology
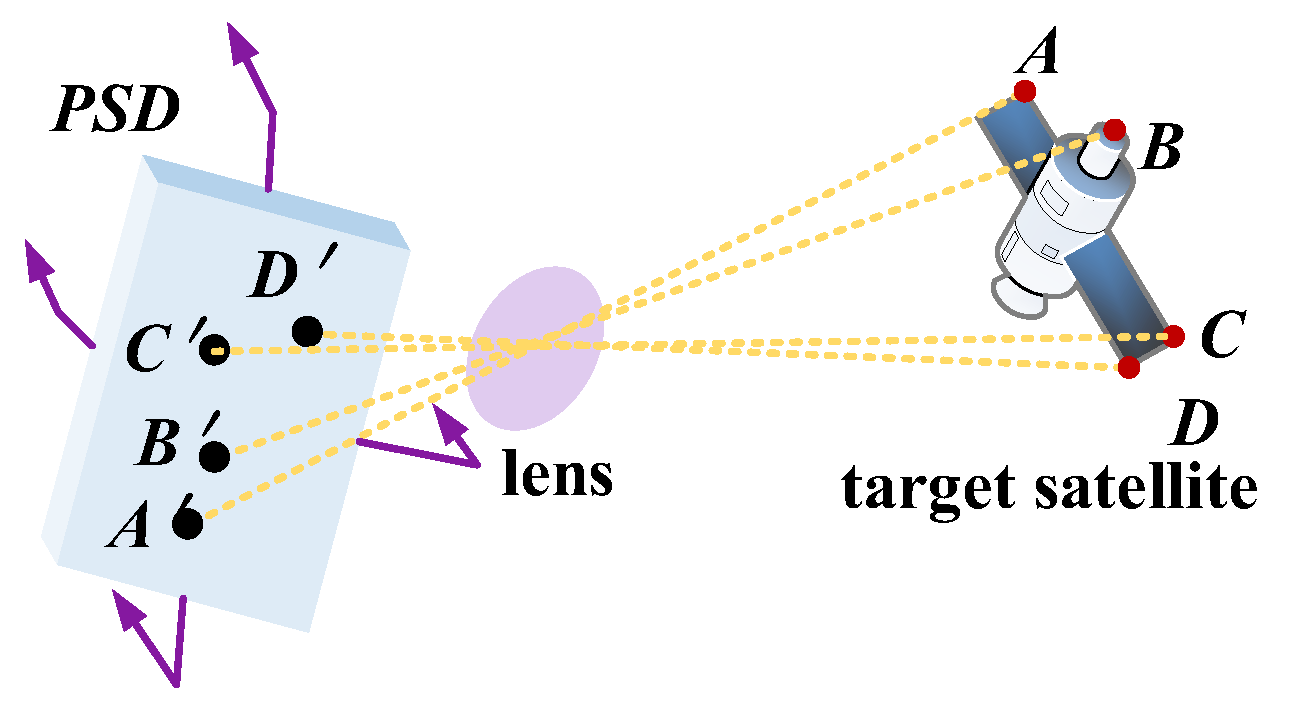
3.4. Visible Light Vision Measurement Technology
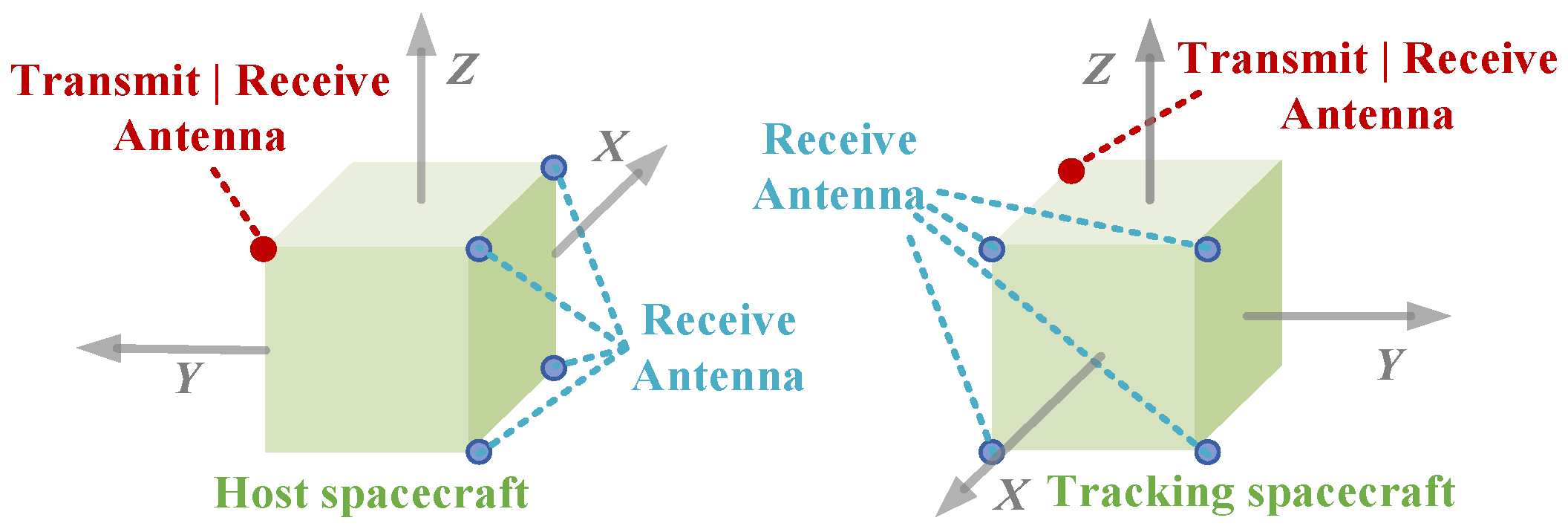
3.5. Radio-Based Autonomous Measurement Technology
3.6. Composite Relative Measurement Technology of Spacecraft Formation
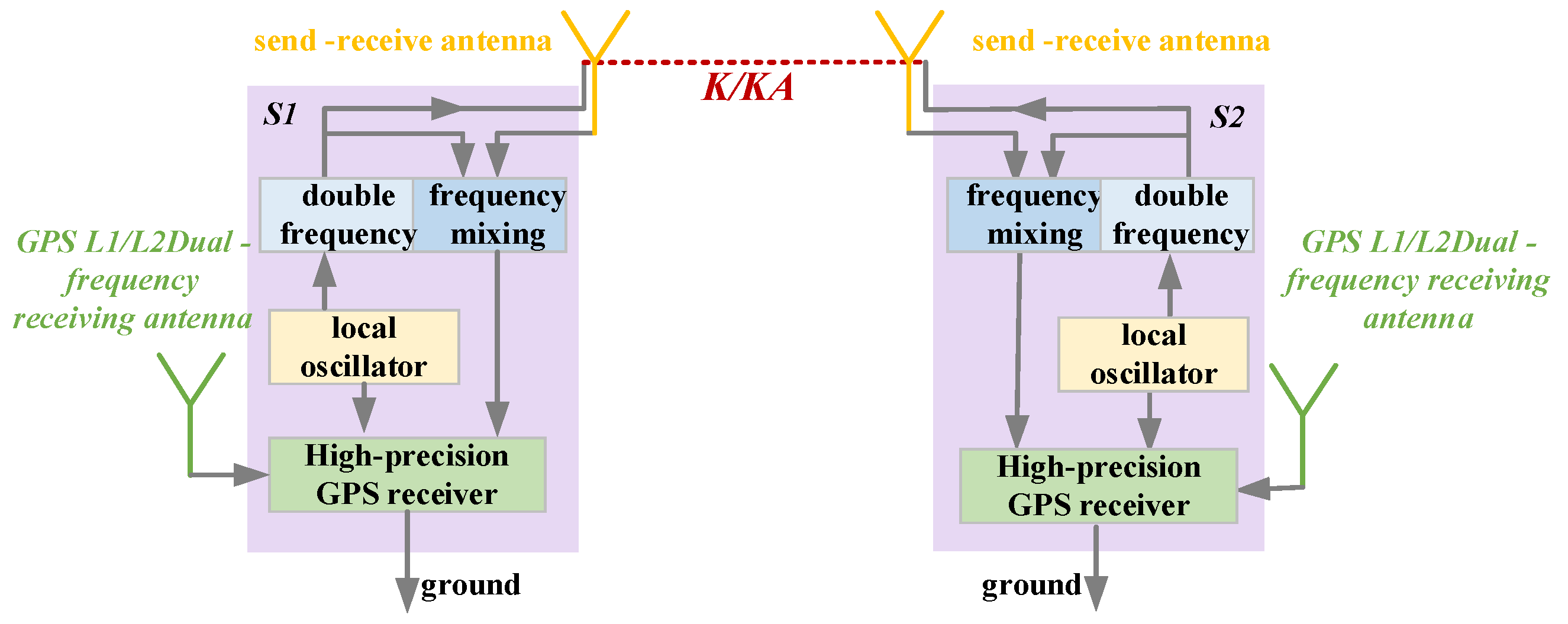
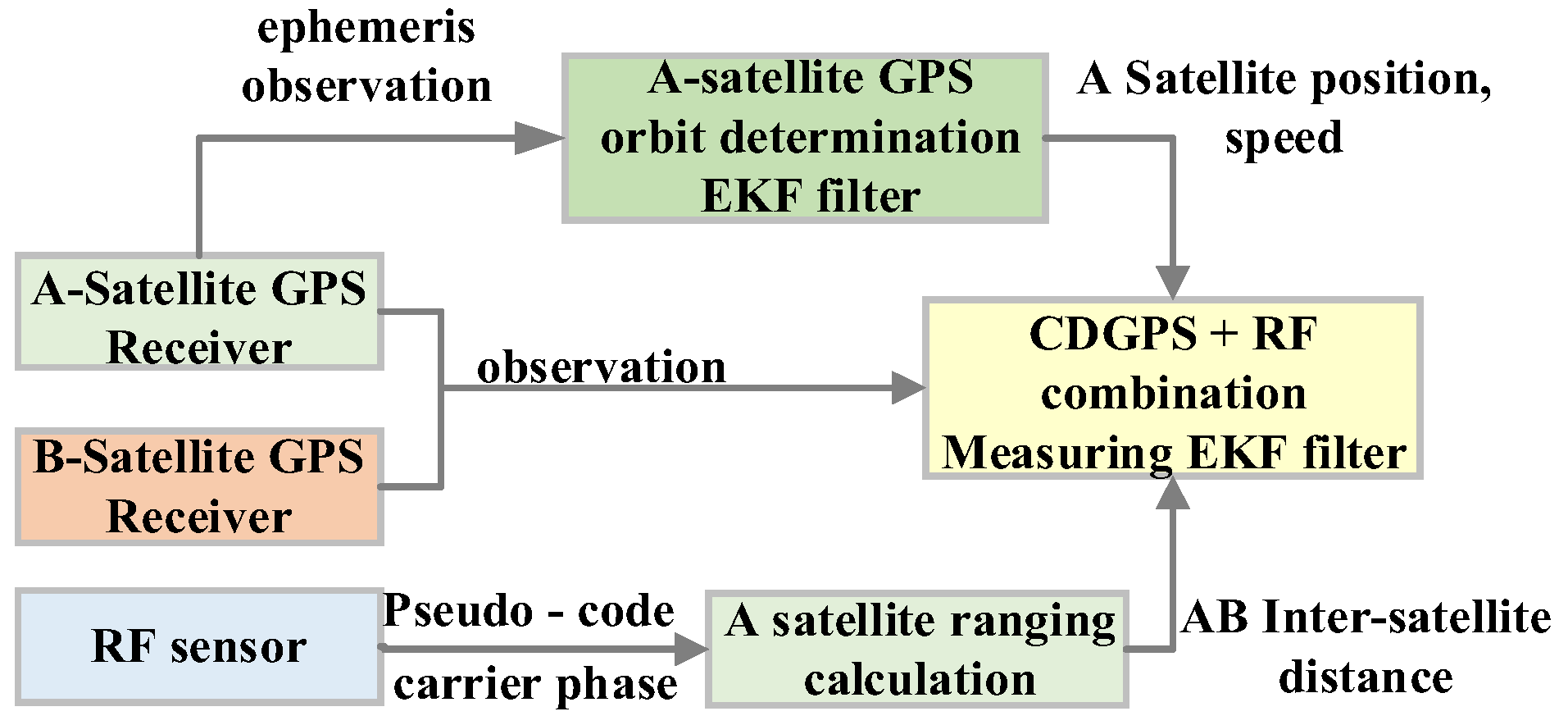
3.6.1. GPS + RF Coupling Measurement Technology
3.6.2. GPS + Laser Coupling Measurement Technology
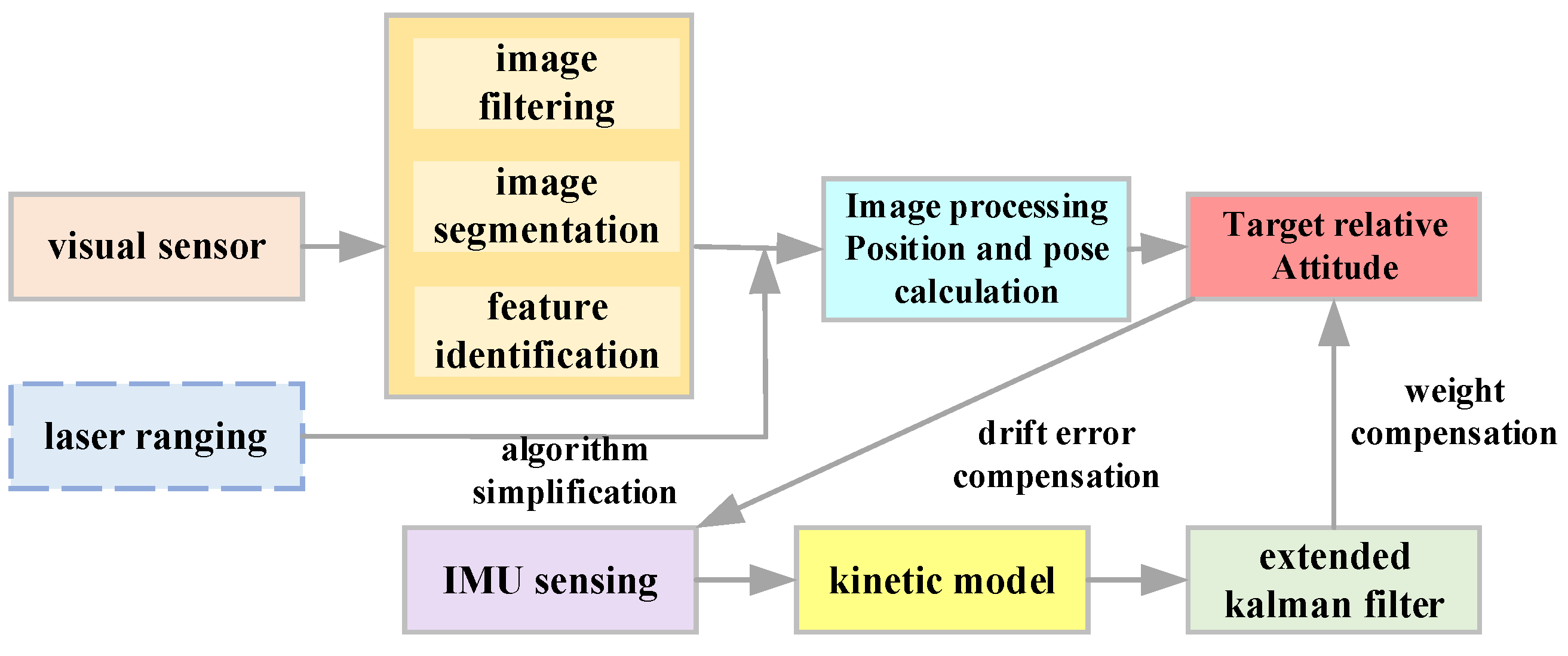
3.6.3. GPS + Vision Coupling Measurement Technology
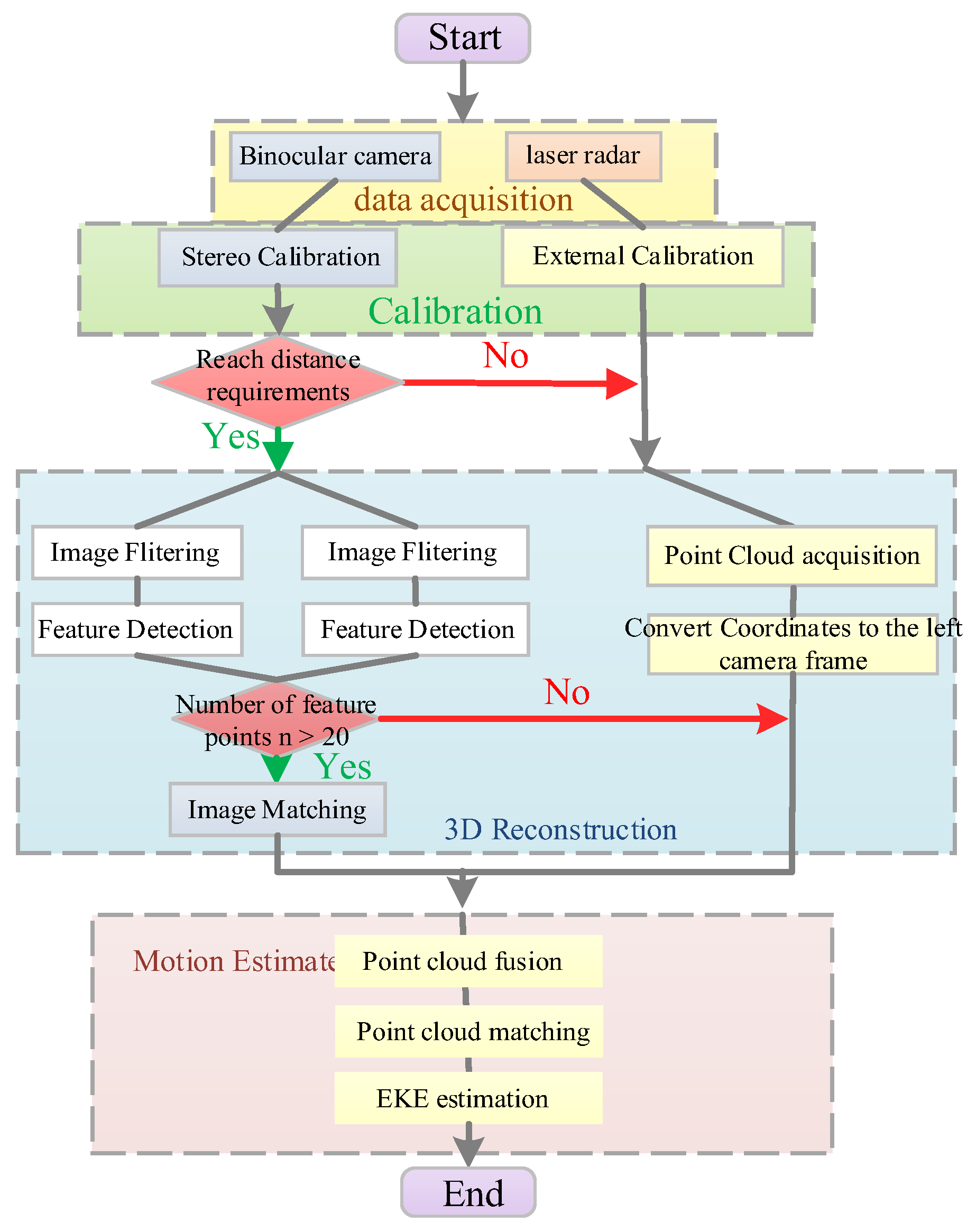
3.6.4. Visual Composite Close-Range Measurement Technology
3.6.5. Vision + RF Coupling Measurement Technology
3.6.6. Vision + Laser Coupling Measurement Technology
3.6.7. Laser + RF Coupling Measurement Technology
3.6.8. Laser + Infrared Coupling Measurement Technology
3.6.9. Laser Multiple Guidance Composite Measurement Technology
4. Relative State Measurement Technology Trends and Optimization
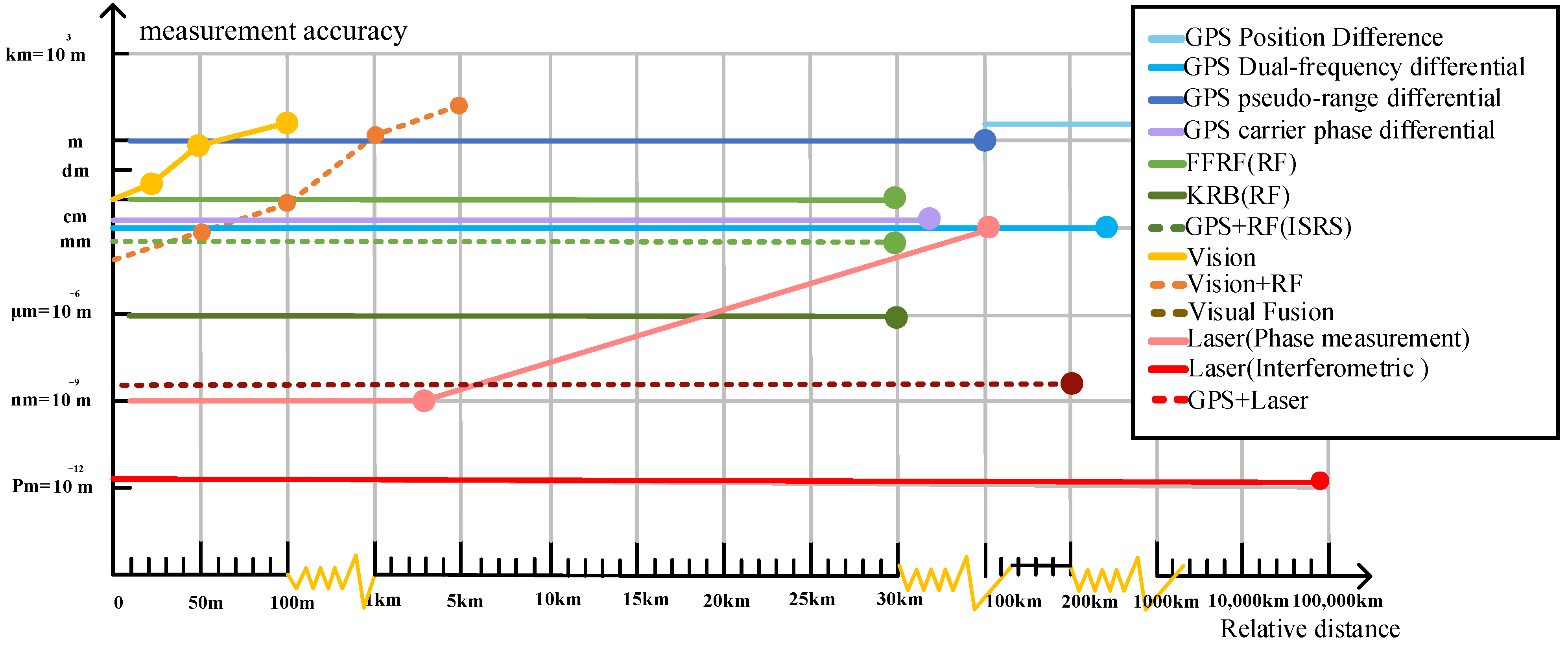
4.1. Summary of the Relative State Measurement Technology Current Status
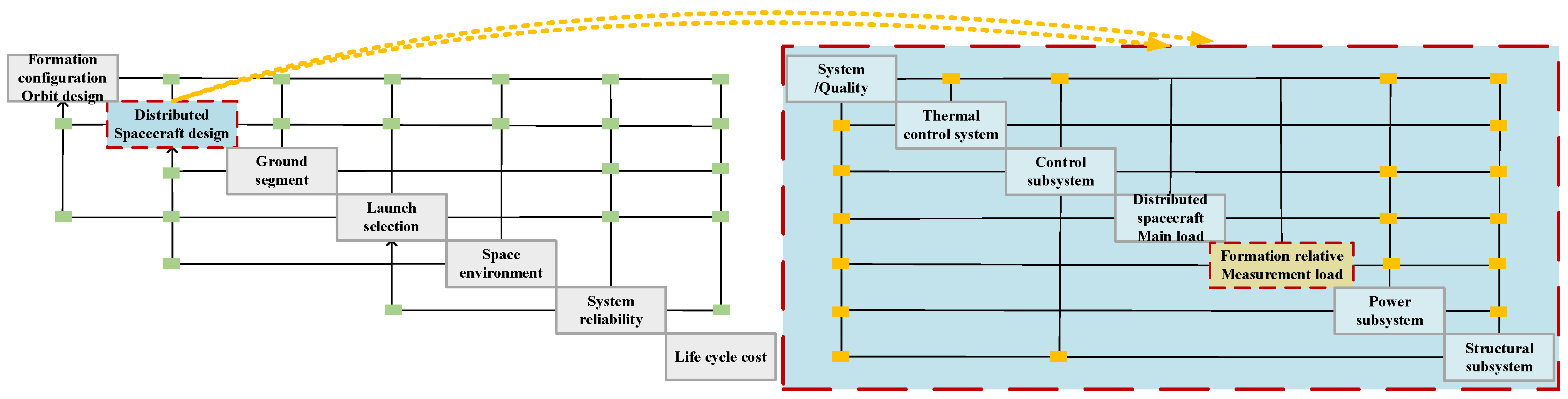
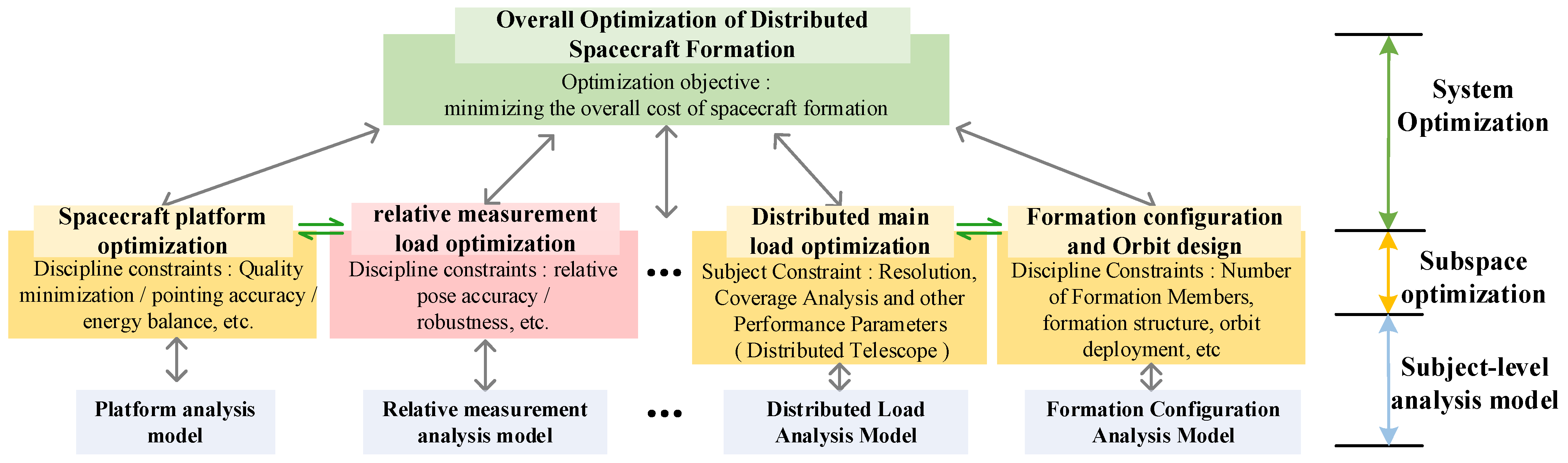
4.2. Multidisciplinary Optimized Architecture for Relative State-Measurement Payloads
4.3. Development Trend
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goswami, S.; Francis, S.P.; Bandikova, T.; Spero, R.E. Analysis of GRACE Follow-On Laser Ranging Interferometer Derived Inter-Satellite Pointing Angles. IEEE Sens. J. 2021, 21, 19209–19221. [Google Scholar] [CrossRef]
- Zink, M.; Moreira, A.; Hajnsek, I.; Rizzoli, P.; Wessel, B. TanDEM-X: 10 Years of Formation Flying Bistatic SAR Interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3546–3565. [Google Scholar] [CrossRef]
- Hughes, M.; Norris, S. An Overview of the Technology Satellite of the 21st Century (TechSat 21) Program. In Smaller Satellites: Bigger Business? Springer: Dordrecht, The Netherlands, 2002; Volume 6, pp. 381–382. [Google Scholar] [CrossRef]
- Das, A.; Cobb, R. TechSat 21—Space Missions Using Collaborating Constellations of Satellites. In Proceedings of the 12th AIAA/USU Conference on Small Satellites, Logan, UT, USA, 31 August–11 September 1998. [Google Scholar]
- Cockell, C.S.; Herbst, T.; Léger, A.; Absil, O.; Beichman, C.; Benz, W.; Brack, A.; Chazelas, B.; Chelli, A.; Cottin, H. Darwin—An Experimental Astronomy Mission to Search for Extrasolar Planets. Exp. Astron. 2009, 23, 435–461. [Google Scholar] [CrossRef]
- Grelier, T.; Guidotti, P.Y.; Delpech, M.; Harr, J.; Leyre, X. Formation Flying Radio Frequency Instrument: First Flight Results from the PRISMA Mission. In Proceedings of the Satellite Navigation Technologies & European Workshop on Gnss Signals & Signal Processing, Toulouse, France, 8–9 December 2011. [Google Scholar]
- Persson, S.; Veldman, S.; Bodin, P. PRISMA—A formation Flying Project in Implementation Phase. Acta Astronaut. 2009, 65, 1360–1374. [Google Scholar] [CrossRef]
- Parmar, A.N.; Hasinger, G.; Arnaud, M.; Barcons, X.; Barret, D.; Blanchard, A.; Boehringer, H.; Cappi, M.; Comastri, A.; Courvoisier, T.; et al. XEUS—The X-ray Evolving Universe Spectroscopy Mission. In Proceedings of the Conference on Space Telescopes and Instrumentation II: Ultraviolet to Gamma Ray, Orlando, FL, USA, 15 June 2006. [Google Scholar]
- Arnaud, M.; Barcons, X.; Barret, D.; Bautz, M.; Bellazzini, R.; Bleeker, J.; Böhringer, H.; Boller, T.; Brandt, W.N.; Cappi, M.; et al. XEUS: The Physics of the Hot Evolving Universe. Exp. Astron. 2009, 23, 139–168. [Google Scholar] [CrossRef][Green Version]
- Jennrich, O. LISA Technology and Instrumentation. Class. Quantum Gravity 2009, 26, 153001–153032. [Google Scholar] [CrossRef]
- Schütze, D.; Stede, G.; Müller, V.; Gerberding, O.; Mahrdt, C.; Sheard, B.; Heinzel, G.; Danzmann, K. LISA-like Laser Ranging for GRACE Follow-on. Proceedings of 9th LISA Symposium, Paris, France, 21–25 May 2012. [Google Scholar]
- Stephens, M.; Craig, R.; Leitch, J.; Pierce, R.; Nerem, R.; Bender, P.; Loomis, B. Demonstration of an Interferometric Laser Ranging System for a Follow-On Gravity Mission to GRACE. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006. [Google Scholar]
- Shahzad, M.W.; Burhan, M.; Ang, L.; Ng, K.C. Energy-water-Environment Nexus Underpinning Future Desalination Sustainability. Desalination 2017, 413, 52–64. [Google Scholar] [CrossRef]
- Watkins, M.; Flechtner, F.; Morton, P.; Webb, F. Status of the GRACE Follow-On Mission. Egu Gen. Assem. 2014, 141, 117–121. [Google Scholar] [CrossRef]
- Orr, N.G.; Eyer, J.K.; Larouche, B.P.; Zee, R.E. Precision Formation Flight: The Can X-4 and Can X-5 Dual Nanosatellite Mission. In Proceedings of the Esa Special Publication, Karlsruhe, Germany, 15–17 September 2008. [Google Scholar]
- Landgraf, M.; Mestreau-Garreau, A. Formation Flying and Mission Design for Proba-3. Acta Astronaut. 2013, 82, 137–145. [Google Scholar] [CrossRef]
- Llorente, J.S.; Agenjo, A.; Carrascosa, C.; de Negueruela, C.; Mestreau-Garreau, A.; Cropp, A.; Santovincenzo, A. PROBA-3: Precise Formation Flying Demonstration Mission. Acta Astronaut. 2013, 82, 38–46. [Google Scholar] [CrossRef]
- Kurahashi, T.; Menini, A. TanDEM-X: A Satellite Formation for High-Resolution SAR Interferometry. IET 2009, 45, 3317–3341. [Google Scholar] [CrossRef]
- Moreira, A.; Krieger, G.; Hajnsek, I.; Hounam, D.; Settelmeyer, E. TanDEM-X: A TerraSAR-X Add-On Satellite for Single-Pass SAR Interferometry. In Proceedings of the Geoscience and Remote Sensing Symposium, IGARSS ’04, Anchorage, AK, USA, 20–24 September 2004. [Google Scholar]
- Guarnieri, A.M.; Tebaldini, S.; Rocca, F.; Broquetas, A. GEMINI: Geosynchronous SAR for Earth Monitoring by Interferometry and Imaging. In Proceedings of the Geoscience & Remote Sensing Symposium, Munich, Germany, 22–27 July 2012. [Google Scholar]
- Park, J.P.; Park, S.Y.; Lee, K.; Oh, H.J.; Kim, T.H. Mission Analysis and CubeSat Design for CANYVAL-X Mission. In Proceedings of the 14th International Conference on Space Operations, Daejeon, Korea, 16–20 May 2016. [Google Scholar]
- Jun, L.; Linghao, A.; Yanli, A.; Zicong, A.; Weigang, B.; Yanzheng, B.; Jiahui, B.; Bin, C.; Wenbo, C.; Chen, C.; et al. A Brief Introduction to the TianQin project. Acta Sci. Nat. Univ. Sunyatseni 2021, 60, 1–19. [Google Scholar]
- Hu, Y.; Mei, J.; Luo, J. TianQin Project and International Collaboration. Chin. Sci. Bull.-Chin. 2019, 64, 2475–2483. [Google Scholar] [CrossRef]
- Liu, H.S.; Luo, Z.R.; Sha, W. In-Orbit Performance of the Laser Interferometer of Taiji-1 Experimental Satellite. Int. J. Mod. Phys. A 2021, 36, 2140004. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, P.; Deng, J.; Cai, Z.; Wang, Z.; Wang, Z.; Yu, J.; Wu, Y.; Kang, Q.; Li, H.; et al. The Drag-Free Control Design and in-Orbit Experimental Results of “Taiji-1”. Int. J. Mod. Phys. A 2021, 36, 2140019. [Google Scholar] [CrossRef]
- Buinhas, L.; Philips-Blum, M.; Frankl, K.; Pany, T.; Eissfeller, B.; Forstner, R. Formation Operations and navigation Concept Overview for the IRASSI space Interferometer. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018; IEEE: Big Sky, MT, USA, 2018; pp. 1–16. [Google Scholar]
- Buinhas, L.; Linz, H.; Philips-Blum, M.; Foerstner, R. iSCOUT: Science-Task Planning and Formation Maneuver Design for the IRASSI Space Interferometer. Adv. Space Res. 2021, 67, 3840–3867. [Google Scholar] [CrossRef]
- Scharf, D.P.; Hadaegh, F.Y.; Kang, B.H. A Survey of Spacecraft Formation Flying Guidance and Control (part 1): Guidance. In Proceedings of the American Control Conference, Boston, MA, USA, 30 June–2 July 2004. [Google Scholar]
- Yuan, J.; Jia, H.; Fang, Q. Application of GPS to space Vehicles: Analysis of Space environment and Errors. IEEE Aerosp. Electron. Syst. Mag. 1998, 13, 25–30. [Google Scholar] [CrossRef]
- Montenbruck, O.; Ebinuma, T.; Lightsey, E.G.; Leung, S. A Real-Time Kinematic GPS Sensor for Spacecraft Relative Navigation. Aerosp. Sci. Technol. 2002, 6, 435–449. [Google Scholar] [CrossRef]
- Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M. Uncooperative Pose Estimation with a LIDAR-Based System. Acta Astronaut. 2015, 110, 287–297. [Google Scholar] [CrossRef]
- Gao, P.; Zheng, Y. Characters of Laser Ranging on Inter-Satellite Relative Position Measurement. In Proceedings of the International Conference on Recent Advances in Space Technologies, Istanbul, Turkey, 14–16 June 2007. [Google Scholar]
- Zhu, Y.; Sun, Y.; Zhao, W.; Huang, B.; Wu, L. Relative navigation for Autonomous Aerial Refueling Rendezvous Phase. Optik 2018, 174, 665–675. [Google Scholar] [CrossRef]
- Erkec, T.Y.; Hajiyev, C. Vision-Based Approaches of the Small Satellites Relative Navigation. Wseas Trans. Comput. Res. 2021, 9, 13–20. [Google Scholar] [CrossRef]
- Qian, F.; Zhu, Z.H.; Quan, P.; Hou, X. Relative State and Inertia Estimation of Unknown Tumbling Spacecraft by Stereo Vision. IEEE Access 2018, 6, 54126–54138. [Google Scholar] [CrossRef]
- Sabatini, M.; Palmerini, G.B.; Gasbarri, P. A testbed For Visual Based Navigation and Control during Space Rendezvous Operations. Acta Astronaut. 2015, 117, 184–196. [Google Scholar] [CrossRef]
- Yoshida, K. Engineering Test Satellite VII Flight Experiments for Space Robot Dynamics and Control: Theories on Laboratory Test Beds Ten Years Ago, Now in Orbit; Springer: Berlin/Heidelberg, Germany, 2003; Volume 22, pp. 321–335. [Google Scholar] [CrossRef]
- Shoemaker, J.; Wright, M. Orbital Express Space Operations Architecture Program. Proc. SPI—Int. Soc. Opt. Eng. 2004, 5088, 1–9. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, S.; Suk, J. Parametric Study of Sensor Placement for Vision-Based Relative Navigation System of Multiple Spacecraft. Acta Astronaut. 2017, 141, 36–49. [Google Scholar] [CrossRef]
- Pan, H.; Huang, J.; Qin, S. High Accurate Estimation of Relative Pose of Cooperative Space Targets Based on Measurement of Monocular Vision Imaging. Opt.-Int. J. Light Electron Opt. 2014, 125, 3127–3133. [Google Scholar] [CrossRef]
- Segal, S.; Carmi, A.; Gurfil, P. Stereovision-Based Estimation of Relative Dynamics Between Noncooperative Satellites: Theory and Experiments. IEEE Trans. Control. Syst. Technol. 2014, 22, 568–584. [Google Scholar] [CrossRef]
- An, S.; Haodong, P.; Huixian, D. Trinocular Stereo Visual Measurement Method for Spatial Non-Cooperative Target. Acta Opt. Sin. 2021, 41, 0615001. [Google Scholar] [CrossRef]
- Liu, Y.; Xie, Z.; Liu, H. Three-Line Structured Light Vision System for Non-Cooperative Satellites in Proximity Operations. Chin. J. Aeronaut. 2020, 33, 1494–1504. [Google Scholar] [CrossRef]
- Ning, M.; Zhang, S.; Wang, S. A Non-Cooperative Satellite Feature Point Selection Method for Vision-Based Navigation System. Sensors 2018, 18, 854. [Google Scholar] [CrossRef]
- Christian, J.A.; Robinson, S.B.; D’Souza, C.N.; Ruiz, J.P. Cooperative Relative Navigation of Spacecraft Using Flash Light Detection and Ranging Sensors. J. Guid. Control. Dyn. 2014, 37, 452–465. [Google Scholar] [CrossRef]
- Peng, J.; Xu, W.; Yuan, H. An Efficient Pose Measurement Method of a Space Non-Cooperative Target Based on Stereo Vision. IEEE Access 2017, 5, 22344–22362. [Google Scholar] [CrossRef]
- Gao, X.; Liang, B.; Du, X.; Xu, W. Pose measurement of large Non-Cooperative Satellite Using Structured Light Vision Sensor. In Proceedings of the 2012 IEEE International Conference on Information Science and Technology, Wuhan, China, 23–25 March 2012. [Google Scholar] [CrossRef]
- He, D.L.; Cao, X.B. Relative States Autonomous Determination of Satellites Formation Flying. In Proceedings of the 2006 International Conference on Machine Learning and Cybernetics, Dalian, China, 13–16 August 2006; pp. 742–748. [Google Scholar]
- Weiqing, M.; Liu, R.; Xinxin, Y.; Kamel, E. Analysis of Precision Estimation of RF Metrology in Satellite Formation Flying. In Proceedings of the 2015 International Conference on Wireless Communications & Signal Processing (wcsp), Nanjing, China, 15–17 October 2015; IEEE: New York, NY, USA, 2015. [Google Scholar]
- Grelier, T.; Guidotti, P.Y.; Delpech, M.; Harr, J.; Leyre, X. Formation Flying Radio Frequency Instrument: First Flight Results from the PRISMA Mission. In Proceedings of the Satellite Navigation Technologies & European Workshop on Gnss Signals & Signal Processing, Noordwijk, The Netherlands, 8–10 December 2010. [Google Scholar]
- Lee, C.K.; Han, S.C.; Bilitza, D.; Chung, J.K. Validation of International Reference Ionosphere Models Using in Situ Measurements from GRACE K-Band Ranging System and CHAMP Planar Langmuir Probe. J. Geod. 2011, 85, 921–929. [Google Scholar] [CrossRef]
- Wang, F. Study on Center of Mass Calibration and K-Band Ranging System Calibration of the Grace Mission; The University of Texas at Austin: Ann Arbor, MI, USA, 2003. [Google Scholar]
- Thevenet, J.-B.; Grelier, T. Formation Flying Radio-Frequency Metrology Validation and Performance: The PRISMA case. Acta Astronaut. 2013, 82, 2–15. [Google Scholar] [CrossRef]
- Mo, S.; Jin, X.; Lin, C.; Zhang, W.; Xu, Z.; Jin, Z. Multi-Satellite Relative Navigation Scheme for Microsatellites Using Inter-Satellite Radio Frequency Measurements. Sensors 2021, 21, 3725. [Google Scholar] [CrossRef]
- Mu, W.; Liu, R.; Wang, Z.; Liu, Y. Antenna Configuration Method for RF Measurement Based on DOPs in Satellite Formation Flying. Int. J. Aerosp. Eng. 2018, 2018, 4216971. [Google Scholar] [CrossRef]
- Liu, C.; An, J.; Zhang, R. Zhang Radio-Based Relative State Measurement Algorithm for Micro-Nano Satellite Formation. In Proceedings of the 2019 IEEE 2nd International Conference on Electronics Technology (ICET), 10–13 May 2019; Chengdu, China; pp. 13–19. [Google Scholar]
- Peng, Y.X.; Scales, W.A.; Edwards, T.R. GPS-Based Satellite Formation Flight Simulation and Applications to Ionospheric Remote Sensing. Navigation 2020, 67, 3–21. [Google Scholar] [CrossRef]
- Dirkx, D.; Prochazka, I.; Bauer, S.; Visser, P.; Noomen, R.; Gurvits, L.I.; Vermeersen, B. Laser and radio tracking for planetary science missions—A comparison. J. Geod. 2019, 93, 2405–2420. [Google Scholar] [CrossRef]
- Sun, W.; Chen, L.; Liu, K. Research on Vision-Based Autonomous Navigation Algorithm for RVD between Spacecrafts. JSCSE 2012, 2, 1–12. [Google Scholar] [CrossRef]
- Fan, G.Q.; Wang, W.; Xiao-Ning, X.I. Application of GPS and Like-GPS Carrier Phase in States Measurement of Formation Constellation. Comput. Simul. 2006, 1, 44–47. [Google Scholar] [CrossRef]
- Allende-Alba, G.; D’Amico, S.; Montenbruck, O. Radio-Frequency Sensor Fusion for Relative Navigation of Formation Flying Satellites. Int. J. Space Sci. Eng. 2015, 3, 129–147. [Google Scholar] [CrossRef]
- Kang, D.-E.; Park, S.-Y.; Son, J. Characteristics of Relative Navigation Algorithms Using Laser Measurements and Laser-GPS Combined Measurements. J. Astron. Space Sci. 2018, 35, 287–293. [Google Scholar] [CrossRef]
- Oh, H.; Park, H.-E.; Lee, K.; Park, S.-Y.; Park, C. Improved GPS-Based Satellite Relative Navigation Using Femtosecond Laser Relative Distance Measurements. J. Astron. Space Sci. 2016, 33, 45–54. [Google Scholar] [CrossRef]
- Barreau, V.; Priot, B.; Calmettes, V.; Sahmoudi, M. A New Approach for Deep Integration of GNSS and Vision-Aided MEMS IMU. In Proceedings of the Ion Gnss, Portland, OR, USA, 21–24 September 2010. [Google Scholar]
- Wang, X.; Shao, X.; Gong, D.; Duan, D. GPS/VISNAV Integrated Relative Navigation and Attitude Determination System for Ultra-Close Spacecraft Formation Flying. J. Syst. Eng. Electron. 2011, 22, 9. [Google Scholar] [CrossRef]
- Bowen, J.; Tsuda, A.; Abel, J.; Villa, M. CubeSat Proximity Operations Demonstration (CPOD) Mission Update. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015. [Google Scholar]
- Roscoe, C.; Westphal, J.J.; Mosleh, E. Overview and GNC design of the CubeSat Proximity Operations Demonstration (CPOD) Mission. Acta Astronaut. 2018, 153, 410–421. [Google Scholar] [CrossRef]
- Giubilato, R.; Chiodini, S.; Pertile, M.; Debei, S. MiniVO: Minimalistic Range Enhanced Monocular System for Scale Correct Pose Estimation. IEEE Sens. J. 2020, 20, 11874–11886. [Google Scholar] [CrossRef]
- Jing, Y.; Zhu, S.; Wang, L. Autonomous Optical Navigation Approach Aided by Radio Beacon for Deep Space Spacecraft. In Proceedings of the 2016 Chinese Control and Decision Conference, Yinchuan, China, 28–30 May 2016. [Google Scholar]
- Wang, X.; Shao, X.; Gong, D.; Duan, D. Radio/VISNAV Integrated Navigation System for Autonomous Spacecraft Rendezvous Using Two-Order Filter. In Proceedings of the 8th World Congress on Intelligent Control and Automation, Jinan, China, 6–9 July 2010; pp. 1735–1740. [Google Scholar]
- Peng, J.; Xu, W.; Liang, B.; Wu, A.G. Pose Measurement and Motion Estimation of Space Non-Cooperative Targets Based on Laser Radar and Stereo-vision Fusion. IEEE Sens. J. 2018, 19, 3008–3019. [Google Scholar] [CrossRef]
- Lestarquit, L.; Harr, J.; Grelier, T.; Peragin, E.; Wilhelm, N.; Mehlen, C.; Peyrotte, C. Autonomous Formation Flying RF Sensor Development for the PRISMA Mission. In Proceedings of the 19th International Technical Meeting of the Satellite Division of the Institute of Navigation (ion Gnss 2006), Fort Worth, TX, USA, 26–29 September 2006. [Google Scholar]
- Guo, C.; Xia, X.; Si, C.; Liu, P.; Yang, D. A Survey of Relative Position and Attitude Measurement for Formation Flying Satellite. Aerosp. Control 2018, 36, 83–89. [Google Scholar]
- Liu, Y.; Dong-Yun, Y.I.; Wang, Z.M. Research on High Precision Measure Methods of Inter-Satellite Baselines of Formation Flying Satellites. J. Astronaut. 2007, 6, 1643–1647. [Google Scholar]
- Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M. A Review of Cooperative and Uncooperative Spacecraft Pose Determination Techniques for Close-Proximity Operations. Prog. Aeosp. Sci. 2017, 93, 53–72. [Google Scholar] [CrossRef]
- Wu, Y.; Cao, X.; Dan, X. Autonomous Relative Navigation for Formation Flying Satellites. In Proceedings of the International Symposium on Systems & Control in Aerospace & Astronautics, Harbin, China, 19–21 January 2006. [Google Scholar]
- Schilling, K. Small Satellite Formations: Challenges in Navigation and its Application Potential. In Proceedings of the 2021 28th Saint Petersburg International Conference on Integrated Navigation Systems (ICINS), Saint Petersburg, Russia, 31 May–2 June 2021; pp. 1–4. [Google Scholar]
- Bucolo, M.; Buscarino, A.; Famoso, C.; Fortuna, L.; Gagliano, S. Imperfections in Integrated Devices Allow the Emergence of Unexpected Strange Attractors in Electronic Circuits. IEEE Access 2021, 9, 29573–29583. [Google Scholar] [CrossRef]
- Hou, R.; Zhao, S.H.; Jie, X.U.; Yong-Jun, L.I.; Ji-Li, W.U. The Effects Analysis of High Particles on the Laser Satellite Communication System. Opt. Commun. Technol. 2008, 9, 55–58. [Google Scholar]
- Maessen, D.C.; Gill, E. Relative State Estimation and Observability for Formation Flying Satellites in the Presence of Sensor Noise. Acta Astronaut. 2013, 82, 129–136. [Google Scholar] [CrossRef]
- Boscherini, M.; Adriani, O.; Bongi, M.; Bonechi, L.; Castellini, G.; D’Alessandro, R.; Gabbanini, A.; Grandi, M.; Menn, W.; Papini, P.; et al. Radiation Damage of Electronic Components in space Environment. Nucl. Instrum. Methods Phys. Res. Sect. A-Accel. Spectrom. Dect. Assoc. Equip. 2003, 514, 112–116. [Google Scholar] [CrossRef]
- Godard; Kumar, K.D. Fault Tolerant Reconfigurable Satellite Formations Using Adaptive Variable Structure Techniques. J. Guid. Control Dyn. 2010, 33, 969–984. [Google Scholar] [CrossRef]
- Salvoldi, M.; Choukroun, D. Intersatellite Laser Ranging and Attitude Robust Measurement Planning. In Proceedings of the Israel Conference on Aerospace Sciences, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Li, J.; Kumar, K.D. Fault Tolerant Attitude Synchronization Control during Formation Flying. J. Aerosp. Eng. 2011, 24, 251–263. [Google Scholar] [CrossRef]
- Sabatini, M.; Reali, F.; Palmerini, G.B. Autonomous State Estimation in Formation Flight. In Proceedings of the 2007 Ieee Aerospace Conference, Big Sky, MT, USA, 3–10 March 2007; IEEE: New York, NY, USA, 2007; Volumes 1–9, p. 628. [Google Scholar]
- Balesdent, M.; Bérend, N.; Dépincé, P. New Multidisciplinary Design Optimization Approaches for Launch Vehicle Design. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2012, 227, 1545–1555. [Google Scholar] [CrossRef]
- Ujiie, R.; Nishi, K. Multi-Disciplinary System Design Optimization for All-Electric Geostationary Communication Satellite. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018; pp. 1–9. [Google Scholar]
- Sobieszczanski-Sobieski, J. Multidisciplinary Design Optimization: An Emerging New Engineering Discipline. In Advances in Structural Optimization; NASA Langley Research Center: Hampton, VA, USA, 1993. [Google Scholar]
- Balesdent, M.; Price, N.; Riche, R.L.; Kim, N.H.; Haftka, R.T. Advanced Space Vehicle Design Taking into Account Multidisciplinary Couplings and Mixed Epistemic/Aleatory Uncertainties. In Space Engineering; Springer International Publishing: Cham, Switzerland, 2016; Volume 114, pp. 1–48. [Google Scholar] [CrossRef]
- Budianto, I.A.; Olds, J.R. A Collaborative Optimization Approach to Design and Deployment of a Space Based Infrared System Constellation. In Proceedings of the Aerospace Conference, Big Sky, MT, USA, 25–25 March 2000. [Google Scholar]
- Curry, M.; Tour, P.L.; Slagowski, S. Multidisciplinary Design Optimization for a High-Resolution Earth-Imaging Constellation. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015. [Google Scholar] [CrossRef]
- Roberto, D.P.; Alfredo, R. A Robust Crater Matching Algorithm for Autonomous Vision-Based Spacecraft Navigation. In Proceedings of the 2021 IEEE 8th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Naples, Italy, 23–25 June 2021; pp. 322–327. [Google Scholar]
- Zhang, C.; Liu, H.; Liu, Y. Combining Stereo Vision and Inertial Navigation for Inspection Spacecraft. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 2369–2374. [Google Scholar]
- Rodrigues Ferreira, P.V.; Paffenroth, R.; Wyglinski, A.M.; Hackett, T.M.; Bilen, S.G.; Reinhart, R.C.; Mortensen, D.J. Multiobjective Reinforcement Learning for Cognitive Satellite Communications Using Deep Neural Network Ensembles. IEEE J. Sel. Areas Commun. 2018, 36, 1030–1041. [Google Scholar] [CrossRef]
- Cheng, Y.-H.; Jiang, B.; Li, H.; Han, X. On-orbit Reconfiguration Using Adaptive Dynamic Programming for Multi-Mission-Constrained Spacecraft Attitude Control System. Int. J. Control Autom. Syst. 2019, 17, 822–835. [Google Scholar] [CrossRef]
- Davis, J.C.; Pernicka, H. Spacecraft Identification Leveraging Unsupervised Learning Techniques for Formation and Swarm Missions. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Long, J.; Qian, Z.; Xie, F.; Ding, Z.; Liu, L. An Improved Multi-Satellite Cooperative Task Planning Method Based on Distributed Multi-Agent System. In Proceedings of the 2021 13th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Beihai, China, 16–17 January 2021; pp. 539–542. [Google Scholar]
- Hu, X.; Liao, X.; Liu, Z.; Liu, S.; Ding, X.; Helaoui, M.; Wang, W.; Ghannouchi, F.M. Multi-Agent Deep Reinforcement Learning-Based Flexible Satellite Payload for Mobile Terminals. IEEE Trans. Veh. Technol. 2020, 69, 9849–9865. [Google Scholar] [CrossRef]
- Hou, R.; Zhao, S.; Xu, J.; Wu, J.; Li, Y.; Zhan, S.; Shi, L.; Fang, S. Influence of Space Charged Particles on Satellite Optical Communication System. Opt. Appl. 2009, 39, 251–265. [Google Scholar]
- Patraev, V.E.; Shangina, E.A.; Dvirny, V.V.; Voroshilova, A.A.; Borisov, S.A. Ensuring the Quality of the Materials Used in the Spacecraft Engineering. In Proceedings of the IX International Multidisciplinary Scientific and Research Conference Modern Issues in Science and Technology/Workshop Advanced Technologies in Aerospace, Mechanical and Automation Engineering, Nanjing, China, 17–19 August 2018; Iop Publishing Ltd.: Bristol, UK, 2018; Volume 450, p. 022010. [Google Scholar]
- Wu, G.; Wang, L.; Ling, F. Research on Software Defined Payload Reconstruction Technology Scheme. In China Satellite Navigation Conference (CSNC) 2020 Proceedings: Volume II; Sun, J., Yang, C., Xie, J., Eds.; Lecture Notes in Electrical Engineering; Springer: Singapore, 2020; Volume 651, pp. 663–672. ISBN 9789811537103. [Google Scholar]
- Maheshwarappa, M.R.; Bridges, C.P. Software Defined Radios for Small Satellites. In Proceedings of the 2014 Nasa/Esa Conference on Adaptive Hardware and Systems (ahs), Leicester, UK, 14–17 July 2014; IEEE: New York, NY, USA, 2014; pp. 172–179. [Google Scholar]
- Wang, J.; Zhang, R.; Yuan, J. Luo Multi-CubeSat Relative Position and Attitude Determination Based on Array Signal Detection in Formation Flying. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 3378–3393. [Google Scholar] [CrossRef]
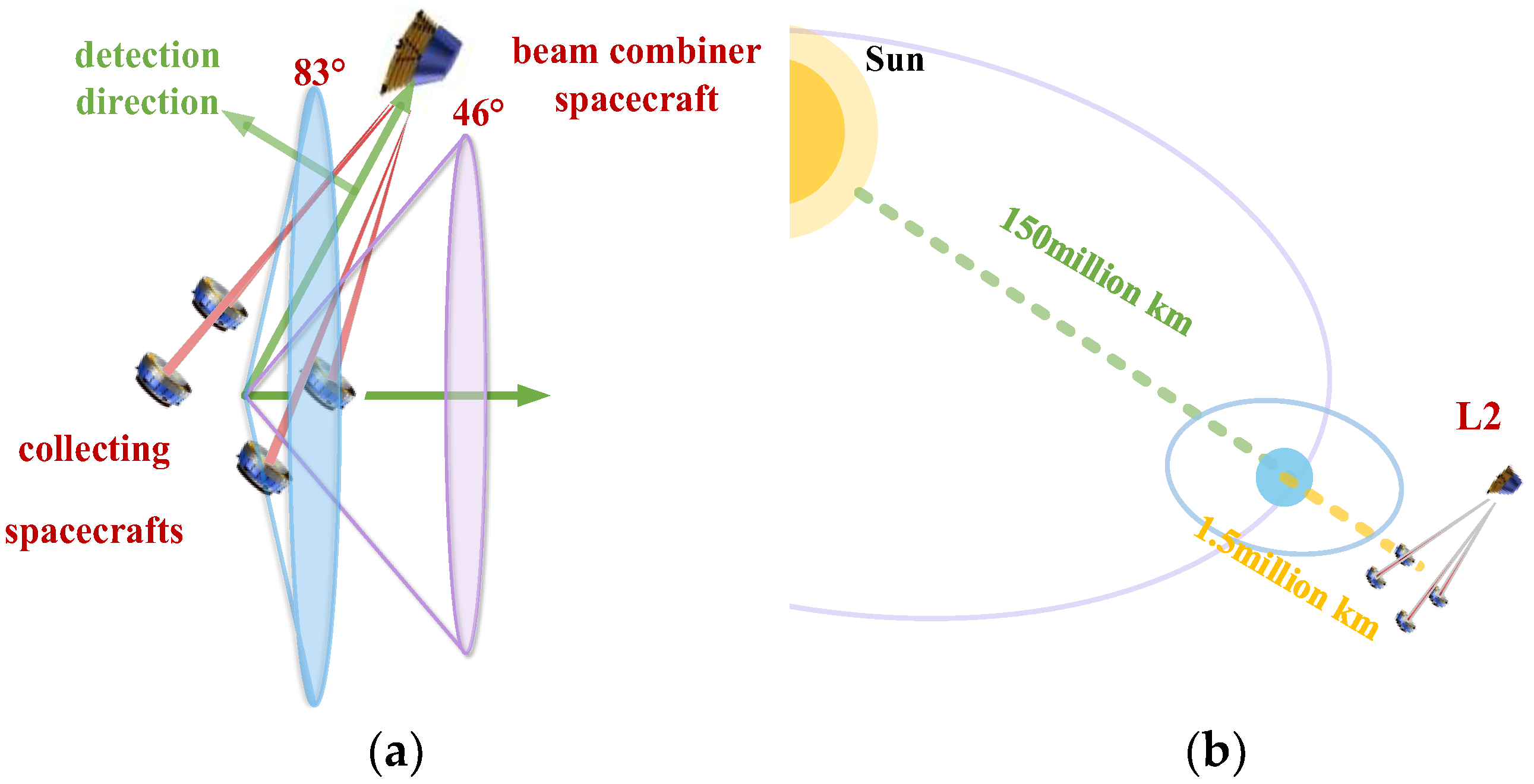
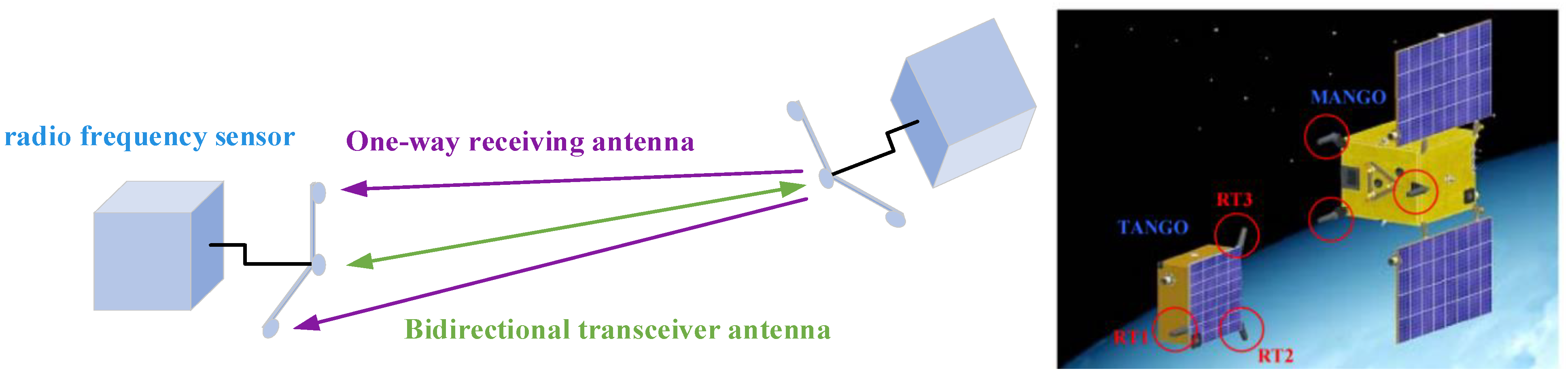
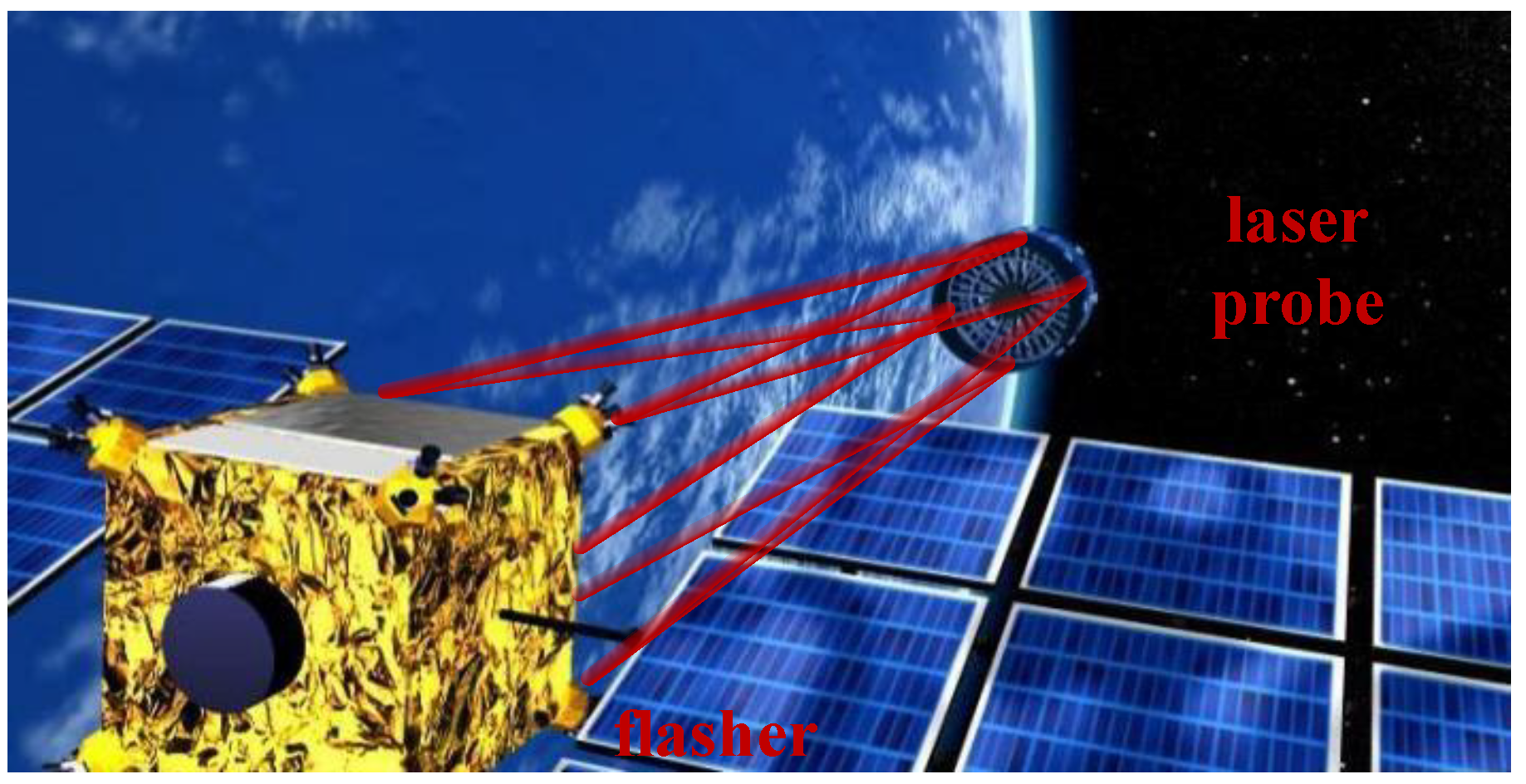
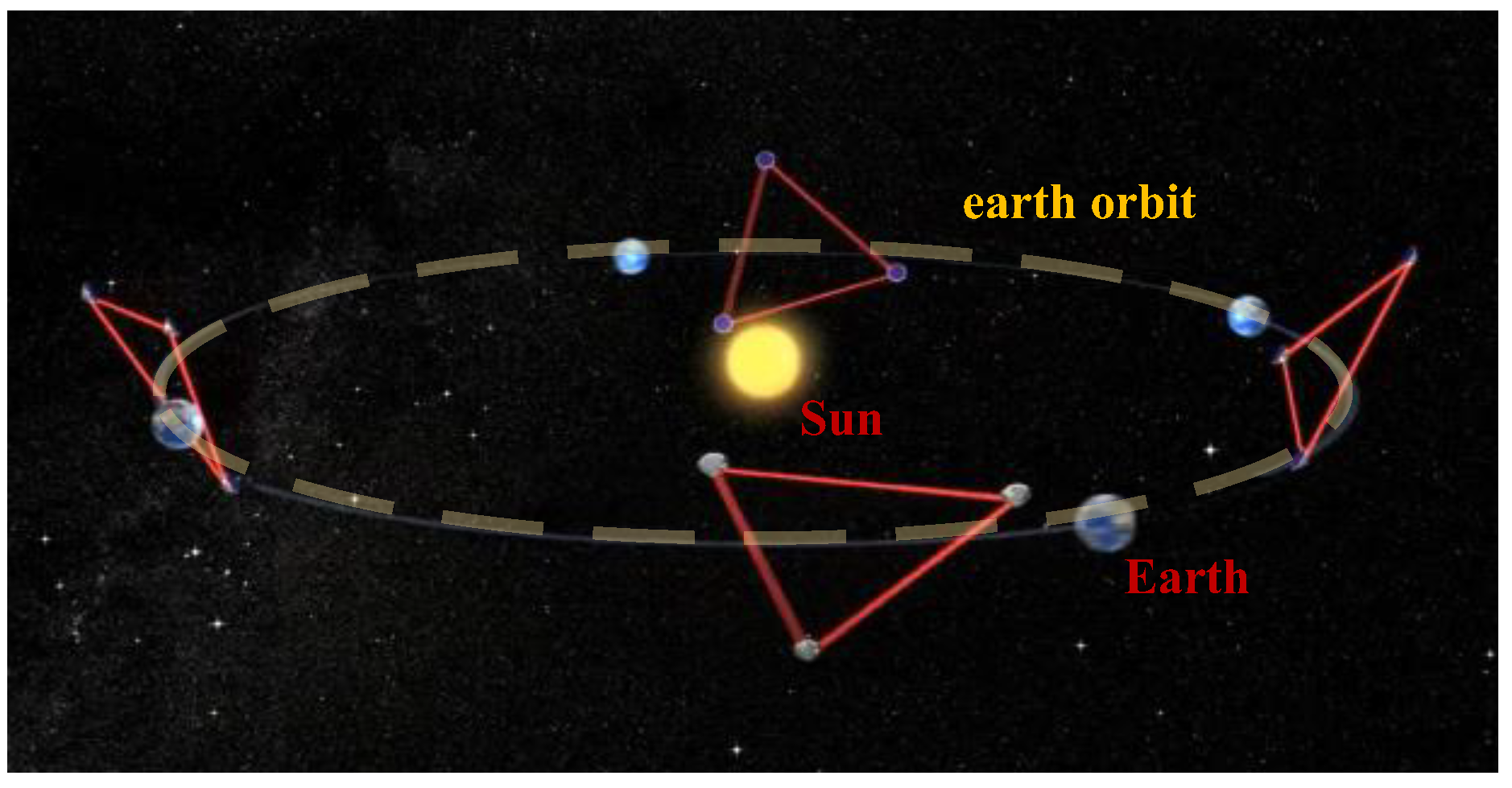

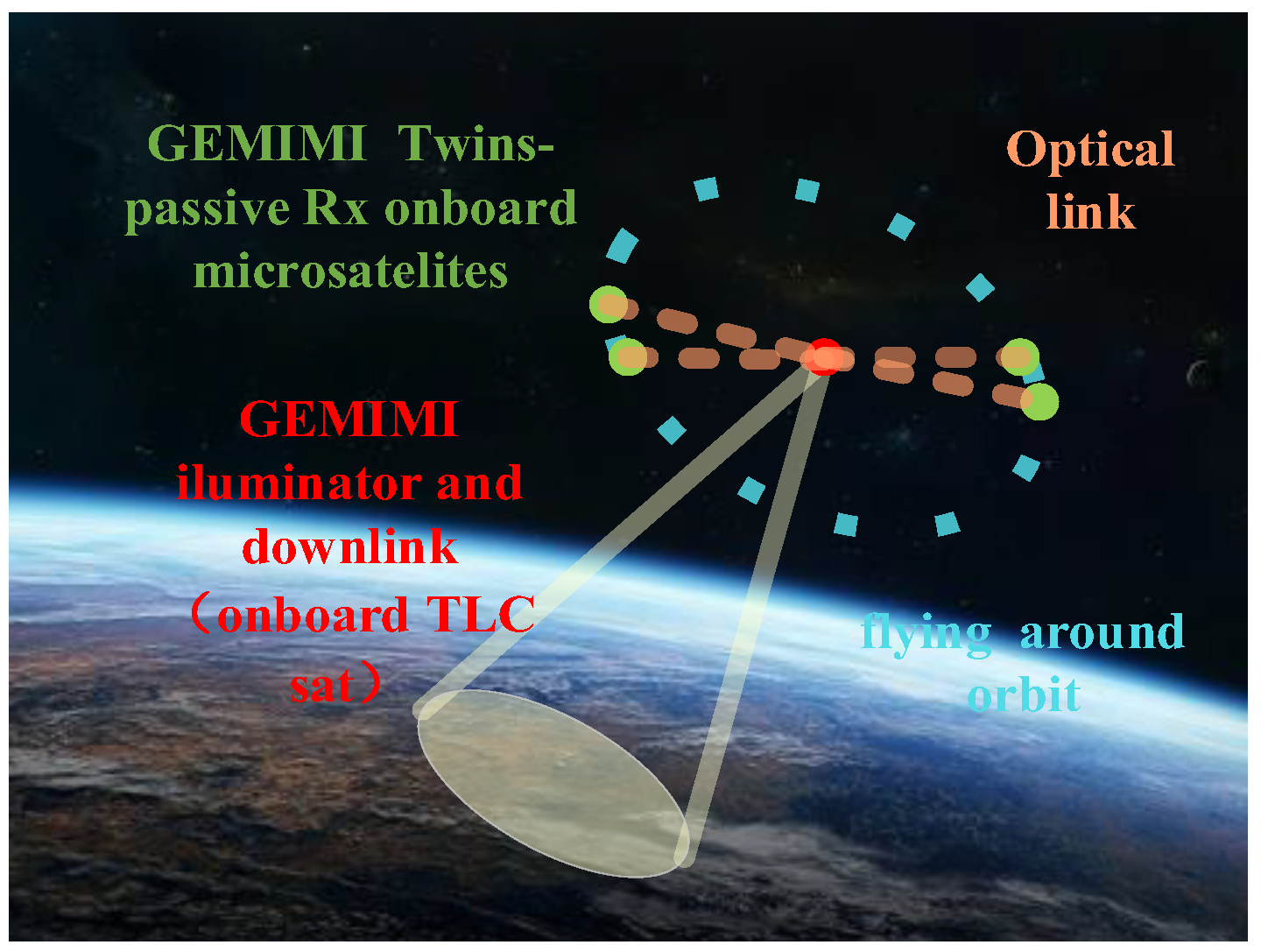
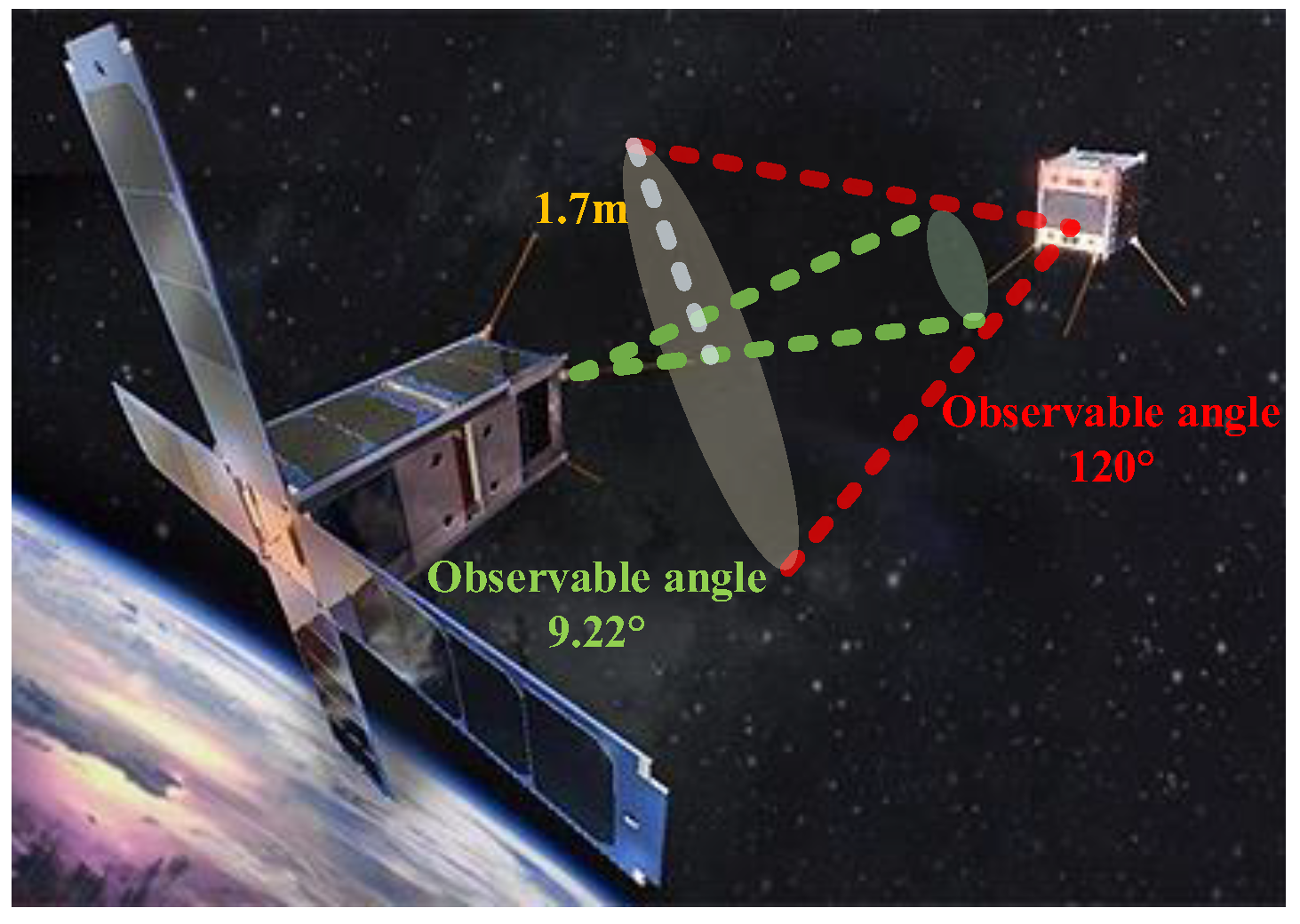
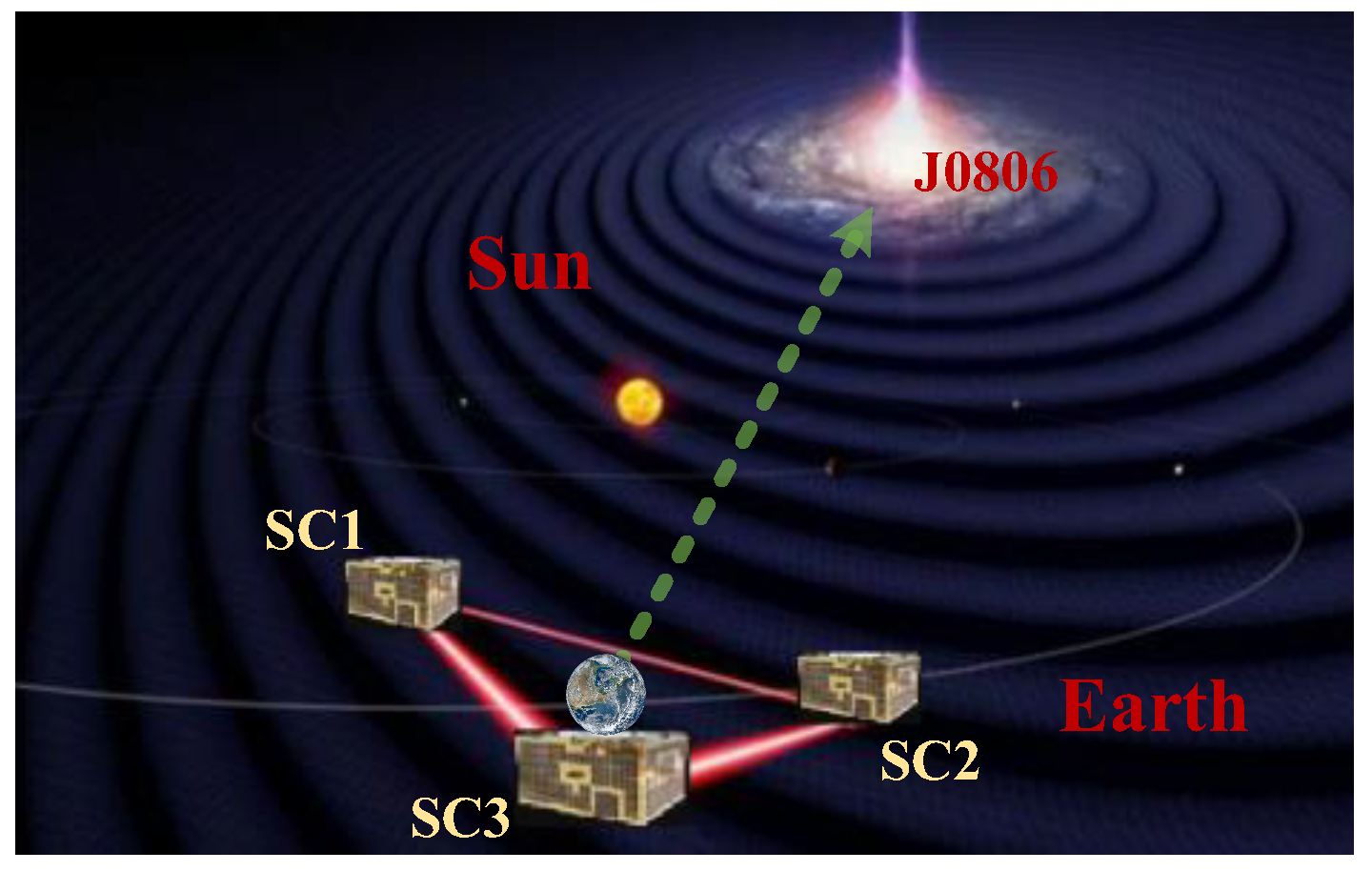

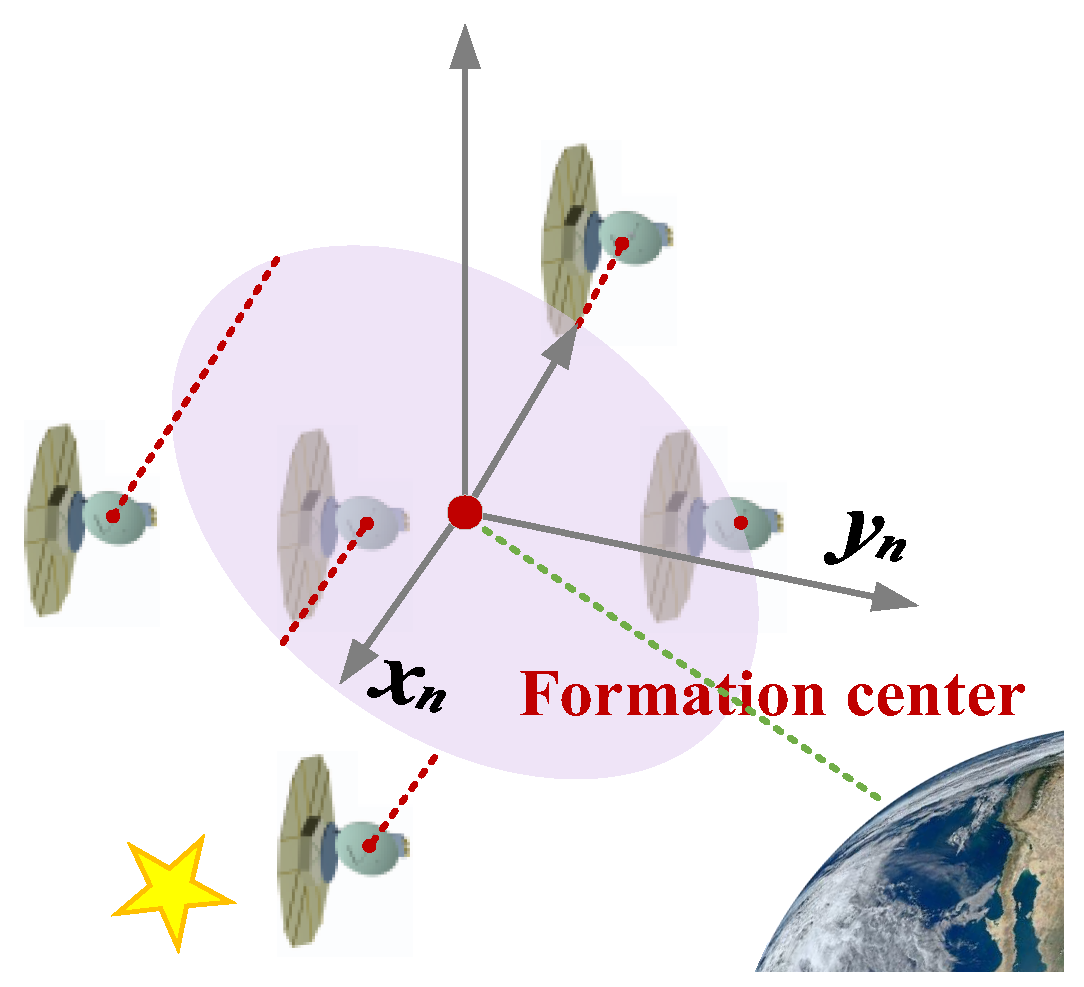







| Formation Flying Type | Mission | Technical Features | Control Precision |
|---|---|---|---|
| Precision Formation | Three-dimensional stereo imaging, virtual telescope, synthetic aperture radar, synthetic aperture optical interferometry, gravitational wave detection | Through autonomous navigation and precision control technology, precise shapes and poses can be maintained between spacecraft over time | Long-term continuous precision measurement control |
| Knowledge Formation | Ground-probing, Intermittent three-dimensional passive navigation | Mutual measurements exist between the spacecraft, but coupling control is not required | Independent control |
| Collaborative Formation | Rendezvous docking, twin formation flight and fly-around | Spacecraft maintain relative measurement and control for short periods of time during the mission | Precision measurement control stages |
| Validation Phase | Measurement Technology | Measurement Range |
|---|---|---|
| Autonomous Formation Flying | Phoenix-S GPS Receiver System Formation Flying Radio Frequency (FFRF) | 20 m~10 km |
| Homing and Rendezvous | Vision-Based Sensor (VBS) | 3 m~100 km |
| Precision Three-dimensional Proximity Operations | Phoenix-S GPS Receiver System Vision-Based Sensor (VBS) | 3~100 m |
| Final Approach and Recede Maneuvers | Vision-Based Sensor (VBS) | 0~3 m |
| Payloads | Measurement Accuracy | Function |
|---|---|---|
| K-band ranging system (KBR) | 1 μm/s | Measuring changes in the Earth’s gravity field |
| Super STAR accelerometer | 1 nm/s2 | Measuring non-gravity-induced acceleration |
| Star sensor | 0.1 mrad | Spacecraft altitude measurement |
| BLACKJACK GPS receiver | 1 mm | Spacecraft relative state determination |
| Laser backward reflector | 1 mm | Auxiliary GPS for precision orbiting |
| Methods | Item | Effective Range | Measurement Accuracy |
|---|---|---|---|
| GPS | Z distance | Perigee | 7.5 cm |
| Apogee | 10 cm | ||
| CLS | X-Y plane offset | 150 m | 1 mm |
| FLLS | Z distance | 25–250 m | 30 μm |
| X-Y plane offset | 20.5 mm | 21 μm |
| Formation Distance | Measurement Accuracy | Control Accuracy |
|---|---|---|
| >100 km | m | 10 m |
| >1 km | cm–dm | m |
| <1 km | mm | cm |
| Project | Country/ Institution | Methods | Modes | Measurement Items | Precision | Number | Whether Launch |
|---|---|---|---|---|---|---|---|
| Techsat-21 | USA | GPS | — | Inter-satellite baseline measurements | 1–10 cm | 8–16 | Canceled |
| TerraSAR-X TanDEM-X | Germany | Laser GPS | — | Inter-satellite baseline measurements | 2–4 mm | 2 | Launched June 2010 |
| PRISMA | Sweden | RF GPS | Rough mode | Z-direction distance (≤30 km) X-Y angle measurement (360°) | 10 cm|5° | 2 | Launched June 2010 |
| Precision mode | Z-direction distance (≤250 m) X-Y angle measurement (10 × 10°) | 1 cm|0.2° | |||||
| CanX-4/5 | Canada | GPS | — | Inter-satellite baseline measurements | Submeter-level | 2 | Launched June 2014 |
| GRACE-FO | USA(NASA) | RF GPS Laser | — | Inter-satellite baseline measurements | 100–10 nm | 2 | Launched May 2018 |
| CANYVAL-X | Korea | Visible light GPS | — | Direction distance X-Y angle measurement | Approximate dm level|1° | 2 | Launched December 2018 |
| TianQin | China | Laser Interference | — | Interferometric ranging | 3 | Partial launched | |
| TaiJi | China | Laser Interference | — | Interferometric ranging | 100 pm | 3 | Partial launched |
| XEUS | ESA | Laser GPS | — | Z-direction distance (40 cm + 1 m) X-Y surface offset (0 m + 1 m) Roll, pitch and yaw angle | 10 μm|125 μm 8″|1″ | 2 | No launch |
| Gemini | Germany | Laser GPS | Rough mode | Z-direction distance (>100 km) | m-level | 1 + 2 × n | No launch |
| Precision mode | Z-direction distance (>1 km) | cm-dm level | |||||
| Ultra-precision mode | Z-direction distance (<1 km) | mm-level | |||||
| Proba-3 | ESA | RF GPS Laser | Rough mode | Z-direction distance (Perigee) Z-direction distance (Apogee) | 7.5 m|10 m | 2 | No launch |
| Precision mode | Z-direction distance (25–250 m) X-Y surface offset (±13 m) X-Y surface offset (±20.5 mm) | 30 μm|1 mm|21 μm | |||||
| Darwin | ESA | Laser GPS | — | Inter-satellite baseline measurements | Submillimeter-level | 5 | No launch |
| LISA | USA (NASA) | Laser Interference | — | Interferometric ranging | 10 pm | 3 | No launch |
| IRASSI | Germany (DLR) | Laser GPS | — | Interferometric ranging Altitude measurement | <5 μm <0.4 arcsec | 5 | No launch |
| FOXST | China | Vision GPS | — | Distance measurement Altitude measurement | mm-level 0.1°-level | 2 × n | Under Study |
| Method | Technical Difficulty | Positioning Accuracy (m) | Scope of Action (km) | |
|---|---|---|---|---|
| Position Differential | Very easy | 10 | 100 | |
| Pseud orange differential | General pseudopitch differential | Easy | 5 | 100 |
| differential smooth pseudo distance of phase | General | 1 | 100 | |
| Wide area differential | Very difficult | 1 | 1000 | |
| Phase differential | Quasi-carrier phase differential | Difficulties | 0.5 | 50 |
| Carrier phase differential | Very difficult | 0.05 | 50 | |
| Project | Mode | Frequency Band | Accuracy | Dynamic Range | Effective Range |
|---|---|---|---|---|---|
| LISA | Outlier type | 0.1–100 mHz | 10 pm | ±12/4 MHz | 5 million km |
| GRACE Follow-on | Outlier type | 0.2–100 mHz | 80 nm | ±10 MHz | 220–270 km |
| Category | Advantages | Disadvantages |
|---|---|---|
| Monocular vision | Simple structure and small size | Lack of in-depth information |
| Stereo Vision | Acquisition of 3D information | Limited range and a complex algorithm |
| Scanning LiDAR | Easier calibration | Time-consuming |
| Flash LiDAR | Large detection distance range | Limited resolution and low accuracy at close range |
| TOF Camera | Low power consumption and compact design | Limited detection distance |
| Measurement Technology | Accuracy | Effective Range | Measurement Items | Advantages | Disadvantages | |
|---|---|---|---|---|---|---|
| GPS | Position difference | Positioning: 10 m magnitude | >100 km | Distance, Altitude | Simple equipment, mature technology | Limited continuous navigation capability, Limited accuracy |
| Pseudo-range difference | Positioning: m magnitude | <100 km | ||||
| Carrier phase difference | Positioning: dm magnitude | <50 km | ||||
| Radio Frequency (RF) | Positioning: cm magnitude altitude determination: <1° | >30 km | Distance, Altitude | Large coverage, communication without external signal assistance | Strong anti-electromagnetic interference | |
| Laser | Positioning: μm–nm magnitude altitude determination: <1″ | m–km | Distance, Altitude | High working frequency, high precision, anti-interference | Narrow beam, needs guidance | |
| Infrared | altitude determination: 1″ | >30 km | Altitude | Simple structure, small size, strong anti-interference | Only provides angular information | |
| Vision | Positioning: mm magnitude Altitude determination: 0.01° | <10 m | Distance, Altitude | Small equipment, simple structure | For close-range measurements only | |
| Visual Composite Measurement | Positioning: mm magnitude altitude determination: 0.01° | <500 m | Distance, Altitude | Small device size, high system robustness | Measurement accuracy decreases rapidly with increasing measurement distance | |
| Vision + RF | Positioning: cm magnitude altitude determination: 0.0001° | 50 km | Distance, Altitude | No Earth-visible arc limit | Limited precision | |
| GPS + RF | Positioning: micron magnitude | >30 km | Distance, Altitude | Improved GPS continuity and navigation initialization process | Composite measurements require consideration of satellite platform volume, mass, resource consumption, etc. | |
| GPS + Laser | Positioning: cm–μm magnitude altitude determination < 0.001° (10 km) | <200 km | Distance, Altitude | Improves GPS accuracy and system robustness | - | |
| GPS + Visual | Positioning: <2 mm altitude determination: < 0.05° | 5 km | Distance, Altitude | Improves GPS robustness, improving the reliability of high-orbit navigation | - | |
| Laser + RF | Laser measurement magnitude | Laser Range | Distance, Altitude | Improves effective range while maintaining precision measurement | - | |
| Laser + Infrared | Laser measurement magnitude | Laser Range | Distance, Altitude | Improves search capability and altitude measurement accuracy | - | |
| Laser Multi-Guidance | Laser measurement magnitude | Laser Range | Distance, Altitude | Increased guidance speed, high robustness and accelerated measurement process | - | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Deng, L.; Feng, J.; Chang, L.; Li, D.; Qin, Y. A Survey of Precision Formation Relative State Measurement Technology for Distributed Spacecraft. Aerospace 2022, 9, 362. https://doi.org/10.3390/aerospace9070362
Zhang Z, Deng L, Feng J, Chang L, Li D, Qin Y. A Survey of Precision Formation Relative State Measurement Technology for Distributed Spacecraft. Aerospace. 2022; 9(7):362. https://doi.org/10.3390/aerospace9070362
Chicago/Turabian StyleZhang, Zhang, Lei Deng, Jiaqi Feng, Liang Chang, Dong Li, and Yilin Qin. 2022. "A Survey of Precision Formation Relative State Measurement Technology for Distributed Spacecraft" Aerospace 9, no. 7: 362. https://doi.org/10.3390/aerospace9070362
APA StyleZhang, Z., Deng, L., Feng, J., Chang, L., Li, D., & Qin, Y. (2022). A Survey of Precision Formation Relative State Measurement Technology for Distributed Spacecraft. Aerospace, 9(7), 362. https://doi.org/10.3390/aerospace9070362





