Abstract
With space technology development, the spatial robotic arm plays an increasingly important role in space activities. Spatial robotic arms can effectively replace humans to complete in-orbit service tasks. The trajectory planning is the basis of robotic arm motion. Its merit has an essential impact on the quality of the completed operation. The research on spatial robotic arm trajectory planning has not yet formed a broad framework categorization, so it is necessary to analyze and deeply summarize the existing research systematically. This paper introduces the current situation of space obstacle avoidance trajectory planning and motion trajectory planning. It discusses the basic principle and practical application of the spatial robotic arm trajectory planning method. The future development trend has also been prospected.
1. Introduction
As humans explore the space domain, space robots or robotic arms gradually become the ultimate solution for various in-orbit missions. Spacecrafts working in orbit need space in-orbit services to help them with maintenance, resupply, assembly, and cleanup [1]. Space technology has always been essential for space robotics as a critical technology for missions in orbit. The use of space robotic arms to replace astronauts in space has become a new trend. The development and application of space robotic arms are of great importance for further human exploration and research in space and bring great value to some aspects, such as the safety and economy of space exploration in countries around the world [2]. The literature [3] summarized the history of successful robot manipulators such as the Shuttle Remote Manipulator System (SRMS) and Space Station Remote Manipulator System (SSRMS). It includes the most famous Canadian arm, Canadarm2, the Japanese Experiment Module (JEM) Remote Manipulator System, and the European Robotic Arm (ERA). In addition, space robotic arm applications include Japan’s first experimental space robot project, Manipulator Flight Demonstration (MFD). Several German space robotic arm projects: Robotic Technology Experiment (ROTEX) [4], Robotics Component Verification on International Space Station (ROKVISS) [5], and Technology Satellite for Demonstration and Validation of Space Systems (TECSAS) [6]. China configured a large robotic arm in the core module of the space station “TIANHE”, named “TIANHE Robotic Arm” [7]. Figure 1 shows the research and application of robotic arms in the space station in the world.
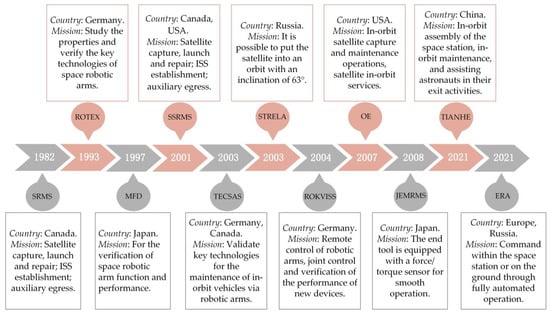
Figure 1.
International Space Station robotic arm research and application.
Trajectory planning is the basis for controlling the motion of the robotic arm, and the merit of trajectory has an essential impact on the quality of the completed operation. Meanwhile, trajectory planning, as a prerequisite for trajectory tracking control, affects the accuracy of robot trajectory tracking control [8,9]. Its performance impacts the motion efficiency, smoothness of motion, and server energy consumption [10]. In the context of modern artificial intelligence research, planning is a process of problem-solving. It starts from the initial of a particular problem and constructs a series of operational steps (operators) to bring it to the goal of solving that problem. The flow chart of trajectory planning in the mission planner is shown in Figure 2. Different trajectory planning tasks need to be performed for the on-orbit robotic arm for different on-orbit operation requirements. To make the end of the robotic arm reach the specified position to complete a specific task, the desired trajectory needs to be planned according to the constraints, i.e., trajectory planning of the robotic arm [11,12]. Nowadays, most scientists would imagine a combined human and robot joint activation in the future, fully exploiting the advantages of both. In this regard, automation and robotics play a vital role in space exploration and ground-based experiments. The development and evolution of complex spacecraft and space exploration missions require the rapid development of intelligent automation systems and robotic equipment [13]. The tasks of space robotic arms include some special space missions in addition to the traditional assembly and repair, such as orbital robots, planetary geological reconnaissance missions [14], and surgical robots for space missions [15]. The special extreme environmental conditions and the extremely high requirements for micro-manipulation make it increasingly important to plan the trajectory of the robotic arm for its manipulation.
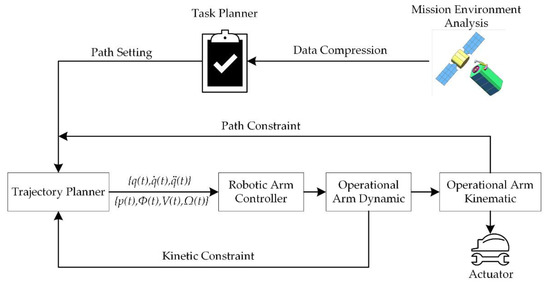
Figure 2.
Diagram of the robotic arm tasks planning.
This paper discusses the basic principles and practical applications of space robotic arm trajectory planning based on the requirements of space robotic arm trajectories, obstacle avoidance, and motion planning. The advantages and shortcomings of the existing trajectory methods are summarized in detail, and the future development trend of space robotic arm trajectory planning is conceived and foreseen. Section 2 describes the obstacle avoidance detection and planning of space robotic arms from the requirement of obstacle avoidance. Section 3 focuses on the current research status of existing space robotic arm motion trajectory planning methods and introduces in detail the basic principle of polynomial interpolation and the gradual application status of modern intelligent trajectory planning methods. Section 4 concludes the article and gives an outlook on future development.
2. Spatial Robotic Arms Trajectory Planning Methods Based on Obstacle Avoidance Requirements
The most significant difference between the space robotic arm and the ground robotic arm is that the base is floating. Since the base of the space arm is not fixed, the base position is not controlled in the free-floating mode of operation, so the linear momentum and angular momentum of the whole robotic arm system are conserved. There is a non-integrity limitation in the robotic arm system, resulting in kinematic and dynamical coupling between the robotic arm and the base during the motion [16]. When planning the motion of the robotic arm, it is necessary to avoid obstacles and reach the target position while satisfying the dynamics of the multi-body dynamics system and the non-complete constraints. The study of obstacle avoidance trajectory planning for free-floating space robot arms is divided into spatial obstacle detection and obstacle avoidance trajectory planning.
2.1. Spatial Obstacle Detection Methods
Usually, the collision detection of space robotic arm with obstacles uses collision of space objects and graphics as the main method. Generally, the space obstacle is represented by the commonly used space specification geometry. Whether the geometry is properly represented determines whether the motion space of the robotic arm can be found in the presence of the obstacle. There are various methods for obstacle detection. The obstacles encountered by the space robotic arm system when performing in-orbit service missions can be divided into two categories. One category is obstacles that are stationary with respect to the space base, and such obstacles include the service satellite and the target satellite. The other category is obstacles in motion with respect to the space base, which includes moving parts on the service satellites and target satellites, and space debris [17]. The application of collision detection algorithms on robotic arms is mainly dynamic collision detection, which is used to detect the relative positions of obstacles and robotic arms. The discrete collision detection algorithm in dynamic detection is to analyze whether a collision occurs in discrete time. The random sampling in the path algorithm mainly considers the collision detection information under the deterministic state point. Therefore, the collision detection of the robot arm uses a discrete collision detection algorithm [18,19].
The discrete collision detection algorithm is the most commonly used dynamic collision detection algorithm. After continuous research and breakthroughs, many feasible collision detection algorithms have been formed, among which the widely used one is the hierarchical wraparound box algorithm [20]. The theory of the envelope box technique is to enclose the complex collection of targets with simple geometry and then construct a tree-like geometry structure to achieve the goal [21]. The main focus of this class of methods is the selection of bracketing boxes. The main bracketing boxes are bracketing sphere, axis-aligned bounding box (AABB), oriented bounding box (OBB), and fixed directions hulls (FDH).
An AABB is defined as the smallest hexahedron that contains the object and whose sides are parallel to the coordinate axes. Therefore, to describe an AABB, only six scalars are needed. The AABB is relatively simple to construct, with small storage space, but poorly compact, especially for irregular geometries, with large redundancy space. It deals with objects that are rigid and convex and is not suitable for complex virtual environment situations that contain soft body deformations. The AABB intersection test is widely used due to its simplicity and better tightness and can also be used for collision detection of soft objects [22]. The enclosing sphere is defined as the smallest sphere that contains the object. To determine the enclosing sphere, the mean values of the x, y, and z coordinates of the vertices of all elements in the set of elementary geometric elements that make up the object are calculated separately to determine the center of the enclosing sphere. Then, the radius r is determined from the distance between the center of the sphere and the point determined by the three maximum coordinates. Collision detection of the enclosing sphere is mainly a comparison of the magnitude of the radius and the distance from the center of the sphere between the two spheres. The enclosing sphere is very similar to the AABB enclosing box, which is simple but still less compact [23]. OBB is the smallest rectangle containing the object with arbitrary orientation with respect to the coordinate axes. The most important feature of OBB is its arbitrary orientation, which allows it to enclose the object as closely as possible according to the shape of the enclosed object. The OBB enclosing box approximates the object more closely than the AABB enclosing box and the enclosing sphere, which can significantly reduce the number of enclosing bodies and thus avoid intersection detection between a large number of enclosed bodies. However, intersection detection between OBBs is more time-consuming than that between AABBs or enclosing spheres. The FDH (or k-DOP) is a special kind of convex package. It inherits the simplicity of AABB, but for it to have good spatial tightness, it must use a sufficient number of fixed directions. The FDH is defined as a convex package that contains the object and the normal vectors of all its faces are taken from a fixed set of directions (k vectors). The FDH encloses the original object more tightly than other enclosing bodies and creates a hierarchical tree with fewer nodes, which reduces more redundant computations when intersection detection is performed, but the intersection operations are more complex with each other [24].
Menasri et al. [25] used spheres for obstacle modeling in robot workspaces, as shown in Figure 3. The idea behind this representation is that the obstacle having any form is shrouded by the smallest hyper-surface which includes all points of the obstacle. This method is also applicable to space robotic arm obstacle detection. Hou [26] and Zhu et al. [27] transformed the obstacles into joint space. They simplified the occupation relationship between the obstacle and the free-floating space robotic arm based on the idea of a spherical enclosing box and spatial superposition. The simplified approach views the collision detection of the robotic arm with a circle as the intersection detection of a line segment with a circle. The method largely simplifies the computation and improves the planning efficiency. Han et al. [28] designed an innovative “sphere and ellipsoid” model to ensure a safe distance for ultra-short orbital approaches. The exclusion zone and limits were designed according to the satellite sphere envelope to keep the whole spacecraft away from any collision threat. Li et al. [29] established the OBB bounding box model for trajectory planning of the robotic arm in the confined environment of the space station experiment box [30]. Figure 4 shows the projection of the mobile manipulator and the obstacles in the experiment. This method is highly efficient in planning routes according to the complexity of the obstacle envelope. Zhang et al. [31] used a convex polyhedral vector inner product detection algorithm for redundant spatial robotic arms to perform a trial search for obstacle avoidance. They use three levels of collision detection problems for robot arm motion, robot arm configuration, and robot arm upper point, respectively. The method consists of the starting configuration moving continuously toward the target configuration according to a certain pattern. If a collision occurs during the movement, the direction of advance is adjusted until a path is found that does not collide with the obstacle. In this way, instead of solving the entire configuration space, only collision detection is required. Wang et al. [32] replace the convex obstacle with a convex polyhedral envelope and non-convex obstacles with multiple convex polyhedral envelopes. The robotic arm is then discretized, and a sufficient number of detection points are selected, which in turn detects whether each point is within the obstacle envelope. A point is selected on each face of the convex polyhedron, and then the inner product of the vector pointing from the point to be detected and the outer normal vector of that face of the convex polyhedron is calculated. If such inner product is positive for all faces of the convex polyhedron, the point to be detected is inside the convex polyhedron. As long as there exists a point to be detected that is inside one of the convex polyhedra, the point to be detected is considered to be inside the obstacle.
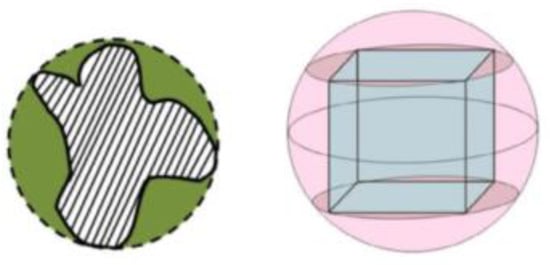
Figure 3.
Obstacles modeling representation in 2D and 3D space.
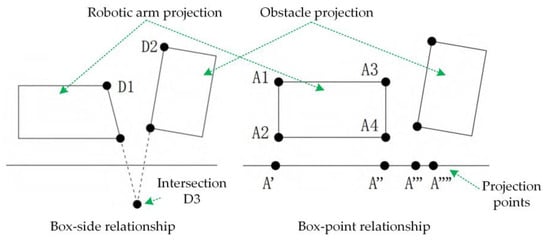
Figure 4.
Projection of the robotic arm and obstacle.
2.2. Spatial Robotic Arms Obstacle Avoidance Trajectory Planning Methods
At the beginning of the collision avoidance study, a hypothesis and test method based on the right-angle coordinate space is mainly used. First of all, it needs to assume that there is a path connecting the initial point and the target point. Then, the path is discrete, and then check whether each discrete interval is a free path (no interference with obstacles). If yes, the collision avoidance path planning is completed. Otherwise, the interfering units are modified and adjusted until they satisfy collision avoidance [33]. Huang et al. [34] considered the obstacle avoidance case and combined the constraints such as dynamics and paths for trajectory planning. Finally, the continuous optimal control problem is discrete transformed using the Gauss Pseudospectral Method (GPM), and the transformed nonlinear planning problem is solved to derive the optimal path.
The hypothesis testing method is relatively simple, but the real-time performance is poor, and the path cannot be optimized by time or energy index. Therefore, the collision penalty function method based on the right-angle coordinate space appears. This method first defines a penalty function for the obstacles, which decreases rapidly as the distance between obstacles increases. Moreover, a penalty term is added to the deviation from the shortest path. The penalty function value for each obstacle is added together, and the total penalty function value can be calculated. This method is very suitable for the collision avoidance planning of mobile robotic arms. Kang et al. [35] modified the traditional impulse obstacle avoidance algorithm for spacecraft trajectory planning applications with a strong dependence on transient thrust and high fuel consumption by using an energy optimal dynamic obstacle avoidance algorithm. They introduced the motion error offset of dynamic obstacles with normal distribution probability into the collision avoidance safety distance model to enhance the reliability of obstacle avoidance.
The main collision-free trajectory planning algorithms widely used for robotic arms are the pseudo-inverse algorithm, the artificial potential field method, the C-space method, the algorithm and the rapid-exploration random tree (RRT) algorithm [36]. The pseudo-inverse algorithm uses the pseudo-inverse of the Jacobi matrix to obtain the joint angular velocity and the null space projection to obtain the chi-solution to avoid obstacles [37]. Pseudo-inverse type methods [38] have been extensively studied in the last decades. These methods generally represent the solution as the sum of the least parametric particular solution and the chi-square solution and require solving the pseudo-inverse of the Jacobi matrix associated with the positive kinematics of the robot arm. The limitations of the pseudo-inverse type methods include the difficulty in handling the joint constraints and the computational intensity in performing the pseudo-inverse [39]. Pisculli et al. [40] proposed a minimal state variable approach to describe the dynamics of a free-floating space manipulator (FFSM) under the action of gravity and gravitational gradient forces. They used a combination of reaction zeros and Jacobi transpose controllers to implement the control and explored the advantages and disadvantages of the method. Sabatini et al. [41] performed an experimental campaign using an air-floating table and a free-floating platform to simulate the spatial manipulator used in the pursuer platform. They adjusted the gain mainly by the distance between the target and the tracker. The method is similar to Jacobi pseudo-inverse control but is only used to manipulate the robotic system.
To overcome the drawbacks of pseudo-inverse type methods, quadratic programming (QP) methods have been developed and widely studied [42]. Stolfi et al. [43], to absorb the impact energy, described the space manipulator end-effector as a mass-spring-damping system without considering the base reaction force, as shown in Figure 5. Tringali et al. [44] based on the optimization of the kinetic energy integral over a finite subset of the future end-effector path points so that the manipulator’s joints move towards the minimum kinetic energy. Their proposed method outperforms the pseudo-inverse-based method. Li et al. [45] proposed a trajectory optimization method that considers frictional contact. The method combines a direct approach to trajectory optimization with a contact model based on complementary constraints in nonlinear programming. The resulting optimization problem is solved by a combined mechanism of sequential quadratic programming. The method allows optimization of spatial robot trajectories satisfying contact constraints without requiring prior knowledge of the contact sequence. Locally optimal trajectories are successfully found in different cases. The method will greatly extend the deceleration, capture, and manipulation strategies of space robots. Lu et al. [46] considered end-effector trajectory tracking constraints and joint angle/velocity/acceleration constraints in the trajectory planning problem of the FFSM model. The trajectory planning problem can be further formulated as a constrained convex quadratic programming problem. They avoid the dynamic singularity of the FFSM based on the obtained optimization algorithm. For the SSRMS configuration robotic arm widely used in space in-orbit services, an inverse kinematic solution method based on the combination of cyclic coordinate descent method and joint angle parameterization method (CCDJAP-IK) is proposed in the literature, which reduces the blindness of parameter taking and increases the success rate of the solution [47].
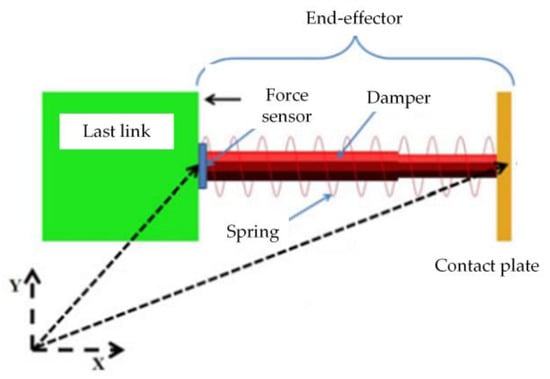
Figure 5.
Schematic diagram of end-effector structure.
Subsequently, Khatib [48] introduced the concept of artificial potential field based on the penalty function method. The artificial potential field method (APF) means that the obstacle is surrounded by a repulsive potential field and a gravitational potential field surrounds the target. The repulsive force increases rapidly with the decrease of the distance between the robotic arm linkage and the obstacle, and the attractive force decreases with the approach of the end and the target posture. Then, selected test points on the robotic arm linkage are solved in real-time for the repulsive potential with each obstacle and the attractive potential with the target. Zhan et al. [49] proposed an accelerated potential field (AccPF) method to plan the tumbling velocity trajectory of a spatial manipulator to eliminate the perturbation of non-cooperative targets. Their attractive potential field eliminates the initial momentum, while the repulsive potential field forces the manipulator away from the obstacle. Gao et al. [50] proposed a fast exploration random tree optimization algorithm based on obstacle avoidance independent potential field guidance for a space robot robotic arm. Some responding layer factors related to operational cost are used as optimization objectives to improve operational reliability. On this basis, a potential field whose gradient is calculated off-line is established to guide the expansion of rapidly exploring the random trees. The potential field mainly considers indexes about the manipulator itself, such as the minimum singular value of the Jacobian matrix, manipulability, condition number, and joint limits of a manipulator. Thus, it can stay the same for different obstacle avoidance path planning tasks.
The artificial potential field method is considered for obstacle avoidance, the gravitational potential field acts in a larger range. In contrast, the repulsive potential field only acts in a local range, and the region far from the obstacle is not affected by the obstacle repulsive potential field. Therefore, this method is also called the local method, which only solves the local space within the obstacle avoidance. However, it is very widely used due to its ease of mathematical description and its applicability to multi-degree-of-freedom robotic arms.
In the early 1980s, Lozano-Perez [51] proposed a C-space-based free-space method, which many scholars affirmed. The robot’s motion is described by the C-space, at this time, the state of the robot forms a one-to-one correspondence with C-space. Suppose the obstacles are also described by a C-space and all obstacles are mapped to the C-space. In that case, the problem of collision-free path planning is transformed into finding a free region in C-space connecting the start point and the target point, as shown in Figure 6. When the robot moves along this path, it can guarantee no collision with obstacles. Existing collision-free trajectory planning algorithms need to obtain C-space obstacle boundaries. Obstacles of the workspace are generally hypersurfaces in the C-space. When applying planning in a C-space, the obstacles in the robot’s workspace are generally described mathematically in C-space.
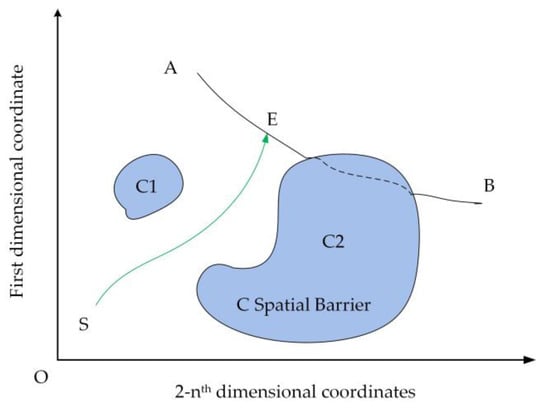
Figure 6.
Robot arm C-spatial trajectory planning schematic.
The obstacle is represented in the robot’s configuration space as:
where denotes the relationship between the robot and the joint variable . When , then the robot interferes with the obstacle .
Maciejewski et al. [52] proposed a path planning method based on C-space topology. Some special points and lines in the obstacles are mapped into the C-space. The obstacle avoidance path planning problem is transformed into finding the connection channel connecting the initial position subspace and the target position subspace on the connectivity graph. Kondo [53] proposed a two-way heuristic search method, which features a direct graph search method in the C-space to search out the free path in both directions from the initial and target points. This method can effectively avoid solving the whole C-space information.
The traditional algorithm is a trajectory planning method that searches optimally way for nodes and points other than nodes [54]. However, the traditional algorithm does not take into account the situation when passing the vertices of the obstacles during the search process to avoid them, which can easily cause unsafe factors. Therefore, Chen et al. [55] further proposed a new fault-tolerant workspace with a load-carrying capacity (FTWLCC) concept to evaluate the fault-tolerance performance and improve the classical algorithm to search feasible task trajectories according to the requirements of load-carrying tasks. Guo et al. [56] proposed a global and local fusion path planning method for planetary exploration. First, an integrated smoothness map was generated based on the digital elevation model (DEM) of the planetary surface, and then a fused path planning method was proposed that combines the improved algorithm and the dynamic window method [57]. A heuristic function was designed based on the integrated smoothness information to guide the algorithm to generate the globally optimal path. The dynamic window method is applied for real-time path planning to generate smooth paths that satisfy the planetary rover capability constraint, which improves the success and reliability of planetary exploration missions.
Moreover, since the RRT algorithm does not require an explicit obstacle representation, it is widely used in various motion planning tasks [58], such as space obstacle avoidance detection tasks. Rybus et al. [59] used the RRT algorithm to plan a collision-free manipulator trajectory. The bi-directional approach is used in the construction of the tree in order to plan a trajectory from the given initial state to the specific final state. The feasibility of the proposed method was also demonstrated in a numerical simulation of a chaser satellite equipped with a 2-DOF (degree of freedom) manipulator in the planar case. Their improvements include reducing the number of dimensions of the state space to simplify the tree construction. A new method is used to select control signals during tree construction to obtain better state-space coverage. Numerical simulations performed in a simplified planar case validate the proposed trajectory planning method. James et al. [60] integrated the RRT method and a new time-scale transformation method to obtain the desired joint trajectory, thus reducing the spacecraft attitude perturbations and satisfying the corresponding state constraints. Guan et al. [61] proposed an improved RRT algorithm. If the accuracy of the target motion state estimation is not high enough, this improved RRT algorithm can be used to plan a safe trajectory. Yan [62] proposed an RRT optimization strategy combined with a probabilistic artificial potential field method for the spatial robotic arm path replanning task with variable task objectives so that the robotic arm can adapt to the changes in task environment and objectives when performing sampling tasks.
In summary, the current status of space robotic arm trajectory planning research based on obstacle avoidance requirements is summarized in Table 1.

Table 1.
Summary of spatial robotic arm obstacle avoidance planning study.
3. Spatial Robotic Arms Trajectory Planning Methods Based on Motion Requirements
3.1. Research on Basic Spatial Trajectory Planning Methods
The basic spatial trajectory planning of a spatial robotic arm can be divided into two categories. One is joint space planning, which generates motion trajectories based on the changes of each joint angle, angular velocity, and angular acceleration of the robotic arm in the process of calculating the end from the initial position to the target position; the other is cartesian space trajectory planning, which is a path generation method selected according to the task requirements [63]. A comparison of their performance characteristics is shown in Table 2.

Table 2.
The comparison of spatial robotic arm trajectory planning performance characteristics.
The common point between the two types of planning approaches is that both need to satisfy velocity and acceleration continuity and ensure smooth trajectory. For joint space planning, such as the determination of position during docking and separation of spacecraft in orbit, truss handling work in the orbit, and other tasks. It needs to describe its starting and target states, i.e., the starting value and target value of the coordinate tool system, also called the motion at this time as point-to-point motion. For the cartesian space trajectory planning operations, such as the robotic arm in orbit maintenance tasks, surface machining tasks, and in-orbit assembly. The task’s realization requires specifying the start and abort points of the actuator and specifying the number of points between the two points, which become path points. It must be made possible to move along a specific path, which becomes continuous path motion or contour motion. The joint space trajectory planning directly plans the motion of a joint, which needs to be solved as a function of joint angle, angular velocity, angular acceleration, and time, while planning the motion trajectory of an end-effector is part of cartesian space trajectory planning. Among them, the concept of trajectory planning in the operation space is intuitive but requires a large number of matrix calculations. Moreover, the parameters in operation space are difficult to obtain directly through sensors, which is difficult to use for real-time control. The trajectory planning in the joint space can adjust the position, angular velocity, and angular acceleration of each joint of the robot arm in time according to the design requirements, which can effectively avoid the problems of mechanism singularity and redundancy of the robot arm. Therefore, joint space trajectory planning is widely used.
The joint space trajectory planning is to describe the joint angle value as a function of time without describing the path between two points in the operation space, which is less computational. There are mainly polynomial interpolation methods and spline interpolation methods for joint space trajectory planning [68]. The cubic spline function interpolation method is easy to understand, simple to use, and can ensure the continuity of velocity and acceleration during the motion. Locked joint failures are inevitable for space robotic arms in non-stop load tasks, so optimization of joint parameters is particularly important. Joint spatial trajectories are mostly parameterized by higher-order polynomials, and the free parameters are optimized by sequential quadratic programming. Tortopidis et al. [69] studied the incomplete behavior of a spatial manipulator actuator in free-floating mode. They used higher-order polynomials as parameters of the cosine function to specify the desired path directly in the joint space. The accessibility of the configuration was extended. An et al. [70] studied the joint trajectory planning of a modular reconfigurable satellite in space, and they proposed a virtual joint coordinate system, as shown in Figure 7. The D-H method based on the virtual joint coordinate system can effectively solve the problem of space orientation asymmetry of reconfigurable joints axis on both sides of the base coordinate system of SMRS. The joint trajectories of the modular reconfigurable satellite are parameterized by using sixth- and seventh-order polynomial curves to ensure the continuity of position, velocity, and acceleration of the joint motion. Cui et al. [71] used 5th and 6th order polynomial interpolation to approximate the trajectory of the joint motion of the free-floating space robot and used sequential quadratic programming to optimally solve the trajectory of the joint hinge motion. The computed trajectories of each joint hinge and control inputs are continuous and smooth by numerical simulation. The planning method has good convergence, high computational efficiency and strong boundary search capability, which are the most outstanding advantages compared with other optimization algorithms. Papadopoulos et al. [72] used smooth continuous functions, such as polynomials, to drive the system to the desired configuration in a finite and prescribed time. Limitations on reaching arbitrary final configurations were discussed and examples were presented.
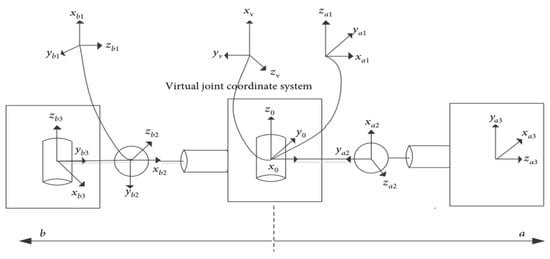
Figure 7.
Virtual coordinate system of SMRS.
Additionally, in the context of the enhanced real-time problem, Misra et al. [73] investigated point-to-point trajectory planning in sequential convex planning (SCP) framework, culminating in an expression for the end-effector positional constraints and their subsequent convex relaxation. Xin et al. [74] generated joint rotation trajectories based on cosine functions through inverse kinematic theory. The rotation trajectories were subsequently discretized to achieve minimum residual vibration suppression for the space manipulator.
For simple point-to-point motions, the polynomial interpolation algorithm satisfies the basic requirements of the trajectory. However, for higher accuracy as well as smoothness requirements, improved planning algorithms are required. The main methods used are B spline curves and non-uniform rational B-splines (NURBS) [75]. B spline curves are parametric curve representations, which are generalizations of Bezier curves and are capable of local modifications, which are important for multi-segment trajectory planning [76]. According to the nodal vector distribution, B spline curves are classified as uniform, quasi-uniform, and nonuniform B spline curves. Quasi-uniform B spline curves retain the properties of Bezier curves and ensure that the first and last points pass through the control vertices, which can be used for point-to-point trajectory planning in joint space. The nonuniform B-sample curve is not equally distributed among control points and can be distributed arbitrarily, which brings convenience to the free variation of trajectories [77]. NURBS curve is also called the nonuniform rational B-sample curve. Node vectors of the NURBS spline function are non-uniformly distributed along the parameter axis, forming different basis functions, and the basis function weight factor is added to the algorithm. The added weight factor reflects the degree of influence of the nodes on the trajectory and is used to change the contribution of the control vertices to the trajectory [78]. Wang et al. [79] presented an optimal joint trajectory planning method using forward kinematics equations of free-floating space robots, while joint motion laws were delineated with the application of the concept of reaction null-space. Bézier curves, in conjunction with the null-space column vectors, were applied to describe the joint trajectories. Considering the forward kinematics equations of the free-floating space robot, the trajectory planning issue was consequently transferred to an optimization issue while the control points to construct the Bézier curve are the design variables. A constrained differential evolution (DE) scheme with a premature handling strategy was implemented to find the optimal solution for the design variables while specific objectives and imposed constraints are satisfied [80]. Rybus et al. [81] presented a planning strategy while dynamic singularities of free-floating space robots were handled by modification of the Bézier curve shape. Figure 8 shows a comparison of a line trajectory and a trajectory based on a Bézier curve in joint space. They explored the idea of using a specific type of parametric curves, the cubic Bézier curves, as trajectories for the free-floating manipulator. These curves can be used to generate trajectories that allow avoidance of system singular configuration. In the considered case of free-floating manipulator dynamic body, Jacobian was used to find dynamically singular configurations (these configurations differ from the kinematically singular configurations obtained for a fixed-base manipulator). Sakayori et al. [82] proposed an energy-aware trajectory planning method for mobile robots in rugged terrain. They interpolated the terrain around the robotic robot with a B spline curve to accurately determine the contact location and analyzed the robot state using three consecutive Bezier curves, which showed a high degree of continuity and controllability. Finally, it was demonstrated through simulation that the planning method can achieve any type of mobile robot traversing rugged terrain with minimum energy trajectory.
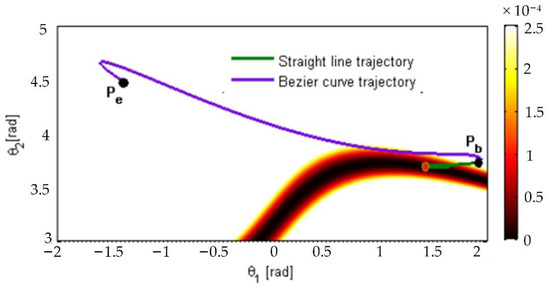
Figure 8.
Comparison of a line trajectory and a trajectory based on a Bézier curve in joint space.
3.2. Research on Optimal Trajectory Optimization Methods
The traditional polynomial interpolation trajectory planning method can achieve effective obstacle avoidance and reasonable trajectory selection of robotic arms but fails to obtain the trajectory with optimal performance. In recent years, researchers have applied intelligent algorithms to space robotic arm trajectory planning to obtain optimal trajectories that satisfy kinematic and dynamical constraints. The commonly used intelligent methods include genetic algorithms [83], particle swarm algorithms [84], and reinforcement learning algorithms [85].
3.2.1. Genetic Algorithm
The genetic algorithm (GA), an intelligent optimization algorithm, has been used extensively in trajectory optimization solutions because of its efficiency in solving optimization problems [86]. The general process when planning is performed by the GA is as follows:
- (1)
- Randomize the initial population and set the main parameters such as variation probability, crossover probability, the maximum number of iterations, and the number of populations;
- (2)
- Selecting populations according to specific rules (e.g., roulette method) based on the fitness function;
- (3)
- Perform crossover variation operation on individuals of the population;
- (4)
- Discriminate whether the maximum number of iterations is reached or not. If the maximum number of iterations is reached, the algorithm ends, otherwise returns to step (2).
The genetic algorithm provides a general framework for solving optimization problems of complex systems, which does not depend on the specific domain of the problem and is robust to the kind of problem and is widely used in robotic arm trajectory planning. Many scholars have researched genetic algorithms. Ge et al. [87] introduced the genetic algorithm in optimal control instead of the traditional Newtonian iterative method. A numerical algorithm for optimal control of motion planning based on the genetic optimization method was proposed. The effectiveness of the method is demonstrated by simulation calculations, and the motion planning problem of the non-complete constrained space robotic arm system is solved. Qi et al. [88] applied the GA to solve the requirement of in-orbit trajectory planning of the space robotic arm. They established the genetic algorithm fitness rating function about the end trajectory length of the Cartesian space robotic arm, the motion angle of the robotic arm in joint space, the maximum torque of the joint during motion, the total motion time of the robotic arm, and the collision case by the weighted coefficient method. Finally, the genetic algorithm is applied to plan an ideal trajectory in the joint space with no collision, kinetic characteristics satisfying the margin requirement, and short trajectory length and motion time. Shrivastava et al. [89] used a genetic algorithm to optimize the trajectory based on the energy conservation criterion. Their proposed method enables the operation of floating bodies in unknown environments with manipulator joint failures. The optimized onboard fuel has a significant impact on the satellite’s lifetime. Fallah et al. [90] proposed a new “feature-based” path optimization technique for planetary exploration vehicles. In this method, they discretized the specified path into segments and extracted the energy-related data of these segments from the search environment map. Subsequently, A genetic algorithm was integrated to search for the best feasible solution for the path planner in conjunction with a meshed environment map using cubic spline interpolation to search for the best feasible solution for the path planner.
From the above analysis, it can be seen that although the genetic algorithm can deal with multiple individuals in the population at the same time, reducing the risk of falling into a locally optimal solution. However, the algorithm itself is a random search algorithm, which requires multiple calculations, and the solutions obtained are often approximate solutions near the optimal solution, and the reliability is not easily guaranteed.
3.2.2. Particle Swarm Optimization Algorithm
Another intelligent optimization method is the particle swarm optimization algorithm (PSO) [91]. The PSO algorithm has a simple structure and easily adjustable parameters, and it is also widely used in trajectory time optimization. The key to this algorithm is the determination of algorithm parameters: some parameters in PSO, such as , the number of particles and iterations are often dependent on the specific problem and are determined based on application experience and after several tests and are not universal. Therefore, how to select algorithm parameters conveniently and efficiently is also an urgent research problem [92].
The particle swarm algorithm and polynomial are mostly used for trajectory planning, and the general process is as follows: firstly, the polynomial expression is derived according to the initial and termination conditions of the robot arm motion. Then the particle swarm method is used to optimize the time, and each joint motion time is treated as a particle, which is written as: “”, where n is the number of robotic arm joints. The fitness values of all particles are determined by the objective function, and each particle has a velocity that determines its search direction and distance. The optimal solution is then obtained by iteration. The traditional particle swarm algorithm can be represented by:
where is the d-dimensional component of the flight velocity in the iteration of the particle, is the d-dimensional component of the position in the iteration of the particle, is the optimal position in the particle, is the best position of the particle, are random numbers of [0, 1], are weight factors, and is the inertia weight.
Jie et al. [93] proposed the particle swarm optimization algorithm of “adaptation value correction + natural selection”. By modifying the adaptation value function, they transformed the attitude perturbation control problem of the floating base into an unconstrained optimization problem in free space and achieved high optimization accuracy. Liu et al. [94] proposed a multi-objective particle swarm optimization (MOPSO) method. The method significantly improves the load handling capability of the space robot system by simultaneously optimizing the joint moments, base perturbations, and system energy. The optimal solution set based on the MOPSO algorithm has good convergence and diversity, and all Pareto optimal solutions can satisfy various constraints, which is easy to implement in engineering. At the same time, the method has a certain universality for solving multi-constrained multi-objective trajectory optimization problems with tandem robotic arms with more degrees of freedom. Xia et al. [95] proposed a trajectory optimization strategy based on the chaotic particle swarm algorithm (CPSO) to study the trajectory planning problem of minimizing the base attitude perturbation in the free-floating state. The CPSO ensures the diversity of particle populations with the advantages of randomness and ergodicity of chaotic motion, improves the ability of particle swarm algorithms to get rid of local extrema, and maintains the advantages of fast convergence of particle swarm optimization algorithms. Xu et al. [96] designed a trajectory planning algorithm in a cartesian coordinate system using the incomplete motion characteristics of the free-floating space robot system, combined with the particle swarm optimization algorithm to search for the optimal solution of the objective function and explored the trajectory planning problem of the space robotic arm in capturing the runaway spin satellite from the perspective of engineering practice. Liu et al. [97] solved the multi-objective trajectory planning problem with the Newton-Raphson iterative method and multi-objective particle swarm optimization algorithm for the free-floating robotic arm model, respectively. Huang et al. [98] used the PSO algorithm to search the global time-optimal trajectory of a spatial manipulator. The time-optimal trajectory planning method based on the particle swarm algorithm is verified by examples to have good performance and practical engineering significance.
Compared with the genetic algorithm, the particle swarm algorithm is slightly slow to converge but better in terms of global search capability. Although neither is guaranteed to obtain an optimal solution, genetic algorithms are more likely to fall into a local optimum when solving large-scale computational volume problems. Particle swarm optimization is an emerging heuristic global search algorithm based on population intelligence, which is easy to understand, easy to implement, and has a strong global search capability.
3.2.3. Application of Reinforcement Learning Algorithms
Most of the above trajectory planning for space robotic arms is implemented based on multi-body dynamics models. If the robotic arm with flexible components is encountered, its dynamics model is difficult to establish, and the population intelligence algorithm usually falls into local optimal solutions. Along with the boom of artificial intelligence technology research, self-learning algorithms represented by reinforcement learning and deep learning are widely used in space robotic arm motion planning problems [99]. The advantages of applying machine learning algorithms for spatial robotic arm trajectory planning are their high applicability, the possibility of training simulation under the condition of no model, and even the possibility of prediction and advanced decomposition of planning behavior. Xu et al. [100] used the Sarsa(λ) reinforcement learning method to achieve autonomous trajectory planning for target tracking and obstacle avoidance in an on-orbit operation environment with unknown target characteristics. Lee et al. [101] established a spatial obstacle avoidance type, by optimally adjusting the path points in the collision-free region to satisfy the dynamic constraints based on the target trajectory of elastic optimization (EO). They used the dynamic movement primitives (DMPs) to learn the optimized trajectories and reprogram them to avoid unknown obstacles. Given global waypoints, the hypothesis and test method can generate a global desired trajectory to perform safe air missions. Xie et al. [102] used a standard actor-critic algorithm framework to study the autonomous planning problem of on-orbit fuel replenishment and migrated the trained policy network from the simulation scenario to the real physical test system to make the robotic arm with end-to-end visual servo capability.
The study of the space robotic arm in-orbit capture task is currently one of the research hotspots for reinforcement learning in space robotic arm applications. Wu et al. [103] proposed a model-free reinforcement learning strategy, namely the deep deterministic policy gradient (DDPG) algorithm. The learning framework of this algorithm is given in Figure 9. The online trajectory planning strategy is trained without modeling the dynamics and kinematics of the spatial robotic arm, enabling the spatial robotic arm to quickly schedule and execute actions. Li et al. [104] used the deep deterministic policy gradients algorithm to achieve complex constrained planning for the flip motion of a robotic arm for the complex constrained motion planning problem of a free-floating two-arm space robotic arm as in Figure 10. The application of the DDPG algorithm made the motion planning have good robustness, which means that for the randomly selected initial point and end point within a certain range, the optimal trajectory can always be obtained by the trained policy. Therefore, the proposed approach can be applied to various space operation tasks. Subsequently, they combined deep reinforcement learning algorithms with artificial potential fields to improve convergence and robustness [105]. Yu [106] used the DDPG framework to learn a redundant robotic arm dual-arm path planning strategy to achieve the capture of target satellites by a spatial spherical-revolute-spherical (SRS) redundant robotic arm. Liang et al. [107] designed a robot deep reinforcement learning motion control model based on the actor-critic algorithm, which unifies the evaluation criteria of distance and angle by transforming the reward function with trigonometric functions. The convergence efficiency is greatly improved, and the target capture of a six-degree-of-freedom spatial robot arm is realized in the simulation platform. Zhao et al. [108] proposed an improved deep deterministic policy gradients algorithm to establish a multi-intelligence self-learning system with each joint as the decision intelligence to achieve rapid capture of the robot arm for uniform motion targets in all directions.
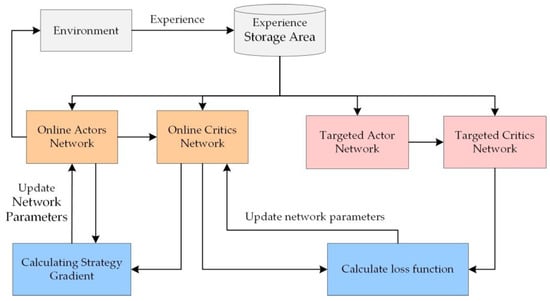
Figure 9.
The structure of the DDPG algorithm.
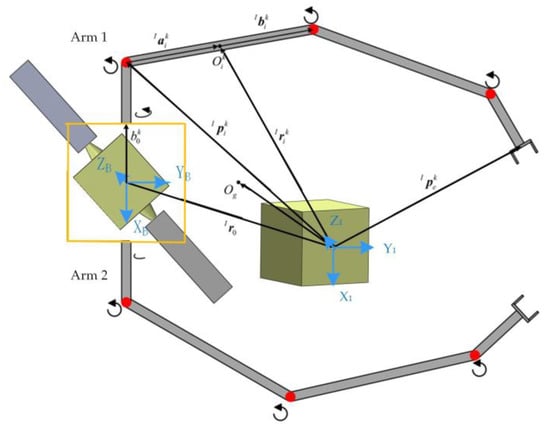
Figure 10.
Schematic diagram of free-floating dual-arm space robot arm capture.
Meanwhile, neural networks are widely used to solve various problems in robot arm kinematics and trajectory planning. Pflueger et al. [109] presented an inverse reinforcement learning architecture using a soft value iteration network (SVIN). The system implicitly learns to solve navigation planning problems using training data derived from other planners or historical rover driving data. They have analyzed how the SVIN formulation can improve training gradients for problems with deterministic state transition dynamics and have seen that improvement empirically on the grid world dataset. Hu et al. [110] proposed a learning-based global path planning method that outperforms conventional searching and sampling-based methods in terms of planning speed. They designed a hierarchical framework consisting of step iterations and block iterations. For the planning of each step, an end-to-end step planner based on deep reinforcement learning is proposed. The planner uses a two-branch residual network for action value estimation and is trained on an ensemble of simulated maps. The method can significantly improve the planning speed of remote coarse yarns while adapting to maps of arbitrary size. Zhang et al. [111] proposed a novel Deep Convolutional Neural Networks architecture with double branches—(DB-CNN) to make paths for planetary rovers directly from orbital images, which requires no prior knowledge about the planetary orbital images. Then, they presented the complete global path planning algorithm based on DB-CNN. Finally, they analyzed why DB-CNN works well through model ablation analysis and visualization analysis.
The current status of research on space robotic arm trajectory planning based on motion planning requirements is summarized in Table 3.

Table 3.
Spatial robotic arm motion trajectory planning study summary table.
4. Summary and Outlook
This paper summarizes and analyzes the existing space robotic arm trajectory planning methods. Starting from two aspects of trajectory planning requirements, in-depth analysis is carried out through the principle’s introduction and application case analysis, and the article has the following summary.
(1) Spatial obstacle detection is an important prerequisite and guarantees obstacle avoidance trajectory planning. We analyze the widely used discrete collision detection algorithms and present their application scenarios. After that, the common obstacle avoidance planning methods for spatial robotic arms are discussed in chronological order: from simple spatial assumptions to the introduction of collision penalty functions. Subsequently, the pseudo-inverse method, the artificial potential field method, the C-space method, algorithm and Genetic Algorithm, etc. which are now widely used, are introduced. A complete system of obstacle avoidance planning is formed from local planning to global planning.
(2) Ensuring the smooth and stable trajectory of the robot arm is the core goal of trajectory planning. We describe in detail the polynomial interpolation planning methods under different types. The traditional polynomial interpolation can meet the basic requirements of trajectory planning, but for the occasions with higher stability requirements, it is still necessary to improve the planning algorithm, which mainly includes B spline, NURBS curve, etc. With the development of modern artificial intelligence, intelligent algorithms are also gradually applied to trajectory planning, and we focus on analyzing the application status of genetic algorithms, particle swarm algorithms, and reinforcement learning algorithms in trajectory planning to provide theoretical a basis and reference significance for the selection of subsequent trajectory planning methods.
From the above analysis, it is clear that each method has limitations in itself, and multiple methods need to be used in combination to bring their respective advantages into play, however, in the process of practical application, there are still some problems to explore, and the following aspects need to be solved urgently. The following problems exist in the current research in trajectory planning for autonomous in-orbit service robotic arms.
(1) For a space-controlled pedestal robotic arm, its motion trajectory is sometimes required to meet multiple performance indicators when performing some specific operational tasks. For example, it is required to move faster, or it is required to move with less vibration and smooth trajectory, or it is required to consume less energy, etc. Several indicators may be required to be considered.
(2) The existing trajectory planning research mainly focuses on the construction of interpolation curves and the use of solution algorithms with good performance. The higher order of interpolation curves increases the difficulty of solving and decreases the efficiency of operation. Although many scholars have studied high-order curve fitting, the optimal selection of curves for different tasks needs to be further improved.
(3) Many existing scholars use intelligent algorithms instead of traditional mathematical calculation methods for trajectory planning solutions, simplifying the complicated mathematical calculation and obtaining trajectories with better performance. However, there is not yet an algorithm that can simultaneously meet the solution requirements of global convergence, real-time solving, accuracy, generality, and simplicity of the solution process. Thus, it can be seen that the application of intelligent algorithms in trajectory planning solutions is still a research hotspot in the future.
The process and method of space robotic arm trajectory planning are much more complicated and tedious than that of the robot arm fixed on the base on the ground, as can be seen from the comparative analysis of different planning methods above. Most of the trajectory planning methods are not quite perfect, and the future development of this research field has the following application prospects.
(1) From the above analysis, it is clear that each method has its limitations and multiple methods need to be used in combination to exploit their respective advantages. Future research can utilize the advantages of polynomial interpolation to achieve robotic arm spatial trajectory planning by combining incomplete constraints with bio intelligence algorithms.
(2) Throughout the existing trajectory planning research literature, most of them only establish the simplified optimization model of trajectory planning for the main influencing factors and find the corresponding optimal solution. However, in the actual on-orbit trajectory planning process, multi-objective optimal trajectory planning considering the actual working condition is needed to improve the working life of the robotic arm while ensuring the quality of spatial operations.
(3) Due to the poor real-time performance of the bio-intelligence method, the solution obtained each time is not unique and is mostly an approximate solution near the optimal value, which should be fully integrated with the environment modeling and specific application context in the future to seek a more rapid and effective path planning algorithm. At present, trajectory planning research combined with machine learning has become another emerging trend in intelligent planning methods. The introduction of machine learning and other artificial intelligence technologies will greatly enhance the intelligence of trajectory planning.
Author Contributions
Conceptualization, Y.D. and C.X.; methodology, Y.D. and Y.Z.; investigation, C.X., Y.J., W.Q. and Q.Z.; writing—original draft preparation, C.X.; writing—review and editing, Y.D. and Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The study is supported by the National Natural Science Foundation of China (Grant No. 52075134); Natural Science Foundation of Heilongjiang Province of China (Grant No. LH2019E062); Postdoctoral Scientific Research Developmental Fund of Heilongjiang Province of China (Grant No. LBH-Q20097).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Flores-Abad, A.; Ma, O.; Pham, K.; Ulrich, S. A review of space robotics technologies for on-orbit servicing. Prog. Aerosp. Sci. 2014, 68, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Zhu, R.Z.; Wang, H.F. Review of manned spacecraft operator systems (continued). Manned Spacefl. 2010, 16, 48–58. [Google Scholar] [CrossRef]
- Haidegger, T. Advanced Robotic Arms in Space. In Proceedings of the International Astronautical Federation—55th International Astronautical Congress, Vancouver, BC, Canada, 4–8 October 2004; Volume 4, pp. 2584–2593. [Google Scholar]
- Hirzinger, G.; Brunner, B.; Dietrich, J. ROTEX-The First Remotely Controlled Robot in Space. IEEE Trans. Robot. Autom. 1994, 6, 2604–2611. [Google Scholar]
- Preusche, C.; Reintsema, D.; Landzettel, K.; Hirzinger, G. Robotics Component Verification on ISS ROKVISS—Preliminary Results for Telepresence. Int. Conf. Intell. Robot. Syst. 2006, 9, 9–15. [Google Scholar]
- Martin, E.; Dupuis, E.; Piedboeuf, J.C.; Doyon, M. The TECSAS Mission From a Canadian Perspective. In Proceedings of the i-SAIRAS 2005, the 8th International Symposium on Artificial Intelligence, Robotics and Automation in Space, Munich, Germany, 5–8 September 2005; Volume 2, pp. 5–8. [Google Scholar]
- Wang, X.; Wang, W. An overview of key technology features of Tiangong space station. China Sci. Technol. Sci. 2021, 51, 1287–1298. [Google Scholar]
- Wang, M.Y.; Li, J. Research on trajectory planning algorithm for six-degree-of-freedom industrial robots. Precis. Manuf. Autom. 2017, 4, 47–49, 62. [Google Scholar] [CrossRef]
- Cao, Z.Y.; Wang, H.; Wu, W.R. Time-optimal and pulsation-optimal trajectory planning for slurry spraying manipulator. J. Cent. South Univ. 2013, 44, 114–121. [Google Scholar]
- Zhu, S.Q.; Liu, S.G.; Wang, X.Y. Time-optimal pulsating continuous trajectory planning algorithm for robots. J. Mech. Eng. 2010, 46, 47–52. [Google Scholar] [CrossRef]
- Oda, M.; Kibe, K.; Yamagata, F. ETS-VII, space robot in-orbit experiment satellite. IEEE 1996, 1, 739–744. [Google Scholar] [CrossRef]
- Zhai, Y.B. Research on Space Robotic Arm Trajectory Planning and Ground Simulation Method. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2013. [Google Scholar]
- Acquatella, P. Development of automation & robotics in space exploration. In Proceedings of the AIAA SPACE Conference & Exposition, Pasadena, CA, USA, 27–30 June 2006. [Google Scholar]
- Anderson, R.C.; Adamo, D.; Buczkowski, D.; Dohm, J.; Haidegger, T.; Jones, T.; Podnar, G.; Wyrick, D. Next frontier in planetary geological reconnaissance: Low-latency telepresence. Icarus 2021, 368, 114558. [Google Scholar] [CrossRef]
- Haidegger, T.; Benyo, Z. Surgical robotic support for long duration space missions. Acta Astronaut. 2008, 63, 996–1005. [Google Scholar] [CrossRef]
- Yoshida, K.; Hashizume, K.; Abiko, S. Zero reaction maneuver: Flight validation with ETS-VII space robot and extension to kinematically redundant arm. In Proceedings of the IEEE International Conference on Robotics & Automation, Seoul, Korea, 21–26 May 2001. [Google Scholar]
- Li, Q.Z.; Gu, W.K.; Ye, X.Q.; Xiang, Z.Y. Research on intelligent pre-scanning control method for path tracking of mobile robots. Robot 2002, 252–255. [Google Scholar] [CrossRef]
- Ferguson, D.; Kalra, N.; Stentz, A. Replanning with RRTs. In Proceedings of the IEEE International Conference on Robotics & Automation, Orlando, FL, USA, 15–19 May 2006. [Google Scholar]
- Yin, B. Research on Redundant Robotic Arm Kinematics and Obstacle Avoidance Path Planning. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2014. [Google Scholar]
- Luo, F. Fast Collision Detection and Intersection Calculation for 3D Mesh Models. Master’s Thesis, Zhejiang University, Zhejiang, China, 2005. [Google Scholar]
- Zeng, C. Research on Space Robotic Arm Motion and Mission Planning Methods for On-Orbit Services. Diploma Thesis, Dalian University of Technology, Dalian, China, 2013. [Google Scholar]
- Wang, Z.P. Research on Motion Planning of Robotic Arm in Constrained Space. Master’s Thesis, Beijing University of Posts and Telecommunications, Beijing, China, 2017. [Google Scholar]
- Jiang, G.Y. Research and Application of Collision Detection Algorithm Based on Wraparound Box. Master’s Thesis, University of Electronic Science and Technology, Chengdu, China, 2012. [Google Scholar]
- Bai, W.D.; Zhou, Z.P.; Zhang, S.B.; Wu, J.Y. A study on inter-object collision detection in VRML. Comput. Appl. Res. 2004, 6, 128–130+133. [Google Scholar]
- Menasri, R.; Nakib, A.; Daachi, B.; Oulhadj, H.; Siarry, P. A trajectory planning of redundant manipulators based on bilevel optimization. Appl. Math. Comput. 2015, 250, 934–947. [Google Scholar] [CrossRef]
- Hou, Z.C. Spatial Capture-Oriented Robot Path Planning and Controller Design. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2011. [Google Scholar]
- Zhu, Z.X.; Jing, S.; Zhong, J.F.; Wang, M.M. Spatially redundant robotic arm obstacle avoidance path planning based on collision detection. J. Northwestern Polytech. Univ. 2020, 38, 183–190. [Google Scholar] [CrossRef]
- Han, F.; Wang, Z.; He, L.; Wu, H.; Yang, G.; Duan, G. Trajectory plan for an ultra-short distance on-orbit service based on the Gaussian pseudo-spectral method. IEEE/CAA J. Autom. Sin. 2018, 1–9. [Google Scholar] [CrossRef]
- Li, Y.C.; Jiang, Q.; Wang, C.H. Adaptive trajectory planning of robotic arms in confined spaces. Electron. Compon. Inf. Technol. 2021, 5, 53–54. [Google Scholar] [CrossRef]
- Li, B.H.; Zhang, Y.P.; Wu, Z.Y.; Yu, D.S.; Yang, Y.Z.; Du, S.Y. Research and implementation of ROS-based SLAM for mobile robots. Electron. Compon. Inf. Technol. 2020, 4, 51–52. [Google Scholar] [CrossRef]
- Zhang, C.F.; Chen, M.H.; Hou, Y.Y.; Zhang, W.J. Redundant space robotic arm trial search obstacle avoidance strategy. Aerosp. Shanghai 2022, 39, 1–7. [Google Scholar] [CrossRef]
- Wang, Y.; Jia, Y.H.; Xu, S.J. Collision-free trajectory planning algorithm for redundant space robotic arm coarse capture segment. Chin. Space Sci. Technol. 2012, 32, 49–56. [Google Scholar]
- Zhuang, H.Z.; Du, S.X.; Wu, J. Research on robot path planning and related algorithms. Bull. Sci. Technol. 2004, 20, 6. [Google Scholar]
- Huang, Y.S.; Tian, D.; Li, H.J.; Jiao, R.H. A tumbling non-cooperative spacecraft approach and flight avoidance trajectory planning and tracking control method. Space Control Technol. Appl. 2021, 47, 8. [Google Scholar]
- Kang, G.H.; Zhang, H.; Wei, J.Y.; Wu, J.Q.; Zhang, L. Energy-optimal spacecraft continuous dynamic obstacle avoidance trajectory planning. J. Astronaut. 2021, 42, 305–313. [Google Scholar]
- Lozano-Perez, T. Spatial Planning: A Configuration Space Approach. IEEE Trans. Comput. 2006, C-32, 108–120. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Sun, H.; Jia, Q.; Lei, H. A Novel Division Based Self-Motion Algorithm for Avoiding Obstacles for Redundant Manipulators. In Proceedings of the IEEE International Conference on Automation & Logistics, Jinan, China, 18–21 August 2007. [Google Scholar]
- Beiner, L.; Mattila, J. An improved pseudoinverse solution for redundant hydraulic manipulators. Robotica 1999, 17, 173–179. [Google Scholar] [CrossRef]
- Jin, L.; Li, S.; La, H.M.; Luo, X. Manipulability Optimization of Redundant Manipulators Using Dynamic Neural Networks. IEEE Trans. Ind. Electron. 2017, 64, 4710–4720. [Google Scholar] [CrossRef]
- Pisculli, A.; Felicetti, L.; Gasbarri, P.; Palmerini, G.B.; Sabatini, M. A reaction-null/Jacobian transpose control strategy with gravity gradient compensation for on-orbit space manipulators. Aerosp. Sci. Technol. 2014, 38, 30–40. [Google Scholar] [CrossRef]
- Sabatini, M.; Gasbarri, P.; Palmerini, G.B. Coordinated control of a space manipulator tested by means of an air bearing free floating platform. Acta Astronaut. 2017, 139, 296–305. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L. Whole-body collision avoidance control design using quadratic programming with strict and soft task priorities. Robot. Comput. Integr. Manuf. 2020, 62, 101882. [Google Scholar] [CrossRef]
- Stolfi, A.; Gasbarri, P.; Sabatini, M. Spazio. Performance Analysis and Gains Tuning Procedure for a Controlled Space Manipulator Used for Non-Cooperative Target Capture Operations. Aerotec. Missili Spaz. 2018, 97, 3–12. [Google Scholar] [CrossRef]
- Tringali, A.; Cocuzza, S. Finite-Horizon Kinetic Energy Optimization of a Redundant Space Manipulator. Appl. Sci. 2021, 11, 2346. [Google Scholar] [CrossRef]
- Li, C.; Zheng, Z.X.; Yuan, J.P. A trajectory optimization method with frictional contacts for on-orbit capture. Acta Astronaut. 2020, 175, 90–98. [Google Scholar] [CrossRef]
- Lu, X.; Jia, Y. Trajectory Planning of Free-Floating Space Manipulators With Spacecraft Attitude Stabilization and Manipulability Optimization. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 7346–7362. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Zhao, J.D.; Zhao, L.L.; Yang, X.H. A method for solving the inverse kinematics of SSRMS configuration space robotic arm. J. Mech. Eng. 2022, 58, 15. [Google Scholar]
- Kathib, O. Real-Time Obstacle Avoidance for Manipulators and Mobile Robots; Springer: New York, NY, USA, 1986. [Google Scholar]
- Zhan, B.; Jin, M.; Yang, G.; Zhang, C. A novel strategy for space manipulator detumbling a non-cooperative target with collision avoidance. Adv. Space Res. 2020, 66, 785–799. [Google Scholar] [CrossRef]
- Gao, X.; Wu, H.; Zhai, L.; Sun, H.; Jia, Q.; Wang, Y.; Wu, L. A rapidly exploring random tree optimization algorithm for space robotic manipulators guided by obstacle avoidance independent potential field. Int. J. Adv. Robot. Syst. 2018, 15. [Google Scholar] [CrossRef]
- Lozano-Perez, T. Automatic Planning of Manipulator Transfer Movements. IEEE Trans. Syst. Man Cybern. 1981, 11, 681–698. [Google Scholar] [CrossRef] [Green Version]
- Maciejewski, A.A.; Fox, J.J. Automation. Path planning and the topology of configuration space. IEEE Trans. Robot. Autom. 1993, 9, 444–456. [Google Scholar] [CrossRef]
- Kondo, K. Motion planning with six degrees of freedom by multistrategic bidirectional heuristic free-space enumeration. IEEE Trans. Robot. Autom. 1991, 7, 267–277. [Google Scholar] [CrossRef]
- Zhao, Z.M. Path planning for service-oriented robots based on weighted A* algorithm. J. Huazhong Univ. Sci. Technol. Nat. Sci. Ed. 2008, 3. [Google Scholar] [CrossRef]
- Chen, G.; Yuan, B.; Jia, Q.; Sun, H.; Guo, W. Failure tolerance strategy of space manipulator for large load carrying tasks. Acta Astronaut. 2018, 148, 186–204. [Google Scholar] [CrossRef]
- Guo, J.F.; Yu, X.Q.; Zheng, H.X.; Yan, P. Autonomous detection and fusion path planning for planetary vehicles. Unmanned Syst. Technol. 2020, 3, 17–23. [Google Scholar]
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef] [Green Version]
- Valle, S.; Kuffner, J.J., Jr. Randomized kinodynamic planning. Int. J. Robot. Res. 2001, 15, 378–400. [Google Scholar]
- Rybus, T. Point-to-Point Motion Planning of a Free-Floating Space Manipulator Using the Rapidly-Exploring Random Trees (RRT) Method. Robotica 2019, 38, 957–982. [Google Scholar] [CrossRef]
- James, F.; Shah, S.V.; Singh, A.K.; Krishna, K.M.; Misra, A.K. Reactionless Maneuvering of a Space Robot in Precapture Phase. J. Guid. Control Dyn. 2016, 39, 2419–2425. [Google Scholar] [CrossRef]
- Guan, Y.Z.; Song, C.L. Path Planning of the Free-floating Manipulator for Capturing a Moving Target. Robot 2017, 39, 803–811. [Google Scholar]
- Yan, S. Development of Intelligent Analysis and Planning System for Space Robotic Arm Table-Taking Sampling Strategy. Master’s Thesis, Beijing University of Posts and Telecommunications, Beijing, China, 2020. [Google Scholar]
- Hoffmann, W.; Sauer, T. A spline optimization problem from robotics. Rend. Mat. Appl. 2006, 26, 221–230. [Google Scholar]
- Garrido, J.; Wen, Y.; Li, X. Robot trajectory generation using modified hidden Markov model and Lloyd’s algorithm in joint space. Eng. Appl. Artif. Intell. 2016, 53, 32–40. [Google Scholar] [CrossRef]
- Wen, Y.F.; Sun, L.N. Trajectory optimization algorithm for surface-modified redundant robot joint space. Mech. Sci. Technol. Aerosp. Eng. 2018, 37, 1870–1874. [Google Scholar]
- Valero, F.; Mata, V.; Besa, A. Trajectory planning in workspaces with obstacles taking into account the dynamic robot behaviour. Mech. Mach. Theory 2006, 41, 525–536. [Google Scholar] [CrossRef]
- Zhang, P.; Gong, J.; Ning, H.; Zeng, Y.; Liu, Y.; Wei, L. Study on Trajectory Combination and Connection Problems of Spray-painting Robot for Large Curvature Combination Surfaces. Adv. Eng. Sci. 2016, 48, 217–222. [Google Scholar] [CrossRef]
- Saramago, S.; Steffen, V.; Theory, M. Optimization of the Trajectory Planning of Robot Manipulators Taking into Account the Dynamics of the System. Mech. Mach. Theory 1998, 33, 883–894. [Google Scholar] [CrossRef]
- Tortopidis, I.; Papadopoulos, E. On point-to-point motion planning for underactuated space manipulator systems. Robot. Auton. Syst. 2007, 55, 122–131. [Google Scholar] [CrossRef]
- An, J.; Li, X.; Zhang, Z.; Man, W.; Zhang, G. Joint Trajectory Planning of Space Modular Reconfigurable Satellites Based on Kinematic Model. Int. J. Aerosp. Eng. 2020, 2020, 1–17. [Google Scholar] [CrossRef]
- Cui, H. Polynomial interpolation method for motion planning of free-floating space robots. J. Beijing Inf. Sci. Technol. Univ. 2019, 34, 8. [Google Scholar]
- Papadopoulos, E.; Tortopidis, I.; Nanos, K. Smooth Planning for Free-floating Space Robots Using Polynomials. In Proceedings of the IEEE International Conference on Robotics & Automation, Barcelona, Spain, 18–22 April 2006. [Google Scholar]
- Misra, G.; Bai, X. Dynamics. Optimal Path Planning for Free-Flying Space Manipulators via Sequential Convex Programming. J. Guid. Control Dyn. 2017, 40, 3019–3026. [Google Scholar] [CrossRef]
- Xin, P.; Rong, J.; Yang, Y.; Xiang, D.; Xiang, Y. Trajectory planning with residual vibration suppression for space manipulator based on particle swarm optimization algorithm. Adv. Mech. Eng. 2017, 9. [Google Scholar] [CrossRef] [Green Version]
- Li, M. Research on Spatial Robotic Arm Trajectory Planning. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2019. [Google Scholar]
- Dudek, G.; Jenkin, M.; Kambhampati, S.; Latombe, J.C. Robot Motion Planning; Kluwer Academic Publishers: Alphen aan den Rijn, The Netherlands, 1990. [Google Scholar]
- Li, L.F.; Ma, H. A Research on the Cubic Uniform B-spline Curve and Its Application on Trajectory Planning Algorithm of Industry Robot. Sci. Technol. Eng. 2013, 13, 3621–3625+3646. [Google Scholar]
- Meike, D.; Ribickis, L. Industrial robot path optimization approach with asynchronous fly-by in joint space. In Proceedings of the IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011. [Google Scholar]
- Wang, M.; Luo, J.; Fang, J.; Yuan, J. Optimal trajectory planning of free-floating space manipulator using differential evolution algorithm. Adv. Space Res. 2018, 61, 1525–1536. [Google Scholar] [CrossRef]
- Nanos, K.; Papadopoulos, E. Systems, E. Avoiding dynamic singularities in Cartesian motions of free-floating manipulators. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2305–2318. [Google Scholar] [CrossRef]
- Rybus, T.; Barcinski, T.; Lisowski, J.; Seweryn, K.; Nicolaukuklinski, J.; Grygorczuk, J.; Krzewski, M.; Skup, K.; Szewczyk, T.; Wawrzaszek, R. Experimental demonstration of singularity avoidance with trajectories based on the Bézier curves for free-floating manipulator. In Proceedings of the International Workshop on Robot Motion & Control, Kuslin, Poland, 3–5 July 2013. [Google Scholar]
- Sakayori, G.; Ishigami, G. Energy-aware trajectory planning for planetary rovers. Adv. Robot. 2021, 35, 21–22. [Google Scholar] [CrossRef]
- Wang, M.; Luo, J.; Walter, U. Trajectory planning of free-floating space robot using Particle Swarm Optimization (PSO). Acta Astronaut. 2015, 112, 77–88. [Google Scholar] [CrossRef]
- Khare, A.; Rangnekar, S. A review of particle swarm optimization and its applications in Solar Photovoltaic system. Appl. Soft Comput. 2013, 13, 2997–3006. [Google Scholar] [CrossRef]
- Wang, M.; Wang, P.; Lin, J.S.; Li, X.; Qin, X.B. Nonlinear Inertia Classification Model and Application. Math. Probl. Eng. 2014, 2014, 987686. [Google Scholar]
- Yang, X.T.; Ku, X.C.; Zhao, H.L.; Mi, X.; Ma, D.Y. Time-optimal trajectory planning based on improved genetic algorithm. Manuf. Technol. Mach. Tools 2022, 03, 74–79. [Google Scholar] [CrossRef]
- Ge, X.S.; Sun, P.W. Particle swarm optimization algorithm for incomplete motion planning of free floating space robotic arm. J. Mech. Eng. 2007, 04, 34–38. [Google Scholar] [CrossRef]
- Qi, R.L.; Zhou, W.J.; Wang, T.J. A genetic algorithm-based trajectory planning method for spatial robotic arm obstacle avoidance. Robotics 2014, 36, 263–270. [Google Scholar]
- Shrivastava, A.; Dalla, V.K. Engineering. Failure control and energy optimization of multi-axes space manipulator through genetic algorithm approach. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 1–17. [Google Scholar] [CrossRef]
- Fallah, S.; Yue, B.; Vahid-Araghi, O.; Khajepour, A. Energy Management of Planetary Rovers Using a Fast Feature-Based Path Planning and Hardware-in-the-Loop Experiments. IEEE Trans. Veh. Technol. 2013, 62, 2389–2401. [Google Scholar] [CrossRef]
- Liu, R.J.; Wang, F.; Zhang, Q.; Nan, L. Research on Trajectory Planning of ROS-based Robot Arm. Navig. Position. Timing 2016, 3, 82–88. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. Swarm Intell. 1995, 1, 33–57. [Google Scholar]
- Jie, D.Y.; Lu, H.R.; Wu, H.L.; Ni, F.L. Transporting trajectory optimization method for large space manipulator system. Acta Aeronaut. Et Astronaut. Sin. 2018, 39, 111–119. [Google Scholar]
- Liu, Y.; Jia, Q.X.; Chen, G. Multi-objective particle swarm optimization algorithm based on load-maximizing trajectory optimization for free-floating space robots. Robotics 2014, 36, 9. [Google Scholar]
- Xia, H.W.; Zhai, Y.B.; Ma, G.C.; Deng, Y. Spatial robotic arm trajectory planning algorithm based on chaotic particle swarm optimization algorithm. Chin. J. Inert. Technol. 2014, 6. [Google Scholar]
- Xu, W.F.; Liu, Y.; Liang, B.; Xu, Y.S.; Qiang, W.Y. Autonomous Path Planning and Experiment Study of Free-floating Space Robot for Target Capturing. J. Intell. Robot. Syst. 2008, 51, 303–331. [Google Scholar] [CrossRef]
- Liu, Y.; Du, Z.; Wu, Z.; Liu, F.; Li, X.J. Multiobjective preimpact trajectory planning of space manipulator for self-assembling a heavy payload. Int. J. Adv. Robot. Syst. 2021, 18, 1–26. [Google Scholar] [CrossRef]
- Huang, P.; Xu, Y. PSO-Based Time-Optimal Trajectory Planning for Space Robot with Dynamic Constraints. In Proceedings of the IEEE International Conference on Robotics & Biomimetics, Kunming, China, 17–20 December 2007. [Google Scholar]
- Sharp, M.; Ak, R.; Hedberg, T. A survey of the advancing use and development of machine learning in smart manufacturing. J. Manuf. Syst. 2018, 48, 170–179. [Google Scholar] [CrossRef]
- Xu, W.; Lu, S. Research on path planning of space robotic arm based on Sarsa(λ) reinforcement learning. J. Astronaut. 2019, 40, 435–443. [Google Scholar]
- Lee, H.; Seo, H.; Kim, H.G. Trajectory Optimization and Replanning Framework for a Micro Air Vehicle in Cluttered Environments. IEEE Access 2020, 8, 135406–135415. [Google Scholar] [CrossRef]
- Xie, Y.C.; Wang, Y.; Chen, A. Learning-based operation technology for space robots in orbit service. Space Control. Technol. Appl. 2019, 45, 13. [Google Scholar]
- Wu, Y.H.; Yu, Z.C.; Li, C.Y.; He, M.J.; Chen, Z.M. Reinforcement learning in dual-arm trajectory planning for a free-floating space robot. Aerosp. Sci. Technol. 2020, 98, 105657. [Google Scholar] [CrossRef]
- Li, Y.; Li, S. Technology. Constrained Motion Planning of Free-Float Dual-Arm Space Manipulator Via Deep Reinforcement Learning. Aerosp. Sci. Technol. 2020, 109, 106446. [Google Scholar] [CrossRef]
- Li, Y.K.; Li, D.Y.; Zhu, W.S.; Sun, J.; Zhang, X.L.; Li, S. Constrained Motion Planning of 7-DOF Space Manipulator via Deep Reinforcement Learning Combined with Artificial Potential Field. Aerospace 2022, 9, 163. [Google Scholar] [CrossRef]
- Yu, Z.C. Research on Multi-Arm Space Robot Planning Technology for On-Orbit Service. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2020. [Google Scholar]
- Liang, B.Y.; Chen, Z.L.; Guo, M.S.; Wang, Y.; Wang, Y.B. Space Robot Target Intelligent Capture System Based on Deep Reinforcement Learning Model. J. Phys. Conf. Ser. 2021, 1848, 012078. [Google Scholar] [CrossRef]
- Zhao, Y.; Guan, G.S.; Guo, J.F.; Yu, X.Q.; Yan, P. Spatial robotic arm trajectory planning based on multi-intelligent reinforcement learning. Acta Aeronaut. Et Astronaut. Sin. 2021, 42, 266–276. [Google Scholar]
- Pflueger, M.; Agha, A.; Sukhatme, G.S. Rover-IRL: Inverse Reinforcement Learning With Soft Value Iteration Networks for Planetary Rover Path Planning. IEEE Robot. Autom. Lett. 2019, 4, 1387–1394. [Google Scholar] [CrossRef]
- Hu, R.; Zhang, Y. Fast Path Planning for Long-Range Planetary Roving Based on a Hierarchical Framework and Deep Reinforcement Learning. Aerospace 2022, 9, 101. [Google Scholar] [CrossRef]
- Zhang, J.; Xia, Y.Q.; Shen, G.H. A novel learning-based global path planning algorithm for planetary rovers. Neurocomputing 2019, 361, 69–76. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).