Quantifying the Resilience Performance of Airport Flight Operation to Severe Weather
Abstract
:1. Introduction
- This paper discusses the coupling relationship between severe weather and the resilience of airport flight operations in depth and proposes a resilience metric to quantify the influence of severe weather events on the airport.
- This study extended existing resilience research methods to a wider range of severe weather using a variety of severe weather conditions, rather than just one type of severe weather, and drew general and practical conclusions.
- The results show that the metric can be used to evaluate the resilience of airport flight operation to severe weather events effectively. Additionally, the research method and approach demonstrated in this paper is transferable to other infrastructure systems.
2. Materials and Methods
2.1. Airport Flight Operation Resilience Capability
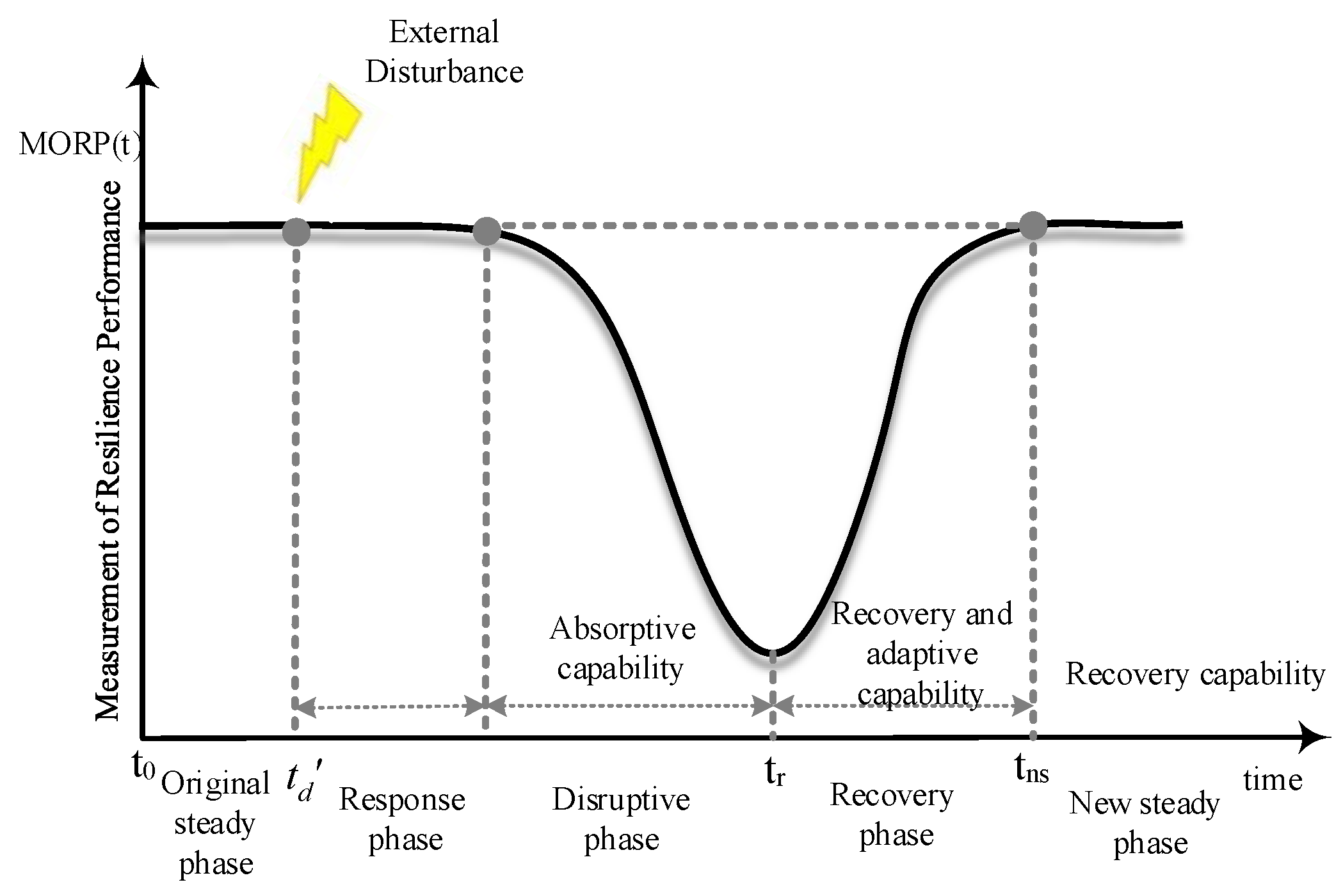
2.2. Resilience Measurement
- 1.
- The first phase is the initial stable phase. The time period is the initial stable stage of the system, when the system is not disturbed by the outside world, and the system performance level is the initial performance value.
- 2.
- The second phase is the response phase. The time period is the response stage of the system under external interference, during which the system has been disturbed, but the system performance level still remains at the initial performance value. During this phase, the system’s susceptibility capability can be assessed by identifying appropriate measures. The selection of the appropriate MORP depends on the specific service provided by the system under analysis. It is assumed that disruptive events occur at and the MORP value drops at . It should be noted that in many cases, might not be equal to , and the delay depends on the selection of the MORP and disruptive event. For instance, it could take several hours for passengers to lose air services due to general severe weather events, while it might only take seconds for same passengers to lose services due to natural hazards, such as earthquakes. System sensitivity could be used to characterize the performance of this stage. System susceptibility is defined as “the inability of a system to avoid being hit by a threat mechanism” [36].
- 3.
- The third phase is the disruptive phase (DP), in which the system performance starts dropping at time , until the lowest level is reached at time . During this phase, the system absorptive capability can be assessed by identifying appropriate measures.
- 4.
- The fourth phase is the recovery phase, in which the system performance increases until the new steady level is achieved. During this phase , the adaptive and restorative capabilities of the system can be assessed by developing appropriate measures.
- 5.
- The fifth phase is the new stable phase, in which system performance reaches and maintains a new steady level. It should be noted that the new stable level may be equal to, lower than, or even higher than the initial level. During this phase, the system recovery capability can be assessed by identifying appropriate measures.
- 1.
- System performance immediately drops to its lowest level under the disturbance (, i.e., no absorptive capability);
- 2.
- System performance never increases past the lower level, R, which is the new steady phase (, i.e., no adaptive and restorative capability).
3. Data Description and Preprocessing
3.1. Data Description
3.2. Data Preprocessing
4. Results and Discussion
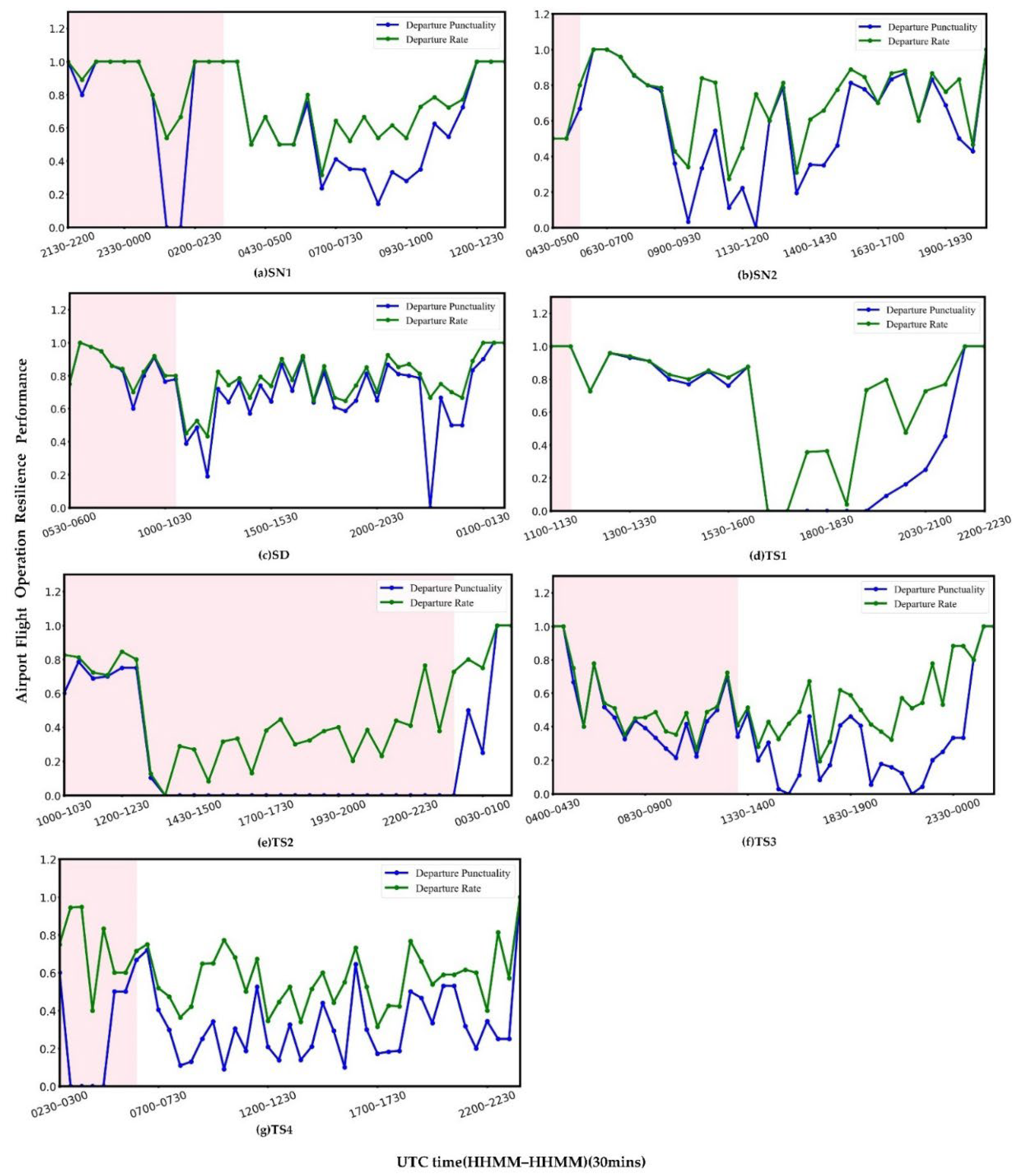
4.1. Departure Punctuality and Departure Rate
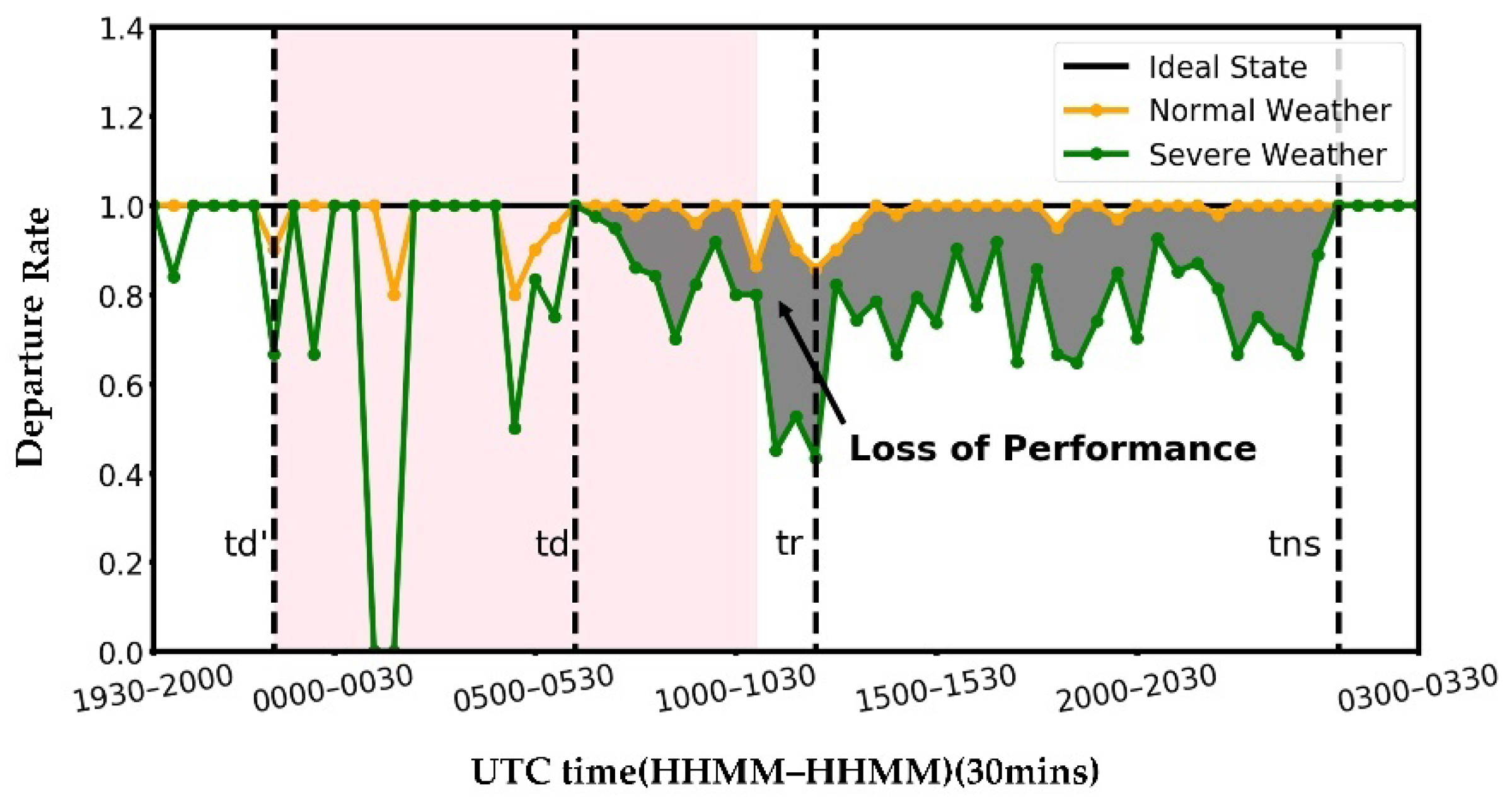
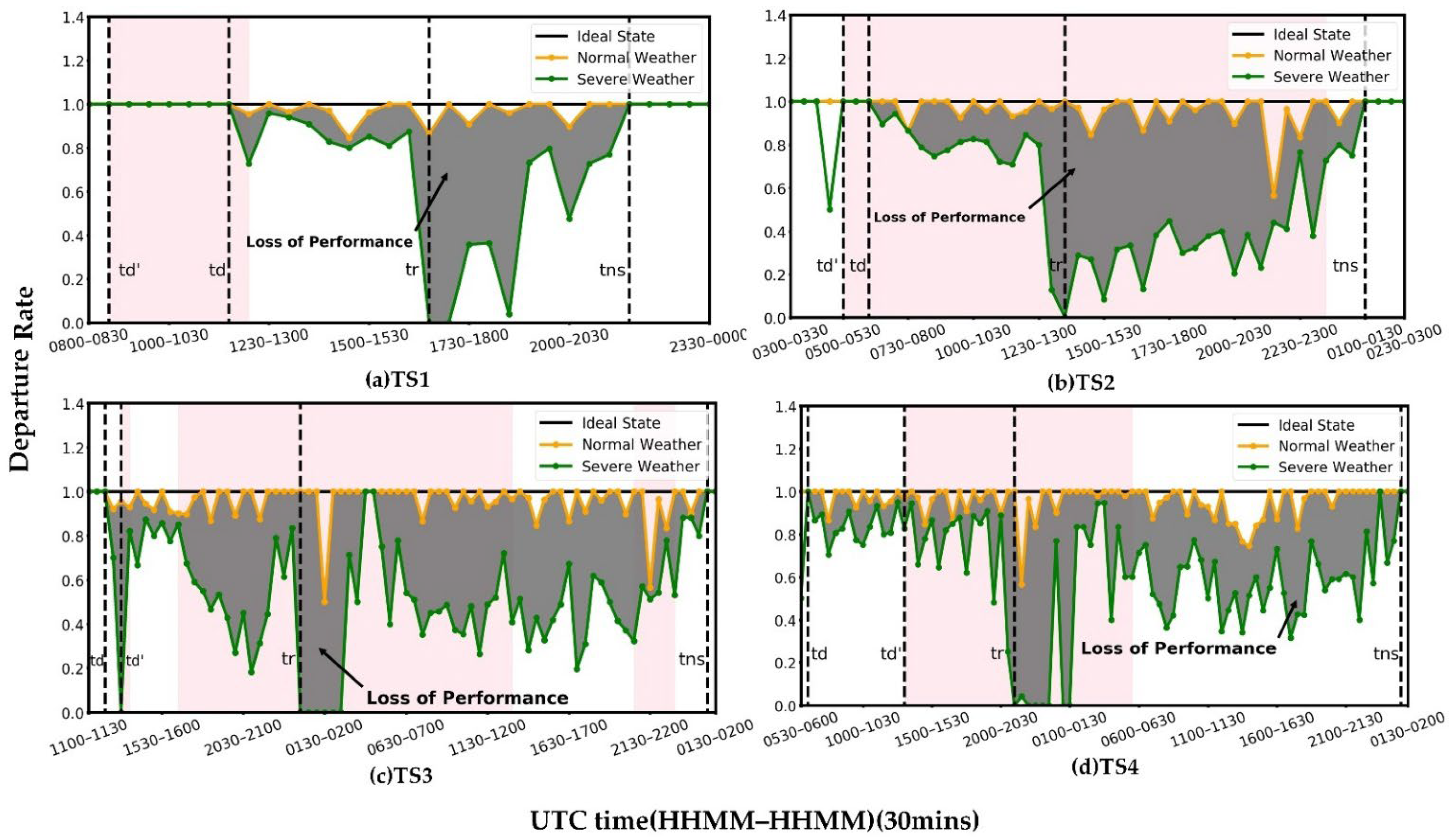
4.2. Resilience Assessment of Airport Flight Operations under Severe Weather
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, S.M. Research on the Impact of Severe Weather on Flight Delay. Master Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2017. (In Chinese). [Google Scholar]
- Zhou, L.; Chen, L. Measuring the performance of airport resilience to severe weather events. Transp. Res. Part D Transp. Environ. 2020, 83, 102–362. [Google Scholar] [CrossRef]
- Civil Aviation Administration of China. 2020 Civil Aviation Industry Development Statistical Bulletin. Available online: http://www.caac.gov.cn/XXGK/XXGK/TJSJ/202006/t20200605_202977.html (accessed on 10 October 2021).
- Kicinger, R.; Sabhnani, G.; Krishna, S. Comparison of the Impacts of Airport Terminal/Surface Weather Hazards. In Proceedings of the Aiaa Guidance, Navigation, & Control Conference, Portland, OR, USA, 8–11 August 2011. [Google Scholar]
- Markovic, D.; Hauf, T.; Röhner, P. A statistical study of the weather impact on punctuality at Frankfurt Airport. Meteorol. Appl. 2010, 15, 293–303. [Google Scholar] [CrossRef]
- Inniss, T.R.; Ball, M.O. Estimating one-parameter airport arrival capacity distributions for air traffic flow management. Air Traffic Control Q. 2004, 12, 223–251. [Google Scholar] [CrossRef] [Green Version]
- Holling, S.C. Resilience and Stability of Ecological Systems. Annu. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Hosseini, S.; Barker, K.; Ramirez-Marquez, J.E. A Review of definitions and measures of system resilience. Reliab. Eng. Syst. Saf. 2015, 145, 47–61. [Google Scholar] [CrossRef]
- Murray-Tuite, P.M. A comparison of transportation network resilience under simulated system optimum and user equilibrium conditions. In Proceedings of the 2006 Winter Simulation Conference, Monterey, CA, USA, 3–6 December 2006; pp. 1398–1405. [Google Scholar]
- Ip, W.H.; Wang, D. Resilience and friability of transportation networks: Evaluation, analysis and optimization. IEEE Syst. J. 2011, 5, 189–198. [Google Scholar] [CrossRef]
- Nogal, M.; O’Connor, A.; Caulfield, B. Resilience of traffic networks: From perturbation to recovery via a dynamic restricted equilibrium model. Reliab. Eng. Syst. Saf. 2016, 156, 84–96. [Google Scholar] [CrossRef]
- Zhang, L.; Zeng, G.; Li, D. Scale-free resilience of real traffic jams. Proc. Natl. Acad. Sci. USA 2019, 116, 8673–8678. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.; Barzel, B.; Barabási, A.L. Universal resilience patterns in complex networks. Nature 2016, 530, 307–312. [Google Scholar] [CrossRef]
- Gomes, J.O.; Woods, D.D.; Carvalho, P.V.R. Resilience and brittleness in the offshore helicopter transportation system: The identification of constraints and sacrifice decisions in pilot’s work. Reliab. Eng. Syst. Saf. 2009, 94, 311–319. [Google Scholar] [CrossRef]
- Gargiulo, F.; Pascarella, D.; Errico, A. Resilience management problem in ATM systems as a shortest path problem. J. Air Transp. Manag. 2016, 56, 57–65. [Google Scholar]
- Palumbo, R.; Filippone, E. A Quantitative Approach to Resilience Engineering for the Future ATM System: Case Studies Results. In Proceedings of the 12th USA/Europe Air Traffic Management Research and Development Seminar (ATM2017), Seattle, WA, USA, 26–30 June 2017. [Google Scholar]
- Chandramouleeswaran, K.R.; Tran, H.T. Data-driven resilience quantification of the US Air transportation network. In Proceedings of the 2018 Annual IEEE International Systems Conference (SysCon), Vancouver, BC, Canada, 23–26 April 2018; pp. 1–7. [Google Scholar]
- Wang, X.L.; Miao, S.F.; Tang, J.Q. Vulnerability and Resilience Analysis of the Air Traffic Control Sector Network in China. Sustainability 2020, 129, 3749. [Google Scholar] [CrossRef]
- Wang, X.L.; Shi, Z.B.; Chen, Z.Y. Air traffic network motif recognition and sub-graph structure resilience evaluation. Acta Aeronaut. Astronaut. Sin. 2021, 42, 558–568. (In Chinese) [Google Scholar]
- Wang, X.; Miao, S. Structural characteristics and resilience assessment of airspace sector network. J. Beijing Univ. Aeronaut. Astronaut. 2021, 47, 904–911. (In Chinese) [Google Scholar]
- Li, B.J.; Du, W.B.; Liu, C. Topologic and dynamic resilience model of Chinese airport network. In Proceedings of the 11th IEEE International Conference on Control & Automation (ICCA), Taichung, China, 18–20 June 2014; pp. 1460–1465. [Google Scholar]
- Aksu, D.T.; Ozdamar, L. A mathematical model for post-disaster road restoration: Enabling accessibility and evacuation. Transp. Res. Part E Logist. Transp. Rev. 2014, 61, 56–57. [Google Scholar] [CrossRef]
- Kepaptsoglou, K.L.; Konstantinidou, M.A.; Karlaftis, M.G.; Stathopoulos, A. Planning postdisaster operations in a highway network: Network design model with interdependencies. Transp. Res. Rec. 2014, 2459, 1–10. [Google Scholar] [CrossRef]
- Testa, A.C.; Furtado, M.N.; Alipour, A. Resilience of coastal transportation networks faced with extreme climatic events. Transp. Res. Rec. 2015, 2532, 29–36. [Google Scholar] [CrossRef]
- Janić, M. Modelling the resilience, friability and costs of an air transport network affected by a large-scale disruptive event. Transp. Res. 2015, 71, 1–16. [Google Scholar]
- Xu, X.H. Research on Robustness of Air Transportation Network and Flight Delay Correlation. Master Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2018. (In Chinese). [Google Scholar]
- Wang, Y.; Zhan, J.; Xu, X. Measuring the resilience of an airport network. Chin. J. Aeronaut. 2019, 32, 2694–2705. [Google Scholar] [CrossRef]
- Bruneau, M.; Chang, S.E.; Eguchi, R.T. A framework to quantitatively Assess and enhance the seismic resilience of communities. Earthq. Spectra 2003, 19, 733–752. [Google Scholar] [CrossRef] [Green Version]
- Chang, S.E.; Shinozuka, M. Measuring Improvements in the Disaster Resilience of Communities. Earthq. Spectra 2004, 20, 739–755. [Google Scholar] [CrossRef]
- McDaniels, T.; Chang, S.; Cole, D. Fostering resilience to extreme events within infrastructure systems: Characterizing decision contexts for mitigation and adaptation. Glob. Environ. Chang. 2008, 18, 310–318. [Google Scholar] [CrossRef]
- Bueno, N.P. Assessing the resilience of small socio-ecological systems based on the dominant polarity of their feedback structure. Syst. Dyn. Rev. 2012, 28, 351–360. [Google Scholar] [CrossRef]
- Filippini, R.; Silva, A. A modeling framework for the resilience analysis of networked systems-of-systems based on functional dependencies. Reliab. Eng. Syst. Saf. 2014, 125, 82–91. [Google Scholar] [CrossRef]
- Alessandri, A.; Filippini, R. Evaluation of Resilience of Interconnected Systems Based on Stability Analysis. In Proceedings of the International Workshop on Critical Information Infrastructures Security, Lillehammer, Norway, 17–18 September 2012. [Google Scholar]
- Henry, D.; Ramirez-Marquez, J.E. Generic metrics and quantitative approaches for system resilience as a function of time. Reliab. Eng. Syst. Saf. 2012, 99, 114–122. [Google Scholar] [CrossRef]
- Nan, C.; Sansavini, G. A quantitative method for assessing resilience of interdependent infrastructures. Reliab. Eng. Syst. Saf. 2017, 157, 35–53. [Google Scholar] [CrossRef]
- Vugrin, E.; Warren, D.; Ehlen, M. A Framework for Assessing the Resilience of Infrastructure and Economic Systems. In Sustainable and Resilient Critical Infrastructure Systems; Springer: Heidelberg, Germany, 2010; pp. 77–116. [Google Scholar]

| Phases | Time Scope | Capabilities | Measurements |
|---|---|---|---|
| Original steady phase | - | - | |
| Response phase | Susceptibility | RST | |
| Disruptive phase | Absorptive capability | R, RAPIDP, DSS | |
| Recovery phase | Recovery and adaptive capability | RCT, RAPIRP | |
| New steady phase | Recovery capability | RA |
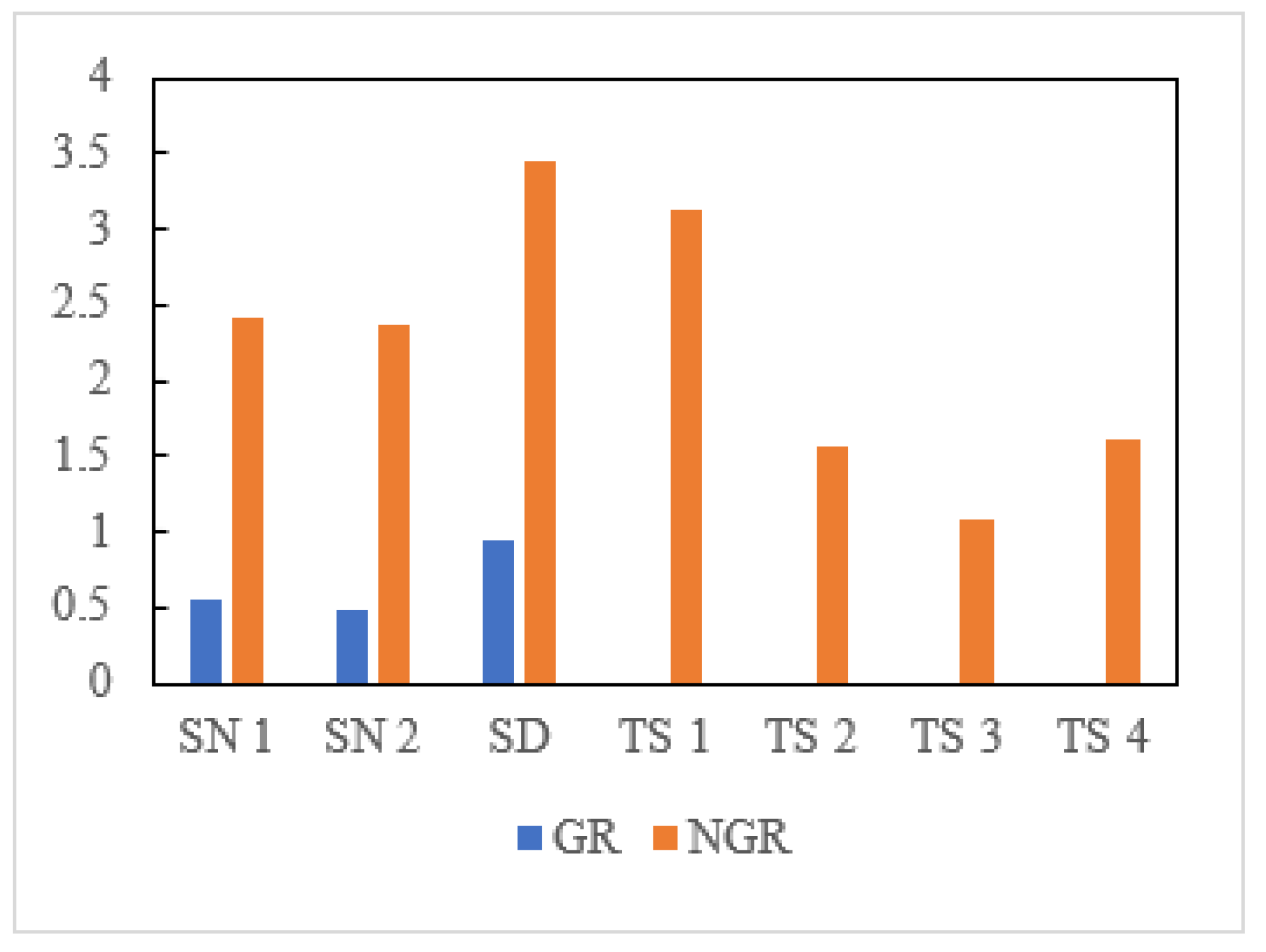
| Severe Weather Events | LOP of Ideal State | LOP of Normal Weather | Difference | Percentage Error |
|---|---|---|---|---|
| SN 1 | 6.1872 | 5.2629 | 0.9243 | 17.56% |
| SN 2 | 8.2305 | 7.3232 | 0.9073 | 12.38% |
| SD | 8.5345 | 7.8235 | 0.7110 | 9.09% |
| TS 1 | 7.0419 | 6.3723 | 0.6696 | 10.51% |
| TS 2 | 17.5957 | 15.8681 | 1.7276 | 10.89% |
| TS 3 | 33.9503 | 30.7412 | 3.2091 | 10.44% |
| TS 4 | 32.5233 | 28.6823 | 3.8410 | 13.39% |
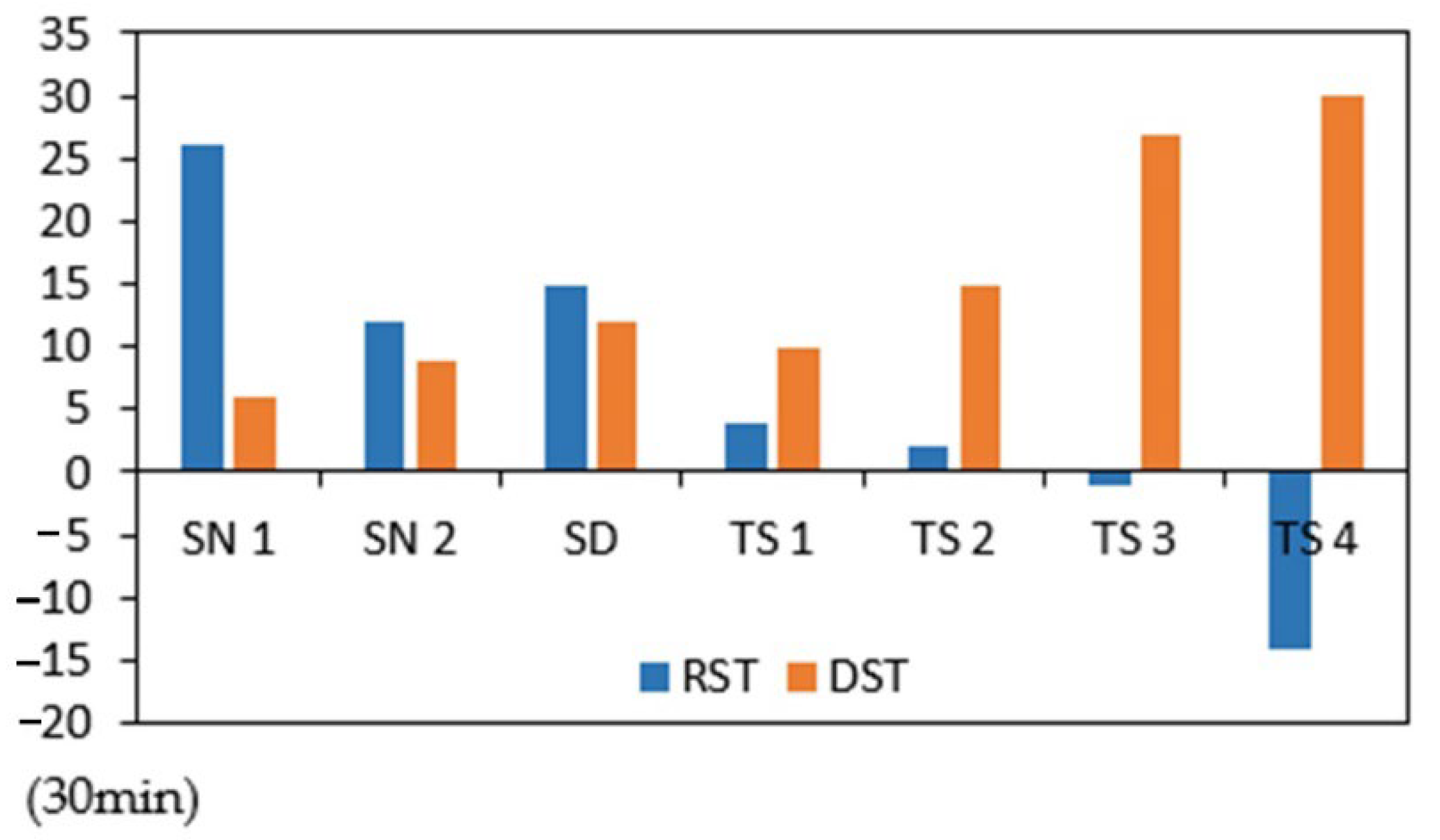
| Severe Weather Events | RST (30 mins) | DST (30 mins) | RCT (30 mins) | RAPIDP | RAPIRP |
|---|---|---|---|---|---|
| SN 1 | 26 | 6 | 11 | 0.1140 | 0.0622 |
| SN 2 | 12 | 9 | 19 | 0.0808 | 0.0383 |
| SD | 15 | 12 | 26 | 0.0472 | 0.0218 |
| TS 1 | 4 | 10 | 10 | 0.1 | 0.1 |
| TS 2 | 2 | 15 | 23 | 0.0667 | 0.0435 |
| TS 3 | −2 | 24 | 50 | 0.0417 | 0.0200 |
| TS 4 | −14 | 30 | 56 | 0.0333 | 0.0179 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Chen, Z.; Li, K. Quantifying the Resilience Performance of Airport Flight Operation to Severe Weather. Aerospace 2022, 9, 344. https://doi.org/10.3390/aerospace9070344
Wang X, Chen Z, Li K. Quantifying the Resilience Performance of Airport Flight Operation to Severe Weather. Aerospace. 2022; 9(7):344. https://doi.org/10.3390/aerospace9070344
Chicago/Turabian StyleWang, Xinglong, Ziyan Chen, and Kenan Li. 2022. "Quantifying the Resilience Performance of Airport Flight Operation to Severe Weather" Aerospace 9, no. 7: 344. https://doi.org/10.3390/aerospace9070344
APA StyleWang, X., Chen, Z., & Li, K. (2022). Quantifying the Resilience Performance of Airport Flight Operation to Severe Weather. Aerospace, 9(7), 344. https://doi.org/10.3390/aerospace9070344






