Numerical Investigation of the Aerofoil Aerodynamics with Surface Heating for Anti-Icing
Abstract
:1. Introduction
2. Methodology
3. Case Validation
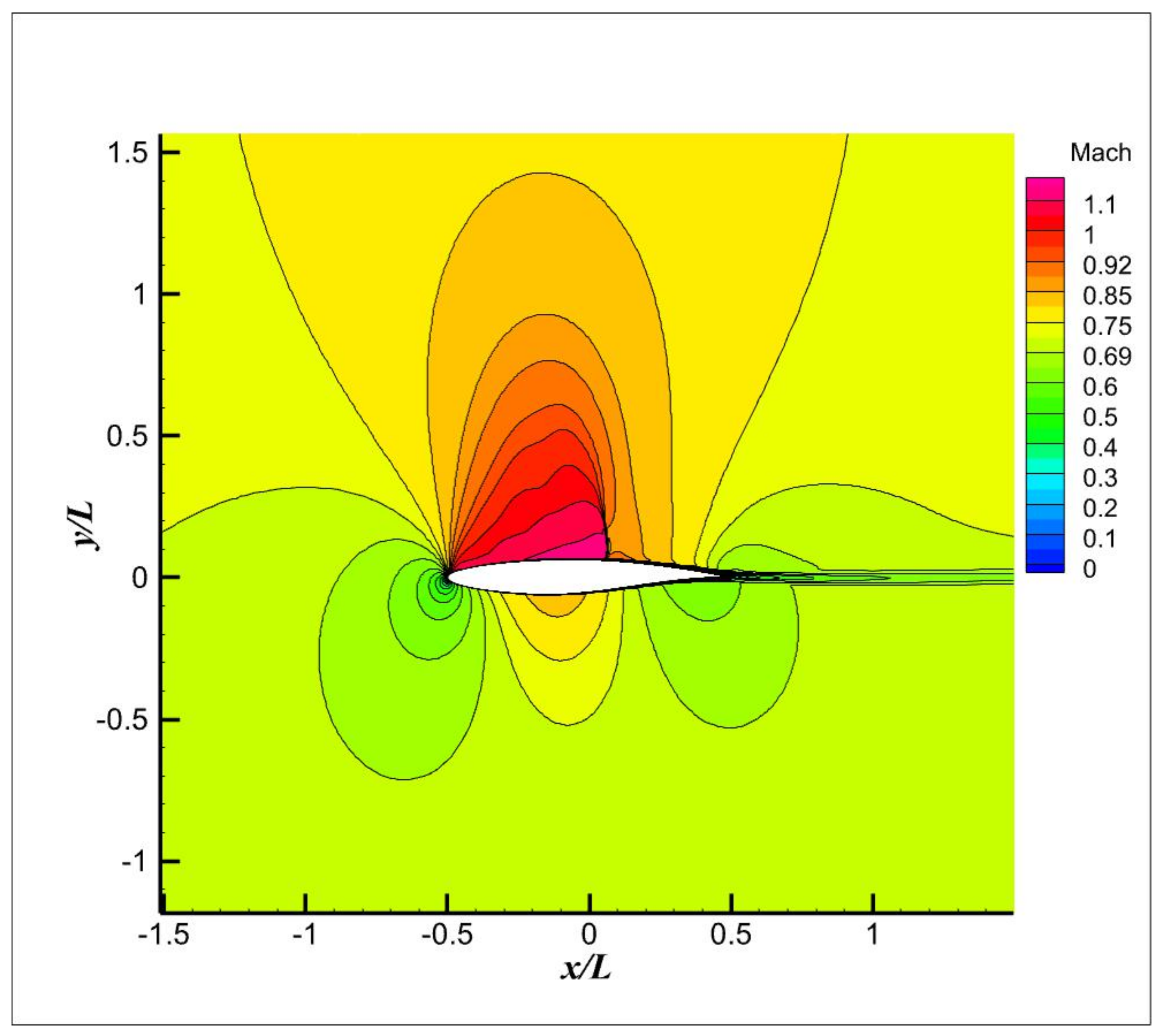
3.1. NACA0012
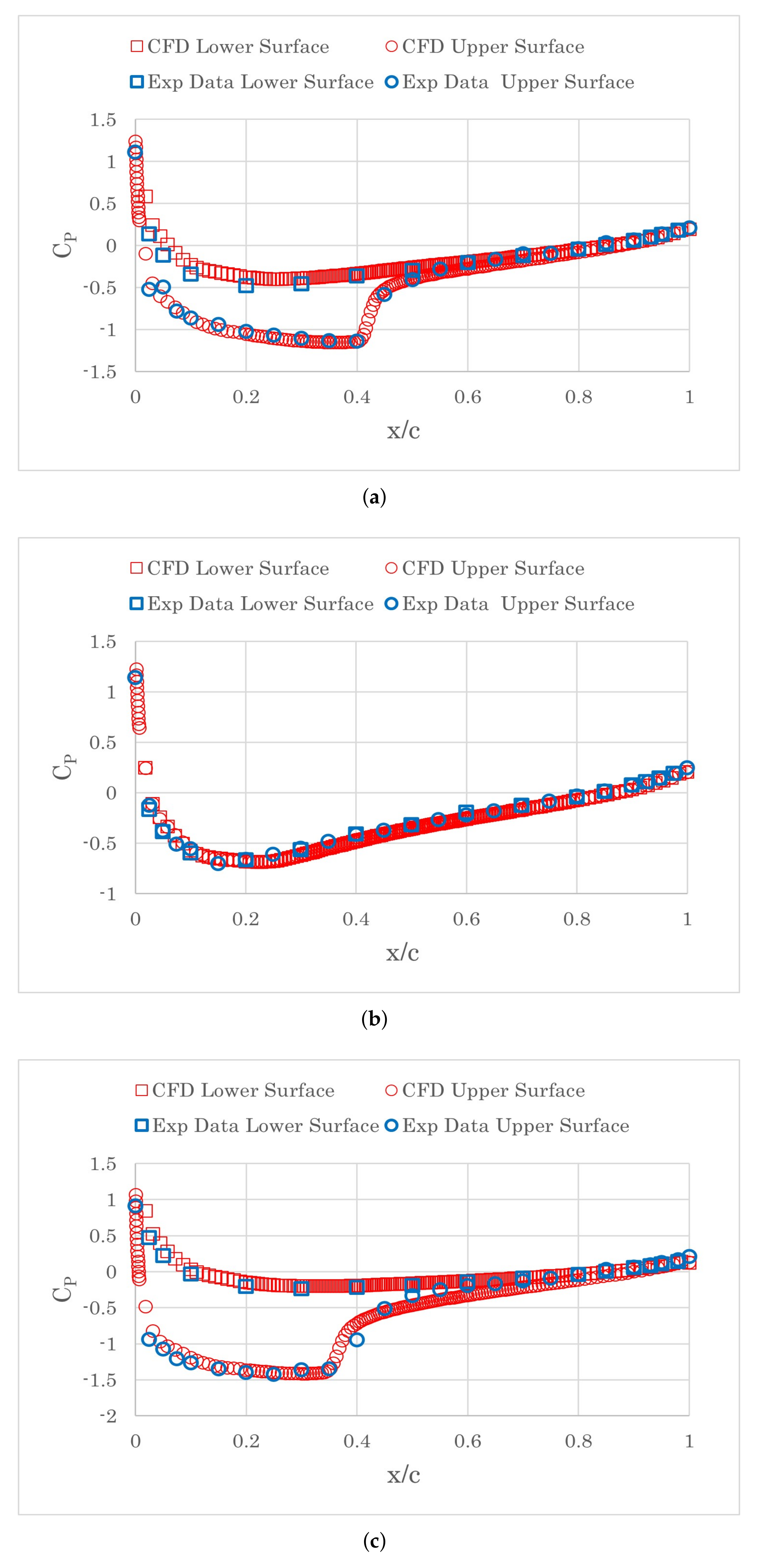
3.2. RAE2822
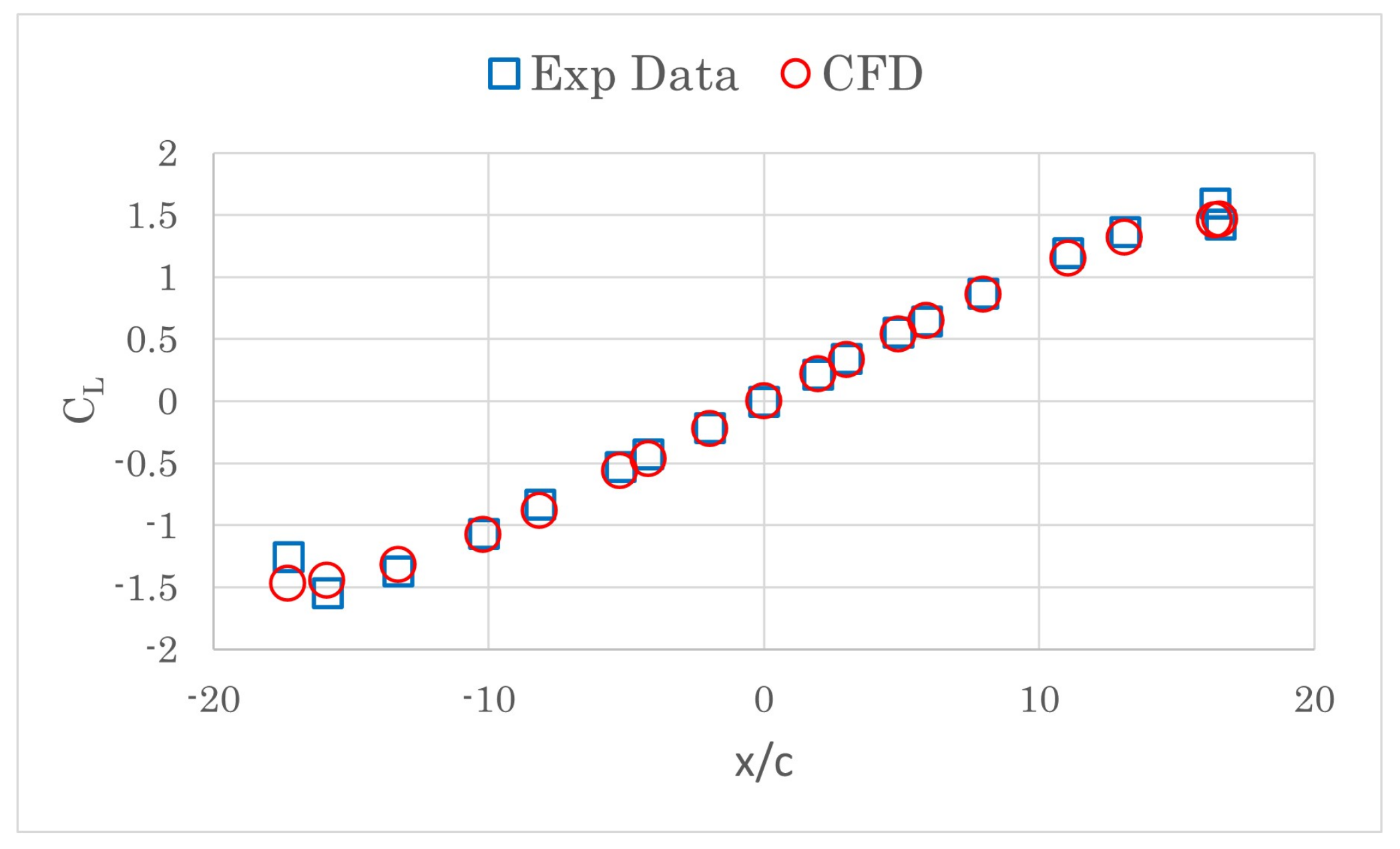
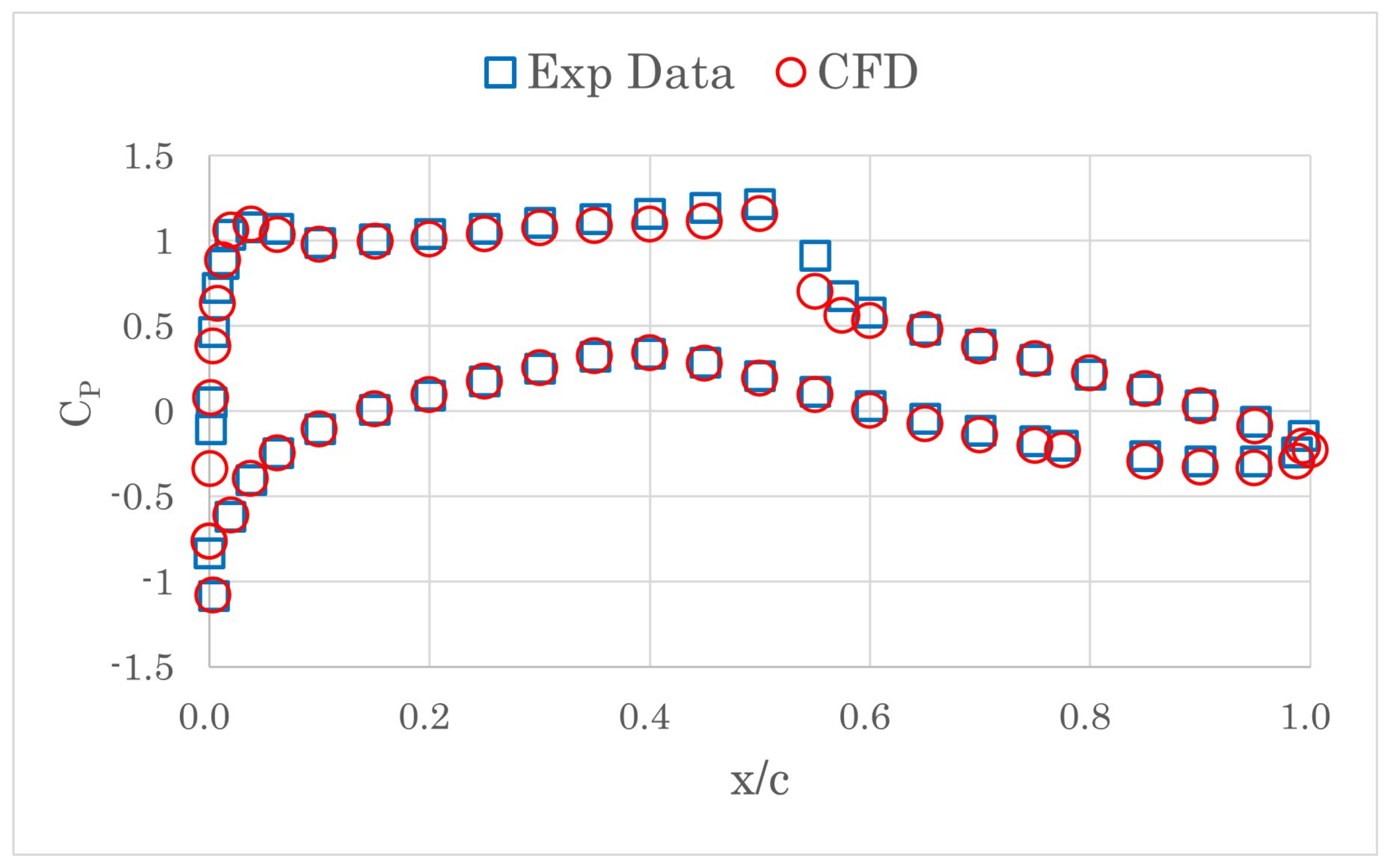
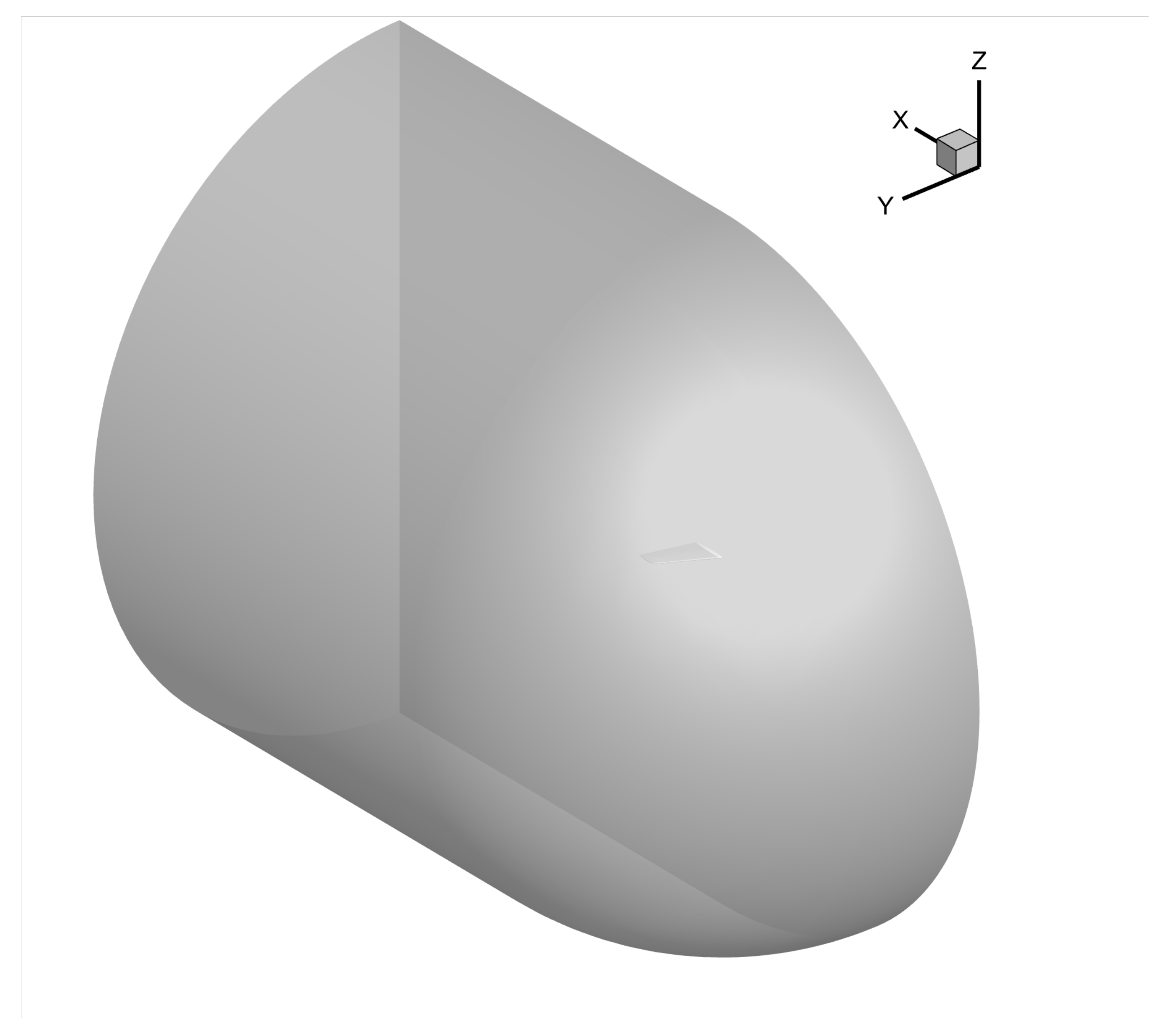
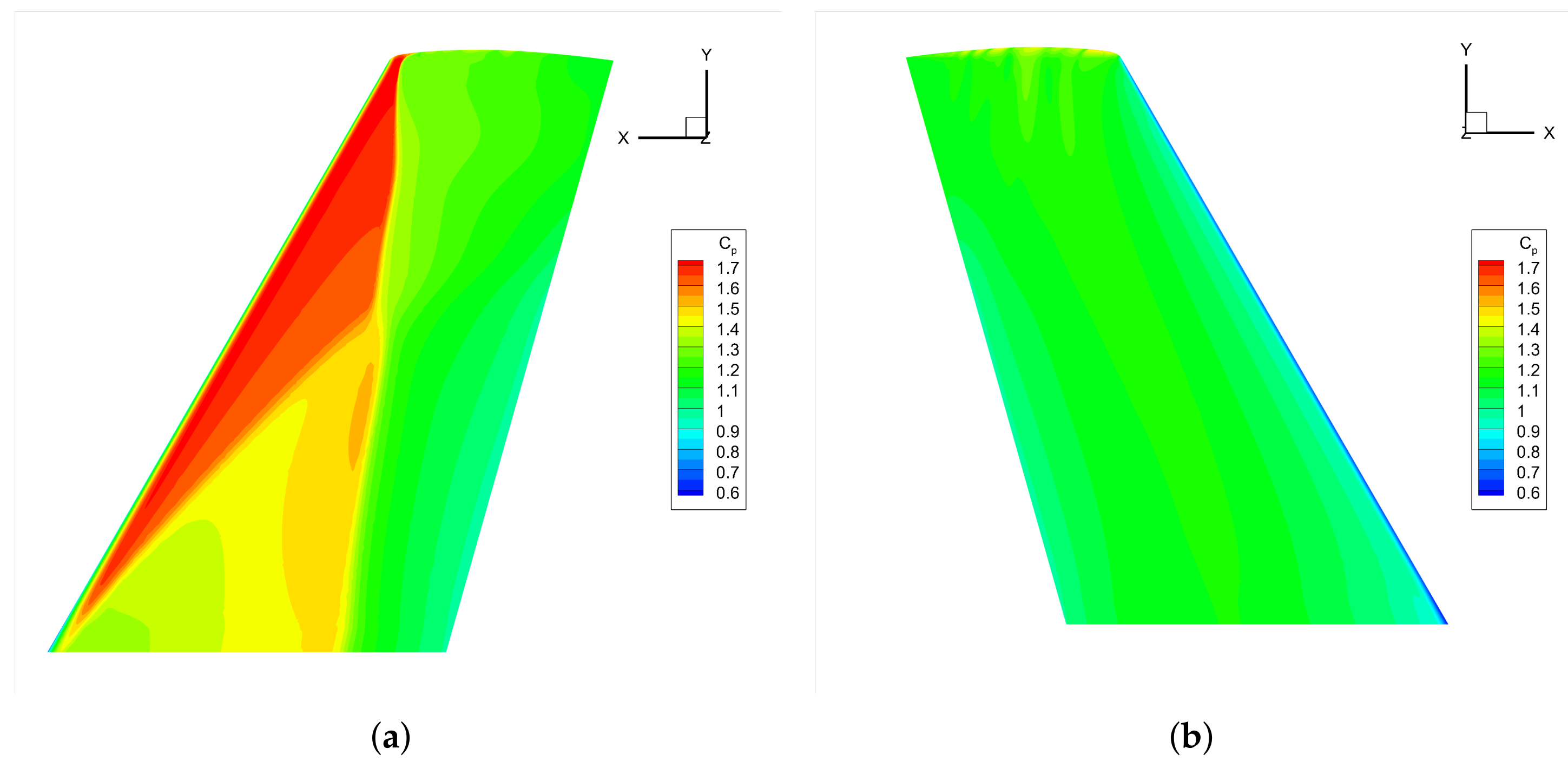
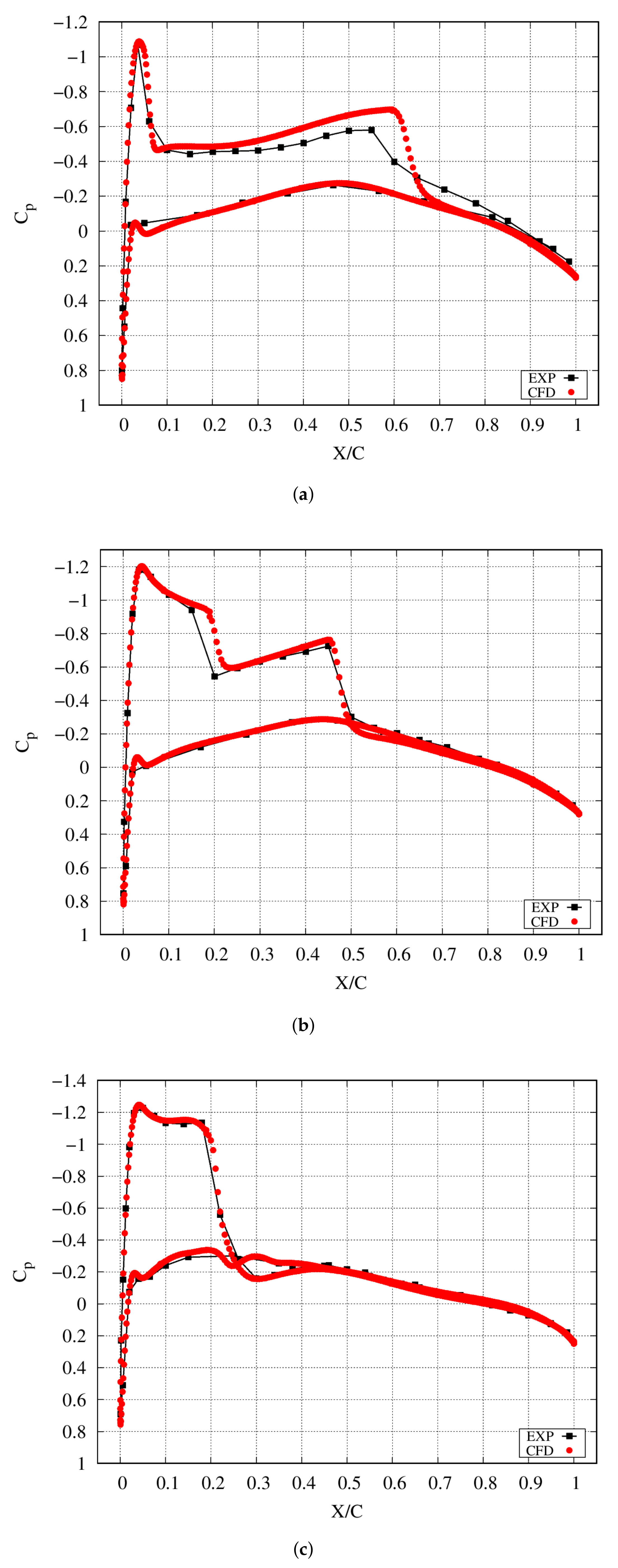
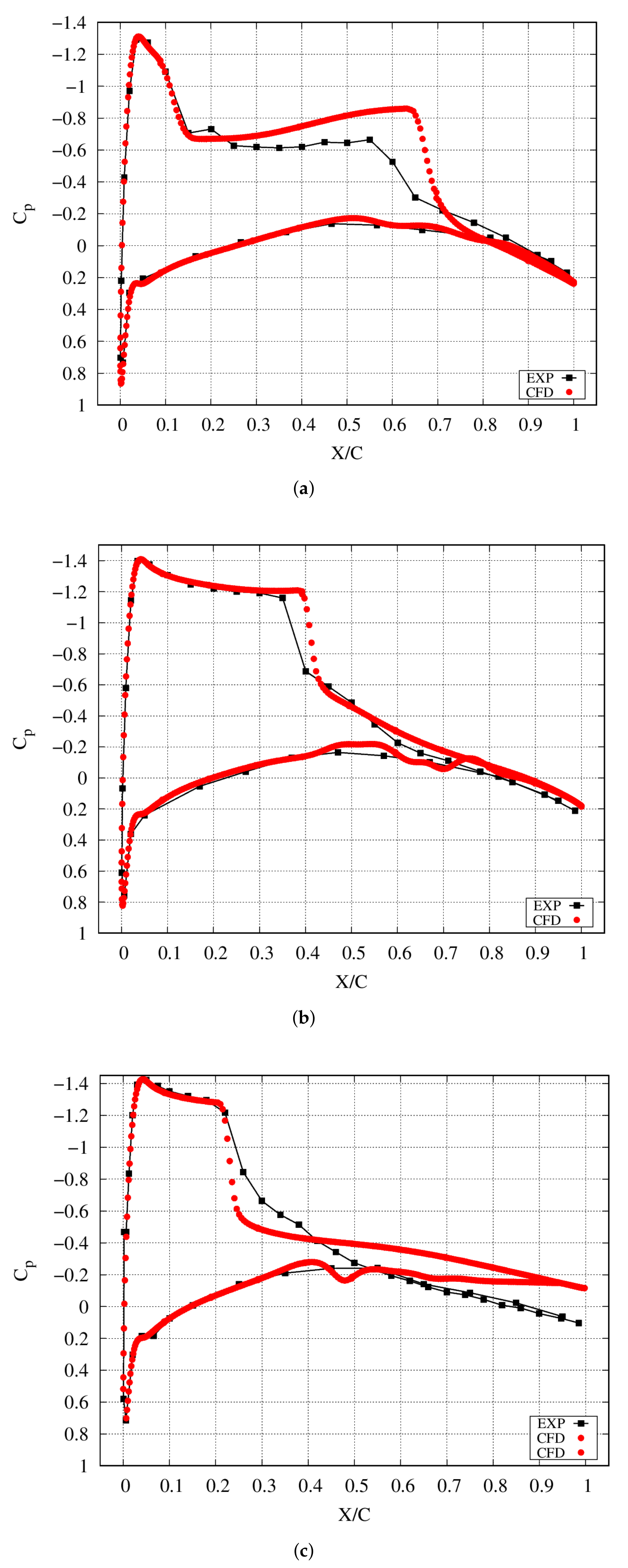
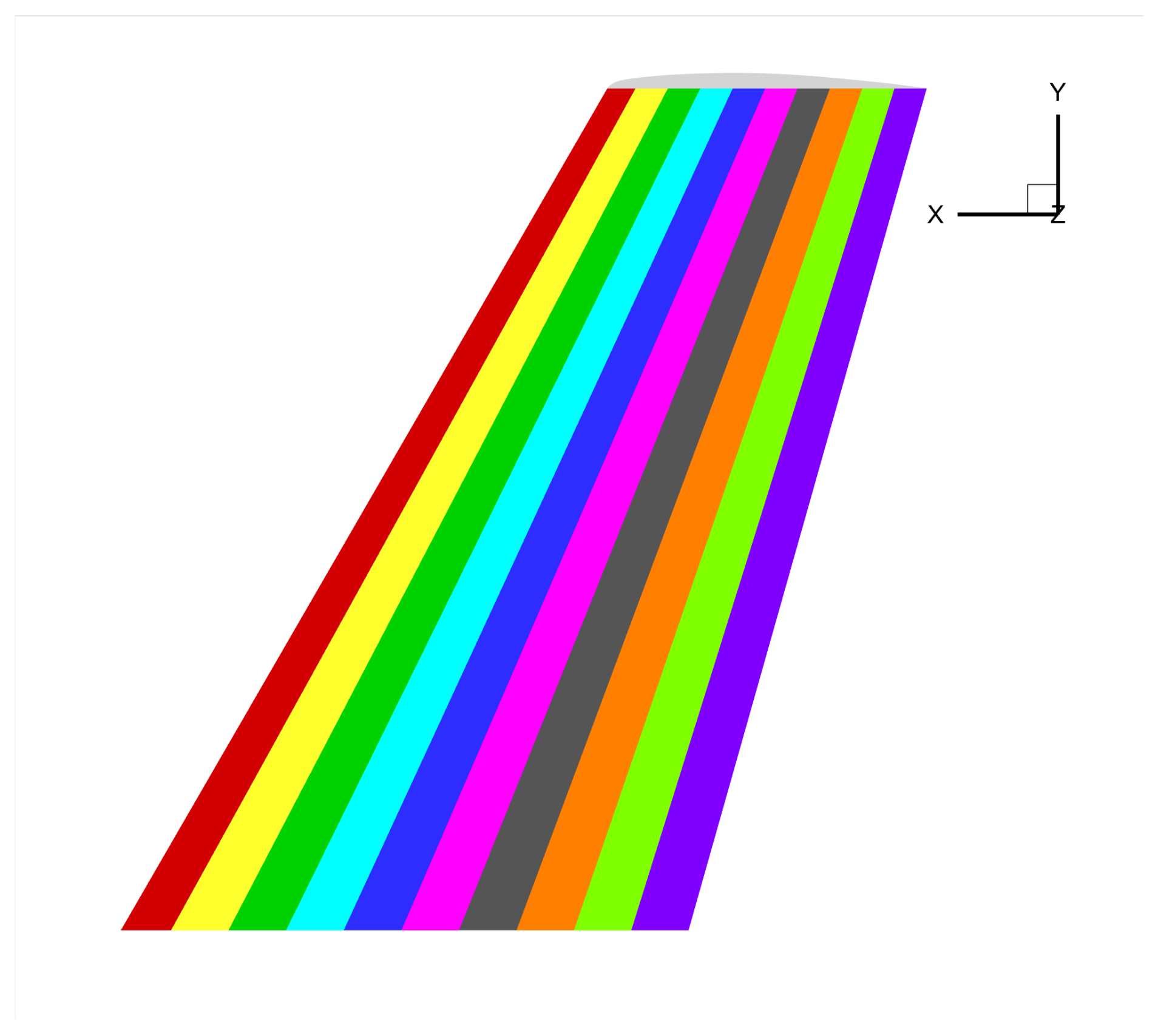
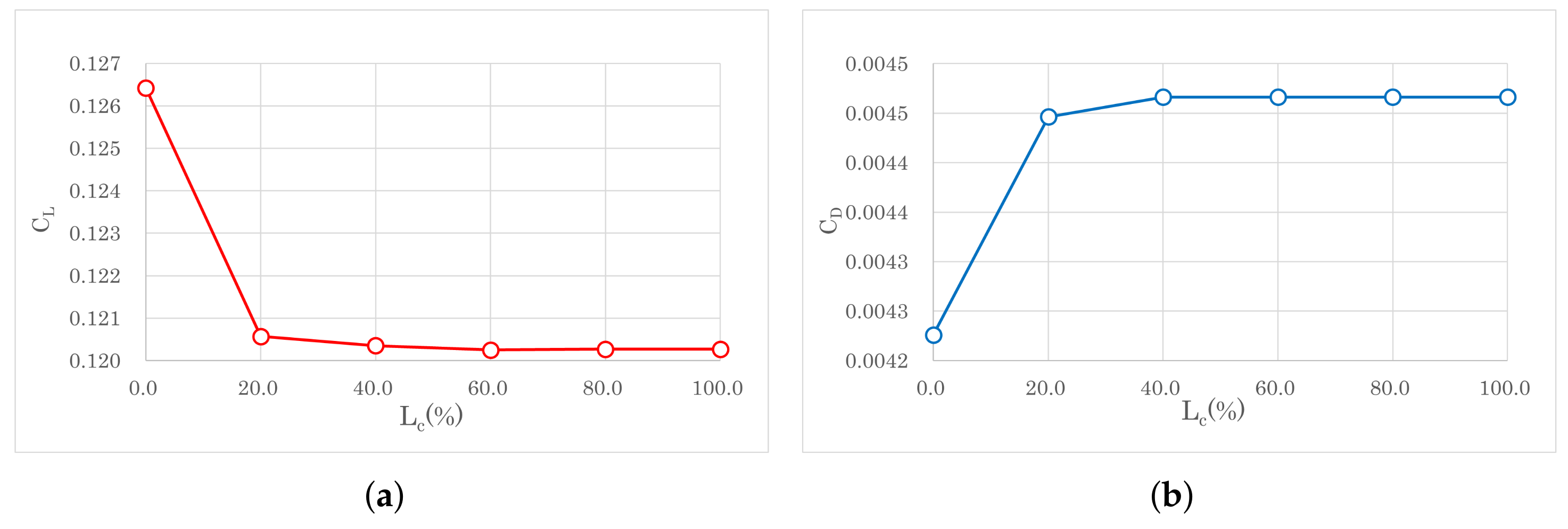
3.3. ONERA M6 Wing
4. Results
4.1. NACA0012
4.1.1. Unheated Flow
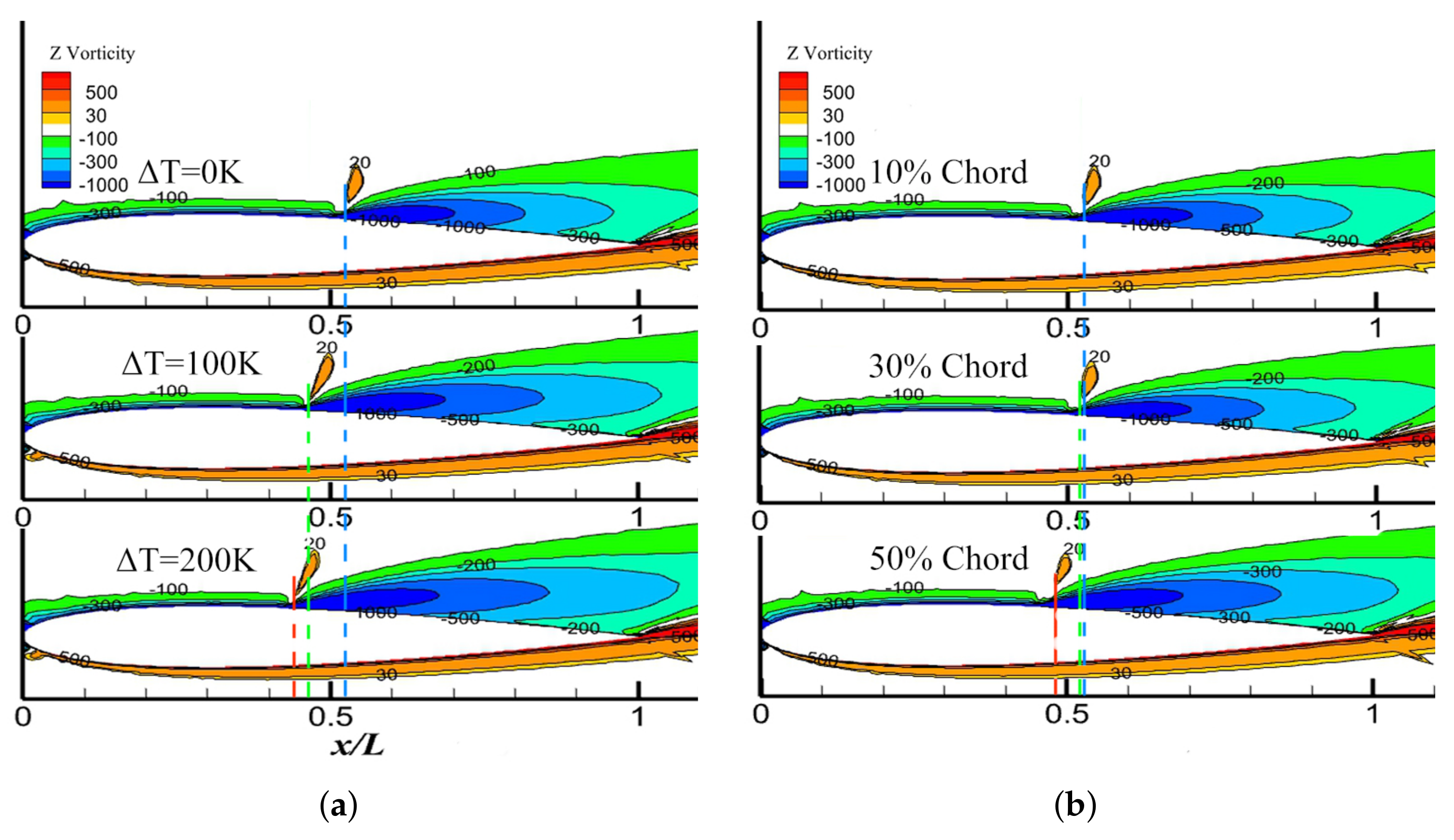
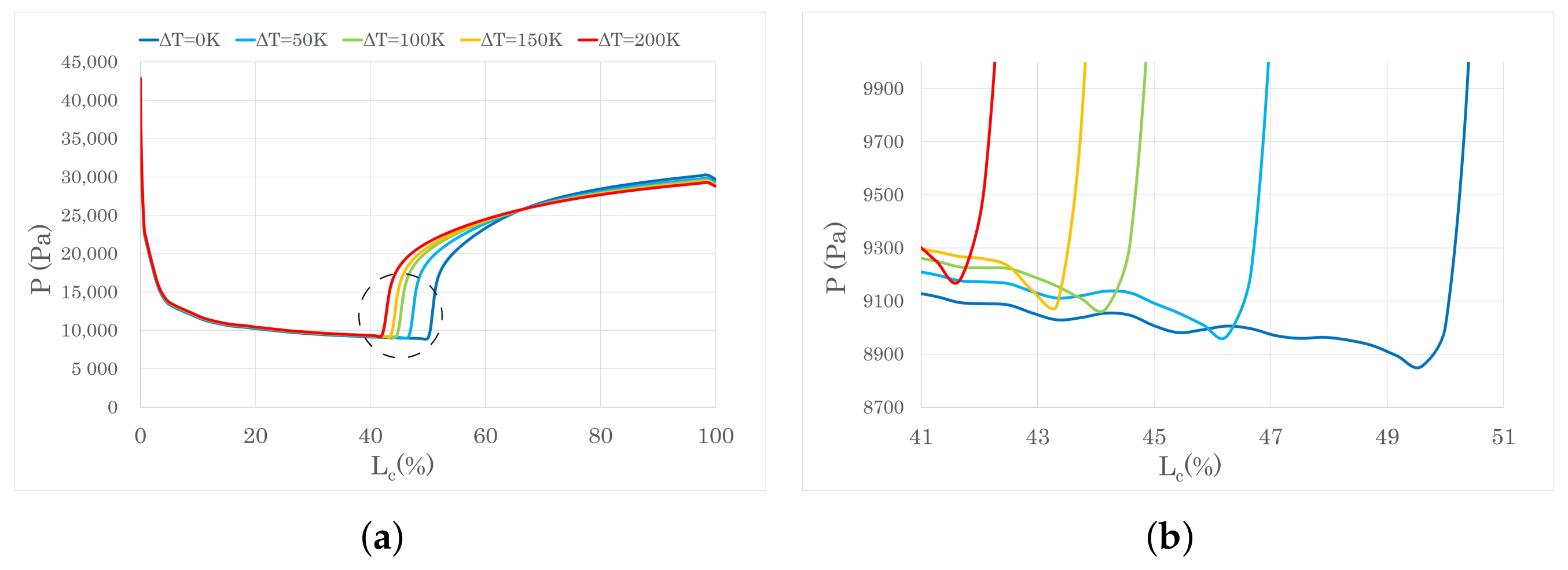
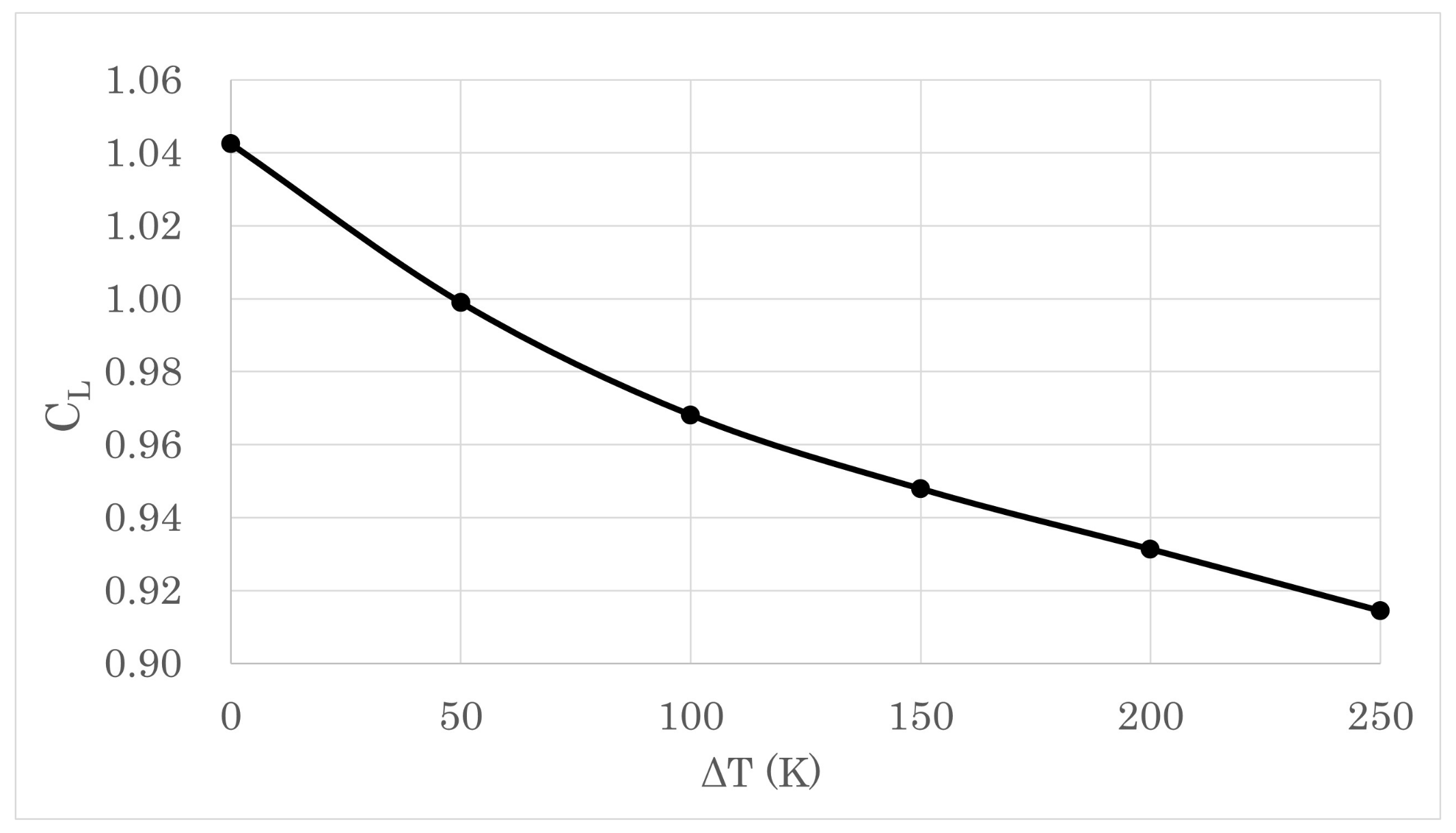
4.1.2. Uniform Surface Heating
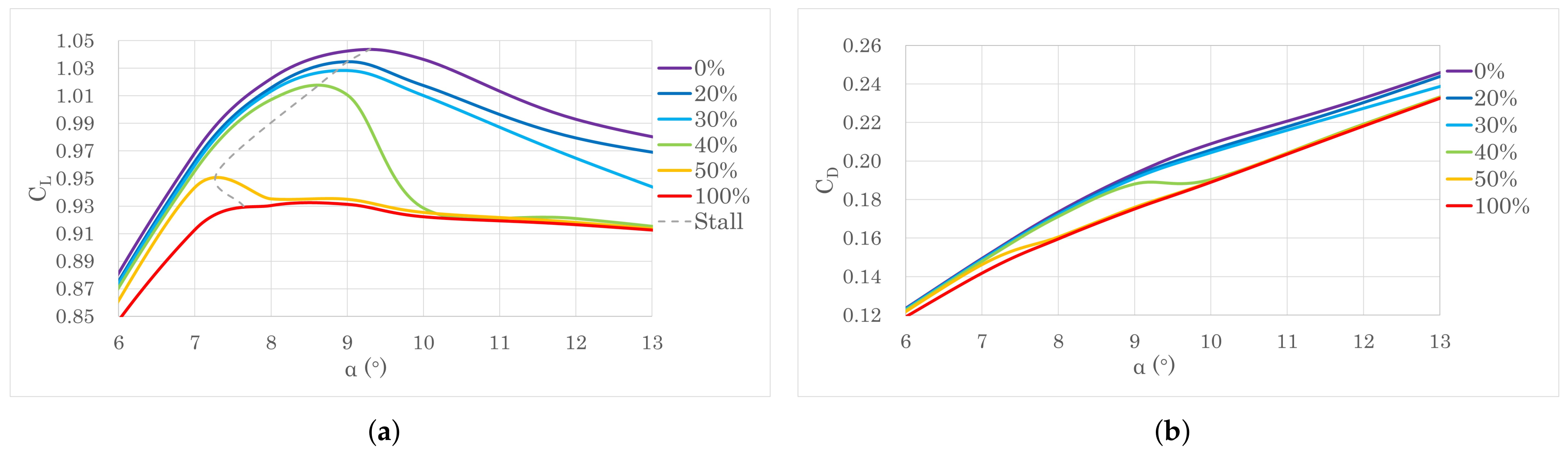
4.1.3. Non-Uniform Part-Chord Surface Heating
4.1.4. Mechanism of Surface Heating on Aerofoil Performance
4.1.5. The Heating Strategy for NACA0012
4.2. RAE2822
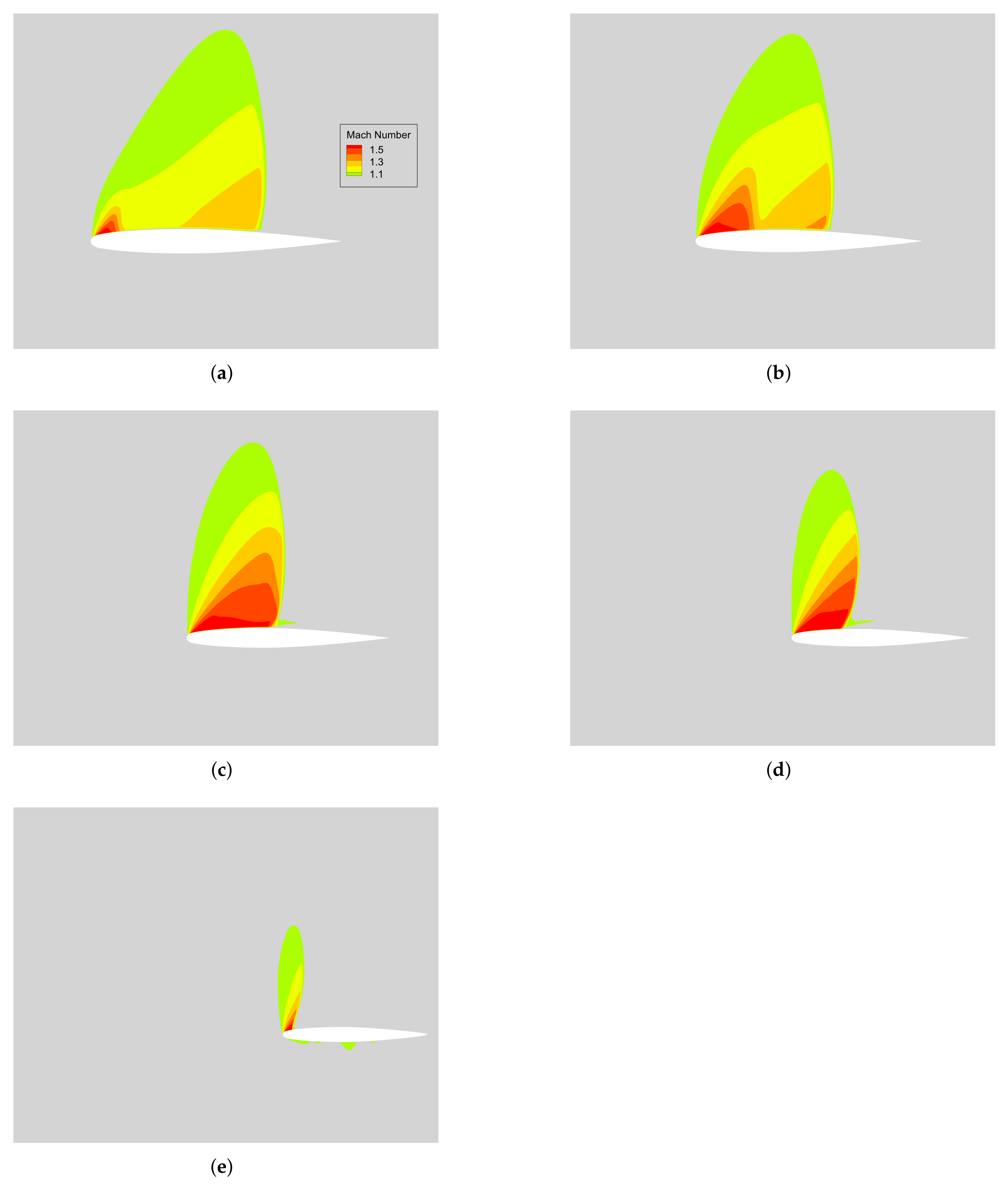
4.3. ONERA M6 Wing
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LE | Leading Edge |
| AOA | Angel of Attack |
| RANS | Reynolds-averaged Navier-Stokes |
| TE | Traling Edge |
| TI | Turbulence Intensity |
References
- Green, S. A study of US inflight icing accidents and incidents, 1978 to 2002. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; p. 82. [Google Scholar]
- Foundation, A.A.S. Aircraft Icing. In Proceedings of the Safety-Advisors, AOPA Air Safety Foundation 421 Aviation Way, Frederick, MD, USA, 8–14 May 2008; p. 16. [Google Scholar]
- Pourbagian, M.; Habashi, W.G. Aero-thermal optimization of in-flight electro-thermal ice protection systems in transient deicing mode. Int. J. Heat Fluid Flow 2015, 54, 167–182. [Google Scholar] [CrossRef]
- Filburn, T. Anti-ice and Deice Systems for Wings, Nacelles, and Instruments. In Commercial Aviation in the Jet Era and the Systems that Make it Possible; Springer: Berlin/Heidelberg, Germany, 2020; pp. 99–109. [Google Scholar]
- Goraj, Z. An overview of the deicing and anti-icing technologies with prospects for the future. In Proceedings of the 24th International Congress of the Aeronautical Sciences, Yokohama, Japan, 29 August–3 September 2004; Volume 29. [Google Scholar]
- Pourbagian, M.; Talgorn, B.; Habashi, W.G.; Kokkolaras, M.; Le Digabel, S. Constrained problem formulations for power optimization of aircraft electro-thermal anti-icing systems. Optim. Eng. 2015, 16, 663–693. [Google Scholar] [CrossRef]
- Al-Khalil, K.; Horvath, C.; Miller, D.; Wright, W.; Al-Khalil, K.; Horvath, C.; Miller, D.; Wright, W. Validation of NASA thermal ice protection computer codes. III-The validation of ANTICE. In Proceedings of the 35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1997; p. 51. [Google Scholar]
- Li, R.; Zhu, G.; Zhang, D. Investigation on the Mechanism of Heat Load Reduction for the Thermal Anti-Icing System. Energies 2020, 13, 5911. [Google Scholar] [CrossRef]
- Kim, J.; Rusak, Z.; Koratkar, N. Small-scale airfoil aerodynamic efficiency improvement by surface temperature and heat transfer. AIAA J. 2003, 41, 2105–2113. [Google Scholar] [CrossRef]
- Kazakov, A.; Kogan, M.; Kuparev, V. Optimization of laminar-turbulent transition delay by means of local heating of the surface. Fluid Dyn. 1995, 30, 563–570. [Google Scholar] [CrossRef]
- Landrum, D.; Macha, J. Influence of a heated leading edge on boundary layer growth, stability, and transition. In Proceedings of the 19th AIAA, Fluid Dynamics, Plasma Dynamics, and Lasers Conference, Honolulu, HI, USA, 8–10 June 1987; p. 1259. [Google Scholar]
- Blohm, R.W. Heat Transfer Effects on a Subsonic Delta Wing. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1973. [Google Scholar]
- Norton, D.J.; Macha, J.M.; Young, J.C. Surface temperature effect on subsonic stall. J. Spacecr. Rocket. 1973, 10, 581–587. [Google Scholar] [CrossRef]
- Stetson, K.F.; Kimmel, R.L. Surface temperature effects on boundary-layer transition. AIAA J. 1992, 30, 2782–2783. [Google Scholar] [CrossRef]
- Uranai, S.; Fukudome, K.; Mamori, H.; Fukushima, N.; Yamamoto, M. Numerical Simulation of the Anti-Icing Performance of Electric Heaters for Icing on the NACA 0012 Airfoil. Aerospace 2020, 7, 123. [Google Scholar] [CrossRef]
- Afghari, M.R.; Vaziry, M.A.; Mostofizadeh, A.R. Computational fluid dynamics investigation of finding appropriate location of fluidic anti-icing protective panel on leading edge of wing. Proc. Inst. Mech. Eng. Part J. Aerosp. Eng. 2019, 233, 698–709. [Google Scholar] [CrossRef]
- Dragan, V. Influences of surface temperature on a low camber airfoil aerodynamic performances. INCAS Bull. 2016, 8, 49. [Google Scholar]
- Fluent, A. Ansys Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2020; pp. 3–4. [Google Scholar]
- Peter. Airbus A320 Specs. Available online: https://modernairliners.com/airbus-a320-introduction/airbus-a320-specs/ (accessed on 15 October 2020).
- Sutherland, W. LII. The viscosity of gases and molecular force. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1893, 36, 507–531. [Google Scholar] [CrossRef] [Green Version]
- Handbook–Airframe, Aviation Maintenance Technician; (FAA-H-8083-31); US Department of Transportation, Federal Aviation Administration: Washington, DC, USA, 2012; Volume 2.
- Jespersen, D.C.; Pulliam, T.H.; Childs, M.L. Overflow Turbulence Modeling Resource Validation Results; NASA Technical Report, No. ARC-E-DAA-TN35216; NASA: Greenbelt, MD, USA, 2016.
- McDevitt, J.B.; Okuno, A.F. Static and Dynamic Pressure Measurements on a NACA 0012 Airfoil in the Ames High Reynolds Number Facility; National Aeronautics and Space Administration, Scientific and Technical: Washington, DC, USA, 1985; Volume 2485.
- Cook, P.; McDonald, M.; Firmin, M. Aerofoil rae 2822-pressure distributions, and boundary layer and wake measurements. experimental data base for computer program assessment. AGARD Rep. AR 1979, A6-1, 182–258. [Google Scholar]
- Slater, J.W. RAE 2822 Transonic Airfoil: Study 4. 2002. Available online: https://www.grc.nasa.gov/www/wind/valid/raetaf/raetaf04/raetaf04.html (accessed on 10 February 2021).
- Schmitt, V. Pressure distributions on the ONERA M6-wing at transonic mach numbers, experimental data base for computer program assessment. AGARD AR-138 1979, B1-1, 327–370. [Google Scholar]
- Cao, Y.; Tan, W.; Wu, Z. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018, 75, 353–385. [Google Scholar] [CrossRef]


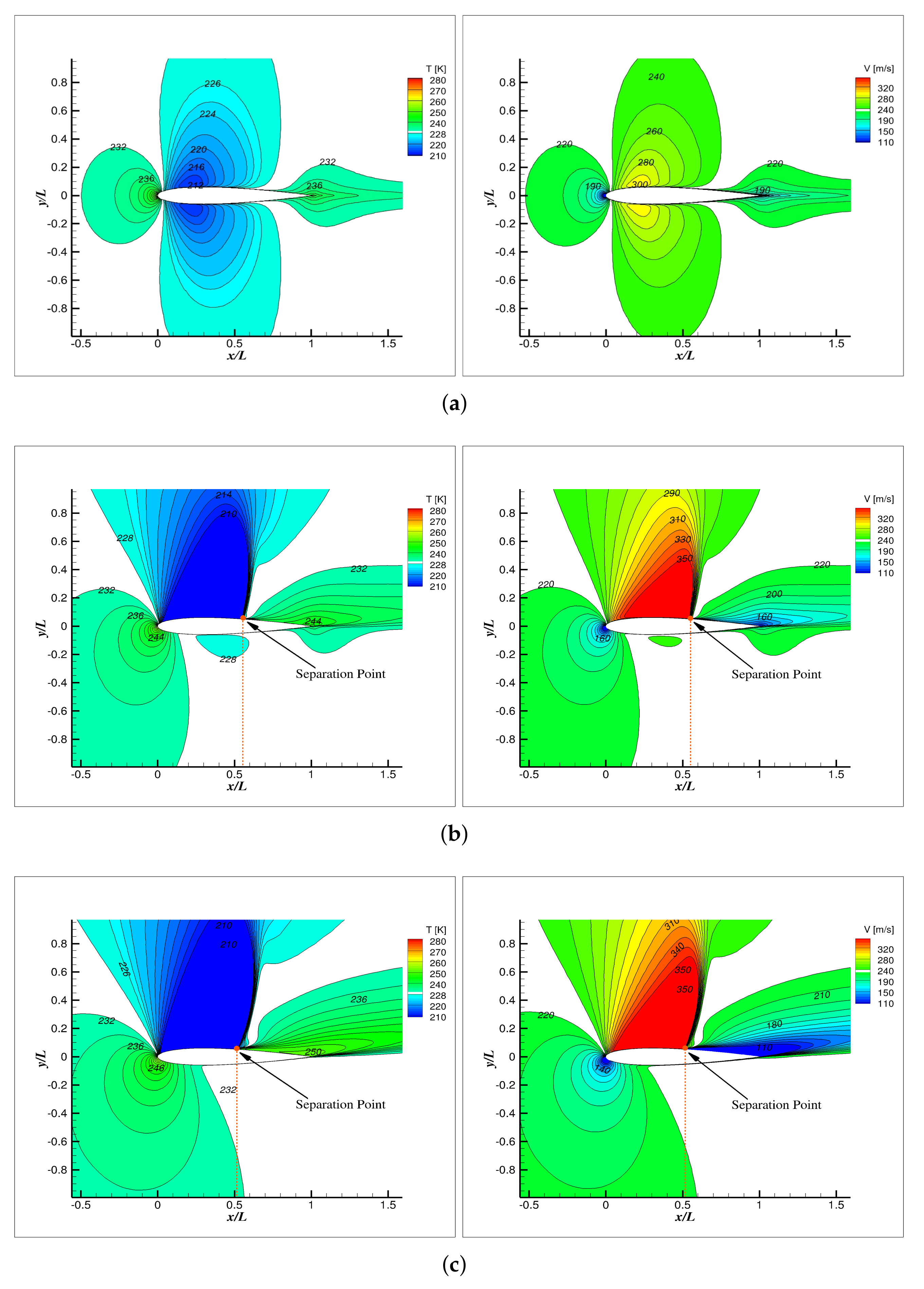
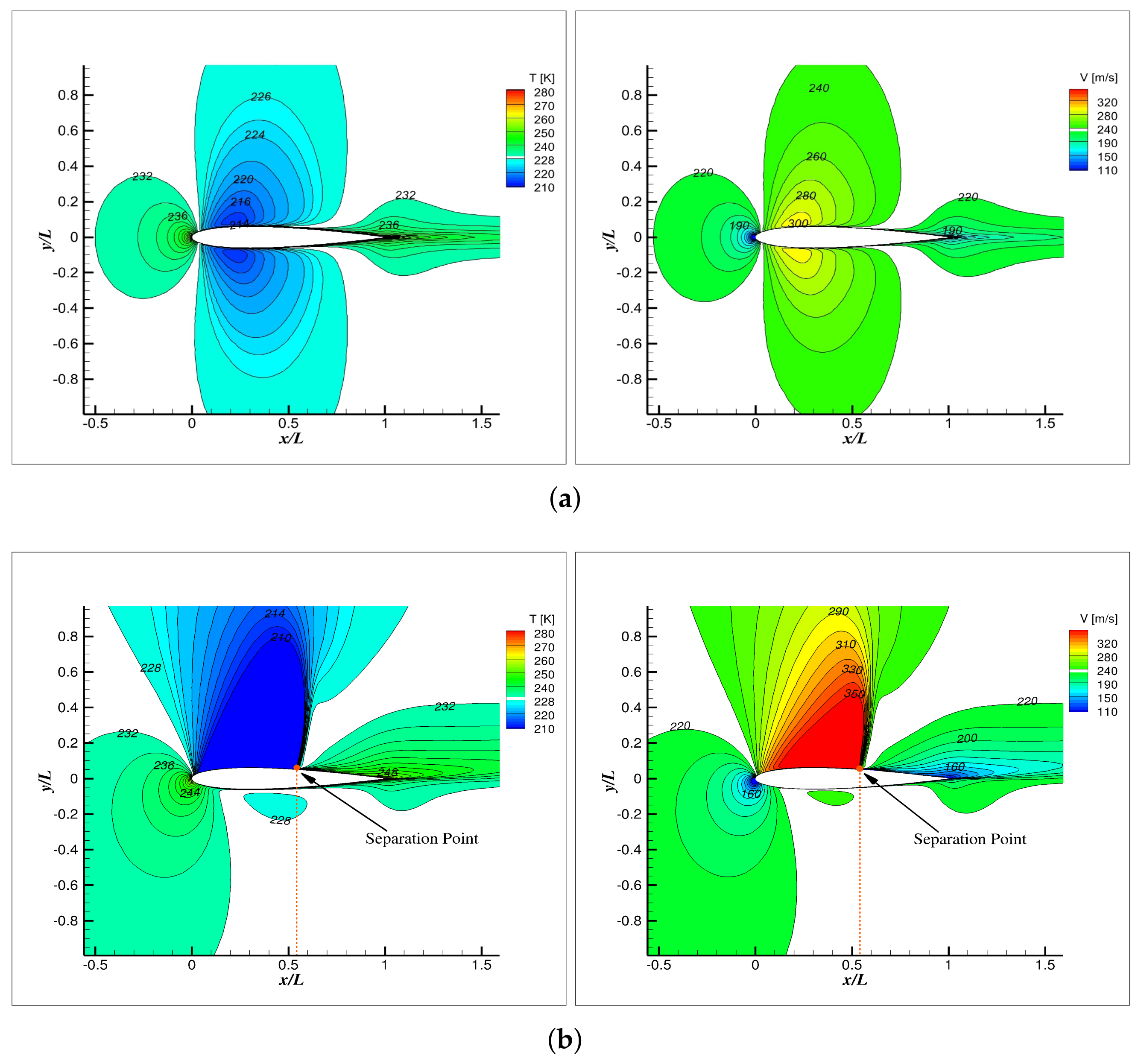
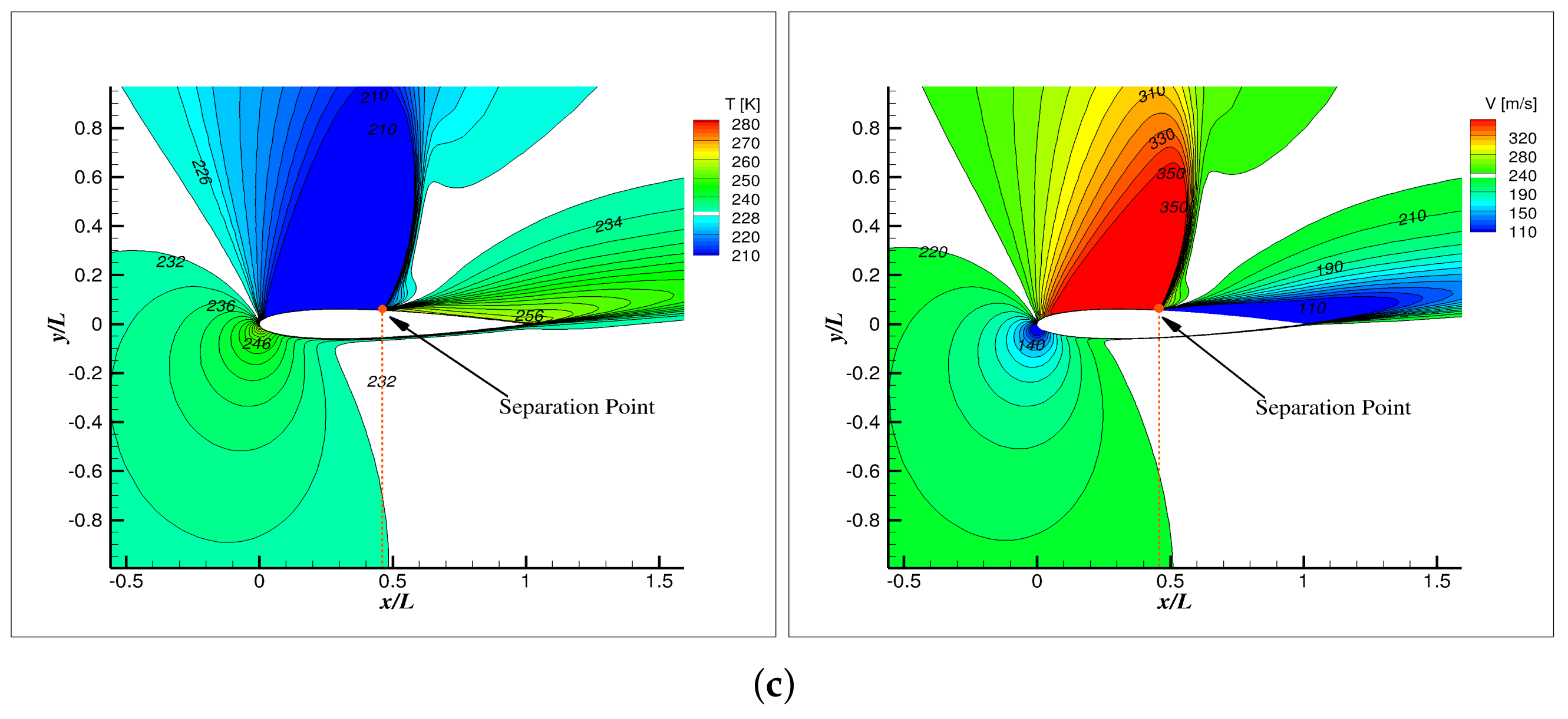
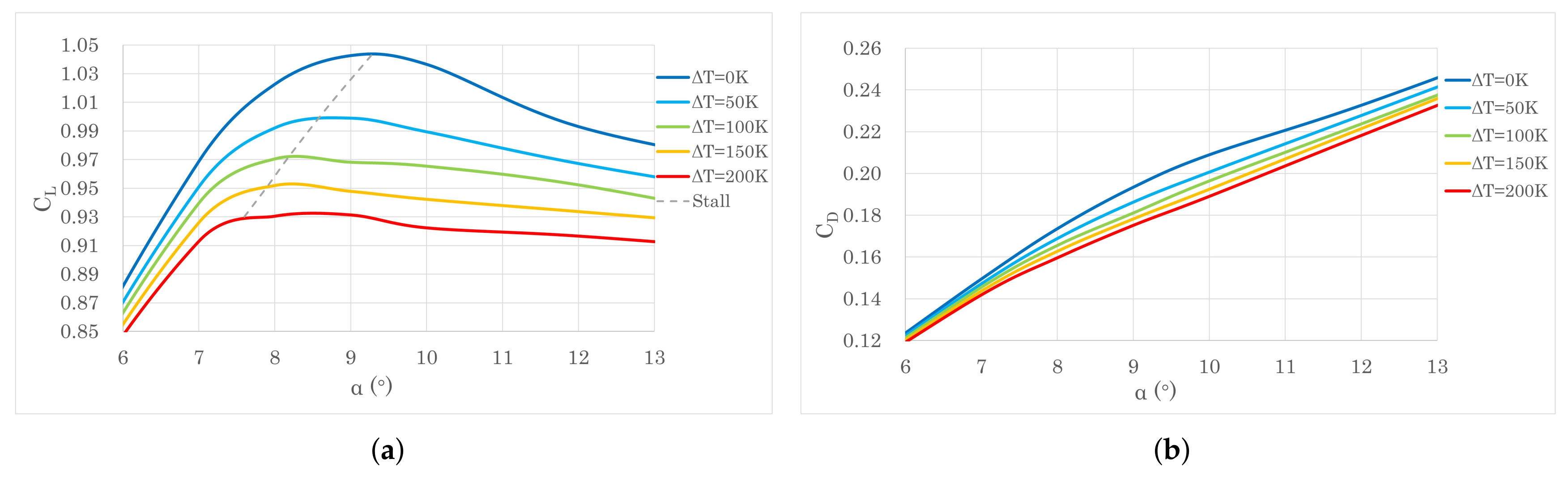



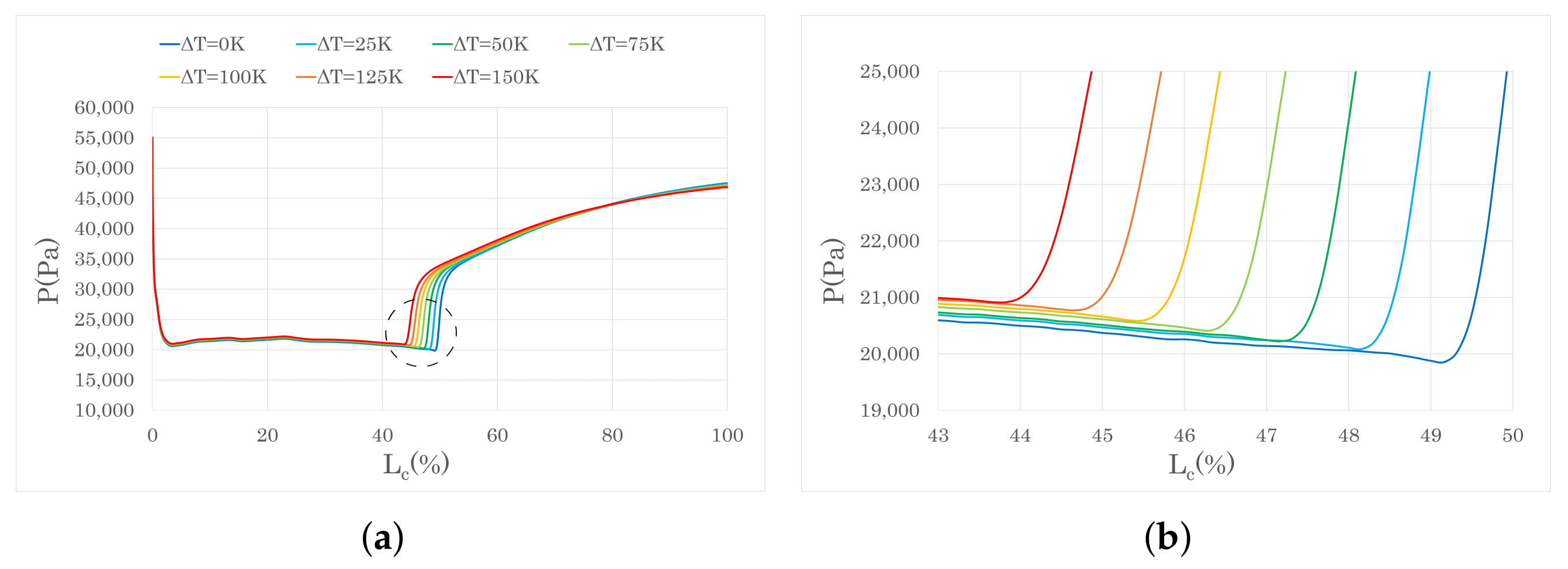
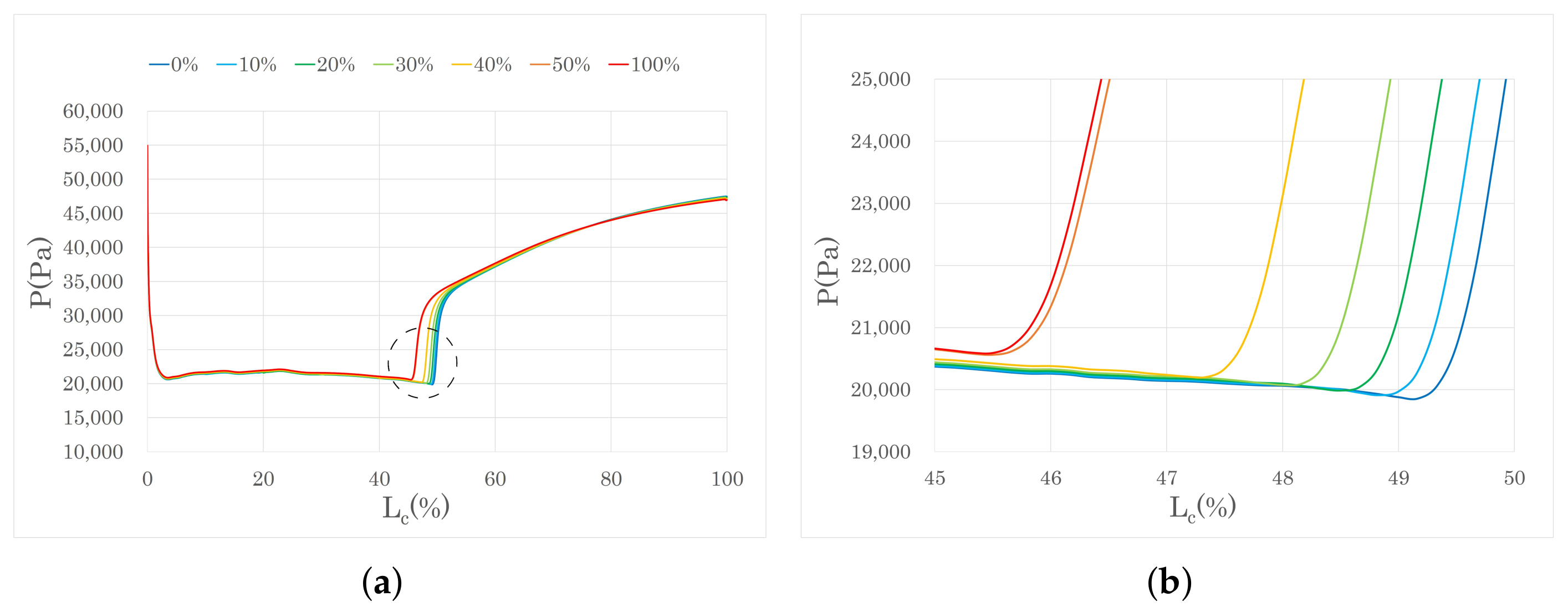
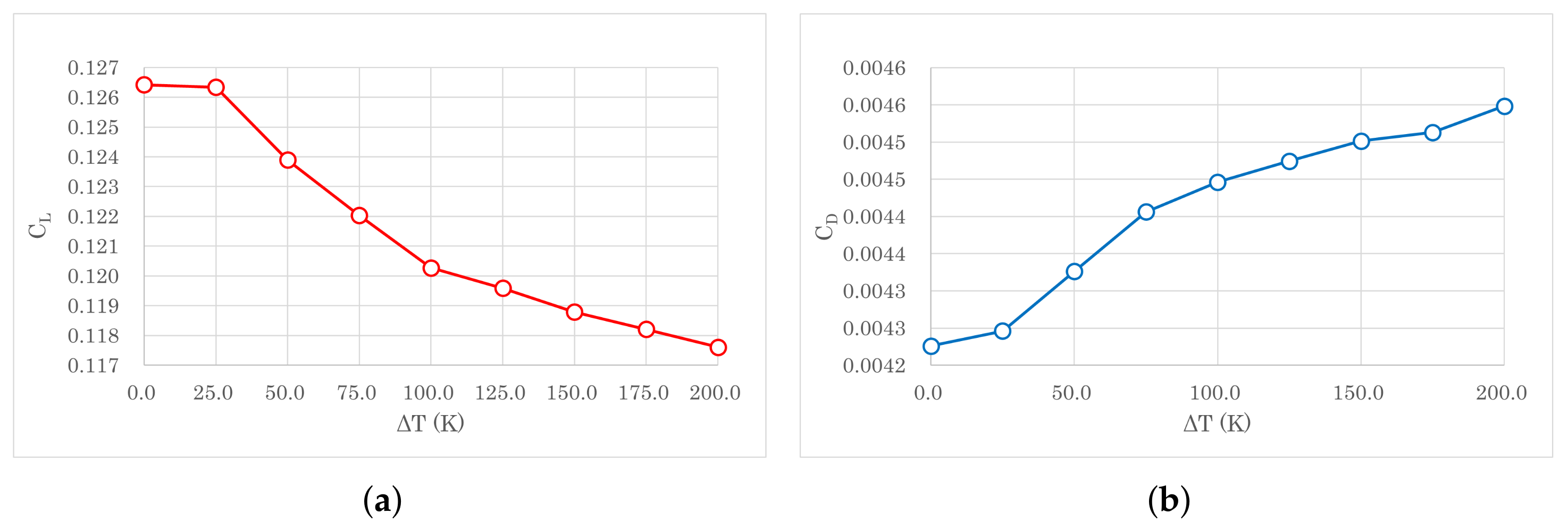
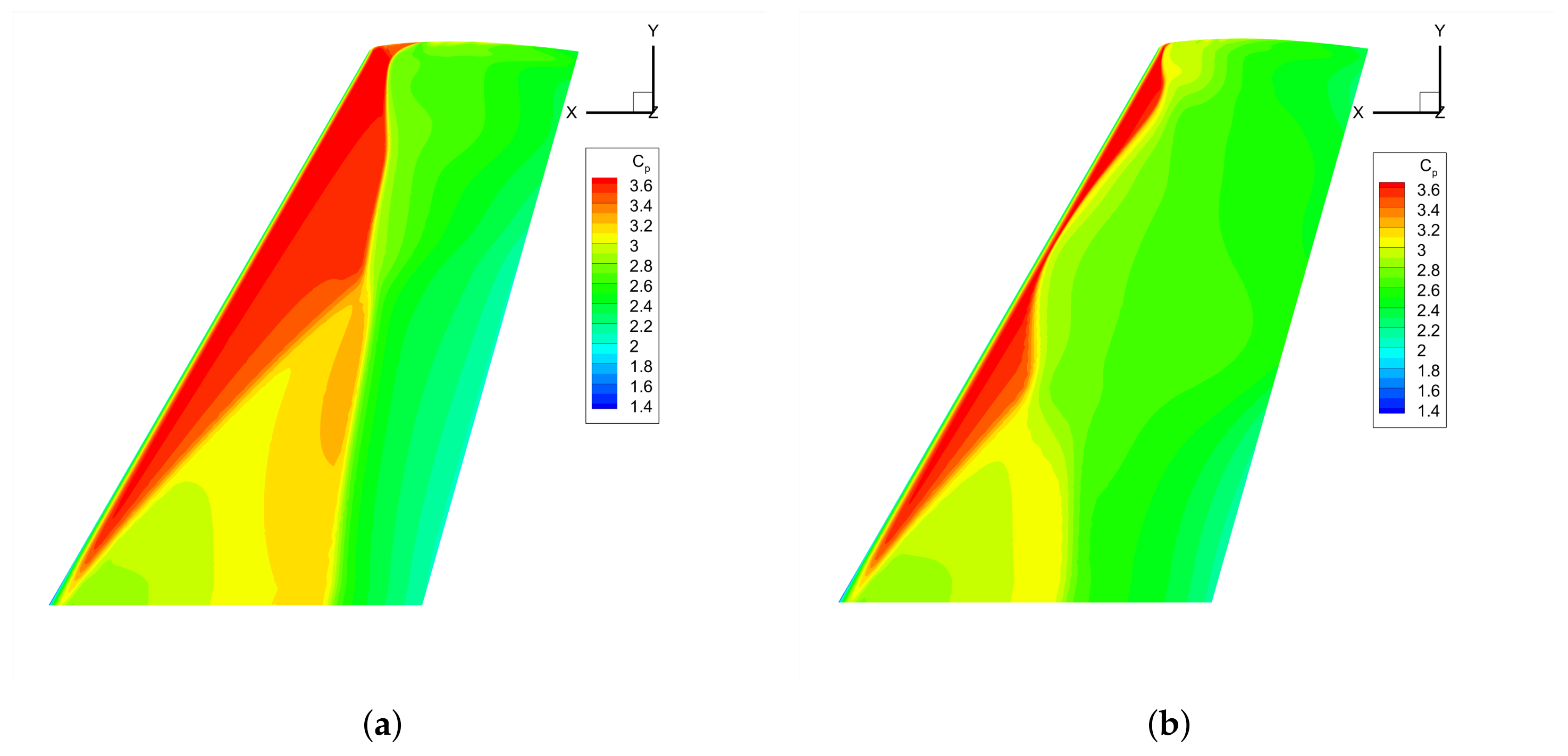

| ΔT = 100 K | ||
| 30% | 1.0355 | 0.1922 |
| 40% | 1.0292 | 0.1911 |
| ΔT = 150 K | ||
| 30% | 1.0302 | 0.19136 |
| ΔT = 175 K | ||
| 20% | 1.0354 | 0.19222 |
| Heating Scheme | ||
|---|---|---|
| Unheated | 1.0425 | 0.1935 |
| Uniform heating ΔT = 100 K | 0.9681 | 0.1811 |
| Optimal heating | 1.0325 | 0.1915 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Sun, Q.; Xiao, D.; Zhang, W. Numerical Investigation of the Aerofoil Aerodynamics with Surface Heating for Anti-Icing. Aerospace 2022, 9, 338. https://doi.org/10.3390/aerospace9070338
Li B, Sun Q, Xiao D, Zhang W. Numerical Investigation of the Aerofoil Aerodynamics with Surface Heating for Anti-Icing. Aerospace. 2022; 9(7):338. https://doi.org/10.3390/aerospace9070338
Chicago/Turabian StyleLi, Bowen, Qiangqiang Sun, Dandan Xiao, and Wenqiang Zhang. 2022. "Numerical Investigation of the Aerofoil Aerodynamics with Surface Heating for Anti-Icing" Aerospace 9, no. 7: 338. https://doi.org/10.3390/aerospace9070338
APA StyleLi, B., Sun, Q., Xiao, D., & Zhang, W. (2022). Numerical Investigation of the Aerofoil Aerodynamics with Surface Heating for Anti-Icing. Aerospace, 9(7), 338. https://doi.org/10.3390/aerospace9070338






