Structural Damage Assessment Using Multiple-Stage Dynamic Flexibility Analysis
Abstract
:1. Introduction
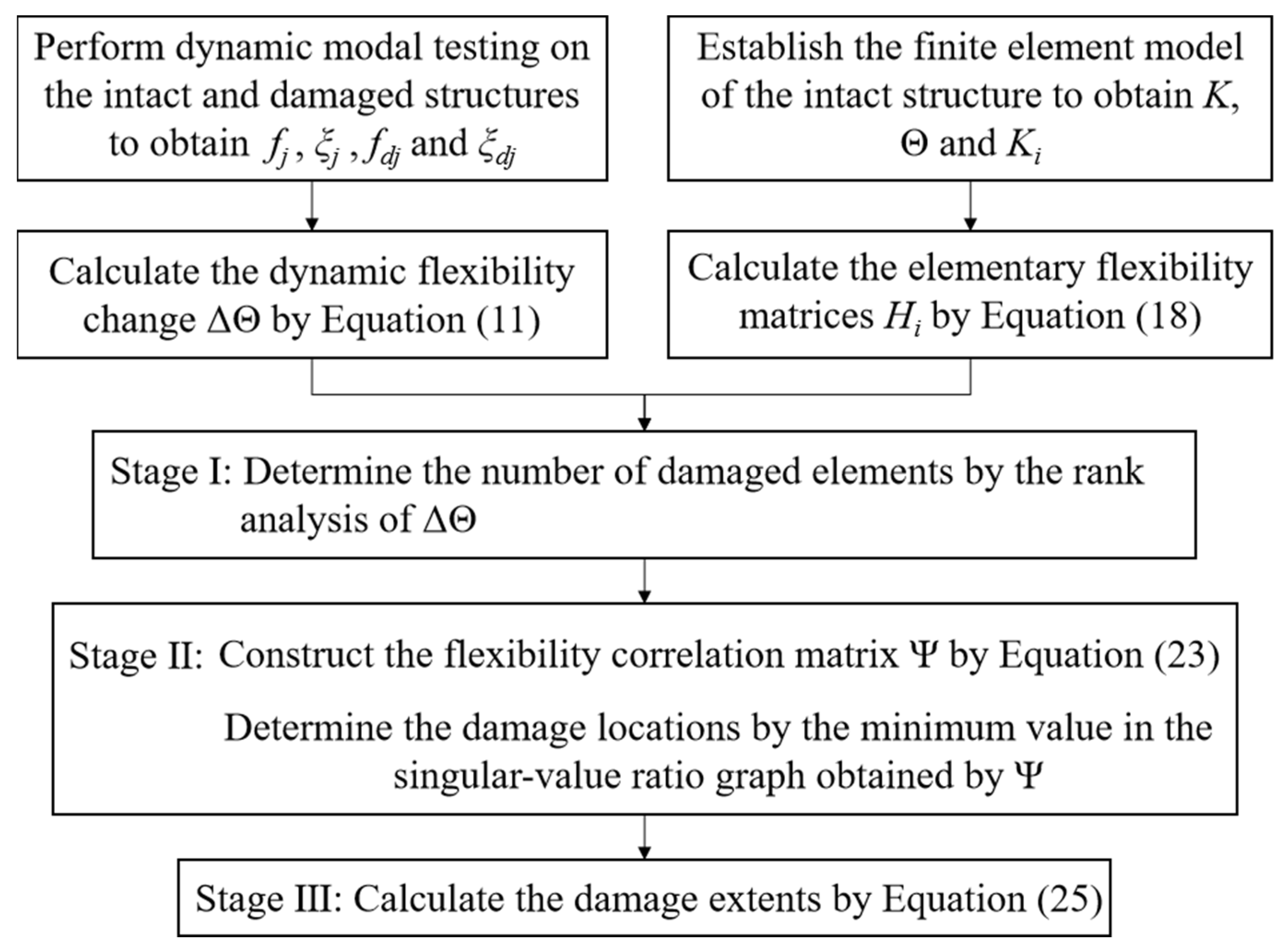
2. Theoretical Development
2.1. Stage I: Judging Whether Damage Occurs by the Rank Analysis of Dynamic Flexibility Change
2.2. Stage II: Determining Damage Locations by the Minimum Rank of Flexibility Correlation Matrices
2.3. Stage III: Quantifying Damage Extent
3. Numerical Example
3.1. Single Damage Condition
3.2. Multiple Damage Condition
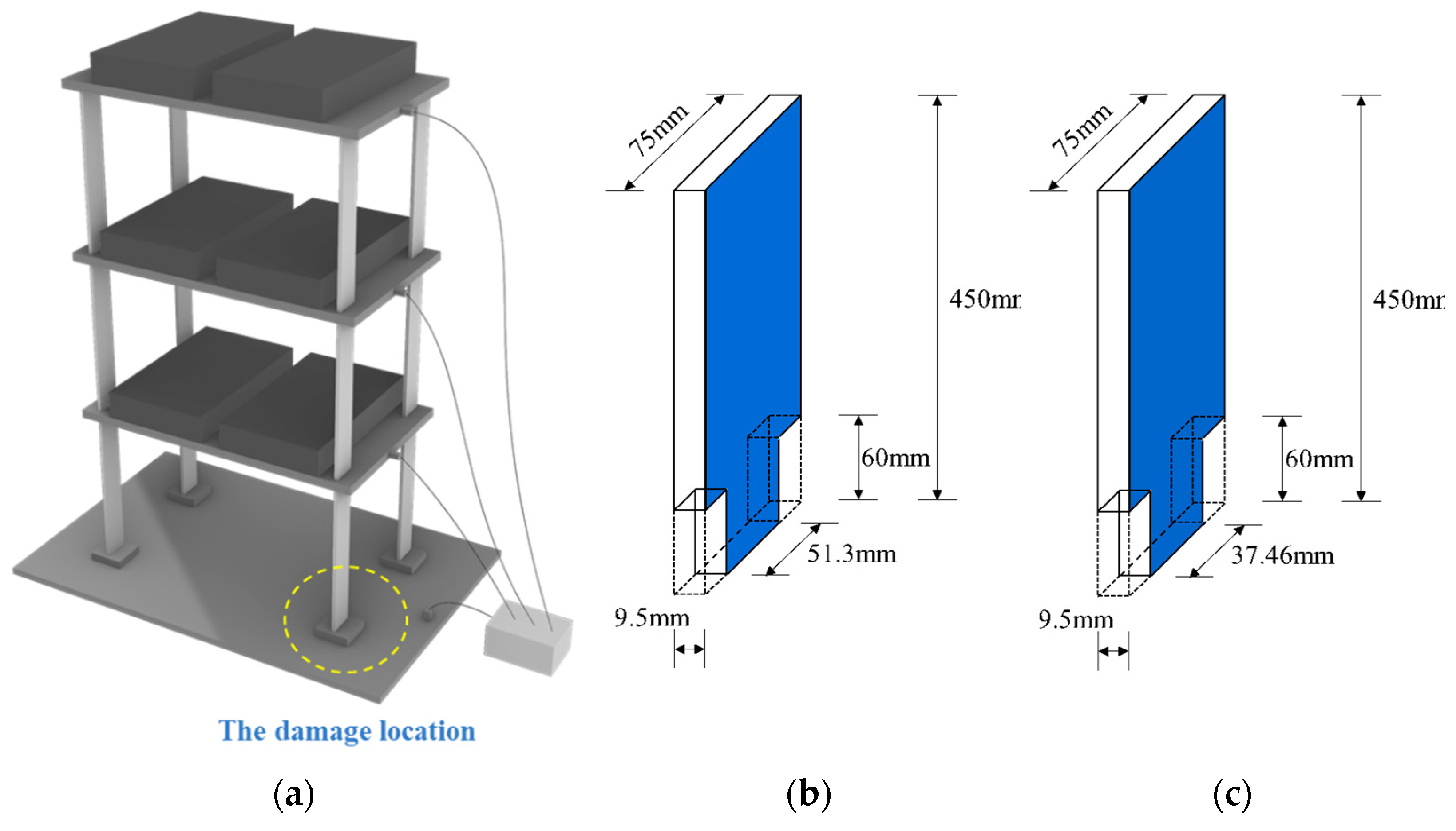
4. Verification by the Experimental Data of Reference
4.1. Damage Case 1
4.2. Damage Case 2
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Roeck, G.D. The state-of-the-art of damage detection by vibration monitoring: The SIMCES experience. J. Struct. Control. 2003, 10, 127–134. [Google Scholar] [CrossRef]
- Yan, Y.J.; Cheng, L.; Wu, Z.Y.; Yam, L.H. Development in vibration-based structural damage detection technique. Mech. Syst. Signal Processing 2007, 21, 2198–2211. [Google Scholar] [CrossRef]
- Cruz, P.J.S.; Salgado, R. Performance of vibration-based damage detection methods in bridges. Comput. -Aided Civ. Infrastruct. Eng. 2009, 24, 62–79. [Google Scholar] [CrossRef]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to Machine Learning and Deep Learning applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Vestroni, F.; Capecchi, D. Damage detection in beam structures based on frequency measurements. J. Eng. Mech. 2000, 126, 761–768. [Google Scholar] [CrossRef]
- Kessler, S.S.; Spearing, S.M.; Atalla, M.J.; Cesnik, C.E.; Soutis, C. Damage detection in composite materials using frequency response methods. Compos. Part B Eng. 2002, 33, 87–95. [Google Scholar] [CrossRef]
- Hwang, H.Y.; Kim, C. Damage detection in structures using a few frequency response measurements. J. Sound Vib. 2004, 270, 1–14. [Google Scholar] [CrossRef]
- Limongelli, M.P. Frequency response function interpolation for damage detection under changing environment. Mech. Syst. Signal Process. 2010, 24, 2898–2913. [Google Scholar] [CrossRef]
- Bandara, R.P.; Chan, T.H.T.; Thambiratnam, D.P. Structural damage detection method using frequency response functions. Struct. Health Monit. 2014, 13, 418–429. [Google Scholar] [CrossRef]
- Sha, G.; Radzieński, M.; Cao, M.; Ostachowicz, W. A novel method for single and multiple damage detection in beams using relative natural frequency changes. Mech. Syst. Signal Process. 2019, 132, 335–352. [Google Scholar] [CrossRef]
- Kim, J.T.; Ryu, Y.S.; Cho, H.M.; Stubbs, N. Damage identification in beam-type structures: Frequency-based method vs mode-shape-based method. Eng. Struct. 2003, 25, 57–67. [Google Scholar] [CrossRef]
- Qiao, P.; Lu, K.; Lestari, W.; Wang, J. Curvature mode shape-based damage detection in composite laminated plates. Compos. Struct. 2007, 80, 409–428. [Google Scholar] [CrossRef]
- Yazdanpanah1a, O.; Seyedpoor, S.M. A new damage detection indicator for beams based on mode shape data. Struct. Eng. Mech. 2015, 53, 725–744. [Google Scholar] [CrossRef]
- Rucevskis, S.; Janeliukstis, R.; Akishin, P.; Chate, A. Mode shape-based damage detection in plate structure without baseline data. Struct. Control. Health Monit. 2016, 23, 1180–1193. [Google Scholar] [CrossRef]
- Umar, S.; Bakhary, N.; Abidin, A.R.Z. Response surface methodology for damage detection using frequency and mode shape. Measurement 2018, 115, 258–268. [Google Scholar] [CrossRef]
- Catbas, F.N.; Brown, D.L.; Aktan, A.E. Use of modal flexibility for damage detection and condition assessment: Case studies and demonstrations on large structures. J. Struct. Eng. 2006, 132, 1699–1712. [Google Scholar] [CrossRef]
- Sung, S.H.; Koo, K.Y.; Jung, H.J. Modal flexibility-based damage detection of cantilever beam-type structures using baseline modification. J. Sound Vib. 2014, 333, 4123–4138. [Google Scholar] [CrossRef]
- Grande, E.; Imbimbo, M. A multi-stage approach for damage detection in structural systems based on flexibility. Mech. Syst. Signal Process. 2016, 76, 455–475. [Google Scholar] [CrossRef]
- Wickramasinghe, W.R.; Thambiratnam, D.P.; Chan TH, T. Damage detection in a suspension bridge using modal flexibility method. Eng. Fail. Anal. 2020, 107, 104194. [Google Scholar] [CrossRef]
- Li, J.; Wu, B.; Zeng, Q.C.; Lim, C.W. A generalized flexibility matrix based approach for structural damage detection. J. Sound Vib. 2010, 329, 4583–4587. [Google Scholar] [CrossRef]
- Liu, H.; Li, Z. An improved generalized flexibility matrix approach for structural damage detection. Inverse Probl. Sci. Eng. 2020, 28, 877–893. [Google Scholar] [CrossRef]
- Liu, H.; Wu, B.; Li, Z. The generalized flexibility matrix method for structural damage detection with incomplete mode shape data. Inverse Probl. Sci. Eng. 2021, 29, 2019–2039. [Google Scholar] [CrossRef]
- Maizuar, M.; Zhang, L.; Miramini, S.; Mendis, P.; Thompson, R.G. Detecting structural damage to bridge girders using radar interferometry and computational modelling. Struct. Control. Health Monit. 2017, 24, 1–6. [Google Scholar] [CrossRef]
- Alani, A.M.; Aboutalebi, M.; Kilic, G. Use of non-contact sensors (IBIS-S) and finite element methods in the assessment of bridge deck structures. Struct. Concr. 2014, 15, 240–247. [Google Scholar] [CrossRef]
- Raja, B.; Miramini, S.; Duffield, C.; Chen, S.; Zhang, L. A Simplified Methodology for Condition Assessment of Bridge Bearings Using Vibration Based Structural Health Monitoring Techniques. Int. J. Struct. Stab. Dyn. 2021, 21, 2150133. [Google Scholar] [CrossRef]
- Li, W.; Hancock, C.; Yang, Y.; Meng, X. Dynamic deformation monitoring of an offshore platform structure with accelerometers. J. Civ. Struct. Health Monit. 2021, 12, 275–287. [Google Scholar] [CrossRef]
- Zini, G.; Betti, M.; Bartoli, G. A pilot project for the long-term structural health monitoring of historic city gates. J. Civ. Struct. Health Monit. 2022, 12, 537–556. [Google Scholar] [CrossRef]
- Aminullah, A.; Suhendro, B.; Panuntun, R.B. Optimal Sensor Placement for Accelerometer in Single-Pylon Cable-Stayed Bridge. In Proceedings of the 5th International Conference on Sustainable Civil Engineering Structures and Construction Materials; Springer: Singapore, 2022; pp. 63–79. [Google Scholar]
- Cocking, S.; Alexakis, H.; Dejong, M. Distributed dynamic fibre-optic strain monitoring of the behaviour of a skewed masonry arch railway bridge. J. Civ. Struct. Health Monit. 2021, 11, 989–1012. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Nguyen, T.Q.; Nhat, T.N.; Nguyen-Xuan, H.; Ngo, N.K. A novel approach based on viscoelastic parameters for bridge health monitoring: A case study of Saigon bridge in Ho Chi Minn City-Vietnam. Mech. Syst. Signal Process. 2020, 141, 106728.1–106728.17. [Google Scholar] [CrossRef]
- Capilla, J.J.; Au, S.K.; Brownjohn, J.; Hudson, E. Ambient vibration testing and operational modal analysis of monopole telecoms structures. J. Civ. Struct. Health Monit. 2021, 11, 1077–1091. [Google Scholar] [CrossRef]
- Li, L. Numerical and Experimental Studies of Damage Detection for Shear Buildings; Huazhong University of Science and Technology: Wuhan, China, 2005. [Google Scholar]
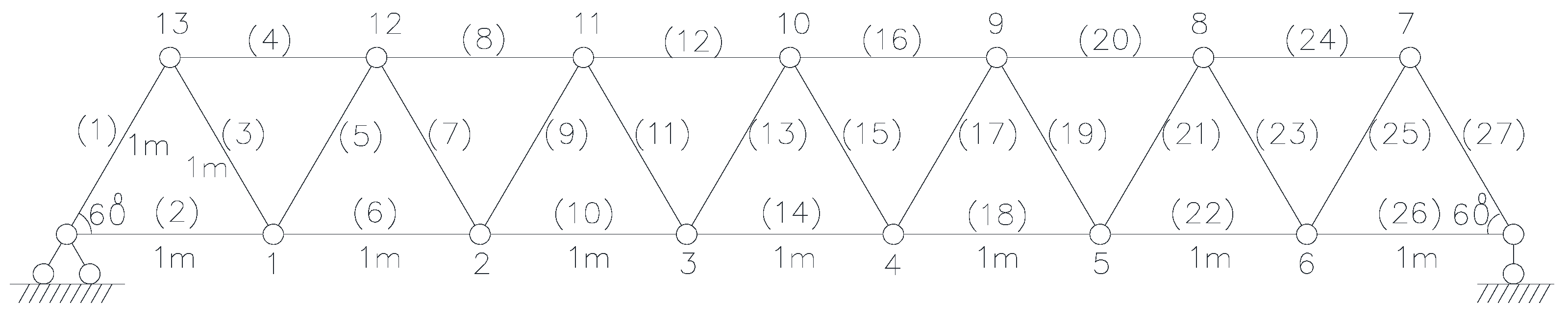
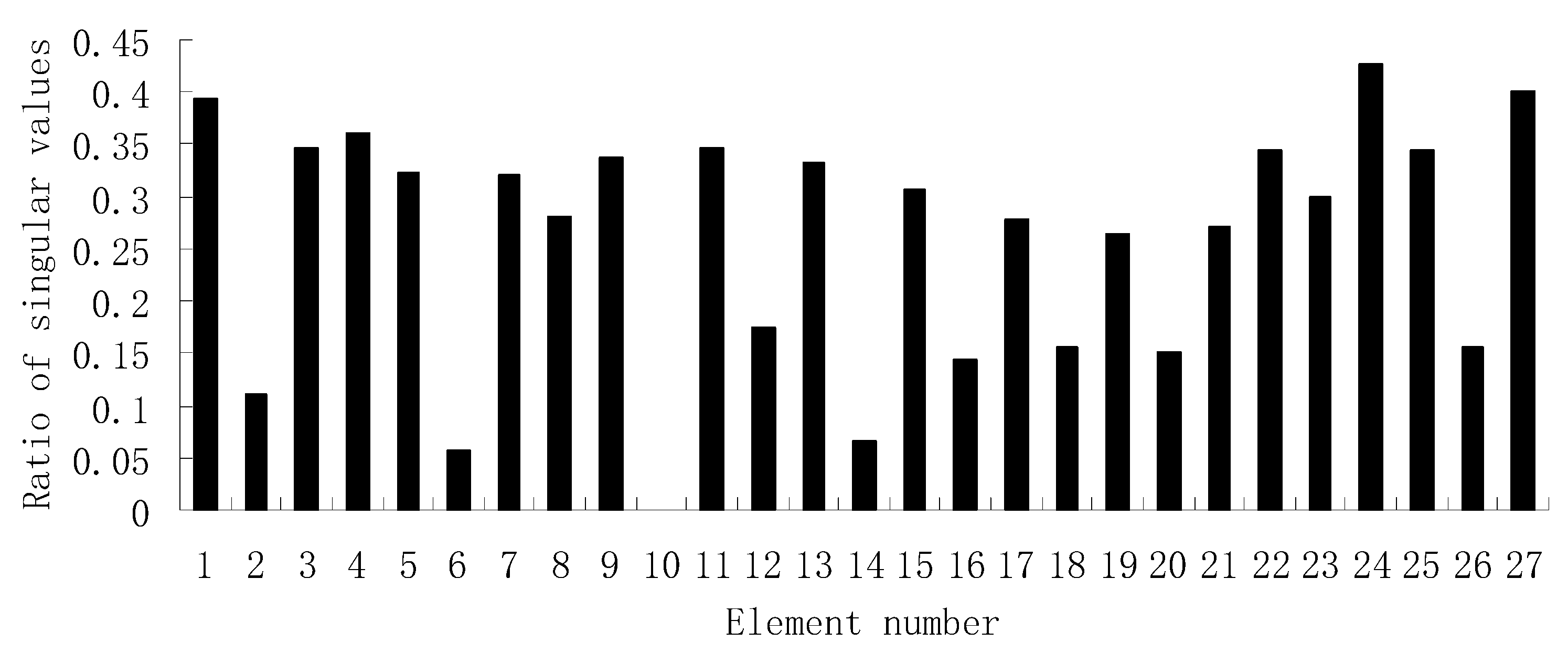
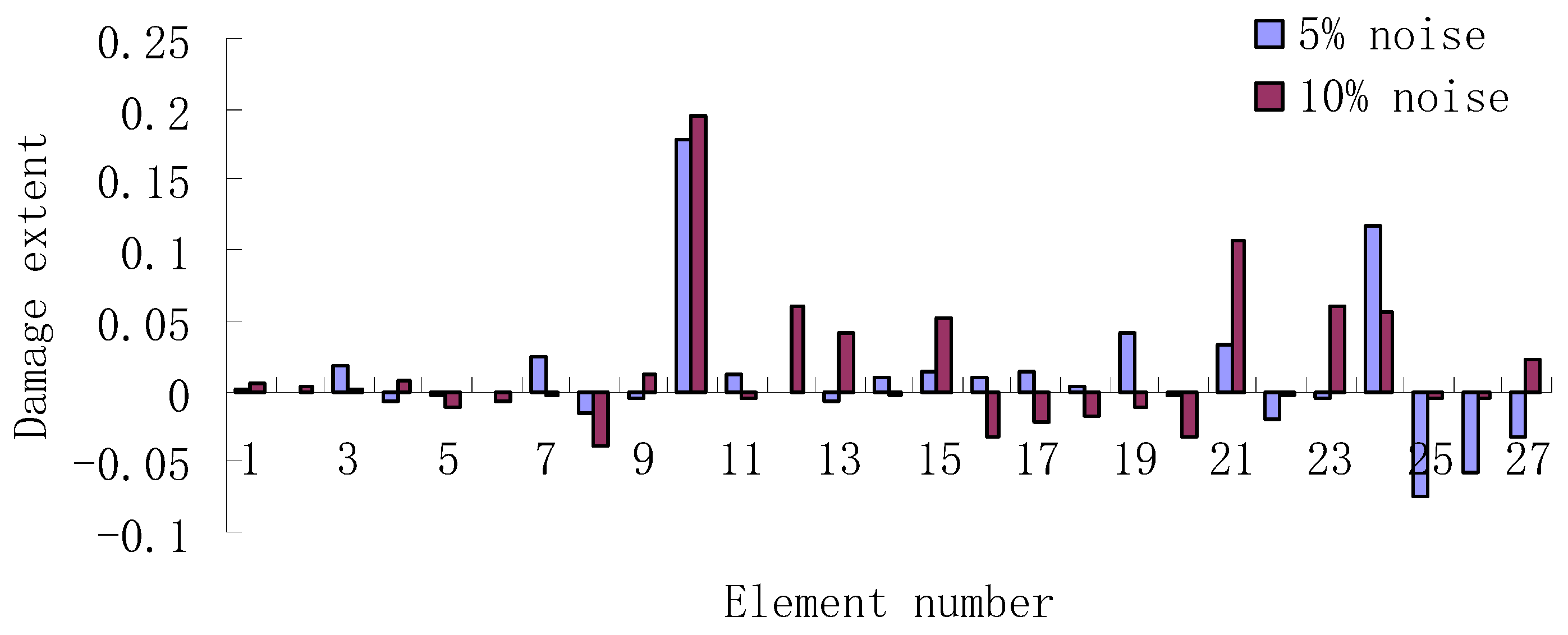
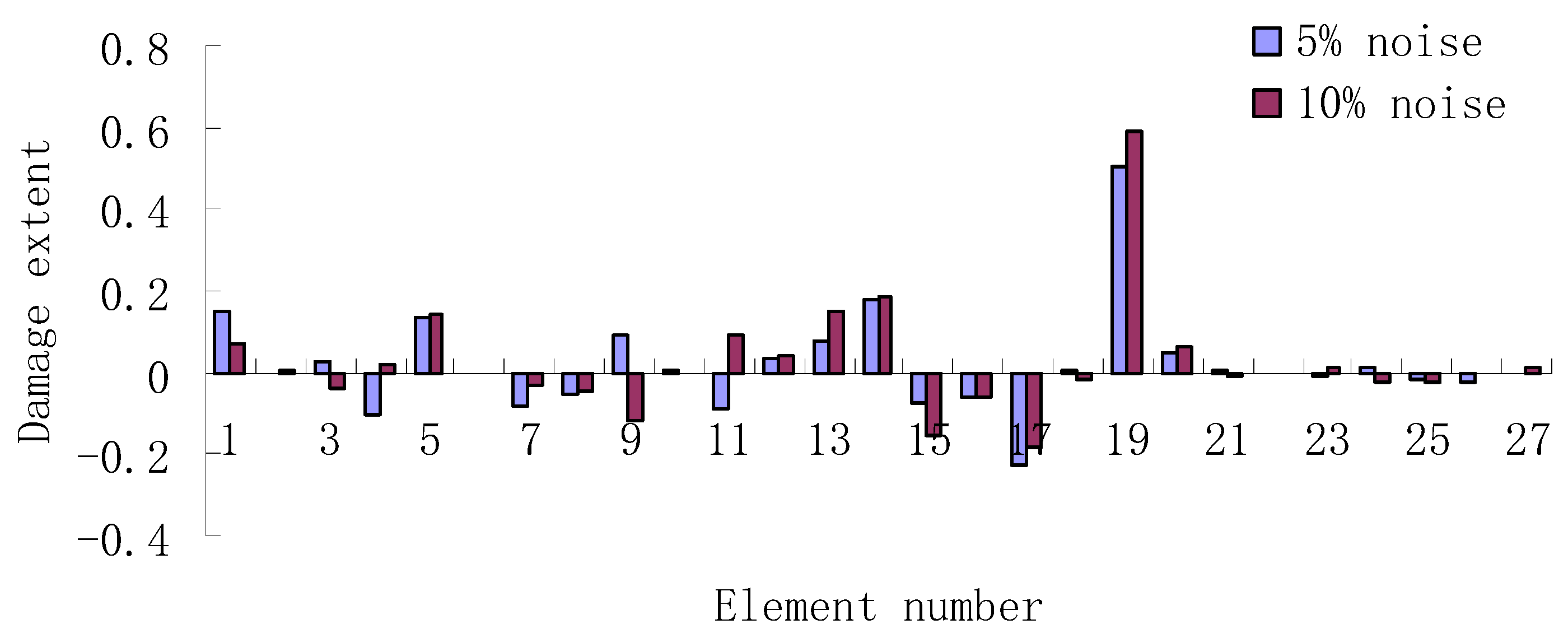
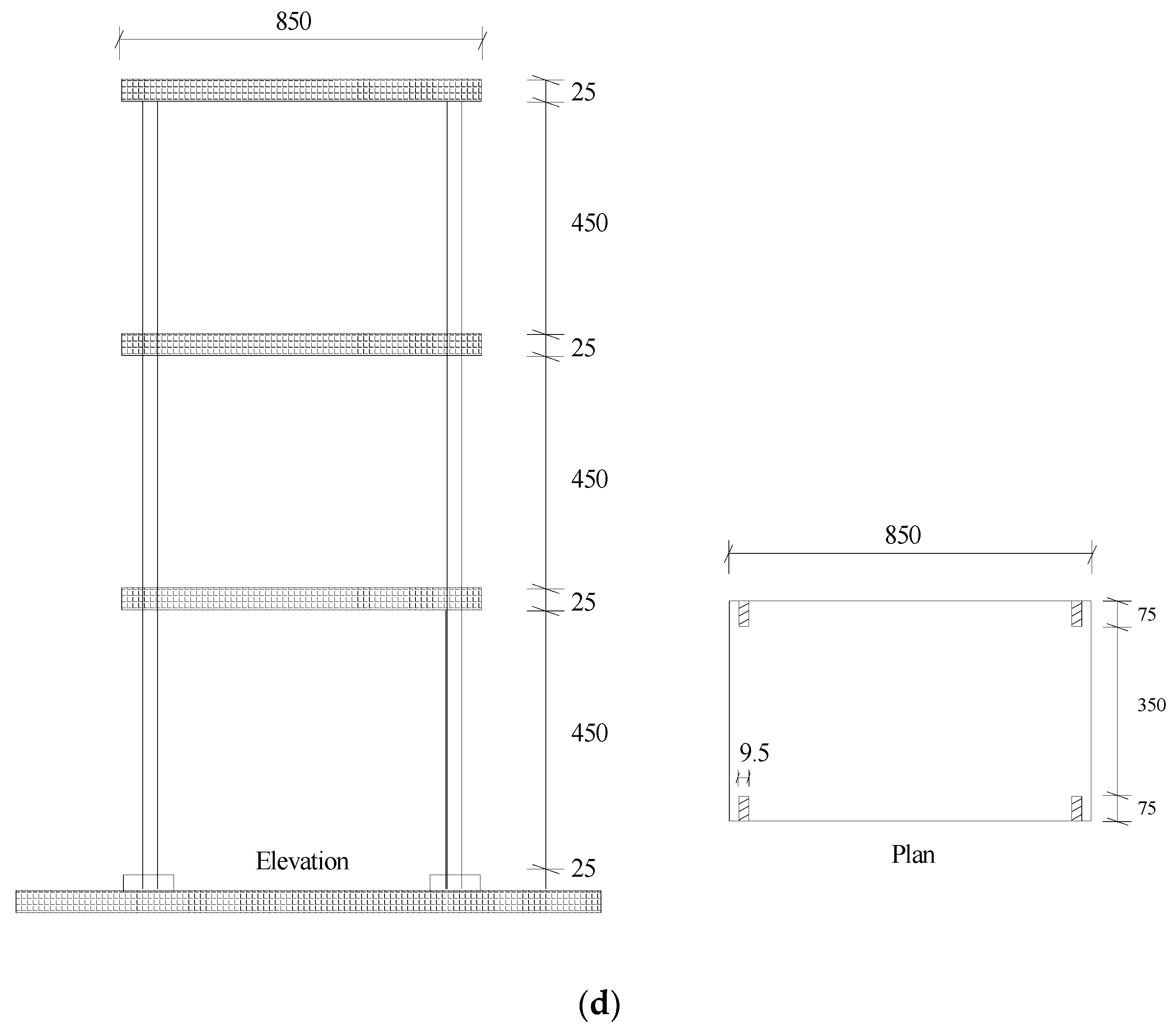
| Frequency Number | Undamaged | Single Damage | Multiple Damage |
|---|---|---|---|
| 1 | 43.4 | 43.0 | 42.9 |
| 2 | 109.7 | 108.8 | 109.5 |
| 3 | 150.9 | 150.9 | 150.6 |
| 4 | 257.7 | 257.4 | 252.9 |
| 5 | 338.9 | 337.5 | 336.7 |
| Element Number | Singular-Values (×10−6) | Identified Column Rank |
|---|---|---|
| 1 | 0.0173, 0.0068 | 2 |
| 2 | 0.1009, 0.0111 | 2 |
| 3 | 0.0171, 0.0059 | 2 |
| 4 | 0.0174, 0.0063 | 2 |
| 5 | 0.0168, 0.0054 | 2 |
| 6 | 0.0987, 0.0057 | 2 |
| 7 | 0.0164, 0.0053 | 2 |
| 8 | 0.0333, 0.0093 | 2 |
| 9 | 0.0161, 0.0054 | 2 |
| 10 | 0.0912, 0.0000 | 1 |
| 11 | 0.0159, 0.0055 | 2 |
| 12 | 0.0561, 0.0097 | 2 |
| 13 | 0.0159, 0.0053 | 2 |
| 14 | 0.0726, 0.0049 | 2 |
| 15 | 0.0160, 0.0049 | 2 |
| 16 | 0.0739, 0.0106 | 2 |
| 17 | 0.0162, 0.0045 | 2 |
| 18 | 0.0477, 0.0075 | 2 |
| 19 | 0.0164, 0.0043 | 2 |
| 20 | 0.0775, 0.0117 | 2 |
| 21 | 0.0167, 0.0045 | 2 |
| 22 | 0.0243, 0.0084 | 2 |
| 23 | 0.0169, 0.0050 | 2 |
| 24 | 0.0170, 0.0073 | 2 |
| 25 | 0.0171, 0.0059 | 2 |
| 26 | 0.0160, 0.0025 | 2 |
| 27 | 0.0173, 0.0069 | 2 |
| 5% Noise Level | 10% Noise Level |
|---|---|
| Stage I: (1) The eigenvalues of can be calculated as: 0.6228 × 10−7, 0.0076 × 10−7, 0.0025 × 10−7, 0.0006 × 10−7, 0, 0, …. (2) The rank of can be determined as 1 due to 0.0076/0.6228 = 1.22% < 5%. (3) It can be judged that only one element is damaged. | Stage I: (1) The eigenvalues of can be calculated as: 0.6324 × 10−7, 0.0142 × 10−7, 0.0090 × 10−7, 0.0034 × 10−7, 0, 0, …. (2) The rank of can be determined as 1 due to 0.0142/0.6324 = 2.25% < 5%. (3) It can be judged that only one element is damaged. |
| Stage II: (1) The ratio graph of singular values for the correlation matrices follows: 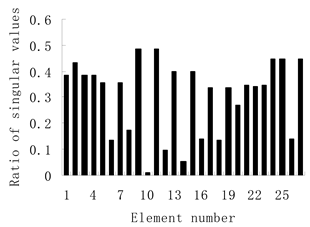 (2) Element 10 can be determined as the damaged bar according to the minimum value in the ratio graph. | Stage II: (1) The ratio graph of singular values for the correlation matrices follows: 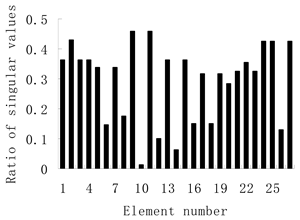 (2) Element 10 can be determined as the damaged bar according to the minimum value in the ratio graph. |
| Stage III:The damage extent can be calculated as = 18.87%. | Stage III:The damage extent can be calculated as = 20.32%. |
| Element Combination | Singular-Values (×10−7) | Identified Column Rank |
|---|---|---|
| 1 and 2 | 1.006, 0.133, 0.058 | 3 |
| 3 and 5 | 0.1648, 0.0633, 0.0322 | 3 |
| 4 and 6 | 0.9844, 0.0889, 0.0577 | 3 |
| 7 and 8 | 0.3307, 0.0795, 0.0439 | 3 |
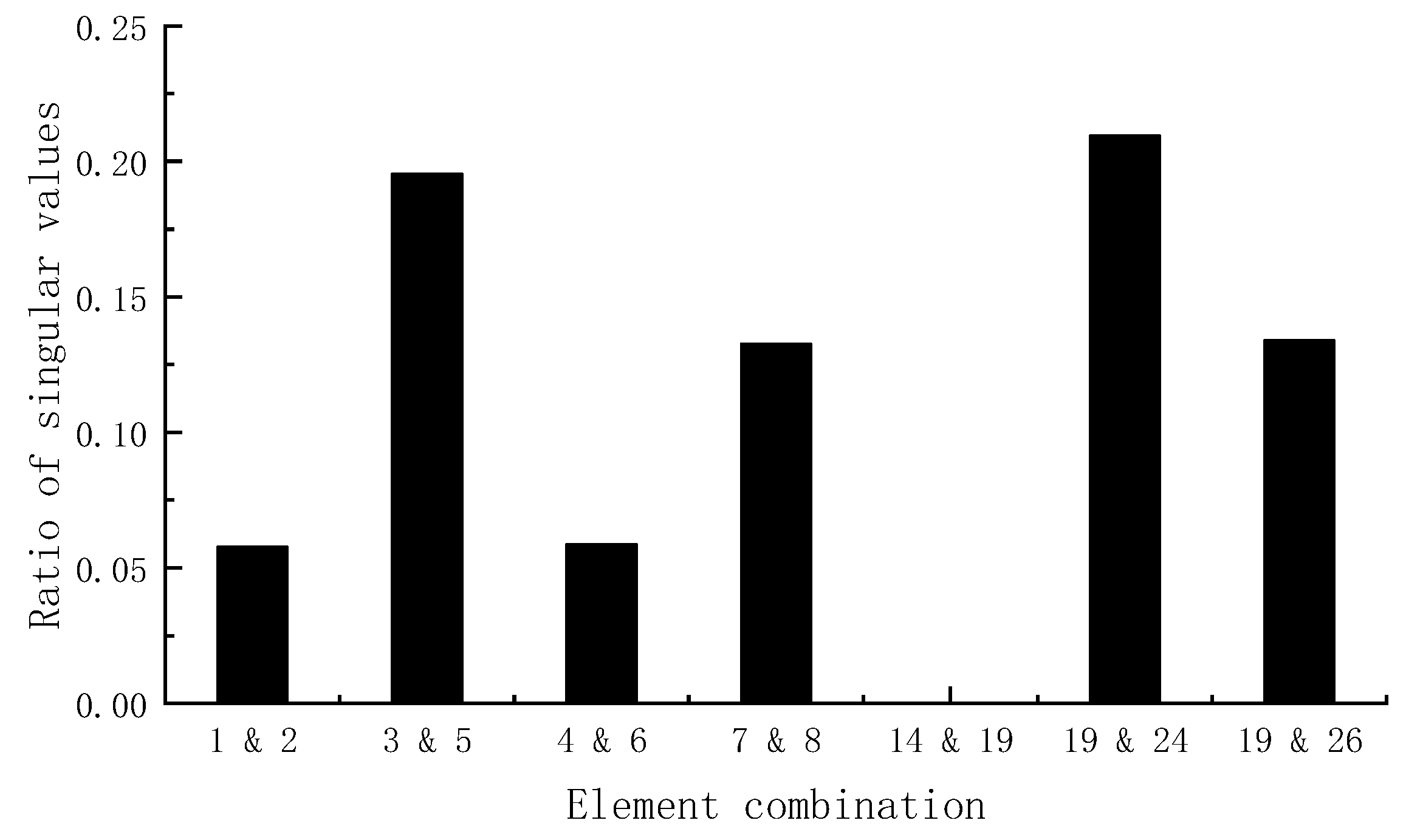
| 14 and 19 | 0.7249, 0.0446, 0.0000 | 2 |
| 19 and 24 | 0.1604, 0.0685, 0.0336 | 3 |
| 19 and 26 | 0.1464, 0.0404, 0.0196 | 3 |
| 5% Noise Level | 10% Noise Level |
|---|---|
| Stage I: (1) The eigenvalues of can be calculated as: 0.6508 × 10−7, 0.0355 × 10−7, 0.0043 × 10−7, 0.0032 × 10−7, 0, 0, …. (2) The rank of can be determined as 2 due to 0.0355/0.6508 = 5.45% > 5% and 0.0043/0.6508 = 0.66% < 5%. (3) It can be judged that two elements are damaged. | Stage I: (1) The eigenvalues of can be calculated as: 0.6444 × 10−7, 0.0384 × 10−7, 0.0095 × 10−7, 0.0071 × 10−7, 0, 0, …. (2) The rank of can be determined as 2 due to 0.0384/0.6444 = 5.96%>5% and 0.0095/0.6444 = 1.47% < 5%. (3) It can be judged that two elements are damaged. |
| Stage II: (1) The ratio graph of singular values for the correlation matrices follows: 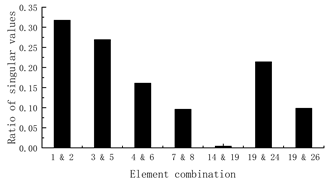 (2) Elements 14 and 19 can be determined as the damaged bars according to the minimum value in the ratio graph. | Stage II: (1) The ratio graph of singular values for the correlation matrices follows: 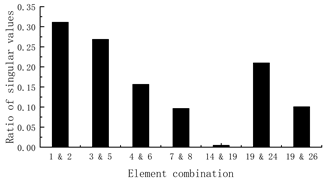 (2) Elements 14 and 19 can be determined as the damaged bars according to the minimum value in the ratio graph. |
| Stage III: The damage extents can be calculated as = 18.34% and = 24.92%. | Stage III: The damage extents can be calculated as = 17.64% and = 34.71%. |
| Mode Number | Natural Frequency | Mode Shape |
|---|---|---|
| 1 | = 3.369 | = (0.02118,0.03922,0.048427)T. |
| 2 | = 9.704 | = (0.048758,0.02031,-0.03923)T |
| 3 | = 14.282 | = (0.037936,-0.04866,0.022852)T |
| Mode Number | Natural Frequency | Mode Shape |
|---|---|---|
| 1 | = 3.259 | = (0.022735,0.039331,0.047594)T |
| 2 | = 9.485 | = (0.049417,0.017683,-0.03968)T |
| 3 | = 14.209 | = (0.035798,-0.04982,0.02379)T |
| Mode Number | Natural Frequency | Mode Shape |
|---|---|---|
| 1 | = 3.003 | = (0.022172,0.040166,0.047161)T |
| 2 | = 9.082 | = (0.053402,0.012675,−0.03629)T |
| 3 | = 13.330 | = (0.031506,-0.05023,0.028513)T |
| Proposed Method | Generalized Flexibility Method |
|---|---|
| Stage I: (1) The eigenvalues of can be calculated as: 7.52 × 10−7, -0.274 × 10−7, -0.012 × 10−7. (2) The rank of can be determined as 1 due to 0.274/7.52 = 3.64% < 5%. (3) It can be judged that only one element is damaged. | The damage extent calculated by the generalized flexibility method follows: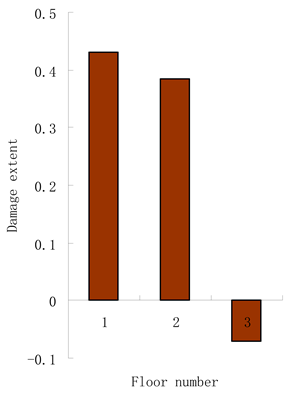 |
| Stage II: (1) The ratio graph of singular values for the correlation matrices follows: 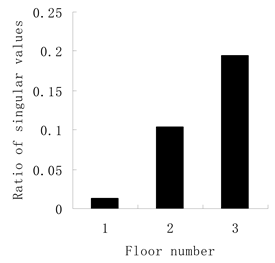 (2) The first floor can be determined as the damaged element according to the minimum value in the ratio graph. | |
| Stage III: The damage extent can be calculated as = 13.11%. | The damage extent of the first floor is = 17.89%. |
| Proposed Method | Generalized Flexibility Method |
|---|---|
| Stage I: (1) The eigenvalues of can be calculated as: 2.5344 × 10−6, 0.2196 × 10−6, −0.01053 × 10−6. (2) The rank of can be determined as 2 due to 0.2196/2.5344 = 8.66% > 5% and 0.01053/2.5344 = 0.42% < 5%. (3) It can be judged that two elements are damaged. | The calculated damage extent by the generalized flexibility method follows: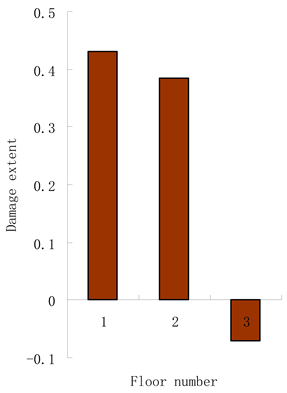 |
| Stage II: (1) The ratio graph of singular values for the correlation matrices follows. 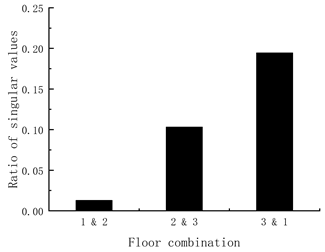 (2) The first and second floors can be determined as the damaged elements according to the minimum value in the ratio graph. | |
| Stage III: The damage extent can be calculated as = 33.62% and = 26.9%. | The damage extent of the first and second floors are = 43.02% and = 38.48%. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun , Y.; Yang, Q.; Peng, X. Structural Damage Assessment Using Multiple-Stage Dynamic Flexibility Analysis. Aerospace 2022, 9, 295. https://doi.org/10.3390/aerospace9060295
Sun Y, Yang Q, Peng X. Structural Damage Assessment Using Multiple-Stage Dynamic Flexibility Analysis. Aerospace. 2022; 9(6):295. https://doi.org/10.3390/aerospace9060295
Chicago/Turabian StyleSun , Yun, Qiuwei Yang, and Xi Peng. 2022. "Structural Damage Assessment Using Multiple-Stage Dynamic Flexibility Analysis" Aerospace 9, no. 6: 295. https://doi.org/10.3390/aerospace9060295
APA StyleSun , Y., Yang, Q., & Peng, X. (2022). Structural Damage Assessment Using Multiple-Stage Dynamic Flexibility Analysis. Aerospace, 9(6), 295. https://doi.org/10.3390/aerospace9060295







