Aerodynamic Modelling of the Airfoil Immersed in Two-Dimensional Jet Flow

Abstract

In order to study the aerodynamic interaction of the airfoil and jet flow, the free streamline model and the panel method are combined to develop a fast calculation method for the airfoil in two-dimensional inviscid jet flow. The vortex strength and position of the jet boundary are determined by using the free streamline model and the constant total pressure difference assumption, the circulation of the airfoil is solved by the vortex panel method, and the whole process is coupled by relaxation iteration. Firstly, the convergence and effectiveness of the present method are verified. Next, the influence of the length ratio of jet height to airfoil chord, the velocity ratio of jet velocity to freestream velocity, and the ground effect on airfoil aerodynamics are studied. The results show that the aerodynamic characteristics of the airfoil in finite width jet flow and in freestream have a large difference, and it is important to consider the jet deflection for jet/airfoil interaction. In jet flow, the velocity ratio can be regarded as an aerodynamic similarity parameter for the airfoil. When the jet flow is deflected, the airfoil will not only generate lift but also drag, and the ground effect can be used to decrease drag. The developed method in this paper can not only capture the jet deflection but also has higher calculation efficiency than Computational Fluid Dynamic (CFD), which is beneficial for the preliminary design of a powered-lift device.

1. Introduction

For the airfoil in freestream, people have enough understanding about its aerodynamic characteristics. For the airfoil in jet flow, understanding is limited. In recent years, powered-lift technology has attracted more and more attention because of the development of fixed-wing vertical take-off and landing (VTOL) aircraft [1,2,3,4]. In the condition of zero freestream or small freestream, traditional fixed-wing aircraft cannot take off normally due to insufficient lift. However, for such aircraft, by deflecting the propulsion jet flow, the wing can generate extra lift, enabling vertical or short take-off. Therefore, a clear understanding of the aerodynamic characteristics of the airfoil immersed in jet flow is very important for the design of such a powered-lift device.

Jet/wing interaction is a complex aerodynamic problem. Because CFD methods can give more flow field details, some researchers have used CFD to study this problem. Li [5] calculated the aerodynamic force of an externally blown flap based on the RANS (Reynolds-averaged Navier-Stokes) method, and showed that the up and down position of the engine relative to the flap has an important influence on the aerodynamic force of the flap; Cui [6] studied the deflection of propeller slipstream and indicated that the horizontal distance between propeller and wing has a small effect on the slipstream deflection; Chadha [7] used the fan boundary condition in FLUENT to simulate slipstream effects on an airfoil, and pointed out that the stall angle of the airfoil was delayed remarkably.

Although the accuracy of the CFD method is high, it needs more time expense, which is inconvenient for the preliminary design. Thus, other scholars have developed simplified methods to study the interaction of jet/wing. Kuhn and Obert [8,9] used momentum theory and semi-empirical formulations to estimate the influence of slipstream on the wing, and the model needed wind tunnel data for correction; Liu [10,11] studied jet/airfoil interaction by solving the stream function equation, but this method is based on the finite difference method and the whole flow field needs to be discretized; Ting and Lan [12,13] adopted image vortex correction for jet/airfoil interaction. Because of the small perturbation assumption, this method is limited to the state of small deformation for a jet boundary. There are also some semi-empirical wake models [14,15], but all belong to fixed-wake methods.

From the above introduction, it can be seen that for jet/wing interaction problems, complex methods have high time expense, and the applicability of simplified methods is limited. Especially under the condition of a high-velocity ratio, there is still a lack of simple and fast aerodynamic estimation methods in engineering. However, in the vertical take-off stage, the jet velocity of the propulsion is usually high, and the contraction [16] and deflection [17] of the jet flow is usually obvious. Therefore, it is necessary for the calculation method to capture wake deformation properly in such flow conditions.

As studied by Lewis [18], the free streamline model regards the wake boundary as a streamline, which can consider wake deformation conveniently. He used the free streamline model to simulate the deflection of a two-dimensional jet over a ridge. Similarly, Shollenberger [19,20] developed a simplified method to calculate the aerodynamic force of the plate in two-dimensional jet flow based on the free streamline model. Bontempo [21,22,23] studied the slipstream contraction of the uniformly loaded propeller by the free streamline model, which further verified the effectiveness of this model.

The panel method [24] can be considered a semi-analytical method, which can exclude the influence of the viscosity and is convenient to change the camber and thickness of the airfoil in aerodynamic design. In order to develop a fast calculation method for the jet/airfoil interaction problem, the panel method and the free streamline model are combined properly in this study. Compared with fixed-wake methods, the developed method in this paper can simulate the deflection of jet flow at any velocity ratio. Compared with CFD methods, the proposed method can effectively reduce the computation cost, which is beneficial for the preliminary design.

This paper is divided as follows. Firstly, the relevant theory of the jet flow and the procedure of the coupled method is introduced. Then, the convergence and validation of the proposed method are tested. Next, the aerodynamic characteristics of the airfoil in two-dimensional jet flow with different flow conditions are calculated, and the different effects of jet and freestream on the airfoil are compared as well. Finally, the influence of the ground effect on the aerodynamic force of airfoil in jet flow is also analyzed. The developed method and conclusions in this paper can provide assistance in understanding the jet/airfoil interaction.

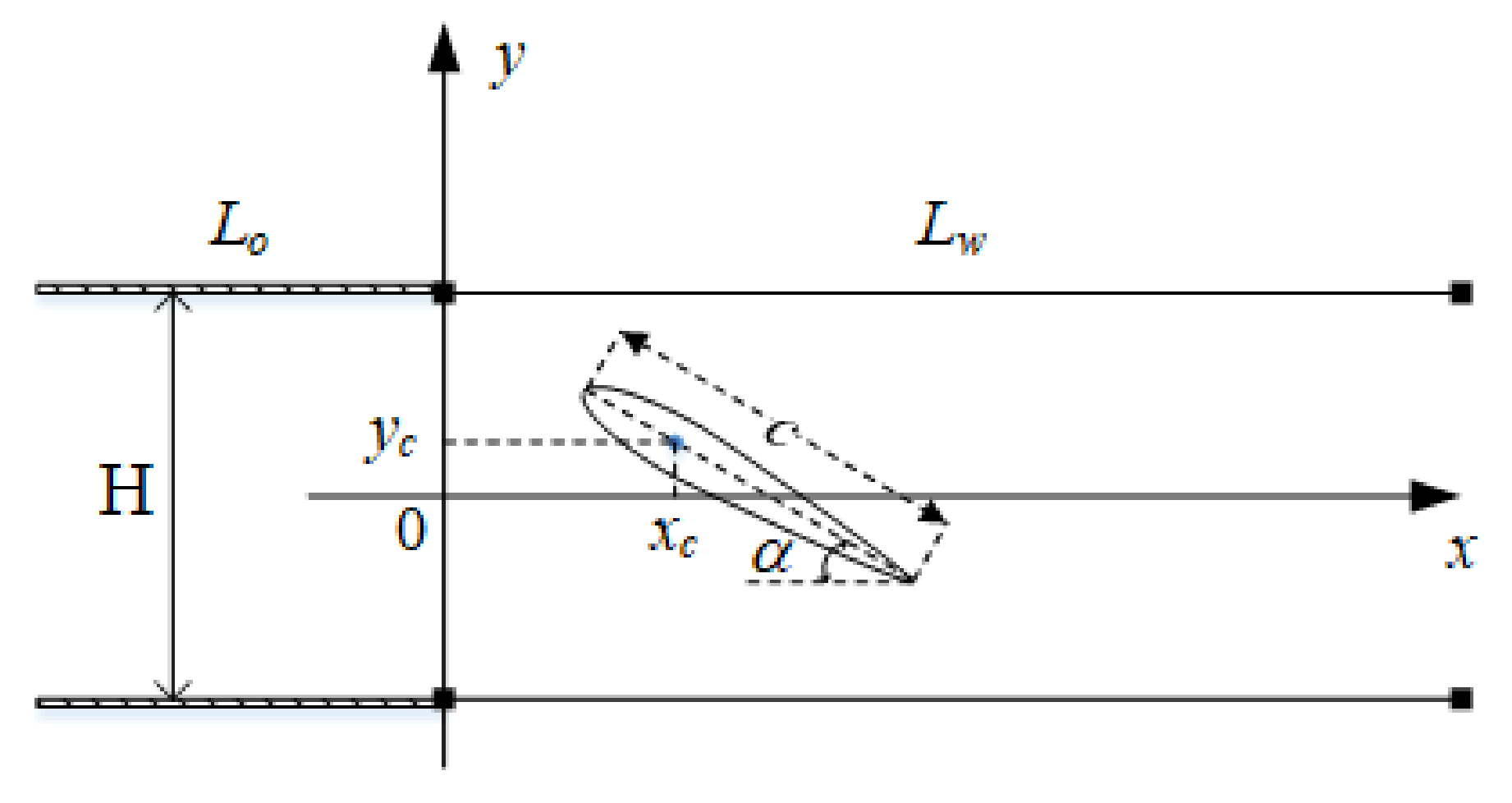
2. Basic Theory

The jet flow usually has a higher velocity than the ambient flow, and the boundary between them is called the free shear layer [25], where the tangential velocity is discontinuous. The vortex sheet can describe such discontinuity, so it is used to represent the jet boundary in this paper.

The developed method in this study is based on the following assumptions:

• The flow is inviscid, and the influence of the viscosity is omitted,
• The flow is two-dimensional and incompressible,
• The total pressure difference between inside and outside jet flow remains constant.

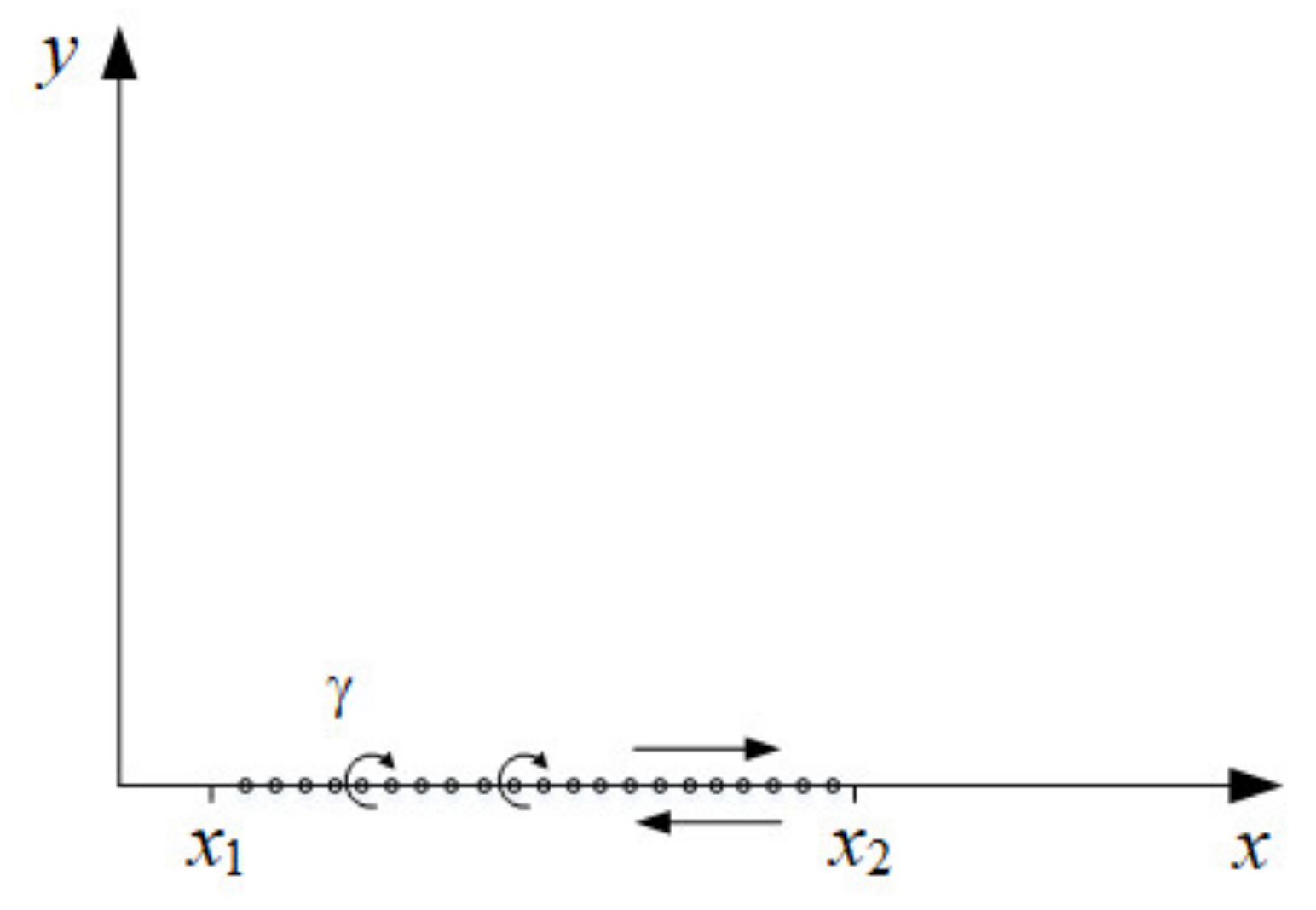
2.1. Infinite Vortex Sheet

Firstly, the induced velocity of the finite vortex sheet is introduced. The vortex strength $\gamma$ remains constant along the x-axis in Figure 1, and the clockwise direction is positive.

According to Katz [24], the induced velocity of a finite constant-strength vortex sheet at the position $(x,y)$ can be calculated as follows:

$$u_{ind}(x,y)=\frac{1}{2\pi }{\displaystyle {\int }_{x_1}^{x_2}\gamma \frac{y}{{(x-x_0)}^2+y^2}}d{x}_0$$

(1)

$$v_{ind}(x,y)=-\frac{1}{2\pi }{\displaystyle {\int }_{x_1}^{x_2}\gamma \frac{x-x_0}{{(x-x_0)}^2+y^2}}d{x}_0$$

(2)

When the length of the vortex sheet approaches infinite, $x_1\to -\infty$, $x_2\to +\infty$, by the integration, the induced velocity can be obtained in Equation (3).

$$\left\{\begin{array}{ll}{u}_{ind}(x,y)=\frac{\gamma }{2},& y>0\\ u_{ind}(x,y)=-\frac{\gamma }{2},& y<0\\ v_{ind}(x,y)=0& \end{array}\right.$$

(3)

In Equation (3), the velocity induced by a single infinite vortex sheet divides the plane into two parts. The velocity above the sheet is $\frac{\gamma }{2}$, and the induced velocity below the sheet is $-\frac{\gamma }{2}$.

For two infinite vortex sheets with opposite strength in Figure 2, the vortex sheet $-\gamma$ is placed at $y=\frac{H}{2}$, and the other is placed at $y=-\frac{H}{2}$, both along the x-direction. The velocity field in this condition is:

$$\left\{\begin{array}{ll}{u}_{ind}(x,y)=\gamma ,& \left|y\right|<\frac{H}{2}\\ u_{ind}(x,y)=0,& \left|y\right|>\frac{H}{2}\\ v_{ind}(x,y)=0& \end{array}\right.$$

(4)

It can be seen from Equation (4) that the velocity field induced by two infinite vortex sheets with opposite strength is equivalent to a jet flow with a height of $H$. Besides, the velocity inside the jet flow is independent of the height $H$, which is equal to the vortex strength $\gamma$. If the jet height becomes wide enough, $H\to +\infty$, the velocity field can also be equivalent to freestream flow.

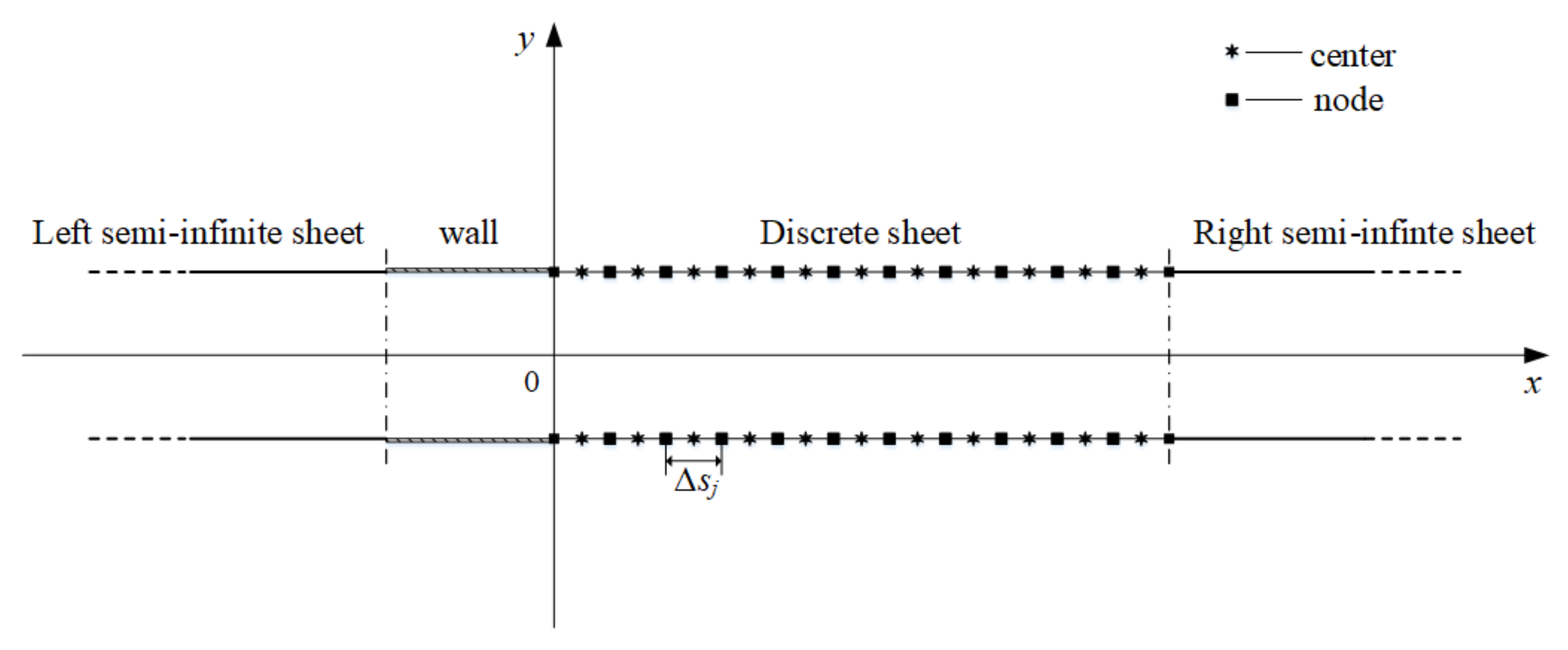
2.2. Discrete Jet Model

In numerical calculation, the jet boundary should be discretized properly. In this study, the outlet of the jet is represented by two walls without thickness. In order to consider the deflection of the jet boundary, the upper and lower discrete vortex sheet with finite length is adopted as well. The final jet model is shown in Figure 3.

The discrete jet model includes a left semi-infinite sheet, jet outlet walls, discrete sheet, and right semi-infinite sheet. The induced velocity of the left and right semi-infinite sheets can be found in the literature [18]. Based on this discrete jet model, the aerodynamic characteristics of the airfoil in jet flow will be studied.

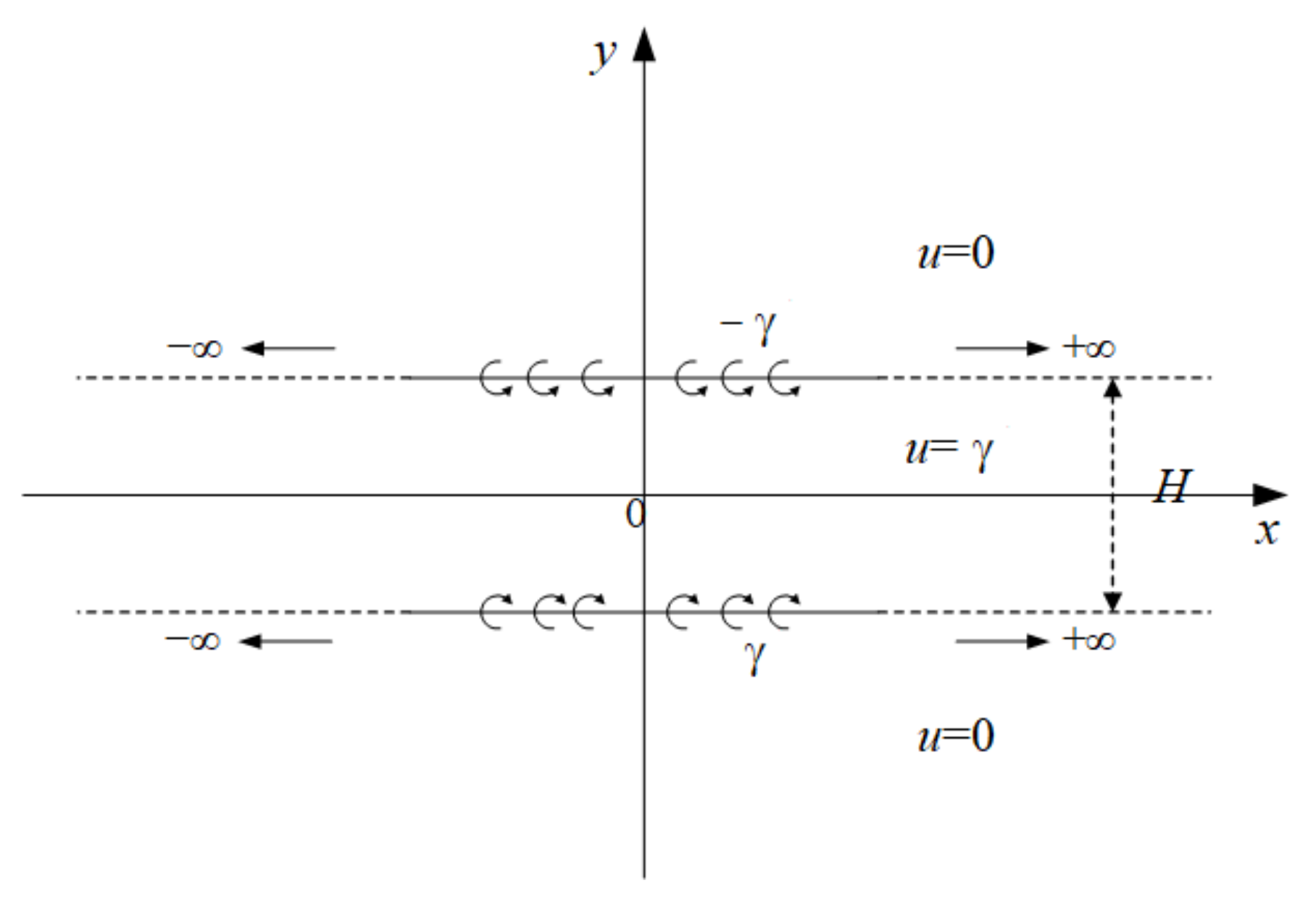
2.3. Jet Bouzndary Condition

For a given jet flow, the jet velocity is $V_w$, and the freestream velocity is $V_{\infty }$, both are along the horizontal direction. The total pressure inside and outside the jet is defined as $p_{total}^{in}$ and $p_{total}^{out}$, respectively. Without the influence of the airfoil, the jet does not deflect, and the static pressure in jet flow is always equal to the ambient pressure, so the total pressure difference inside and outside the jet can be obtained as follows:

$$\Delta p_t=p_{total}^{in}-p_{total}^{out}=\left[p_{\infty }+\frac{1}{2}{\rho }_{\infty }{V}_w^2\right]-\left[p_{\infty }+\frac{1}{2}{\rho }_{\infty }{V}_{\infty }^2\right]=\frac{1}{2}{\rho }_{\infty }{V}_w^2-\frac{1}{2}{\rho }_{\infty }{V}_{\infty }^2$$

(5)

When the airfoil exists in the jet, the pressure and velocity at the jet boundary will change. If the total pressure difference keeps constant, for one point at the jet boundary in Figure 4, Equation (5) returns

$$\Delta p_t=p_{total}^{in}-p_{total}^{out}=\left[p_{in}+\frac{1}{2}{\rho }_{\infty }{V}_{in}^2\right]-\left[p_{out}+\frac{1}{2}{\rho }_{\infty }{V}_{out}^2\right]$$

(6)

Because the free vortex sheet is force-free, which means $p_{in}=p_{out}$ at the jet boundary. Equation (6) can be rearranged as,

$$\Delta p_t=\frac{1}{2}{\rho }_{\infty }{V}_{in}^2-\frac{1}{2}{\rho }_{\infty }{V}_{out}^2=\frac{1}{2}{\rho }_{\infty }(V_{in}-V_{out})(V_{in}+V_{out})$$

(7)

The velocity at the jet boundary is defined as $V_{sheet}=\frac{V_{in}+V_{out}}{2}$, and the vortex strength is ${\gamma }_{sheet}=V_{in}-V_{out}$. Finally, the total pressure difference at the jet boundary can be written as

$$\Delta p_t={\rho }_{\infty }{\gamma }_{sheet}{V}_{sheet}$$

(8)

Equation (8) is the calculation boundary condition of the jet boundary in this paper and can be used to update the vortex strength of the discrete jet boundary.

2.4. The Free Streamline Model

The free streamline model considers the jet boundary to be a streamline. For a discrete vortex sheet, the node position of the vortex sheet can be updated according to the velocity of every element on the vortex sheet [18].

In Figure 3, a single discrete sheet contains $N_w$ elements with $N_w+1$ nodes. The length of an element is $\Delta s_j$, and the velocity at the center is $(u_{j,}{v}_j)$, $j=0,\cdots N_w-1$. The starting point of the discrete sheet is $(x_0,y_0)$, which remains constant. From the second node, the position of each node on the sheet can be updated as follows,

$$x_i=x_0+{\displaystyle \sum _{j=0}^{i-1}\frac{u_j}{\sqrt{u_j^2+v_j^2}}\Delta s_j},y_i=y_0+{\displaystyle \sum _{j=0}^{i-1}\frac{v_j}{\sqrt{u_j^2+v_j^2}}\Delta s_j},i=1,\cdots N_w$$

(9)

Equation (9) will be used for the jet boundary iteration. When the position of the vortex sheet does not change, the calculation is converged.

2.5. Vortex Panel Method

In this study, the lumped vortex is used to represent the jet wall, and the vortex panel is adopted to discretize the surface of the airfoil, the details of which can be found in reference [24]. All walls form a global coefficient matrix, and the Gaussian elimination method is used to solve the linear equations. It is worth noting that, for the jet flow, except for the velocity of freestream, the induced velocity of the jet boundary should be also included in the constant term of equations.

2.6. Generalized Kutta-Joukowski Theorem

The classic Kutta-Joukowski (K-J) theorem is only suitable for a single airfoil in an unbounded freestream. However, the flow field in this study contains multiple free vortex and bound vortex, and the classic K-J theorem does not hold for such problems. Bai [26,27] generalized the classic K-J theorem and extended it to the case of multiple free vortex and bound vortex flow. Thus, this study will use the Generalized K-J theorem to calculate the aerodynamic force of the airfoil in the jet flow.

The freestream velocity $V_{\infty }$ is assumed horizontal. If $N$ panels are placed at the airfoil surface, the lift and drag can be calculated as follows,

$$\left\{\begin{array}{l}L={\displaystyle \sum _{i=0}^{N-1}{\rho }_{\infty }(V_{\infty }+V_{i,x}){\Gamma }_i}\\ D=-{\displaystyle \sum _{i=0}^{N-1}{\rho }_{\infty }{V}_{i,\mathrm{y}}{\Gamma }_i}\end{array}\right.$$

(10)

In Equation (10), $V_{i,x}$ and $V_{i,\mathrm{y}}$ are the horizontal and vertical induced velocity of the $i\mathrm{th}$ panel caused by other free vortex or bound vortex except for the airfoil itself. ${\Gamma }_i$ is the circulation of the $i\mathrm{th}$ panel.

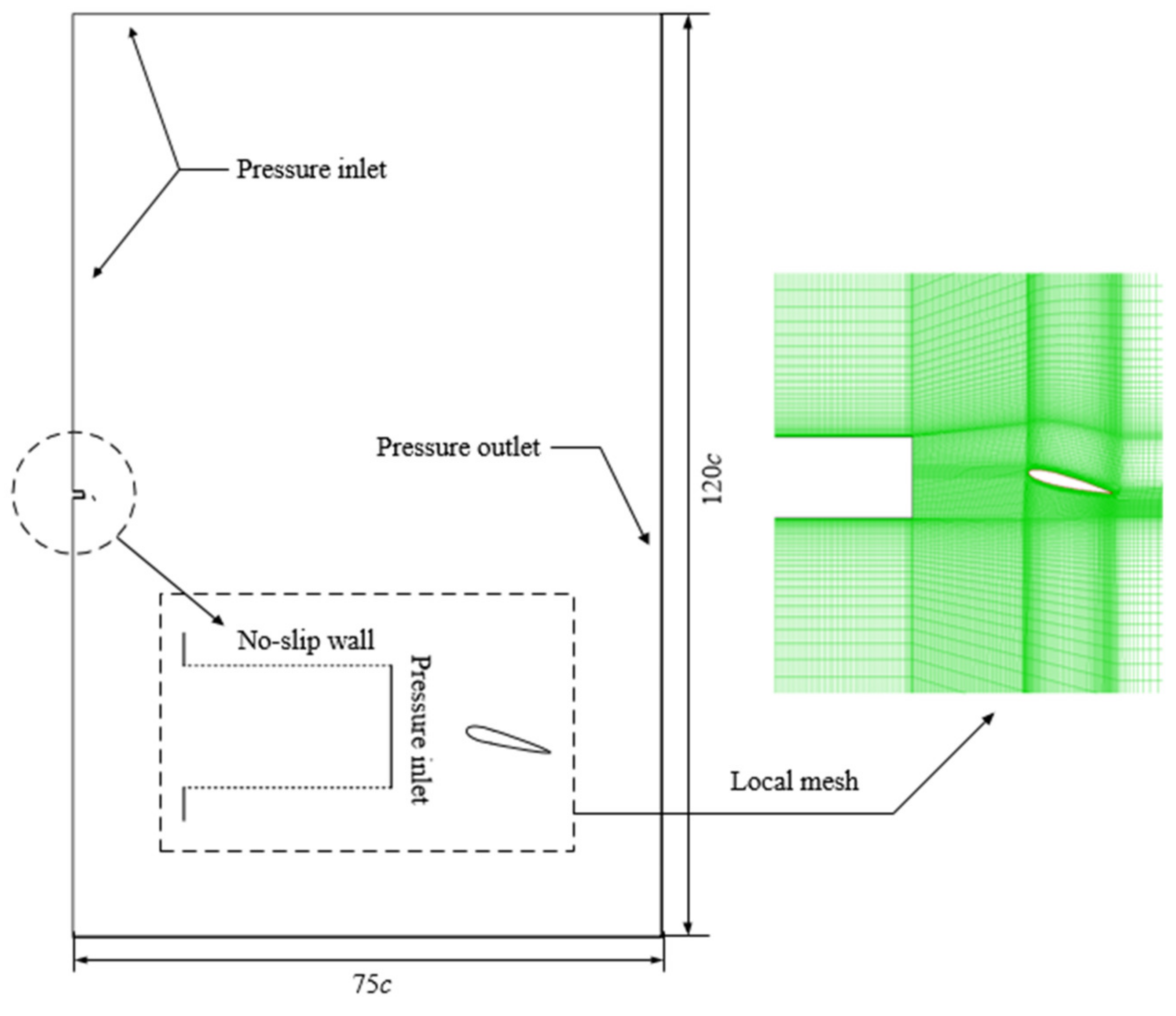
3. Method Validation

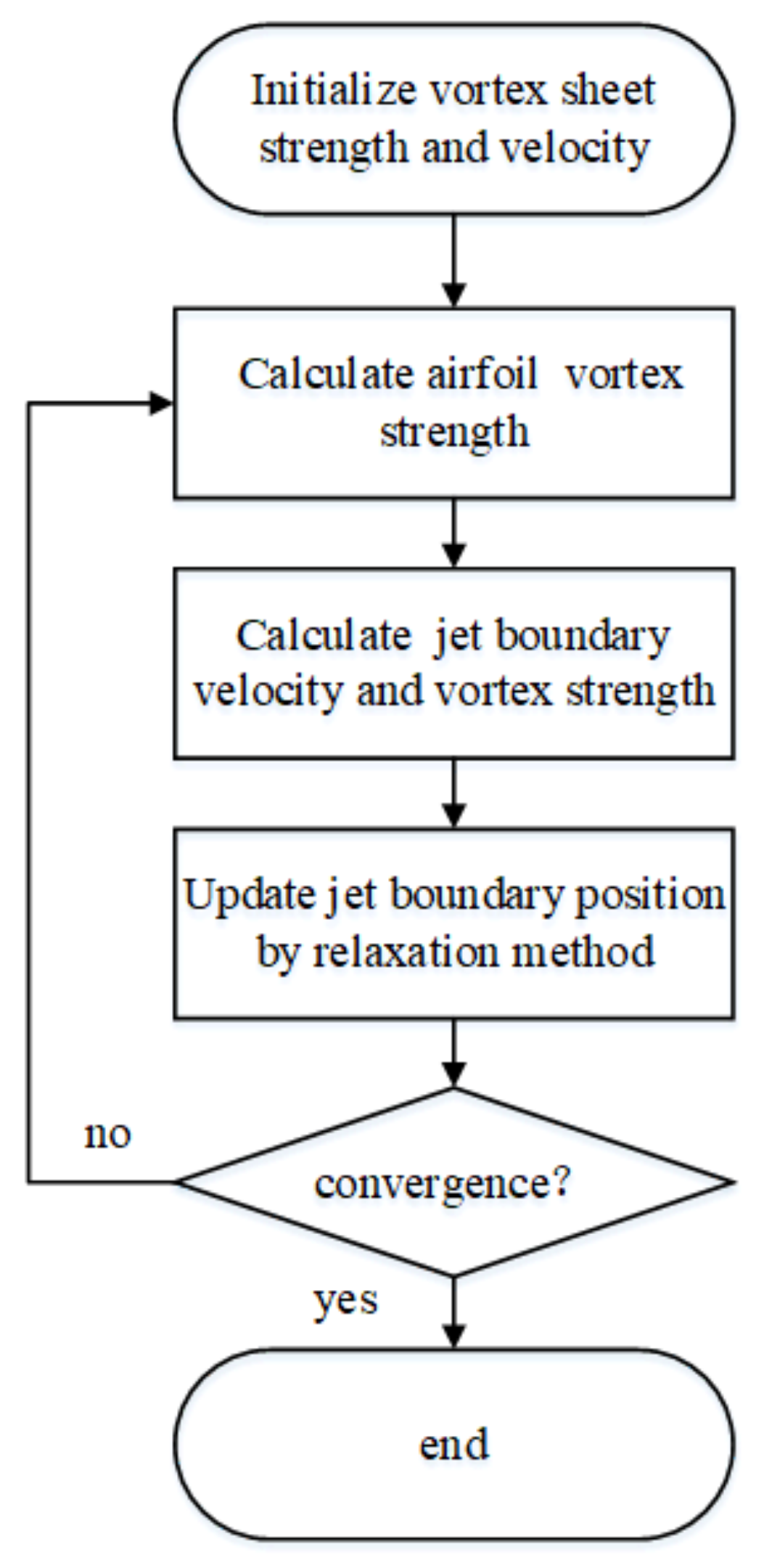
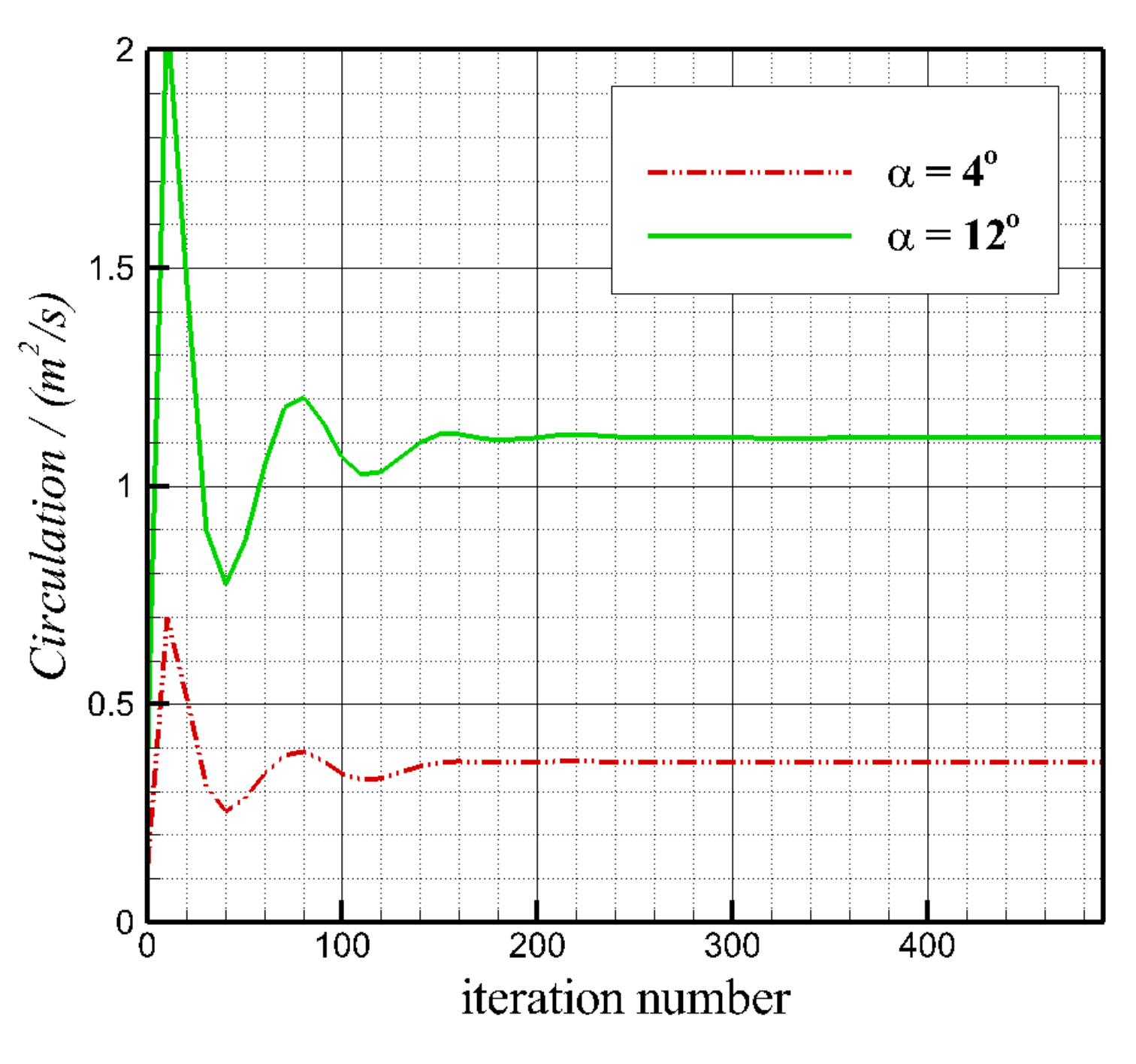
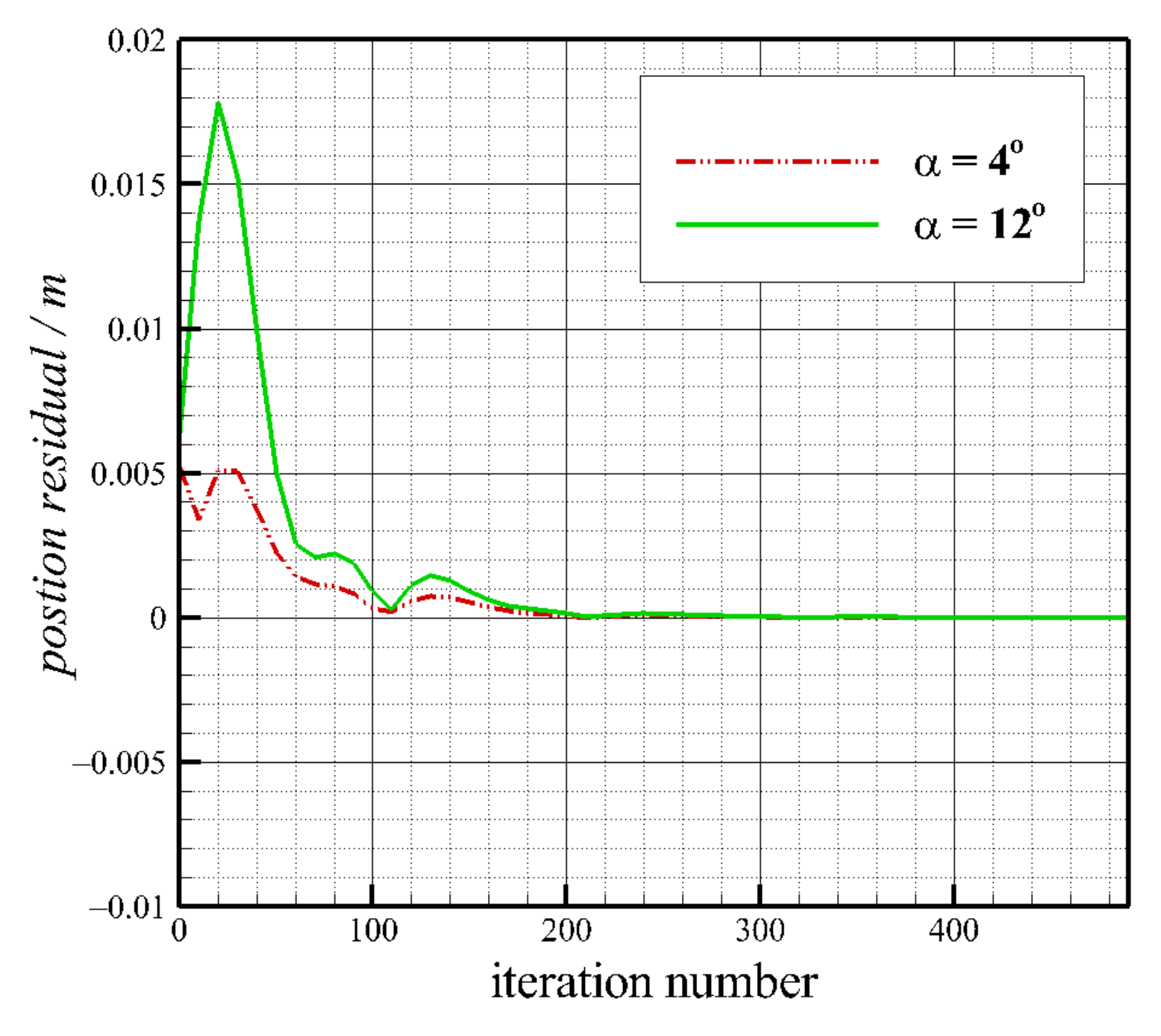
3.1. The Solution Process

After introducing the relevant theory, the calculation procedure of the developed method in this paper is given as follows:

(1)

Input the geometry parameter of the jet and airfoil, and initialize vortex sheet strength and velocity.

If the velocity of the jet and the freestream is $V_w$ and $V_{\infty }$, the initial vortex strength of the jet boundary can be determined in Equation (11).

$${\gamma }_0=V_w-V_{\infty }$$

(11)

(2)

Calculate the induced velocity of the wall surfaces (jet outlet walls and the airfoil) including the effects of jet boundary and freestream.

(3)

Solve linear equations, and update the vortex strength and circulation on the wall surface.

(4)

Update the position of the discrete jet boundary by Equation (9).

(5)

Calculate the vortex strength of the discrete jet boundary by Equation (8).

(6)

Repeat (2)–(5), until the airfoil circulation and the jet position converge.

During the calculation, the position and the vortex strength of the left semi-infinite sheet remain constant. For the right semi-infinite sheet, the vortex strength keeps constant but the position will vary with the position of the last node on the discrete vortex sheet. The whole process is carried out by the relaxation iteration method and is shown in Figure 5.

The main geometric parameters in this paper include the jet height $H$, the length of the outlet wall $L_o$, the chord of the airfoil $c$, and the length of the discrete vortex sheet $L_w$. The rotation center of the airfoil is defined at $0.25c$, $(x_c,y_c)$ in the computational coordinates, and the angle of attack is $\alpha$. The origin of the computational coordinates is located at the center of the jet outlet, as shown in Figure 6.

The lift and drag coefficients of the airfoil in jet flow are calculated by the following equation.

$$c_l=\frac{L}{\frac{1}{2}{\rho }_{\infty }{V}_w^{2}c}, c_d=\frac{D}{\frac{1}{2}{\rho }_{\infty }{V}_w^{2}c}$$

(12)

In Equation (12), the lift coefficient is $c_l$, the drag coefficient is $c_d$, the air density is ${\rho }_{\infty }$, and the jet velocity is $V_w$. In particular, for the freestream flow without the jet, Freestream velocity $V_{\infty }$ will still be used as the reference velocity for the calculation of the aerodynamic coefficient.

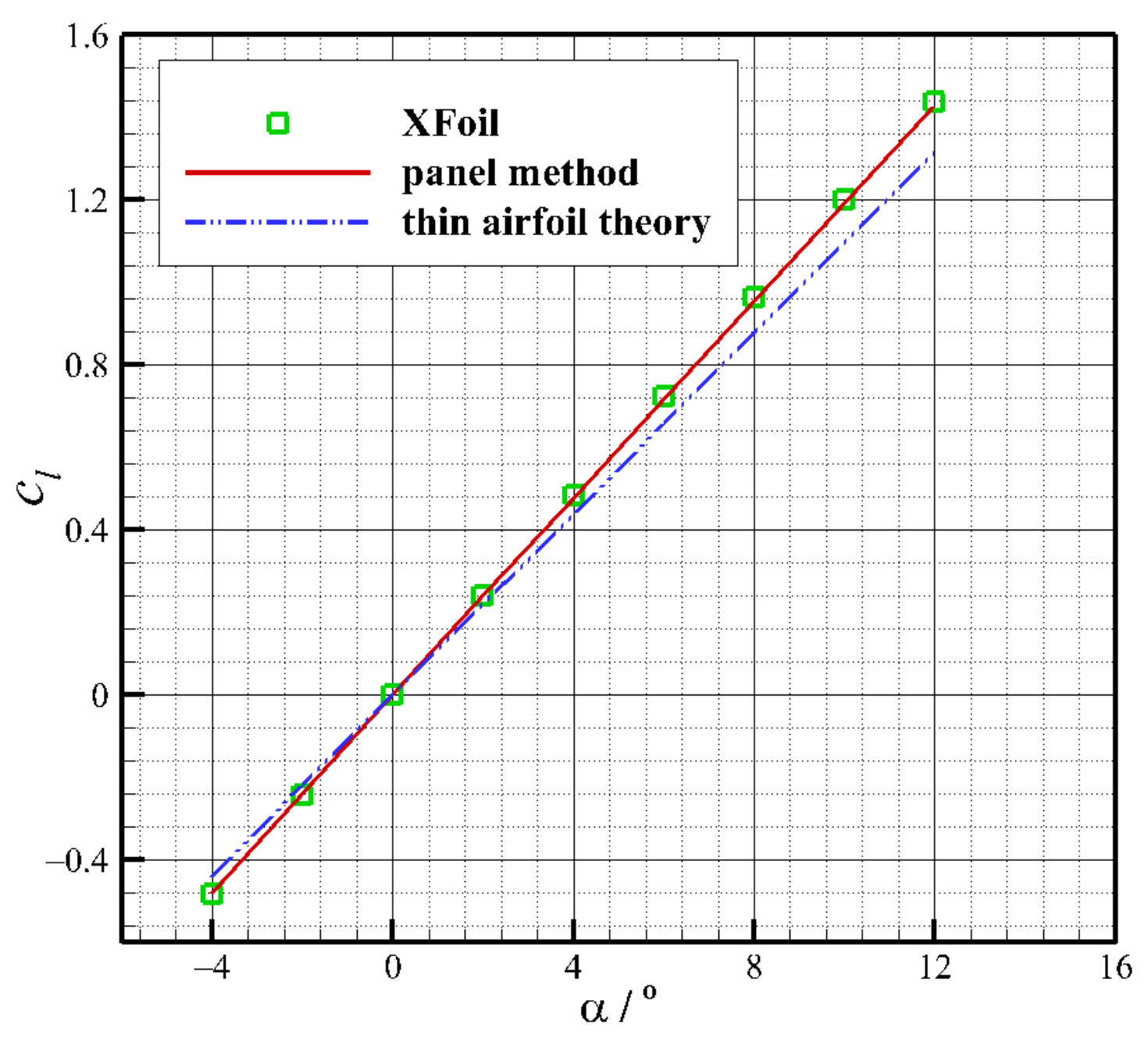
3.2. Airfoil in Freestream

Firstly, the airfoil in inviscid freestream is used to verify the vortex panel method in this study. NACA 0012 airfoil is selected to calculate the lift coefficient and will be compared with the inviscid solution of software XFoil [28].

The panel elements of the airfoil are $N=256$, and the angle of attack range from −4° to 12°, the lift coefficients obtained by different methods are shown in Figure 7.

In Figure 7, the solid line refers to the result of the vortex panel method. It can be seen that the lift coefficient calculated by the vortex panel method is in good agreement with the result of XFoil, which indicates the validity of the panel method in this study.

3.3. Single Jet Flow

The single jet flow with $H=0.16 \mathrm{m}$ is calculated to verify the validity of the discrete jet model. The length of the outlet wall is $L_o=3.2 \mathrm{m}$, and the number of the lumped vortex is 96. The length of the discrete sheet is $L_w=4 \mathrm{m}$, and the element number gives $N_w=180$, $200$, $250$ and $300$ separately, in order to test the influence of the discretization for the velocity field.

The freestream velocity is $V_{\infty }=1 \mathrm{m}/\mathrm{s}$, and the jet velocity is $V_w=30 \mathrm{m}/\mathrm{s}$. For a line segment centered at $x=0.32 \mathrm{m}$, along the $y$-axis, with $0.9H$ length, the velocity on it is compared in Figure 8.

In Figure 8, it can be seen that the discretization will bring discretization error, so the velocity in jet flow will be different from the theory. However, the error can be decreased gradually by increasing the element number. For $N_w\ge 200$, the relative error of axial velocity does not exceed 0.2%. Thus, $N_w=300$ will be adopted in this paper for accuracy.

3.4. Airfoil in Jet Flow

The jet height is $H=0.16 \mathrm{m}$, and the discrete sheet length is $L_w=4 \mathrm{m}$ with $N_w=300$, NACA 0012 airfoil is selected again, and the chord is $c=0.2 \mathrm{m}$, located at $x_c=0.32 \mathrm{m}$, $y_c=0 \mathrm{m}$, angle of attack range from −4° to 20°. The freestream velocity is $V_{\infty }=1 \mathrm{m}/\mathrm{s}$, and the jet velocity is $V_w=30 \mathrm{m}/\mathrm{s}$, along the $x$-axis. The velocity ratio of jet velocity to freestream velocity is 30, which is typical in the take-off stage.

The last node of the lower discrete vortex sheet is used to judge the convergence. For $\alpha =4^{\mathrm{o}}$ and 12°, the convergence curves of airfoil circulation and jet position error for the developed method are given in Figure 9 and Figure 10.

In Figure 9 and Figure 10, it can be seen that the circulation and the position of the jet boundary do not change after about 200 iterations. Thus, the developed method is convergent.

Because there is no relevant experiment data, CFD calculation will be used as a reference to verify the developed method. The commercial software FLUENT is used for CFD calculation. The boundary condition and mesh for CFD are shown in Figure 11.

CFD computation domain contains 55,344 mesh elements, which is sufficient to ensure the accuracy of results. The far-field boundary adopts pressure inlet and pressure outlet boundary conditions, and the total pressure and static pressure of freestream are given. The jet outlet adopts the pressure inlet boundary condition, and the total pressure is calculated according to the jet velocity. The airfoil adopts a no-slip condition for viscous simulation.

The flow condition and geometric parameters remain the same, the S-A and SST k-w turbulence models are used for RANS calculation. Because the panel method cannot consider the friction, the drag obtained by CFD will only take the pressure drag.

The developed method is named FSM (free streamline model) and the aerodynamic force of the airfoil is calculated by the Generalized K-J theorem. The comparisons between FSM and CFD are shown in Figure 12.

It can be seen that FSM agrees well with the results of CFD. The lift curve keeps linear within 20-degree angle of attack due to the contribution of the jet. Besides, the drag is not equal to zero for an airfoil in jet flow even if the flow is inviscid, and the reason will be analyzed in the next section.

For $\alpha =4^{\mathrm{o}}$ and 12°, pressure coefficients obtained by different methods are compared in Figure 13.

In Figure 13, the pressure coefficient obtained by FSM is also in good agreement with the results of CFD. Because the jet velocity is used as the reference velocity, the pressure coefficient at the stagnation point is 1 for the airfoil. Thus, the proposed method in this paper is reliable.

For $\alpha ={12}^{\mathrm{o}}$, the converged shape of the jet boundary is also shown in Figure 14.

It can be seen in Figure 14 that the FSM can capture the jet deflection properly, which further validates the developed method at a high-velocity ratio.

For the time cost, CFD calculation needs about 4.0 minutes for the convergence at every angle of attack, but FSM needs no more than one minute at the same condition. Thus, the developed method in this paper is preferred for the preliminary design.

In the following, the developed method will be used to study the aerodynamic characteristics of an airfoil in jet flow.

4. Method Application

In this section, the established method will be used for the application and study of the factors affecting the aerodynamic force of an airfoil in jet flow.

The length ratio of jet height to airfoil chord is defined as $R_1$, $R_1=H/c$, and the velocity ratio of jet velocity to freestream velocity is defined as $R_2$, $R_2=V_w/V_{\infty }$. In the following calculations, NACA 0012 airfoil with $c=0.2 \mathrm{m}$ is adopted again, and the relative position of the airfoil to the jet outlet remains unchanged.

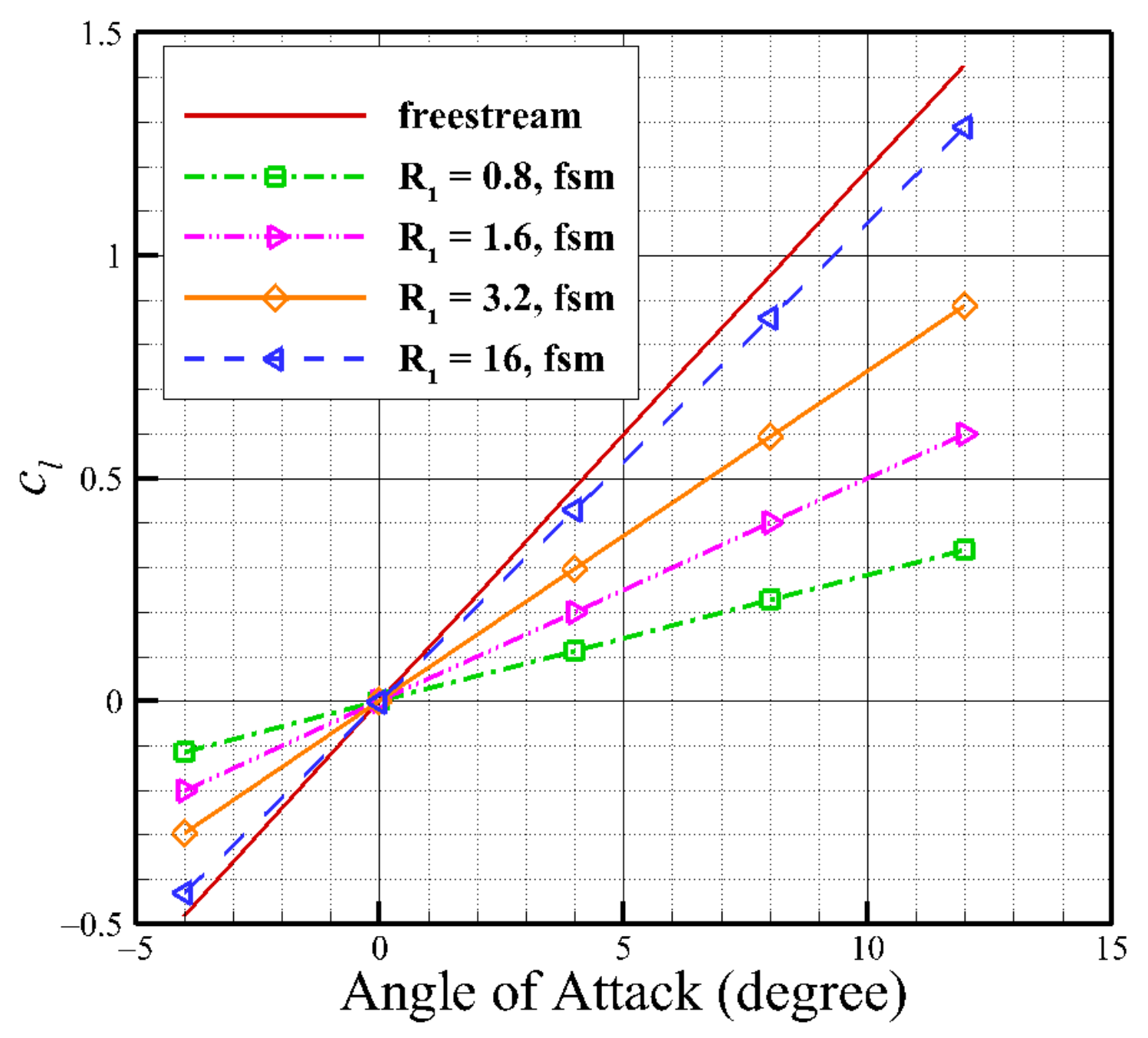
4.1. The Length Ratio of Jet Height to Airfoil Chord

By changing the jet width, the influence of the height-chord ratio on the aerodynamic characteristics of the airfoil in the jet flow is studied.

The freestream velocity is $V_{\infty }=1 \mathrm{m}/\mathrm{s}$ and the jet velocity is $V_w=30 \mathrm{m}/\mathrm{s}$. The jet height is $H=0.16 \mathrm{m}$, $0.32 \mathrm{m}$, $0.64 \mathrm{m}$ and $3.2 \mathrm{m}$, corresponding to $R_1=0.8$, 1.6, 3.2, and 16. The lift coefficients of the airfoil at different height-chord ratios are shown in Figure 15.

In Figure 15, the curve “freestream” means the lift coefficient of the airfoil in inviscid freestream flow. It can be seen that because of the jet deflection, the lift of airfoil in finite width jet is smaller than that in unbounded freestream flow. With the increase in height-chord ratio, the lift curve slope increases, and the difference between the jet and freestream flow decreases gradually. Thus, if calculation methods do not consider the jet deflection in finite height-chord ratio, the airfoil in jet and freestream will always have the same lift coefficient, which is unphysical.

For $\alpha ={12}^{\mathrm{o}}$, the deflections of the upper discrete jet boundary at different height-chord ratios are given in Figure 16.

It can be seen from the above figure that with the increase of the height-chord ratio, the deflection of the jet boundary gradually decreases. This is mainly due to the increased distance between the jet boundary and the airfoil, the influence of the airfoil on the jet boundary becomes smaller.

Most of the existing research about jet/airfoil interaction focus on the lift. In this study, the drag characteristics of the airfoil in jet flow are also analyzed. Continuing to increase the jet height, the variation of drag coefficient with the height-chord ratio at 12° is shown in Figure 17.

When the height is small, the drag of the airfoil in the jet will first increase with the increase of the height-chord ratio. However, for $R_1>>5$, the drag decreases with the increase of the height-chord ratio. This variation can be illustrated by the Generalized K-J theorem.

After the jet deflects, the jet boundary will induce a downward velocity (which can be regarded as downwash) on the airfoil surface in Figure 18. According to the Generalized K-J theorem (Equation (10)), the drag is related to the downwash and circulation. When $R_1$ is small, the circulation increases rapidly with the increase of the height-chord ratio. Although the downwash decreases, the drag still increases at first. When $R_1$ is large enough, the flow around the airfoil will be gradually close to freestream. The circulation changes slowly with the increase of the height-chord ratio, but the downwash decreases rapidly. Thus, the drag will decrease and be close to zero in the inviscid flow at last.

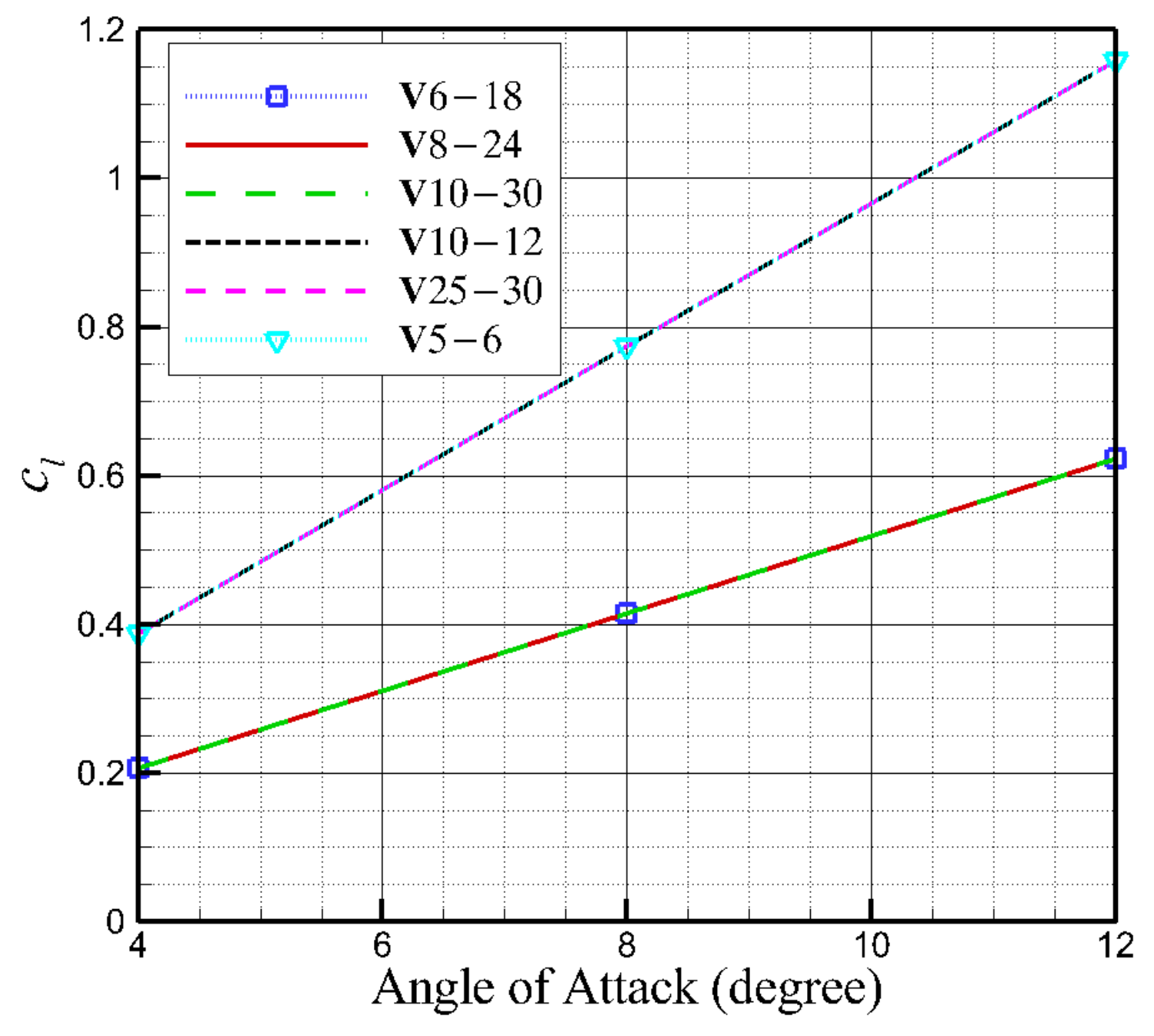
4.2. The Velocity Ratio of Jet Velocity to Freestream Velocity

During the take-off stage, the velocity of the freestream increases continuously while the jet velocity usually decreases. Thus, the effect of different velocity ratios $V_w/V_{\infty }$ on the airfoil should be studied.

The jet height keeps $H=0.16 \mathrm{m}$ and the airfoil parameters remain constant as before. The freestream velocity increases from $V_{\infty }=1 \mathrm{m}/\mathrm{s}$ to $V_{\infty }=20 \mathrm{m}/\mathrm{s}$, and the jet velocity remains $V_w=30 \mathrm{m}/\mathrm{s}$. For angles from 4° to 12°, the variation of lift coefficient of an airfoil with velocity ratio $R_2$ is shown in Figure 19.

It can be seen in Figure 19 that the lift curve slope will increase with the decrease of the velocity ratio. For a large velocity ratio, the vortex strength of the jet boundary is also large (Equation (11)) and the downwash induced by the jet boundary is remarkable, which leads to a smaller lift. When the velocity ratio $R_2$ decreases, the vortex strength of the jet boundary decreases, and the contribution of freestream to lift will become dominant, which contributes to the increase of the lift. For $R_2=1.0$, the vortex strength of the jet boundary will be zero and the composite flow will degrade to a single freestream flow finally.

For inviscid flow, it is known that the lift coefficient of the airfoil in freestream is related to the angle of attack and independent of the velocity magnitude. Once the lift coefficient curve is determined, people can use it at different velocities and do not need to double calculate. However, for the above composite flow, the lift coefficient of the airfoil in jet flow is also related to the velocity magnitude of the freestream. In order to avoid double calculation, it is helpful if there exists a non-dimensional parameter to describe this composite flow.

By changing the velocity of the freestream and the jet at the same time, more flow conditions will be calculated. For angles from 4° to 12°, the lift coefficients of the airfoil at different flow conditions are shown in Figure 20.

In Figure 20, there exist six curves, corresponding to six different flow conditions. Symbol “V6–18” means $V_{\infty }=6 \mathrm{m}/\mathrm{s}$ and $V_w=18 \mathrm{m}/\mathrm{s}$, and other symbols are similar. It is interesting to see that the lift coefficient curve of “V6–18”, “V8–24”, and“V10–30” are coincident, corresponding to $R_2=3$, and the lift coefficient curve of the other three are also coincident, corresponding to $R_2=1.2$. In a word, with the same velocity ratio, the lift coefficient of the airfoil in the jet flow is equal, and the drag coefficient also has the same conclusion.

In order to explain this phenomenon, for $\alpha =$12°, the jet boundaries at different flow conditions are given in Figure 21.

It can be seen that the deflection of the jet is different under different velocity ratios, but at the same velocity ratio, the deflection of the wake is exactly the same no matter how the velocity magnitude of the jet and freestream is. In other words, for the composite flow, the velocity ratio can be regarded as a similarity parameter for this composite system. For the same velocity ratio, the flow field is similar. Therefore, if the geometric parameters remain unchanged, the aerodynamic coefficients of the airfoil in the jet flow will keep constant with the same velocity ratio. So, double calculation will be avoided at the same velocity ratio.

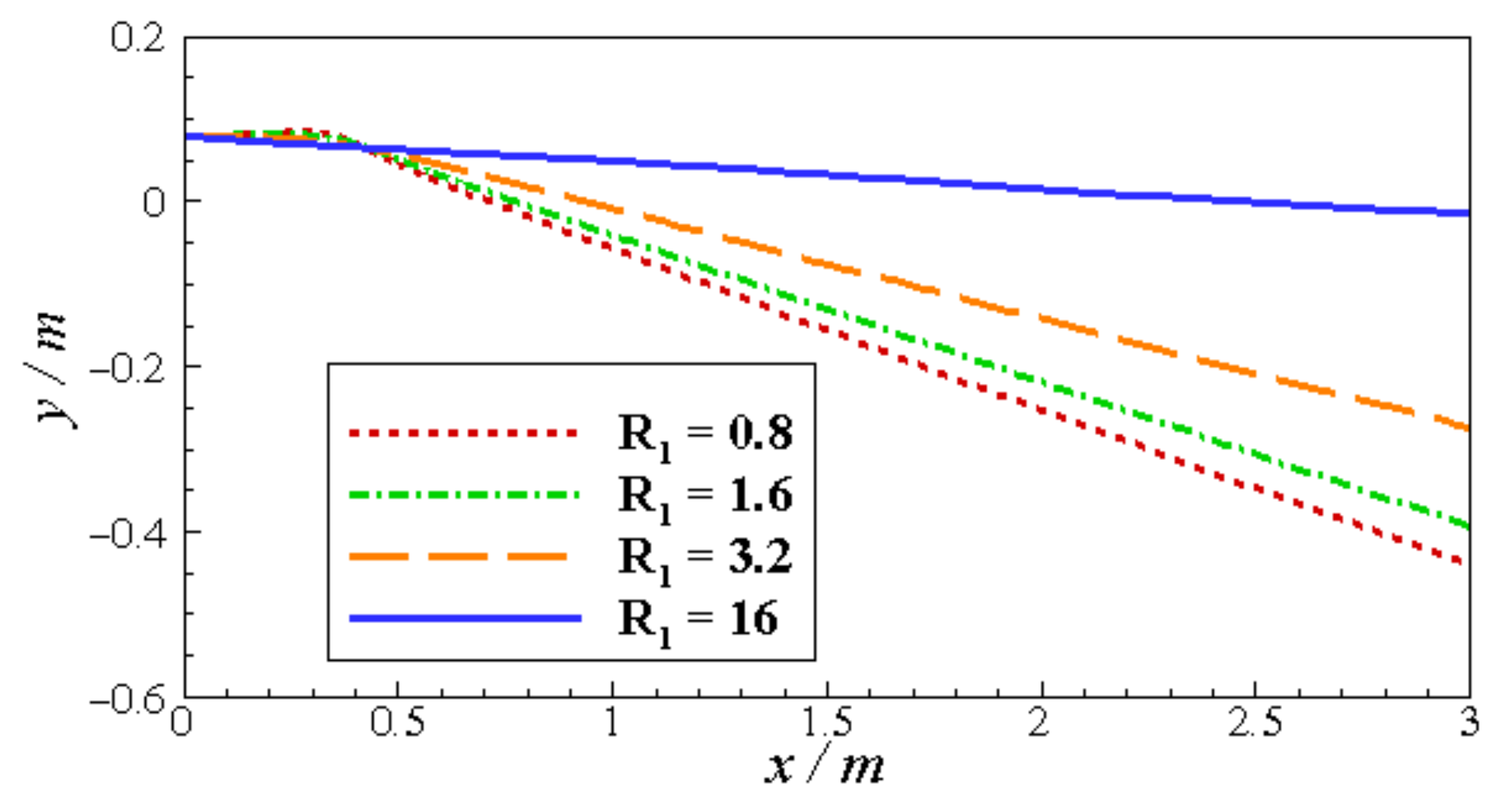
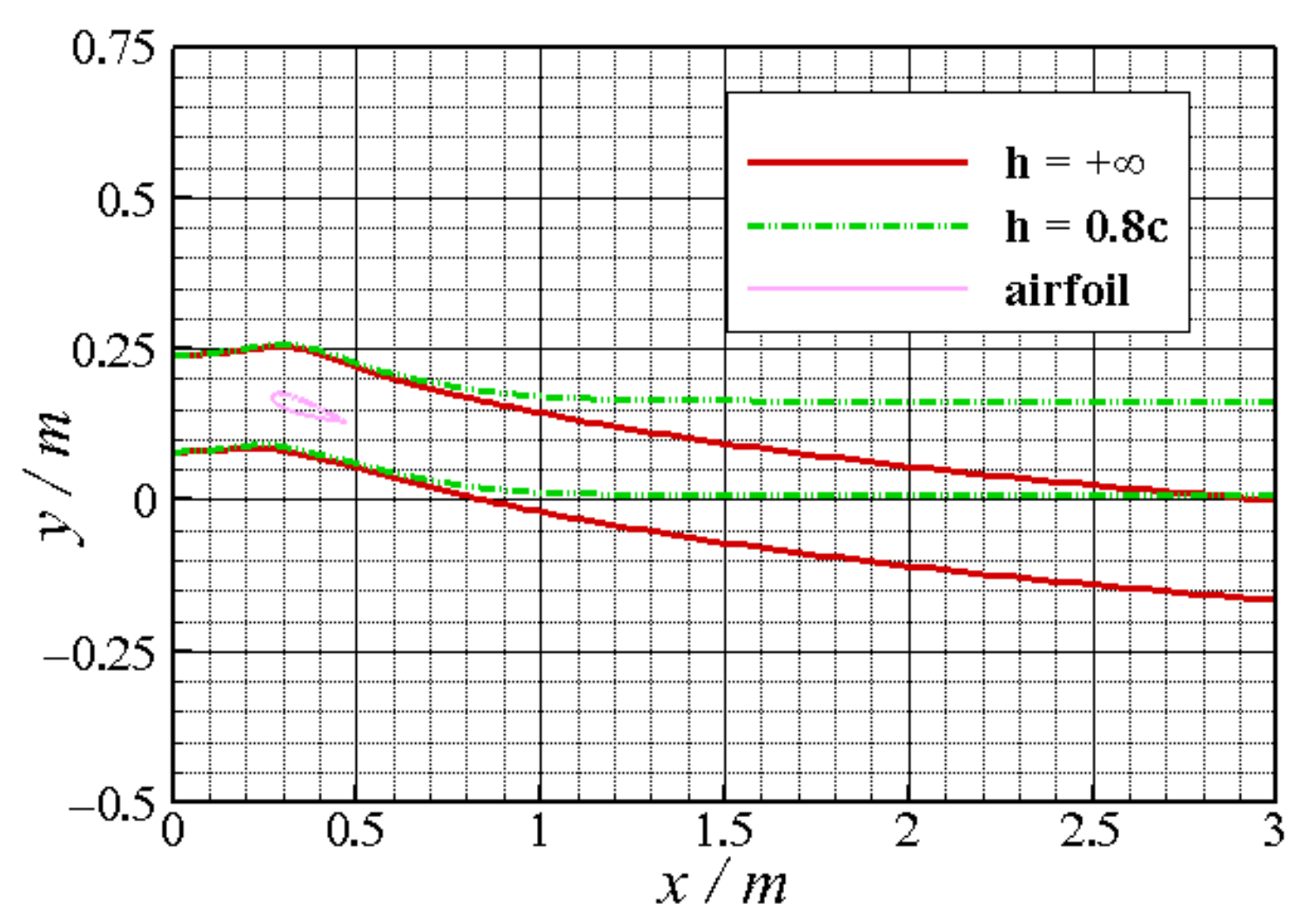
4.3. Ground Effect for the Airfoil in Jet Flow

According to the above study, it is clear that due to the deflection of the jet boundary, the airfoil in jet flow will not only generate the lift but also generate the drag. Reference [29] points out that the ground effect can increase lift and reduce drag for the airfoil in freestream. In this study, the influence of the ground effect on the aerodynamic force for the airfoil in the jet flow is also analyzed.

The image method [25] is combined with the FSM method to calculate the ground effect. The freestream velocity is $V_{\infty }=10 \mathrm{m}/\mathrm{s}$, and the jet velocity is $V_w=30 \mathrm{m}/\mathrm{s}$. The jet height is $H=0.16 \mathrm{m}$, and the position of the airfoil remains unchanged. The height above the ground is shown in Figure 22.

The ground height changes from $h=0.8c$ to $h=5.0c$ and the results of FSM will also be compared with CFD. For $\alpha =$ 8° and 12°, the aerodynamic coefficients of NACA 0012 airfoil at different ground heights are compared as follows:

As can be seen in Figure 23, the variation trends of aerodynamic coefficients are similar by different methods. When the ground height decreases, the lift becomes larger and the drag decreases. Thus, for the airfoil in the jet flow, the ground effect can be used to increase the lift and reduce the drag.

For $\alpha =$ 12°, the different shapes of the jet boundary at $h=0.8c$ and $h=+\infty$ are compared in Figure 24.

In Figure 24, for $h=+\infty$, there is no ground effect, and the deflection of the jet boundary is free along the flow direction. However, for $h=0.8c$, due to the obstruction of the ground, the jet flow returns to the horizontal direction soon after passing the airfoil. The existence of the ground decreases the downward deflection for the jet boundary, and the downwash velocity decreases finally. Therefore, the drag of the airfoil is reduced, which is beneficial for the take-off.

5. Conclusions

Based on the free streamline model, a fast calculation method for an airfoil in inviscid jet flow is developed in this paper. Using the developed method, the effects of the length ratio of jet height to airfoil chord, the velocity ratio of jet velocity to freestream velocity, and the ground effect are studied. The work in this paper contributes to a comprehensive understanding of the aerodynamic characteristics of an airfoil in jet flow. The main conclusions are as follows:

(1)

The proposed method in this study can capture the deflection of the jet flow with a low time cost and can be used at a high-velocity ratio, which is suitable for the preliminary design of a powered-lift wing.

(2)

In a finite-width jet, the airfoil will not only generate lift but also drag because of the jet deflection. Besides, the slope of the lift curve in jet flow is lower than the situation in freestream flow. The lift and drag appear in different variations with the increase in the height-chord ratio. When the height-chord ratio is large enough, the aerodynamic characteristics of the airfoil will be close to the freestream condition.

(3)

For the inviscid jet flow, the velocity ratio of jet and freestream can be regarded as a similarity parameter, which can be used to describe this composite flow. Keeping the same geometric parameters, the aerodynamic coefficients of the airfoil will be equal at the same velocity ratio no matter how the velocity magnitude of the jet and freestream is.

(4)

For the airfoil in the jet flow, by resisting the deflection of the jet boundary, the ground effect can be used to increase lift and decrease drag, which is helpful for short take-off.

When the thrust of the propulsion is known, the aerodynamic model developed in this paper can also be applied to the study of the three-dimensional jet/wing interaction, such as the ducted fan/wing interaction problem [30]. Firstly, the FSM method can be used to calculate the aerodynamic force of the airfoil in a two-dimensional jet flow. Combined with the Lifting-line methods [31,32,33], the aerodynamic force of the three-dimensional wing including the influence of three-dimensional jet flow will be quickly estimated.