Track Segment Association Method Based on Bidirectional Track Prediction and Fuzzy Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Holt-Winters Method
2.2. Fuzzy Track Association Algorithm
2.3. Fuzzy Track Segment Association Algorithm
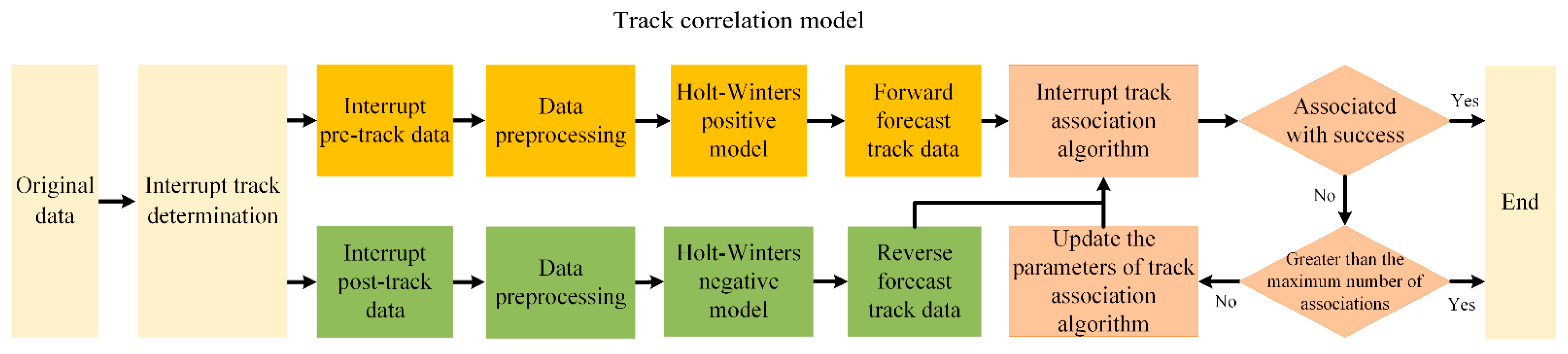
2.4. Holt-Winters Prediction and Fuzzy Analysis Model
- Track segment judgment: real-time judgment of incoming track points, if the latest track point is not received after the set time, it is considered that the current track is in an interrupted state, and the procedure goes to the next step;
- Track segment data processing: convert the pre-interruption track data into the format required by the program and use the processed pre-interruption track data to train the Holt-Winters forward model while waiting for the recovery of the track point. If the point data are considered to be in an interrupted state at the end of the track, the program goes to the next step;
- Track segment data prediction: the processed track data before the interruption and the track data after the interruption are processed and sent to the Holt-Winters model, and the Holt-Winters method is used to predict from two directions. After the prediction is completed, the program goes to the next step;
- Track segment association: a fuzzy track association algorithm is used to correlate data before and after interruption. If the association fails and the number of repeated associations does not exceed the preset maximum number of times, end the program. If the association fails, perform the secondary association: first jump to step 3 to update the prediction result and then replace the Equation (7) of the algorithm with Equation (9) in the fourth step of the program, and then perform the fuzzy track. The association algorithm is shown below.
3. Results
3.1. Data Set
3.2. Experimental Setup
3.3. Prediction Experiment
- TCN [23]: The input step is 10, the learning rate is 1 × 10−3; epoch: 300.
- Prophet [29]: Parameters: default; the prediction frequency is 10 s.
- Holt-Winters: “Trend” is set to “add”. Except that, the three feature parameters x, and vx are slightly different, the “damped trend” of other feature column parameters is set to “true” and “seasonal” is set to “add”.
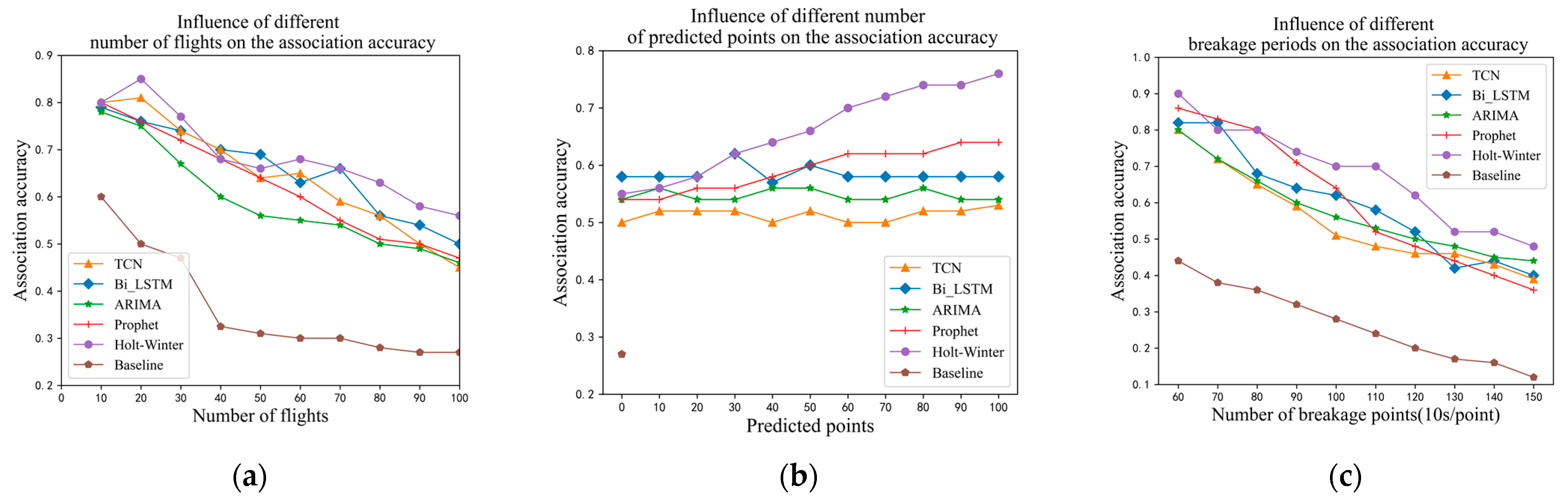
3.4. Track Association Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, T.; Chen, H.; Sun, S.; Corchado, J.M. Joint Smoothing and Tracking Based on Continuous-Time Target Trajectory Function Fitting. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1476–1483. [Google Scholar] [CrossRef] [Green Version]
- Rong Li, X.; Jilkov, V.P. Survey of maneuvering target tracking. Part I. Dynamic models. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1333–1364. [Google Scholar] [CrossRef]
- Rong Li, X.; Jilkov, V.P. Survey of Maneuvering Target Tracking. Part II: Motion Models of Ballistic and Space Targets. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 96–119. [Google Scholar]
- Rong Li, X.; Jilkov, V.P. Survey of maneuvering target tracking. Part V. Multiple-model methods. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1255–1321. [Google Scholar] [CrossRef]
- Zhou, J.; Li, T.; Wang, X.; Zheng, L. Target Tracking with Equality/Inequality Constraints Based on Trajectory Function of Time. IEEE Signal Process. Lett. 2021, 28, 1330–1334. [Google Scholar] [CrossRef]
- Singer, R.A. Estimating Optimal Tracking Filter Performance for Manned Maneuvering Targets. IEEE Trans Aerosp. Electron. Syst. 1970, 6, 473–482. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Jaffer, A.G. Adaptive linear Filtering for Tracking with Measurements of Uncertain Origin. In Proceedings of the 1972 IEEE Conference on Decision and Control and 11th Symposium on Adaptive Processes, New Orleans, LA, USA, 13–15 December 1972. [Google Scholar]
- Fortmann, T.E.; Bar-Shalom, Y.; Scheffe, M. Multi-target tracking using joint probabilistic data association. In Proceedings of the 19th IEEE Conference on Decision and Control including the Symposium on Adaptive Processes, Albuquerque, NM, USA, 10–12 December 1980. [Google Scholar]
- Singer, R.A.; Sea, R.G. A New Filter for Optimal Tracking in Dense Multi-target Environments. In Proceedings of the Ninth Allerton Conference Circuit and System Theory, Monticello, VA, USA, 6–8 October 1971. [Google Scholar]
- Reid, D.B. An Algorithm for Tracking Multiple Targets. IEEE Trans. Autom. Control. 1979, 24, 843–854. [Google Scholar] [CrossRef]
- Blackman, S.S.; Popoli, R. Design and Analysis of Modern Tracking Systems; Artech House: Norwood, MA, USA, 1999. [Google Scholar]
- Hachour, S.; Delmotte, F.; Mercier, D.; Lefevre, E. Object tracking and credal classification with kinematic data in a multi-target context. Inf. Fusion 2014, 20, 174–188. [Google Scholar] [CrossRef]
- Schultz, D.; Burgard, W.; Fox, D. Tracking Multiple Moving Targets with a Mobile Robot Using Particle Filters and Statistical Data Association. IEEE Int. Conf. Robot. Autom. 2001, 2, 1665–1670. [Google Scholar]
- Bar-Shalom, Y.; Rong Li, X.; Tugnait, J.K. Estimation with Applications to Tracking and Navigation: Theory, Algorithms and Software; Wiley-Interscience Publication: Hoboken, NJ, USA, 2001; pp. 179–490. [Google Scholar]
- Holt, C.C. Forecasting seasonals and trends by exponentially weighted moving averages. Int. J. Forecast. 2004, 20, 5–10. [Google Scholar] [CrossRef]
- Winters, P.R. Forecasting Sales by Exponentially Weighted Moving Averages. Math. Models Mark. A Collect. Abstr. 1976, 132, 384–386. [Google Scholar]
- Suseelatha, A.; Sudheer, G. Short term load forecasting using wavelet transform combined with Holt-Winters and weighted nearest neighbor models. Int. J. Electr. Power Energy Syst. 2015, 64, 340–346. [Google Scholar]
- Grubb, H.; Mason, A. Long lead-time forecasting of UK air passengers by Holt-Winters methods with damped trend. Int. J. Forecast. 2001, 17, 71–82. [Google Scholar] [CrossRef]
- Yar, M.; Chatfield, C. Prediction intervals for the Holt-Winters forecasting procedure. Int. J. Forecast. 1990, 6, 127–137. [Google Scholar] [CrossRef]
- Gelper, S.; Fried, R.; Croux, C. Robust forecasting with exponential and Holt–Winters smoothing. J. Forecast. 2010, 29, 285–300. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Bai, S.; Zico Kolter, J.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271v2. [Google Scholar]
- Xu, F.; Du, Y.A.; Chen, H.; Zhu, J.M. Prediction of Fish Migration Caused by Ocean Warming Based on SARIMA Model. Complexity 2021, 2021, 5553935. [Google Scholar] [CrossRef]
- Kirbas, I.; Sozen, A.; Tuncer, A.D.; Kazancioglu, F.S. Comparative analysis and forecasting of COVID-19 cases in various European countries with ARIMA, NARNN and LSTM approaches. Chaos Solitons Fractals 2020, 138, 110015. [Google Scholar] [CrossRef]
- Aasim; Singh, S.N.; Mohapatra, A. Repeated wavelet transform based ARIMA model for very short-term wind speed forecasting. Renew. Energy 2019, 136, 758–768. [Google Scholar] [CrossRef]
- Ordonez, C.; Sanchez Lasheras, F.; Roca-Pardinas, J.; de Cos Juez, F.J. A hybrid ARIMA-SVM model for the study of the remaining useful life of aircraft engines. J. Comput. Appl. Math. 2019, 346, 184–191. [Google Scholar] [CrossRef]
- De Oliveira, E.M.; Cyrino Oliveira, F.L. Forecasting mid-long term electric energy consumption through bagging ARIMA and exponential smoothing methods. Energy 2018, 144, 776–788. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at Scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Jian, D.; Xuezhi, X. A Fuzzy Track Association Algorithm in Track Interrupt-oriented. Fire Control. Command. Control. 2013, 38, 518–522. [Google Scholar]
| Error | Method | ||||
|---|---|---|---|---|---|
| LSTM | TCN | ARIMA | Prophet | Holt-Winters | |
| x (m) | 0.01031226 | 0.00847442 | 0.00343247 | 0.000282 | 0.00036811 |
| y (m) | 0.01457218 | 0.01379722 | 0.00490498 | 0.000393 | 0.00097181 |
| z (m) | 0.0500951 | 0.04427563 | 0.02846062 | 0.005334 | 0.0077661 |
| vx (m/s) | 0.00623551 | 0.0041277 | 0.00063828 | 0.00068 | 0.000844625 |
| vy (m/s) | 0.0060439 | 0.00399427 | 0.00035111 | 0.000383 | 0.001006425 |
| vz (m/s) | 0.00608286 | 0.00376995 | 0.00048802 | 0.000474 | 0.00061313 |
| ax (m/s2) | 0.00612628 | 0.0041475 | 0.00063779 | 0.000683 | 0.00148328 |
| ay (m/s2) | 0.00591117 | 0.00409016 | 0.00034982 | 0.000384 | 0.001005105 |
| az (m/s2) | 0.00600928 | 0.00384299 | 0.00048726 | 0.000473 | 0.000612425 |
| Time (min) | 120 | 480 | 15 | 15 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Cao, J.; Zhou, Z. Track Segment Association Method Based on Bidirectional Track Prediction and Fuzzy Analysis. Aerospace 2022, 9, 274. https://doi.org/10.3390/aerospace9050274
Cao Y, Cao J, Zhou Z. Track Segment Association Method Based on Bidirectional Track Prediction and Fuzzy Analysis. Aerospace. 2022; 9(5):274. https://doi.org/10.3390/aerospace9050274
Chicago/Turabian StyleCao, Yupeng, Jiangwei Cao, and Zhiguo Zhou. 2022. "Track Segment Association Method Based on Bidirectional Track Prediction and Fuzzy Analysis" Aerospace 9, no. 5: 274. https://doi.org/10.3390/aerospace9050274
APA StyleCao, Y., Cao, J., & Zhou, Z. (2022). Track Segment Association Method Based on Bidirectional Track Prediction and Fuzzy Analysis. Aerospace, 9(5), 274. https://doi.org/10.3390/aerospace9050274





