Abstract
The manuscript presents the conceptual design phase of an unmanned aerial vehicle, with the objective of a systems approach towards the integration of a hydrogen fuel-cell system and Li-ion batteries into an aerodynamically efficient platform representative of future aircraft configurations. Using a classical approach to aircraft design and a combination of low- and high-resolution computational simulations, a final blended wing body UAV was designed with a maximum take-off weight of 25 kg and 4 m wingspan. Preliminary aerodynamic and propulsion sizing demonstrated that the aircraft is capable of completing a 2 h long mission powered by a 650 W fuel cell, hybridized with a 100 Wh battery pack, and with a fuel quantity of 80 g of compressed hydrogen.
1. Introduction
For more than 60 years, since the design of the Boeing 707, civil aviation has shown constant progress towards more efficient aircraft. Initially driven by pure economics for fuel efficiency, recent years have seen efficiency improve also as an effect of concerns for environmental issues such as greenhouse gas emissions—aviation contributes for 2% to 3% of global carbon dioxide emissions, and this number is projected to grow [1,2]—and noise pollution. As a result, there has been a significant push towards “more electrical aircraft,” with a focus on battery as well as hydrogen power. Both hydrogen fuel cells and batteries are electrochemical devices that convert chemical energy into electricity. The difference between the two systems resides in the energy storage method: as hydrogen (in gaseous or liquid for) in an external storage for use in a fuel cell; and inside the electrode material for a battery [3]. Hydrogen fuel cell systems offer high specific energy and are therefore an interesting candidate for replacing the APUs in commercial aircraft [1,2,4,5,6]. In addition, feasibility studies and test flights have been carried out in light aircraft by fitting fuel cells to existing two-seater [6,7,8] and six-seater airframes [9].
Prior to these larger scale efforts in civil aviation, the use of hydrogen fuel cells has been evaluated on small to medium sized unmanned aerial vehicles (UAV) [10], as fuel cells in combination with batteries. The resulting hybrid system exploits the high energy density of hydrogen and high power density of batteries, and from an operation standpoint they combine low environmental impact, low thermal signal, and quiet performance. Since the energy is stored as hydrogen, it is also possible to achieve high endurance without a significant impact on the aircraft weight, keys design factors for successful UAV operations. The most prominent among these demonstrators is the IonTiger designed by the US Naval Research Laboratory, which competed a record-breaking flight of 48 h [11,12].
Several other large-scale projects also tested the concept of fuel-cells for use in fixed-wing UAVs. Within the United States, long endurance small UAVs powered by hydrogen fuel cells have been designed and successfully flown by Georgia Tech [13] and Colorado State University [14], and California State University and Oklahoma State University [15] collaborated with Horizon Fuel Cell Technologies in their design. Medium to large scale efforts were also conducted by Gong et al. [16] in Australia, through ground testing simulation of fuel-cell-based power system for small UAV missions, and in Korea by Gang et al. [17] and Kim et al. [18]. A thorough study, both analytical and flight tested, has also been conducted by Lapeña-Rey et al. at Boeing Europe [19], who analysed the in-flight performance of the fuel cells stack in hot and dry conditions.
In addition to these major efforts, several small UAVs have been designed, primarily as university research efforts, all of which share the same general configuration and mission: high-aspect ratio wings for long endurance, and hydrogen fuel cells enhanced in a hybrid system with LiPo batteries. Some studies are primarily analytical to evaluate the operational aspects of fuel cell stacks, such as Gadalla et Zafar [20], Renau et al. [21], Depick et al. [22], and the design by Verstraete et al. [23], which is a development of the Hyperion blended wing body project, and which was tested in flight for aircraft performance, but not with the hybrid/electric system. Few examples exist, to the best knowledge of the authors, of flight-tested aircraft, such as Özbeck et al. [24] and Savvaris et al. [25]. Most recently, ISAE-Supaero [26] in France has launched a project developing a fixed-wing UAV for ultra-long endurance (the Mermoz Challenge), powered by a hybrid-electric system incorporating a fuel-cell with liquid hydrogen as fuel, which features thin, high aspect ratio wing configuration for dynamic soaring, and TU Delft NederDrone [27], a unique tilt-wing fixed wing drone for maritime operations, which has been flight-tested.
Setting itself apart is the Phoenix Project by AeroDelft, which is of added significance as it is planned to transition from an unmanned version of a specifically designed aircraft, powered by fuel cells utilising gaseous hydrogen, to a crewed aircraft, powered by fuel cells utilising liquid hydrogen [28].
From a commercial perspective, French company Delair [29] is making the case for the transition from battery-powered to hybrid-hydrogen powered fixed-wing drones with the Hydrone project, as it has been recognized that the use of hydrogen fuel cells provide significant advantages in terms of range for industrial applications, in particular with the need of carrying a given payload.
Two aspects have been highlighted by this brief review of known past and current projects: on one hand research in aircraft propulsion is clearly moving towards new, sustainable, and environmentally conscious technologies, while on the other hand little or no emphasis appears to having been given to push the boundaries in terms of aircraft configurations towards high aerodynamic efficiency, for optimized use of these new green technologies. An exception to this approach is the work by Guynn et al. [30], in which the application of hydrogen fuel cells, in combination with the aerodynamically efficient blended wing body (BWB) aircraft configuration was evaluated. Most recently, this philosophy of combining zero-net emissions and high aerodynamic efficiency was adopted by Airbus in its ZEROe program [31]. Literature has indicated that BWB configurations may may result in improvements in fuel consumption of up to 10% for a nominal mission of 6000 nmi and 300 passenger, compared to a classical tube-and-wing configuration in the same class [32,33].
It is therefore the objective of this multidisciplinary engineering work to develop a UAV test-platform centred on the integration of a hybrid/electric hydrogen fuel cell system in an aerodynamically efficient blended wing body configuration representative of a potential configuration for future transport aircraft in the wide-body class.
The structure of the manuscript follows the steps of a traditional aircraft conceptual design process. Section 1 presents the background review of the existing work in the topic of hybrid electric-fuel cell aircraft, and the goals and objectives of the current work are stated. Section 2 summarizes the design process and mission specifications and provides the background information for the definition of the design constraints, as well as presenting the educational aspect of the project. In Section 3, the initial sizing is discussed, covering the weight and aerodynamic sizing as independent parameters to the final aircraft configuration. Starting from a design maximum take-off mass of 25 kg, the structural and mass energy fractions are estimated as 0.565 and 0.160 of the full mass of the aircraft. Reflex airfoils were selected to retain the natural pitching stability of the aircraft. The conceptual design phase is discussed in Section 4 describing the design constraints for the body-section of the aircraft, and the design choice of a 4 m span, 30 swept wing with positive 4 dihedral and spanwise varying twist angle for enhanced performance. A stall angle of 9 at a maximum lift coefficient of 0.8 is shown. The preliminary power analysis and fuel cell and hybridization are discussed in Section 5, where a 650 W fuel cell in connection with a 100 Wh battery is shown to be sufficient to complete a flight of the duration in excess of 60 min in ideal conditions. Conclusions are presented in Section 7.
2. Pre-Conceptual Phase
2.1. Educational Aspects
An accompanying aspect of the project presented in the manuscript is the introduction of aspects of net-zero carbon offset aviation research within the academic curricula. Broad scoped research and education oriented projects with a strong emphasis on multidisciplinarity outside of the controlled environment of a scheduled course, as well as a strong emphasis on practical work are not commonly available within school curricula, making the current work an added value to education at KTH, The Royal Institute of Technology. The combination of two aspects—research and education—are addressed at the core of the project.
The work presented in the manuscript is built on the teaching concept of “Conceive-Design-Implement-Operate” (CDIO) [34] as a series of complementary projects and master thesis work, with topics aligned with the existing curricula within KTH, enhanced through a multidisciplinary perspective so that no single project is “stand-alone” but is built on previous work and becomes the basis for future work. This aspect mimics in part work conducted in a research-focused environment as well as industry, emphasizing the need for collaborative work. Student involved in the project have the opportunity of improving technical skills within their “field of expertise” whilst at the same time exposing them to learning soft skills necessary in industry.
Within each phase of the work, students are faced with challenges found in research and industry. Throughout the pre-conceptual phase, students must assess the needs for future aviation and highlight a “gap” in technology. In this particular case, this process resulted in the choice of a hydrogen fuel cell and blended-wing-body aircraft as a good balance between existing technology and knowledge to be developed. At every step of the design phase, students need to select the appropriate tools and assess their suitability and limitations and at times adapt well-tried methodologies to novel topics.
Finally, students involved in the project are developing soft skills comparable to those necessary to those required in industry dynamically and in a synergistic approach with the need of being aware of the project as a whole, in an approach rarely found in course work.
2.2. Design Methodology
The design methodology for the current conceptual work followed that presented by Raymer [35], and shown in Figure 1, from Mission Requirements to the Final Configuration, or design freeze. One aspects differs from the conceptual design process described by Raymer [35], and that is the Technology Available here is replaced with Novel Technology and placed at an equal level with Mission Requirements as this is a driver for the design and mission specification. In addition, only introductory studies of the stability of the aircraft are discussed.
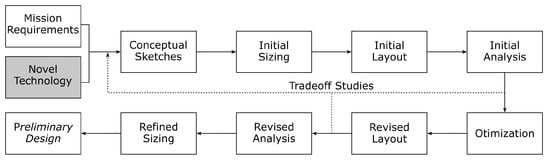
Figure 1.
Design Methodology [35].
2.3. Mission Specifications and Design Parameters
The first step in the design process is to determine the mission specifications that drive the design and which ultimately define the configuration.
The purpose of the aircraft is to act as a flying test platform for compressed hydrogen fuel-cell/battery electrical hybrid system. The aircraft is required to have a target endurance of 1 h, at a cruise altitude of 500 m, and is expected to operate from paved runways. The mission profile is shown in Figure 2. The long-duration mission requires beyond-line-of-sight (BVLOS) and autonomous flight capabilities, which is beyond the scope of the work presented herein and will be explored at later stages of the project.
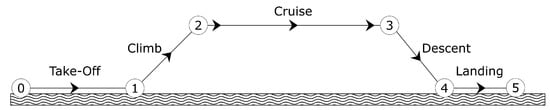
Figure 2.
Mission Profile.
A comparison of fuel-cell powered aircraft that completed flight testing was conducted to provide a design frame for the current project, in particular the relation between fuel-cell power and maximum take off weight, as presented in Table 1.

Table 1.
Existing Demonstrators.
The data in Table 1 show that heavier UAVs require fuel-cells with power exceeding 500 W, and that in general all models evaluated have high aspect ratios representative of glider-type aircraft as well as relatively low cruise velocities. Based on these values and on the emphasis of designing a UAV with a configuration applicable to future commercial aircraft, target values have been defined of a maximum take-off mass (MTOM) of 25 kg (maximum take-off weight MTOW 245.3 N), which corresponds to the EU class C3C4 for UAV certification, a maximum wingspan of 4 m, a design cruise velocity of 20 m/s, and a stall speed of 12 m/s [10,13,23,25]. A fuel cell in the range of 500 W to 800 W is used for the initial sizing. The initial parameters and sought aircraft configuration set the current design beyond the boundaries of existing work.
3. Initial Sizing
For the conceptual phase of the design, a progressive approach was implemented, starting from a classical method, which applies regression models based on available data [35,36]. The size of the fuselage section of the aircraft was determined by the constraints imposed by the dimensions of the fuel cell, which was preliminary defined by averaging the size of commercially available models in the range of 500–800 W and 2 L to 3 L compressed hydrogen tanks, pressurized at 300 bar [37,38].
3.1. Weight Estimation
The conceptual sizing was conducted initially using Raymer’s approach [35,36], subsequently transitioning to the preliminary weight estimation method by Gundlach [39]. The approach by Gundlach was preferred when considering two aspects of a small to medium size, unmanned aerial vehicle:
- The approach takes the aspects of electric or hybrid-electric fuel cell-based propulsion into consideration;
- The breakdown of the weight components is more detailed, as in lighter aircraft it is more critical to differentiate the weight of subsystems and avionics from the generic empty weight, as they might have more significant impact in terms of weight fractions.
The maximum take-off weight is then estimated using Equation (1) [39]:
where the subscripts Struct, Subs, Prop, Avion, PL, and Energy correspond to the structural, subsystems, propulsion system, avionics, payload, and energy storage weights. The term refers to the weight of items in the UAV that do not belong to any of the standard categories, and will be neglected in the current design. This is because the mission of the UAV under development is to test the hybrid/electric propulsion system, and any instrumentation required for in-flight measurements is included in the payload category.
Preliminary weight estimations of fixed items is shown in Table 2, where a total of six motors+propeller-esc have been estimated, and a total of 15 servos have been estimated to take into consideration multi control-surface designs for aircraft stability.

Table 2.
Fixed items weight.
Equation (1) can then be rewritten in terms of component weight fraction WF with respect to the take-off weight, and careful attention must be paid to the weight fraction of the propulsion and of the energy storage , as the estimation needs to be broken down into sub-components for a fuel-cell powered aircraft. The mass fraction of the propulsion is estimated, taking the weight of the fuel-cells stack into consideration, along with the associated propulsion chain controller-motor-propeller. For a fuel-cell powered aircraft, the propulsion mass fraction is:
As can be seen from Equation (2), the mass fraction of the propulsion is directly related to the power output P of the fuel-cell, so it was important to have an initial estimation of the power output required. In addition, the scaling factor in Equation (2) is based on the assumption that all items in the propulsion chain which are down-the-line from the powerplant are scaled directly with the engine power. In the current initial evaluation, the value for is assumed to be equal to 1, as the term () include all installation items and propeller, meaning that the term is set to zero. It is acknowledged that this assumption underpredicts the mass fraction of the propulsion.
The weight of the compressed hydrogen, of the tank, and of any additional batteries for the UAV are included in the category of energy weight , and the energy mass fraction is therefore estimated by calculating the ratio between the mass fraction of the weight of the hydrogen and the storage, and by adding the mass fraction of the estimated additional batteries required for high energy maneuvers and/or reservoir energy:
The mass fraction of the storage of the compressed hydrogen must be estimated taking the weight of the compressed hydrogen itself into consideration:
The remainder of the mass fractions, namely avionics and subsystems, were calculated by adding up weights of the expected components, which have been listed in Table 2 in Section 3.1. Finally, the weight fraction of the structure was initially estimated following Gundlach’s recommendation of a starting value of 0.6 [39], as there is no existing available data for this class of aircraft, and Raymer’s fudge factor of 0.95 for composite material was applied [35], resulting in a wight fraction of the structure of 0.565. The mass fractions and corresponding absolute weights are presented in Table 3, including the values for payload, which are a function of the fixed MTOW.

Table 3.
Aircraft Initial Weight Sizing.
3.2. Aerodynamic Sizing
The definition of the aerodynamic shapes of the aircraft are a compromise between the required volume and dimensions imposed by the pre-selected fuel-cell system, and the aerodynamic and stability constraints of a tailless BWB configuration, with the need of reflex cambered airfoils to naturally restore the pitching moment stability of the aircraft [40,41,42]. These constraints resulted in the selection of the Martin Hepperle MH 104 airfoil for the body section with 15% thickness for additional combined favourable aerodynamic and geometric properties, and the MH61 for the wing sections with 10% thickness. Specifications for the two airfoils are presented in Table 4. Airfoil profiles are shown in Figure 3.

Table 4.
Airfoil Profiles [43].
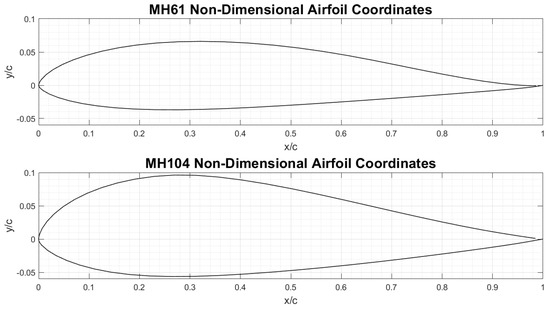
Figure 3.
Profiles of the MH61 and MH104 reflex airfoils.
The performance of these two airfoils was analyzed using the open-source software XFOIL [44], obtaining lift and drag polars for both airfoils at a range of Reynolds number between 250,000 and 5,000,000, providing preliminary estimations of and . The initial sizing of the lift coefficient for a wing of finite span was obtained by classical approach [35,45], where the indicative value of is calculated by simplifying the geometry of the wing and treating it as a “constant airfoil section wing” based on averaging the maximum lift coefficient of the wing root and wig tip, corrected for 3-dimensionality of the wing flow and quarter chord sweep at 30 as shown in Equation (5).
The value of the maximum lift coefficient of this simplified wing was then used to define the initial planform area required for an initially defined stall speed of 12 m/s. Subsequently, for the design maximum take-off weight of 245 N, the initial value of the planform area was estimated [45,46]. Finally, the sizing of the drag coefficient can be obtained, with the simplified assumption that the minimum drag coefficient is equivalent to the zero-lift drag coefficient [36]:
Wing sweep was set at 30 to be representative of a larger scale transport aircraft, and the Oswald efficiency factor was calculated both for the unswept (or < 30) (Equation (7)) and swept wings (or > 30) (Equation (8)) configurations, and the values averaged [35].
The initial value for zero-lift drag was taken from references [36,47,48] for small, fixed wing UAVs, and it must be noted that it is a statistical value obtained for a class of UAVs, rather than based on a specific configuration. It is expected that, for an aerodynamically efficient BWB, the zero-lift drag of the final design will be lower than this initial estimation. The value for the aerodynamic sizing, and the related geometric parameters are summarized in Table 5.

Table 5.
Initial Aerodynamic Sizing Parameters.
4. Conceptual Design Phase
The next phase in the design was to complete the iterative process of defining the final aircraft configuration, based on the initial design specifications of 25 kg MTOM and 4 m maximum wingspan presented in Section 3, the initial geometric and aerodynamic sizing discussed in Section 3.2, and the requirement of fitting the fuel cell system in the main section of the body. Three additional aerodynamic parameters have been considered in the iterative process of the design: spanwise wing lift distribution, stall characteristics, and natural static stability of the aircraft. Optimization of the wing design focused on approximating the lift distribution towards an elliptical shape for increased efficiency [49]. Wing sweep promotes both longitudinal and directional stability, although an undesirable effect of wing sweep is the first onset of stall occurring at the wing tip. To counteract this phenomenon, and delay and shift the onset of stall towards mid-wing to retain aileron effectiveness and roll control at high angles of attack, geometric twist was evaluated. Dihedral angle, which provides inherent lateral stability, was evaluated as well.
4.1. Configuration Layout
With the BWB configuration being a lifting body, the first step in the design process is to define the three sections of the aircraft: fuselage, fuselage-to-wing blending section, and wing. As previously discusses, the design of the fuselage was driven by the geometry and size of the fuel cell system for which the thicker MH104 airfoil was used. The sizing parameters of the fuel cell are presented in Table 6.

Table 6.
Fuel Cell System Initial Sizing.
The result of the design process is a fuselage with a centreline chord () length of 1.7 m and an outboard chord of 1.52 m. The main section of the fuselage has a width of 0.4 m, a maximum thickness of 0.259 m at 0.449 m from the nose of the aircraft, and a sectional planform area of 0.644 m.
Keeping the geometry of the fuselage section fixed, the design was subsequently parametrized using OpenVSP [50], an open-source software provided by NASA for the conceptual design phase of an aircraft, for fast geometry optimization process of the blending section and the wing. The wing shape was then aerodynamically optimized in xflr5 [51] using classical methods such as vortex lattice, panel, and the non-linear lifting line theory methods discussed in Section 4.2.1. Final geometric parameters and aerodynamic analysis data are discussed in Section 4.3. The final configuration is shown in Figure 4. The aircraft geometric parameters are presented in Table 7.
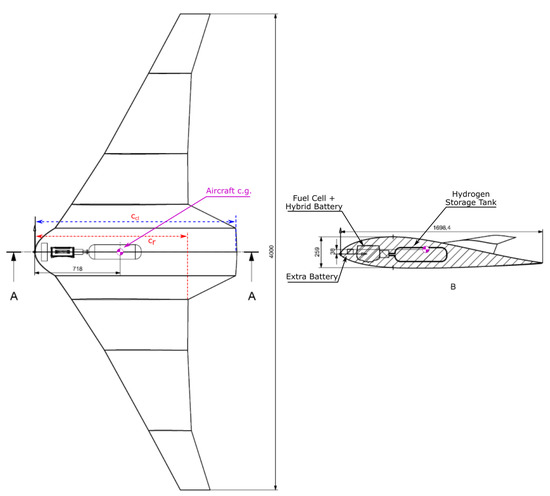
Figure 4.
Aircraft Dimensions. All dimensions are in [mm].

Table 7.
Aircraft Geometry.
The root chord corresponds to the distance from the leading edge at the centreline to the projected trailing edge of the wing, as shown in Figure 4.
The final step concerned the geometric definition of the centre of gravity based on the components which, apart from the structure of the aircraft, impact the location, namely those belonging to the “Energy and Storage” section as presented in Table 2. Each component was modelled as a point mass centroid. The structure of the aircraft was initially estimated as a carbon fiber shell and the centroid estimated using OpenVSP.
As previously mentioned, the volume and shape of the fuel cell and the hydrogen storage constrained the size of the fuselage section of the aircraft, resulting in the hydrogen tank being positioned in the thickest part of the fuselage and the fuel cell and hybrid battery ahead of it towards the nose. These geometric constraints limited the movement of the components along the longitudinal axis leaving the extra battery as the primary mass for shifting the centre of gravity, resulting in the battery being placed at the nose of the aircraft. The preliminary centre of gravity is from the nose of the aircraft. The location of these components and the centre of gravity are shown graphically in Figure 4.
4.2. Aerodynamic Analysis Methodology
4.2.1. Low-Fidelity Numerical Methods
The choice of a low-fidelity analysis approach was implemented as it allowed to quickly and efficiently iterate the design at a low computational cost for both aerodynamic and stability parameters [52]. Three viscous solutions were considered: the vortex lattice method (VLM2) based on ring vortex analysis, and the panel method, which are both linear solutions, and the non-linear lifting line theory (LLT) approach as it is able to indicatively predict stall conditions as the solution includes non-linear approximations [51]. These methods were employed in parallel to obtain an overall initial understanding of the aerodynamic performance, since all of them present limitations in the analysis with respect to the current design [44,51]. The VLM2 method considers only the airfoil mean camber line for the analysis and assumes the small angle approach in the aerodynamic analysis, limiting the accuracy of the coefficient of lift at extreme (outside the linear region of the lift curve, therefore near stall) low and high values of angles of attack, resulting in the trailing vortices being misaligned with respect to the free-stream velocity. In addition, viscous parameters for the coefficient of lift are obtained from a preceding airfoil analysis using XFOIL [44], therefore adding an additional degree of approximation in the solution. Oppositely, the non-linear LLT method has been primarily developed for high-aspect ratio and low-sweep wings [51], such as those for sailplanes, and therefore of limited application to the current design. The panel method is the only approach that takes the wing thickness into consideration and is expected to lead to more accurate lift and drag initial estimations, at least within the linear region of the lift curve. These results are discussed in Section 4.3.
4.2.2. CFD Methodology
Numerical Set-Up: A higher resolution analysis has been conducted using computational fluid dynamics (CFD) by means of Star-CCM+ commercial software by Siemens (Release 16.02.008). A Reynolds-Averaged Navier–Stokes (RANS) model has been applied (Equations (9) and (10)):
Two approaches have been used, with the RANS coupled with: the turbulence model equations in the SST formulation; and with the Spalart–Allmaras model. Menter [53] has shown that the RANS SST model provides excellent approximation of pressure-induced separation and the resulting viscous-inviscid interaction in comparison to other closures. Specifically designed for aerospace applications involving wall-bounded flows, the Spalart–Allmaras model has been shown to give similarly good results for boundary layers subjected to adverse pressure gradients [54].
As most of the RANS turbulent closures, both and Spalart–Allmaras are based on the Boussinesq Hypothesis, where the traceless part of the Reynolds stress tensor is assumed to be proportional to the Strain Rate Tensor with the coefficient for eddy viscosity [55]:
By dimensional analysis, it holds that is proportional to the product of a turbulence velocity and length scale. The models consist of solving a transport equation for the turbulent kinetic energy k and the turbulent frequency , which allows the derivation of the turbulence scales and closes the system.
The RANS and turbulence model equations have been discretized through a second order upwind scheme. A steady-state solving approach has been employed to reduce the computational expense. The inlet turbulence intensity has been set to 1% and the Turbulent Viscosity Ratio to 10. While the intensity is in accordance with Spalart and Rumsey [56] for external aeronautics-applied flows, the default value of viscosity ratio in Star-CCM+ has been kept for simplicity and is a few units above the one suggested in Spalart and Rumsey [56]. Further analysis performed within the project showed that this boundary parameter has nearly no influence in the output aerodynamic coefficients for this case-study and thus proved the reliability of the condition.
Mesh Validation: Following best practice cases for domain definition, a box-shaped domain (4c–6c box) has been constructed, with dimensions shown in Figure 5. With the goal of preventing the introduction of an unknown error related to the presence of the domain’s external walls, a “slip” boundary condition has been introduced in their correspondence. Furthermore, in order to optimize computational time, only half of the geometry has been simulated, with a symmetry plane imposed on the xz-plane along the axis of symmetry. In order to resolve the boundary layer, an inflation of high aspect-ratio cells has been designed in the near-wall region of the aircraft geometry, as shown in Figure 5. Preliminary boundary layer calculations have been performed with the turbulent flat plate formulas, yielding a total thickness of mm, which is prescribed as the maximum thickness of layers inflation. Moreover, to ensure and fully resolve the viscous sublayer region, a first cell thickness of has been set.
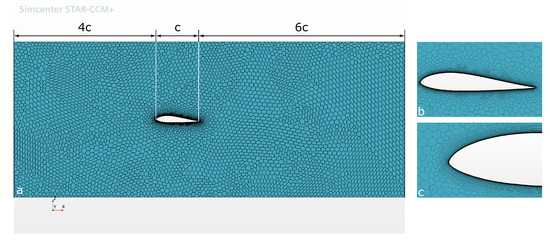
Figure 5.
Volume Mesh.
The automated mesh algorithm of STAR-CCM+ allows to build a high-quality polyhedral mesh provided some general input parameters are given. For each of the surfaces to be meshed, the user can prescribe a “minimum target size” (MSS) and a “target surface size” (TSS). The former represents the minimum allowed cell dimension in the most curved surface region, i.e., where the algorithm tends to refine the mesh to capture the curved geometrical features. For instance, this parameter comes into play in the wing leading edge limiting the refinement in its correspondence (Figure 6a). The latter sets a maximum cell size in the regions where the algorithm tends to build a coarser mesh, i.e., in the least curved or flat surfaces. For instance, this parameter is used to limit the mesh coarsening at the wing upper and lower surfaces (Figure 6b,c) and at the far-field of the external domain boundaries (Figure 5a). Furthermore, Star-CCM+ allows the design of simple geometrical shapes to delimit domain regions where a mesh refinement can be introduced. Hence, in order to better capture the wingtip vortices and thus better predict the induced drag, a truncated-cone in the wingtip proximity has been designed.

Figure 6.
Surface Mesh.
The mesh validity has been assessed through a grid-convergence study, at an angle of attack of , and the dependence of the aerodynamic coefficients on the following mesh parameters has been explored:
- The wing minimum surface size, which in practice defines the wing leading edge smallest surface cell dimension;
- The wing target surface size, i.e., the upper and lower wing surface cell maximum dimension;
- The external domain boundaries target surface size, i.e., the far-field maximum cell surface dimension;
- The characteristic cell dimension within the cone-delimited wingtip mesh region.
The initial steps in the validation process consists in evaluating the wing minimum surface size, for which a cell-size range between 5 mm to 0.5 mm was selected. Results indicated that a cell dimension of 1 mm is the equilibrium between numerical accuracy and computation time. Similarly, the wing target surface cell size has been evaluated for a range between 30 mm to 7.5 mm, with mesh independence reached at a cell value of 7.5 mm. Finally, the external domain boundaries target surface size and the wingtip cone cell size were evaluated, the first for a range between 600 mm to 75 mm, and the second for a range between 50 mm and 10 mm. Results show that mesh independence is reached at a size of 150 mm for the simulation domain target surface size, and at a cell size of 30 mm for the wingtip cone mesh.
The far-field domain shape and extension should be chosen to allow a safe boundary condition setup without introducing non-physical impositions to the problem, and without affecting the resulting aerodynamic coefficients. Further literature research showed that for low Mach number flows, it is recommended to employ a bullet-shaped domain rather than a box-shaped one [57]. Goetten et al. [57] also provide an overview of desirable and safe domain extensions, which turn to be much larger than the ones employed in this study. For instance, they report Versteeg’s and Malalasekera’s [58] suggestion to position the inlet and the outlet significantly more than ten body lengths behind the geometry. These findings highlight the necessity to further prove the validity of the results obtained using the initial box-shaped domain shown in Figure 5. Hence, two additional extended domains, one box-shaped and one bullet-shaped as shown in Figure 7, have been investigated. The cases simulated are summarized in Table 8, with dimensions expressed, in this case, in terms of wingspans.

Figure 7.
Box (left) vs. Bullet (right) Domains.

Table 8.
Domain Evaluation for Spalart–Allmaras Turbulence Model.
Results showed that in both flow regimes, i.e., attached flow and stalled flow, the lift and drag coefficient vary in a range below 2.5%. In particular, the lift and drag coefficients show respectively a 2.3% and 1.6% discrepancy at low angles of attack, and a 0.3% and 2.2% at stalled angles of attack. The lower lift coefficient variation in the latter configuration is probably due to the higher numerical random errors which characterize this flow regime. This very limited error in the CFD computations can be considered acceptable for the conceptual design purposes of the present work, and thus proves the reliability of the limited-extension domain initially designed.
Final Set-Up: After completing the mesh studies, initial aerodynamic evaluations have shown a more stable convergence of the solution provided by the Spalart–Allmaras turbulence model in comparison to the one of SST at high angles of attack, where the flow is partially stalled, as it will be discussed in Section 4.3. In contrast, the results of the two models are almost perfectly matching at low angles of attack, where the flow is attached. Hence, in order to derive more reliable results at high angles of attack, and ultimately predict a reasonable , Spalart–Allmaras was selected for the remainder of the study. A similar choice has been performed by Panagiotou and Yakinthos [47]. They compared the models for the prediction of aerodynamic forces on UAVs, and based on their studies opted for the use of the Spalart-Allmaras turbulence model in their subsequent work involving a BWB configuration [36,48].
Domain 4c–6c Box in Table 8 has been used for the remainder of the work, mesh parameters are summarized in Table 9 and shown graphically in Figure 6.

Table 9.
Final Mesh with 4c inlet and 6c outlet (4c–6c Box).
4.3. Aerodynamic Performance
The preliminary configuration was tested using OpenVSP and xflr5 for fast iteration of the effects of geometry variation on the aerodynamic performance of the aircraft. Nominally, twist angle effects were iterated with the objective of refining aerodynamic efficiency and obtaining a nearly elliptical lift distribution at cruise flight conditions, and dihedral angle to provide natural lateral stability. The final configuration had a wing dihedral of 5 (not including the blending and fuselage sections), and a twist distribution, from the longitudinal axis y = 0.0 m, of 2.5 up to y = 0.2 m, of 3 at 0.2 m 1.5 m, and twist of 0 at the wing tip. Tip stall was negatively affected, but this twist variation improved the overall lift span distribution.
Results are presented in Table 10. These results are referenced to the initial aerodynamic parameters listed in Table 5 where available. All data were obtained at the cruise velocity of 20 m/s, at a range of angles of attack between −4 and 12.

Table 10.
Comparison of aerodynamic parameters.
Here, a is the lift curve slope, is the maximum lift coefficient, the maximum angle of attack, the zero-lift drag, and the change of pitching moment coefficient with respect to angle of attack . Lift, drag, and moment coefficients with respect to angle of attack are shown in Figure 8.
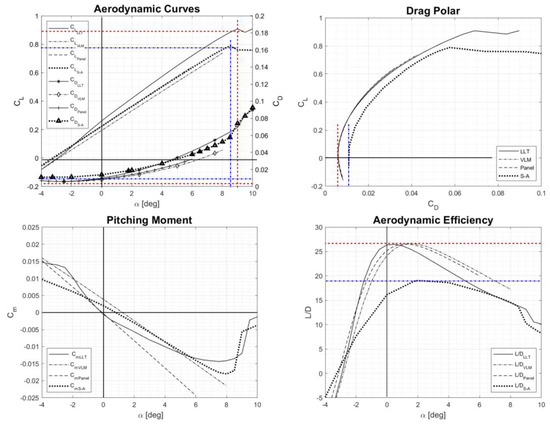
Figure 8.
Aerodynamic results comparison. vs. and vs. (top left), vs. (top right), vs. (bottom right), and vs. (bottom left).
The comparison of the lift curves obtained with the three methods indicate good agreement between the results of the panel method and the CFD simulations in terms of lift curve slope, with an error of 3.4%. The large difference in lift curve slope with respect to data obtained using non-linear LLT method has already been witnessed.
The comparison of the drag coefficients shows a consistently larger drag coefficient value in the CFD results, and this is expected as it is known that the analytical models used in xflr5, due to the way friction and form drag are applied, underpredict drag. At low angles of attack, where viscosity has a smaller effect as the flow is fully attached, this results in a discrepancy of only 2–3 counts of drag, and this difference progressively increases as the angle of attack is increased and viscous effects become more significant.
This aspect of modelling viscosity also affects the prediction of lift in the non-linear LLT model in particular, for which the curve slope is steeper, and lift is over predicted with respect to the CFD result. On the other hand, the lift curve slope obtained with the CFD model agrees well with the VLM2 and panel method predictions, to a value of . Results obtained with the panel method agree particularly well, as shown in Figure 8, as the values of the lift coefficients in the linear section of the curve are within less than a difference. As a consequence of the larger drag predicted by the CFD simulations, the aerodynamic efficiency is severely affected and decreases from a value of approximately 26 to a value of approximately 19, impacting the performance of the aircraft, as can be seen in Figure 8.
As previously mentioned, the non-linear LLT is the only analytical method capable of estimating the maximum lift coefficient and stall angle, providing an initial prediction and a first level of validation comparing to the classical initial aerodynamic sizing described in Section 3.2. As shown in Table 10, a overprediction of maximum lift coefficient occurs between the initially estimated value and that obtained with the non-linear LLT, a difference that becomes more significant, in excess of , if compared with the value predicted by the CFD solution. On the other hand, the non-linear LLT and CFD results appear to be quite consistent when predicting the maximum angle of attack, with only a 0.5 difference, which could be improved by decreasing the angular steps between two simulations currently set at 0.25.The stall angle is in agreement with aircraft of similar size and comparable configuration [48].
The prediction of the longitudinal static stability parameters appears to be highly dependent of the solution methodology applied, although all models indicate a stable aircraft, as is negative. Of the three analytical methods, the non-linear LLT and panel methods predict a and a stable aircraft up to = 6. The pitching moment coefficient obtained from CFD simulation shows a similar trend extending the limit of the longitudinal stability to = 8 at the onset of stall and confirming a positive value of . Post-stall, with a departure of the aerodynamic centre from the quarter chord due to flow separation, the prediction of the longitudinal stability becomes more complex and therefore the current values should be considered indicative
To fully assess the stall conditions of the aircraft, the phenomenon was evaluated in more in detail by looking at the surface pressure fields on the top surface of the aircraft. As shown in Figure 9, at an angle of attack of 6 the flow is fully attached to the surface of the wing, while the surface pressure distribution at 8 indicates that the desired onset of stall at mid-wing for keeping control surface effectiveness is achieved prior to separation extending towards the wingtip. Finally at a 10 angle of attack, the flow is fully stalled over the outer section of the wing, but it remains locally attached on the fuselage of the aircraft with clean flow allowing more design options for the integration of the propulsion system at trailing section of the fuselage. Qualitatively, the stall behaviour is also shown via plotted streamlines, in Figure 10.
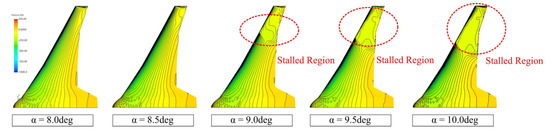
Figure 9.
Development of stall pattern.

Figure 10.
Stall Pattern at .
5. Power Requirements and Battery Definition
5.1. Power Required Analysis
Literature has shown [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25] that existing UAVs have implemented propeller driven propulsion as it is normally less energy demanding and therefore preferred for long endurance designs. Oppositely, work on BWB at full-aircraft scale [30,31,32,33] has favoured configurations with air-breathing engines. As the propulsion system of the current design is yet to be defined, both power and thrust required have been estimated. The use of power in the calculations for the sizing of the fuel cell and extra battery do not indicate a pre-selection of a propulsion system. The values expressed in Watts are used for consistency in the calculations in Section 5.2
Preliminary estimations were completed using aerodynamic data obtained through CFD simulations, at a velocity range between 5 m/s and 30 m/s [46] where the power required curve is calculated through the components of the aircraft drag (Equation (12)):
Preliminary power and thrust required curves are presented in Figure 11, where data for velocities below 10 m/s are not available, as the aircraft is not capable of sustained flight below that speed in clean wing configuration. Results indicate that, at the target velocity of 20 m/s, the aircraft requires 262 W of power, or 13 N of thrust, at a trim angle of 1.7 to 2, demonstrating that, for target flight conditions, sufficient excess power is available, even when taking into consideration that these values are normally an underestimation as they do not take the efficiency losses inherent to the propulsive system into consideration.
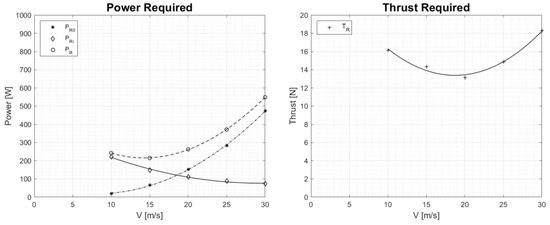
Figure 11.
Power require (left) and thrust required (right) vs. Velocity.
5.2. Hybrid Hydrogen Fuel Cell/Battery System
Based on the power demand of the UAV discussed in Section 5.1, a typical 2 h mission is designed and presented in Figure 12. It corresponds to a 10 min take-off at 1.2 kW, 100 min cruise at 600 W and 10 min landing procedure requiring 1 kW. A sizing strategy using the power demand as an input for designing hybrid fuel cell/battery systems was previously developed by the authors for underwater applications [59], and was adapted for the UAV application. It finds the best, i.e., most compact or lightest, combination of fuel cell stack and battery pack in order to fulfill the given mission. Results showed that a hybrid system combining a 650 W Proton Exchange Membrane Fuel Cell (PEMFC), with a tank containing 80 g pressured hydrogen, and a 100 Wh battery pack is the most suitable (lightest) for the hybrid electric propulsion system. Only certain fuel cell power sizes were considered, based on what is available commercially. As a comparison, this described hybrid energy system weights around 5 kg, whereas, based on the assumptions from [59], a full secondary battery system with the same amount of energy weights around 9 kg.
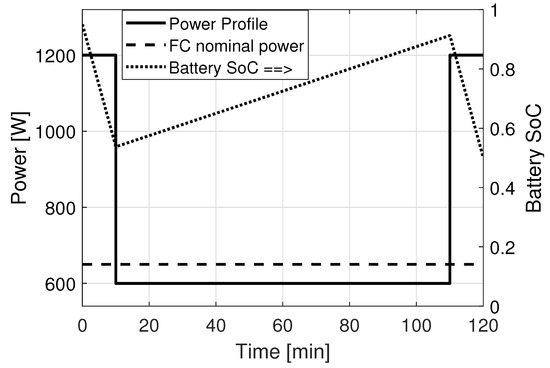
Figure 12.
Electric power profile and estimated battery SoC of the typical mission consisting of three phases, 10 min take off, 100 min cruising and 10 min landing. The simulation considers a fuel cell stack with 650 W nominal power, 80 g hydrogen, and a 100 Wh battery with an initial SoC at 95%.
Parameters used for simulating a mission are shown in Table 11. The amount of hydrogen left in the tank during the mission can be calculated using Equation (14), with the fuel cell output power , the Low Heating Value of hydrogen at 25 °C and the fuel cell efficiency . As a result, the fuel cell delivers the base power while the battery is used to reach high-power demands and is being recharged by the fuel cell during times with low power demand. This configuration means that the flexibility of the UAV, in terms of power and therefore speed, mostly depends on the battery pack.

Table 11.
Electrochemical Parameters for the hybrid fuel cell and battery system.
The battery State-of-Charge (SoC) corresponds to the ratio between the energy content of the battery pack at a given time, and its energy content when fully charged. It can be estimated as shown in Equation (15), where is the battery power (positive during discharge and negative during charge), is the energy content of the battery when fully charged and is the battery efficiency for charging or discharging. Going to very high or very low SoC can accelerate the degradation of the battery [61], so to avoid degradation the acceptable SoC-window was therefore set to SoC in the simulations. To compare different charge and discharge rates the charging rate, , is often used. A of 1C means that it takes one hour to fully charge the battery from a SoC of 0%, and 2C means it takes 30 min. The maximum reached during the mission is estimated using Equation (16).
A procedure for checking if the mission can be fulfilled with the chosen fuel cell, hydrogen storage and battery size was developed by the Chiche et al. [60]. If the hydrogen tank is depleted or the battery SoC goes outside its chosen window at any time then the mission is considered unsuccessful. It also considers that when the battery SoC is at 95%, charging stops. Results, in Figure 12, show that the mission is fulfilled. In addition, the battery SoC goes from being at 95% SoC to 55% during the take-off phase and is then recharged up to 90% during the cruise period. The landing phase also deplete battery power, when the SoC decreases to 50% at the end of the mission. Furthermore, the maximum reached during the mission is 5.5, meaning that the battery will have to be power-optimized. There is no clear boundary for a high , however, a is usually considered high. Most batteries can handle higher discharge currents than charge currents, so it is almost always the charge step that is limiting for battery design and selection [62]. A power-optimized battery can handle relatively high , but generally has a reduced energy density. It is interesting to note that the fuel cell power remains constant at 650 W, in other words, the fuel cell continuously works at steady-state at a high efficiency point. At the end of the mission, there is 8 g of hydrogen left in the tank.
6. Future Work
Work is currently ongoing for the continuous development of the aircraft, as well as targeting specific issues encountered in the conceptual phase of the design.The work is a combination of applied research within the frame of the educational and research emphasis of the project itself.
Further aerodynamic work is being conducted focusing on the improvement of the stall characteristics of the aircraft—namely to delay it to higher angles of attack and therefore increase the maximum lift coefficient—through the use of passive flow control. This work also focuses on a more detailed comparison of low-fidelity and CFD simulations towards a more robust design process when non-conventional configurations are concerned.
As noticeable in the literature [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25], the overwhelming majority of UAVs powered by fuel cells are propeller aircraft as they are less energy demanding, while future aircraft of the BWB design are expected to be powered by air-breathing engines [31]. Consequently, detailed work is being carried out comparing the use of electrical ducted fans (EDF) and brushless-motors with propellers, to determine the number of motors needed for each configuration and the propeller size. Characterization of the performance of an acquired fuel cell from those evaluated in the literature and that are commercially available [37,38] is being carried out to improve the power analysis, and will be followed by bench tests of the full propulsion architecture with additional focus on energy management.
The design process is also transitioning to ground testing first through the planning of a preliminary wind tunnel campaign to validate the aerodynamic loads obtained through CFD simulations and improve the understanding of the stability of the aircraft by testing for both angle of attack and sideslip/yaw angle. These tests will enable the full understanding of the aerodynamic and stability characteristics of the aircraft and provide information for future development of the aircraft.
Data obtained experimentally will be imported in commercially available flight simulation software to study further the behaviour of the aircraft, coupled with the design and manufacturing of a geometrically representative sub-scale version for flight testing.
The results from simulations and experimental campaigns will provide the necessary foundation knowledge for any redesign prior to commencing the final phase of the development involving the structural design and manufacturing of the full scale aircraft.
7. Conclusions
The present work focuses on the conceptual design of a hybrid-electric, fuel-cell powered blended wing body UAV representative of a future aircraft configuration. A simple mission was defined for the aircraft to act as a test platform for data acquisition, with a target endurance of 60 min. Future work covering all aspects of aircraft design has been discussed showing the broad scope of the project. The platform is to act as the first stepping stone for the development of a new research topic at KTH, Royal Institute of Technology.
Design constraints were based on existing, successfully flown, fuel-cell powered UAVs, leading to sizing constraints of a MTOM of 25 kg, a wing span of 4 m, and a cruise velocity of 20 m/s. The technical specifications of the UAV and of the desired mission, the multidisciplinarity aspects of the work, and the long-term emphasis and perspective on novel configurations for future aviation in combination to the efforts in embedding the project within the education curricula at KTH sets the current project apart from the majority of existing work reported in the literature.
A classical design approach was initially implemented supported by recognized analytical tools for aircraft design such as XFOIL, OpenVSP, and xflr5 for rapid design iterations. The aerodynamic analysis was enhanced using CFD methods for improved understanding of the performance of the aircraft. These results indicate that the classical design approach has limitations when departing from a traditional aircraft configuration and emphasize the need to implement more advanced methods and tools already at early stages of the design process, as also previously shown by Panagiotou et al. [36]. At the same time, this classical approach can still provide a quick “rule of thumb” approximation and starting point for the design process.
The current design features a fuselage and wing section with reflex airfoils for natural longitudinal stability, and a wing sweep of 30. Dihedral and sweep angles were set to optimise the aerodynamic efficiency in cruise and the natural lateral stability of the aircraft. An aerodynamic efficiency of 19 was achieved, and a maximum coefficient of lift of 0.789 at 8.5. Initial longitudinal stability analysis shows a longitudinally stable aircraft between −4 and 8, according to results from CFD simulations. Post-stall pitching moment is more difficult to predict as a result of the departure of the aerodynamic centre from quarter chord due to flow separation, and therefore data should be taken as indicative.
Power calculations demonstrated that a 650 W fuel-cell, complemented by a tank of 80 g of compressed hydrogen and a 100 Wh lithium-ion battery is capable of completing the mission required by the specifications.
Author Contributions
Data curation, S.S., A.P., A.O., H.G., A.C. and R.M.; Formal analysis, S.S., A.P., A.O. and R.M.; Investigation, S.S.; Methodology, H.G. and A.C.; Project administration, R.M.; Supervision, R.M. and G.L.; Writing—original draft, A.C. and R.M.; Writing—review & editing, H.G. and G.L. All authors have read and agreed to the published version of the manuscript.
Funding
The project has been funded by the KTH Integrated Transport Research Lab, KTH Industry Transformation Platform, the KTH Energy Platform, KTH XPRES, and KTH Excellenta Utnildningsmiljöer (KTH Excellence in Education.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Data is contained within the article.
Acknowledgments
Malin Åkermo for financial support through XPRES, Selma Rahman and Mattias Olausson for providing high-quality CAD models of the aircraft, which were used in the CFD simulations, and finally Alessio Galfione and Enrico Trevisan for the engineering drawing.
Conflicts of Interest
The authors confirm that there are no potential or existing conflict of interests associated with their work or the funding.
References
- Centracchio, F.; Rossetti, M.; Iemma, U. Approach to the weight estimation in the conceptual design of hybrid-electric-powered unconventional regional aircraft. J. Adv. Transp. 2018, 2018, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Hordé, T.; Achard, P.; Metkemeijer, R. PEMFC Application for aviation: Experimental and numerical study of sensitivity to altitude. Int. J. Hydrogen Energy 2012, 37, 10818–10829. [Google Scholar] [CrossRef]
- Winter, M.; Brodd, R.J. What Are Batteries, Fuel Cells, and Supercapacitors? J. Chem. Rev. 2003, 104, 4245–4269. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baroutaji, A.; Wilberforce, T.; Ramadan, M.; Ghani Olabi, A. Comprehensive investigation on hydrogen and fuel cell technology in the aviation and aerospace sectors. Renew. Sustain. Energy Rev. 2019, 106, 31–40. [Google Scholar] [CrossRef] [Green Version]
- Peters, R.; Samsun, R.C. Evaluation of multifunctional fuel cell systems in aviation using a multistep process analysis methodology. Appl. Energy 2013, 111, 46–63. [Google Scholar] [CrossRef]
- Guida, D.; Muntillo, M. Design methodology for a PEM fuel cell power system in a more electrical aircraft. Appl. Energy 2017, 192, 446–456. [Google Scholar] [CrossRef]
- Romeo, G.; Borello, F.; Correa, G. Setup and test flights of all-electric two-seater aeroplane powered by fuel cells. J. Aircr. 2011, 48, 1331–1341. [Google Scholar] [CrossRef]
- Romeo, G.; Borello, F.; Correa, G.; Cestino, E. ENFICA-FC: Design of transport aircraft powered by fuel cell & flight test of zero emission 2-seater aircraft powered by fuel cells fueled by hydrogen. Int. J. Hydrogen Energy 2013, 28, 469–479. [Google Scholar]
- Barrett, S. ZeroAvia completes first hydrogen-electric passenger plane flight. Fuel Cells Bull. 2020, 6. [Google Scholar]
- Gong, A.; Verstraete, D. Fuel cell propulsion in small fixed-wing unmanned aerial vehicles: Current status and research needs. Int. J. Hydrogen Energy 2017, 42, 21311–21333. [Google Scholar] [CrossRef]
- Swider-Lyons, K.E.; MacKrell, J.A.; Rodgers, J.A.; Page, G.S.; Schuette, M.; Stroman, R.O. Hydrogen fuel cell propulsion for long endurance small UAVs. In Proceedings of the Name of the Conference, AIAA Centennial of Naval Aviation Forum “100 Years of Achievement and Progress”, Virginia Beach, VA, USA, 21–22 September 2011. [Google Scholar]
- Stroman, R.O.; Schuette, M.W.; Swider-Lyons, K.; Rodgers, J.A.; Edwards, D.J. Liquid hydrogen fuel system design and demonstration in a small long endurance air vehicle. Int. J. Hydrogen Energy 2014, 39, 11279–11290. [Google Scholar] [CrossRef]
- Bradley, T.H.; Moffitt, B.A.; Mavris, D.M.; Parekh, D.E. Development and experimental characterization of a fuel cell powered aircraft. J. Power Sources 2007, 39, 11279–11290. [Google Scholar] [CrossRef]
- Rhoads, G.D.; Wagner, N.A.; Taylor, B.J.; Keen, D.B.; Bradley, T.H. Design and flight test results for a 24 h fuel cell unmanned air vehicle. In Proceedings of the 8th Annual International Energy Conversion Engineering Conference, Nashville, TN, USA, 25–28 July 2010. [Google Scholar]
- Herwerth, C.; Chiang, C.; Ko, A.; Matsuyama, S.; Choi, S.B.; Mirmirani, M.; Gamble, D.; Paul, R.; Sanchez, V.; Arena, A.; et al. Development of a Small Long Endurance Hybrid PEM Fuel Cell Powered UAV; Aerospace Technology Conference and Exposition, SAE Technical Paper; SAE International: Warrendale, PE, USA, 2007. [Google Scholar]
- Gong, A.; Palmer, J.L.; Brian, G.; Harvey, J.R.; Verstraete, D. Performance of a hybrid, fuel-cell-based power system during simulated small unmanned aircraft missions. Int. J. Hydrogen Energy 2016, 41, 11418–11426. [Google Scholar] [CrossRef]
- Gang, B.G.; Kim, H.; Kwon, S. Ground simulation of a hybrid power strategy using fuel cells and solar cells for high-endurance unmanned aerial vehicles. Energy 2017, 141, 1547–1554. [Google Scholar] [CrossRef]
- Kim, K.; Kim, T.; Kwon, S. Fuel cell systems with sodium borohydride as hydrogen source for unmanned aerial vehicles. J. Power Sources 2011, 196, 9069–9075. [Google Scholar] [CrossRef]
- Lapena-Rey, N.; Blanco, J.A.; Ferreyra, E.; Lemus, J.L.; Pereira, S.; Serrot, E. A fuel cell powered unmanned aerial vehicle for low altitude surveillance missions. Int. J. Hydrogen Power 2017, 42, 6926–6940. [Google Scholar] [CrossRef]
- Gadalla, M.; Zafar, S. Analysis of a hydrogen fuel cell-PV power system for small UAV. Int. J. Hydrogen Energy 2016, 41, 6422–6432. [Google Scholar] [CrossRef]
- Renau, J.; Lozano, A.; Barroso, J.; Miralles, J.; Martín, J.; Sánchez, F.; Barreras, F. Use of fuel cell stacks to achieve high altitudes in light unmanned aerial vehicles. Int. J. Hydrogen Energy 2015, 40, 14573–14583. [Google Scholar] [CrossRef] [Green Version]
- Depcik, C.; Cassady, T.; Collicott, B.; Burugupally, S.P.; Li, X.; Alam, S.S.; Arandia, J.R.; Hobeck, J. Comparison of lithium ion batteries, hydrogen fueled combustion engines, and a hydrogen fuel cell in powering a small unmanned aerial vehicle. Energy Convers. Manag. 2020, 207, 112514. [Google Scholar] [CrossRef]
- Verstraete, D.; Lehmkuehler, K.; Wong, K.C. Design of a Fuell Cell Powered Blended Wing Body UAV. In Proceedings of the ASME 2012 International Mechanical Engineering Conference & Exposition, IMECE 2012, Houston, TX, USA, 9–15 November 2012. IMECE2012-88871. [Google Scholar]
- Özbek, E.; Yalin, G.; Ekici, S.; Karakoc Hikmet, T. Evaluation of design methodology, limitations, and iterations of a hydrogen fuelled hybrid fuel cell mini UAV. Energy 2020, 213, 118757. [Google Scholar] [CrossRef]
- Savvaris, A.; Xie, Y.; Malandrakis, K.; Lopez, M.; Tsourdos, A. Development of a fuel cell hybrid-powered unmanned aerial vehicle. In Proceedings of the 24th Mediterranean Conference on Control and Automation (MED), Athens, Greece, 21–24 June 2016. [Google Scholar]
- Project for an Unmanned Airplane with Zero Emissions to cross the South Atlantic. Available online: https://www.isae-supaero.fr/en/news/project-for-an-unmanned-airplane-with-zero-emissions-to-cross-the-south/ (accessed on 2 March 2021).
- De Wagter, C.; Remes, B.; Smeur, E.; van Tienen, F.; Ruijsink, R.; van Hecke, K.; van der Horst, E. The NederDrone: A hybrid lift, hybrid energy hydrogen UAV. Int. J. Hydrogen Energy 2021, 46, 16003–16018. [Google Scholar] [CrossRef]
- Project Phoenix. Available online: https://aerodelft.nl/project-phoenix/ (accessed on 12 May 2022).
- DELAIR. Available online: https://delair.aero/delair-commercial-drones/hydrone/ (accessed on 7 September 2021).
- Guynn, M.D.; Freeh, J.E.; Olson, E.D. Evaluation of a Hydrogen Fuel Cell Powered Blended-Wing-Body Aircraft Concept for Reduced Noise and Emissions. In NASA/TM-2004-212989; National Aeronautics and Space Administration: Washington, DC, USA, 2004. [Google Scholar]
- ZEROe, towards the World’s First Zero-Emission Commercial Aircraft. Available online: https://www.airbus.com/innovation/zero-emission/hydrogen/zeroe.html (accessed on 7 September 2021).
- Reist, T.A.; Zingg, D.W. Aerodynamic design of blended wing body and lifting-fuselage aircraft. In Proceedings of the 34th AIAA Applied Aerodynamics Conference, Session: Innovative Aerodynamic Concepts & Designs, Washington, DC, USA, 13–17 June 2016. AIAA 2016-3874. [Google Scholar]
- Bradley, K.R. A sizing methodology for the conceptual design of blended-wing-body transports. In NASA/CR-2004-213016; National Aeronautics and Space Administration: Washington, DC, USA, 2004. [Google Scholar]
- Crawley, E.F.; Malmqvist, J.; Östlund, S.; Brodeur, D.R.; Edström, K. Rethinking Engineering Education. The CDIO Approach, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Raymer, D.P. Aircraft Design: A Conceptual Approach, 6th ed.; AIAA Educational Series; AIAA: Reston, VA, USA, 2018; pp. 27–94; discussion 834–838. [Google Scholar]
- Panagiotou, P.; Fotiadis-Karras, S.; Yakinthos, K. Conceptual design of a Blended Wing Body MALE UAV. Aerosp. Sci. Technol. 2018, 73, 32–47. [Google Scholar] [CrossRef]
- HES Energy Systems. Available online: https://www.hes.sg/ (accessed on 7 September 2021).
- Intelligent Energy. Available online: https://www.intelligent-energy.com/ (accessed on 7 September 2021).
- Gundlach, J. Designing Unmanned Aircraft Systems: A Comprehensive Approach, 3rd ed.; AIAA Educational Series; AIAA: Reston, VA, USA, 2012. [Google Scholar]
- Liebeck, R.H. Design of the blended wing body subsonic transport. J. Aircr. 2004, 41, 10–25. [Google Scholar] [CrossRef] [Green Version]
- Qin, N.; Vavalle, A.; Le Moigne, A.; Laban, M.; Hackett, K.; Weinerfelt, P. Aerodynamic considerations of blended wing body aircraft. Prog. Aerosp. Sci. 2004, 40, 321–343. [Google Scholar] [CrossRef]
- Qin, N.; Vavalle, A.; Le Moigne, A. Spanwise lift distribution for blended wing body aircraft. J. Aircraft 2005, 42, 356–365. [Google Scholar] [CrossRef]
- Airfoil Tools. Available online: http://airfoiltools.com/search/index (accessed on 7 September 2021).
- Drela, M. XFOIL: An Analysis and Design System for Low Reynolds Number Airfoils. In Lectures Noted in Engineering, Proceedings of the Conference in Low Reynolds Number Aerodynamics, Notre Dame, IN, USA, 5–7 June 1989; Mueller, T.J., Ed.; Springer: Berlin, Germany, 1989. [Google Scholar]
- Anderson, J.D. Aircraft Performance and Design; McGraw-Hill Int. Editions: Singapore, 1999. [Google Scholar]
- Pamadi, B.N. Performance, Stability, Dynamics and Control of Airplanes; AIAA Educational Series; AIAA: Reston, VA, USA, 1998. [Google Scholar]
- Panagiotou, P.; Yakinthos, K. Parametric aerodynamic study of Blended-Wing-Body platforms at low subsonic speeds for UAV applications. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, AIAA AVIATION Forum, Denver, CO, USA, 5–9 June 2017. AIAA 2017-3737. [Google Scholar]
- Panagiotou, P.; Kaparos, P.; Salpingidou, C.; Yakinthos, K. Aerodynamic design of a MALE UAV. Aerosp. Sci. Technol. 2016, 50, 127–138. [Google Scholar] [CrossRef]
- Koster, J.; Balaban, S.; Hillery, D.; Hmbargar, C.; Nasso, D.; Serani, E.; Velazco, A. Design of a Blended Wing Body UAS with Hybrid Propulsion. In Proceedings of the ASME 2011 International Mechanical Engineering Congress & Exposition, IMECE2011, Denver, CO, USA, 11–17 November 2011. IMECE2011-62126. [Google Scholar]
- McDonald, R.A.; Gloudemans, J.R. Open Vehicle Sketch Pad: An Open Source Parametric Geometry and Analysis Tool for Conceptual Aircraft Design. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- xflr5. Available online: http://www.xflr5.tech/xflr5.htm (accessed on 7 September 2021).
- Tomac, M.; stenfelt, G. Predictions of stability and control for a flying wing. Aerosp. Sci. Technol. 2014, 39, 179–186. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Douvi, E.C.; Tsavalos, I.A.; Margaris, P.D. Evaluation of the turbulence models for the simulation of the flow over a National Advisory Committee for Aeronautics (NACA) 0012 airfoil. J. Mech. Eng. Res. 2012, 4, 100–111. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Spalart, P.R.; Rumsey, C.L. Effective inflow conditions for Turbulence Models in Aerodynamic calculations by Spalart and Rumsey. AIAA J. 2007, 45, 2544–2553. [Google Scholar] [CrossRef]
- Goetten, F.; Finger, D.F.; Marino, M.; Bil, C. A revire of guidelines and best practices for subsonic aerodynamic simulations unsing RANS CFD. In Proceedings of the Asia Pacific International Symposium on Aerospace Technology, Gold Coast, Australia, 4–6 December 2019; ISBN 978-1-925627-40-4. [Google Scholar]
- Versteeg, H.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson: London, UK, 2007. [Google Scholar]
- Chiche, A.; Lindbergh, G.; Stenius, I.; Lagergren, C. A Strategy for Sizing and Optimizing the Energy System on Long-Range AUVs. IEEE J. Ocean. Eng. 2021, 1132–1143. [Google Scholar] [CrossRef]
- Chiche, A.; Andruetto, C.; Lagergren, C.; Lindbergh, G.; Stenius, I.; Peretti, L. Feasibility and impact of a Swedish fuel cell-powered rescue boat. Ocean. Eng. 2021, 234, 109259. [Google Scholar] [CrossRef]
- Wikner, E.; Thiringer, T. Extending Battery Lifetime by Avoiding High SOC. Appl. Sci. 2018, 8, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Sturm, J.; Frank, A.; Rheinfeld, A.; Erhard, S.V.; Jossen, A. Impact of electrode and cell design on fast charging capabilities of cylindrical lithium-ion batteries. J. Electrochem. Soc. 2020, 167, 130505. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).