Cooperative Smooth Nonsingular Terminal Sliding Mode Guidance with Tracking Differentiator for Active Aircraft Defense
Abstract
1. Introduction
- In the design process of the two-way cooperative algorithm, we build a two-dimensional second-order nonlinear system based on the zero-effort miss distance (ZEM), zero-effort velocity (ZEV), and their integral values, by which the SNTSM was used to design a cooperative guidance law. In comparison to the present methods that deal with this problem, the proposed algorithm is of faster convergence speed, higher guidance accuracy, stronger robustness, and lower sensitivity to the time-to-go estimation error, which are demonstrated by the theoretical derivation and simulation experimental results.
- For the overload saturation phenomenon caused by excessive initial command error, the tracking differentiator is introduced to arrange the transition process based on the SNTSM design method, and the experimental simulation results show that the overload constraint requirements of the defense missile and the target are met.
- In the one-way cooperative engagement scenario where the target adopts an independent evasion maneuver, the one-way cooperative SNTSM guidance strategy is proposed, which does not require knowledge of the target evasion strategy. The proposed sliding mode surface convergence rate is faster, the guidance accuracy is higher, and the overload distribution is more consistent with the principle of energy management.
2. Model Description
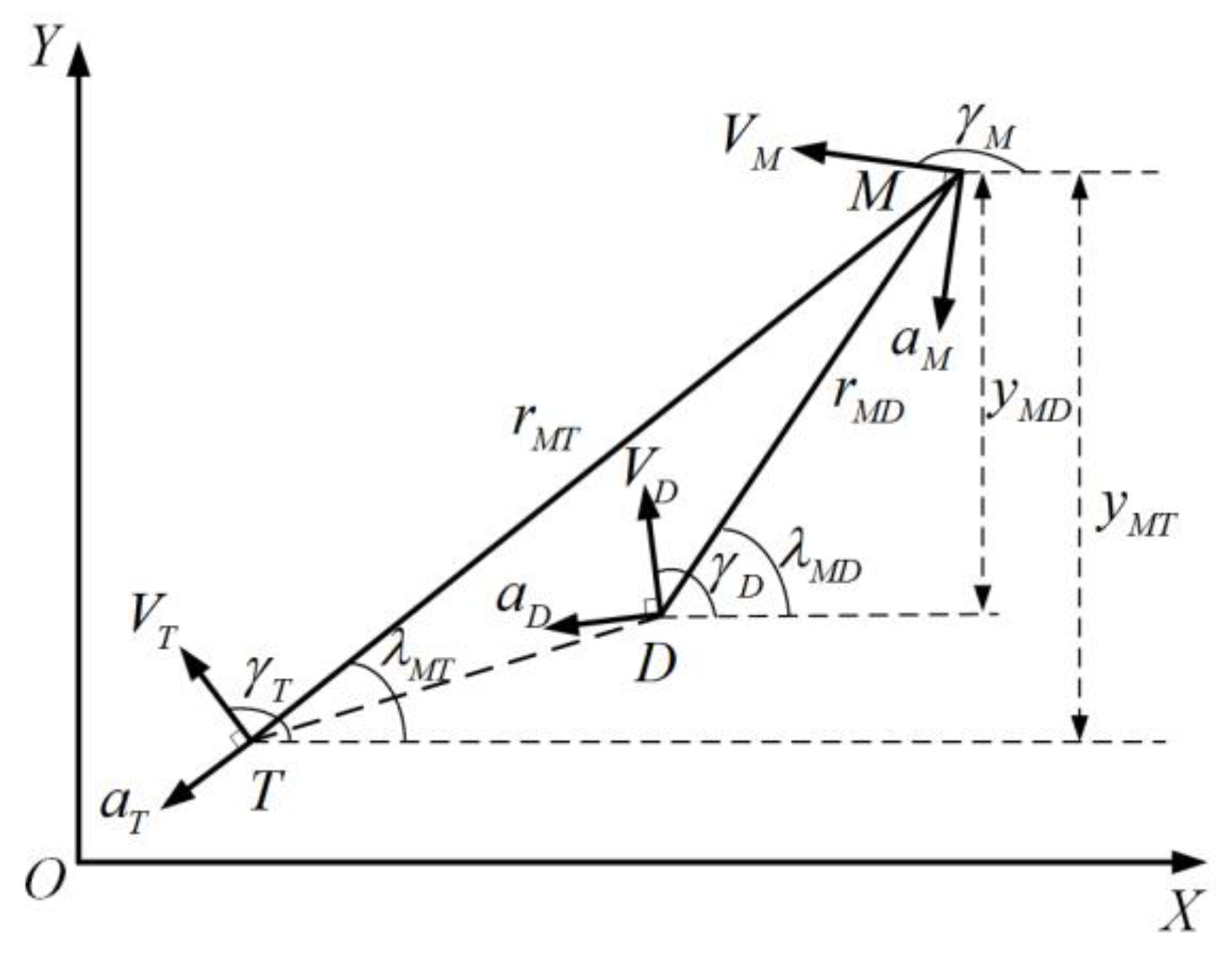
2.1. Nonlinear Engagement Kinematics
2.2. Linear Engagement Kinematics
2.3. Timeline
2.4. Order Reduction and Zero-Effort Transformations
3. Two-Way Cooperative SNTSM Guidance Design with TD
3.1. Principle and Stability Proof Smooth Nonsingular Terminal Sliding Mode
3.2. Two-Way Cooperative SNTSM Guidance Design
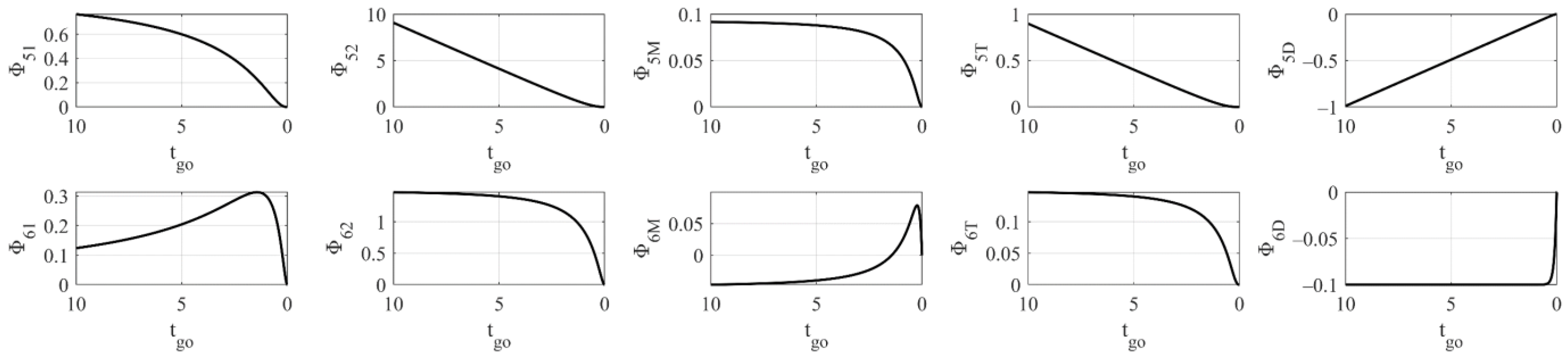
3.3. Tracking Differentiator
4. One-Way Cooperative Smooth Nonsingular Terminal Sliding Guidance Design
5. Simulation Study
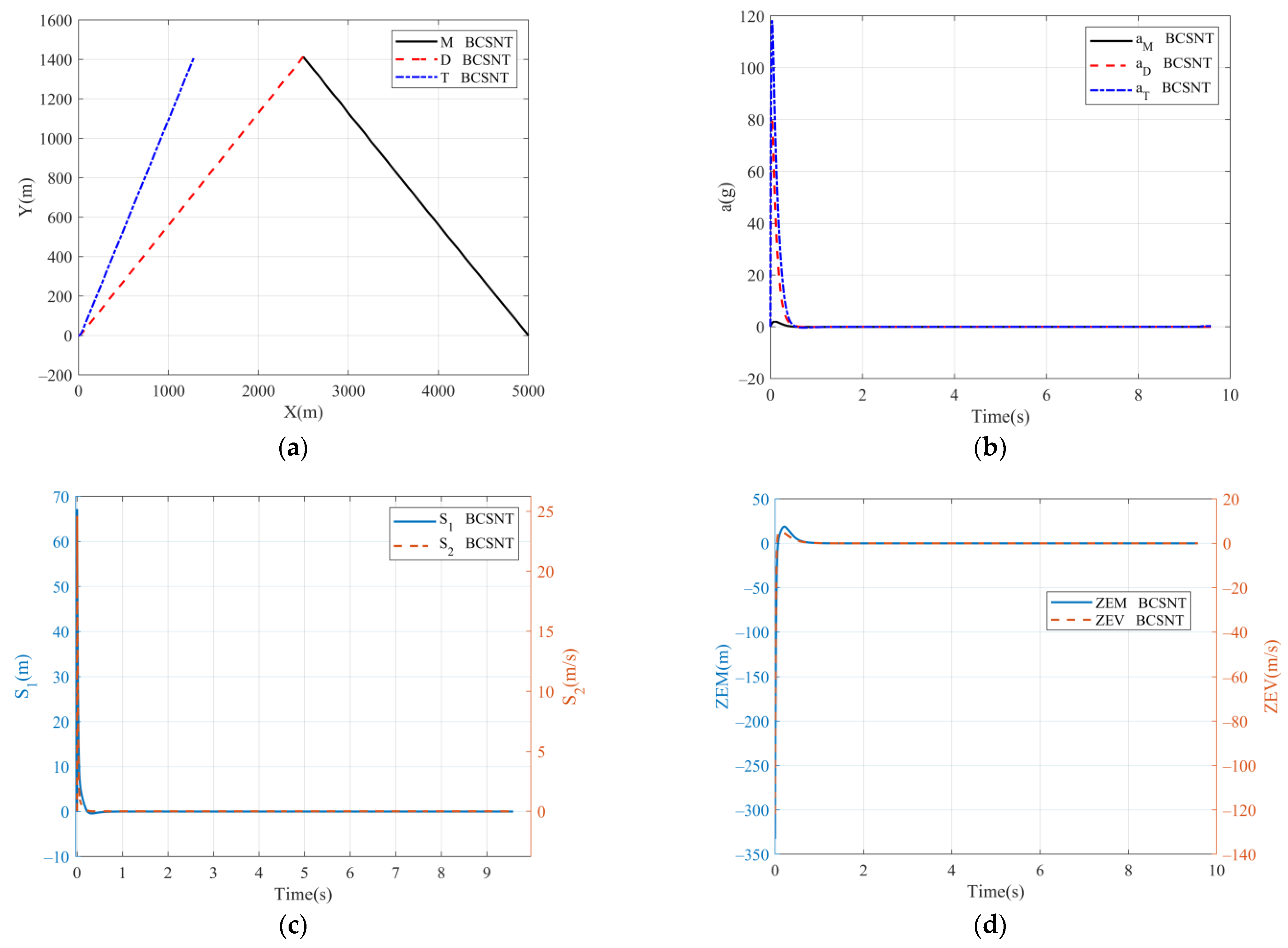
5.1. Two-Way Cooperative SNTSM Guidance without a TD
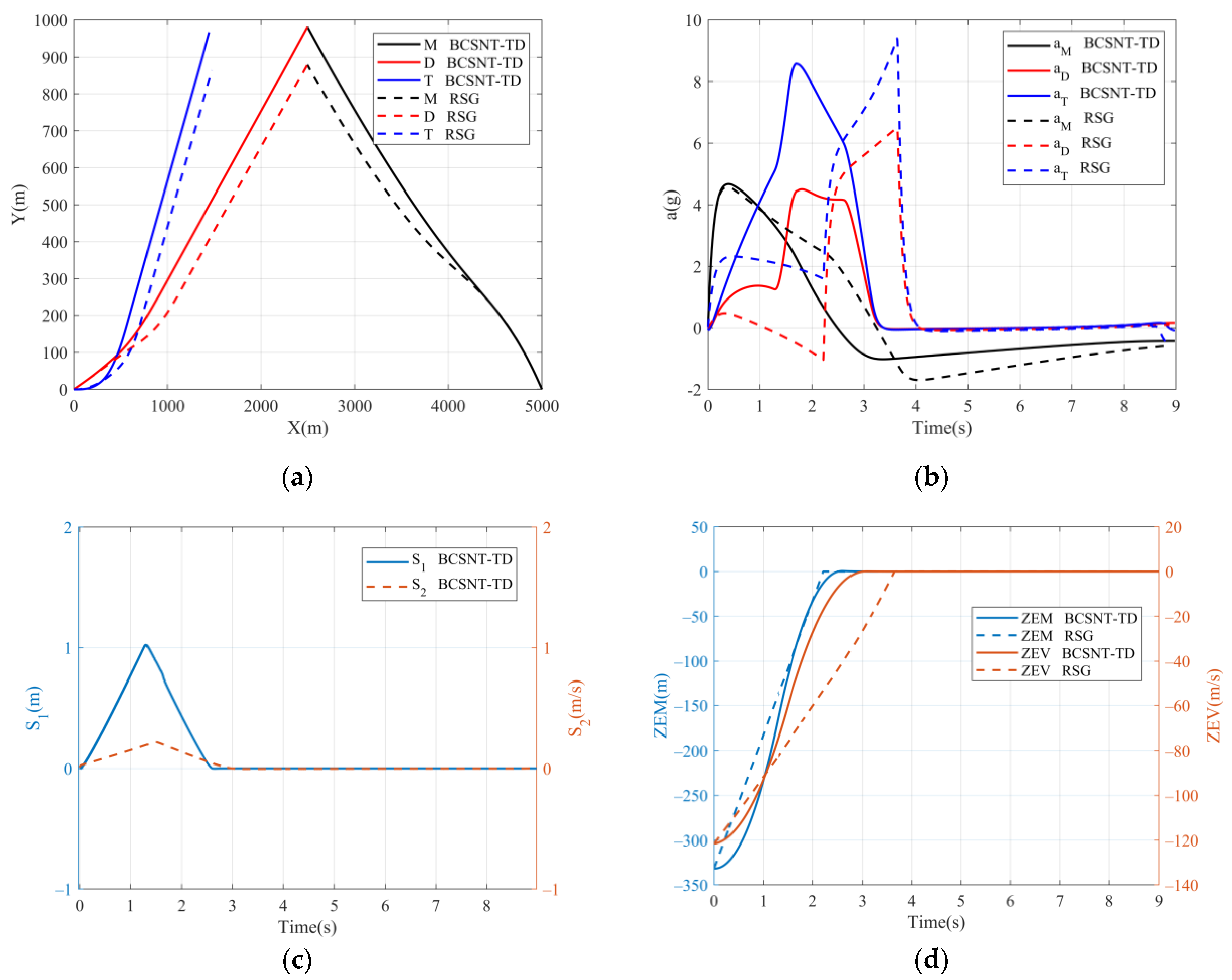
5.2. Comparation for Two-Way Cooperative SNTSM Guidance with TD and Reduced-Sensitivity Guidance
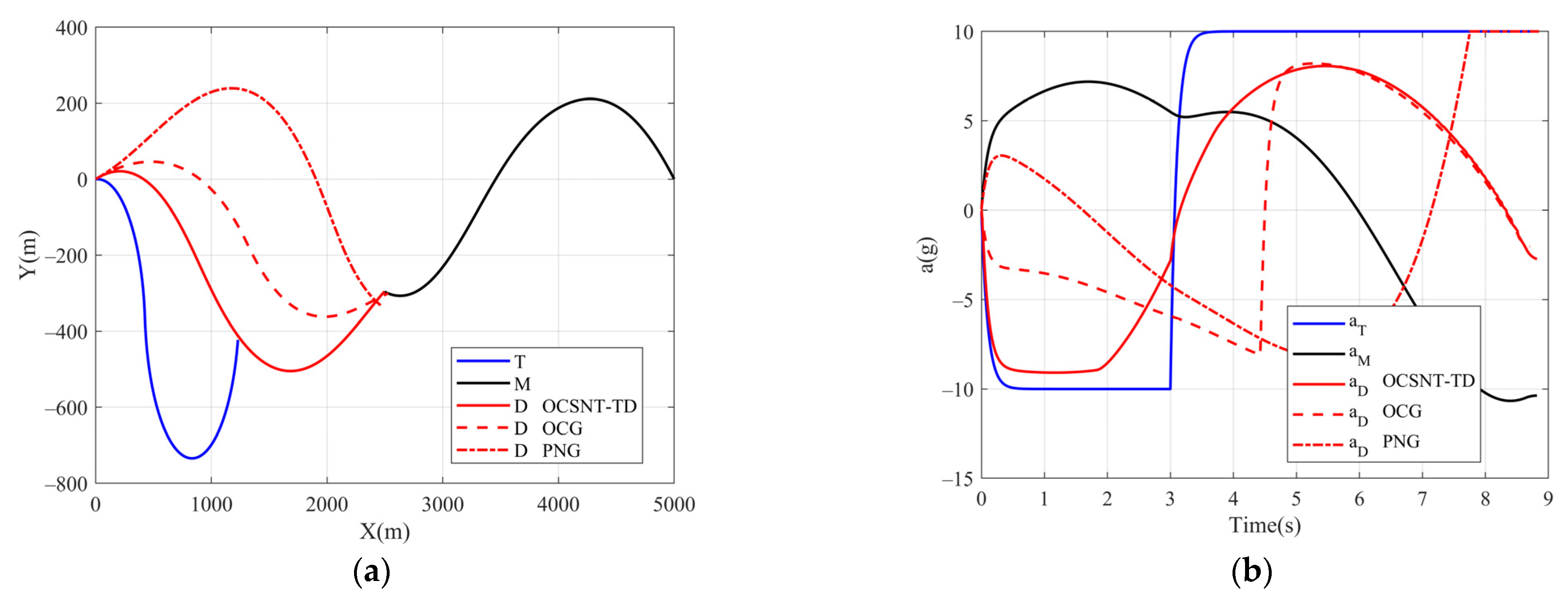
5.3. Comparation for One-Way Cooperative SNTSM Guidance with a TD, One-Way Cooperative Guidance, and Proportional Navigation Guidance (PNG)
6. Conclusions and Future Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yamasaki, T.; Takano, H. Modified command to line-of-sight intercept guidance for aircraft defense. J. Guid. Control Dyn. 2013, 36, 898–902. [Google Scholar] [CrossRef]
- Ratnoo, A.; Shima, T. Line-of-sight interceptor guidance for defending an aircraft. J. Guid. Control Dyn. 2013, 34, 522–532. [Google Scholar] [CrossRef]
- Ratnoo, A.; Shima, T. Guidance strategies against defended aerial targets. J. Guid. Control Dyn. 2013, 35, 1059–1068. [Google Scholar] [CrossRef]
- Kumar, S.R.; Mukherjee, D. Cooperative active aircraft protection guidance using line-of-sight approach. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 957–967. [Google Scholar] [CrossRef]
- Prokopov, O.; Shima, T. Linear quadratic optimal cooperative strategies for active aircraft protection. J. Guid. Control Dyn. 2013, 36, 753–764. [Google Scholar] [CrossRef]
- Garcia, E.; Casbeer, D.W.; Pachter, M. Cooperative strategies for optimal aircraft defense from an attacking missile. J. Guid. Control Dyn. 2015, 38, 1510–1520. [Google Scholar] [CrossRef]
- Shima, T. Optimal cooperative pursuit and evasion strategies against a homing missile. J. Guid. Control Dyn. 2011, 34, 414–425. [Google Scholar] [CrossRef]
- Weiss, M.; Shima, T. Minimum effort pursuit/evasion guidance with specified miss distance. J. Guid. Control Dyn. 2016, 39, 1069–1079. [Google Scholar] [CrossRef]
- Fang, F.; Cai, Y. Optimal cooperative guidance with guaranteed miss distance in three-body engagement. P. I. Mech. Eng. G-J. Aer. 2018, 232, 492–504. [Google Scholar] [CrossRef]
- Weiss, M.; Shima, T.; Castaneda, D.; Rusnak, I. Combined and cooperative minimum-effort guidance algorithms in an active aircraft defense scenario. J. Guid. Control Dyn. 2017, 40, 1241–1254. [Google Scholar] [CrossRef]
- Garcia, E.; Casbeer, D.W.; Pachter, M. Active target defense using first order missile models. Automatica 2017, 78, 139–143. [Google Scholar] [CrossRef]
- Perelman, A.; Shima, T. Cooperative differential games strategies for active aircraft protection from a homing missile. J. Guid. Control Dyn. 2011, 34, 761–773. [Google Scholar] [CrossRef]
- Saurav, A.; Kumar, S.R.; Maity, A. Cooperative guidance strategies for aircraft defense with impact angle constraints. In AIAA SciTech Forum, 7–11 January 2019; Online: San Diego, CA. USA.
- Rubinsky, S.; Gutman, S. Three-player pursuit and evasion conflict. J. Guid. Control Dyn. 2014, 37, 98–110. [Google Scholar] [CrossRef]
- Shaferman, V.; Shima, T. Cooperative multiple model adaptive guidance for an aircraft defending missile. J. Guid. Control Dyn. 2010, 33, 1801–1813. [Google Scholar] [CrossRef]
- Fang, F.; Cai, Y.; Yu, Z. Adaptive estimation and cooperative guidance for active aircraft defense in stochastic scenario. Sensors 2019, 19, 979. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Yan, B.; Zhang, X.; Liu, W.; Yan, J. Fractional-order sliding mode guidance law for intercepting hypersonic vehicles. Aerospace 2022, 9, 53. [Google Scholar] [CrossRef]
- Kumar, S.R.; Shima, T. Cooperative nonlinear guidance strategies for aircraft defense. J. Guid. Control Dyn. 2017, 40, 124–138. [Google Scholar] [CrossRef]
- Ates, H.U. Lyapunov based nonlinear impact angle guidance law for stationary targets. In AIAA Guidance, Navigation, and Control Conference, 5–9 January 2015; Online: Kissimmee, FL, USA.
- Zhang, Y.; Jiao, G.; Sun, M.; Chen, Z. Finite Time Convergent Guidance Law with Impact Angle Constraint Based on Sliding Control. In Proceedings of the 30th Chinese Control Conference, Yantai, China, 22–24 July 2011; pp. 2597–2601. [Google Scholar]
- He, S.; Lin, D. Adaptive nonsingular sliding mode based guidance law with terminal angular constraint. Int. J. Aeronaut. Space 2014, 15, 146–152. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Han, F. On nonsingular terminal sliding-mode control of nonlinear systems. Automatica 2013, 49, 1715–1722. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Khoo, S.; Xie, L.; Man, Z. Robust finite-time consensus tracking algorithm for multirobot systems. IEEE-ASME T. Mech. 2009, 14, 219–228. [Google Scholar] [CrossRef]
- Kumar, S.R.; Rao, S.; Ghose, D. Nonsingular terminal sliding mode guidance with impact angle constraints. J. Guid. Control Dyn. 2014, 37, 1–17. [Google Scholar] [CrossRef]
- Wang, X.; Wang, J. Partial integrated missile guidance and control with finite time convergence. J. Guid. Control Dyn. 2013, 36, 1399–1409. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, K.; Chen, P. Adaptive terminal sliding mode guidance law with impact angle constraint. J. Beijing Univ. Aeronaut. Astronaut. 2016, 42, 1566–1574. [Google Scholar]
- Song, J.; Song, S.; Zhou, H. Adaptive nonsingular fast terminal sliding mode guidance law with impact angle constraints. Int. J. Control Autom. 2016, 14, 99–114. [Google Scholar] [CrossRef]
- Zou, X.; Zhou, D.; Du, R.; Liu, J. Adaptive nonsingular terminal sliding mode cooperative guidance law in active defense scenario. P. I. Mech. Eng. G-J. Aer. 2015, 230, 307–320. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, J. Smooth sliding mode control for missile interception with finite-time convergence. J. Guid. Control Dyn. 2015, 38, 1311–1318. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, H.; Zou, J.; Zheng, G. Tracking differentiator-based dynamic surface control for the power control of the wind generation system in the wind farm. P. I. Mech. Eng. G-J. Aer. 2013, 227, 275–285. [Google Scholar] [CrossRef]
- Zhang, H.; Xie, Y.; Long, Z. Fault detection based on tracking differentiator applied on the suspension system of maglev train. Math. Probl. Eng. 2015, 2015, 1–9. [Google Scholar] [CrossRef][Green Version]
- Lou, W.; Zhu, M.; Guo, X. Spatial trajectory tracking control for unmanned airships based on active disturbance rejection control. P. I. Mech. Eng. G-J. Aer. 2019, 233, 2231–2240. [Google Scholar] [CrossRef]
- Yan, M.; Xue, C.; Xie, X. A novel model free adaptive controller with tracking differentiator. In Proceedings of the 2009 IEEE International Conference on Mechatronics and Automation, Changchun, China, 9–12 August 2009; pp. 4191–4196. [Google Scholar]
- Wang, Z.; Long, Z.; Xie, Y.; Ding, J.; Luo, J.; Li, X. A discrete nonlinear tracking-differentiator and its application in vibration suppression of maglev system. Math. Probl. Eng. 2020, 2020, 1–9. [Google Scholar] [CrossRef]
- Zarchan, P. Tactical and Strategic Missile Guidance, 7th ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2019. [Google Scholar]
- Ben-Asher, J.Z. Linear quadratic pursuit-evasion games with terminal velocity constraints. J. Guid. Control Dyn. 1996, 19, 499–501. [Google Scholar] [CrossRef]
- Ben-Asher, J.Z.; Yaesh, I. Optimal guidance with reduced sensitivity to time-to-go estimation errors. J. Guid. Control Dyn. 1997, 20, 158–163. [Google Scholar] [CrossRef]
- Xie, Y.; Long, Z.; Li, J.; Zhang, K.; Luo, K. Research on a new nonlinear discrete-time tracking-differentiator filtering characteristic. In Proceedings of the 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008; pp. 6750–6755. [Google Scholar]

| Guidance Algorithm | BCSNT-TD | RSG |
|---|---|---|
| Mean | 0.4401 | 0.6360 |
| Standard deviation | 0.3561 | 0.4909 |
| RMS | 0.5559 | 0.7897 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Fan, Y.; Yan, T.; Liang, X.; Yan, J. Cooperative Smooth Nonsingular Terminal Sliding Mode Guidance with Tracking Differentiator for Active Aircraft Defense. Aerospace 2022, 9, 221. https://doi.org/10.3390/aerospace9040221
Li Q, Fan Y, Yan T, Liang X, Yan J. Cooperative Smooth Nonsingular Terminal Sliding Mode Guidance with Tracking Differentiator for Active Aircraft Defense. Aerospace. 2022; 9(4):221. https://doi.org/10.3390/aerospace9040221
Chicago/Turabian StyleLi, Quancheng, Yonghua Fan, Tian Yan, Xuechao Liang, and Jie Yan. 2022. "Cooperative Smooth Nonsingular Terminal Sliding Mode Guidance with Tracking Differentiator for Active Aircraft Defense" Aerospace 9, no. 4: 221. https://doi.org/10.3390/aerospace9040221
APA StyleLi, Q., Fan, Y., Yan, T., Liang, X., & Yan, J. (2022). Cooperative Smooth Nonsingular Terminal Sliding Mode Guidance with Tracking Differentiator for Active Aircraft Defense. Aerospace, 9(4), 221. https://doi.org/10.3390/aerospace9040221






