Intelligent Discrete Sliding Mode Predictive Fault-Tolerant Control Method for Multi-Delay Quad-Rotor UAV System Based on DIECOA
Abstract
:1. Introduction
- 1.
- The above two papers deal with the actuator fault of the system, and this paper deals with the sensor fault. In the system model, Ref. [31] has not considered time delays and the parameter uncertainties of the system, and Ref. [30] only considered state time delay. First, the augmented system is constructed in system structural transformation, and the sensor fault is added to the system state.
- 2.
- About the design of sliding mode controller, different from the linear sliding surface in the predictive model [30] and the delta operator approach [31], the quasi-integral sliding mode surface is adopted in this paper to deal with discrete sliding mode control problems which can eliminate the sliding mode approach process and ensure the global robustness of the system.
- 3.
- For the sensor fault, various disturbances, and multiple time delays, this paper designs an intelligent double-power function reference trajectory considering fault and disturbance compensation term, which effectively reduces the adverse effect of multi-delay and improves the precision of fault-tolerant control.
- 4.
- Regarding the design of rolling optimization, which is what [31] lacks, this paper adopts the dynamic information exchange coyote optimization algorithm (DIECOA), which introduced a dynamic information exchange strategy (DIE) to further improve the individual change mechanism of the coyote optimization algorithm (COA). Compared with the multi-agent particle swarm optimization algorithm (MAPSO) proposed in [31], DIECOE improves the local solution capability of the control law optimization in this paper and has the advantages of faster convergence and higher accuracy.
2. Problem Statement and Preliminaries
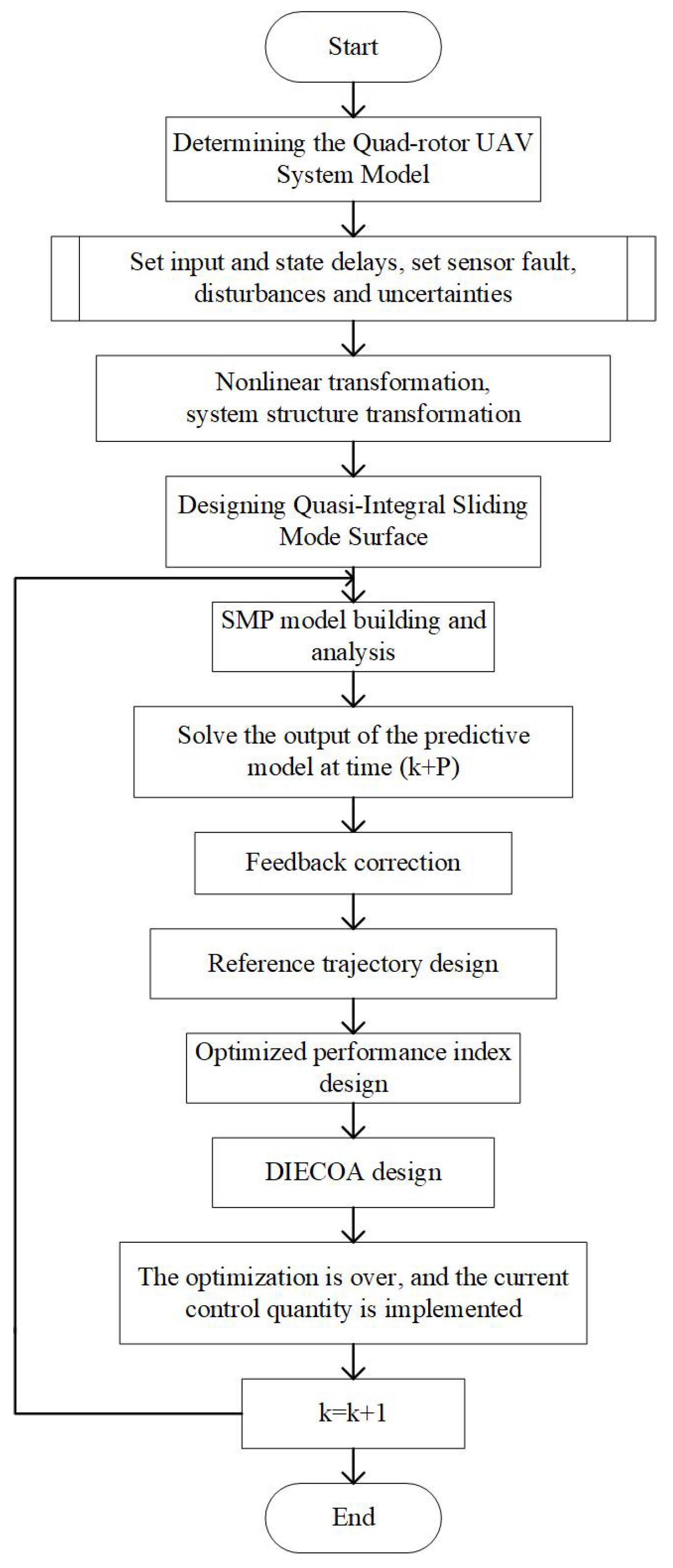
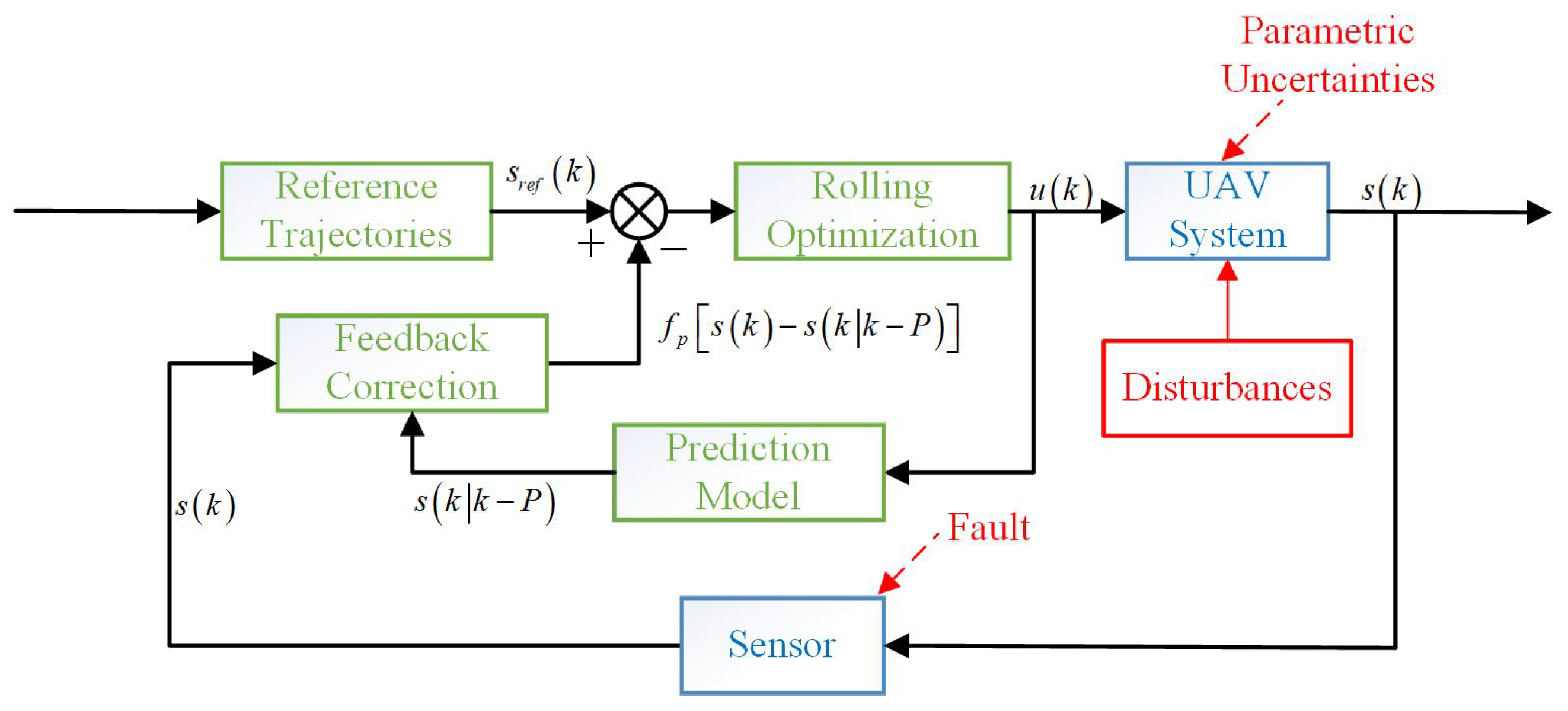
3. SMP-FTC Method Design
3.1. SMP Model Analysis
3.2. Stability Analysis of the SMP Model
3.3. Feedback Correction
3.4. Reference Trajectory Design
3.5. Rolling Optimization Design Based on DIECOA
4. Stability Analysis
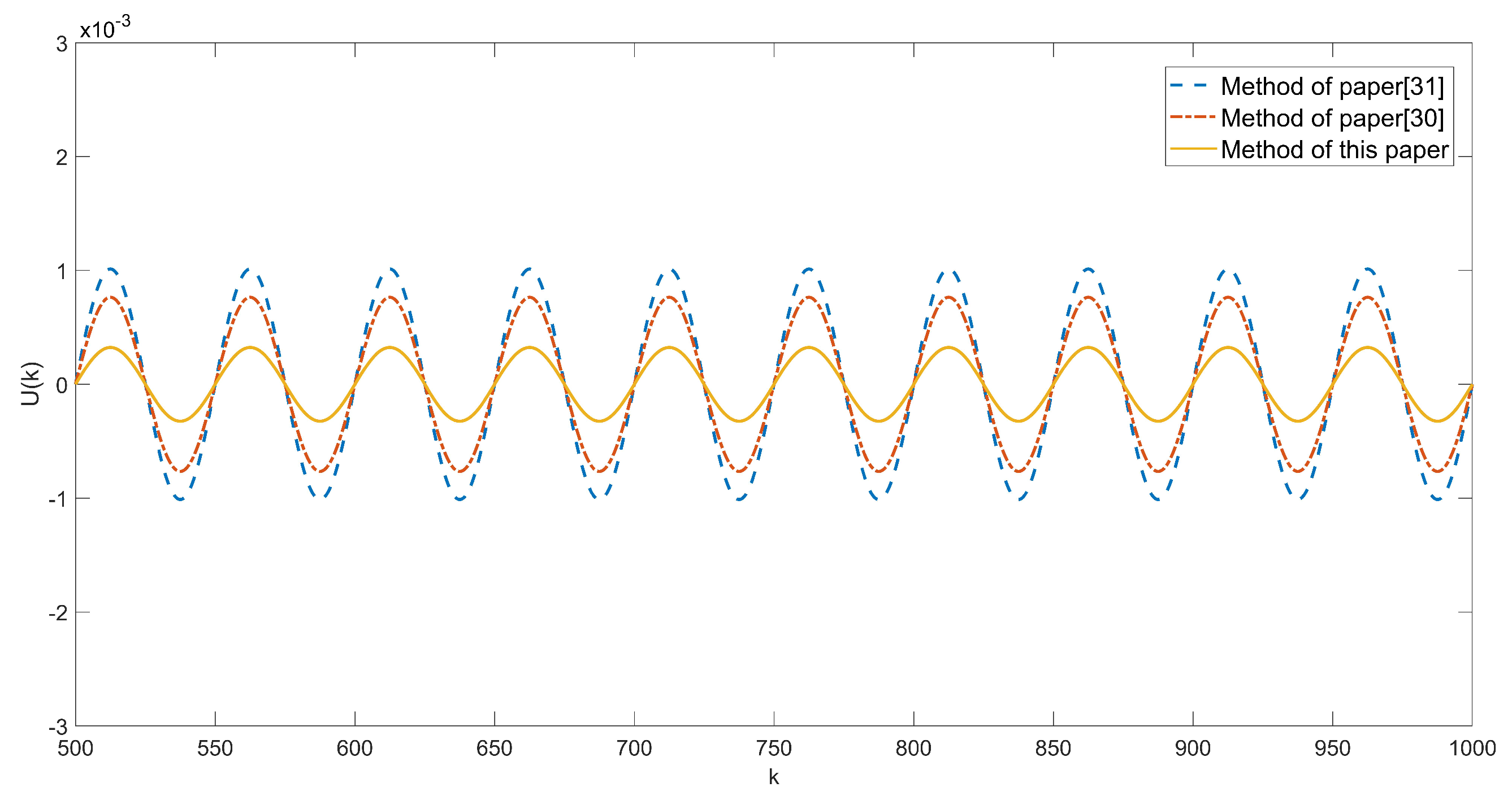
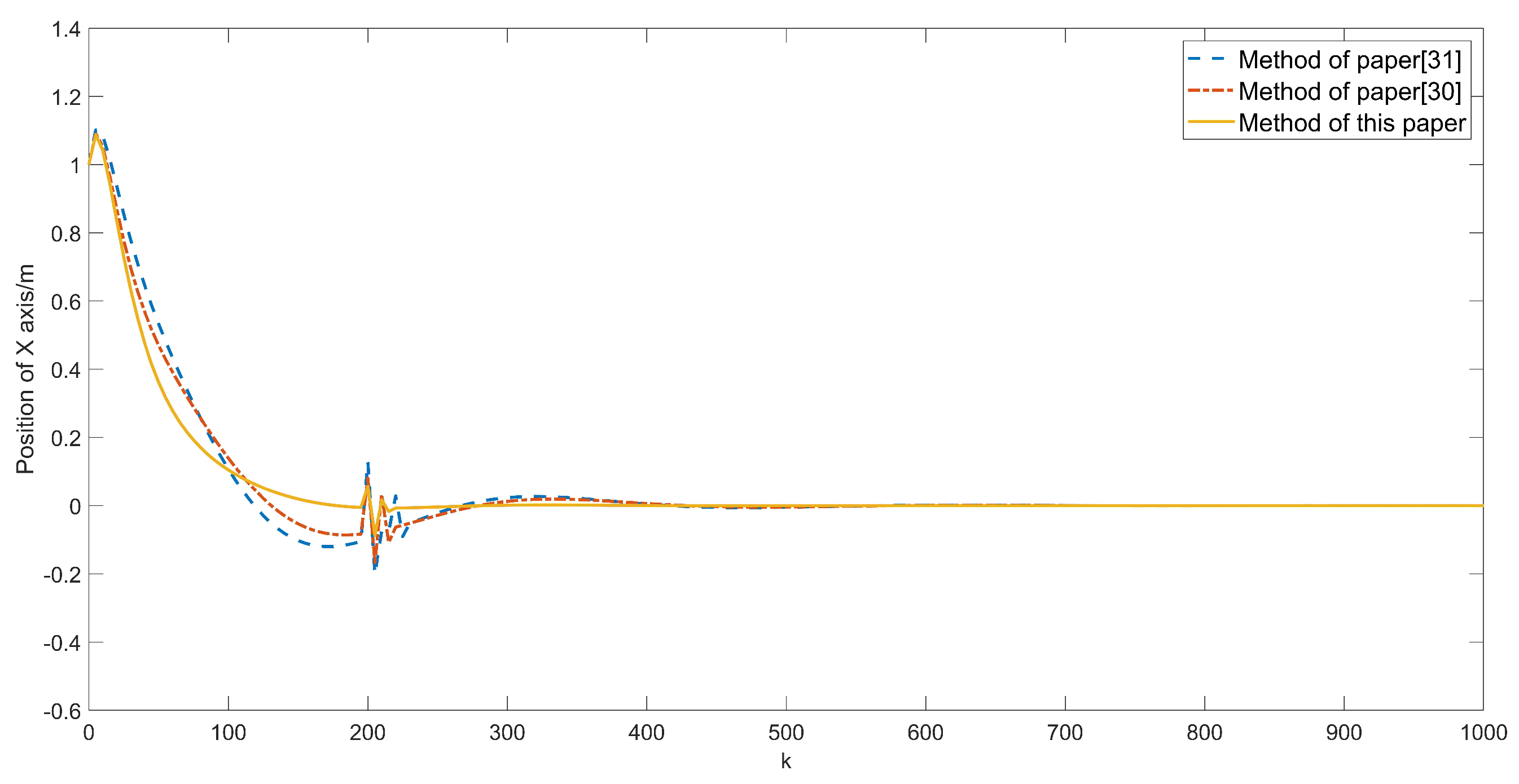
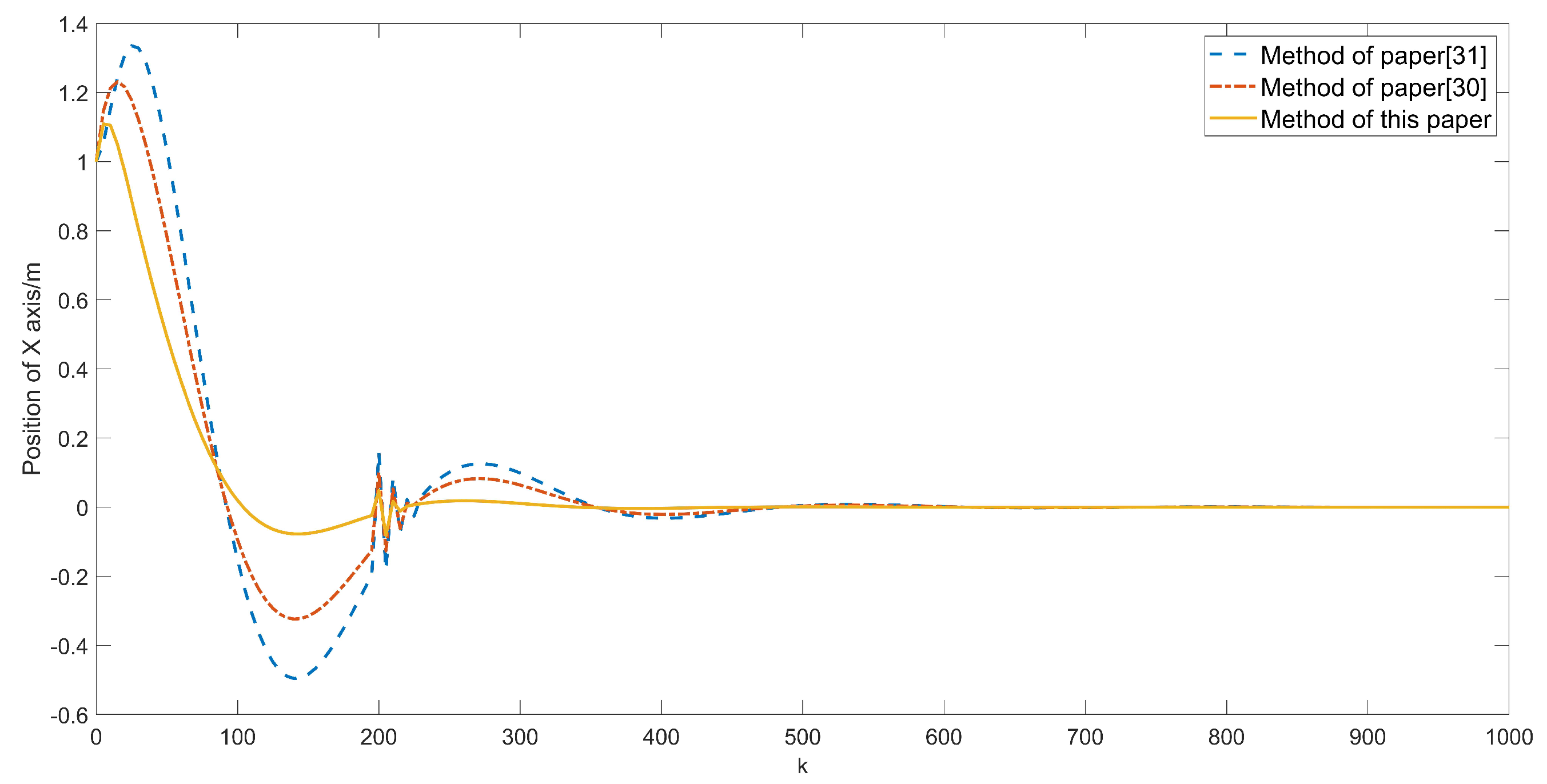
5. Simulation Settings and Analysis
5.1. Model Introduction and Parameter Settings
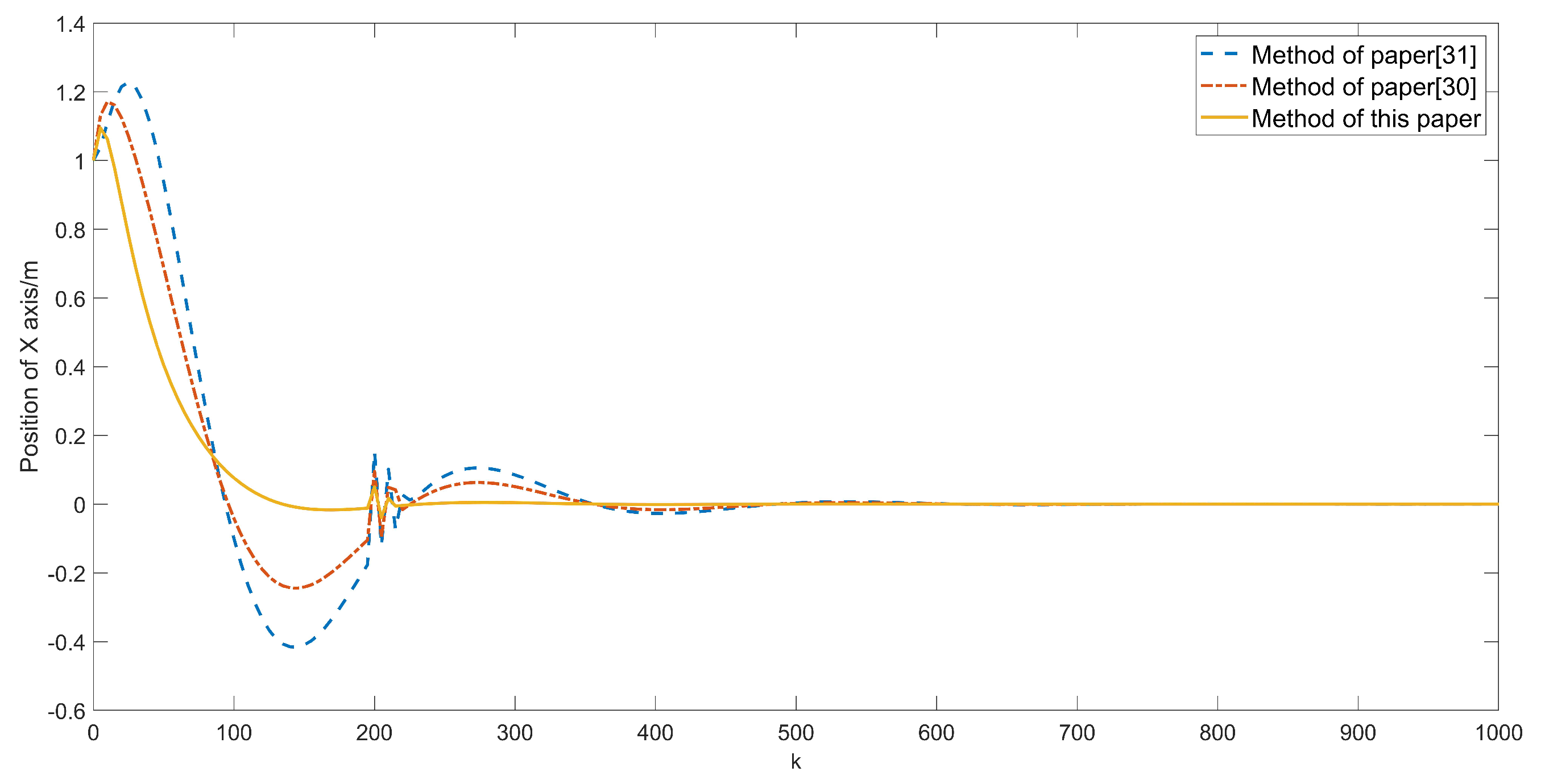
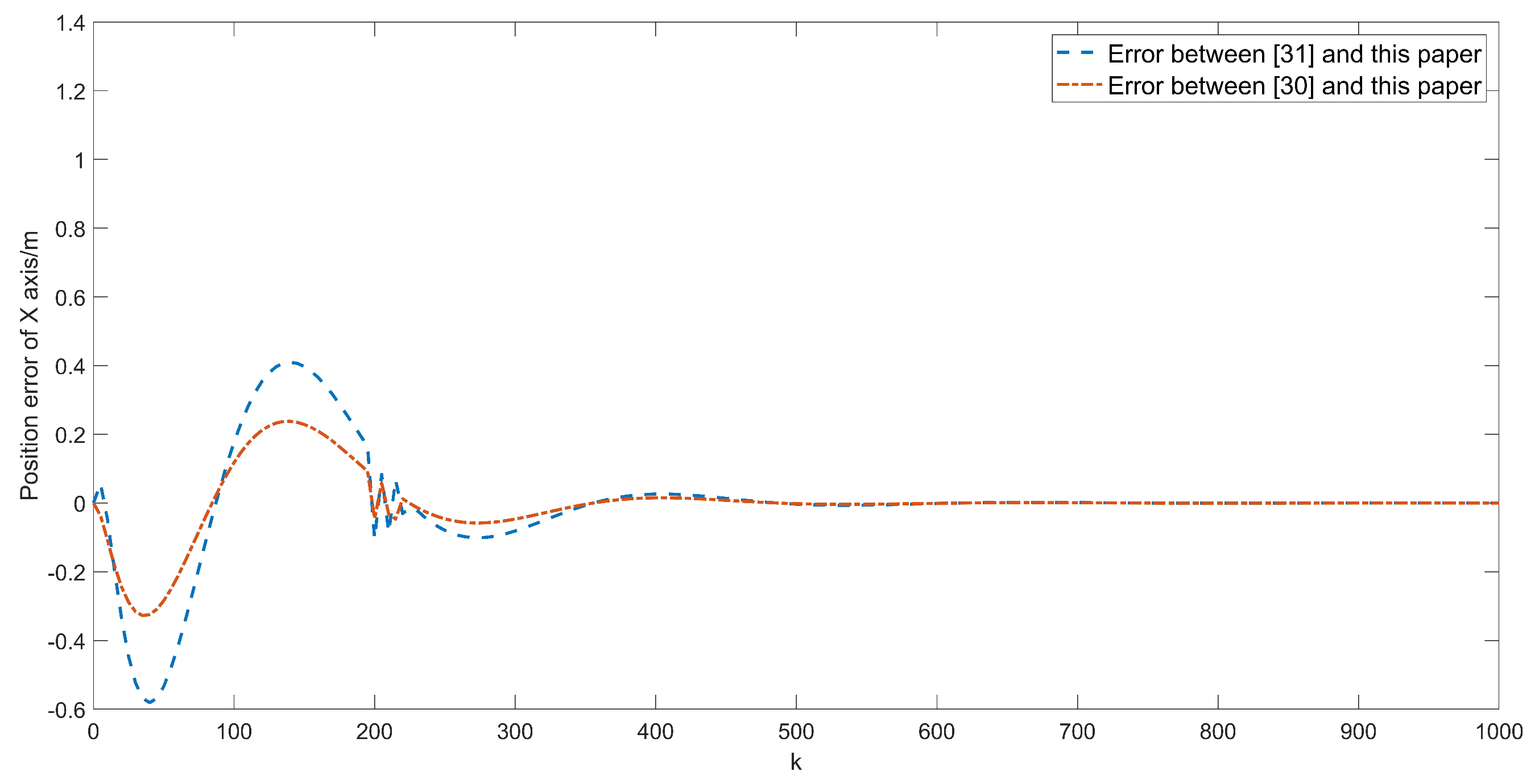
5.2. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aouaouda, S.; Chadli, M. Robust fault tolerant controller design for Takagi-Sugeno systems under input saturation. Int. J. Syst. Sci. 2019, 50, 1163–1178. [Google Scholar] [CrossRef]
- Hao, L.Y.; Zhang, H.; Yue, W.; Li, H. Fault-tolerant compensation control based on sliding mode technique of unmanned marine vehicles subject to unknown persistent Ocean Disturbances. Int. J. Control Autom. Syst. 2020, 18, 739–752. [Google Scholar] [CrossRef]
- Wang, X.; Kampen, E.J.; Chu, Q. Quadrotor fault-tolerant incremental nonsingular terminal sliding mode control. Aerosp. Sci. Technol. 2019, 95, 105514. [Google Scholar] [CrossRef]
- Xiao, S.; Dong, J. Robust adaptive fault-tolerant tracking control for uncertain linear systems with time-varying performance bounds. Int. J. Robust Nonlinear Control 2019, 29, 849–866. [Google Scholar] [CrossRef]
- Qian, M.; Shi, Y.; Gao, Z.; Zhang, X. Integrated fault tolerant tracking control for rigid spacecraft using fractional order sliding mode technique. J. Frankl. Inst. 2020, 357, 10557–10583. [Google Scholar] [CrossRef]
- Yao, L.; Wu, Y. Robust fault diagnosis and fault-tolerant control for uncertain multiagent systems. Int. J. Robust Nonlinear Control 2020, 30, 8192–8205. [Google Scholar] [CrossRef]
- Kuantama, E.; Vesselenyi, T.; Dzitac, S.; Tarca, R. PID and Fuzzy-PID control model for quadcopter attitude with disturbance parameter. Int. J. Comput. Commun. Control 2017, 12, 519–532. [Google Scholar] [CrossRef] [Green Version]
- Noormohammadi-Asl, A.; Esrafilian, O.; Arzati, M.A.; Taghirad, H.D. System identification and H∞-based control of quadrotor attitude. Mech. Syst. Signal Process. 2020, 135, 106358. [Google Scholar] [CrossRef]
- Eren, U.; Prach, A.; Koçer, B.B.; Raković, S.V.; Kayacan, E.; Açıkmeşe, B. Model predictive control in aerospace systems: Current state and opportunities. J. Guid. Control Dyn. 2017, 40, 1541–1566. [Google Scholar] [CrossRef]
- Labbadi, M.; Cherkaoui, M. Robust integral terminal sliding mode control for quadrotor UAV with external disturbances. Int. J. Aerosp. Eng. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Xuan-Mung, N.; Hong, S.K. Robust adaptive formation control of quadcopters based on a leader–follower approach. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419862733. [Google Scholar] [CrossRef] [Green Version]
- Ferdaus, M.M.; Pratama, M.; Anavatti, S.; Garratt, M.A.; Pan, Y. Generic evolving self-organizing neuro-fuzzy control of bio-inspired unmanned aerial vehicles. IEEE Trans. Fuzzy Syst. 2018, 28, 1542–1556. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Zheng, Z.; Sun, L.; Zhu, M. Saturated adaptive sliding mode control for autonomous vessel landing of a quadrotor. IET Control Theory Appl. 2018, 12, 1830–1842. [Google Scholar] [CrossRef]
- Xu, Q. Digital integral terminal sliding mode predictive control of piezoelectric-driven motion system. IEEE Trans. Ind. Electron. 2015, 63, 3976–3984. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, Y. An adaptive fault-tolerant sliding mode control allocation scheme for multirotor helicopter subject to simultaneous actuator faults. IEEE Trans. Ind. Electron. 2017, 65, 4227–4236. [Google Scholar] [CrossRef] [Green Version]
- Barghandan, S.; Badamchizadeh, M.A.; Jahed-Motlagh, M.R. Improved adaptive fuzzy sliding mode controller for robust fault tolerant of a quadrotor. Int. J. Control Autom. Syst. 2017, 15, 427–441. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, P.; Li, D.; Xu, M. Sliding mode prediction fault-tolerant control method based on whale optimization algorithom. Int. J. Innov. Comput. Inf. Control 2019, 15, 2119–2133. [Google Scholar]
- Xiao, L.; Sattarov, R.R.; Liu, P.; Lin, C. Intelligent Fault-Tolerant Control for AC/DC Hybrid Power System of More Electric Aircraft. Aerospace 2022, 9, 4. [Google Scholar] [CrossRef]
- Rabasa, J.A.; López-Estrada, F.R.; Gonzalez-Contreras, B.M.; Valencia-Palomo, G.; Chadli, M.; Perez-Patricio, M. Actuator fault detection and isolation on a quadrotor unmanned aerial vehicle modeled as a linear parameter-varying system. Meas. Control 2019, 52, 1228–1239. [Google Scholar] [CrossRef] [Green Version]
- Tang, P.; Zhang, F.; Ye, J.; Lin, D. An integral TSMC-based adaptive fault-tolerant control for quadrotor with external disturbances and parametric uncertainties. Aerosp. Sci. Technol. 2020, 109, 106415. [Google Scholar] [CrossRef]
- Gomez-Peate, S.; López-Estrada, F.R.; Valencia-Palomo, G.; Rotondo, D.; Guerrero-Sánchez, M.E. Actuator and sensor fault estimation based on a proportional multiple-integral sliding mode observer for linear parameter varying systems with inexact scheduling parameters. Int. J. Robust Nonlinear Control 2021, 25, 339–361. [Google Scholar]
- Patan, M.G.; Caliskan, F. Sensor fault-tolerant control of a quadrotor unmanned aerial vehicle. J. Aerosp. Eng. 2022, 236, 417–433. [Google Scholar] [CrossRef]
- Chen, F.; Jiang, G.; Wen, C. Sensor cascading fault estimation and control for hypersonic flight vehicles based on a multidimensional generalized observer. Int. J. Robust Nonlinear Control 2019, 2019, 3027–3041. [Google Scholar] [CrossRef]
- Du, D.; Jiang, B.; Shi, P. Sensor fault estimation and accommodation for discrete-time switched linear systems. IET Control Theory Appl. 2014, 8, 960–967. [Google Scholar] [CrossRef]
- Kolmanovskii, V.B.; Richard, J.P. Stability of some linear systems with delays. IEEE Trans. Autom. Control 1999, 44, 984–989. [Google Scholar] [CrossRef]
- Tao, H.; Paszke, W.; Rogers, E.; Yang, H.; Gałkowski, K. Finite frequency range iterative learning fault-tolerant control for discrete time-delay uncertain systems with actuator faults. ISA Trans. 2019, 95, 152–163. [Google Scholar] [CrossRef] [PubMed]
- Tong, S.; Yang, G.; Zhang, W. Observer-based fault-tolerant control against sensor failures for fuzzy systems with time delays. Int. J. Appl. Math. Comput. Sci. 2011, 21, 617–627. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.B.; Yang, G.H. Robust adaptive fault-tolerant tracking control of multiple time-delays systems with mismatched parameter uncertainties and actuator failures. Int. J. Robust Nonlinear Control 2015, 25, 2922–2938. [Google Scholar] [CrossRef]
- Gao, Z.; Breikin, T.; Wang, H. Reliable observer-based control against sensor failures for systems with time delays in both state and input. IEEE Trans. Syst. Man Cybern. Part A Syst. Humans 2008, 38, 1018–1029. [Google Scholar]
- Yang, P.; Guo, R.; Pan, X.; Li, T. Study on the sliding mode fault tolerant predictive control based on multi agent particle swarm optimization. Int. J. Control Autom. Syst. 2017, 15, 2034–2042. [Google Scholar] [CrossRef]
- Gao, Y.; Wu, L.; Shi, P.; Li, H. Sliding mode fault-tolerant control of uncertain system: A delta operator approach. Int. J. Robust Nonlinear Control 2017, 27, 4173–4187. [Google Scholar] [CrossRef]
- Abidi, K.; Xu, J.X.; Xinghuo, Y. On the discrete time integral sliding mode control. IEEE Trans. Autom. Control 2007, 52, 709–715. [Google Scholar] [CrossRef] [Green Version]
- Qu, S.; Xia, X.; Zhang, J. Dynamics of discrete_time sliding_mode_control uncertain systems with a disturbance compensator. IEEE Trans. Ind. Electron. 2013, 61, 3502–3510. [Google Scholar] [CrossRef] [Green Version]
- Pierezan, J.; Coelho, L. Coyote optimization algorithm: A new metaheuristic for global optimization problems. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; Volume 2018, pp. 1–8. [Google Scholar]



| Physical Meaning | Expression |
|---|---|
| Dynamic equation of X-axis | |
| Lift generated by the rotor F | |
| Actuator dynamics | |
| State space expression form of : |
| Physical Meaning | Value |
|---|---|
| Body mass | kg |
| The positive gain | N |
| Actuator bandwidth | rad/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, P.; Zhang, Z.; Geng, H.; Jiang, B.; Hu, X. Intelligent Discrete Sliding Mode Predictive Fault-Tolerant Control Method for Multi-Delay Quad-Rotor UAV System Based on DIECOA. Aerospace 2022, 9, 207. https://doi.org/10.3390/aerospace9040207
Yang P, Zhang Z, Geng H, Jiang B, Hu X. Intelligent Discrete Sliding Mode Predictive Fault-Tolerant Control Method for Multi-Delay Quad-Rotor UAV System Based on DIECOA. Aerospace. 2022; 9(4):207. https://doi.org/10.3390/aerospace9040207
Chicago/Turabian StyleYang, Pu, Zhiqing Zhang, Huiling Geng, Bin Jiang, and Xukai Hu. 2022. "Intelligent Discrete Sliding Mode Predictive Fault-Tolerant Control Method for Multi-Delay Quad-Rotor UAV System Based on DIECOA" Aerospace 9, no. 4: 207. https://doi.org/10.3390/aerospace9040207
APA StyleYang, P., Zhang, Z., Geng, H., Jiang, B., & Hu, X. (2022). Intelligent Discrete Sliding Mode Predictive Fault-Tolerant Control Method for Multi-Delay Quad-Rotor UAV System Based on DIECOA. Aerospace, 9(4), 207. https://doi.org/10.3390/aerospace9040207







