Optimization of Geostationary Orbit Transfers via Combined Chemical–Electric Propulsion
Abstract
1. Introduction
2. Materials and Methods
2.1. Dynamic Model
2.2. Optimal Control Theory
2.3. Steps of Solving Hybrid Transfer Problem
- Apply the ICEA algorithm to search the approximate solutions of the initial costate vector , the timing and magnitude of impulsive burn and numerical Lagrange multipliers to the high-thrust short-duration transfer problem .
- Take the approximate solutions of step 1 as the initial guess to provide the accurate solution of the high-thrust short-duration transfer problem . Go back to step 1 if it does not converge.
- Set and begin the thrust continuation process. Reduce the thrust by , i.e., . Employ the solution of the previous problem as an initial guess to solve the new problem . If it does not converge, reduce and repeat this step. Let if it converges.
- When , set and begin the transfer time continuation process. Increase the transfer time by , i.e., . Employ the solution of the previous problem as an initial guess to solve the new problem . If it does not converge, reduce and repeat this step. Let if it converges.
- When , output the desired solutions of the hybrid transfer problem .
3. Results
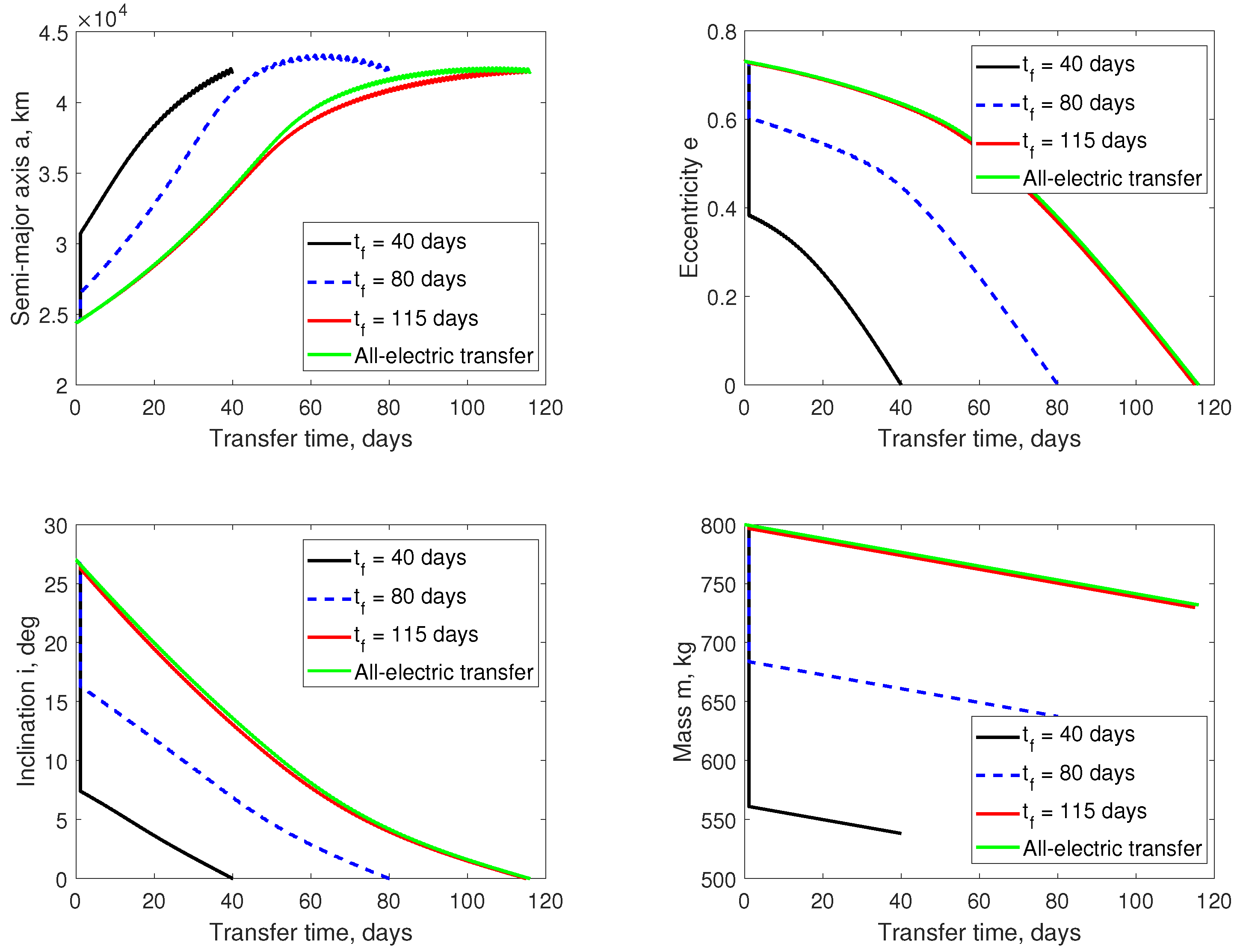
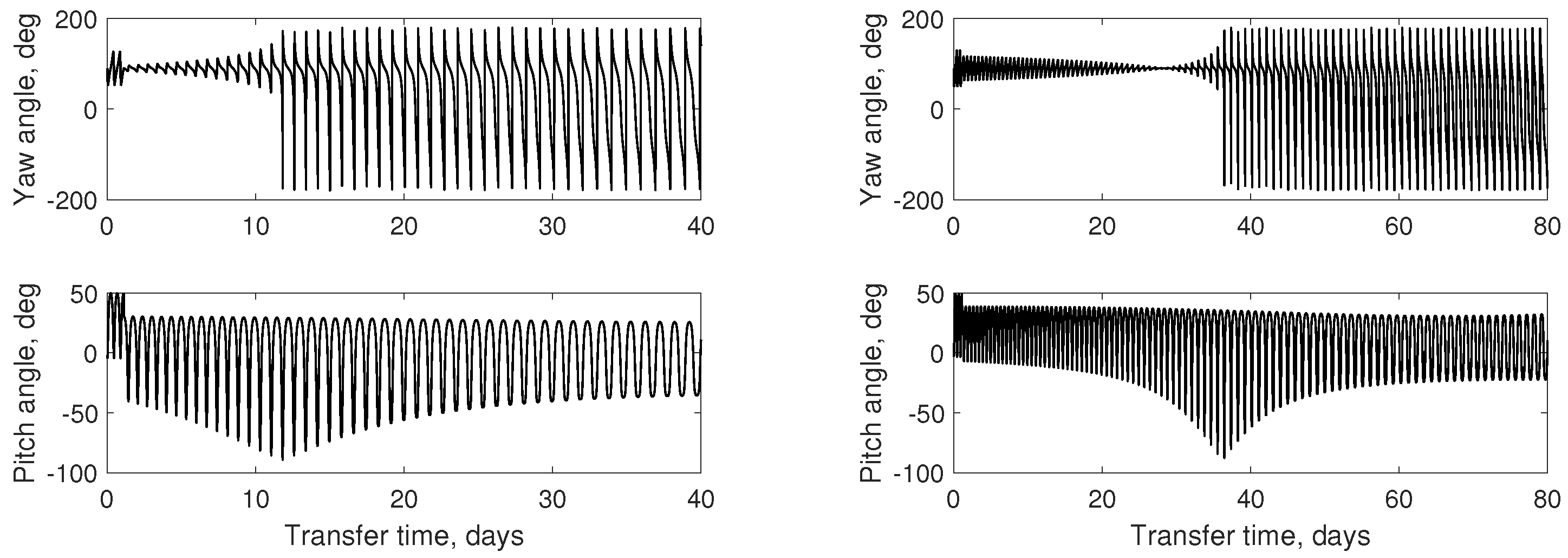
3.1. Solution of Hybrid Minimum-Fuel Hybrid Transfer
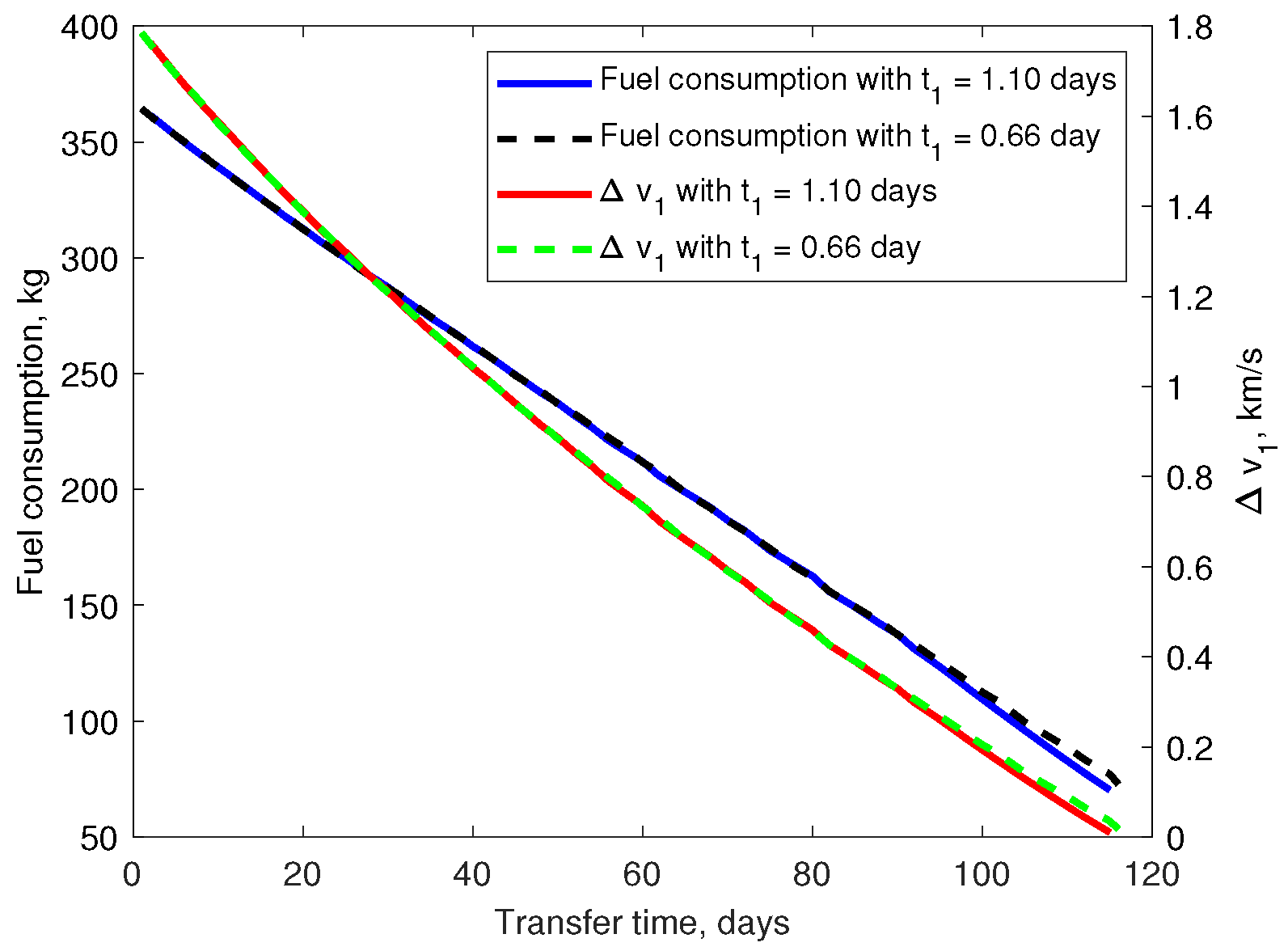
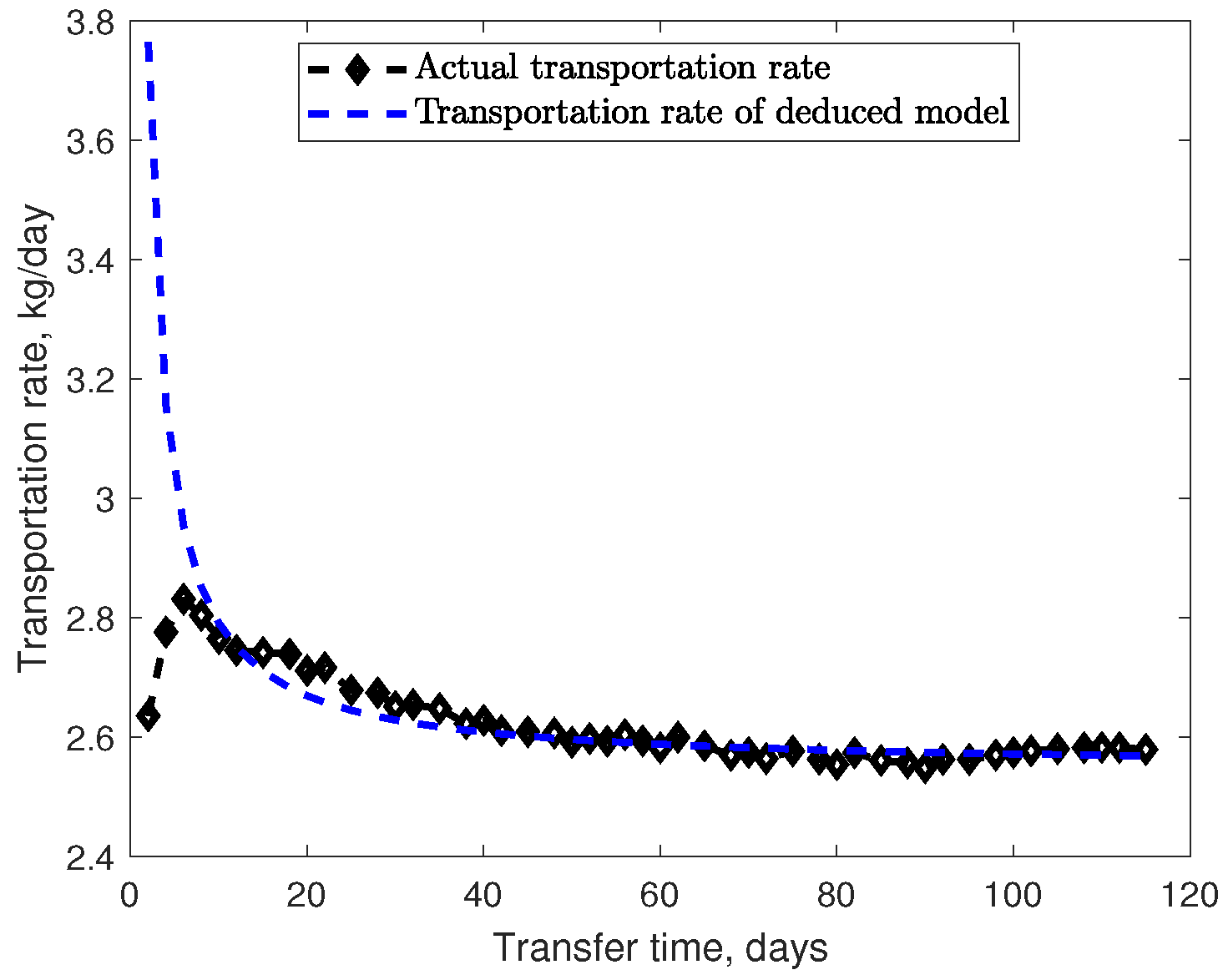
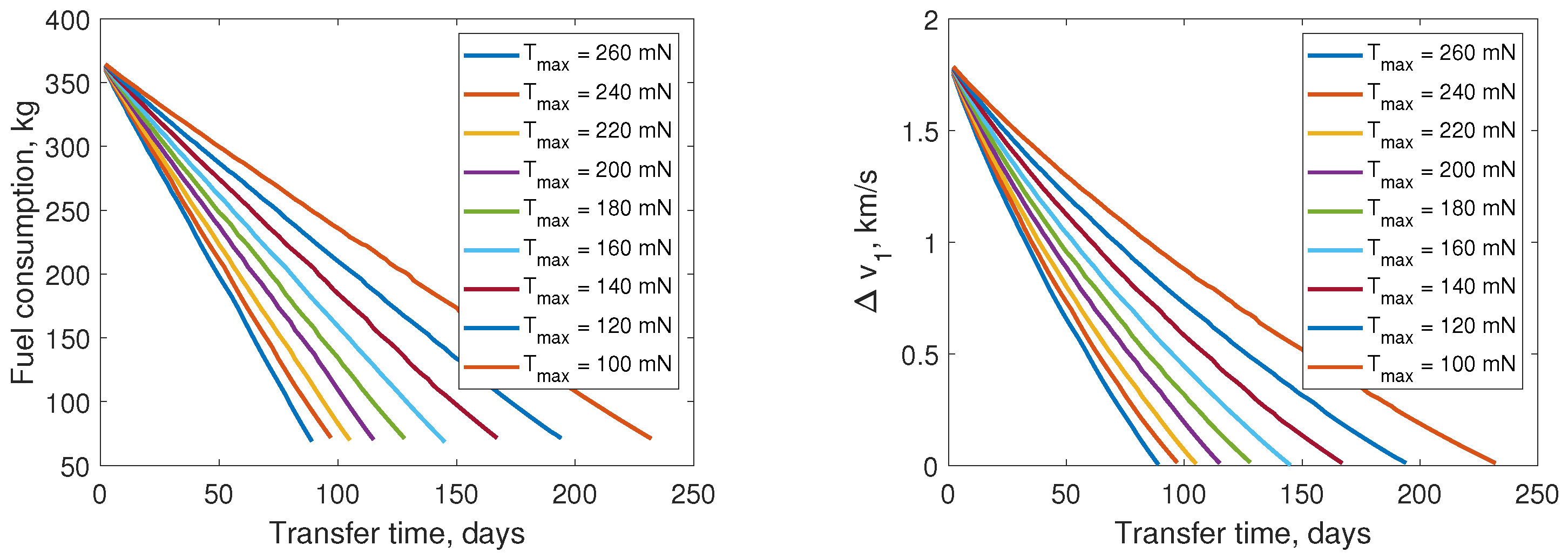
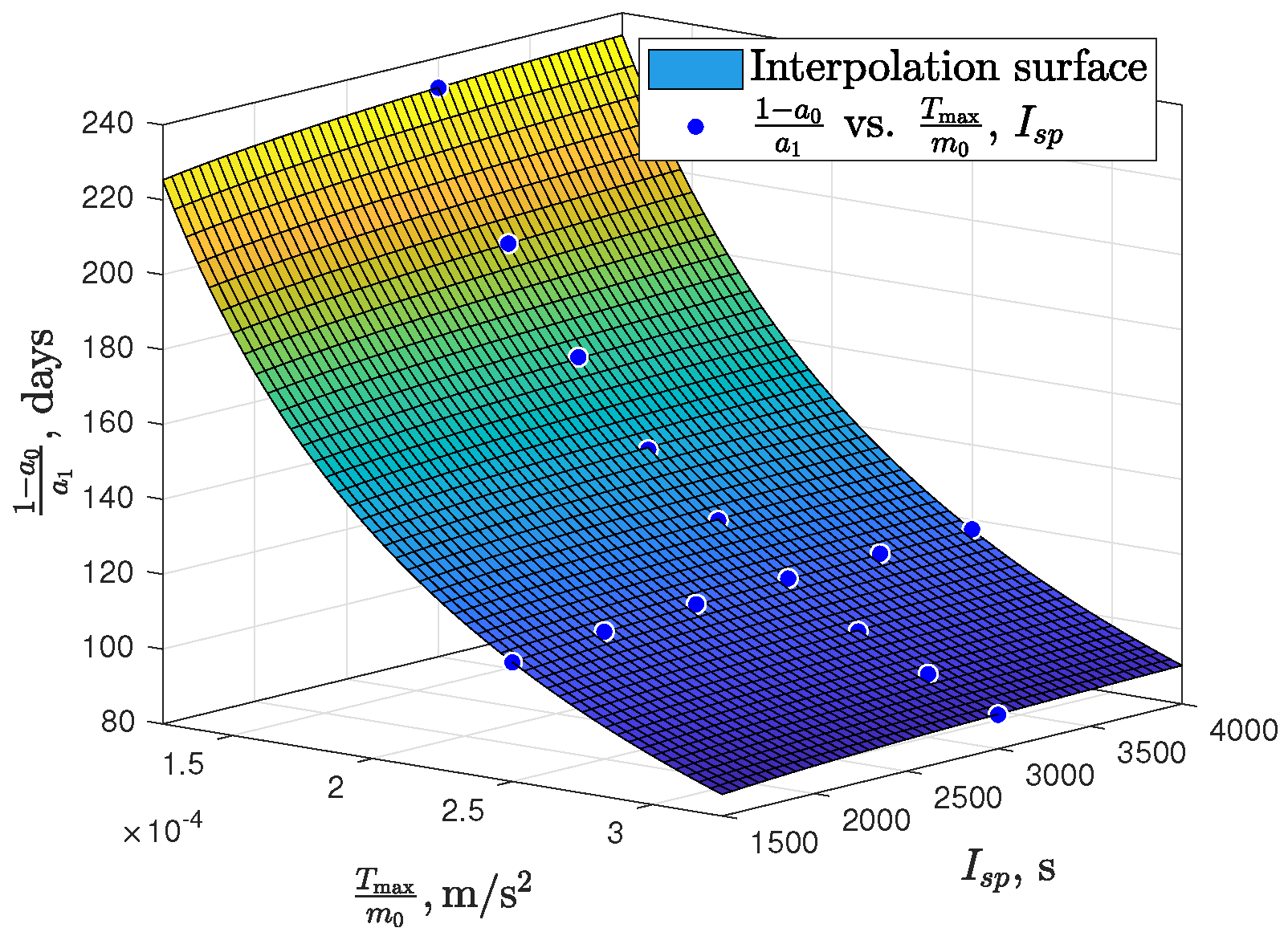
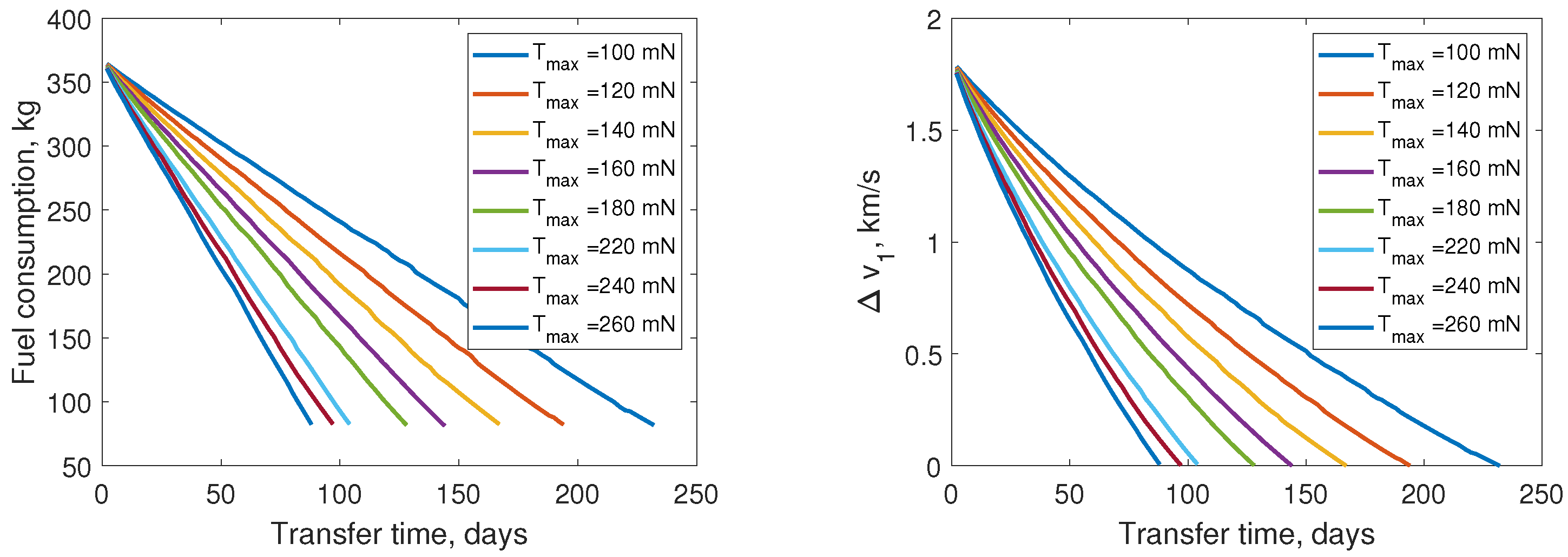
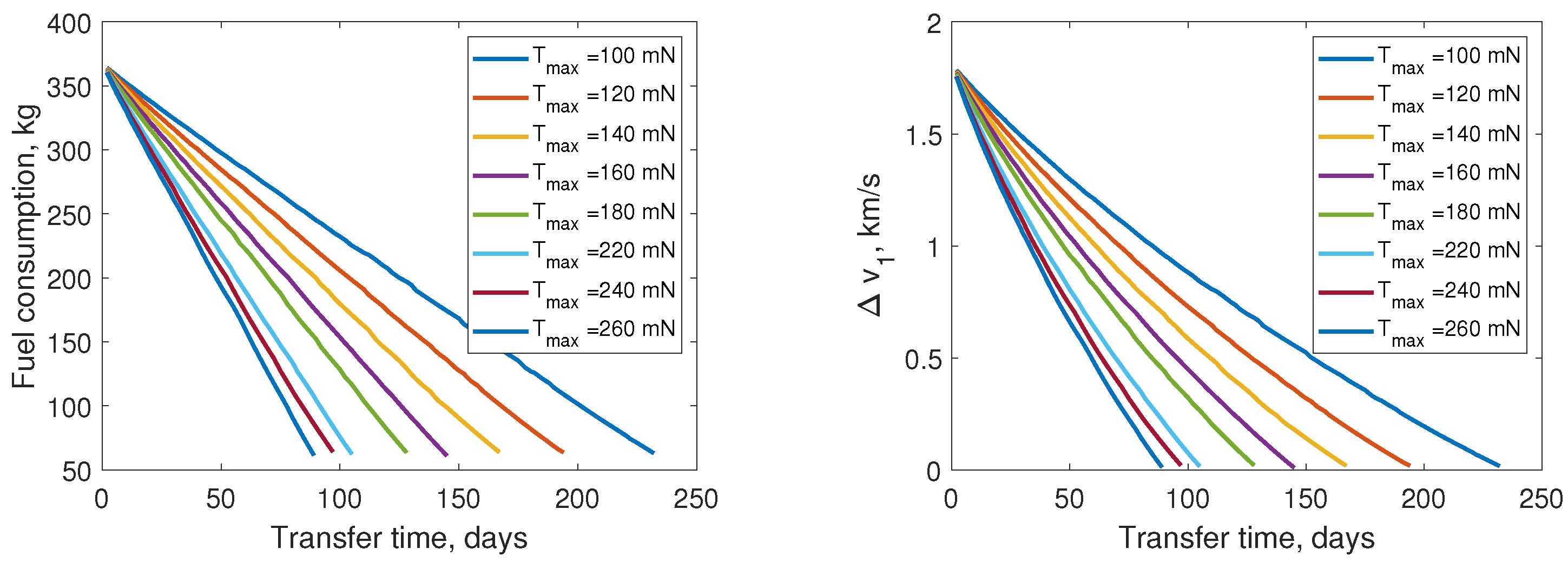
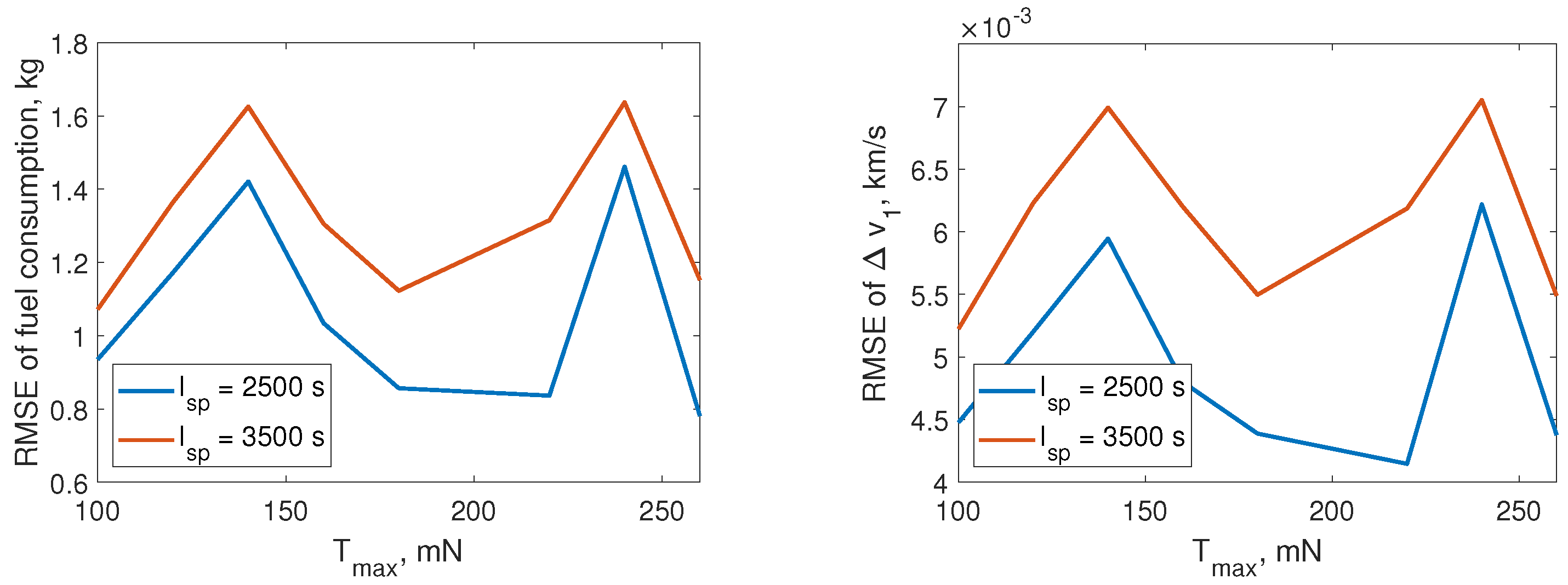
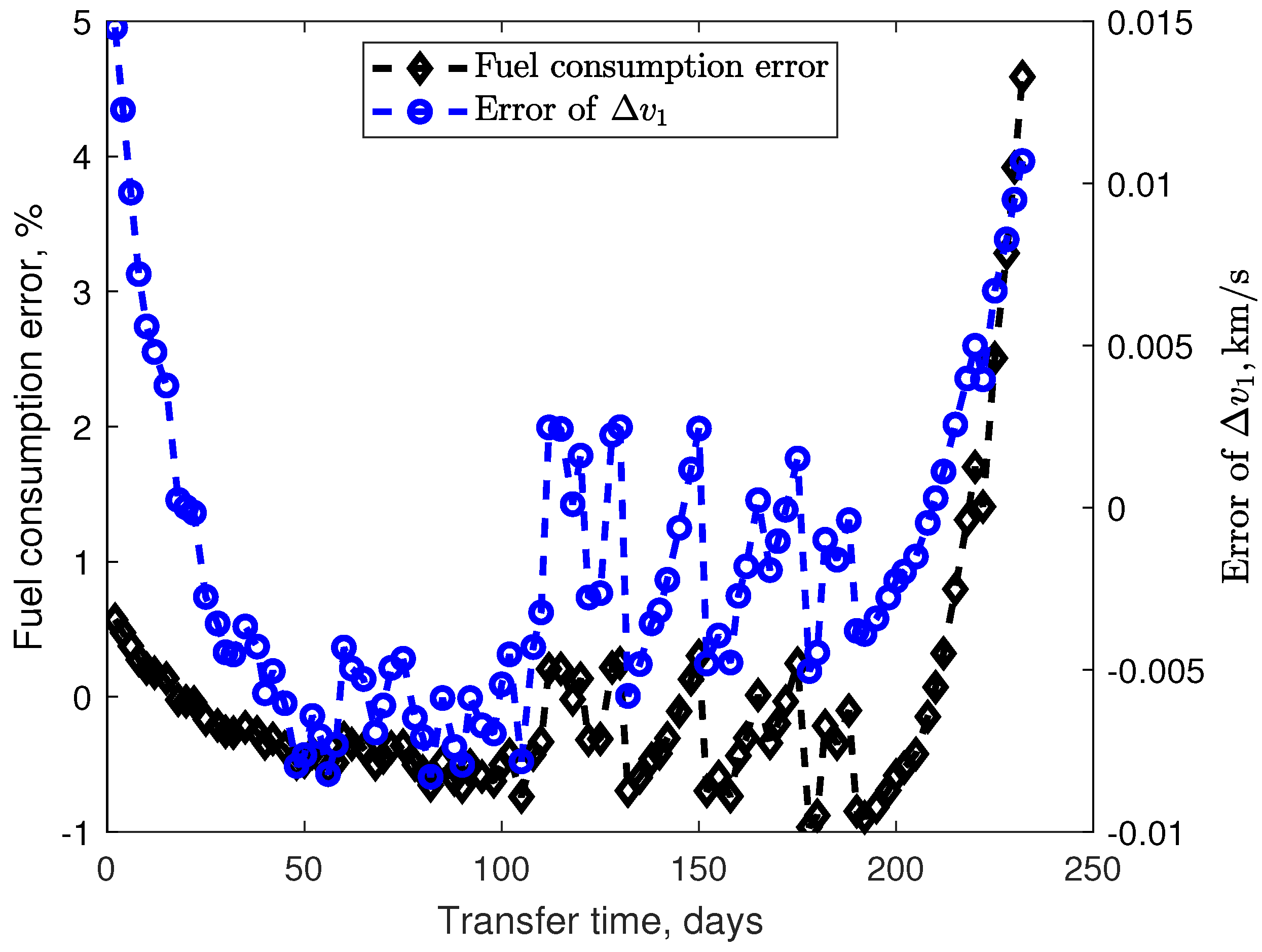
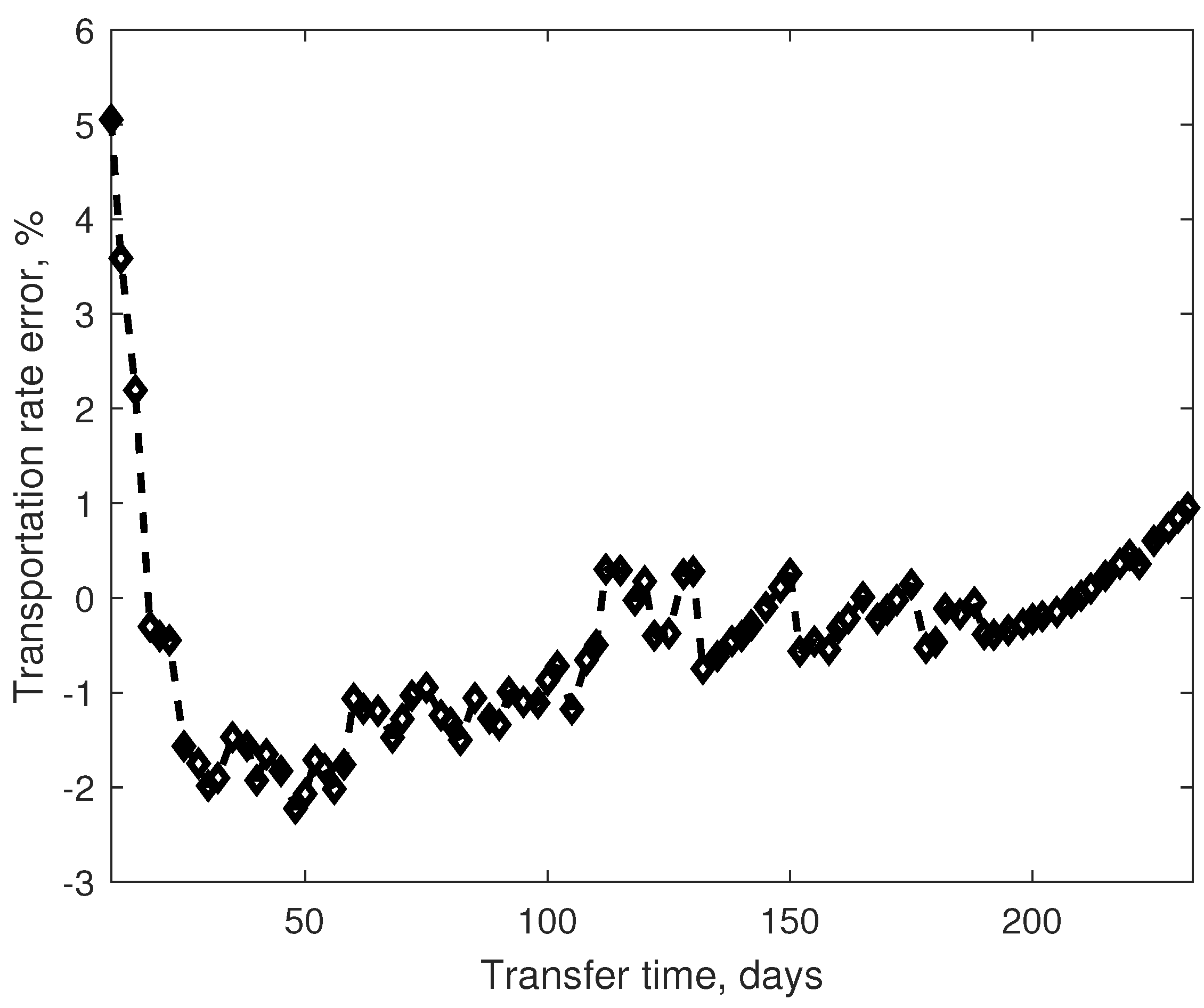
3.2. Performance of Hybrid Transfer with Various Low-Thrust Maximum Magnitude and Specific Impulse
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Martinez-Sanchez, M.; Pollard, J.E. Spacecraft electric propulsion-an overview. J. Propuls. Power 1998, 14, 688–699. [Google Scholar] [CrossRef]
- Yang, G. Direct optimization of low-thrust many-revolution earth-orbit transfers. Chin. J. Aeronaut. 2009, 22, 426–433. [Google Scholar] [CrossRef][Green Version]
- Scheel, W.A.; Conway, B.A. Optimization of very-low-thrust, many-revolution spacecraft trajectories. J. Guid. Control Dyn. 1994, 17, 1185–1192. [Google Scholar] [CrossRef]
- Dalin, Y.; Bo, X.; Youtao, G. Optimal strategy for low-thrust spiral trajectories using Lyapunov-based guidance. Adv. Space Res. 2015, 56, 865–878. [Google Scholar] [CrossRef]
- Hargraves, C.R.; Paris, S.W. Direct Trajectory Optimization Using Nonlinear Programming and Collocation. J. Guid. Control Dyn. 1987, 10, 338–342. [Google Scholar] [CrossRef]
- Haberkorn, T.; Martinon, P.; Gergaud, J. Low thrust minimum-fuel orbital transfer: A homotopic approach. J. Guid. Control Dyn. 2004, 27, 1046–1060. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G.; Bassetto, M. Optimal solar sail transfers to circular Earth-synchronous displaced orbits. Astrodynamics 2020, 4, 193–204. [Google Scholar] [CrossRef]
- Gao, Y.; Kluever, C. Low-Thrust Interplanetary Orbit Transfers Using Hybrid Trajectory Optimization Method with Multiple Shooting. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; Volume 2. [Google Scholar] [CrossRef]
- Ilgen, M.R. A hybrid method for computing optimal low thrust otv trajectories. Spacefl. Mech. 1994, 2, 941–958. [Google Scholar]
- Petropoulos, A.E. Simple Control Laws for Low-Thrust Orbit Transfers; Jet Propulsion Laboratory, National Aeronautics and Space Administration: Pasadena, CA, USA, 2003. [Google Scholar]
- Ilgen, M.R. Low thrust OTV guidance using Liapunov optimal feedback control techniques. Astrodynamics 1994, 85, 1527–1545. [Google Scholar]
- Bassetto, M.; Quarta, A.A.; Mengali, G.; Cipolla, V. Spiral trajectories induced by radial thrust with applications to generalized sails. Astrodynamics 2021, 5, 121–137. [Google Scholar] [CrossRef]
- Feuerborn, S.A.; Perkins, J.; Neary, D.A. Finding a way: Boeing’s all electric propulsion satellite. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint PropulsionConference, San Jose, CA, USA, 15–17 July 2013; p. 4126. [Google Scholar]
- Rovey, J.L.; Lyne, C.T.; Mundahl, A.J.; Rasmont, N.; Glascock, M.S.; Wainwright, M.J.; Berg, S.P. Review of multimode space propulsion. Prog. Aerosp. Sci. 2020, 118, 100627. [Google Scholar] [CrossRef]
- Oleson, S.R.; Myers, R.M.; Kluever, C.A.; Riehl, J.P.; Curran, F.M. Advanced propulsion for geostationary orbit insertion and north-south station keeping. J. Spacecr. Rocket. 1997, 34, 22–28. [Google Scholar] [CrossRef]
- Mailhe, L.M.; Heister, S.D. Design of a hybrid chemical/electric propulsion orbital transfer vehicle. J. Spacecr. Rocket. 2002, 39, 131–139. [Google Scholar] [CrossRef]
- Oh, D.Y.; Randolph, T.; Kimbrel, S.; Martinez-Sanchez, M. End-to-end optimization of chemical-electric orbit-raising missions. J. Spacecr. Rocket. 2004, 41, 831–839. [Google Scholar] [CrossRef]
- Jenkin, A. Representative mission trade studies for low-thrust transfers to geosynchronous orbit. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2004; p. 5086. [Google Scholar]
- Kluever, C.A. Optimal geostationary orbit transfers using onboard chemical-electric propulsion. J. Spacecr. Rocket. 2012, 49, 1174–1182. [Google Scholar] [CrossRef]
- Kluever, C.A. Designing transfers to geostationary orbit using combined Chemical–Electric propulsion. J. Spacecr. Rocket. 2015, 52, 1144–1151. [Google Scholar] [CrossRef]
- Morante, D.; Sanjurjo Rivo, M.; Soler, M. A survey on low-thrust trajectory optimization approaches. Aerospace 2021, 8, 88. [Google Scholar] [CrossRef]
- Hughes, S.P.; Qureshi, R.H.; Cooley, S.D.; Parker, J.J. Verification and validation of the general mission analysis tool (GMAT). In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, San Diego, CA, USA, 4–7 August 2014; p. 4151. [Google Scholar]
- Sauer, J.R.C. Optimization of multiple target electric propulsion trajectories. In Proceedings of the 11th Aerospace Sciences Meeting, Washington, DC, USA, 10–12 January 1973; p. 205. [Google Scholar]
- Walker, M.; Ireland, B.; Owens, J. A set modified equinoctial orbit elements. Celest. Mech. 1985, 36, 409–419. [Google Scholar] [CrossRef]
- Bryson, A.E. Applied Optimal Control: Optimization, Estimation and Control; CRC Press: Boca Raton, FL, USA, 1975. [Google Scholar]
- Fehlberg, E. Classical fifth-, sixth-, seventh-, and eighth-order Runge-Kutta formulas with stepsize Control. NASA Tech. Rep. 1968, R-287. [Google Scholar]
- Lei, H.; Xu, B.; Sun, Y. Earth–Moon low energy trajectory optimization in the real system. Adv. Space Res. 2013, 51, 917–929. [Google Scholar] [CrossRef]
- Caillau, J.B.; Gergaud, J.; Noailles, J. 3D geosynchronous transfer of a satellite: Continuation on the thrust. J. Optim. Theory Appl. 2003, 118, 541–565. [Google Scholar] [CrossRef]
- Pan, B.; Lu, P.; Pan, X.; Ma, Y. Double-homotopy method for solving optimal control problems. J. Guid. Control Dyn. 2016, 39, 1706–1720. [Google Scholar] [CrossRef]
- Moré, J.J.; Garbow, B.S.; Hillstrom, K.E. User Guide for MINPACK-1; Technical Report, CM-P00068642; Cern Libraries: Geneva, Italy, 1980. [Google Scholar]
- Powell, M.J. A hybrid method for nonlinear equations. In Numerical Methods for Nonlinear Algebraic Equations; Gordon and Breach: London, UK, 1970. [Google Scholar]
- Moré, J.J.; Cosnard, M.Y. Numerical solution of nonlinear equations. ACM Trans. Math. Softw. (TOMS) 1979, 5, 64–85. [Google Scholar] [CrossRef]
- Broyden, C.G. A class of methods for solving nonlinear simultaneous equations. Math. Comput. 1965, 19, 577–593. [Google Scholar] [CrossRef]
- Li, H.; Baoyin, H.; Topputo, F. Neural Networks in Time-Optimal Low-Thrust Interplanetary Transfers. IEEE Access 2019, 7, 156413–156419. [Google Scholar] [CrossRef]
- Graham, K.F.; Rao, A.V. Minimum-time trajectory optimization of multiple revolution low-thrust earth-orbit transfers. J. Spacecr. Rocket. 2015, 52, 711–727. [Google Scholar] [CrossRef]
- Yue, X.; Yang, Y.; Geng, Z. Indirect optimization for finite-thrust time-optimal orbital maneuver. J. Guid. Control Dyn. 2010, 33, 628–634. [Google Scholar] [CrossRef]
- Ramos Moron, N. Indirect Optimization of Electric Propulsion Orbit Raising to GEO with Homotopy. Master’s Thesis, Politecnico di Milano—School of Industrial and Information Engineering, Milan, Italy, 27 July 2017. [Google Scholar]




| () | e | ||||
|---|---|---|---|---|---|
| 3.82 | 0.731 | 27 | 0 | 0 | 0 |
| (Days) | (Days) | MinPack-1 | Hybrid | Discrete Newton | Broyden |
|---|---|---|---|---|---|
| 40 | 42 | 1.8 s 257.22 kg | 1.2 s 257.22 kg | 4.7 s 257.22 kg | 1.4 s 257.22 kg |
| 70 | 72 | 4.9 s 182.28 kg | 3.0 s 182.28 kg | 8.6 s 182.28 kg | 2.7 s 182.28 kg |
| 100 | 105 | 6.9 s 96.59 kg | 5.2 s 96.59 kg | 19.5 s 96.59 kg | 8.6 s 96.59 kg |
| −3.99577 | 0.03540 | −0.70065 | −0.98333 | −0.65100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Xu, B.; Li, X. Optimization of Geostationary Orbit Transfers via Combined Chemical–Electric Propulsion. Aerospace 2022, 9, 200. https://doi.org/10.3390/aerospace9040200
Yang S, Xu B, Li X. Optimization of Geostationary Orbit Transfers via Combined Chemical–Electric Propulsion. Aerospace. 2022; 9(4):200. https://doi.org/10.3390/aerospace9040200
Chicago/Turabian StyleYang, Shihai, Bo Xu, and Xin Li. 2022. "Optimization of Geostationary Orbit Transfers via Combined Chemical–Electric Propulsion" Aerospace 9, no. 4: 200. https://doi.org/10.3390/aerospace9040200
APA StyleYang, S., Xu, B., & Li, X. (2022). Optimization of Geostationary Orbit Transfers via Combined Chemical–Electric Propulsion. Aerospace, 9(4), 200. https://doi.org/10.3390/aerospace9040200






