Abstract
Aiming at the problem of autonomous decision making and trajectory planning (ADMTP) for launch vehicles under power failure conditions, the target degradation order strategy (TDOS) and the trajectory online planning method were studied in this paper. Firstly, the influence of power failure on the orbit-injection process was analyzed. Secondly, the TDOS was proposed according to the mission attribute, failure mode, and multi-payload combination. Then, an online planning method based on the adaptive target update iterative guidance method (ATU-IGM) and radial basis neural network (RBFNN) was proposed, where the ATU-IGM adopted the basic TDOS criterion for generating optimal orbit-injection samples and online guidance instructions, and the RBFNN was used for orbit-injection samples training and online generation of orbital missions. Finally, the comparative simulation analysis was performed under multi-failure conditions. The results showed that the TDOS proposed in this paper could meet the requirements of the mission decision making under different failures, target orbit types, orbit-injection methods, and payload compositions. The online trajectory-planning capability deviation was less than 5%, and the mission decision-making and trajectory-planning time were less than 10 ms. This study provides theoretical support for autonomous decision making and planning of space launch missions.
1. Introduction
With the increasing demand for launch vehicle missions, power system failures have become the main cause of launch vehicle mission failure [1]. Therefore, advanced launch vehicle technology with high reliability and failure tolerance has attracted extensive attention and research. Currently, launch vehicles are required to have omnidirectional sensing ability and a high degree of autonomous decision-making ability. The improvement of perception capability can be realized by distributed sensors and satellite communication technologies, and the fault information acquisition and the control system reconstruction have become possible with the development and maturity of the design technology of the asynchronous fault detection observer and the data-driven control technology, which can meet the requirements of the random system [2,3]; therefore, the autonomous decision making of flight missions and trajectory planning under power failure conditions becomes the major challenge in the development of launch technology. With the rapid development of machine learning, RBFNN and other machine-learning methods with powerful mapping capability have been gradually used to solve the trajectory-planning problem [4,5].
Launch vehicle ascent trajectory-planning methods are mainly divided into two categories, including analytical methods based on optimal control principles and numerical methods that transform and solve the problem parametrically. The iterative guidance method (IGM) was proposed and developed in the 1960s. The IGM has been applied successfully to the Saturn V launch vehicle of the U.S. and the Long March vehicles of China [6,7]. In references [8,9,10,11], an improved IGM can cope with more terminal constraints and achieve guidance accuracy of less than 10 m through an injection-point position update and shutdown strategy adjustment. Therefore, it can be said that the IGM has become one of the most important launch vehicle online planning methods. With the development of numerical methods, numerical methods such as particle swarm optimization, Gaussian pseudo-spectral, and convex optimization methods have been gradually introduced into launch vehicle trajectory planning.
Although the numerical methods have great potential for launch vehicle trajectory planning, issues still affect its engineering applications, such as algorithm convergence and computational efficiency. For example, in the literature [12,13], the Gaussian pseudo-spectral method was used to discretize the trajectory-planning problem based on the optimal control expression for the ascent section of the launch vehicle. Although the initial guessing technique and the homogeneous technique were adopted to improve the algorithm’s convergence, it still could not meet the demand of real-time trajectory online planning under failures or large disturbance conditions. In the literature [14], the orbit-injection problem was transformed into a series of simple convex subproblems by convex optimization, which were solved step by step by serial iterative methods. Although this method can deal with more complex constraints, the number of discrete points and the trust domain’s setting will affect the algorithm’s accuracy and convergence under different working conditions. Moreover, the existing equipment on the launch vehicle cannot bear the computation load of the iterative solution of continuum subproblem in the convexity of sequence. Therefore, to ensure the algorithm’s reliability and timeliness, an improved ATU-IGM is adopted for the online planning of trajectories based on mission parameters.
As of now, there has been little research on launch vehicle orbital mission decision making. Most studies are concentrated on the decision optimization of the upper stage orbit transfer of launch vehicles by using optimization algorithms and the determination of optimal orbit in the original target orbit plane. A two-particle hierarchical optimization framework for the multi-pulse orbit transfer of spacecrafts was investigated in the literature [15]. The literature [16] used various optimization methods such as genetic algorithms and gradient optimization algorithms within a multidisciplinary optimization platform to optimize the payload quality and launch cost involved in launch missions. Although numerous scenarios in actual launch missions were considered, the orbit mission under power failure conditions could still not be reconfigured. The literature [17] used a joint-convex optimization method to optimize the orbit mission and trajectory under power failures, with high planning accuracy and timeliness. In this research, selecting the initial value of the target orbital elements and prioritizing the orbit height before correcting the orbital position deviation are of great engineering significance. However, the research method still has some application limitations because only simple orbit shapes are considered, and the properties of the target orbit, the orbit-injection mode, and the multi-payload combination are not studied.
The main innovations of the method proposed in this paper are as follows:
- (1)
- The mission decision-making model and trajectory online planning method were creatively put forward to meet the requirements of the launch vehicle’s different mission attributes, failure modes, and multi-payload combinations.
- (2)
- The TDOS was designed to adapt to multiple mission modes, including ① multiple target orbit types: low-inclination LEO, SSO, and elliptical orbit; ② different orbit-injection modes: direct orbiting and transfer orbiting; ③ different payload compositions: integral and detachable.
- (3)
- The autonomous mission decision-making model based on RBFNN was proposed to meet the requirements of mission diversity, rapidity of the decision-making process, and accuracy of decision-making results.
- (4)
- The online trajectory-planning method was presented based on the TDOS and TAU-IGM, which had the characteristics of high precision and rapidity.
Aiming at the ADMTP problem of launch vehicles under the power system failure, this paper proposes the TDOS that can meet the requirements of different mission attributes, failure modes, and multiple payload combinations and puts forward an autonomous mission decision-making and trajectory online planning model based on TAU-IGM and RBFNN. Firstly, a launch vehicle motion model considering power system failure is established, and the influence of the failure mode is briefly analyzed; secondly, the TDOS, which can better meet the requirements of engineering applications, is proposed by analyzing different orbit types, injection modes, and multi-payload combinations. Moreover, the online trajectory-planning method based on the ATU-IGM and RBFNN is studied to meet the timeliness requirement of online mission decision making and trajectory planning. When offline, the ATU-IGM and the TDOS are used to generate failure samples for RBFNN training; when online, the trained decision model of the RBFNN is used to generate mission target parameters and supply the ATU-IGM to complete online trajectory planning. Finally, the effectiveness of the method is analyzed by simulation experiments.
2. Motion Model and Failure Effect
The launch vehicle power system consists of turbopumps, combustion chambers, piping, valves, and other important parts. Common power failures include turbopump failure, thrust chamber failure, piping and valve failure, etc. Since the generation of all these faults reduces engine thrust, the power failures can be equivalented to engine thrust loss.
This paper establishes the kinetic equations in the launch inertial coordinate system [18] (the origin is the launch point; the axis is in the horizontal plane of the launch point, pointing in the aiming direction; the axis points upward, perpendicular to the horizontal plane of the launch point; the axis and the other two axes constitute a right-handed system, and the coordinate system remains motionless in inertial space).
where denote the position and velocity vector of the launch vehicle, respectively; denotes the gravitational acceleration vector; is the sea level gravitational acceleration value; denotes the aerodynamic vector; is the equivalent power system failure factor; denotes the engine thrust vector; is the launch vehicle mass; is the second consumption; is the fuel-specific impulse.
The injection stage of new-generation launch vehicles usually has a secondary switching ability to adapt to more complex missions. However, different failure modes have different influences on the secondary switching ability of launch vehicle engines, and mission requirements and engine performance will jointly determine the injection mode of launch vehicles. For example, in the event of turbopump wear failure, speed drop failure, or partial engine failure, the remaining normal parts of the engine and even the affected engine itself can still switch on and off again. When fire and thrust chamber failure occurs, the engine should be shut down immediately and not allowed to rework. When the turbine pump bearings are damaged, the opening of pipes and valves is not enough, and the closing is not strict, the engine can continue to work in the current mode to avoid the deterioration of the fault or failure to start up when restarted. In addition to causing decreased engine thrust, the different failure modes will also affect its ability to perform the orbital transfer. Therefore, the authors artificially divided the launch vehicle orbit-injection mode under power system failure into direct orbiting and transfer orbiting.
The target orbit is usually described using the orbital elements, including semimajor axis , eccentricity , inclination , longitude of the ascending node , argument of periapsis , and true anomaly . Among them, and determine the shape of the orbit, , , and determine the spatial position of the orbit, and determines the position of the vehicle in orbit. When the target orbit is circular, the definitions of the argument of perigee and true anomaly are meaningless, and the geocentric magnitude angle formed between the ascending nodal line and the geocentric vector of the injection point has physical significance in any case, which can be used to describe the target orbit. The target orbit can be described as follows [19]:
where denotes the geocentric gravitational constant; , , and denote the three components of .
Constraints on the altitudes of perigee and apogee of the target orbit are required to ensure the safety and mission viability of the payload in the target orbit:
where is the perigee altitude of the target orbit; is the minimum safe altitude, which is set to 110 km in this paper; is the altitude of the failure point; is the height adjustment margin, which is set to 5 km in this paper.
The launch vehicle flies at a programmed angle in the first stage at a low altitude, which is influenced by the atmosphere, so there are limited flight adjustment measures when the launch vehicle power system failure occurs. In contrast, the launch vehicle flies at a higher altitude in the second flight stage, where the influence of aerodynamic forces can usually be ignored, and there is more room for adjustment when the power system failure occurs. Therefore, the main flight stages studied are the secondary and higher vacuum flight phases.
3. Target Degradation Strategy (TDOS)
The TDOS relies on the injection capability judgment (ICJ), which is proposed to judge the reachability of the original orbit by whether the remaining flight time calculated by the ATU-IGM is greater than the maximum working time supported by the remaining fuel. When the launch vehicle does not have the flight capability of the original orbit, the orbit-injection strategy based on the target degradation rule is used to adjust the orbit parameters to reduce the mission loss caused by the power failure.
The basic degradation methods are divided into two categories: the payload reduction method and the energy reduction method. A payload reduction method refers to a launch mission carrying multiple payloads with the same or similar function, but there is only a weak dependence between these payloads. After the fairing is thrown off, part of the payload can be released in advance so that the remaining payloads can enter the predetermined target orbit or safe orbit. An energy reduction method refers to matching the remaining flight capability of the launch vehicle after the power failure by reducing the energy required for the target orbit. In the second stage of flight, due to the smaller thrust of the launch vehicle itself, the thrust-to-weight ratio after a power failure is even smaller, the impact of the payload reduction method on the acceleration effect and climbing efficiency of the subsequent flight stages of the launch vehicle is not significant, and if the payload can be kept at an altitude lower than the original target orbit but higher than the minimum safety orbit, the mission can be saved to the greatest extent by the payload’s orbit change capability or space rescue. Therefore, an energy reduction method is normally preferred over a load reduction method. The schematic diagram of the target degradation rule based on the orbit-injection strategy is shown in Figure 1.
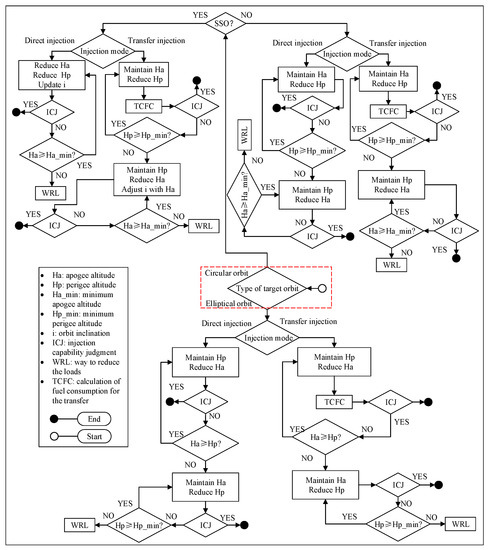
Figure 1.
Orbit-injection strategy based on target degradation rules.
3.1. Energy Reduction Method
The energy of the target orbit can be described as follows [19]:
This paper downgrades the perigee altitude and apogee altitude of the target orbit to adjust the eccentricity and semimajor axis (energy).
where and are the perigee altitudes of the target orbit from the and degradations, respectively; and are the apogee altitudes of the target orbit from the and degradations, respectively, the mean radius of the Earth , and the altitude degradation gradient . The perigee and apogee altitudes of the target orbit need to be degraded at the same time according to the failure and mission attributes.
Although transfer orbiting is more fuel-efficient than direct orbiting, the final orbiting approach still needs to be selected according to the mission and engine failure attributes. When the power system failure mode requires the launch vehicle to minimize the orbit-injection time or the mission requires a fast response, the launch vehicle should adopt the direct orbiting method; otherwise, the launch vehicle adopts the transfer orbiting method. In this study, the elliptical orbit with the apogee altitude equal to the perigee altitude of the target orbit and the perigee altitude equal to the minimum safety height is selected as the transfer orbit.
- (1)
- Downgrading strategy when the original target mission is a circular orbit
First, it is necessary to determine whether the original target orbit is a sun-synchronous orbit (SSO).
- (a)
- SSO downgrade strategy
In the case of an SSO, it is necessary to adjust the target orbit inclination according to the relationship between the SSO orbit inclination and orbit altitude while adjusting the orbit altitude [20].
The mission degradation schematic diagram of SSO is shown in Figure 2.
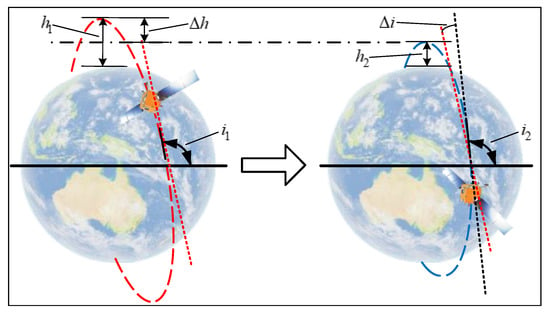
Figure 2.
Schematic diagram of sun-synchronous orbit degradation.
Specifically: ① when adopting the direct orbiting approach, the perigee altitude and apogee altitude need to be reduced simultaneously, and the target orbit inclination needs to be updated simultaneously; when it is reduced to , if the launch vehicle still does not have the orbit-injection capability, the payload reduction approach will be adopted; ② when adopting the transfer orbiting approach, it is assumed that the injection occurs at the apogee. First, the apogee altitude is maintained, the perigee altitude is reduced, and the fuel consumption of the transfer process is calculated. When the perigee altitude is reduced to , if the launch vehicle still does not have the capability of transfer orbit, it needs to maintain the minimum perigee altitude, reduce the apogee altitude, and update the target orbit inclination according to the change of apogee altitude. When the apogee altitude drops to , if the launch vehicle still cannot enter the orbit, it will switch to the payload reduction mode.
- (b)
- Non-SSO circular orbit degradation strategy
① When the direct orbiting approach is adopted, the perigee altitude should be lowered for the analysis of the orbiting capability; when it is lowered to , if the launch vehicle still does not have the orbiting capability, the minimum perigee altitude is maintained, and the apogee altitude is lowered; when it is lowered to , if the launch vehicle still does not have the orbiting capability, the payload lowering approach will be adopted. ② When the transfer orbiting approach is adopted, it is assumed that the launch vehicle will be orbited at the apogee of the transfer orbit. When the perigee altitude is reduced to , if the launch vehicle still cannot enter the orbit of the transfer orbit, the minimum perigee altitude is maintained, and the apogee altitude is reduced; when the apogee altitude is reduced to , if the launch vehicle still cannot enter the orbit of the orbit, the reduced payload mode will be adopted.
- (2)
- Downgrading strategy when the original target mission is an elliptical orbit
- (a)
- When the direct orbiting mode is adopted, priority should be given to maintaining the perigee height of the target orbit and reducing the apogee height so that the payload can enter the degraded orbit near the perigee of the original target orbit for secondary orbital transfer of the payload; when it is lowered to if the launch vehicle still does not have the orbit-injection capability, the minimum apogee altitude is maintained, and the perigee altitude is lowered; when the perigee altitude is lowered to , if the launch vehicle still cannot enter the orbit for the transfer orbit, it will switch to the payload drop mode. Since the launch vehicle has a high flight altitude in the second stage and the altitude adjustment margin is reserved, there will be no situation where the apogee altitude after degradation is less than the perigee altitude at the last degradation.
- (b)
- When the transfer orbiting approach is adopted, the perigee altitude of the target orbit is maintained, the apogee altitude is lowered, the fuel consumption for orbit transfer is calculated, and the launch vehicle’s orbiting capability is judged; when it is lowered to if the launch vehicle still does not have the orbiting capability of the target orbit, the minimum apogee altitude is maintained, the perigee altitude is lowered, the fuel consumption for orbit transfer is calculated again, and the launch vehicle’s orbiting capability is judged; when the perigee altitude drops to , if the launch vehicle still does not have the orbit-injection capability, it will switch to the payload reduction mode.
3.2. Payload Reduction Method
When the minimum orbit-injection requirement cannot be achieved by taking the energy reduction approach or when the orbit energy reduction will seriously affect the payload system function, the launch vehicle will be forced to abandon part of the payload under power failure.
Usually, multiple payloads carried on the same mission are different, and for the simplification of the problem, the mass reduction at each payload drop is assumed to be , and the payload mass of the launch vehicle after load drops can be described as:
where denotes the total mass of the payload after degradation; denotes the initial mass of the payload; denotes the number of times the maximum payload is degraded.
Considering the altitude degradation gradient in the energy reduction method and the mass degradation gradient in the payload reduction method, the capacity generated by the mission decision making will be no less than the actual optimal capacity.
4. Trajectory-Planning Method
The flight status and the TDOS of the failure point can provide the direction of mission degradation when the failure occurs, and the ATU-IGM can determine the target orbit-injection capability of the launch vehicle after each degradation step. Therefore, the combination of the ATU-IGM and the TDOS can be used to determine the launch vehicle’s orbit-injection ability under different failures. Then, an effective and sufficient decision-making sample can be obtained by traversing the failure states. On this basis, the RBFNN can train the decision-making samples to obtain a decision-making model under power failures for online trajectory planning of launch vehicles. When the launch vehicle carries out mission online planning under failure conditions, the optimal orbital elements can be obtained from the flight status, the failure information, and the TDOS. Finally, the ATU-IGM is used to complete the online trajectory planning of the mission. The method proposed in this paper can enter the enabled state at the time of fault because it can judge the carrying capacity in real time through the fault information and decide whether to re-plan the mission and trajectory independently.
For the generation of failure samples, the ATU-IGM only needs to obtain the remaining flight time required to enter the target orbit and obtain the maximum flight time of available fuel during transfer by calculating fuel consumption to determine whether the launch vehicle has enough fuel for the target orbit. The ATU-IGM needs to calculate the complete flight trajectory for online trajectory planning and give real-time guidance. Due to the limitation of article length, the RBFNN section is not described in this paper. In summary, the launch vehicle trajectory-planning process under power failures is shown in Figure 3.
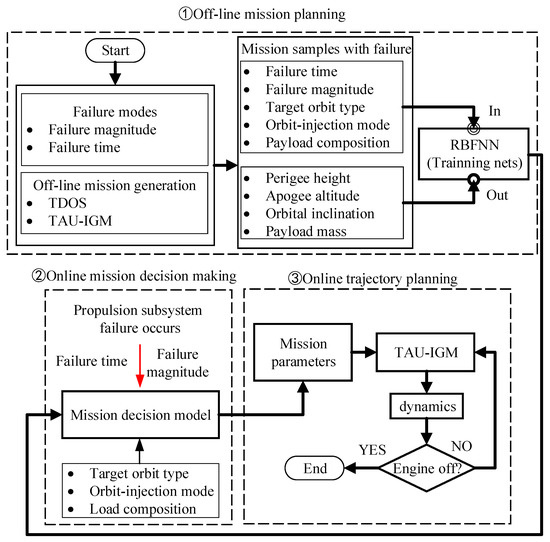
Figure 3.
Launch vehicle trajectory-planning method.
4.1. RBFNN Mission Decision-Making Model
Using the approximation ability of RBFNN for any unknown nonlinear function, this paper uses RBFNN for the training of post-fault mission samples and the generation of online mission decision-making models. Euclidean radial basis function is adopted to construct RBFNNs activation functions [2].
where is the input, is the center of the kernel function of the neuron in the hidden layer, and is the width parameter of the function.
The output of RBFNN is:
where is the weight coefficient from the -th neuron in the hidden layer to the -th output of the output layer; is the number of neurons in the hidden layer.
The number of input nodes is six, and the input attribute vectors are fault moment, fault magnitude, whether the target orbit is circular, whether the target orbit is an SSO, entry mode, and payload composition form. The number of output nodes is three. The output label vectors are perigee, apogee, and payload mass. The OLS algorithm can obtain the number of neurons and weight coefficients of the hidden layer. The mission decision-making samples generated offline in the previous paper are divided into training and test sets according to the ratio of 80% versus 20%, and the mission decision-making model is obtained by neural network training using RBFNN. When used online, the mission decision-making results under the corresponding fault conditions can be obtained according to the RBFNN input attributes at the fault moment for online trajectory planning by the ATU-IGM.
4.2. Calculation of Fuel Consumption during Transfer (TCFC)
When the launch vehicle adopts the transfer orbiting mode after the power system failure occurs, the fuel consumption from the transfer orbit to the target orbit needs to be calculated and set aside. The capacity of the launch vehicle to enter the target orbit is characterized by the flight capability of the launch vehicle entering into the transfer orbit with the remaining fuel. The velocity pulse is used to enter the target orbit when the launch vehicle flies to the apogee of the transfer orbit, and the velocity increment can be expressed as:
where and represent the perigee altitude and apogee altitude of the transfer orbit, respectively.
The fuel consumption corresponding to the velocity increment when adopting the transfer orbiting approach can be solved iteratively by Qi’s formula, and the solution process is shown in Figure 4.
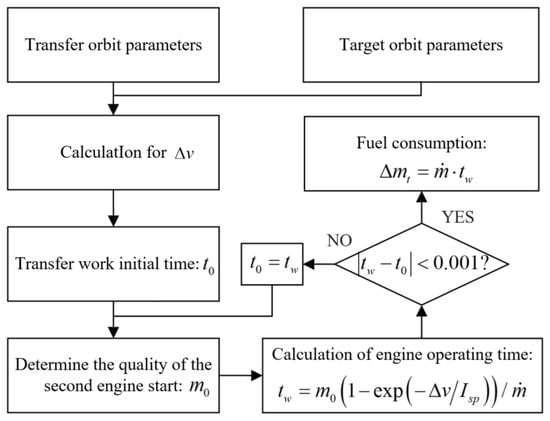
Figure 4.
Transfer orbit fuel consumption calculation.
4.3. Adaptive Target Update Iterative Guidance Method (ATU-IGM)
The ATU-IGM is a trajectory online planning method specially designed for mission target degradation based on the IGM. The idea of the adaptive target updating strategy (ATU) is similar to the iterative learning control (ILC), that is, using the previous result information to modify the system input to achieve more accurate control of the target task [21]. The ATU-IGM obtains the baseline mission target parameters by the TDOS at sample generation or the RBFNN at online planning; meanwhile, the ATU-IGM determines the spatial position of the target orbit () using the flight state at failure point and failure parameters; then, TAU-IGM adaptively adjusts the launch vehicle’s injection position in orbit according to the predicted terminal position deviation.
When the power system failure occurs in the secondary flight segment, the launch vehicle is already in the flight plane determined by the launch point and launch direction, so the orbital inclination and longitude of the ascending node determined by the state of the failure point can be used as the target orbital inclination and longitude of the ascending node after the failure occurs.
where are the position vector and velocity vector of the failure point, respectively, is the orbital angular momentum per unit mass, and , , and are the components.
As the engine thrust will decrease after the failure occurs, the geocentric amplitude angle of the launch vehicle entering the target orbit increases, and the initial value of the increased target orbit geocentric amplitude angle can be given by the failure factor . Although the geocentric amplitude angle can be determined autonomously by the ATU-IGM, a more reasonable initial value of the geocentric amplitude angle is still needed. Let the geocentric amplitude angle corresponding to the failure point state be and the geocentric angle between the failure point and the original target orbit-injection point be , the initial value of the target orbit geocentric amplitude angle after the failure occurs is:
According to the principle of optimal control, the analytical solution of iterative guidance in the coordinate guidance system [9] can be written as Equation (13):
where and are the primary attitude angles used to ensure terminal velocity, and , , , and are coefficients of the secondary attitude angles for terminal position deviation correction, which can be expressed as follow [11]:
Therefore, the predicted terminal position deviation can be obtained from the target point position in the direction and the current point state (, ).
The ATU-IGM updates the position of the injection point to eliminate the terminal position deviation. The original target point is marked as , and the updated target point is marked as . The parallel line of the axis is made through the point and intersects with the semimajor axis at the point . The auxiliary line perpendicular to the axis is made through the point and intersects the axis at the point . The initial true anomaly is ; is the change amount of the true anomaly before and after updating. The above geometric relationship is shown in Figure 5.
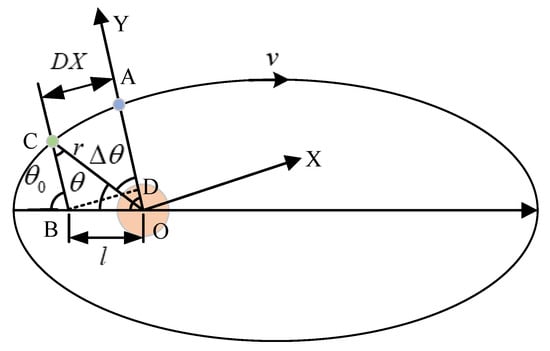
Figure 5.
Schematic diagram of the adaptive target update algorithm.
The orbital dynamics can be described as Equation (18):
Equation (18) can be expanded as Equation (19):
Assuming , is a small amount in a single guidance cycle, which can be obtained by Equation (20):
Based on the transformation relationship between the orbital elements and the state quantity, the updated coordinate components of the target orbit-injection point can be calculated as Equation (21):
5. Results
5.1. Simulation Conditions
In this paper, based on the Long March 7 launch vehicle, the overall parameters of the launch vehicle for the required simulation experiments were obtained through reasonable adjustment of the overall parameters, and the main parameters are listed in Table 1.

Table 1.
General parameters of the launch vehicle.
The list of parameters for designing a standard mission is shown in Table 2.

Table 2.
Standard mission.
Among the three standard mission sets, the SSO mission has a capacity of 6.50 t, the elliptical orbit mission has a capacity of 7.50 t, and the low-inclination LEO mission has a capacity of 9.00 t. The following four sets of failure conditions are based on the mission attributes and failure modes, as shown in Table 3.

Table 3.
List of fault conditions.
5.2. Feasibility Analysis of Mission Decision Making
The training results of the mission decision-making model using RBFNN are shown in Figure 6.
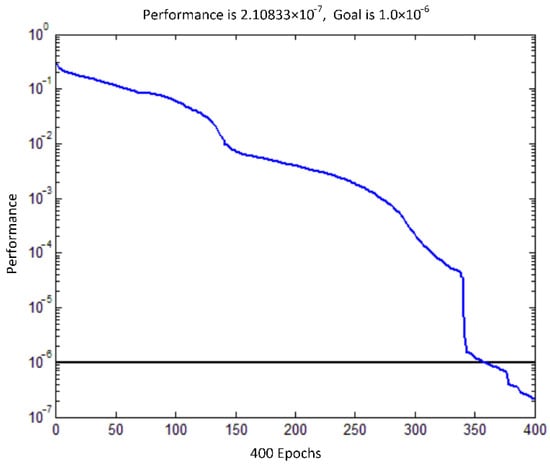
Figure 6.
RBFNN training residual curve.
For the given four groups of fault cases, the mission decision making and trajectory planning are performed using the trained RBFNN and the ATU-IGM, and the simulation results are obtained as shown in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11.
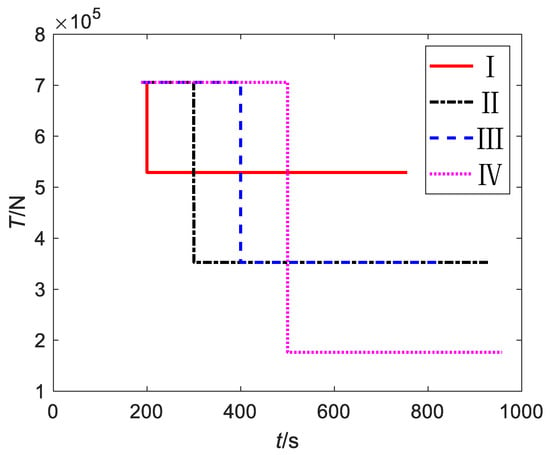
Figure 7.
Engine thrust.
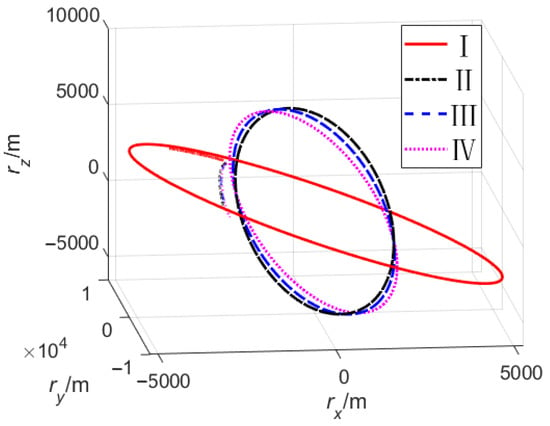
Figure 8.
Flight trajectory and terminal orbit.
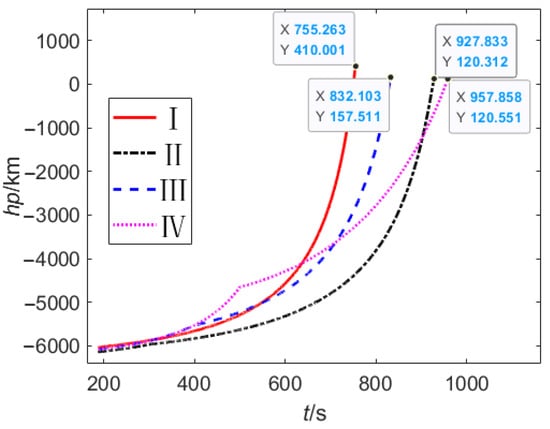
Figure 9.
Perigee altitude.
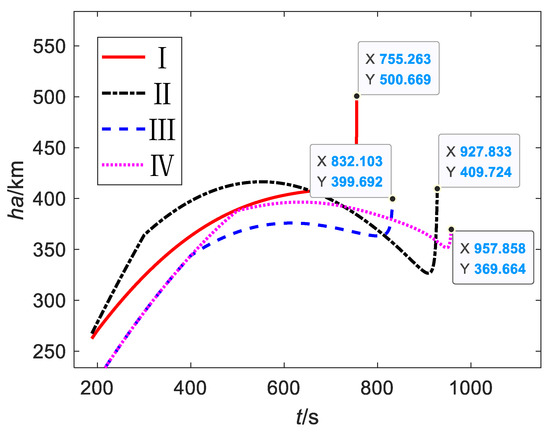
Figure 10.
Apogee altitude.
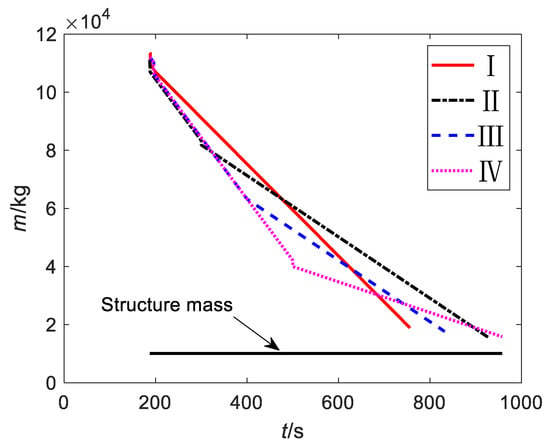
Figure 11.
Mass.
For the transfer orbit entry form, this paper calculates the fuel consumption mass by the TCFC and then leaves the 3% fuel margin for the actual orbit transfer and takes the perigee height and apogee height of the final target orbit as the result of the mission planning and the entry deviation into the transfer orbit as the accuracy of trajectory planning. The results of mission decision making and trajectory planning can be obtained as shown in Table 4.

Table 4.
Feasibility results of mission decision making and trajectory planning.
The above results show that the proposed method can plan a reasonable and feasible new mission under different fault conditions and mission attributes. For fault I, the launch vehicle lost 90 km at perigee height, but all payloads (9.00 t) entered the mission orbit with sufficient accuracy. For fault II, the launch vehicle firstly entered 410 km × 490 km transfer orbit and finally entered the 490 km SSO due to the large magnitude and late occurrence of the fault; the decision-making model enabled the launch vehicle to complete high-precision orbit-injection when it was as close to the original target orbit height as possible and retained most of the payload. For fault III, the launch vehicle lost 50% thrust at the later fault time; the apogee height of the mission orbit decreased by a small amount due to the height limit at fault time and the constraint of the integral direct orbiting, and the carrying capacity could only be matched by significantly reducing the perigee height. The perigee height of 157 km also meant that the launch vehicle was close to the edge of mission failure. For fault IV, although the magnitude and time of fault occurrence were larger and later than fault III, the launch vehicle could reduce the mission loss by transfer orbiting and discarding part of the payload thanks to its better mission attribute requirements. Besides proving the feasibility of the proposed method, these results also confirmed that the mission attribute had a significant impact on mission decision making and loss under power failure conditions.
5.3. Effectiveness Analysis of Trajectory Planning
To verify the effectiveness of the mission-planning results, the proposed method is simulated in comparison with particle swarm optimization (PSO) by taking failure cases I and IV as examples. For failure case I, the orbital semimajor axis is optimized by fixing the payload mass and apogee height; for failure case IV, the payload mass is optimized by fixing the target orbit parameters.
This paper uses the PSO algorithm with improved global search performance by Shi and Eberhart [22]. Ignoring the adjustment of the launch vehicle to the motion plane after the failure, the initial pitch angle and the slope of the two pitch angles according to the time averaging are the particle positions, and the squared sum of the perigee altitude deviation, apogee altitude deviation, and payload mass deviation is the value of the fitness function. The number of populations is set to 30, and the maximum number of iterations is 200. Comparative simulation results after optimization can be obtained, as shown in Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17.
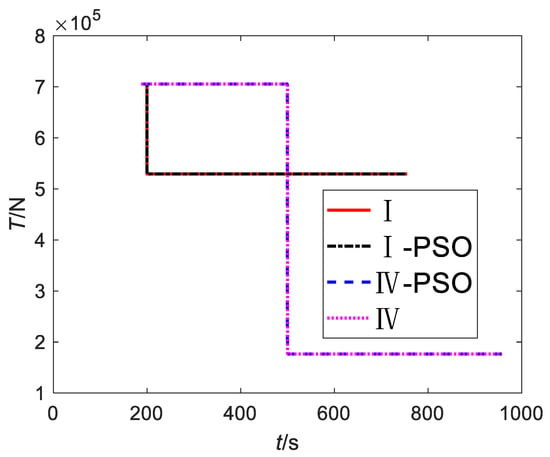
Figure 12.
Engine thrust.
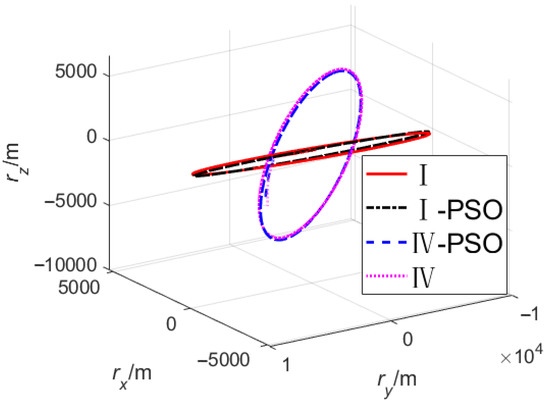
Figure 13.
Flight trajectory and terminal orbit.
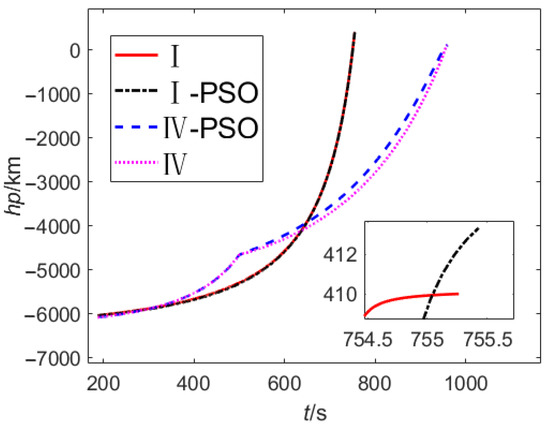
Figure 14.
Perigee altitude.
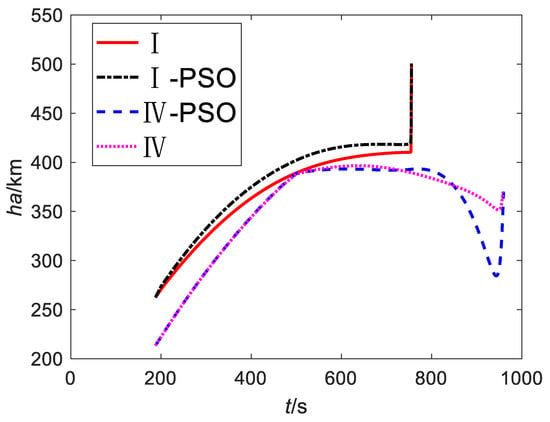
Figure 15.
Apogee altitude.
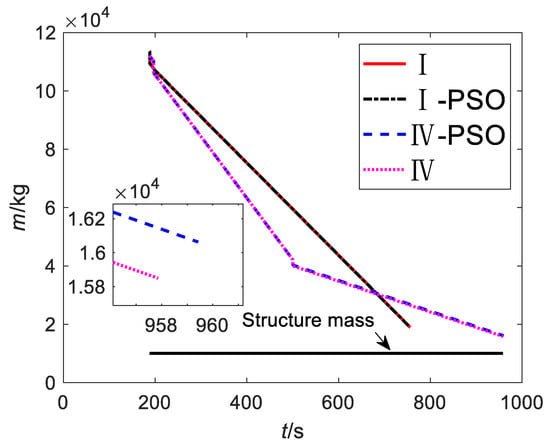
Figure 16.
Mass.
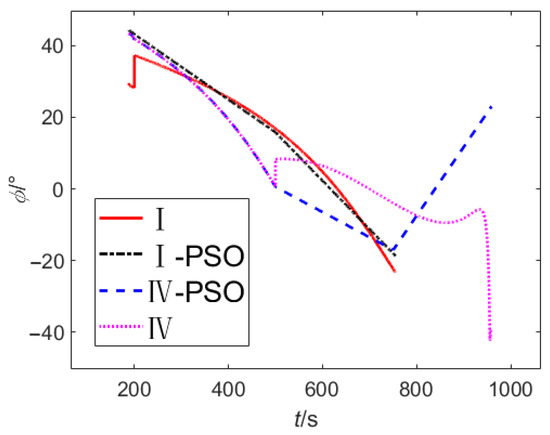
Figure 17.
Pitch angle.
The results of Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17 are shown in Table 5.

Table 5.
Effectiveness results of mission decision making and trajectory planning.
The results show that, under the same fault condition, the mission loss obtained by the proposed method is slightly larger than that of the PSO, but the calculation cost is far less than that of the PSO. Theoretically, the optimal results will be obtained when the population size, particle dimension of the PSO, and the number of iterations are large enough; the degradation gradients used in this paper to simplify the neural network modeling process limit the optimality of the method. However, this paper uses the RBFNN, the TDOS, and the ATU-IGM to generate guidance commands, which make the control angle and states smoother and can better meet the actual flight requirements; the PSO guidance commands obtained by parameterizing the control have obvious parameterization characteristics (for example, the linearized model adopted by the PSO in this paper) and are not only different from the actual flight commands but also easy to make the states fluctuate greatly, as shown in Figure 15 and Figure 17.
In summary, it can be seen that the proposed method is almost at the same level with the traditional numerical solution method in terms of the accuracy of mission planning and trajectory planning, but mission adaptability and solution efficiency have been greatly improved. The population size and initial guesses greatly influence the convergence and computational speed of the PSO method. In contrast, the proposed method in this paper uses the RBFNN for mission decision making, which simplifies the calculation process, and the ATU-IGM for trajectory planning to generate the guidance instructions in analytic form. Therefore, the timeliness of mission planning is effectively ensured.
6. Conclusions
To solve the problem of autonomous decision making and trajectory planning for launch vehicles under power failures, this paper investigates the orbit-injection strategy based on the target degradation rule and proposes an online trajectory-planning method based on the combination of the ATU-IGM and the RBFNN. The TDOS performs gradient degradation of the target mission from orbital energy and payload mass by analyzing mission attributes, failure modes, and multi-payload composition. To meet the requirement of flight timeliness, this paper proposes an online trajectory-planning method based on the offline decision-making learning model and online parameter-mapping method. For the offline decision-making learning model, RBFNN is used to train the optimal decision-making samples under power failures generated by the combination of the TDOS and the ATU-IGM; for the online parameter-mapping method, the main orbital elements are generated from the trained decision-making model according to the mission requirements and the failure states. Then, the remaining orbital elements are generated based on the TDOS, and the ATU-IGM is used for parameter adjustment and online trajectory planning.
To test the feasibility of the proposed method, simulation analysis was conducted under four sets of typical missions with failure conditions. The results show that the proposed method can generate effective mission-planning results and achieve high trajectory-planning accuracy for different mission types and fault states. To further test the effectiveness of the mission planning, the particle swarm optimization method was used to perform the optimization comparison simulation under power failure. The results show that the mission-planning results of the proposed method are conservative compared with the optimization results. The maximum mission-planning deviation is 4.96%, determined by the optimal failure mission samples’ height and payload mass degradation gradient. In addition, the deviation of the decision-making model can be reduced by reducing the gradient values. In summary, the proposed method can adapt to various mission situations and has obvious computational efficiency advantages, providing theoretical support for autonomous decision making and planning of space launch missions.
Author Contributions
Conceptualization, Y.D. and J.P.; methodology, Y.D.; software, H.X.; investigation, R.M.; writing—original draft preparation, Y.D.; writing—review and editing, Y.D.; funding acquisition, J.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Laboratory Opening Funding of Technology of Micro-Spacecraft (Grant No. HIT.KLOF.MST.2018028).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Chang, I.-S. Investigation of space launch vehicle catastrophic failures. J. Spacecr. Rocket. 2015, 33, 198–205. [Google Scholar] [CrossRef]
- Cheng, P.; Wang, H.; Stojanovic, V.; He, S.; Shi, K.; Luan, X.; Liu, F.; Sun, C. Asynchronous fault detection observer for 2-D Markov jump systems. IEEE Trans. Cybern. 2021, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Djordjevic, V.; Stojanovic, V.; Tao, H.; Song, X.; He, S.; Gao, W. Data-driven control of hydraulic servo actuator based on adaptive dynamic programming. Discret. Contin. Dyn. Syst.-S 2021. [Google Scholar] [CrossRef]
- Luan, T.; Sun, M.; Xia, G.; Chen, D. Evaluation for sortie generation capacity of the carrier aircraft based on the variable structure RBF neural network with the fast learning rate. Complexity 2018, 2018, 6950124. [Google Scholar] [CrossRef]
- Perk, B.E.; Inalhan, G. Safe motion planning and learning for unmanned aerial systems. Aerospace 2022, 9, 56. [Google Scholar] [CrossRef]
- Chandler, D.C.; Smith, I.E. Development of the iterative guidance mode with its application to various vehicles and missions. J. Spacecr. Rocket. 1967, 4, 898–903. [Google Scholar] [CrossRef]
- Lv, X.G.; Song, Z.Y. Guidance methods of long-march launch vehicles. J. Astronaut. 2017, 38, 895–902. [Google Scholar]
- Ru, J.X. An iterative guidance method for liquid launch vehicles. Sci. China Ser. E-Technol. Sci. 2009, 39, 696–706. [Google Scholar]
- Han, X.Y.; Ma, Y.; Zhang, Z.G.; Yu, M.L. Study on application of iterative guidance algorithm with injection attitude constraints. J. Astronaut. 2018, 39, 508–515. [Google Scholar]
- Goodman, J. Roland jaggers and the development of space shuttle powered explicit guidance (PEG). In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–15 and 19–21 January 2021. [Google Scholar]
- Zhang, L.; Wei, C.; Diao, Y.; Cui, N. On-line orbit planning and guidance for advanced upper stage. Aircr. Eng. 2019, 91, 634–647. [Google Scholar] [CrossRef]
- Huang, P.X.; Wei, C.Z.; Gu, Y.; Gui, N. Hybrid optimization approach for rapid endo-atmospheric ascent trajectory planning. Aircr. Eng. Aerosp. Technol. 2016, 88, 473–479. [Google Scholar] [CrossRef]
- Zhang, Z.G.; Yu, M.L.; Geng, G.Y.; Song, Q. Research on application of the pseudo spectral method in online guidance method for a launch vehicle. J. Astronaut. 2017, 38, 262–269. [Google Scholar]
- Benedikter, B.; Zavoli, A.; Colasurdo, G.; Pizzurro, S.; Cavallini, E. Convex approach to three-dimensional launch vehicle ascent trajectory optimization. J. Guid. Control Dyn. 2021, 44, 1116–1131. [Google Scholar] [CrossRef]
- He, H.; Shi, P.; Zhao, Y. Hierarchical optimization algorithm and applications of spacecraft trajectory optimization. Aerospace 2022, 9, 81. [Google Scholar] [CrossRef]
- Dupont, C.; Tromba, A.; Missonnier, S. New strategy to preliminary design space launch vehicle based on a dedicated MDO platform. Acta Astronaut. 2018, 158, 103–110. [Google Scholar] [CrossRef]
- Song, Z.Y.; Wang, C.; Gong, Q.H. Joint dynamic optimization of the target orbit and flight trajectory of a launch vehicle based on state-triggered indices. Acta Astronaut. 2020, 174, 82–93. [Google Scholar] [CrossRef]
- Wang, J.G.; Pu, J.L.; Cui, N.G.; Li, Y.; Han, Y. Ascent adaptive guidance for power system fault of heavy lift launch vehicle. In Proceedings of the IEEE CSAA Guidance, Navigation and Control Conference (GNCC), Xiamen, China, 10–12 August 2018. [Google Scholar]
- Markley, F.L.; Crassidis, J.L. Orbital Dynamics. In Fundamentals of Spacecraft Attitude Determination and Control; Springer: New York, NY, USA, 2014; Volume 33, pp. 365–402. [Google Scholar]
- Macdonald, M.; McKay, R.; Vasile, M.; De Frescheville, F.B. Extension of the Sun-Synchronous Orbit. J. Guid. Control Dyn. 2015, 33, 1935–1940. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, Z.H.; Tao, H.F.; Chen, Y.Y.; Stojanovic, V.; Paszke, W. Iterative learning control for repetitive tasks with randomly varying trial lengths using successive projection. Int. J. Adapt. Control Signal Process. 2022, 1–20. [Google Scholar] [CrossRef]
- Shi, Y.H.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).