Abstract
In this work, we investigate the behavior of low-energy trajectories in the dynamical framework of the spatial elliptic restricted 4-body problem, developed using the Hamiltonian formalism. Introducing canonical transformations, the Hamiltonian function in the neighborhood of the collinear libration point (or ), can be expressed as a sum of three second order local integrals of motion, which provide a compact topological description of low-energy transits, captures and quasiperiodic libration point orbits, plus higher order terms that represent perturbations. The problem of small denominators is then applied to the order three of the transformed Hamiltonian function, to identify the effects of orbital resonance of the primaries onto quasiperiodic orbits. Stationary solutions for these resonant terms are determined, corresponding to quasiperiodic orbits existing in the presence of orbital resonance. The proposed model is applied to the Jupiter-Europa-Io system, determining quasiperiodic orbits in the surrounding of Jupiter-Europa considering the 2:1 orbital resonance between Europa and Io.
1. Introduction
Low-energy trajectories have long been used in space exploration, starting from missions to the libration points of the Sun–Earth system [1,2,3,4,5] and including lunar transfers passing close to the intermediate Earth–Moon libration point [6,7,8], named internal transfers, or extending beyond the orbit of the Moon to take advantage of the Sun gravitational attraction [9,10], named external transfers.
The spatial Circular Restricted 3-Body Problem (CR3BP) [11] represents an effective model for the preliminary analysis of both missions to the libration points [12,13,14,15] and low-energy transfers [16,17,18]. As proved by Conley [19], in this dynamical framework the ultimate behavior of low-energy trajectories can be determined based on their phase space description in the neighborhood of the collinear libration points [20], a property which has been extensively used in mission oriented works, since it allows a rapid design of low-energy missions [21,22,23,24,25].
More accurate solutions can be generated based on more sophisticated models, such as the Elliptic Restricted 3-Body Problem (ER3BP) [26], in which the primaries move along elliptic orbits, or the Circular Restricted 4-Body Problem (CR4BP), in which the spacecraft dynamics evolves under the gravitational attraction of four primaries (i.e., the Sun–Earth–Moon system) [27]. Unfortunately, because no integrals of motion, such as the Jacobi constant for the CR3BP, are known for neither the ER3BP nor the CR4BP, a general characterization of low-energy trajectories in these dynamical frameworks has not been derived yet.
In fact, the phase space description derived for the CR3BP in the surrounding of the libration point (or ) can actually provide pivotal results for the design of missions also in the presence of non negligible, but limited, eccentricity in the motion of the primaries [28] and gravitational attraction from a fourth body [29]. This result has its foundation on a theorem by Conley and Easton [30], stating that the basic topological properties of the phase space flow of the CR3BP are persistent in the presence of perturbations, whose validity was verified also by means of numerical analyses [31,32].
In this paper, we present a novel model that allows characterizing low-energy trajectories for a system consisting of a central body and two natural satellites moving along elliptic orbits, therefore in the dynamical framework of the spatial Elliptic Restricted 4-Body Problem (ER4BP). Typically, this task is performed based on the results of the CR3BP, corrected and compensated to take into account the perturbations introduced by the eccentric motion of the primaries or by the gravitational attraction of a third primary. The model proposed in this paper provides results which do not require any further correction and, furthermore, allows determining new solutions corresponding to quasiperiodic orbits existing when the primaries are in orbital resonance.
The ER4BP is modeled using the Hamiltonian formalism, where canonical transformations of the state variables allow reducing the Hamiltonian function for the ER4BP to a form equivalent to that of the CR3BP in the neighborhood of plus higher order terms, thus the complexity of the problem is transferred in the definition of a coordinate transformation. Following this approach, the low-energy trajectories can be characterized in terms of the new phase space variables, using the same techniques developed for the CR3BP [33], then the corresponding physical (position and velocity) coordinates can be derived applying the inverse coordinate transformation.
The effect of orbital resonance between two of the primaries is finally examined. Under this circumstance, any attempt of introducing a canonical transformation to absorb the higher order terms defaults, because of the small denominators problem [34], and the Hamiltonian function for the ER4BP, is transformed to that of the CR3BP plus an additional resonant term.
Specific phase space states in the transformed coordinates correspond to equilibrium conditions for the resonant term and these are actually periodic solutions in physical coordinates. The problem is here applied to the specific case of the Jupiter–Europa–Io system, in which the two moons are in a 2:1 resonance, to determine quasiperiodic trajectories in the neighborhood of Jupiter–Europa . Here, a satellite can be deployed to perform, or support, space science missions to the Jovian moon, which has attracted the interest of space agencies because of its geodynamically active icy crust, which makes Europa a major candidate for the search of life in the solar system [35,36].
The paper is organized as it follows, in Section 2 a model for the ER4BP is developed in space and velocity coordinates and converted to Hamiltonian variables. In Section 3 the Hamiltonian function for the ER4BP is set in a form equivalent to that of the CR3BP by means of canonical transformations. In Section 4 the resonant terms, depending on the true anomalies of the primaries, are identified, by means of small denominators problem, and the corresponding quasiperiodic solutions are determined. An application to the Jupiter–Europa–Io system is provided in Section 5, comparing the analytical solution obtained in Section 4 to the numerical results obtained from integrating the full nonlinear equations of motion associated to the ER4BP.
2. The Elliptic Restricted 4-Body Problem
2.1. Dynamical Model
The dynamics of a restricted 4-body system, with masses , is hereafter described under the following hypotheses:
- The center of mass of the system is indicated as O;
- The relative motion of with respect to describes a Keplerian orbit onto the plane with semimajor axis a and eccentricity e;
- The relative motion of with respect to describes a Keplerian orbit onto the plane with semimajor axis and eccentricity ;
- The orbital plane is tilted of an angle with respect to ;
where the subscript p is used to explicit the parameters referring to the perturbing fourth body . This model is suitable to represent a multi-moon environment, which is typical for the outer planets, or gas giants, in the solar system.
An inertial reference frame is introduced. is centered in O, with orthogonal to , parallel to the line that connects and at the initial time , and completing the rectangular reference frame. For the sake of simplicity, it is assumed that at the primary is at the apocenter of its orbit around and lies onto the plane. It shall be noted that this hypothesis does not cause any loss of generality.
The dynamic equations of motion for m in the inertial reference frame are reported below
where indicate the coordinates of the i-th primary, and indicates the distance between m and the i-th primary.
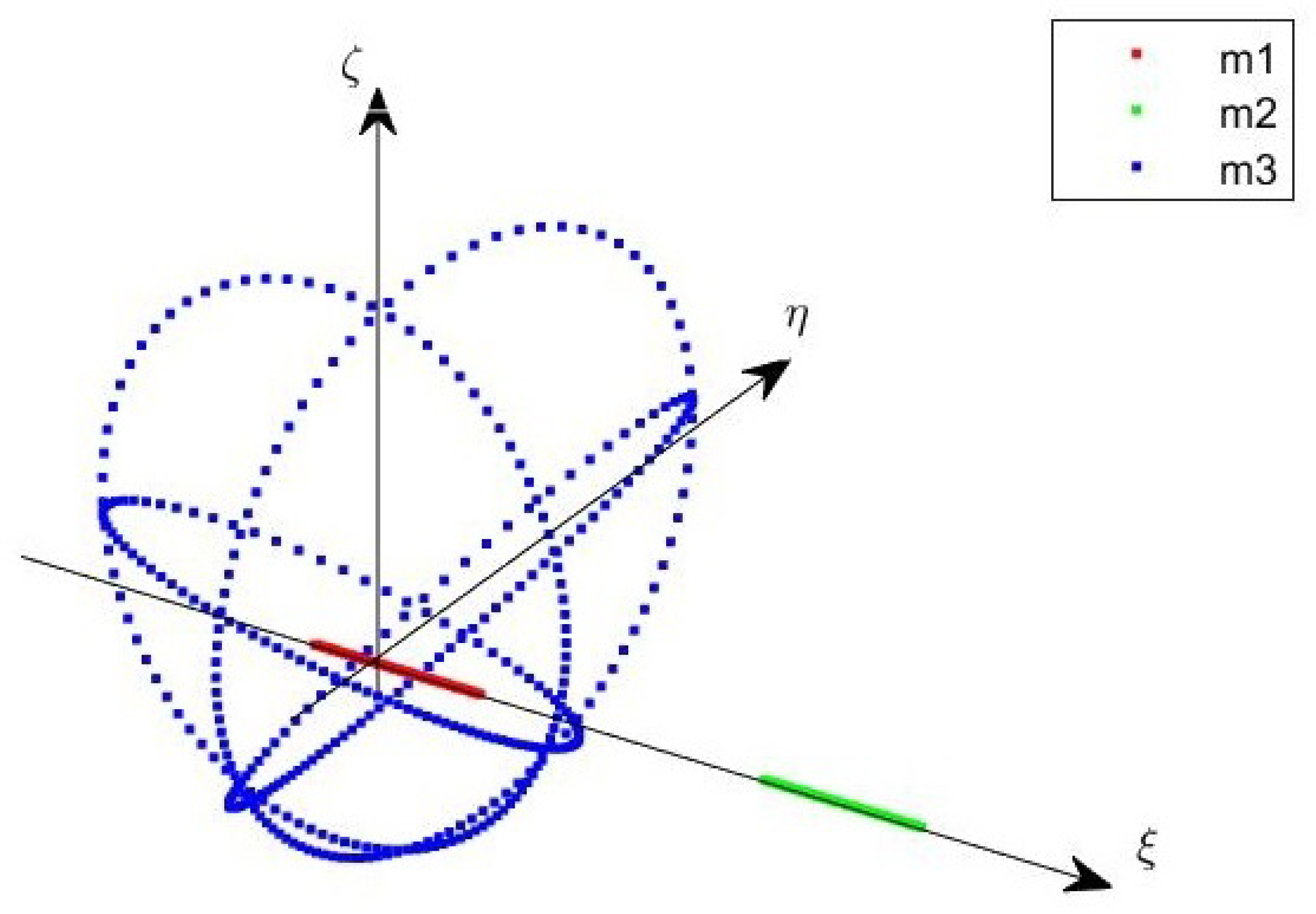
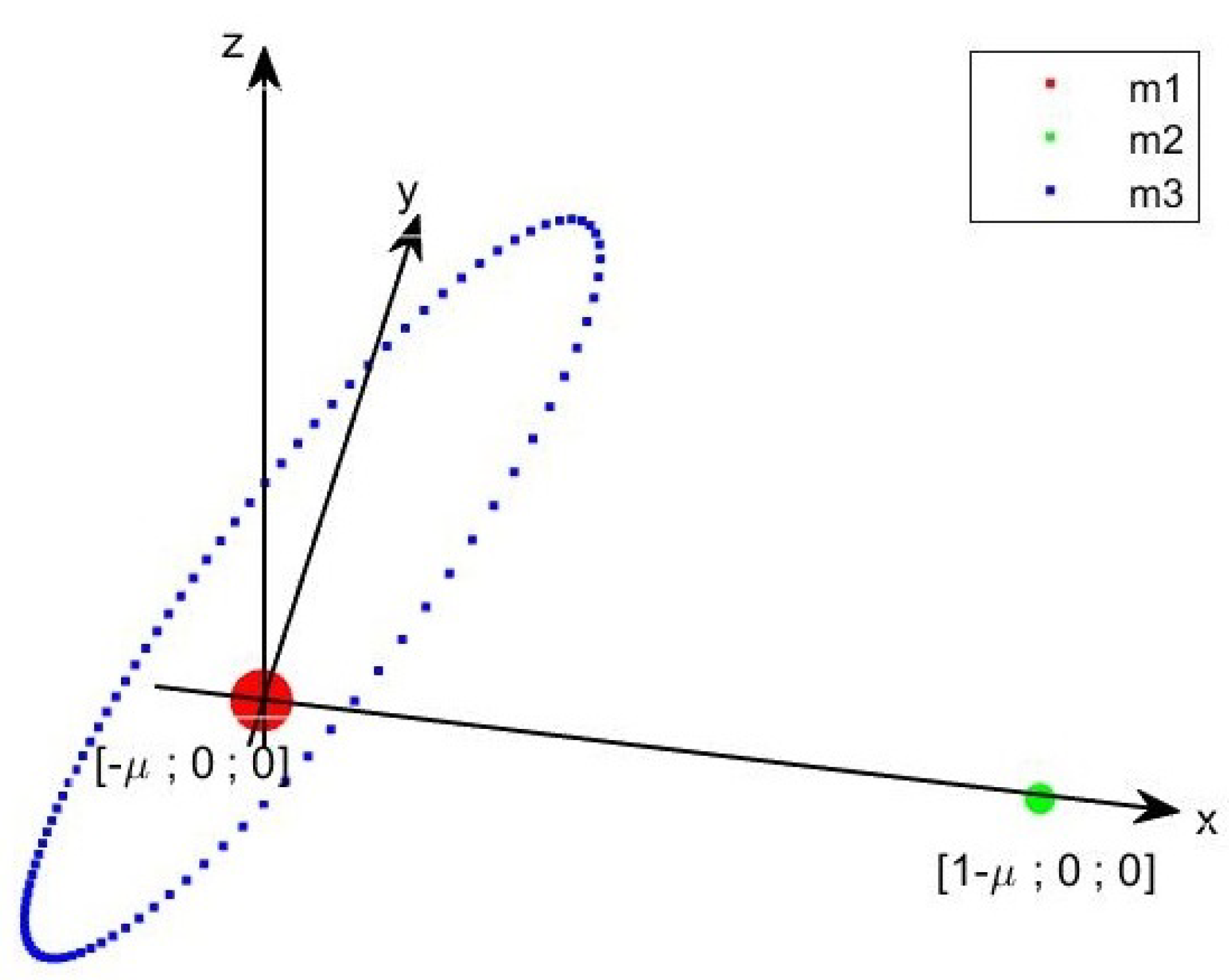
System (1) can be conveniently converted into rotating-pulsating coordinates, after introducing the reference frame , which rotates rigidly with the primaries and . In particular, is parallel to at , with axis pointing from to , axis orthogonal to and axis completing the orthogonal reference frame. As sketched in Figure 1 (the trajectory of the primaries in Figure 1 and Figure 2 does not correspond to an actual system and is produced for the sake of representation, selecting: km, km, , , deg, kg, kg, kg), in the rotating frame the primaries and oscillate along the axis . The trajectory of the primary is more complex and results from the combination of the periodic motion of around O and the periodic rotation of . Converting the inertial coordinates into rotating ones produces the following form for the dynamic equations of motion [37]
where and is the true anomaly of .
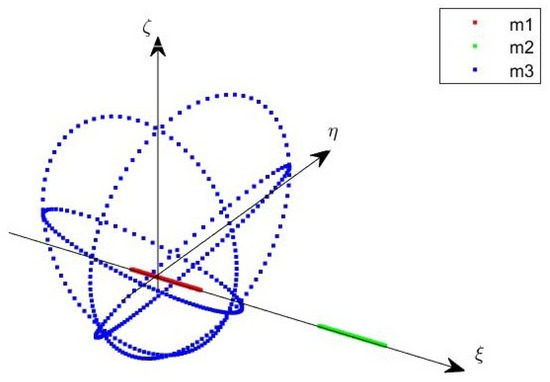
Figure 1.
Motion of the primaries in the rotating frame.
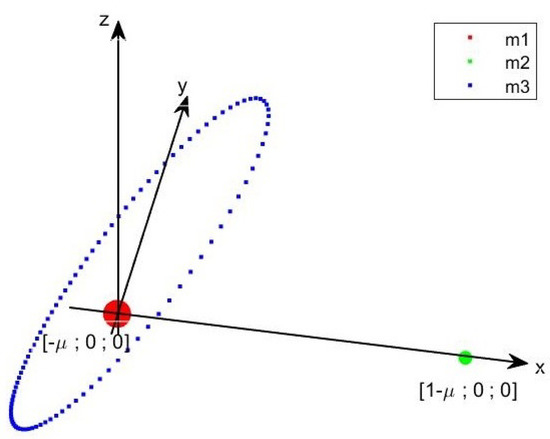
Figure 2.
Motion of the primaries in rotating-pulsating coordinates. Only one orbit of is shown.
Introducing the normalization factors for the mass , distance and time , allows transforming the rotating coordinates into rotating-pulsating ones , and, finally, rearranging System (2) in a dimensionless form, with the dependence on time being replaced by that on [38]
where , , , and the apostrophe indicates the derivative with respect to . As shown in Figure 2, the position of the primaries and in rotating-pulsating coordinates corresponds to, respectively, and with . As in the rotating frame, the primary evolves along a three-dimensional trajectory which in this case depends also on the periodic motion of the rotating-pulsating reference frame along axis .
The second order equations in System (3) are typically expressed as a set of first order equations for the position and velocity coordinates
The reader will notice that setting the Systems (1)–(4) reduce to the corresponding ones for the CR3BP. In Section 3 it will be shown how to express the dynamics of the ER4BP to a form equivalent to that of the CR3BP also when e, , and are small but not negligible. To achieve this goal, the Hamiltonian formalism is introduced.
2.2. Hamiltonian Formalism
System (4) can be represented using the Hamiltonian formalism after deriving the Hamiltonian function for the ER4BP (see [26,39])
which depends on the variables and , where the bold style is used to indicate the vectors, named the positions and conjugate momenta
The dynamic equations of motion are obtained by the definitions [40] and , leading to
Introducing Equation (6) into Equation (7) results in System (4), proving the equivalence between the Hamiltonian and the position space representations.
Considering the non-polynomial terms of H
the dependence on e, , and can be isolated after expanding in power series about the expansion point , indicated by the superscript
with
where collects the terms of order higher than one in e, , and . For the sake of clarity, the long expressions for the partial derivatives of are reported in Appendix A.
3. Classification of Low-Energy Trajectories in the Elliptic Restricted 4-Body Problem
3.1. Persistence of the Topological Properties
In Section 2, the Hamiltonian function of the ER4BP was expressed as the sum of the Hamiltonian for the CR3BP and the terms depending on the orbital eccentricity of the primaries and on the gravitational attraction of the third primary .
It is worth recalling now that for the CR3BP, the ultimate behavior of low-energy trajectories can be determined based on the topological properties of the linear flow in the phase space surrounding the collinear libration points (or ) [20], called the equilibrium region. According to a theorem by Conley and Easton, the properties of the flow in the equilibrium region are persistent also in the presence of perturbations [30], therefore for small e, and , it shall be possible to transform the Hamiltonian function of the ER4BP to a form equivalent to that of the CR3BP in the equilibrium region, hereafter indicated as .
The expression of is derived hereafter. First, the origin of the system is translated to the libration point (equivalent solutions can be derived for the second libration point by simply replacing with ), setting
Then the non polynomial terms of Equation (14) are rearranged as follows
and expanded in power series up to order two in , obtaining
where is the x coordinate of the libration point, and
Introducing Equations (18) and (19) into Equation (15) and excluding terms inessential in the Hamilton equations of motion leads to
with .
In the following sections, two canonical transformations are introduced. The first one leads the second order Hamiltonian function for the ER4BP to a form equivalent to Equation (20), the second one allows expressing the resulting second order Hamiltonian function as the sum of three local integrals of motion.
3.2. Normal Forms for the Elliptic Restricted 4-Body Problem
A canonical transformation from the old to a new set of Hamiltonian variables is designed by means of the generating function S, which verifies the condition
and links the old and new variables as
The authors proved that selecting the generating function reported below (see Appendix B)
The canonical transformation can absorb the second order terms in Equation (15) that depend on the perturbations , hereafter explicited (please note that terms depending on the perturbation do not appear in Equation (23) because they are of a order higher than two)
Then, the second order Hamiltonian in the new variables reduces to , where
and the full Hamiltonian is given by
where collects terms of order 3 or higher.
It is worth to summarize the result here. Applying the canonical transformation defined in Equation (21) with the generating function described by Equation (23), the second order Hamiltonian function for the ER4BP results in Equation (25), whose form is equivalent to that of the second order Hamiltonian for the CR3BP, given by Equation (20). Because the topological properties of the phase space flow in the equilibrium region depend on the local form of the Hamiltonian function [20], the equivalence in the form of and indicates that the topological properties of the CR3BP are equivalent to those of the ER4BP, substantiating the theorem by Conley and Easton [30].
3.3. Topological Characterization of Low-Energy Trajectories
A second canonical transformation , originally proposed by Siegel and Moser [41] and extensively used for the CR3BP [29,33,42], allows expressing as the sum of three terms
where , , and are, respectively, the real and the two imaginary eigenvalues of the linear system associated to and h indicates the constant value of , named the energy level.
As proved by Moser [43], the three terms in Equation (27) are local integrals of motion, each one depending on a different couple of variables . The two integrals associated with the imaginary eigenvalues represent harmonic oscillators and characterize, respectively, the in-plane and out-of-plane oscillations, corresponding to the and z components in position space coordinates.
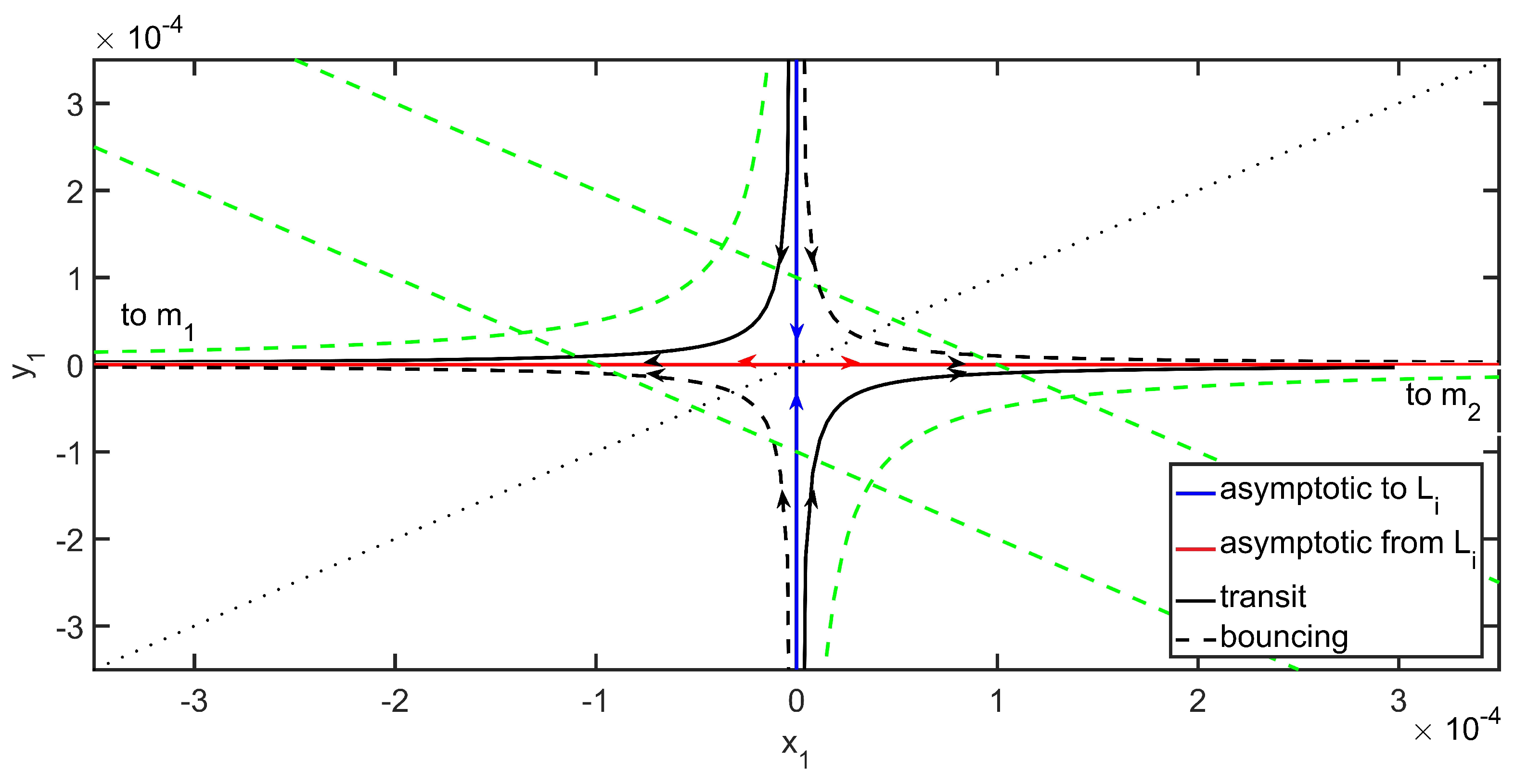
The level surface describes the linear phase space flow in the neighborhood of the saddle point , as sketched in Figure 3.
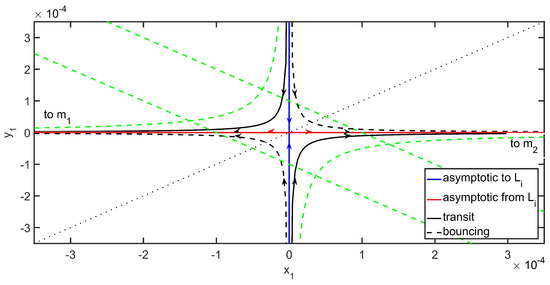
Figure 3.
Representation of the phase space flow in .
Low-energy trajectories can be characterized based on their state projection in and are classified as follows [20]:
- Lissajous quasiperiodic orbits, characterized by , which evolve inside the equilibrium region;
- Transit trajectories, corresponding to the hyperbolic segments , which cross the equilibrium region twice, once towards and once towards , in a finite interval of time;
- Bouncing trajectories, corresponding to the hyperbolic segments , which never cross the equilibrium region;
- Long-term ballistic captures, characterized by either or , which cross the equilibrium region twice, over an indefinitely long interval of time.
Inasmuch, some relevant results proved that the CR3BP can be extended to the ER4BP, indicating that correlations exist between the osculating orbital elements of ballistic captures in the proximity of the primaries and their state in the equilibrium region [33,44].
As detailed in the next section, the model proposed can provide further information on the dynamical evolution of quasiperiodic orbits under the effect of perturbations included in higher order terms. In particular, the impact of orbital resonance between the primaries is examined.
4. Resonant Terms and Quasiperiodic Solutions
4.1. Identification of Resonant Terms
The focus now is on investigating the effects of residual perturbations, included in the higher order terms, onto quasiperiodic orbits . In particular, the case of orbital resonance between the primaries is examined, which allows setting , where n is an integer number.
The Hamiltonian function including the higher order terms can be easily derived, by applying the canonical transformation by Siegel and Moser to , producing , and adding this term to Equation (27), resulting in
A new canonical transformation , aiming at absorbing the order three terms in Equation (28), is now introduced. Operating as in Section 3, the canonical transformation is defined by means of a generating function S, which verifies
and
Using symbolic algebra, the authors proved that setting the following expression for the generating function (see Appendix B)
Allows absorbing the order three terms of Equation (28), leading to
where collects the terms of order higher than three.
As expected from the small denominator problem [34], in case of resonance, the denominators of some coefficients in are equal to zero and the canonical transformation defaults. In particular, this occurs in and for and in and for , where is an arbitrarily small constant.
The residual order three terms of the Hamiltonian function are reported below
where and are constant coefficients depending on e, and and are determined from the change of coordinates in Equation (30).
4.2. Determination of Stationary Points
The model developed here allows determining periodic solutions existing because of orbital resonance. Before proceeding with their determination, the following property of the canonical transformation by Siegel and Moser shall be recalled [40,41]
Introducing Equation (34) into Equation (33) and applying Euler’s formula, to express the exponential terms as trigonometric functions, the expression of is transformed to
Here the dependence on the true anomaly can be absorbed by introducing the canonical transformation defined by the following generating function
Corresponding to the change of coordinates reported below (the variables not reported are not transformed)
Which transforms Equation (35) as follows
Stationary points exist for Equation (38), corresponding to
The reader shall note that the sequence of transformations from to , hereafter indicated as and producing , depend on the commensurable and . Applying the inverse of to any stationary solution defined by Equation (39) results in a quasiperiodic trajectory in and related position and velocity components.
5. Numerical Analysis
In the previous sections, we derived a model which allows designing quasiperiodic libration point orbits existing in case of resonance between the primaries. This model is here verified by means of numerical analysis on the Jupiter–Europa–Io system, whose parameters are reported in Table 1 (from the values in Table 1 it is possible to compute ). This system is characterized by the 2:1 orbital resonance between Europa and Io, corresponding to .

Table 1.
Parameters of the Jupiter–Europa–Io system.
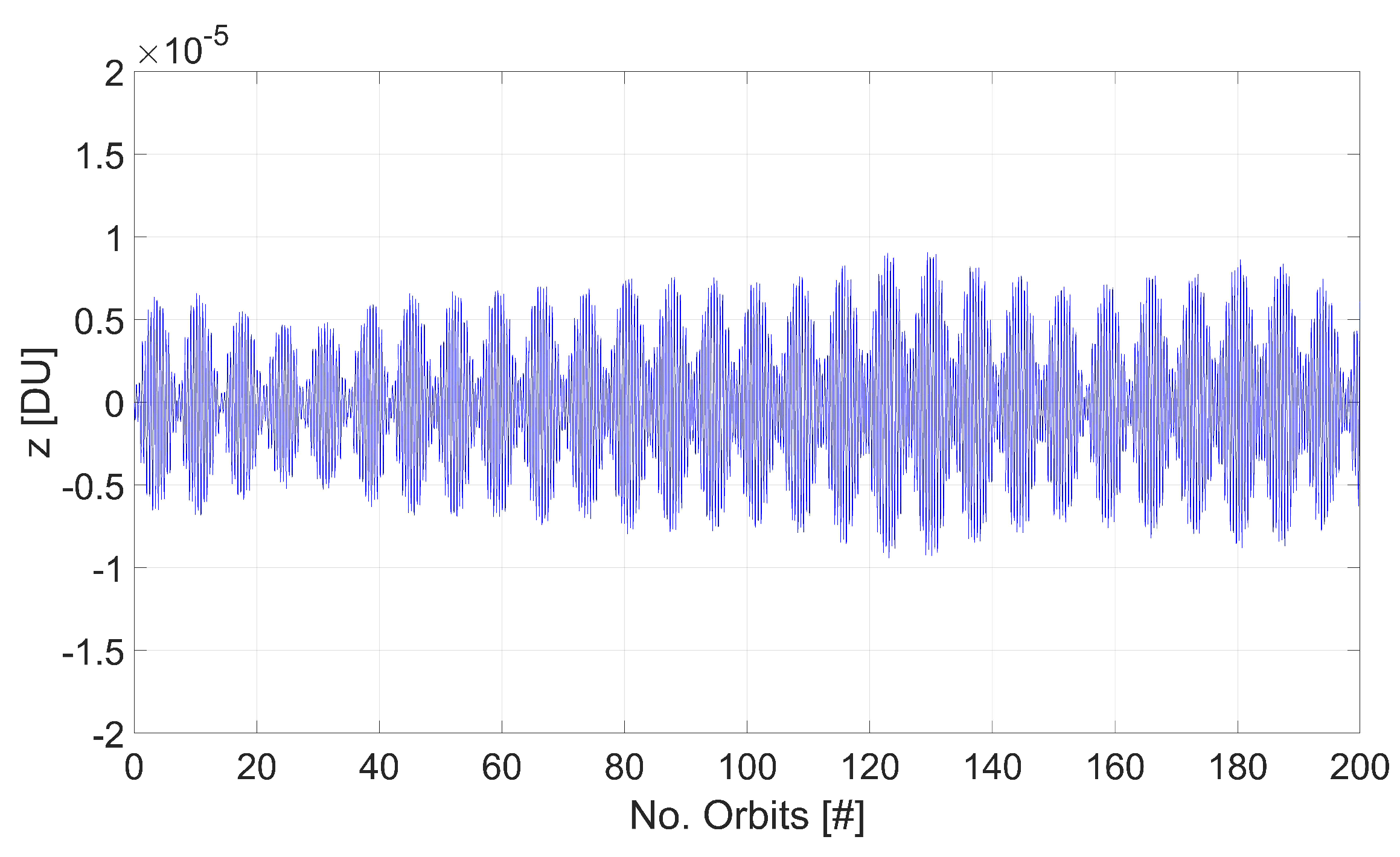
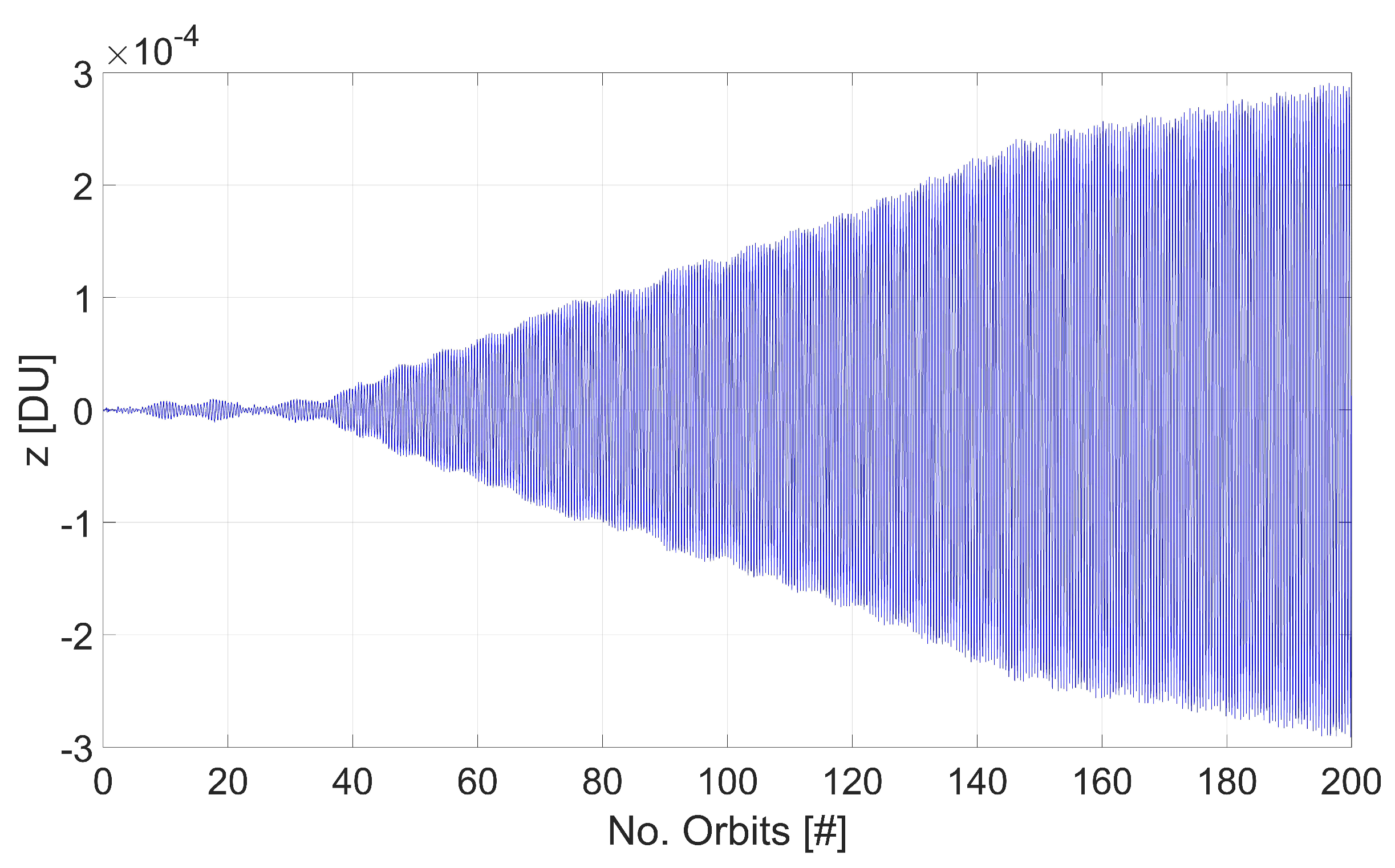
The effects of the orbital resonance is investigated on quasiperiodic orbits in the neighborhood of Jupiter–Europa , characterized by and . Since , the condition is verified. In particular, the case of an out of plane periodic orbit is presented below. The initial conditions, selected from Equation (39) for , are and and correspond to , , , , and . From this initial state, the full nonlinear equations of motion in System (4) are integrated using ode113 solver in Matlab, for a total time equal to 200 times the orbital period of Europa around Jupiter, which corresponds to about 708 Earth days. The time behavior of the oscillations is shown in Figure 4, where the distance is normalized by .
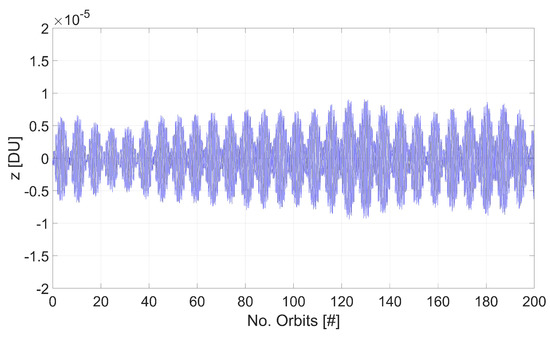
Figure 4.
Behavior of the vertical oscillator associated to a stationary point.
The solution is compared to the one obtained ignoring the order three terms, corresponding to the state , , , , and . The time behaviour of the oscillations is represented in Figure 5, showing that the orbital perturbation of Io produces an increase of the amplitude up to DU in the time interval considered. Differently, the amplitude of oscillations for the quasiperiodic orbit obtained from the stationary point never exceeds the value DU.
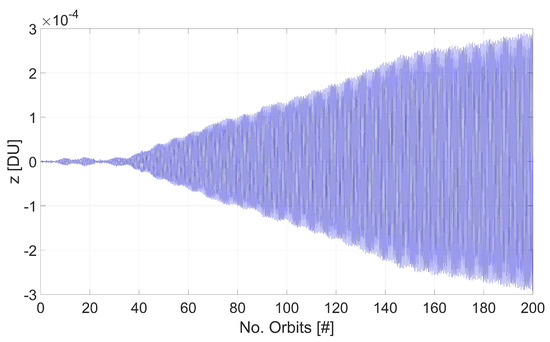
Figure 5.
Behavior of a vertical oscillator determined neglecting order three terms.
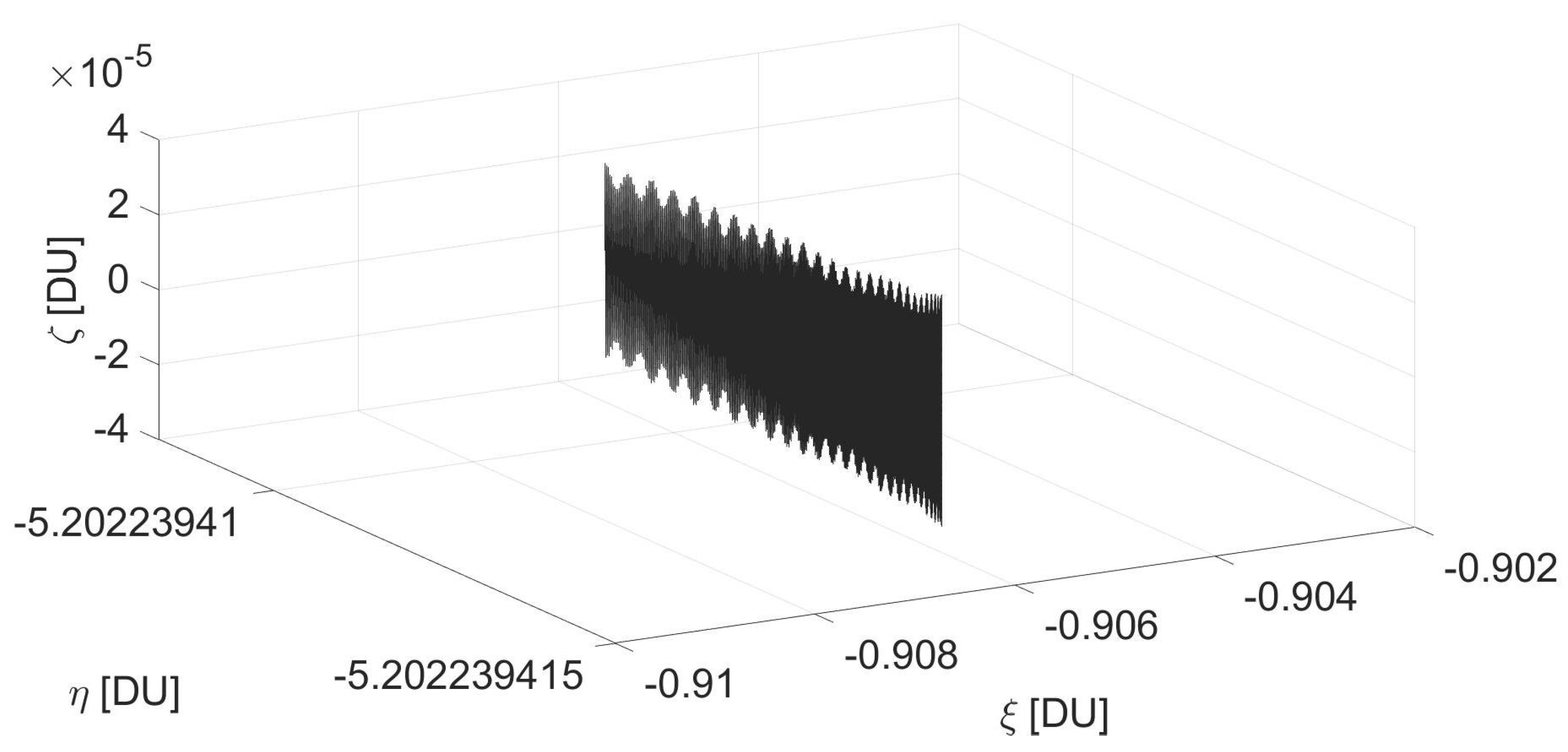
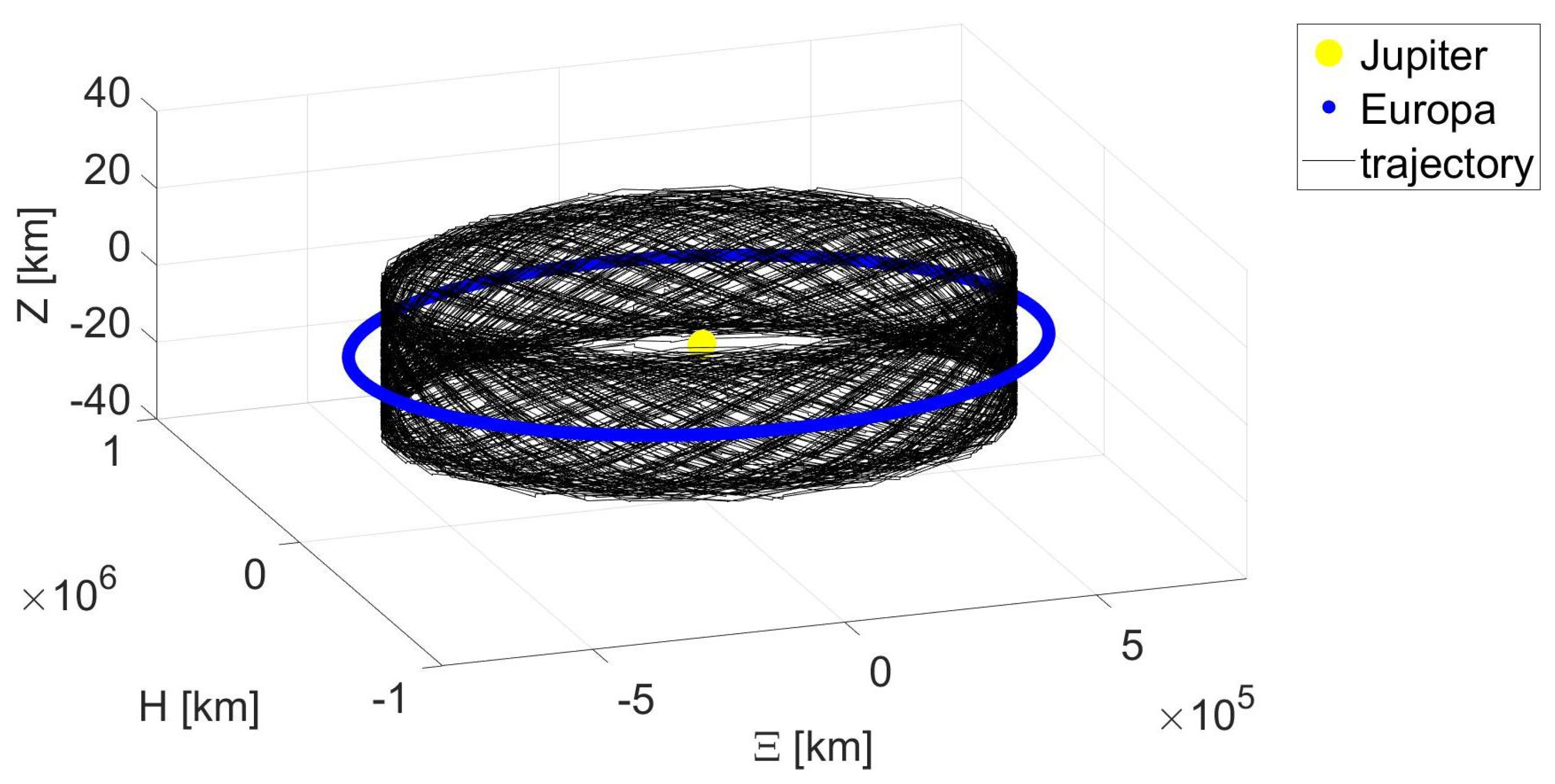
A representation of the quasiperiodic trajectory in the rotating frame is shown in Figure 6. It can be observed that the vertical component oscillates as in Figure 4, while the in-plane components have a negligible drift towards the negative values, resulting from higher order perturbations. It shall be emphasized that over the 200 orbits, the drift of the in-plane components is four orders of magnitude lower than the amplitude of the vertical oscillations. To provide a better insight on the shape of the quasiperiodic orbit corresponding to the stationary point, the trajectory is represented in Figure 7 in the inertial reference frame .
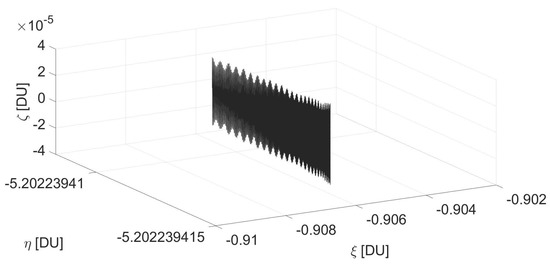
Figure 6.
Representation of the vertical oscillator associated to a stationary point in the rotating frame.
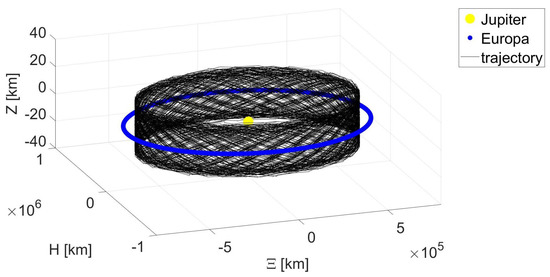
Figure 7.
Representation of the vertical oscillator associated to a stationary point in the inertial frame.
6. Conclusions
In this manuscript we presented a model to extend the topological characterization of low-energy trajectories from the dynamical framework of the CR3BP to that of the ER4BP. This goal is achieved, defining a sequence of canonical transformations which convert the Hamiltonian function of the ER4BP, evaluated in the neighborhood of the libration point (or ) to a form equivalent to that of the CR3BP.
The higher order terms of the Hamiltonian function in the normal form, which depend on the true anomalies of the primaries, can be absorbed by a further canonical transformation. This transformation defaults in case of orbital resonance between the primaries, as indicated by the problem of small denominators.
For the terms of the Hamiltonian function that cannot be absorbed by the canonical transformation, in virtue of the orbital resonance, stationary points can be computed, which correspond to quasiperiodic orbits in the position space coordinates.
The above mentioned model was verified, by means of numerical analyses, to investigate the behavior of quasiperiodic orbits for the Jupiter–Europa–Io system, characterized by the 1:2 resonance of Io and Europa. The full nonlinear equations of motion for the ER4BP were integrated for an initial condition corresponding to the vertical harmonic oscillator at Jupiter-Europa .
The results clearly showed that neglecting the terms of order three results in a trajectory in which the amplitude of the oscillations increases indefinitely in time, driven by the orbital resonance between the primaries. Instead, using the initial conditions associated to stationary points determined for the order three resonant Hamiltonian, reported in Equation (27), the amplitude of oscillations does not diverge and the resulting orbits are quasiperiodic.
Author Contributions
Conceptualization, S.C., M.P. and P.T.; methodology, S.C. and P.T.; software, S.C.; validation, M.P. and P.T.; formal analysis, S.C. and M.P.; investigation, S.C.; resources, P.T.; data curation, M.P.; writing—original draft preparation, S.C.; writing—review and editing, M.P. and P.T.; visualization, S.C. and M.P.; supervision, P.T.; project administration, P.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Terms of the Power Series Expansion
Appendix B. Canonical Transformations
In this section, it is described the process to derive the canonical transformations absorbing the order two (Appendix B.1) and the order three terms (Appendix B.2) depending on e, and .
Appendix B.1. Second Order
The expression of the Hamiltonian function derived in Section 2 for the ER4BP is given by Equation (15). In particular, the second order terms are collected in Equation (24), reported hereafter for the sake of completeness
where
Introducing the generating function defined by Equation (23)
The following transformation from the old to the new canonical coordinates is obtained
Leading to the following expression of the second order Hamiltonian function
with .
To reduce the Hamiltonian to a form equivalent to that of the CR3BP, reported in Equation (24), the terms multiplying and shall be set equal to zero. This corresponds to solving the following set of differential equations depending on the variable and including the parameters e, and
The complex system of Equations (A12) is solved using symbolic algebra tools in Matlab. It shall be outlined that the equations depending on the in-plane and the out-of-plane variables are not coupled, therefore they can be solved separately, reducing the use of computational resources. The process results in the following expression for the transformed Hamiltonian function
where collects the terms of order three and higher.
Appendix B.2. Third Order
Applying the transformation developed by Siegel and Moser [41], the Hamiltonian variables are transformed as follows (see [29,40] for the derivation of matrix )
Introducing Equation (A14) to Equation (A13) leads to the following form for the Hamiltonian
where collects the terms of order three and higher.
Because the interest of this analysis is investigating quasiperiodic orbits, the condition is verified, then Equation (A15) can be written in the following form, which includes all terms up to order three
where the long expressions for the coefficients were not reported, but can be derived from the procedure described in the previous paragraphs.
A canonical transformation is here introduced to absorb the order three Hamiltonian, operating as in Appendix B.1. The expression for the generating function, given by Equation (31), is reported below for the sake of clarity
Resulting in the following transformation from the old to the new canonical coordinates
Introducing the Equation (A18) into Equation (A16) results in two sets of ordinary differential equations, one for , , and , related on the in-plane variables , and one for , , , and , related to the out of plane variables . These sets of ordinary differential equations are solved using symbolic algebra tools in Matlab, producing the following form for the Hamiltonian function
where collects the terms of order four and higher.
As discussed in Section 4, the canonical transformation defaults in case of resonance, occurring for and , where is an arbitrarily small constant. In this case the denominator of some coefficients in functions , , , and are equal to zero, and residual terms of the Hamiltonian, reported in Equation (35), can be threaded as indicated in Section 4 to determine stationary points corresponding to quasiperiodic solutions.
References
- Rathsman, P.; Kugelberg, P.; Bodin, P.; Racca, D.G.; Foing, B.; Stagnaro, L. SMART-1: Development and Lessons Learnt. Acta Astronaut. 2005, 56, 455–468. [Google Scholar] [CrossRef]
- Lo, M.W.; Williams, B.G.; Bollman, W.E.; Han, D.S.; Hahn, Y.S.; Bell, J.L.; Hirst, E.; Corwin, R.; Hong, R.; Howell, K.; et al. Genesis mission design. J. Astronaut. Sci. 2011, 49, 169–184. [Google Scholar] [CrossRef]
- Folta, D.C.; Woodard, M.; Howell, K.; Patterson, C.; Schlei, W. Applications of multi-body dynamical environments the ARTEMIS transfer trajectory design. Acta Astronaut. 2012, 73, 237–249. [Google Scholar] [CrossRef]
- Roncoli, R.B.; Fujii, K.K. Mission design overview for the gravity recovery and interior laboratory GRAIL mission. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Toronto, ON, Canada, 2–5 August 2010. [Google Scholar]
- Farquhar, R.W. The Flight of ISEE-3/ICE Origins, Mission History, and a Legacy. J. Astronaut. Sci. 2001, 49, 23–73. [Google Scholar] [CrossRef]
- Dunham, D.W.; Jen, S.J.; Roberts, C.E.; Seacord, A.W., II; Sharer, P.J.; Folta, D.C.; Muhonen, D.P. Transfer trajectory design for the SOHO libration-point mission. In Proceedings of the 43rd International Astronautical Congress, Washington, DC, USA, 28 August–5 September 1992. [Google Scholar]
- Sharer, P.; Harrington, T. Trajectory Optimization for the ACE Halo Orbit Mission. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, San Diego, CA, USA, 29–31 July 1996. AIAA paper 96-3601-CP. [Google Scholar]
- Franz, H.; Sharer, P.; Ogilvie, K.; Desch, M. WIND Nominal Mission Performance and Extended Mission Design. J. Astronaut. Sci. 2001, 49, 145–167. [Google Scholar] [CrossRef]
- Uesugi, K.; Matuso, H.; Kawaguchi, J.; Hayashi, T. Japanese first double Lunar swingby mission HITEN. Acta Astronaut. 1991, 25, 347–355. [Google Scholar] [CrossRef]
- Belbruno, E.; Miller, J. Sun-perturbed Earth-to-Moon transits with balistic capture. J. Guid. Control Dyn. 1993, 16, 770–775. [Google Scholar] [CrossRef]
- Szebehely, V. Theory of Orbit the Restricted Problem of Three Bodies; Academic Press: London, UK, 1967. [Google Scholar]
- Goḿez, G.; Masdemont, J. Some zero cost transfers between libration points orbits. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, Clearwater, FL, USA, 23–26 January 2000. Paper AAS 00-177. [Google Scholar]
- Breakwell, J.V.; Brown, J.V. The halo family of 3-dimensional periodic orbits in the Earth–Moon restricted 3-body problem. Celest. Mech. Dyn. Astron. 1979, 20, 389–404. [Google Scholar] [CrossRef]
- McCarthy, B.P.; Howell, K.C. Leveraging quasi-periodic orbits for trajectory design in cislunar space. Astrodynamics 2021, 5, 139–165. [Google Scholar] [CrossRef]
- Farquhar, R.W.; Kamel, A.A. Quasi-periodic orbits about the translunar libration point. Celest. Mech. Dyn. Astron. 1973, 7, 458–473. [Google Scholar] [CrossRef]
- Moeckel, R. A variational proof of existence of transit orbits in the restricted three-body problem. Dyn. Syst. Int. J. 2005, 20, 45–58. [Google Scholar] [CrossRef][Green Version]
- Anderson, R.L.; Easton, R.W.; Lo, M.W. Isolating blocks as computational tools in the circular restricted three-body problem. Physica D 2017, 343, 38–50. [Google Scholar] [CrossRef]
- Giancotti, M.; Pontani, M.; Teofilatto, P. Lunar capture trajectories and homoclinic connections through isomorphic mapping. Celest. Mech. Dyn. Astron. 2012, 114, 55–76. [Google Scholar] [CrossRef]
- Conley, C.C. Low energy transit orbits in the restricted three-body problem. J. Appl. Math. 1968, 16, 732–746. [Google Scholar] [CrossRef]
- Conley, C.C. On the Ultimate Behavior of Orbits with Respect to an Unstable Critical Point l. Oscillating, Asymptotic, and Capture Orbits. J. Differ. Equ. 1969, 5, 136–158. [Google Scholar] [CrossRef]
- Koon, W.S.; Lo, M.W.; Marsden, J.E.; Ross, S.D. Low Energy transit to the Moon. Celest. Mech. Dyn. Astron. 2001, 81, 63–73. [Google Scholar] [CrossRef]
- Giancotti, M.; Pontani, M.; Teofilatto, P. Cylindrical isomorphic mapping applied to invariant manifold dynamics for Earth-Moon Missions. Celest. Mech. Dyn. Astron. 2014, 120, 249–268. [Google Scholar] [CrossRef]
- Anderson, R.L.; Lo, M.W. Spatial approaches to moons from resonance relative to invariant manifolds. Acta Astronaut. 2014, 105, 335–372. [Google Scholar] [CrossRef]
- Khaja Fayaz, H.; Khaja Faisal, H.; Carletta, S.; Teofilatto, P. Deployment of a microsatellite constellation around the Moon using chaotic multi body dynamics. In Proceedings of the 71st International Astronautical Congress, Dubai, United Arab Emirates, 25–29 October 2021. [Google Scholar]
- Carletta, S.; Pontani, M.; Teofilatto, P. Earth-Mars microsatellite missions using ballistic capture and low-thrust propulsion. In Proceedings of the 71st International Astronautical Congress, Dubai, United Arab Emirates, 25–29 October 2021. [Google Scholar]
- Szebehely, V.; Giacaglia, G.E.O. On the elliptic restricted problem of three bodies. Astronaut. J. 1964, 69, 230–235. [Google Scholar] [CrossRef]
- Michalodimitrakis, M. The circular restricted four-body problem. Astrophys. Space Sci. 1981, 75, 289–305. [Google Scholar] [CrossRef]
- Carletta, S.; Pontani, M.; Teofilatto, P. Station-keeping about sun-mars three-dimensional quasi-periodic collinear libration point trajectories. Adv. Astronaut. Sci. 2020, 173, 299–311. [Google Scholar]
- Carletta, S.; Pontani, M.; Teofilatto, P. Long-term capture orbits for low-energy space missions. Celest. Mech. Dyn. Astron. 2018, 130, 46. [Google Scholar] [CrossRef]
- Conley, C.; Easton, R. Isolated invariant sets and isolating blocks. Trans. Am. Math. Soc. 1971, 158, 35–61. [Google Scholar] [CrossRef]
- Graziani, F.; Sparvieri, N.; Carletta, S. A low-cost Earth-Moon-Mars Mission Using a Microsatellite Platform. In Proceedings of the 71st International Astronautical Congress, Online Event, 12–14 October 2020. [Google Scholar]
- Carletta, S. Design of fuel-saving lunar captures using finite thrust and gravity-braking. Acta Astronaut. 2021, 181, 190–200. [Google Scholar] [CrossRef]
- Carletta, S.; Pontani, M.; Teofilatto, P. Dynamics of three-dimensional capture orbits from libration region analysis. Acta Astronaut. 2019, 165, 331–343. [Google Scholar] [CrossRef]
- Arnold, V.I. Small denominators and problems of stability of motion in classical and celestial mechanics. In Collected Works; Vladimir I. Arnold—Collected Works; Givental, A.B., Khesin, B.A., Marsden, J.E., Varchenko, A.N., Vassiliev, V.A., Viro, O.Y., Zakalyukin, V.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 1. [Google Scholar]
- Blanc, M.; Alibert, Y.; André, N.; Atreya, S.; Beebe, R.; Benz, W.; Bolton, S.J.; Coradini, A.; Coustenis, A.; Dehant, V.; et al. LAPLACE: A mission to Europa and the Jupiter System for ESA’s Cosmic Vision Programme. Exp. Astron. 2009, 23, 849–892. [Google Scholar] [CrossRef][Green Version]
- Phillips, C.B.; Pappalardo, R.T. Europa Clipper Mission Concept: Exploring Jupiter’s Ocean Moon. EOS 2014, 95, 165–167. [Google Scholar] [CrossRef]
- Carletta, S.; Pontani, M.; Teofilatto, P. Design of low-energy capture trajectories in the elliptic restricted four-body problem. In Proceedings of the 70th International Astronautical Congress, Washington, DC, USA, 21–25 October 2019. [Google Scholar]
- Liu, C.; Gong, S. Hill stability of the satellite in the elliptic restricted four-body problem. Astrophys. Space Sci. 2018, 363, 162. [Google Scholar] [CrossRef]
- Llibre, J.; Piñol, C. On the elliptic restricted three-body problem. Celest. Mech. Dyn. Astron. 1990, 48, 319–345. [Google Scholar] [CrossRef]
- Meyer, K.R.; Hall, G.R.; Offin, D. Introduction to Hamiltonian Dynamical Systems and the N-Body Problem. In Applied Mathematical Sciences; Springer Science+Business Media: New York, NY, USA, 2009. [Google Scholar]
- Siegel, C.L.; Moser, J.K. Lectures on Celestial Mechanics Reprint of the 1971 Edition; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Koon, W.S.; Lo, M.W.; Marsden, J.E.; Ross, S.D. Dynamical Systems, the Three-Body Problem and Space Mission Design; Marsden Books, 2011; Available online: https://www.researchgate.net/publication/328913173_Dynamical_Systems_the_Three-Body_Problem_and_Space_Mission_Design (accessed on 20 February 2022).
- Moser, J. On the generalization of a theorem of A. Liapounoff. Commun. Pure Appl. Math. 1958, 11, 257–271. [Google Scholar] [CrossRef]
- Carletta, S.; Pontani, M.; Teofilatto, P. Dynamics of capture orbits from libration region analysis. In Proceedings of the 69th International Astronautical Congress, Bremen, Germany, 1–5 October 2018. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).