A Parallelized Genetic Algorithm to Evaluate Asteroid Impact Missions Using Electric Propulsion
Abstract
1. Introduction
2. NEXT-C Ion Thruster
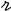 , where
, where 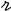 is the magnitude of separation. The data from Fisher et al. [19] was used to set the propellant flow rate as and the thrust efficiency as . When , the thrust power was and the available thrust was .
is the magnitude of separation. The data from Fisher et al. [19] was used to set the propellant flow rate as and the thrust efficiency as . When , the thrust power was and the available thrust was .3. Mission Parameters
4. Parallelized Evaluation Process
4.1. Launch
4.2. Impact
4.3. Heliocentric Trip
5. Genetic-Algorithm-Based Optimization of Parameters
5.1. Crossover
5.2. Mutations
5.3. Annealing
6. Results and Discussion
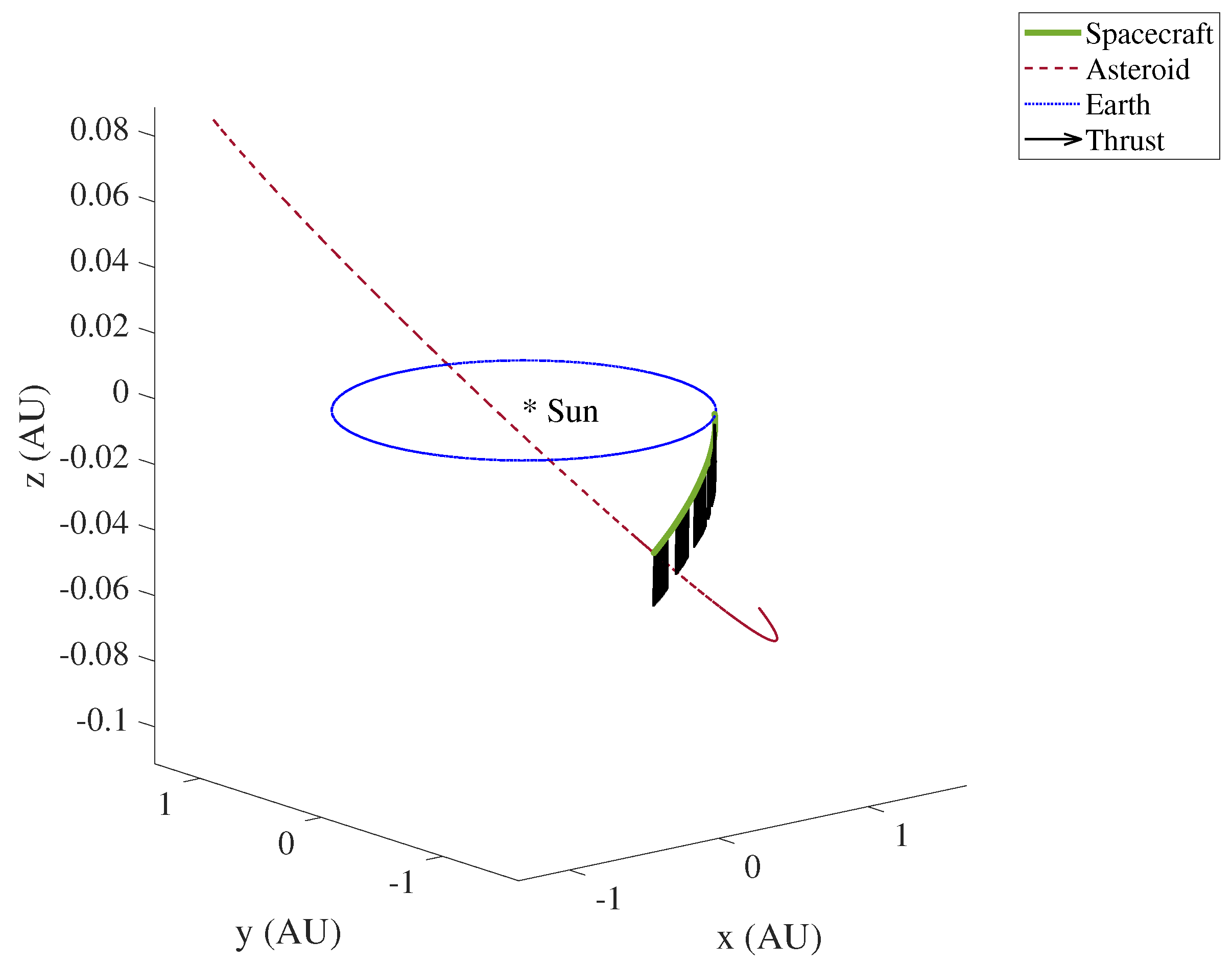
6.1. Baseline
6.2. Comparable Trip Time
6.2.1. Varying Available Propellant Mass
6.2.2. Varying Available Power
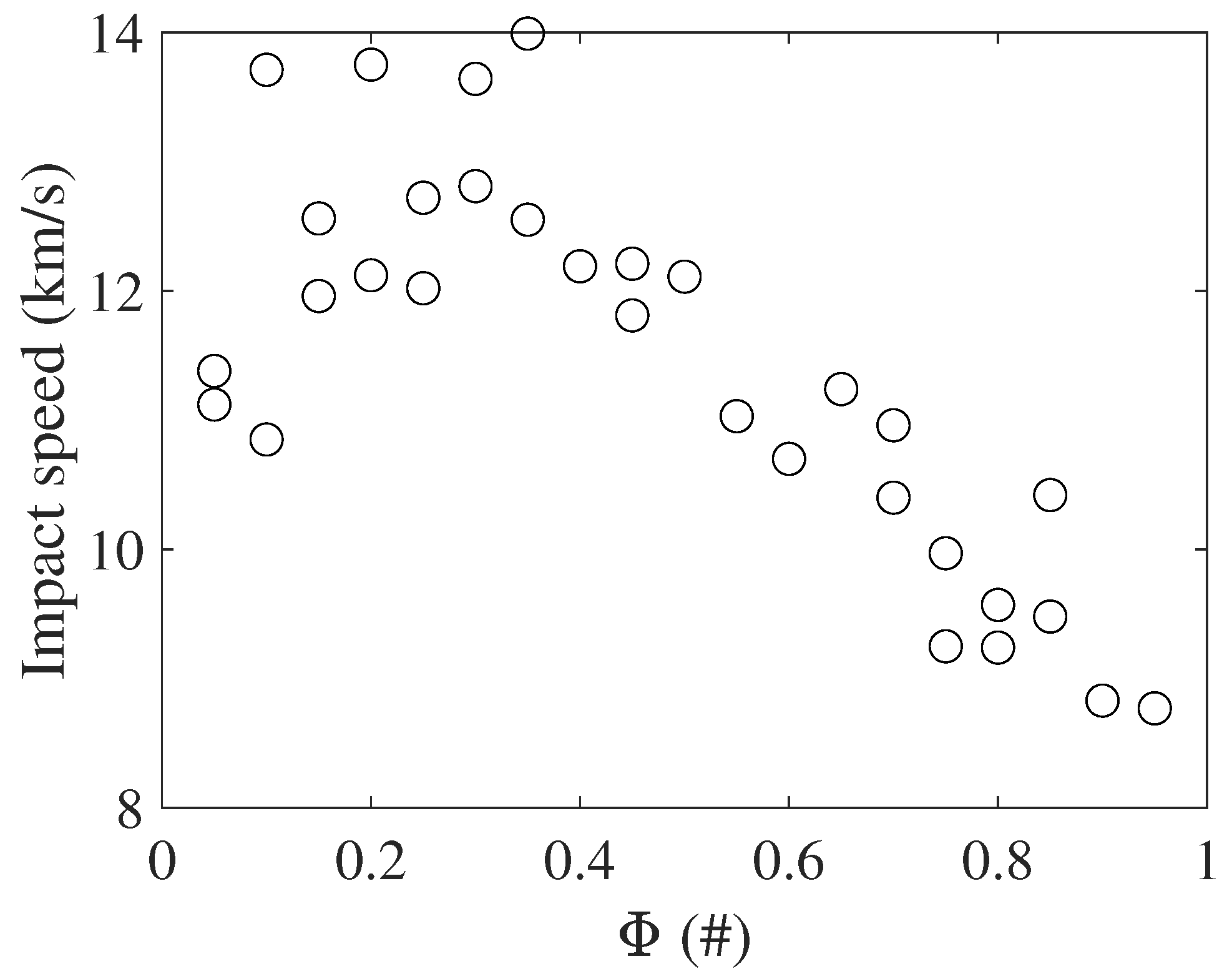
6.2.3. Varying Survivor Selection
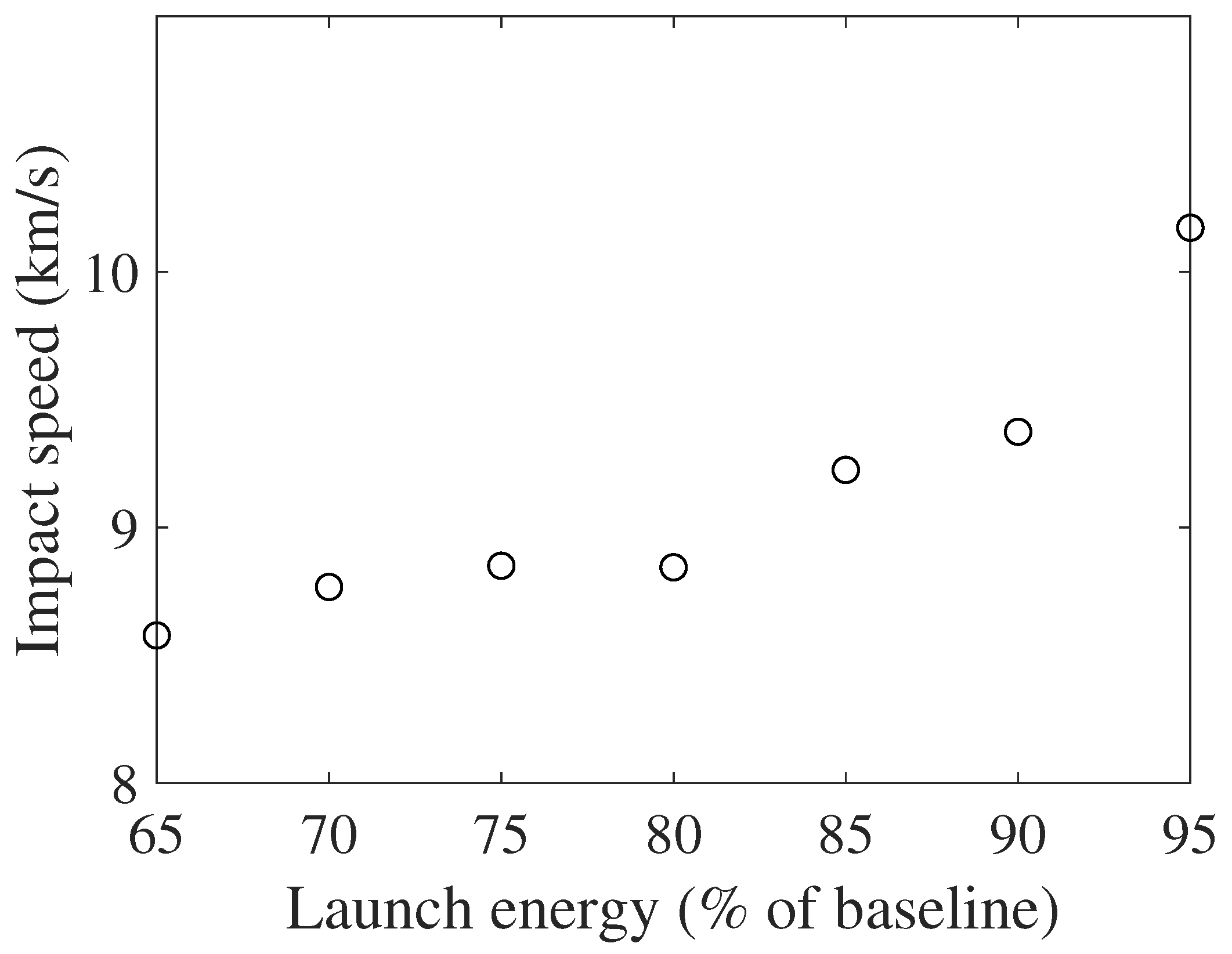
6.2.4. Varying Launch Energy
6.3. Short Trip Time
7. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Acceleration of the spacecraft due to thrust (AU s) | |
| Function used to optimize coasting (#) | |
| Thrust exerted on the spacecraft (kg AU s) | |
| Mass of the spacecraft (kg) | |
| Radial, angular, and off-plane position of the spacecraft (AU, rad, AU) | |
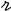 | Magnitude of separation of the spacecraft from the Sun (AU) |
| ESOI | Earth’s sphere of influence |
| T | Trip time from leaving ESOI to impact (s) |
| Radial, tangential, and off-plane velocity of the spacecraft (AU/s) | |
| Angular location in the ecliptic plane at ESOI (rad) | |
| In-plane and off-plane angles of velocity at ESOI (rad) | |
| In-plane and off-plane directions of thrust (rad) | |
| Thrust efficiency (#) | |
| Fraction of “parents” chosen based on proximity vs. impact speed (#) | |
| Input function to (rad) |
References
- Stahl, B.; Braun, R. Low-Thrust Trajectory Optimization Tool to Assess Options for Near-Earth Asteroid Deflection. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; AIAA: Honolulu, HI, USA, 2008; p. 6255. [Google Scholar] [CrossRef][Green Version]
- Sankaran, K.; French, A.; Gady, S.; Wisniewski, T.; Woodkey, M. Evaluation of Electric Propulsion Systems for Asteroid and Comet Sample-Return Missions. In Proceedings of the AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014; AIAA: Cleveland, OH, USA, 2014; p. 3720. [Google Scholar] [CrossRef]
- Englander, J.; Conway, B. An Automated Solution of the Low-Thrust Interplanetary Trajectory Problem. J. Guid. Control Dyn. 2016, 40, 15–27. [Google Scholar] [CrossRef] [PubMed]
- Casalino, L.; Simeoni, F. Indirect optimization of asteroid deflection missions with electric propulsion. J. Guid. Control Dyn. 2012, 35, 423–433. [Google Scholar] [CrossRef]
- Kantsiper, B. The Double Asteroid Redirection Test (DART) mission electric propulsion trade. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017; IEEE: Big Sky, MT, USA, 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Knittel, J.; Englander, J.; Ozimek, M.; Atchison, J.; Gould, J. Improved Propulsion Modeling for Low-Thrust Trajectory Optimization. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, San Antonio, TX, USA, 5–9 February 2017; AAS: San Antonio, TX, USA, 2017; pp. 1–19. [Google Scholar]
- Jean, I.; Misra, A.; Ng, A. Controlled Spacecraft Trajectories in the Context of a Mission to a Binary Asteroid System. J. Astronaut. Sci. 2021, 68, 38–70. [Google Scholar] [CrossRef]
- Cheng, A.; Michel, P.; Reed, C.; Galvez, A.; Carnelli, I. DART: Double Asteroid Redirection Test. In Proceedings of the European Planetary Science Congress (EPSC), Madrid, Spain, 23–28 September 2012; Volume 7, p. 935. [Google Scholar]
- Atchison, J.; Ozimek, M.; Kantsiper, B.; Cheng, A. Trajectory options for the DART mission. Acta Astronaut. 2016, 123, 330–339. [Google Scholar] [CrossRef]
- Sarli, B.; Ozimek, M.; Atchison, J.; Englander, J.; Barbee, B. NASA Double Asteroid Redirection Test (DART) Trajectory Validation and Robustness. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, San Antonio, TX, USA, 5–9 February 2017; AAS: San Antonio, TX, USA, 2017; pp. 1–17. [Google Scholar]
- Ozimek, M.; Atchison, J. NASA Double Asteroid Redirection Test (DART) Low-Thrust Trajectory Concept. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, San Antonio, TX, USA, 5–9 February 2017; AAS: San Antonio, TX, USA, 2017; pp. 1–20. [Google Scholar]
- Sarli, B.; Atchison, J.; Ozimek, M.; Englander, J.; Barbee, B. Double Asteroid Redirection Test Mission: Heliocentric Phase Trajectory Analysis. J. Spacecr. Rocket. 2019, 56, 546–558. [Google Scholar] [CrossRef]
- Patterson, M.; Foster, J.; Haag, T.; Rawlin, V.; Soulas, G.; Roman, R. NEXT: NASA’s Evolutionary Xenon Thruster. In Proceedings of the AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Indianapolis, IN, USA, 7–10 July 2002; AIAA: Indianapolis, IN, USA, 2002; p. 3832. [Google Scholar] [CrossRef]
- Janin, G.; Gómez-Tierno, M. The Genetic Algorithms for Trajectory Optmization. In Proceedings of the 36th Congress of the International Astronautical Federation (IAF-85), Stockholm, Sweden, 7–12 October 1985; p. 244. [Google Scholar]
- Hartmann, J.; Coverstone-Carroll, V.; Williams, S. Optimal Interplanetary Spacecraft Trajectories via a Pareto Genetic Algorithm. J. Astronaut. Sci. 1998, 46, 267–282. [Google Scholar] [CrossRef]
- Vavrina, M.; Englander, J.; Philiips, S.; Hughes, K. Global, Multi-Objective Trajectory Optmization with Parametric Spreading. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, San Antonio, TX, USA, 5–9 February 2017; AAS: San Antonio, TX, USA, 2017; pp. 1–20. [Google Scholar]
- Darani, S.; Abdelkhalik, O. Space Trajectory Optmization Using Hidden Genes Genetic Algorithms. J. Spacecr. Rocket. 2018, 55, 764–774. [Google Scholar] [CrossRef]
- Van Noord, J. Lifetime Assessment of the NEXT Ion Thruster. In Proceedings of the AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cincinnati, OH, USA, 8–11 July 2007; AIAA: Cincinnati, OH, USA, 2007; p. 5274. [Google Scholar] [CrossRef]
- Fisher, J.; Ferriauolo, B.; Hertel, T.; Monheiser, J.; Barlog, C.; Allen, M.; Myers, R.; Hoskins, A.; Bontempo, J.; Nazario, M.; et al. NEXT-C Flight Ion Propulsion System Development Status. In Proceedings of the International Electric Propulsion Conference (IEPC), Atlanta, GA, USA, 8–12 October 2017; ERPS: Atlanta, GA, USA, 2017; p. 218. [Google Scholar]
- Abdelkhalik, O.; Taheri, E. Approximate On-Off Low-Thrust Space Trajectories Using Fourier Series. J. Spacecr. Rocket. 2012, 49, 962–965. [Google Scholar] [CrossRef]
- Sankaran, K.; Hamming, B.; Grochowski, C.; Hoff, J.; Spaun, M.; Rollins, M. Evaluation of Existing Electric Propulsion Systems for the OSIRIS-REx Mission. J. Spacecr. Rocket. 2013, 50, 1292–1295. [Google Scholar] [CrossRef]
- Stefano, I.; Cappuccio, P.; Iess, L. The BepiColombo solar conjunction experiments revisited. Class. Quantum Gravity 2020, 38, 055002. [Google Scholar] [CrossRef]
- Dormand, J.R.; Prince, P.J. A family of embedded Runge-Kutta formulae. J. Comput. Appl. Math. 1980, 6, 19–26. [Google Scholar] [CrossRef]
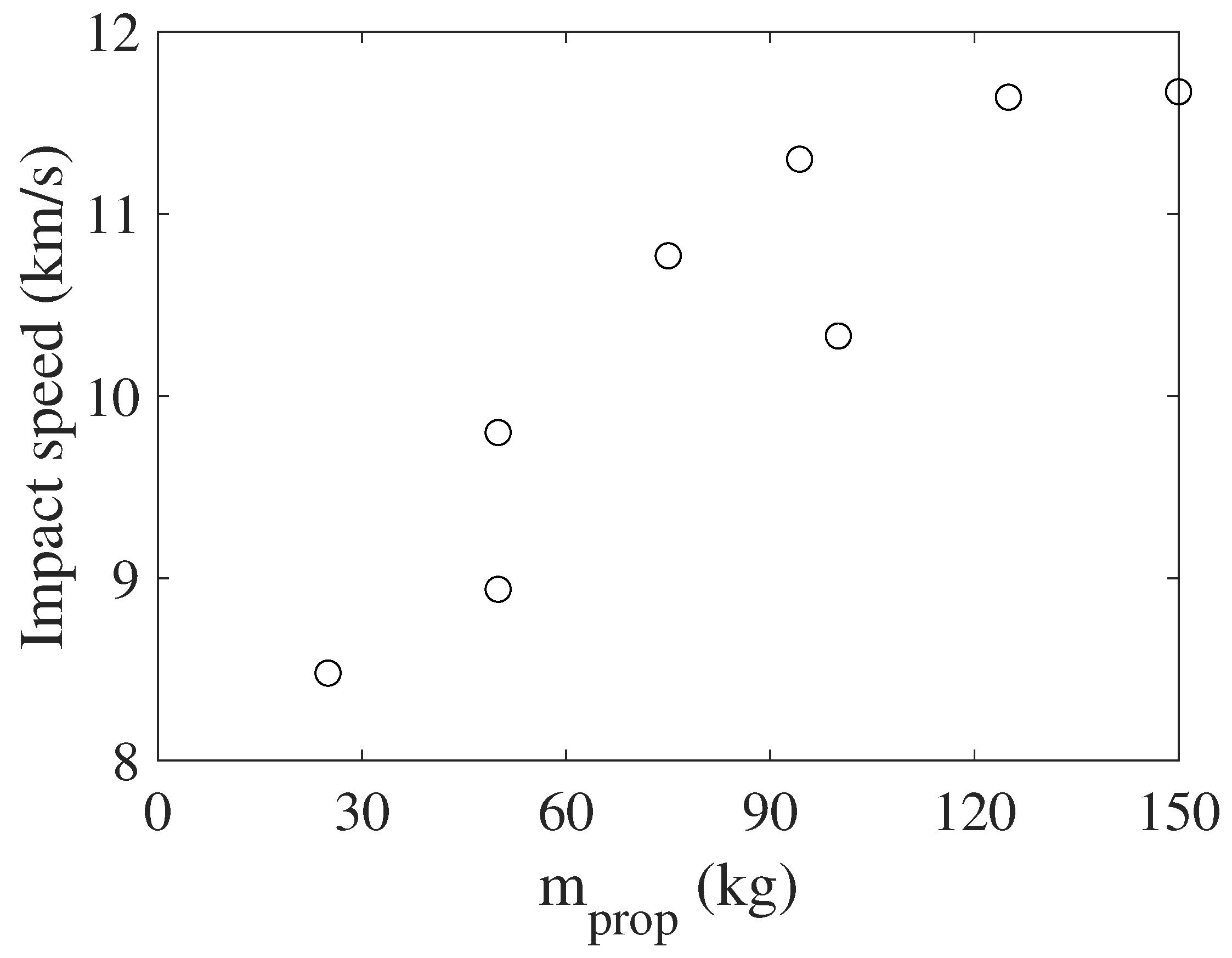

| Variable | Range |
|---|---|
| T | 1.0–1.5 yrs |
| ± rad | |
| 0– rad | |
| ± rad | |
| ± rad | |
| ± rad | |
| ± rad |
| (Rad) | (Rad) | (Rad) | T (Days) | |
|---|---|---|---|---|
| −1.8 | 1.7 | −0.9 | 435.69 | 6.64 |
| −1.6 | 1.7 | −0.9 | 435.44 | 6.63 |
| −1.5 | 1.8 | −0.9 | 435.33 | 6.62 |
| −0.8 | 1.8 | −0.9 | 434.55 | 6.58 |
| −0.6 | 1.9 | −0.9 | 434.16 | 6.57 |
| −0.3 | 1.9 | −0.9 | 433.72 | 6.57 |
| 0.1 | 1.9 | −0.9 | 432.77 | 6.59 |
| 0.3 | 1.9 | −0.9 | 432.41 | 6.60 |
| 0.5 | 1.9 | −0.9 | 432.21 | 6.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sankaran, K.; Griffith, S.A.; Thompson, N.C.; Lochridge, M.D.; O’Kins, A.S. A Parallelized Genetic Algorithm to Evaluate Asteroid Impact Missions Using Electric Propulsion. Aerospace 2022, 9, 116. https://doi.org/10.3390/aerospace9030116
Sankaran K, Griffith SA, Thompson NC, Lochridge MD, O’Kins AS. A Parallelized Genetic Algorithm to Evaluate Asteroid Impact Missions Using Electric Propulsion. Aerospace. 2022; 9(3):116. https://doi.org/10.3390/aerospace9030116
Chicago/Turabian StyleSankaran, Kamesh, Scott A. Griffith, Noah C. Thompson, Matthew D. Lochridge, and Andrew S. O’Kins. 2022. "A Parallelized Genetic Algorithm to Evaluate Asteroid Impact Missions Using Electric Propulsion" Aerospace 9, no. 3: 116. https://doi.org/10.3390/aerospace9030116
APA StyleSankaran, K., Griffith, S. A., Thompson, N. C., Lochridge, M. D., & O’Kins, A. S. (2022). A Parallelized Genetic Algorithm to Evaluate Asteroid Impact Missions Using Electric Propulsion. Aerospace, 9(3), 116. https://doi.org/10.3390/aerospace9030116







