Path Planning for Self-Collision Avoidance of Space Modular Self-Reconfigurable Satellites

Abstract

Space modular self-reconfigurable satellite (SMSRS) is a new type of satellite. The research on self-collision avoidance of SMSRS is important for its on-orbit safety but is not completely solved. This paper offers a new method for joint path planning for self-collision avoidance of SMSRS. Firstly, we establish the collision detection model for SMSRS based on forward kinematics and the spherical nonholonomic envelope to detect the collision occurring in SMSRS. Then, to achieve offline path planning in joint space, we proposed the self-collision avoidance strategy, which splices multiple C-spaces based on the pre-defined joint path into a binary map, and then transforms the binary map into a map with the dangerous potential field, and planning algorithms based on a map with the dangerous potential field is proposed to find the optimal collision-free path. The new method is applied to two cases and both find collision-free joint paths for SMSRS successfully, which demonstrates the feasibility of the method. In addition, this study bridges the gap in the study of self-collision avoidance of super-redundant self-reconfigurable satellites.

1. Introduction

With the large-scale exploitation of outer space and the increasing frequency of spacecraft and satellite launches, future space systems are expected to have low cost, rapid response, and multiple uses [1]. However, the traditional development mode cannot meet the needs of future space systems [2]. For example, traditional space systems are almost specially designed for missions, requiring subsystem-by-subsystem development and numerous iterations, which are slow, repetitive, and expensive [3]. In addition, the structures of these traditional spacecraft systems are essentially permanently fixed and designed to perform a single mission that cannot be reconfigured for other missions. Long development cycles and launch-window limitations also make it difficult for them to respond quickly to emergencies [3].

To overcome these limitations of existing space systems, many new concept satellites have been proposed, and the most representative ones are CubeSats [4,5]. The primary goal of CubeSats is to provide a small, lightweight, low-cost platform for academic and technology demonstration. A CubeSat is a $10 \mathrm{cm}\times 10 \mathrm{cm}\times 10 \mathrm{cm}$ cube. It provides a standard for the design of picosatellites to reduce cost and development time, increase accessibility to space, and sustain frequent launches [6]. The spacecraft bus was designed to be versatile enough to accommodate different payloads that meet the mass, volume, and power constraints. Presently, the CubeSat Projects become attractive for wide fields [7,8], such as exoplanet detection [9,10], space weather [11], weather forecasting [12], and river-flow estimation [13].

However, the utilization of a standard, low-cost satellite bus will reduce the reliability and decrease the lifetime of Cubesats [14,15]. A statistical study performed in 2013 on the first 100 launched CubeSats [16] shows that the mission failures of CubeSats are on a high level [17]. In addition, the structure of CubeSat is fixed, and it carries limited payloads so that they can only perform a single space task.

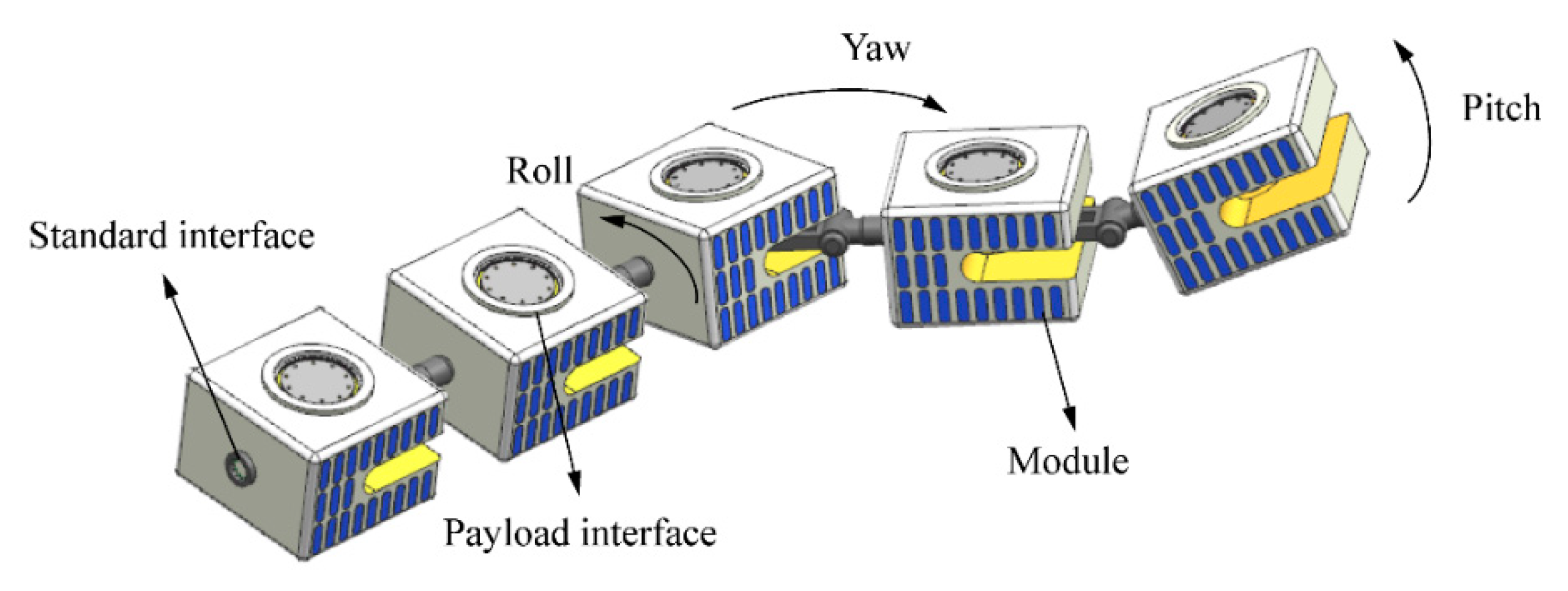
Taking the design concept of CubeSat as the baseline, we proposed a new type of satellite with a reconfigurable structure and adjustable function, named Space Modular Self-Reconfigurable Satellite (SMSRS). SMSRS has the following features:

(1) Modular: SMSRS has a chain structure composed of functional modules and joints. Common satellite subsystems are integrated into unit modules and are called subsystem modules. The unit subsystem modules are installed with standard interfaces for payloads and joints. According to shapes and work positions, the payloads are designed as external structures carrying standard docking interfaces to the subsystem modules, or as unit payload modules. The modular design of SMSRS facilitates the structural folding and packaging before launch and the reconfiguration in space [18].

(2) Scalability: Payload and subsystem modules are functionally independent and physically separated from each other. The volumes and masses of module units are divided into several series from small to large, which can be selected according to the demand of payloads. All modules have standard interfaces, which are used to connect with modular joint modules for ground or in-orbit extension according to the type of space mission. The type and number of modules carried by SMSRS are configured to mission requirements. The model of the SMSRS with five modules is shown in Figure 1.

(3) Structural Reconfigurability: There are three mutually orthogonal joints between modules of SMSRS. The three joints form degrees of freedom (DOFs) between modules in relative rotation, roll, and yaw and enable the SMSRS to self-reconfigure adaptively to mission command.

(4) Risk resistance. The scalability and modularity together determine the risk resistance of SMSRS. Since modules are functionally independent, the failure of a local satellite module makes the satellite not completely fail, and the multiple payloads it carries can still be reprogrammed functionally. In addition, multiple joints between modules allow the modules to maintain some relative motion capability in the event of a single joint failure.

(5) Functional Adjustability: The types of payloads carried by SMSRS include optical cameras, SAR, communication payloads, etc. While carrying different payloads, SMSRS arranges and reorganizes these payloads in different space orientations by structural reconfiguration and therefore achieves the ability to accomplish multiple types of space missions. There are typical application scenarios for SMSRS:

• When SMSRS carries multiple optical cameras, it could change the spatial orientations of these cameras through joint motions. With this, these cameras could achieve an expanded imaging area by stitching together their field of view as shown in Figure 2a, or achieve the reconnaissance of multiple targets as shown in Figure 2b.
• When SMSRS carries multiple communication payloads and adjusts them towards different orientations, it can achieve multi-area communication to the earth, as shown in Figure 2c.

The application scenarios of SMSRS are by no means limited to these, and there are larger expansions. Moreover, in recent years, a large number of small satellite launches have led to space traffic congestion and burdened space traffic management. At the same time, a large amount of space debris is generated, which seriously threatens the safety of satellites in orbit. The multi-functional feature of SMSRS, which allows a single satellite to perform multiple functions adaptively, can reduce the number of satellite launches. It reduces the pressure of space traffic management and the generation of space debris.

The target orbit of SMSRS is Low Earth Orbit (LEO). The advantage of standing high and seeing far in High Earth Orbit (HEO) can be compensated by the feature of SMSRS multi-payload synergy, e.g., the large field of view of HEO satellites can be achieved by using fields of view stitching of SMSRS. In addition, LEO launches can launch heavier mass satellites at a lower cost, providing margin for SMSRS in-orbit scalability.

When running on LEO, the satellite tracking is characterized by low transmission delay, low coverage, low link loss, and low power consumption. The low transmission delay and low loss are beneficial to the command transmission of the reconfiguration for SMSRS, and in solving the low coverage problem, as shown in Figure 2c, adjusting the orientation of the tracking system can be used to expand the tracking range.

As shown in Figure 3, SMSRS are folded and packed on the ground before launch. After getting into orbit, the folded configuration is gradually unfolded and changed from the initial configuration to the work configuration for performing the designed mission. When the SMSRS receives a new mission command, its mission planning system will plan the new mission configuration and send the joint control system command for reconfiguring to the new work configuration. Modules of SMSRS have solar cells attached to each surface to ensure battery recharging in different configurations.

The function switching of SMSRS depends largely on the motion of the joints. However, from Figure 1, it can be seen that the modules of SMSRS are large in size but small in spacing between each other, and the motion of the joints allows the relative positions of these modules to change over a wide range so that collisions between modules can easily occur. When a collision occurs, it is likely to cause structural damage and instability of the system [19]. To avoid self-collisions between modules in whole reconfiguration progress is crucial for the on-orbit safety of the system [20]. In this paper, we will study how to achieve self-collision avoidance in the reconfiguration of SMSRS.

The remaining paper is organized as follows. Section 2 sorts out the related work on self-collision avoidance of self-configuring systems. In Section 3, the collision detection model of SMSRS is established. Section 4 elaborates on the self-collision strategy of SMSRS. In Section 5, the parameters of SMSRS and two self-collision avoidance tasks are set. Section 6 verifies the self-collision avoidance path planning method. Section 7 summarizes the work of this paper.

2. Related Work

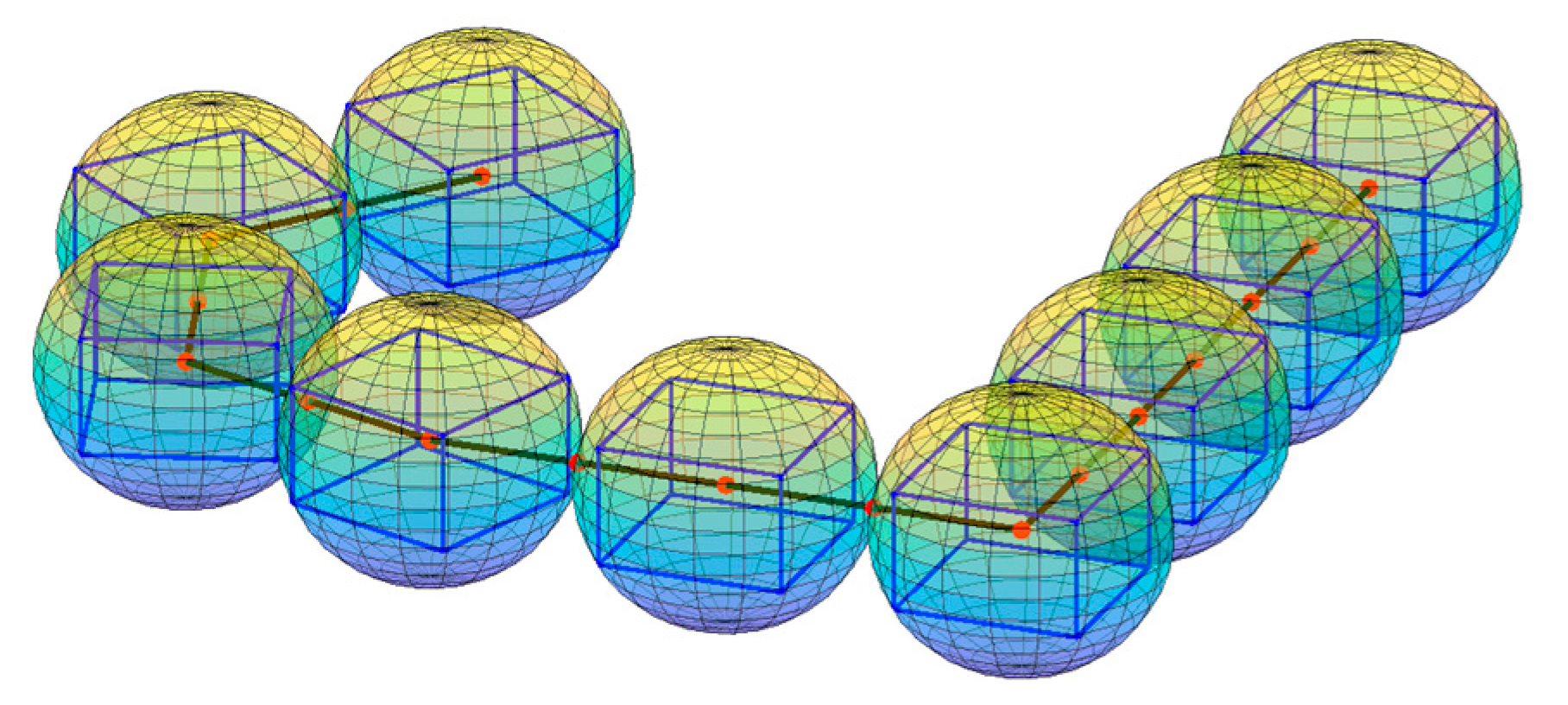
The researches on avoiding self-collision are mainly for redundant robotic arms, and the contents mainly involve two aspects: self-collision detection and self-collision avoidance strategies. Collision detection focuses on establishing an approximate geometric model of the collision-prone structures of the research object to calculate the relative position between them [21] and to judge whether they will collide or have collided. There are two common methods to establish the collision detection model. The first method uses a large number of polygons [22,23] to model the geometrical shapes of collision-prone structures to fit them as closely as possible. This method is generally suitable for systems that have an irregular shape and higher requirements for collision detection accuracy, or are used to perform sophisticated tasks, but it requires higher computational costs. For systems with regular shapes or have low requirements for collision detection accuracy, using the sphere-based model to establish its approximate structural envelope is another method [20,21]. These approximate envelopes can be selected according to the shape of the system, including spheres [21,24], swept-spheres [25], cylinders [20], capsules [26], patch-based bounding volumes [27], etc. Although the second method could not accurately describe the shape of the collision-prone structures, it is computationally economical.

In the present research, self-collision avoidance strategies are usually divided into the online reactive approach [27,28] and offline path planning. Of the two, the online reactive approach does not predetermine the angle motion path but detects collisions in real time during joint movements. Online reactive approaches usually use the distance functions as “repulsive potential” functions and then converts them into joint velocities based on Jacobian Inverse Kinematics (IK) [26] and joint torques for torque control schemes [29], or regards them as a constraint in an optimization-based IK solver to adjusts the joint motion path in real time [28,30], etc. To obtain smooth joint motion trajectories, some researchers have proposed a unified framework to detect collisions by using a series of sensors capable of estimating joint torques and accelerations in real time. However, the use of expensive hardware such as sensors always increases the cost [21]. Although the online reactive approach has a shorter computation time, it is mostly applied to ground-based humanoid robots and is only applicable to systems with fewer DOFs because of its instability.

Offline path planning can be divided into two categories: path planning of end-effector in workspace [31,32] and path planning of joints in joint space [33,34]. As there is no end-effector of SMSRS, we do not discuss the path planning of the end-effector, but focus on the path planning of the joints in joint space. In contrast to the online method, offline path planning predetermines the motion path of joints and there would not be self-collision when joints move along the predetermined path. Compared with the online reactive approach, offline path planning is more stable and efficient, and the planned paths are guaranteed to be optimal, which are more suitable for space systems with higher requirements for stability. Moreover, for SMSRS, offline path planning will not make its joints detour in space, which is also of great significance for energy conservation. Therefore, offline path planning is the more suitable choice for the self-collision avoidance strategy of SMSRS.

Currently, offline path planning for collision avoidance of self-configuration systems such as space robotic arms is mostly focused on avoiding collision with fixed obstacles or target vehicles in the environment [20,35]. The methods to avoid collision with obstacles in the environment include using a random search algorithm to find a collision-free joint path in the Configuration Space (C-Space) of the robotic arm, and commonly used algorithms include the A* algorithm [36] and the Rapid Exploration Random Tree (RRT) algorithm [37,38,39], and using optimization techniques [40], etc. In addition, the current offline path planning only needs to find collision-free joint paths to achieve the desired pose of the end effector, regardless of the pose of other intermediate structures [20]. The researches on self-avoidance are also mainly focused on systems with fewer DOFs. Therefore, current research cannot meet the requirements of self-collision path planning of SMSRS, mainly because it has the following newly derived difficulties:

(1)

SMSRS has a super-redundant structure, and its ultra-high DOFs make collisions between each module possible and easy;

(2)

The pose of each module of SMSRS is changed in real time during reconfiguration, for one module, all other modules are its dynamic obstacles—this also imposes a burden on collision detection; and

(3)

Different from the robots that only achieve the pose of the end effector without collision, SMSRS requires all modules to achieve desired poses without collision after path planning.

In this paper, considering the above difficulties and the actual space mission requirements, we proposed a new self-collision avoidance method for SMSRS, which consists of a collision detection model and a self-collision avoidance strategy. The collision detection model is established based on the Forward Kinematics (FK) and spherical nonholonomic envelope, which has no hardware cost and low computational cost. Among the offline and online strategies, considering the high stability requirements of the SMSRS and reducing additional hardware as much as possible, the offline path planning is selected to realize self-collision avoidance of SMSRS, and a self-collision avoidance path planning strategy based on pre-defined path and spliced C-space is proposed.

The main contributions of this study are as follows: (1) a collision detection model is developed using multiple discrete spherical, which can approximate envelop SMSRS using a few spheres and execute collision detection for SSMSRS at a low computational cost; (2) a method is proposed for splicing multiple C-spaces into a binary map based on a pre-defined path, which transforms the path planning in dynamic C-space into the planning of time sequence of joints on the pre-defined path; and (3) a new collision-free path search algorithm based on the map with dangerous potential fields is proposed to find the safest path without self-collision for SMSRS.

3. Collision Detection of SMSRS

The collision detection model of SMSRS is used to detect whether each module collides with others, and the relative poses of modules are the basis of collision detection. SMSRS consists of a series of rigid bodies and its modules and inter-module connection structures can also be regarded as links, and this structure forms a kinematic chain. We firstly ignore the specific shape of modules and treat them as links, and calculate their space poses by establishing an FK model in Section 3.1. On this basis, the collision detection model will be completed after assigning the shape characteristics of these links in Section 3.2.

3.1. Module Pose

In SMSRS, each moveable joint defines a joint variable, all joints form a joints vector $\mathit{q}=\left({\theta }_1,{\theta }_1,\cdots ,{\theta }_{N_j}\right)$ and the number of joints N_j defines DOFs of SMSRS. Calculating the poses of links using the given values of the joint variables and the link parameters is a forward problem, which is known as FK [41,42]. In FK, the poses of links can be represented by a homogeneous transformation matrix. For example, the homogeneous transformation matrix [43] of the ith link relative to the base coordinate system ${\Sigma }_b$ is:

$${}_i{}^{0}T=\left[\begin{array}{cccc}{n}_{xi}& o_{xi}& a_{xi}& p_{xi}\\ n_{yi}& o_{yi}& a_{yi}& p_{yi}\\ n_{zi}& o_{zi}& a_{zi}& p_{zi}\\ 0& 0& 0& 1\end{array}\right]=\left[\begin{array}{cc}\left[\begin{array}{ccc}{\mathit{n}}_i& {\mathit{o}}_i& {\mathit{a}}_i\end{array}\right]& {\mathit{p}}_i\\ \mathbf{0}& \mathbf{1}\end{array}\right]=\left[\begin{array}{cc}{\mathit{R}}_i& {\mathit{p}}_i\\ \mathbf{0}& 1\end{array}\right]$$

(1)

where, ${\mathit{R}}_i$ represents the attitude matrix and ${\mathit{p}}_i$ presents the position vector of the ith link. To obtain the homogeneous transformation matrix, we should establish the multi-link coordinate system according to certain rules, then select the parameters to describe relative relationships between coordinate systems. In this paper, we select Denavit–Hartenberg (D–H) method to build the homogeneous transformation matrix. According to the principles of the D–H method, we fix every link with a coordinate system as shown in Figure 4, the ${\Sigma }_b$ is usually established at the center of mass of the attitude control module to facilitate the attitude control, and then the multi-link coordinate system of SMSRS is divided into a and b side by ${\Sigma }_b$. In some space systems, such as space dual-arm robots, the joint axis on both sides of ${\Sigma }_b$ are always designed to be symmetrical in direction, so the D–H parameters on both sides are equal [44]. However, the three joints between the modules are orthogonal and are asymmetrical on both sides of ${\Sigma }_b$, which violates principles of the D–H method on establishing coordinate systems. In this case, we proposed the concept of virtual joint coordinate system Jv [18]. Jv is a coordinate system established between the ${\Sigma }_b$ and the first joint coordinate system on the b side. The origin of the Jv coincides with the origin of ${\Sigma }_b$. Then, the pose matrix of the link on the b side only needs to multiply the homogeneous transformation matrix from the Jv to ${\Sigma }_b$ between the first joint coordinate system and ${\Sigma }_b$. Moreover, Jv does not affect the mass and size of SMSRS when its mass and size are set to 0. The insertion of Jv successfully solves the problem caused by the asymmetrical direction of joints on a and b sides.

Then, four parameters between adjacent coordinate systems: linked length A, link twist α, link offset d, and joint angle θ are measured to calculate their relative relationship. In FK, any single translation or rotation can be expressed by a homogeneous transformation matrix, and a series of motions can be expressed by multiplying these homogeneous transformation matrices of single motions. The four selected parameters imply four-step motions from the (i − 1)th coordinate system to the ith coordinate system, so the homogeneous transformation matrix between them can be expressed as:

$$\begin{array}{cc}\hfill {}_i{}^{i-1}T& =Rot\left(x,{\alpha }_{i-1}\right)·Tran\left(A_{i-1},0,0\right)·Rot\left(z,{\theta }_i\right)·Tran\left(0,0,d_i\right)\hfill \\ & =\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& c{\alpha }_{i-1}& -s{\alpha }_{i-1}& 0\\ 0& s{\alpha }_{i-1}& c{\alpha }_{i-1}& 0\\ 0& 0& 0& 1\end{array}\right]·\left[\begin{array}{cccc}1& 0& 0& A_{i-1}\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]·\left[\begin{array}{cccc}c{\theta }_i& -s{\theta }_i& 0& 0\\ s{\theta }_i& c{\theta }_i& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]·\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& d_i\\ 0& 0& 0& 1\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cccc}c{\theta }_i& -s{\theta }_i& 0& A_{i-1}\\ s{\theta }_{i}c{\alpha }_{i-1}& c{\theta }_{i}c{\alpha }_{i-1}& -s{\alpha }_{i-1}& -s{\alpha }_{i-1}{d}_i\\ s{\theta }_{i}s{\alpha }_{i-1}& c{\theta }_{i}s{\alpha }_{i-1}& c{\alpha }_{i-1}& c{\alpha }_{i-1}{d}_i\\ 0& 0& 0& 1\end{array}\right]\hfill \end{array}$$

(2)

The relative poses of non-adjacent links can be obtained by the successive multiplications of adjacent link homogeneous transformation matrices [43]. Equation (3) shows the homogeneous transformation matrix of the ith link relative to ${\Sigma }_b$.

$${}_i{}^{0}T={}_1{}^{0}T\left({\theta }_1\right){}_2{}^{1}T\left({\theta }_2\right){}_3{}^{2}T\left({\theta }_3\right)\cdots {}_i{}^{i-1}T\left({\theta }_i\right)={\displaystyle \prod }_{k=1}^i{}_k{}^{k-1}T\left({\theta }_k\right)$$

(3)

3.2. Self-Collision Detection Model

3.2.1. Spherical Nonholonomic Envelope

A complete self-collision detection model needs to assign shape properties to links based on the obtained link poses. In this paper, the spherical shape is chosen to envelop the modules of SMSRS, which has the following advantages: (1) the single parameter can avoid a large amount of computational consumption and improve the computational speed. (2) The fixed shape of SMSRS modules can be completely enveloped by spheres, and the approximate nature of the spherical envelope makes the collision detection conservative [24], which is suitable for space systems where reliability and safety are vital. Since the volume of the module is much larger than the volume of the inter-module joint structure, we create a spherical envelope only for the module and ignore the joint structures. The spherical nonholonomic envelope could further improve computational efficiency. And the spherical nonholonomic envelope of SMSRS with nine modules is shown in Figure 5.

3.2.2. Self-Collision Detection Criteria

Figure 6 shows the schematic diagram of the spherical nonholonomic envelope of the SMSRS with three modules. The center of the spherical envelope locates at the center of the module body, and the length of the radius R_C is one half of the diagonal length of the module body. In this paper, the distance between the centers of two modules is used to determine whether modules collide. For SMSRS, $\Psi$ is defined as the set of modules. Select two different modules $y,r\in \Psi ,\left(y\ne r\right)$, their position vectors with respect to ${\Sigma }_b$ are ${\mathit{p}}_y$ and ${\mathit{p}}_r$, $d_{yr}$ denotes the distance between the centers of the two modules, and it equals to the 2-norm of the difference between ${\mathit{p}}_y$ and ${\mathit{p}}_r$. The criteria for determining modules $y,r$ have not collided is:

$$d_{yr}=\Vert {\mathit{p}}_y-{\mathit{p}}_r\Vert >2R_C$$

(4)

For a certain configuration of SMSRS, only if $d_{yr}$ of any two modules is larger than $2R_C$, it can be concluded that SMSRS has no collision under this configuration, and as long as there exist any two modules that collide, this configuration has collision.

4. Self-Collision Avoidance Strategy

Collision avoidance is a fundamental problem in offline path planning, and a two-step framework is widely used in collision-free path planning for robotic arms with few DOFs and mobile robots, i.e., building the C-space and then searching for collision-free paths in the C-space. For the offline collision-free problem of SMSRS in time-varying configurations, we propose the spliced C-space based on pre-defined joint paths and the path planning algorithms based on digital maps with the dangerous potential field, which together consist of the self-collision avoidance strategy of SMSRS. It is implemented in several steps as follows to achieve the self-collision avoidance strategy of SMSRS:

(1)

Locate the collision module and record collision start-stop joint angles;

(2)

Determine the planned joints;

(3)

Build linear path-based multiple C-spaces;

(4)

Pre-defined the paths of the planned joints;

(5)

Splice the multiple C-spaces based on the pre-defined paths into the binary map, and check the validity of the binary map;

(6)

Transform the binary map into a map with the dangerous potential field;

(7)

Search collision-free path in the map with the dangerous potential field; and

(8)

Check paths.

The logical relationships of these steps are shown in Figure 7, where steps (1) to (2) are for initialization, (3) to (5) are for C-space construction, and (6) to (8) are for path planning algorithms based on digital maps with the dangerous potential field. The idea and execution process of each step will be described below.

4.1. Locate the Collision Module

The initial configuration and final configuration with corresponding joint angles are given by the mission planning system. The results of the path planning of SMSRS, on a self-collision-free basis, need to satisfy the pose requirements of each link, not only the desired poses of the end link while ignoring the poses of the other links. Therefore, the goal of the path planning of SMSRS is to find feasible paths for all joints so that the SMSRS can move from the initial configuration to the final configuration without collision. We set all joints of SMSRS to move in linear paths from initial angles to final angles, and locate the collision modules under their linear paths. If there are no additional optimization objectives, the linear path is the most economical path, which avoids the energy waste caused by joints moving in complex paths and could facilitate the subsequent joint trajectory optimization.

Under the linear paths of joints, the collision detection model in Section 3.2 is used to determine whether there is a collision between modules in real time, and once a module collision is detected, the two modules are marked as collision modules, and the collision start angles of joints ${\mathit{q}}_{col\_start}$ are recorded. The final configuration of the SMSRS is collision-free, indicating the collision state will not last until the end, allowing the SMSRS to continue moving and recording the collision stop angles of joints ${\mathit{q}}_{col\_end}$.

4.2. Determine the Planned Joints

Once the collision module and the ${\mathit{q}}_{col\_start}$ and ${\mathit{q}}_{col\_end}$ are clarified, there are two options for the selection of the joints to be planned: planning the path of all joints or planning the path of only some selected joints. In this paper, the paths of two joints are selected to plan to avoid the self-collision, which is based on the following considerations: (1) the path planning with few joints can reduce the planning complexity and computational cost, while a large number of stable and efficient path search algorithms for planes can be utilized, which also improves the visibility; (2) SMSRS has wide ranges of joint angles, and by reasonably configuring the two planned joints, the configurations of SMSRS can be substantially adjusted so that new collision-free paths can be found in the collections of these configurations; and (3) each joint needs to return to the desired angle after path planning, and when multiple joint angles are planned at the same time, it is difficult to ensure that.

The principle of configuring the planned joints is the maximum success rate and maximum stability. The so-called maximum success rate means that the selected joint can find the collision-free path as successfully as possible after planning. Maximum stability means that the planned joint will not significantly change the configuration of the collision-free module, resulting in unnecessary collisions. Combining these two principles, we develop the following selection rules for the planned joints:

• For ith joint, when its ${\theta }_{i\_col\_start}\ne {\theta }_{i\_col\_end}$, we call it motion joint, otherwise no motion joint—when there are more than two motion joints between two collision modules, the two adjacent motion joints closest to the end of SMSRS are selected as the planned joints;
• When the selected joints cannot successfully avoid the self-collision after planning, another two adjacent motion joints between collision modules are selected from the end to the middle of SMSRS;
• When the number of motion joints between collision modules is less than two, a no motion joint closest to the end collision module and a motion joint are selected as planned joints;
• Under (3), if it is still not able to find self-collision-free paths, the motion joint and no motion joint are configured from the end to the middle of SMSRS; and
• After selection, we denote the planned joints as ${\theta }_1^p$, ${\theta }_2^p$, their start collision angles as ${\theta }_{1\_start}^p$, ${\theta }_{2\_start}^p$, and end collision angles as ${\theta }_{1\_end}^p$, ${\theta }_{2\_end}^p$.

4.3. Splice Multiple C-Spaces Based on a Pre-Defined Path

4.3.1. Multiple C-Spaces

The concept of C-space originates from collision detection and avoidance of robotics [12,13], which uses the pose parameters of rigid objects in the workspace as its coordinate parameters, and the kinematic relations map the poses of target objects and obstacles from the workspace to the C-space.

C-space is often used for path planning of rigid objects in stationary obstacles. Therefore, C-space can be further divided into two subspaces: obstacle space and free space. The obstacle space refers to the space occupied by obstacles in the C-space, while the free space refers to the space not occupied by obstacles in C-space. Unlike the physical workspace, the dimensions of the C-space are defined as the DOFs of all control variables in the motion system [45]. A schematic of a two-dimensional C-space is shown in Figure 8. When the boundaries of the obstacle space and the free space in the C-space are determined, collision-free path planning is to search for a path in the C-space that connects the start point and end point and does not pass through the obstacles.

For SMSRS, a configuration $ℂ$ can be defined by the $N_j$-dimensional joint vector q, with q denoting the current state of each joint. At this point, $ℂ$ can be designated as a point in the $N_j$-dimensional C-space of SMSRS, and the boundary of this convex C-space is defined by the upper bound ${\mathit{u}}_{\mathit{b}}$ and the lower bound ${\mathit{I}}_{\mathit{b}}$ of joint angles.

$$\begin{array}{c}{\mathit{I}}_{\mathit{b}}={\left[\begin{array}{ccccc}{\theta }_{1_{min}}& {\theta }_{2_{min}}& {\theta }_{3_{min}}& \cdots & {\theta }_{N_{jmin}}\end{array}\right]}^T\\ {\mathit{u}}_{\mathit{b}}={\left[\begin{array}{ccccc}{\theta }_{1_{max}}& {\theta }_{2_{max}}& {\theta }_{3_{max}}& \cdots & {\theta }_{N_{jmax}}\end{array}\right]}^T\end{array}$$

(5)

However, in Section 4.2 we illustrate selecting only two joints for path planning, so there is not necessary to build an $N_j$-dimensional C-space of SMSRS, but only a two-dimensional C-space with the angles of planned joints as coordinate parameters. At a certain moment t, SMSRS has a configuration ${ℂ}_t$. If a collision occurs in SMSRS under ${ℂ}_t$, the point $\left(\begin{array}{cc}{\theta }_1^p\left(t\right),& {\theta }_2^p\left(t\right)\end{array}\right)$ belongs to the obstacle space of the C-space, and if no collision occurs, the point belongs to the free space. Then, the first task is to map the obstacles in the workspace space to C-space. In SMSRS, all non-planned joints will be used to build the obstacle space.

However, unlike the C-space with fixed obstacles, the C-space of SMSRS is with dynamic obstacles as modules are in motion with time, so it is impossible to use computational methods to calculate its obstacle space, this paper uses the random sampling method to determine the obstacle space of the C-space of SMSRS.

At a moment, we could fix the angles of non-planned joints and build the C-space of the planned joints by the random sampling method. While the angles of non-planned joints also need to move with time, we propose the concept of spliced C-space. We select multiple time points in the collision process of SMSRS uniformly, build the C-space at each time point, and splice them together into a spliced C-space. The operation procedures are:

(1) Moderate angle allowance is added into ${\mathit{q}}_{col\_start}$ and ${\mathit{q}}_{col\_end}$ to ensure the states of SMSRS before and after planning are self-collision-free. Assuming that the total time of the collision process is T and joint moves from the ${\mathit{q}}_{col\_start}$ to ${\mathit{q}}_{col\_end}$ linearly, the collision process is equated into N time sequences. The start moment of each time sequence is $T_t,t=1,2\cdots N$, and the joint angles of SMSRS at $T_t$ is ${\mathit{q}}_{{\mathit{T}}_{\mathit{t}}}$. The determination principle of N is: $N=max\left({\left({\theta }_1^p\right)}_{max}-{\left({\theta }_1^p\right)}_{min},{\left({\theta }_2^p\right)}_{max}-{\left({\theta }_2^p\right)}_{min}\right)$ to keep it in a reasonable interval.

(2) At $T_t$, randomly sample (${\theta }_1^p\left(T_t\right),{\theta }_2^p\left(T_t\right)$) with a sampling number ϑ, and the sample intervals are for ${\theta }_1^p\left(T_t\right),{\theta }_2^p\left(T_t\right)$ are $\left(\begin{array}{cc}{\left({\theta }_1^p\right)}_{min},& {\left({\theta }_1^p\right)}_{max}\end{array}\right)$, $\left(\begin{array}{cc}{\left({\theta }_2^p\right)}_{min},& {\left({\theta }_2^p\right)}_{max}\end{array}\right)$, respectively, put all the sampled points into the matrix ${Є}_{{\mathit{T}}_{\mathit{t}}}\in {\mathbf{\Re }}^{\vartheta \times 2}$ in order.

(3) At $T_t$, the angles of the planned joints at the corresponding positions in ${\mathit{q}}_{{\mathit{T}}_{\mathit{t}}}$ are replaced by each set of ${\theta }_1^p\left(T_t\right),{\theta }_2^p\left(T_t\right)$ in ${Є}_{{\mathit{T}}_{\mathit{t}}}$ to form a new joint angle sequence. The new joint angle sequence is saved to the matrix ${\mathrm{Б}}_{{\mathit{T}}_{\mathit{t}}}\in {\mathbf{\Re }}^{\vartheta \times N_j}$.

(4) At $T_t$, each ${\mathit{q}}_{{\mathit{T}}_{\mathit{t}}}$ in ${\mathrm{Б}}_{{\mathit{T}}_{\mathit{t}}}$ is brought into the FK of SMSRS to calculate the module poses, and the self-collision detection model in Section 3.2 is used to judge whether there is a collision occurring in SMSRS under ${\mathit{q}}_{{\mathit{T}}_{\mathit{t}}}$, if there is a collision occurring, the point (${\theta }_1^p\left(T_t\right),{\theta }_2^p\left(T_t\right)$) are counted into the obstacle space, otherwise, it is counted into the free space. Until each ${\mathit{q}}_{{\mathit{T}}_{\mathit{t}}}$ in ${\mathrm{Б}}_{{\mathit{T}}_{\mathit{t}}}$ are judged, the work to build C-space at $T_t$ is finished. Figure 9 shows a schematic diagram of C-space built by random sampling with ϑ = 40,000, from which we can see that as long as the sampling points are sufficient, the boundary of the obstacle space is clear.

(5) Follow steps 2 to 4 to build the C-space at each moment until obtaining the N-multiplicity two-dimensional C-space.

4.3.2. Pre-Defined Path

To find self-collision-free joint paths from the N-multiplicity C-spaces, the primary is to splice the N-multiplicity C-spaces according to certain principles. In this paper, we propose a method for splicing N-multiplicity C-spaces based on a predefined path of planned joints. The idea is to predefine a joint path and splice N-multiplicity C-spaces into a binary map along the predefined path. In the binary map, searching for a collision-free path is essentially the planning of the time sequence of the pre-defined path. Thus, the path planning of joints in N-multiplicity C-spaces is transformed into the planning of its time sequence on a pre-defined path in spliced C-space. Firstly, we propose a method to pre-define the path of the planned joint from ${\theta }_{1\_start}^p, {\theta }_{2\_start}^p$ to ${\theta }_{1\_end}^p, {\theta }_{2\_end}^p$, which is shown in Figure 10.

Figure 10a shows the pre-defined path for two planned joints that are both motion joints. Firstly, the angles of planned joints from $\left({\theta }_{1\_start}^p, {\theta }_{2\_start}^p\right)$ to (${\theta }_{1\_end}^p, {\theta }_{2\_end}^p$) are divided into n equal intervals, $n=max\Vert \left({\theta }_{1\_end}^p-{\theta }_{1\_start}^p,{\theta }_{2\_end}^p-{\theta }_{2\_start}^p\right)\Vert$. The $\left(A_1,B_1\right)$ point is the start point of the path, representing the start collision angle of the planned joint $\left({\theta }_{1\_start}^p, {\theta }_{2\_start}^p\right)$. $\left(A_n,B_n\right)$ is the end of the path, representing the end collision angle of the planned joint $\left({\theta }_{1\_end}^p,{\theta }_{2\_end}^p\right)$. The default pre-defined path is linear: $\left(A_1,B_1\right)\to \left(Ve{r}_x,Ve{r}_y\right)\to \left(A_n,B_n\right)$, and it forms a triangle with $\left(A_1,B_1\right)\to \left(A_n,B_n\right). \left(Ve{r}_x,Ve{r}_y\right)$ is the apex of the obtuse angle, and it has the following three kinds of moving rules:

(1) Equilateral path: along with the $\left(A_n,B_1\right)\to \left(A_1,B_n\right)$ line, $Ve{r}_x$ move from the $A_{\left(n/2+1\right)}$ to both sides of $A_{\left(n/2+1\right)}$, $Ve{r}_y$ move from $B_{\left(n/2+1\right)}$ to both sides of $B_{\left(n/2+1\right)}$.

(2) Non-equilateral path: $Ve{r}_y=B_n,Ve{r}_x$ move from $A_n$ to $A_1$; or $Ve{r}_x=A_n,Ve{r}_x$ move from $B_n$ to $B_1.$

(3) Non-equilateral path: $Ve{r}_y=B_1,Ve{r}_x$ move from $A_1$ to $A_n$; or $Ve{r}_x=A_1,Ve{r}_x$ move from $B_1$ to $B_n$.

Figure 10b shows the pre-defined path method when one of the planned joints is no motion joint. Firstly, the angles of motion joints are divided into n equal intervals from ${\theta }_{1\_start}^p$ to ${\theta }_{1\_end}^p$, and ${\theta }_{2\_end}^p={\theta }_{2\_start}^p$, $n=\Vert {\theta }_{1\_end}^p-{\theta }_{1\_start}^p\Vert$. The $\left(A_1,B_1\right)$ point is the start point of the path, representing the start collision angle of the planned joint $\left({\theta }_{1\_start}^p,{\theta }_{2\_start}^p\right)$. $\left(A_n,B_1\right)$ is the end of the path, representing the end collision angle of the planned joint $\left({\theta }_{1\_end}^p,{\theta }_{2\_end}^p\right).$ The side length of both X and Y directions of a grid are equal. The default pre-defined path is linear: $\left(A_1,B_1\right)\to \left(Ve{r}_x,Ve{r}_y\right)\to \left(A_n,B_1\right)$, and it forms an equilateral triangle with $\left(A_1,B_1\right)\to \left(A_n,B_1\right). \left(Ve{r}_x,Ve{r}_y\right)$ has two kinds of moving rules:

(1) Equilateral path: $\left(Ve{r}_x,Ve{r}_y\right)$ move along $\left(A_{\left(n/2+1\right)},B_2\right)\to \left(A_{\left(n/2+1\right)},B_m\right)$. $B_m\in \left(\begin{array}{cc}{\left({\theta }_2^p\right)}_{min},& {\left({\theta }_2^p\right)}_{max}\end{array}\right)$.

(2) Non-equilateral path: $Ve{r}_x$ move from $A_{\left(n/2+1\right)}$ to both sides of $A_{\left(n/2+1\right)}$ and $Ve{r}_y$ move from $B_1$ to $B_m$. $B_m\in \left(\begin{array}{cc}{\left({\theta }_2^p\right)}_{min},& {\left({\theta }_2^p\right)}_{max}\end{array}\right)$.

We restrict $\left(Ve{r}_x,Ve{r}_y\right)$ can only be located on the grid points in Figure 10, it generates a new pre-defined path for each step forward on the grid. In Figure 10a, if there is no collision-free path in the spliced C-space generated by the current pre-defined path, a new path needs to be pre-defined according to rules (1)~(3) successively, and the pre-defined path needs to be guaranteed the obtuse angle is greater than 100 degrees; In Figure 10b, if all pre-defined paths in rule (1) are proved to be invalid, a new path shall be pre-defined according to rule (2), and the value of the two acute angles of the path should be less than 80 degrees. As shown in Figure 7, if all the compliant pre-defined paths of the currently planned joints are proved invalid, the progress needs to return to the step of determining planned joints.

4.3.3. Splice Multiple C-Space

Finding the time sequence for the planned joints on the pre-defined path with no collisions is our inspiration for splicing N-multiplicity C-spaces. Equate the pre-defined path into S segments. To ensure the length of the path segment is equal to the C-space grid, S = max$\left(A_n-A_1\right),\left(B_n-B_1\right)$. Create an $N\times S$ dimensional matrix $\mathbb{Z}$, calculate the point of joint angles $\left({\theta }_{1\_j}^p,{\theta }_{2\_j}^p\right)$, $j\in 1,2\cdots S$ of the start point of each segment on the predefined path. For jth point, judge whether it is in free space or obstacle space of the ith multiplicity C-space, and, if it is in the free space, $\mathbb{Z}\left(i,j\right)$ = 0; otherwise $\mathbb{Z}\left(i,j\right)$ = 1. After finishing the judgments, the N-multiplicity C-spaces based on the pre-defined paths are spliced into matrix $\mathbb{Z}$, which can be regarded as a two-dimensional digital map composed of the numbers 1 and 0 and is named as the binary map.

The N rows of the binary map present the N-multiplicity C-spaces and the S columns present the S segments of whole movement time along the pre-defined path. If we could find an all-0 path from the top-left to the bottom-right in the binary map, it means that the planned joints could cross the N-multiplicity C-spaces along the pre-defined path collision-freely under a specific time sequence. A binary map is valid if there exists an all-0 path from the top-left to the bottom-right; otherwise, the map is invalid, and a pre-defined path needs to be reselected. We propose an all-0 path search algorithm based on the total path length to determine whether the binary map is valid.

In Figure 11, the binary map is plotted into a map with grids. Every grid has two values, the top value represents its binary value, and the bottom value represents the binary sum of all the grids on the optimal path pushed to the current grid from the start point, denoted by $\mho$.

We specify the path to a grid can only be extended from its upper grid and left grid, e.g., the path to grid G can only be extended from grid F or H, and $\mho =$ 1 for $A\to H$, $\mho =$ 0 for $A\to F$. Therefore, the path from grid F is the more optimal path for grid G. Based on this method, the steps of the all-0 path search algorithm based on the total path length are:

(1) In a binary map, set the top-left grid as the start point and the bottom-right grid as the end point, if one of their binary values is not 0 or none is 0, the binary map is invalid and the pre-defined path should be adjusted to redraw the binary map.

(2) The path to a grid can only be extended from its upper grid and left grid. Based on this principle, we first calculate the $\mho$ of grids in the first row and first column from the start point down and right, respectively. Then, in left to right and top to bottom order, we continue to calculate $\mho$ of each grid until reaches the end point.

(3) Judge whether $\mho$ of the end point is 0, if $\mho$ = 0, as shown in Figure 11a, it proves that there exists an all-0 path from the start point to the endpoint. If $\mho \ne 0$, as shown in Figure 11b, it proves that there exists no all-0 path from the start point to the end point, the map is invalid.

4.4. Path Planning Algorithms

4.4.1. Dangerous Potential Fields

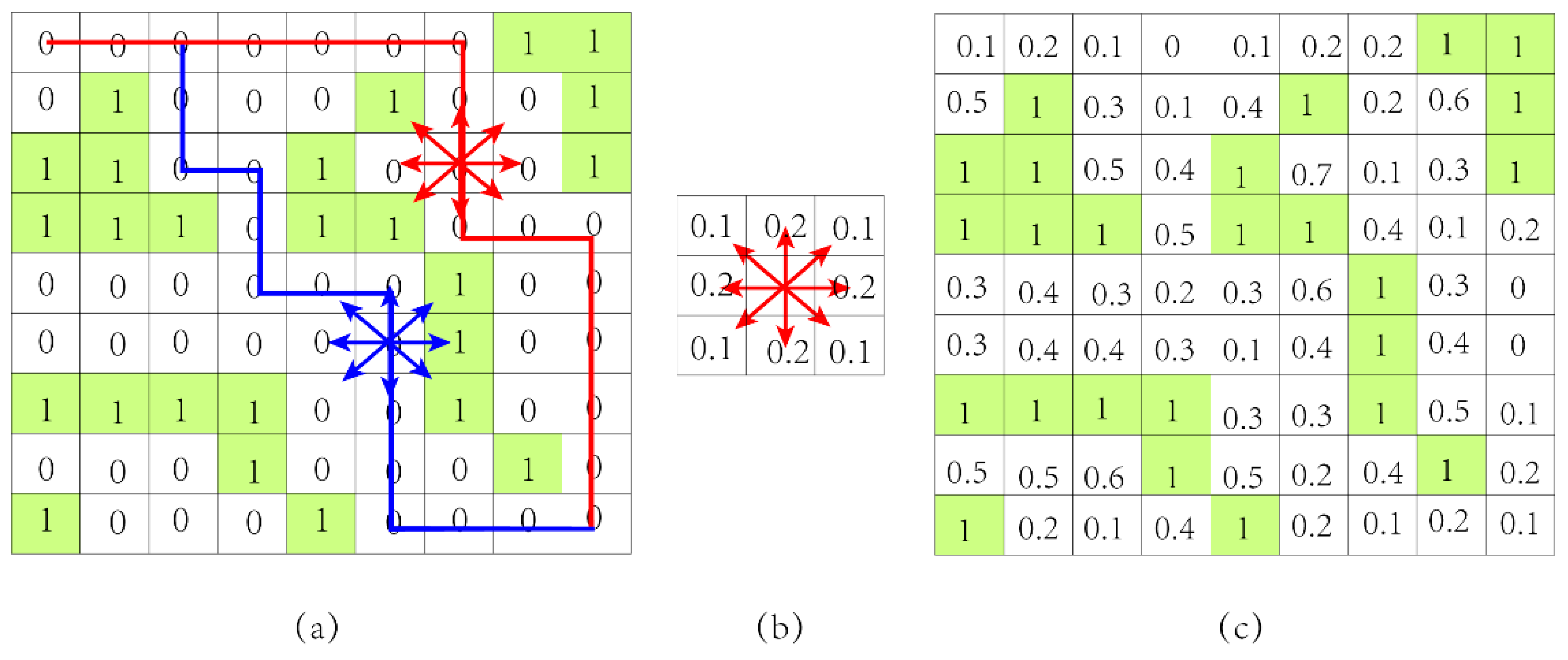
As shown in Figure 12a, a valid binary map may have several collision-free paths from the start point to the end point, to select the optimal path from them, a collision-free path planning algorithm based on a Map with Dangerous Potential Fields (MDPF) is proposed.

The dangerous potential field of the map is used to evaluate the possibility of potential collisions of its grids. As shown in Figure 12b, a grid is centered on the eight surrounding grids, and the values ${\ell }_i$ in the surrounding grids represent their effect weights to the dangerous potential field of the center grid. The dangerous potential field strength of the center grid is $\mathbb{Q}={{\displaystyle \sum }}_{i=0}^8{\ell }_i{ℒ}_i$, where ${ℒ}_i$ is the binary value of its eight surrounding grids, and for the four oblique grids, ${\ell }_i$ = 0.1, for the other grids, ${\ell }_i=$ 0.2. Calculating the dangerous potential field strength of all grids in the binary map, we convert the binary map into a digital map with the dangerous potential field, as shown in Figure 12c. We expect to find an optimal path in the map with the dangerous potential field by the MDPF algorithm. The optimal path has the smallest total value of the dangerous potential field of all grids on the path, that is, the safest path with the lowest collision possibility.

4.4.2. MDPF Algorithm

Same as the all-0 path search algorithm in Section 4.3.3, the MDPF algorithm sets the path start point at the top-left grid and the end point at the bottom-right grid, and $\mho$ of all grids are calculated in the same order. The difference is that the value at the top of the grid represents the value of $\mathbb{Q}$, and the bottom value $\mho$ represents the sum of the $\mathbb{Q}$ of all grids on the optimal path from the start point to it. In addition, the all-0 path search algorithm uses $\mho$ to determine whether a binary map is valid, but the MDPF algorithm aims to find the safest path in the map with the dangerous potential field.

Since $\mho$ of all grids are calculated in the forward direction, the optimal path of one grid from the start point can be retracted based on the $\mho$ value of other grids. For example, in Figure 13, the path to grid G can only extend from grid C or grid D. Then we compare the $\mho$ of grid C and grid D, it can be found that $\mho$ = 0.6 for A→C and $\mho$ = 1.1 for A→D, therefore, the path to grid G is extended from grid C. According to the principle that the sub-path of the optimal path must also be optimal, the sub-path of the current path back one step is also the optimal path. Therefore, the mechanism for the MDPF algorithm is to find the optimal path by backtracking $\mho$ from the end point to the start end in the map with the dangerous potential field.

From the end point, we compare the $\mho$ values of its upper grid and left grid, and mark the grid with smaller $\mho$ as the target grid, then compare the $\mho$ values of the upper grid and left grid of the target grid, Following this step, the target grid can be backtracked to the start grid and all the target grids form the optimal path. The MDPF algorithm achieves the planning of the optimal path without traversing every path.

In the MDPF algorithm, for the current grid, if the $\mho$ value of its upper grid is the same as its left grid, different optimal paths will be obtained when setting different backtracking directions, including priority to the left; priority to the upper; priority to the upper left; and priority to the previous direction, etc.

4.4.3. Check Path

The information contained in the optimal path obtained by the MDPF algorithm is the time sequence for the planned joints to cross the N-multiplicity C-spaces on the pre-defined path, and it can be translated into joint paths. Then, it should be stitched with the linear joint paths of the planned joints together to form the complete joint paths of SMSRS from the initial configuration to the final configuration. Check whether SMSRS has self-collision under the complete joint paths, if there is no collision, it proves that the path is successfully planned, and if there still exits collision, start the next joint path planning program from locating the collision module. Until the complete joint paths are verified collision-free, the path planning ends.

5. Settings

5.1. Parameter Setting of SMSRS

In this paper, SMSRS with nine modules and 25 DOFs is selected as the path planning object, and ${\Sigma }_b$ locates in its middle module, so there are four modules on both the a and b sides of ${\Sigma }_b$. The DOFs of a side are 12, and, the DOFs of the b side are 13 due to the existence of virtual joints. The body diagonal length of the module is 0.23 m. The D–H parameters of SMSRS are shown in

Table 1. D–H parameters of SMSRS.

D–H Parameters of a Side					D–H Parameters of b Side
Link	${\mathsf{\theta }}_{\mathit{i}}^{\mathit{a}}\left(\mathit{d}\mathit{e}\mathit{g}\right)$	${\mathit{d}}_{\mathit{i}}^{\mathit{a}}\left(\mathit{m}\right)$	${\mathsf{\alpha }}_{\mathit{i}-1}^{\mathit{a}}\left(\mathit{d}\mathit{e}\mathit{g}\right)$	${\mathit{A}}_{\mathit{i}-1}^{\mathit{a}}(\mathit{m})$	Link	${\mathsf{\theta }}_{\mathit{i}}^{\mathit{b}}\left(\mathit{d}\mathit{e}\mathit{g}\right)$	${\mathit{d}}_{\mathit{i}}^{\mathit{b}}\left(\mathit{m}\right)$	${\mathsf{\alpha }}_{\mathit{i}-1}^{\mathit{b}}\left(\mathit{d}\mathit{e}\mathit{g}\right)$	${\mathit{A}}_{\mathit{i}-1}^{\mathit{b}}(\mathit{m})$
1	0	0	0	0	v1-0	90	0	90	0
2	90	0	90	0.198	1-v	0	−0.243	90	0
3	−90	0.243	−90	0	2	−90	0	90	0
4	−90	0	−90	0	3	90	0	−90	0.198
5	90	0	90	0.198	4	−90	−0.243	−90	0
6	−90	0.243	90	0	5	−90	0	90	0
7	−90	0	−90	0	6	90	0	−90	0.198
8	90	0	90	0.198	7	−90	−0.243	−90	0
9	−90	0.243	90	0	8	−90	0	90	0
10	−90	0	−90	0	9	90	0	−90	0.198
11	90	0	90	0.198	10	−90	−0.243	−90	0
12	−90	0.243	90	0	11	−90	0	90	0
-	-	-	-	-	12	90	0	-90	0.198

.

The lower and upper limits of the joint angle are set as:

$$\begin{array}{c}{\mathit{I}}_{\mathit{b}}={\left[\begin{array}{ccccc}-90& -90& -90& \cdots & -90\end{array}\right]}^T\\ {\mathit{u}}_{\mathit{b}}=[\begin{array}{ccccc}90& 90& 90& \cdots & {90]}^T\end{array}\end{array}$$

(6)

5.2. Setting of Cases

This paper selects two cases to illustrate the application of the self-collision avoidance method for SMSRS in detail and verifies the feasibility of this method.

5.2.1. Case 1

In case 1, the SMSRS moves from the initial configuration in Figure 14 to the final configuration in Figure 15. ${\mathit{q}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{r}{\mathit{t}}_{\mathit{a}}}, {\mathit{q}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{r}{\mathit{t}}_{\mathit{b}}}$ are, respectively, the initial angles of joints on both a and b sides of ${\Sigma }_b$, and ${\mathit{q}}_{\mathit{e}\mathit{n}{\mathit{d}}_{\mathit{a}}}, {\mathit{q}}_{\mathit{e}\mathit{n}{\mathit{d}}_{\mathit{b}}}$ are, respectively, the final angles of joints on both a and b sides of ${\Sigma }_b$.

$$\begin{array}{c}{\mathit{q}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{r}{\mathit{t}}_{\mathit{a}}}=\left[0,0,0,90,0,0,0,0,0,90,0,0\right]\\ {\mathit{q}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{r}{\mathit{t}}_{\mathit{b}}}=\left[0,0,0,-90,0,-90,0,0,-30,0,0,0\right]\\ {\mathit{q}}_{\mathit{e}\mathit{n}{\mathit{d}}_{\mathit{a}}}=\left[0,0,0,-90,0,-90,0,0,-30,0,0,0\right]\\ {\mathit{q}}_{\mathit{e}\mathit{n}{\mathit{d}}_{\mathit{b}}}=\left[0,0,0,0,0,0,0,0,0,0,0,0\right]\end{array}$$

(7)

As shown in Figure 16, modules will collide when joints of the SMSRS moves in linear joint paths.

5.2.2. Case 2

In case 2, the SMSRS moves from the initial configuration in Figure 17 to the final configuration in Figure 18. ${\mathit{q}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{r}{\mathit{t}}_{\mathit{a}}}, {\mathit{q}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{r}{\mathit{t}}_{\mathit{b}}}$ are, respectively, the initial angles of joints on both a and b sides of ${\Sigma }_b$, and ${\mathit{q}}_{\mathit{e}\mathit{n}{\mathit{d}}_{\mathit{a}}}, {\mathit{q}}_{\mathit{e}\mathit{n}{\mathit{d}}_{\mathit{b}}}$ are, respectively, the final angles of joints on both a and b sides of ${\Sigma }_b$.

$$\begin{array}{c}{\mathit{q}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{r}{\mathit{t}}_{\mathit{a}}}=\left[0,0,0,90,0,90,90,0,0,90,30,0\right]\\ {\mathit{q}}_{\mathit{s}\mathit{t}\mathit{a}\mathit{r}{\mathit{t}}_{\mathit{b}}}=\left[0,0,0,0,0,0,0,0,0,0,0,0\right]\\ {\mathit{q}}_{\mathit{e}\mathit{n}{\mathit{d}}_{\mathit{a}}}=\left[0,0,0,90,0,-90,90,0,0,90,0,0\right]\\ {\mathit{q}}_{\mathit{e}\mathit{n}{\mathit{d}}_{\mathit{b}}}=\left[0,0,0,0,0,0,0,0,0,0,0,0\right]\end{array}$$

(8)

As shown in Figure 19, modules will collide when joints of the SMSRS moves in linear paths.

5.3. Setting of Algorithm

For case 1 and case 2, N = 180, and set the number of samples to ϑ = 40,000. All algorithms are implemented in MATLAB 2012a and run on the same machine with an Intel(R) Core(TM) i5-8300H CPU @ 2.30GHz and 8 G memory.

6. Simulation Results and Analysis

6.1. Case 1

6.1.1. Locate Collide Modules and Determine Planned Joints

Case 1 sets the joints moving from the initial angles to the final angles in linear paths. According to the collision detection model in Section 3 and the method for locating collision modules in Section 4.1, the two terminal modules of SMSRS are located as the collision modules by real-time detection, and the collision time sequence is (71, 364) when the total time of collision process is divided into 1000 segments.

According to the selection principle of the planned joints in Section 4.2, ${\theta }_1^p$ is set as the tenth joint on a side and ${\theta }_2^p$ is set as the seventh joint on a side for case 1. $\left({\theta }_{1\_start}^p,{\theta }_{2\_start}^p\right)=\left(86.31, 3.65\right)$, $\left({\theta }_{1\_end}^p,{\theta }_{2\_end}^p\right)=\left(52.74, 37.26\right),\left(\begin{array}{cc}{\left({\theta }_1^p\right)}_{min}& {\left({\theta }_1^p\right)}_{max}\end{array}\right)=\left(-90, 90\right),\left(\begin{array}{cc}{\left({\theta }_2^p\right)}_{min}& {\left({\theta }_2^p\right)}_{max}\end{array}\right)=\left(-90,90\right)$.

6.1.2. Spliced C-Space

Follow the steps in Section 4.3.1 to create the 180-multiplicity C-spaces. When both of the planned joints are motion joints, their paths are pre-defined as shown in Figure 10a. For each pre-defined path, we judge whether the binary map generated by splicing C-space under this pre-defined path is valid, and, if it is not, we re-select the pre-defined path according to the principles in Section 4.3.2.

After multiple iterations shown in Figure 20, one pre-defined path is found as the needed pre-defined path because the binary map generated by splicing 180-multiplicity C-spaces under it is valid, and it is marked obviously in Figure 20.

Under the final pre-defined path, we splice 180-multiplicity C-spaces following steps in Section 4.3.3 and obtain the binary map shown in Figure 21. In the binary map, (0, 0) is the start point of the path, and (180, 37) is the end point, and there exist accessible paths from the start point to the end point.

6.1.3. Path Planning

The map with the dangerous potential field can be obtained by calculating the dangerous field strength of all grids in the binary map. In the map with the dangerous potential field, the MDPF algorithm could for search the collision-free path. Different paths will be obtained when setting different priority backtracking directions in the MDPF algorithm. Figure 22 shows the different collision-free paths founded by the MDPF algorithm. Among them, the priority backtracking directions set for path 1 is the previous direction, for path 2 is the bottom-left, for path 3 is the below, and for path 4 is the left.

6.1.4. Check Path

The collision-free path in the map with the dangerous potential field contains the information of the time sequence of the planned joint from the first to the Nth multiplicity C-space based on the pre-defined path. we translate the collision-free path into the angle curves of planned joints in Figure 23.

Maintaining the linear curves of joints when no self-collision occurs and inserting planned angle curves in Figure 21 into them, complete curves of all motion joints of the SMSRS are shown in Figure 24. We analyze the reconfiguration processes of SMSRS under these angle curves, and they are shown in Figure 25. Under different angle curves, the reconfiguration processes of SMSRS are different, but they can successfully avoid the self-collision in common.

6.2. Case 2

6.2.1. Locate Collide Modules and Determine Planned Joints

Case 2 sets the joints moving from the initial angles to the final angles in linear paths. According to the collision detection model in Section 3 and the method for locating collision modules in Section 4.1, the first and fifth modules on a side of SMSRS are located as the collision modules by real-time detection, and the collision time sequence is (245, 835) when the total time of collision process is divided into 1000 segments.

6.2.2. Spliced C-Space

According to the principles in Section 4.2 to select planned joints, they are set as two motion joints: ${\theta }_1^p$ is the eleventh joint on a side and ${\theta }_2^p$ is the sixth joint on a side. And $\left({\theta }_{1\_start}^p,{\theta }_{2\_start}^p\right)=\left(24.15, 54.9\right), \left({\theta }_{1\_end}^p,{\theta }_{2\_end}^p\right)=\left(3.45,-69.3\right),\left({\left({\theta }_1^p\right)}_{min},{\left({\theta }_1^p\right)}_{max}\right)=\left(-90,90\right), \left({\left({\theta }_2^p\right)}_{min},{\left({\theta }_2^p\right)}_{max}\right)=\left(-90,90\right)$. The 180-multiplicity C-spaces are built following the steps in Section 4.3.1. However, after pre-defining paths according to the principles in Figure 10a, the binary map generated by splicing C-space under each pre-defined path of current planned joints is invalid, it proves the planned joints cannot avoid self-collision of SMSRS after path planning.

In this case, we reselect the planned joint and set ${\theta }_1^p$ as the eleventh joint on a side and ${\theta }_2^p$ as the tenth joint on a side. At this point, the 180-multiplicity C-spaces are re-built using the random sampling method following steps in Section 4.3.1. After multiple iterations shown in Figure 26, one pre-defined path is found as the needed pre-defined path because the binary map generated by splicing 180-multiplicity C-spaces under it is valid, and it is marked obviously in Figure 26.

Under the final pre-defined path, splice 180-multiplicity C-spaces following steps in Section 4.3.3, and the binary map is shown in Figure 27. In the binary map, (0, 0) is the start point of the path, and (180, 37) is the end point, and there exist accessible paths from the start point to the end point.

6.2.3. Path Planning

The map with the dangerous potential field can be obtained by calculating the dangerous field strength of all grids in the binary map. In the map with the dangerous potential field, the MDPF algorithm could search for the collision-free path. Different paths will be obtained when setting different priority backtracking directions in the MDPF algorithm. Figure 28 shows the different collision-free paths founded by the MDPF algorithm. Among them, the priority backtracking directions for path 1 is the previous direction, for path 2 is the bottom-left, for path 3 is the below, and for path 4 is the left.

6.2.4. Check Path

The collision-free path in the map with the dangerous potential field contains the information of the time sequence of the planned joint from the first to the Nth multiplicity C-space based on the pre-defined path. we translate the collision-free paths into the angle curves of planned joints in Figure 29.

Maintaining the linear curves of joints when no self-collision occurs and inserting planned angle curves in Figure 29 into them, complete curves of all motion joints of the SMSRS are shown in Figure 30. We analyze the reconfiguration processes of SMSRS under these angle curves, and they are shown in Figure 31. Under different angle curves, the reconfiguration processes of SMSRS are different, but they can successfully avoid the self-collision in common.

We observe that some segments of angle curves of planned joints change very sharply, such as the curve of ${\theta }_a^{10}$ in Figure 28, which will lead to rapid changes of joint speeds and accelerations, even beyond their limits. However, the curves only reflect the path of joint angle and with no correspondence to time. Therefore, there are several ways to solve the problem:

• If there is no limitation on the configuration time, we could extend the movement time of segments with sharp changes on the angle curves until the joint speeds and accelerations are within limitations;
• Further improve the collision-free path planning algorithm by adding optimization objectives and constraints to find smoother joint paths; and
• Select key points in the angel curves and deep plan the paths between these points to satisfy the joint velocity and acceleration constraints.

7. Conclusions

SMSRS uses structural reconfiguration to achieve multi-mission capabilities. The research on self-collision avoidance in the reconfiguration process of SMSRS is particularly important for its safety, but it is still vacant because of the original and super-redundant structure. Based on the analysis of the characteristics of SMSRS and the summary of existing studies on the self-collision avoidance problem, we propose a method for self-collision avoidance of SMSRS, which includes a suitable collision detection model and an innovative self-collision avoidance strategy.

The collision detection model based on forward kinematics and the spherical nonholonomic envelope is capable of collision detection at a low computational cost for SMSRS. By comparison, offline path planning is the applicable self-collision avoidance strategy for SMSRS. The idea of splicing the multiple C-spaces based on pre-defined paths into a binary map solves the difficulty in joint path planning resulting from the dynamic change of module position, it successfully transforms the path search in joint space into time sequence planning based on the pre-defined path for planned joints. It provides a basis for collision-free path planning. Converting the binary map into a map with dangerous potential fields and searching for the safest path using the MDPF algorithm was proved can avoid self-collisions successfully. The planned joint angle curve lays the foundation for subsequent in-depth path planning and trajectory planning.

The proposed method of self-collision avoidance meets the needs of SMSRS and proved to be effective, which fills the gap of offline path planning research for self-collision avoidance of new self-configuration satellites to a certain extent. There are also implications for offline path planning of other self-configuration systems. Future works will focus on simplifying the steps of the method and the in-depth path planning and trajectory optimization for SMSRS with single or multiple optimization objectives.