Abstract
The guidance problem of a confrontation between an interceptor, a hypersonic vehicle, and an active defender is investigated in this paper. As a hypersonic multiplayer pursuit-evasion game, the optimal guidance scheme for each adversary in the engagement is proposed on the basis of linear-quadratic differential game strategy. In this setting, the angle of attack is designed as the output of guidance laws, in order to match up with the nonlinear dynamics of adversaries. Analytical expressions of the guidance laws are obtained by solving the Riccati differential equation derived by the closed-loop system. Furthermore, the satisfaction of the saddle-point condition of the proposed guidance laws is proven mathematically according to the minimax principle. Finally, nonlinear numerical examples based on 3-DOF dynamics of hypersonic vehicles are presented, to validate the analytical analysis in this study. By comparing different guidance schemes, the effectiveness of the proposed guidance strategies is demonstrated. Players in the engagement could improve their performance in confrontation by employing the proposed optimal guidance approaches with appropriate weight parameters.
1. Introduction
In recent decades, the technology of hypersonic vehicles (HVs) developed rapidly and has drawn considerable attention among researchers. The generally accepted definition of hypersonic flight is a flight through the atmosphere between 20 km and 100 km at a speed above Mach 5. The advantage of complete controllability of the whole flight process indicates great potential in terms of the military (hypersonic weapon) and civil (hypersonic airliner) applications of HVs. Nevertheless, the disadvantages of HVs are obvious, one of which is easily detected by infrared detectors. Since violent friction with the atmosphere heats the vehicle surface during flight, it will generate intensive infrared radiation. Moreover, the maneuver of HVs relies on aerodynamic force only, which means that their overload and maneuverability are limited. As a result, HVs face serious threats of new interceptors with the development of endoatmosphere interception technology.
In order to reduce the risk of being intercepted, there are two methods to improve HVs’ ability of confrontation: developing guidance laws for one-on-one competition, or carrying defender vehicles and transforming the one-on-one confrontation into a multiplayer game. As for the former, the one-on-one scenario has been researched extensively. The classical guidance laws such as proportional navigation (PN), augmented proportional navigation (APN), and optimal guidance laws (OGLs) were proposed for pursuers [1,2,3,4]. From the perspective of evader, one-on-one pursuit-evasion games can be formulated as two types of problems: a one-side optimization problem or differential game problem. A key assumption of a one-side optimization problem is that the player could obtain maneuvering and guidance information of its rival [5,6,7]. This tight restriction was relaxed by introducing the multiple model adaptive estimator in Ref. [8]. Information sharing and missile staggering were exploited to reduce the dependency of prior information in one-side optimization problems [9]. On the other hand, the differential game approach makes no assumption on the rival’s maneuver but requires each adversary’s state information [10,11]. The results in Ref. [10] demonstrated that PN is actually an optimal intercept strategy. Air-to-air missile guidance laws based on optimal control and differential game strategy were derived in Ref. [11], where the guidance laws based on differential game strategy were proven to be less sensitive to errors in acceleration estimation. Other guidance laws using sliding-mode control, formation control, heuristic method, and artificial neural network were investigated in Refs. [12,13,14,15,16,17]. It is worth noting that HVs are prone to meet saturation problem and chattering phenomenon when using the aforementioned guidance laws, because of their limited overload and maneuverability.
Carrying an active defense vehicle is efficient to reduce the maneuverability requirement of a target in confrontation, as well as to alleviate the problem of control saturation. Other than the high requirement of maneuverability in one-on-one games, the number of adversaries covers the inferiority of maneuverability [18,19,20,21,22,23]. As indicated in Ref. [18], optimal cooperative evasion and pursuit strategies for the target pair and the pursuer were derived. It should be noted that cooperative differential strategies could reduce maneuverability requirements from the target pair but bring difficulties to parameter choice and induce complicated calculations. Shima [19] derived optimal cooperative strategies of concise forms for aircraft and its defending missile by using Pontryagin minimum principle. However, the laws are calculated by a signum function, which causes a chattering phenomenon in control signals. Shaferman and Shima [20] considered a novel scenario in which a team of cooperating interceptors pursue a high-value target, and a relative intercept angle index was introduced to improve the performance of interceptors. In Ref. [21], cooperative guidance laws for aircraft defense were performed in a nonlinear framework by using the sliding-mode control technique. In addition to the above studies, Qi et al. [22] discussed the infeasible and feasible region of initial zero-effort-miss distance in a multiplayer game and provided evasion-pursuit guidance laws for the attacker. Garcia et al. [23] exploited the multiplayer game in a three-dimensional case and derived optimal strategies from the perspective of geometry.
It can be seen that most of the above studies are based on ideal scenarios in which the response of adversaries is rapid, and the dynamics are assumed to be linear. These particular assumptions will cause potential problems in practical application, since the responding speed of HVs, whose overload is generated by aerodynamic force, is commonly low. Thus far, there are few studies focusing on hypersonic, pursuit-evasion games. Chen et al. [24] proposed a fractional calculus guidance algorithm based on nonlinear proportional and differential guidance (PDG) law for a hypersonic, one-on-one pursuit-evasion game. However, the adversaries in multiplayer games commonly have more than one objective, so the family of PID controllers is difficult to be utilized in a multiplayer game. To the best of the authors’ knowledge, research on guidance laws of hypersonic, multiplayer pursuit-evasion games has not been explored in the available literature.
In this paper, we consider a hypersonic multiplayer game in which an HV carrying an active defense vehicle is pursued by an interceptor. In order to match up with nonlinear dynamics, the output of the proposed strategy is set up as the angle of attack (AOA). The main contribution of this paper is proposing linear-quadratic optimal guidance laws (LQOGLs) for adversaries in the game by simultaneously considering energy cost, control saturation, and chattering phenomenon. The optimal guidance strategies are derived through solving the linear-quadratic differential game problem with the aid of the Riccati differential equation. In addition, the satisfaction of the saddle-point condition of the proposed guidance laws is proved analytically. Simulations based on nonlinear kinematics and dynamics are presented, to validate that each adversary can benefit most within its ability by employing the proposed strategies.
This paper is organized as follows: In Section 2, a description of the multiplayer scenario and mathematical model is presented. In Section 3, the linear-quadratic differential strategies are derived and analyzed. In Section 4, simulation analysis is presented. Finally, some conclusions are provided in Section 5.
2. Engagement Formulation
In this section, an engagement is considered in which an HV carrying an active defense vehicle is pursued by an interceptor. In this engagement, the HV plays as a maneuvering target (M), the HV interceptor plays as an interceptor (I), and the active defense vehicle plays as a defender (D). The defender is launched sometime during the end game to protect the HV by destroying the interceptor. The engagement is analyzed in a plane. The three-dimensional version of optimal guidance laws can be obtained by extending the optimal guidance laws in the plane to three-dimensional models [25,26] and, thus, will not be discussed here.
2.1. Problem Statement
A schematic view of the planar engagement geometry is shown in Figure 1, where X-O-Y is the Cartesian reference system. There are two collision triangles in the engagement. One is between the interceptor and the HV (I–M collision triangle), and the other is between the interceptor and the defender (I–D collision triangle). The altitude, velocity, flight path angle, and lift coefficient are represented by , , and , respectively. The distance between each adversary is represented by and , while the angle between the light of sight (LOS) and axis is represented by .
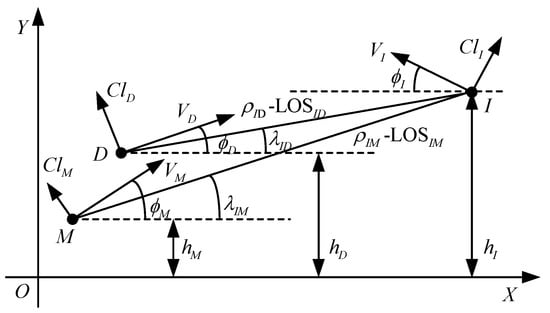
Figure 1.
Planar engagement geometry.
The HV is required to evade the interceptor with the assistance of the defender. Conversely, the mission of the interceptor includes evading the defender and pursuing the HV. Therefore, the guidance laws for target pairs are designed to converge to zero and to maximize , while the guidance laws designed for interceptors should converge to zero and maximize .
2.2. Equations of Motion
Considering the I–M collision triangle, equations of motion can be given by
where is the relative velocity along , and is the lateral speed orthogonal to , which can be calculated by
Additionally, the relative motion of the interceptor and defender in the I–D collision triangle can also be described in a similar manner as Equation (1).
where
The flight path angles of each adversary can be defined as
where is the gravitational constant, and is an operator defined as follows:
where is the dynamic pressure, is the reference cross-sectional area of aircraft, and is the mass of aircraft.
2.3. Linearized Equations of Motion
During the endgame, the adversaries can be considered as constant-speed mass points, since, in most cases, the acceleration generated by thrusters is not significant in the guided phase of the flight [6]. Therefore, the equations of motion can be linearized around the initial collision course according to small-perturbation theory, and the multiplayer game can be formulated as a fixed-time optimal control process.
As a consequence of linearized kinematics, the gravitational force is neglected [6]. Meanwhile, it is reasonable to assume that the dynamics of each agent can be represented by first-order equations as
where is the guidance command.
In this engagement, we were concerned more about the miss distances orthogonal to LOS. Thus, the state variables chosen to represent the engagement are given as
The state functions can be expressed as
Accordingly, the state-space representation of the pursuit-evasion game is obtained.
where
A zero-effort-miss (ZEM) method is introduced to reduce the complexity of the mathematical model, which is the missed distance if both vehicles in collision engagement would apply no control from the current time. The ZEM of interceptor and target is represented by , and that of interceptor and defender is represented by , which can be, respectively calculated as
where and represent interception time, and are constant vectors defined as
Additionally, is the transition matrix which can be calculated by
where is the inverse Laplace transformation, and denotes the identity matrix. Associated with Equations (13)–(17), and can be calculated as follows:
where , and are computed as
As a result, and are calculated by
The derivative of and can be given as follows:
Therefore, the dynamic system corresponding to Equations (13) and (14) is transformed into
where
Remark 1.
According to Equations (22a) and (22b), is independent of guidance laws and only relies on current states. If the current state is determined, can be determined. It can be seen from Equations (23a) and (23b) that the derivative is state-independent. Corresponding to the new state space defined by Equations (24)–(26), an optimal control problem with a fixed terminal time in a continuous system is considered. The objective of the target pair is to design optimal guidance schemes that can converge to zero as while keeping as large as possible. Conversely, the control law of the interceptor is designed to make converge to zero while maintaining as large as possible.
2.4. Timeline
With the linearization assumption, the interception time is fixed and can be calculated by
It is reasonable to assume that the engagement of the interceptor and the defender terminates before that of the interceptor and the target, and thus, . The nonnegative time-to-go of the interceptor–defender engagement and the interceptor–target engagement can be, respectively, calculated as follows:
3. Guidance Schemes
3.1. Cost Function
The quadratic cost function in this problem is chosen as follows:
where
The weights , , , and are nonnegative. Let , , and be optimal guidance laws for interceptor, target, and defender, respectively. Thus, the guidance laws are issued so as to meet the condition set as follows:
3.2. Cost Function
Let be the Lagrange multiplier vector,
The corresponding Hamiltonian is given by
The costate equations and transversality conditions are given by
As the Hamiltonian is second-order continuously differentiable with respect to and , and satisfy
Therefore, the optimal guidance laws can be calculated by
Considering Equation (35), the linear relationship between and can be obtained immediately. Thus, it is reasonable to assume that
where is a square matrix of order two and satisfies
The derivative with respect to time can be calculated by
Substituting the optimal guidance laws (37) into Equation (40), we have
According to Equations (34) and (41), since is satisfied for any , we have
Equation (42) is a well-known Riccati differential equation. Considering the following equation:
Then, by integrating Equation (43) from to and considering Equation (39), the analytical expression of is derived as follows:
Substituting Equation (44) into Equation (38), the LQOGL , and can be calculated by
Now, the solution of optimal guidance laws is presented completely. By using the interpolation method, the desired AOA can be obtained, and this completes the design of the guidance laws.
3.3. Proof of Saddle-Point Condition
The proposed guidance laws , and are functions of state vector , which form closing-loop feedback controls of . It should be proven that the optimal guidance laws given by Equation (45) satisfy the saddle-point condition. Considering Equations (24) and (42), it can be derived that
Integrating Equation (46) from to and taking Equation (29) into account, the cost function can be derived as follows:
If , we have
It is obvious that yields the minimum of , which means
Similarly, if , we have
Thus, yields the maximum of , which means
Combined with two situations (49) and (51), and satisfy the saddle-point condition as follows:
4. Simulation and Analysis
In this section, the performance of the proposed guidance algorithms is investigated through nonlinear numerical examples. A scenario, consisting of an HV as the target (M), an active defense vehicle as the defender (D), and an HV interceptor as the interceptor (I), is considered. The interceptor is assigned the task of capturing the HV and evading the defender. Perfect information for the adversaries’ guidance laws is assumed.
4.1. Simulation Setup
In the simulated scenarios, 3-DOF point mass planetary flight mechanics [27] are employed in each adversary. All players use rocket engines to achieve hypersonic speed; the target and the defender are launched by the same rocket, while each interceptor is launched by a separate small rocket. The target and the defender have higher speeds than the interceptor since the target has a higher range requirement and is launched by a more powerful rocket. Hence, the initial horizontal velocities of the three players are set as , and , respectively. The altitudes are set as , , and , respectively. The endgame starts when the horizontal distance between the target and the interceptor reaches 150 km. The defender is assumed to be launched 20 km in front of the target at the beginning of the scenario. During the endgame, all players are in the glide phase and perform maneuvers, mainly relying on aerodynamic force. The HV is considered as a plane-symmetric lifting-body shape with one pair of air rudders, which can provide high L/D up to 3.5 [28]. Hence, the HV is required to employ bank-to-turn control. The active defense vehicle is a companion vehicle launched by HV whose aerodynamic performance is slightly worse than HV. Conversely, the interceptor is designed as an axisymmetric structure, with two pairs of air rudders, and employed skid-to-turn control for high agility. The desired roll rate of the interceptor can be expected to be much smaller than the HV since the interceptor can reorient the aerodynamic acceleration by changing the ratio of the AOA to the angel of sideslip [29]. This means that the interceptor sacrifices the aerodynamic performance in exchange for mobility and control stability. To compensate for the shortcoming of aerodynamic maneuverability, the interceptor was equipped with a rocket-based reaction-jet system (RCS), to obtain instant lateral acceleration. The RCS can only be turned on for a short time around the collision, due to limited fuel cost. The instantaneous overload of the interceptor is expected to be 9 g when exhausting the RCS. For these practical factors, the AOAs are assumed to be bounded as with bounded changing rates as , and , respectively. Time constant of each player is and , respectively. The simulation parameters of all adversaries are listed in Table 1.

Table 1.
Simulation parameters.
4.2. Numerical Examples
In this subsection, the effectiveness of the proposed LQOGL in Equation (45) is validated through the following three cases:
- The interceptor adopts PN guidance law, the defender adopts PN guidance law, and the target adopts LQOGL (PNvPNvLQOGL);
- The interceptor adopts PN guidance law, the defender adopts LQOGL, and the target adopts LQOGL (PNvLQOGLvLQOGL);
- The interceptor adopts LQOGL, the defender adopts LQOGL, and the target adopts LQOGL (LQOGLvLQOGLvLQOGL).
Generally, high L/D HVs are required for the capabilities of large downrange and cross-range [30]. Thus, unnecessary maneuvers of HV should be avoided since it will increase drag forces and cause kinetic energy cost and range loss. Thus, the LQOGL for the target can be expressed as follows:
Since the defender is designed to sacrifice itself to protect the HV, there is no need to take into account the range loss and control saturation for the defender. Unlike the HV and the defender, endoatmosphereic interceptor missile is generally steered by dual control systems of aerodynamic fins and reaction jets [31]. Thus, fuel cost should be taken into account for the interceptor, and the switching time of the jet engines should be strictly controlled. Inspired by Ref. [31], the maximum duration of the engine is assumed up to 1 s, and the engine is turned on when and . Additionally, the dynamic of the divert thrust generated by jet engines can be assumed to be presented by a first-order equation,
The herein is considered as a complement to lift force in Equation (53). The optimal guidance laws based on Pontryagin minimum principle for a reaction-jet system can be given by
where is the maximum thrust that the engines can provide, which is assumed to be seven times of gravitational force.
The simulation results are concluded in Table 2.

Table 2.
Simulation results.
Case 1.
The performance of the guidance strategies in multiplayer engagement, PNvPNvLQOGL, is investigated in this case. Based on the linear-quadratic differential game, LQOGL for the target is calculated by Equation (53), corresponding to weight parameters.
Simulation results of case 1 are shown in Figure 2, which include the trajectory, ZEM, and AOA of each adversary. It can be seen from Figure 2a,b that the interceptor is pursued tightly by the defender but evades the defender depending on thrust during and then turns its head to the target. The maximum acceleration of the interceptor reaches 10 g when the exhaust pipe is burning. Although the target has a higher L/D, the interceptor is able to intercept the target. The ZEM between the target and the interceptor and the ZEM between the defender and the interceptor both converge to zero swiftly. An interesting situation is observed in which even the target is pursued tightly by the interceptor, and it hardly maneuvers in the middle of the endgame. This situation can be understood as the scenario in which the interceptor is also tightly caught by the defender, which is considered safe by the target according to LQOGL. However, the key is that the jet engines on the interceptor can help it evade the defender when . The ZEM between the interceptor and the defender rises suddenly to 15.01 m when , which is larger than the killing radius of the defender obviously. After that, the engagement is transformed into a one-on-one game, and the target has no time to enlarge the missing distance. Referring to Figure 2c–e, both the target and the interceptor face to control saturation. However, the target is not able to evade the interceptor since the rate of AOA change of the target is limited, while the interceptor can respond quickly by switching on the jet engines when . As can be seen in Figure 2b, the ZEM between the target and the interceptor converges to −0.17 m when , which is smaller than the killing radius of the interceptor.
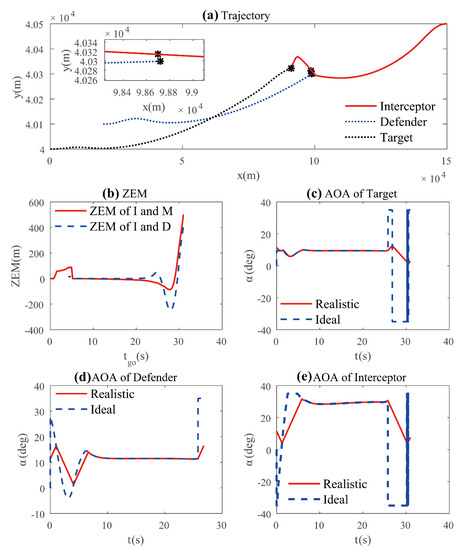
Figure 2.
Simulation results of Case 1: (a) trajectory; (b) ZEM; (c) target’s AOA; (d) defender’s AOA; (e) interceptor’s AOA.
These results demonstrate that the interceptor is able to evade the defender using PN guidance law and successfully intercept the target. Additionally, the accelerations of the three adversaries do not reach the limit in the middle process of this engagement.
Remark 2.
Inspired by Ref. [19], guidance laws for target based on norm differential strategy can be derived from the cost function
The guidance scheme for the target is calculated by
It can be seen from Equation (59) that the guidance laws based on norm differential strategy are calculated by a signum function.
A controlled experiment is performed by replacing the target’s LQOGL with the norm optimal guidance law proposed in Equation (59). The results are shown in Figure 3, showing the trajectory, ZEM, and AOA of the target. It can be seen in Figure 3b that the ZEM between the target and the interceptor is kept around a safe distance. However, as shown in Figure 3c, the target meets with the control saturation problem and severe chattering phenomenon. This is consistent with the expression of norm optimal guidance law. Under the bank-to-turn control mode, the desired roll rate of the target will be very large. Additionally, large-amplitude maneuvering will lead to kinetic energy loss as far as range loss.
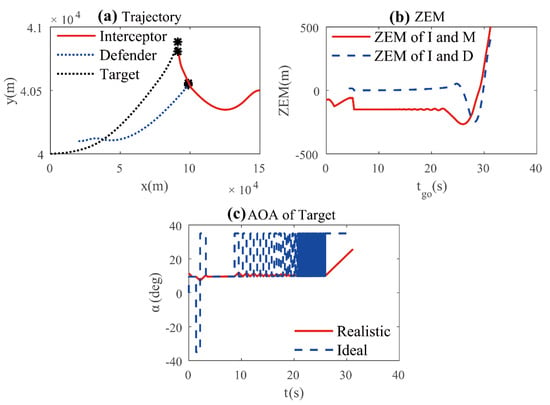
Figure 3.
Simulation results of controlled experiment: (a) trajectory; (b) ZEM; (c) target’s AOA.
Case 2.
The performance of guidance strategies in engagement, PNvLQOGLvLQOGL, is investigated in this case. LQOGLs for target pair are calculated through Equations (45) and (53), corresponding to parameters chosen as follows:
Simulation results of case 2 are shown in Figure 4, which include trajectory, ZEM, and AOA of the target pair. The effectiveness of the proposed guidance laws is confirmed by this case. Figure 4a,b show that the interceptor evades from being intercepted by the defender but fails to catch the target. The ZEM between the interceptor and the defender is −15.03 m when , and the ZEM between the interceptor and the target vehicle is −28.07 m when , which are larger than the killing radius of the defender and the interceptor, respectively. It can be seen from Figure 4a,b that the interceptor is driven away from the target by the defender when and cannot catch up with the target even the interceptor can accelerate by jet engines. Compared with the simulation result of case 1, smooth dynamics of the target and the defender are evident in Figure 4c,d. Moreover, the guidance laws of target pairs are not saturated, and the kinetic energy cost is considerably saved. The chattering phenomenon is also alleviated, which is beneficial to control stability.
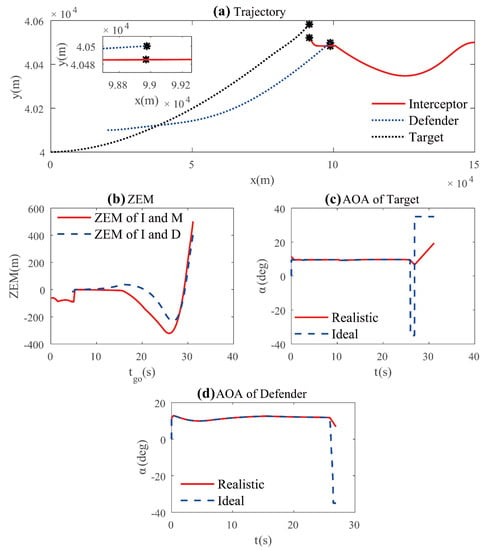
Figure 4.
Simulation results of Case 2: (a) trajectory; (b) ZEM; (c) target’s AOA; (d) defender’s AOA.
Case 3.
The performance of guidance strategies in engagement, LQOGLvLQOGLvLQOGL, is investigated in this case. LQOGLs for three adversaries are calculated through Equations (45), (53), (55), and (56). Weight parameters are chosen as follows:
Figure 5 presents the simulation results of case 3 in order similar to the above cases. As Figure 5a shows, the guidance laws proposed for the target pair are effective. Instead of evading the interceptor persistently, the target acts similar to a bat and lures the interceptor close to the defender. It allows the defender to catch the interceptor more easily. However, contrary to the result of case 2, the interceptor skims the defender without changing heading violently and turns its head to the target. Obviously, it can be seen from Figure 5b that the interceptor is able to attack the target vehicle without being intercepted by the defender. The ZEM between the interceptor and the defender is 15.01 m when , and the ZEM between the interceptor and the target vehicle is −0.17 m when .
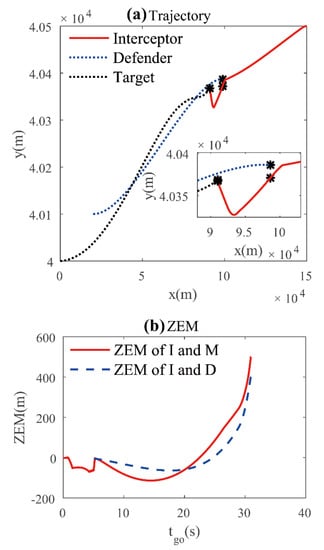
Figure 5.
Simulation results of Case 3: (a) trajectory; (b) ZEM.
5. Conclusions
- In this research, a set of guidance laws for a hypersonic multiplayer pursuit-evasion game is derived based on linear-quadratic differential strategy. The energy cost, control saturation, chattering phenomenon, and aerodynamics were considered simultaneously. The satisfaction of saddle-point condition in a differential game was also proven theoretically.
- Nonlinear numerical examples of the multiplayer game were presented to validate the analysis. The advantage and efficiency of the proposed guidance were verified by the results. The LQOGLs exactly reduce the maneuverability requirement of the target in the pursuit-evasion game. Compared with the norm differential strategy, the proposed guidance strategy reduces the energy cost, alleviates the saturation problem, and avoids the chattering phenomenon, which guarantees task accomplishment and increases guidance phase stability.
- The performance of the interceptor showed that the proposed optimal guidance approach is able to complete the intercept mission if the interceptor possesses superior maneuverability. It is important to note that the saturation problem cannot be avoided completely when all the adversaries employ the LQOGL, since maneuverability is the most important factor in determining whether they will win or lose in the game. The interceptor or the target pair should make their best effort to attack or defend by exhaustedly performing maneuvers.
Author Contributions
Formal analysis, H.C.; funding acquisition, Y.Z.; investigation, J.W. (Jinze Wu); supervision, J.W. (Jianying Wang); visualization, Z.L.; writing—original draft preparation, Z.L.; writing—review and editing, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, Grant No. 62003375 and No. 62103452.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data used during the study appear in the submitted article.
Acknowledgments
The study described in this paper was supported by the National Natural Science Foundation of China (Grant No. 62003375, No. 62103452). The authors fully appreciate their financial support.
Conflicts of Interest
The authors certify that there is no conflict of interest with any individual/organization for the present work.
References
- Zarchan, P. Tactical and Strategic Missile Guidance; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2012. [Google Scholar]
- Yuan, P.J.; Chern, J.S. Ideal proportional navigation. J. Guid. Control Dyn. 1992, 15, 1161–1165. [Google Scholar] [CrossRef]
- Ryoo, C.-K.; Cho, H.; Tahk, M.-J. Optimal Guidance Laws with Terminal Impact Angle Constraint. J. Guid. Control Dyn. 2005, 28, 724–732. [Google Scholar] [CrossRef]
- Li, Y.; Yan, L.; Zhao, J.-G.; Liu, F.; Wang, T. Combined proportional navigation law for interception of high-speed targets. Def. Technol. 2014, 10, 298–303. [Google Scholar] [CrossRef]
- Ben-Asher, J.Z.; Cliff, E.M. Optimal evasion against a proportionally guided pursuer. J. Guid. Control Dyn. 1989, 12, 598–600. [Google Scholar] [CrossRef][Green Version]
- Shinar, J.; Steinberg, D. Analysis of Optimal Evasive Maneuvers Based on a Linearized Two-Dimensional Kinematic Model. J. Aircr. 1977, 14, 795–802. [Google Scholar] [CrossRef]
- Ye, D.; Shi, M.; Sun, Z. Satellite proximate interception vector guidance based on differential games. Chin. J. Aeronaut. 2018, 31, 1352–1361. [Google Scholar] [CrossRef]
- Fonod, R.; Shima, T. Multiple model adaptive evasion against a homing missile. J. Guid. Control Dyn. 2016, 39, 1578–1592. [Google Scholar] [CrossRef]
- Shaferman, V.; Oshman, Y. Stochastic cooperative interception using information sharing based on engagement staggering. J. Guid. Control Dyn. 2016, 39, 2127–2141. [Google Scholar] [CrossRef]
- Ho, Y.; Bryson, A.; Baron, S. Differential games and optimal pursuit-evasion strategies. IEEE Trans. Autom. Control 1965, 10, 385–389. [Google Scholar] [CrossRef]
- Anderson, G.M. Comparison of optimal control and differential game intercept missile guidance laws. J. Guid. Control Dyn. 1981, 4, 109–115. [Google Scholar] [CrossRef]
- Geng, S.-T.; Zhang, J.; Sun, J.-G. Adaptive back-stepping sliding mode guidance laws with autopilot dynamics and acceleration saturation consideration. Proc. Inst. Mech. Eng. Part G: J. Aerosp. Eng. 2019, 233, 4853–4863. [Google Scholar] [CrossRef]
- Eun-Jung, S.; Min-Jea, T. Three-dimensional midcourse guidance using neural networks for interception of ballistic targets. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 404–414. [Google Scholar] [CrossRef]
- Shima, T.; Idan, M.; Golan, O.M. Sliding-mode control for integrated missile autopilot guidance. J. Guid. Control Dyn. 2006, 29, 250–260. [Google Scholar] [CrossRef]
- Yang, Q.M.; Zhang, J.D.; Shi, G.Q.; Hu, J.W.; Wu, Y. Maneuver Decision of UAV in Short-Range Air Combat Based on Deep Reinforcement Learning. IEEE Access 2020, 8, 363–378. [Google Scholar] [CrossRef]
- Wang, L.; Yao, Y.; He, F.; Liu, K. A novel cooperative mid-course guidance scheme for multiple intercepting missiles. Chin. J. Aeronaut. 2017, 30, 1140–1153. [Google Scholar] [CrossRef]
- Song, J.; Song, S. Three-dimensional guidance law based on adaptive integral sliding mode control. Chin. J. Aeronaut. 2016, 29, 202–214. [Google Scholar] [CrossRef]
- Perelman, A.; Shima, T.; Rusnak, I. Cooperative differential games strategies for active aircraft protection from a homing missile. J. Guid. Control Dyn. 2011, 34, 761–773. [Google Scholar] [CrossRef]
- Shima, T. Optimal cooperative pursuit and evasion strategies against a homing missile. J. Guid. Control Dyn. 2011, 34, 414–425. [Google Scholar] [CrossRef]
- Shaferman, V.; Shima, T. Cooperative optimal guidance laws for imposing a relative intercept angle. J. Guid. Control Dyn. 2015, 38, 1395–1408. [Google Scholar] [CrossRef]
- Kumar, S.R.; Shima, T. Cooperative nonlinear guidance strategies for aircraft defense. J. Guid. Control Dyn. 2016, 40, 1–15. [Google Scholar] [CrossRef]
- Qi, N.; Sun, Q.; Zhao, J. Evasion and pursuit guidance law against defended target. Chin. J. Aeronaut. 2017, 30, 1958–1973. [Google Scholar] [CrossRef]
- Garcia, E.; Casbeer, D.W.; Fuchs, Z.E.; Pachter, M. Cooperative missile guidance for active defense of air vehicles. IEEE Trans. Aerosp. Electron. Syst. 2017, 54, 706–721. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, Q.; Liang, Z.; Li, P.; Ren, Z.; Zheng, Y. Fractional Calculus Guidance Algorithm in a Hypersonic Pursuit-Evasion Game. Def. Sci. J. 2017, 67, 688–697. [Google Scholar] [CrossRef]
- Guelman, M.; Shinar, J. Optimal guidance law in the plane. J. Guid. Control Dyn. 1984, 7, 471–476. [Google Scholar] [CrossRef]
- Zhang, Z.; Man, C.; Li, S.; Jin, S. Finite-time guidance laws for three-dimensional missile-target interception. Proc. IMechE Part G J. Aerosp. Eng. 2016, 230, 392–403. [Google Scholar] [CrossRef]
- Yong, E. Study on trajectory optimization and guidance approach for hypersonic glide-reentry vehicle. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2008. [Google Scholar]
- Sziroczak, D.; Smith, H. A review of design issues specific to hypersonic flight vehicles. Prog. Aerosp. Sci. 2016, 84, 1–28. [Google Scholar] [CrossRef]
- Li, H.; Zhang, R.; Li, Z.; Zhang, R. Footprint Problem with Angle of Attack Optimization for High Lifting Reentry Vehicle. Chin. J. Aeronaut. 2012, 25, 243–251. [Google Scholar] [CrossRef]
- Wang, J.; Liang, H.; Qi, Z.; Ye, D. Mapped Chebyshev pseudospectral methods for optimal trajectory planning of differentially flat hypersonic vehicle systems. Aerosp. Sci. Technol. 2019, 89, 420–430. [Google Scholar] [CrossRef]
- Yunqian, L.; Naiming, Q.; Xiaolei, S.; Yanfang, L. Game space decomposition dtudy of differential game guidance law for endoatmospheric interceptor missiles. Acta Aeronaut. Astronaut. Sin. 2010, 8, 1600–1608. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).