Aircraft 4D Trajectory Prediction in Civil Aviation: A Review
Abstract
1. Introduction
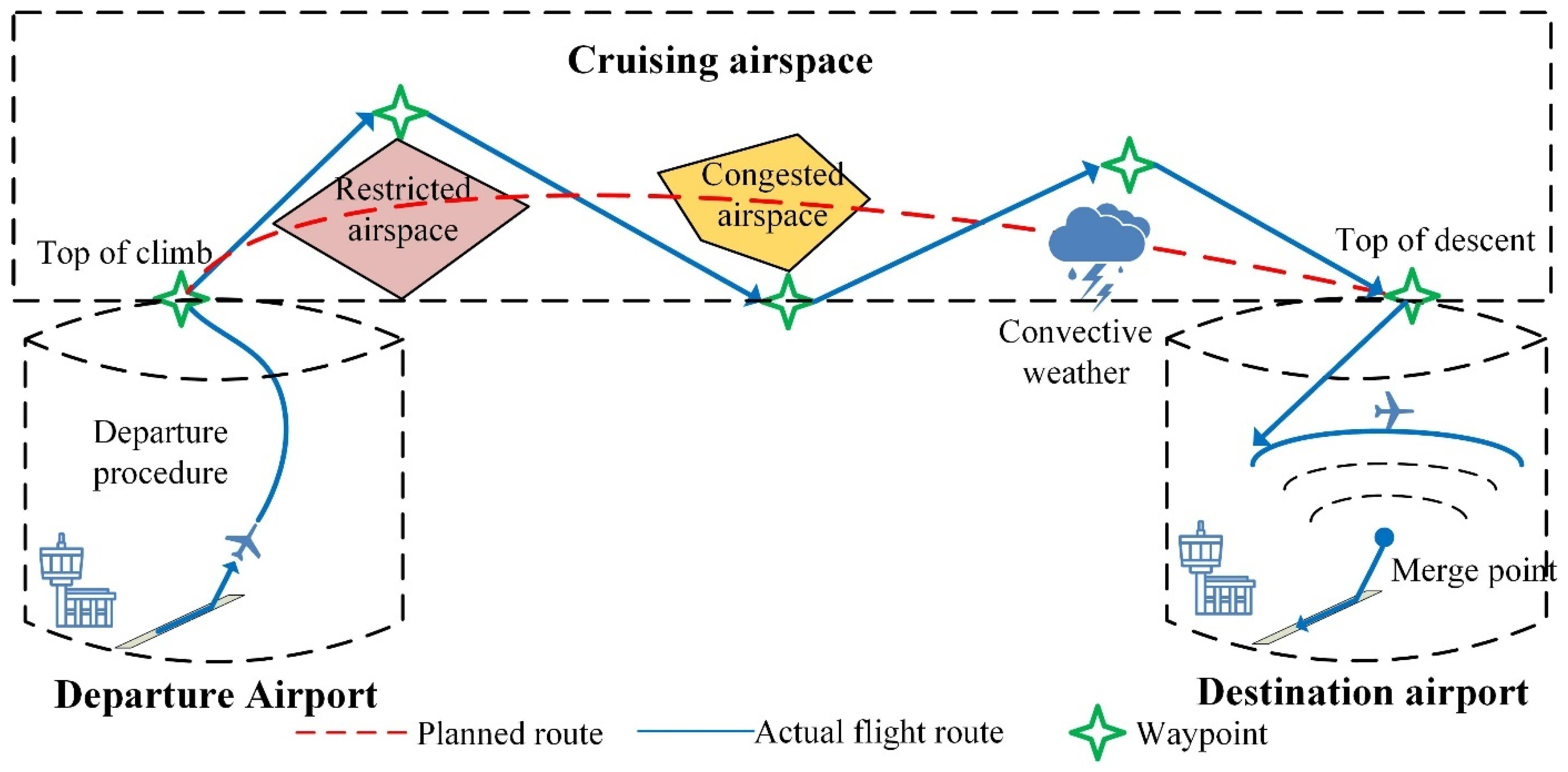
2. Problem Description and Definition
3. Trajectory Prediction Process
4. Prediction Methods
4.1. State Estimation Model
4.1.1. Single Model Estimation
4.1.2. Multi-Model Estimation
4.2. Kinetic Model
4.3. Machine Learning Model
4.3.1. Regression Model
4.3.2. Neural Network
4.3.3. Other Methods
| Regression model | Linear regression: [41,59,60] Stepwise regression: [57] |
| Nonlinear regression: [41,58] | |
| Neural network model | Feedforward neural networks: [61,70,75,84] Elman neural network: [78] LSTM: [62,63,64,65,67,71,72] DNN + LSTM: [40] CNN + LSTM: [66] GRU: [79] Bayesian neural network: [40,69] |
| Generative adversarial network: [68] | |
| Other methods | A gaussian mixture model with clustering: [82] |
| Random forest with clustering: [83] Neural Networks with clustering: [8] Nonparametric interval prediction: [73] Genetic programming: [76] |
5. Evaluation Index
6. Open Database
6.1. Aircraft Performance Data
6.1.1. BADA
6.1.2. ANP
6.2. Aircraft Surveillance Data
6.2.1. Flightradar24
6.2.2. FlightAware
6.2.3. VariFlight Global Flight Tracking Radar
6.2.4. The OpenSky Network
6.3. Meteorological Data
6.3.1. The China Meteorological Data Network
6.3.2. ECMWF
6.3.3. National Environmental Information Center
6.3.4. Relay of Aircraft Meteorological Data
6.3.5. WorldClim
7. Challenges and Future Research
- (1)
- The performance of the trajectory prediction model is closely related to the accuracy of information such as aircraft performance parameters, aircraft intent, and meteorological conditions. These input parameters are more or less in error, and small errors in some parameters can lead to catastrophic prediction results. In order to make more accurate predictions, it is possible to strengthen the real-time sharing and transmission of data such as uncertainty, which is a hotspot of current research; in addition, a more robust prediction model can be established through a method research, which is the focus of future research.
- (2)
- In recent years, ensemble learning is a type of machine learning method that uses multiple models or learners for modeling and uses certain rules to integrate the learning results, so as to obtain a machine learning method that is better than a single model or learner. The existing prediction models have their own advantages and disadvantages, and the application scenarios are different. Therefore, integrating different models to build a track prediction fusion model will improve the accuracy and stability of the model.
- (3)
- In general, air traffic congestion on an aircraft’s planned route affects the flight path. At the same time, aircraft passing through the same route or waypoint will also affect each other. How to fully consider the overall traffic congestion and the interaction between aircraft when building a prediction model will help improve the accuracy of track prediction.
- (4)
- Probabilistic trajectory prediction is often more practical than deterministic trajectory prediction. The performance of many air traffic intelligent decision-making systems depends on the accuracy of trajectory prediction. However, trajectory prediction is often affected by a variety of factors, resulting in errors in the prediction results of deterministic models. Therefore, in some application scenarios, it is often more reasonable to predict the spatiotemporal distribution of the track.
- (5)
- Most of the research and development of decision support tools are mainly focused on the terminal airspace. The effective operation of these automated decision support systems depends on the results of aircraft trajectory prediction with high reliability and accuracy. However, the complex structure of the airport terminal airspace, the high density of flight flow, and the frequent changes of aircraft flight attitudes bring challenges to the high-precision and reliable prediction of flight paths.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schulz, E.; Airbus. Global Networks, Global Citizens. Global Market Forecast 2018–2037; Airbus, Ed.; Airbus: Blagnac Cedex, France, 2018. [Google Scholar]
- Ruiz, S.; Leones, J.L.; Ranieri, A. A novel performance framework and methodology to analyze the impact of 4D trajectory based operations in the future air traffic management system. J. Adv. Transport. 2018, 2018, 1601295. [Google Scholar] [CrossRef]
- Song, Y.; Cheng, P.; Mu, C. An Improved Trajectory Prediction Algorithm Based on Trajectory Data Mining for Air Traffic Management. In Proceedings of the 2012 IEEE International Conference on Information and Automation, Shenyang, China, 6–8 June 2012. [Google Scholar]
- Brudnicki, D.J.; Kirk, D.B. Trajectory modeling for automated en route air traffic control (AERA). In Proceedings of the 1995 American Control Conference-ACC’95, Seattle, WA, USA, 21–23 June 1995. [Google Scholar]
- FAA/EUROCONTROL. Common TP Structure and Terminology in Support of SESAR & NextGen; Techincal Report FAA/EUROCONTROL: Brussels, Belgium, 2010. [Google Scholar]
- Garcia-Chico, J.; Vivona, R.; Cate, K. Characterizing intent maneuvers from operational data: Step towards trajectory prediction uncertainty estimation. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar]
- ICAO. Global Air Traffic Management Operational Concept; ICAO: Montreal, QC, Canada, 2005. [Google Scholar]
- Wang, Z.; Liang, M.; Delahaye, D. Short-Term 4d Trajectory Prediction Using Machine Learning Methods. In Proceedings of the SESAR Innovation Day SID, Belgrade, Serbia, 28–30 November 2017. [Google Scholar]
- Chatterji, G. Short-Term Trajectory Prediction Methods. In Proceedings of the Guidance, Navigation, and Control Conference and Exhibit, Portland, OR, USA, 9–11 August 1999. [Google Scholar]
- Kuchar, J.K.; Yang, L.C. A review of conflict detection and resolution modeling methods. IEEE Trans. Intell. Transp. Syst. 2000, 1, 179–189. [Google Scholar] [CrossRef]
- Radanovic, M.; Eroles, M.A.P.; Koca, T.; Gonzalez, J.J.R. Surrounding traffic complexity analysis for efficient and stable conflict resolution. Transp. Res. Part C Emerg. Technol. 2018, 95, 105–124. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, J.; Hu, R.; Zhu, H. Online four dimensional trajectory prediction method based on aircraft intent updating. Aerosp. Sci. Technol. 2018, 77, 774–787. [Google Scholar] [CrossRef]
- Bronsvoort, J. Contributions to Trajectory Prediction Theory and Its Application to Arrival Management for Air Traffic Control. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 8 October 2014. [Google Scholar]
- Lymperopoulos, I.; Lygeros, J.; Lecchini, A. Model Based Aircraft Trajectory Prediction during Takeoff. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar]
- Porretta, M.; Dupuy, M.D.; Schuster, W.; Majumdar, A.; Ochieng, W. Performance evaluation of a novel 4D trajectory prediction model for civil aircraft. J. Navig. 2008, 61, 393–420. [Google Scholar] [CrossRef]
- Schuster, W.; Ochieng, W.; Porretta, M. High-Performance Trajectory Prediction for Civil Aircraft. In Proceedings of the 29th Digital Avionics Systems Conference, Salt Lake City, UT, USA, 3–7 October 2010. [Google Scholar]
- Schultz, C.; Thipphavong, D.; Erzberger, H. Adaptive Trajectory Prediction Algorithm for Climbing Flights. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012. [Google Scholar]
- Schuster, W.; Porretta, M.; Ochieng, W. High-accuracy four-dimensional trajectory prediction for civil aircraft. Aeronaut. J. 2012, 116, 45–66. [Google Scholar] [CrossRef]
- Benavides, J.V.; Kaneshige, J.; Sharma, S.; Panda, R.; Steglinski, M. Implementation of a Trajectory Prediction Function for Trajectory Based Operations. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Dalmau, R.; Pérez-Batlle, M.; Prats, X. Real-Time Identification of Guidance Modes in Aircraft Descents Using Surveillace Data. In Proceedings of the 2018 IEEE/AIAA 37th Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018. [Google Scholar]
- Dalmau, R.; Prats, X.; Verhoeven, R.; Bussink, F.; Heesbeen, B. Comparison of various guidance strategies to achieve time constraints in optimal descents. J. Guid. Control. Dyn. 2019, 42, 1612–1621. [Google Scholar] [CrossRef]
- Avanzini, G. Frenet-based algorithm for trajectory prediction. J. Guid. Control. Dyn. 2004, 27, 127–135. [Google Scholar] [CrossRef]
- Lymperopoulos, I.; Lygeros, J. Sequential Monte Carlo methods for multi-aircraft trajectory prediction in air traffic management. Int. J. Adapt. Control Signal Process. 2010, 24, 830–849. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, J.-W.; Liu, H. An algorithm for trajectory prediction of flight plan based on relative motion between positions. Front. Inf. Technol. Electron. Eng. 2018, 19, 905–916. [Google Scholar] [CrossRef]
- Choi, P.P.; Hebert, M. Learning and predicting moving object trajectory: A piecewise trajectory segment approach. Robot. Inst. 2006, 337, 1–17. [Google Scholar]
- Ayhan, S.; Samet, H. Aircraft Trajectory Prediction Made Easy with Predictive Analytics. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Lin, Y.; Yang, B.; Zhang, J.; Liu, H. Approach for 4-d trajectory management based on HMM and trajectory similarity. J. Mar. Sci. Technol. 2019, 27, 246–256. [Google Scholar]
- Rezaie, R.; Li, X.R. Trajectory Modeling and Prediction with Waypoint Information Using a Conditionally Markov Sequence. In Proceedings of the 2018 56th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 2–5 October 2018. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Liu, W.; Hwang, I. Probabilistic trajectory prediction and conflict detection for air traffic control. J. Guid. Control. Dyn. 2011, 34, 1779–1789. [Google Scholar] [CrossRef]
- Seah, C.E.; Hwang, I. A Hybrid Estimation Algorithm for Terminal-Area Aircraft Tracking. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007. [Google Scholar]
- Seah, C.E.; Hwang, I. Terminal-area aircraft tracking using hybrid estimation. J. Guid. Control. Dyn. 2009, 32, 836–849. [Google Scholar] [CrossRef]
- Hwang, I.; Seah, C.E. Intent-based probabilistic conflict detection for the next generation air transportation system. Proc. IEEE 2008, 96, 2040–2059. [Google Scholar] [CrossRef]
- Chen, Y.; Cheng, Z.; Wen, S.-L. Modified IMM algorithm for unmatched dynamic models. Syst. Eng. Electron. 2011, 33, 2593–2597. [Google Scholar]
- Jun-Feng, Z.; Xiao-Guang, W.; Fei, W. Aircraft trajectory prediction based on modified interacting multiple model algorithm. J. Donghua Univ. 2015, 32, 180–184. [Google Scholar]
- Yepes, J.L.; Hwang, I.; Rotea, M. New algorithms for aircraft intent inference and trajectory prediction. J. Guid. Control. Dyn. 2007, 30, 370–382. [Google Scholar] [CrossRef]
- Xi, L.; Jun, Z.; Yanbo, Z.; Wei, L. Simulation Study of Algorithms for Aircraft Trajectory Prediction Based on ADS-B Technology. In Proceedings of the 2008 Asia Simulation Conference-7th International Conference on System Simulation and Scientific Computing, Beijing, China, 10–12 October 2008. [Google Scholar]
- Liu, Y.; Li, X.R. Intent based trajectory prediction by multiple model prediction and smoothing. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Choi, H.-C.; Deng, C.; Hwang, I. Hybrid Machine learning and estimation-based flight trajectory prediction in terminal airspace. IEEE Access 2021, 9, 151186–151197. [Google Scholar] [CrossRef]
- Zhang, X.; Mahadevan, S. Bayesian neural networks for flight trajectory prediction and safety assessment. Decis. Support Syst. 2020, 131, 113246. [Google Scholar] [CrossRef]
- Ghasemi Hamed, M.; Gianazza, D.; Serrurier, M.; Durand, N. Statistical prediction of aircraft trajectory: Regression methods vs point-mass model. In Proceedings of the ATM Seminar, Chicago, IL, USA, 10–13 June 2013. [Google Scholar]
- Weitz, L.A. Derivation of a Point-Mass Aircraft Model Used for Fast-Time Simulation; MITRE Corporation: Bedford, MA, USA, 2015. [Google Scholar]
- Schuster, W. Trajectory prediction for future air traffic management—Complex manoeuvres and taxiing. Aeronaut. J. 2015, 119, 121–143. [Google Scholar] [CrossRef][Green Version]
- Fukuda, Y.; Shirakawa, M.; Senoguchi, A. Development and evaluation of trajectory prediction model. In Proceedings of the 27th International Congress of the Aeronautical Sciences, Nice, France, 19–24 September 2010. [Google Scholar]
- Tang, X.-M.; Han, Y.-X. 4D trajectory estimation for air traffic control automation system based on hybrid system theory. Promet Traffic Transp. 2012, 24, 91–98. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S.; Hwang, I. Hybrid system modeling and estimation for arrival time prediction in terminal airspace. J. Guid. Control. Dyn. 2016, 39, 903–910. [Google Scholar] [CrossRef]
- Felix, F.N.; Ruiz, M.V.; Querejeta, C.; Gallo, E.; Leones, J.L. Predicting Aircraft Trajectory. US9250099B2 Patents, 2 February 2016. [Google Scholar]
- Lopez Leones, J. Definition of an aircraft intent description language for air traffic management applications. Ph.D. Thesis, University of Glasgow, Glasgow, UK, 2008. [Google Scholar]
- López-Leonés, J.; Vilaplana, M.A.; Gallo, E.; Navarro, F.A.; Querejeta, C. The aircraft intent description language: A key enabler for air-ground synchronization in trajectory-based operations. In Proceedings of the 2007 IEEE/AIAA 26th Digital Avionics Systems Conference, Dallas, TX, USA, 21–25 October 2007. [Google Scholar]
- Thipphavong, D.P.; Schultz, C.A.; Lee, A.G.; Chan, S.H. Adaptive algorithm to improve trajectory prediction accuracy of climbing aircraft. J. Guid. Control. Dyn. 2013, 36, 15–24. [Google Scholar] [CrossRef]
- Baklacioglu, T.; Cavcar, M. Aero-propulsive modelling for climb and descent trajectory prediction of transport aircraft using genetic algorithms. Aeronaut. J. 2014, 118, 65–79. [Google Scholar] [CrossRef]
- Nuic, A.; Poinsot, C.; Iagaru, M.G.; Gallo, E.; Navarro, F.A.; Querejeta, C. Advanced aircraft performance modeling for ATM: Enhancements to the BADA model. In Proceedings of the 24th Digital Avionics System Conference, Washington, DC, USA, 30 September–3 October 2005. [Google Scholar]
- Alligier, R.; Gianazza, D.; Durand, N. Learning the aircraft mass and thrust to improve the ground-based trajectory prediction of climbing flights. Transp. Res. Part C Emerg. Technol. 2013, 36, 45–60. [Google Scholar] [CrossRef]
- Sun, J.; Ellerbroek, J.; Hoekstra, J.M. WRAP: An open-source kinematic aircraft performance model. Transp. Res. Part C Emerg. Technol. 2019, 98, 118–138. [Google Scholar] [CrossRef]
- Sun, J.; Ellerbroek, J.; Hoekstra, J.M. Aircraft initial mass estimation using Bayesian inference method. Transp. Res. Part C Emerg. Technol. 2018, 90, 59–73. [Google Scholar] [CrossRef]
- Alligier, R.; Gianazza, D. Learning aircraft operational factors to improve aircraft climb prediction: A large scale multi-airport study. Transp. Res. Part C Emerg. Technol. 2018, 96, 72–95. [Google Scholar] [CrossRef]
- De Leege, A.; van Paassen, M.; Mulder, M. A machine learning approach to trajectory prediction. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar]
- Tastambekov, K.; Puechmorel, S.; Delahaye, D.; Rabut, C. Aircraft trajectory forecasting using local functional regression in Sobolev space. Transp. Res. Part C Emerg. Technol. 2014, 39, 1–22. [Google Scholar] [CrossRef]
- Kanneganti, S.T.; Chilson, P.B.; Huck, R. Visualization and prediction of aircraft trajectory using ADS-B. In Proceedings of the NAECON 2018-IEEE National Aerospace and Electronics Conference, Dayton, OH, USA, 23–26 July 2018. [Google Scholar]
- Hong, S.; Lee, K. Trajectory prediction for vectored area navigation arrivals. J. Aerosp. Inf. Syst. 2015, 12, 490–502. [Google Scholar] [CrossRef]
- Le Fablec, Y.; Alliot, J.-M. Using neural networks to predict aircraft trajectories. In Proceedings of the IC-AI, Las Vegas, NV, USA, 28 June–1 July 1999. [Google Scholar]
- Shi, Z.; Xu, M.; Pan, Q.; Yan, B.; Zhang, H. LSTM-based flight trajectory prediction. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar]
- Xu, Z.; Zeng, W.; Chu, X.; Cao, P. Multi-aircraft trajectory collaborative prediction based on social long short-term memory network. Aerospace 2021, 8, 115. [Google Scholar] [CrossRef]
- Zeng, W.; Quan, Z.; Zhao, Z.; Xie, C.; Lu, X. A deep learning approach for aircraft trajectory prediction in terminal airspace. IEEE Access 2020, 8, 151250–151266. [Google Scholar] [CrossRef]
- Yang, K.; Bi, M.; Liu, Y.; Zhang, Y. LSTM-based deep learning model for civil aircraft position and attitude prediction approach. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019. [Google Scholar]
- Ma, L.; Tian, S. A hybrid CNN-LSTM model for aircraft 4D trajectory prediction. IEEE Access 2020, 8, 134668–134680. [Google Scholar] [CrossRef]
- Shi, Z.; Xu, M.; Pan, Q. 4-D flight trajectory prediction with constrained LSTM network. IEEE Trans. Intell. Transp. Syst. 2020, 22, 7242–7255. [Google Scholar] [CrossRef]
- Pang, Y.; Liu, Y. Conditional generative adversarial networks (CGAN) for aircraft trajectory prediction considering weather effects. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Pang, Y.; Liu, Y. Probabilistic aircraft trajectory prediction considering weather uncertainties using dropout as bayesian approximate variational inference. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Wu, Z.-J.; Tian, S.; Ma, L. A 4D trajectory prediction model based on the BP neural network. J. Intell. Syst. 2019, 29, 1545–1557. [Google Scholar] [CrossRef]
- Ma, Z.; Yao, M.; Hong, T.; Li, B. Aircraft surface trajectory prediction method based on LSTM with attenuated memory window. J. Phys. Conf. Ser. 2019, 1215, 012003. [Google Scholar] [CrossRef]
- Zhao, Z.; Zeng, W.; Quan, Z.; Chen, M.; Yang, Z. Aircraft trajectory prediction using deep long short-term memory networks. In Proceedings of the 19th COTA International Conference of Transportation Professionals CICTP 2019, Nanjing, China, 6–8 July 2019; pp. 124–135. [Google Scholar]
- Hamed, M.G. Méthodes Non-Paramétriques pour la Prévision D intervalles avec HAUT niveau de Confiance: Application à la Prévision de Trajectoires D avions. Ph.D. Thesis, Institut National Polytechnique de Toulouse-INPT, Toulouse, France, 2014. [Google Scholar]
- Shen, Z.; Tang, X. A novel 4D track prediction approach combining empirical mode decomposition with nonlinear correlation coefficient. In Proceedings of the COTA International Conference of Transportation Professionals CICTP 2015, Beijing, China, 24–27 July 2015; pp. 25–34. [Google Scholar]
- Gallego, C.E.V.; Comendador, V.F.G.; Carmona, M.A.A.; Valdés, R.M.A.; Nieto, F.J.S.; Martínez, M.G. A machine learning approach to air traffic interdependency modelling and its application to trajectory prediction. Transp. Res. Part C Emerg. Technol. 2019, 107, 356–386. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, X.; Shi, C.; Liu, W. Aircraft trajectory prediction based on genetic programming. In Proceedings of the 2016 3rd International Conference on Information Science and Control Engineering (ICISCE), Beijing, China, 8–10 July 2016. [Google Scholar]
- Chen, Z.; Guo, D.; Lin, Y. A deep gaussian process-based flight trajectory prediction approach and its application on conflict detection. Algorithms 2020, 13, 293. [Google Scholar] [CrossRef]
- Min, W.; Jiawei, W.; Jinhui, G.; Lihua, S.; Bogong, A. Multi-point prediction of aircraft motion trajectory based on GA-Elman-Regularization neural network. Integr. Ferroelectr. 2020, 210, 116–127. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, C.; Xuan, Y.; Tang, S. Real-time prediction of air combat flight trajectory using GRU. Syst. Eng. Electron. Technol. 2020, 42, 2546–2552. [Google Scholar]
- Tang, X.; Chen, P.; Zhang, Y. 4D trajectory estimation based on nominal flight profile extraction and airway meteorological forecast revision. Aerosp. Sci. Technol. 2015, 45, 387–397. [Google Scholar] [CrossRef]
- Fernández, E.C.; Cordero, J.M.; Vouros, G.; Pelekis, N.; Kravaris, T.; Georgiou, H.; Ayhan, S. DART: A machine-learning approach to trajectory prediction and demand-capacity balancing. In Proceedings of the SESAR Innovation Days, Belgrade, Serbia, 28–30 November 2017; pp. 28–30. [Google Scholar]
- Barratt, S.T.; Kochenderfer, M.J.; Boyd, S.P. Learning probabilistic trajectory models of aircraft in terminal airspace from position data. IEEE Trans. Intell. Transp. Syst. 2018, 20, 3536–3545. [Google Scholar] [CrossRef]
- Le, T.H.; Tran, P.N.; Pham, D.T.; Schultz, M.; Alam, S. Short-term trajectory prediction using generative machine learning methods. In Proceedings of the ICRAT 2020 Conference, Tampa, FL, USA, 23–26 June 2020. [Google Scholar]
- Gallego, C.E.V.; Comendador, V.F.G.; Nieto, F.J.S.; Imaz, G.O.; Valdés, R.M.A. Analysis of air traffic control operational impact on aircraft vertical profiles supported by machine learning. Transp. Res. Part C Emerg. Technol. 2018, 95, 883–903. [Google Scholar] [CrossRef]
- Zeng, W.; Xu, Z.; Cai, Z.; Chu, X.; Lu, X. Aircraft trajectory clustering in terminal airspace based on deep autoencoder and gaussian mixture model. Aerospace 2021, 8, 266. [Google Scholar] [CrossRef]
- Nuic, A. User manual for the Base of Aircraft Data (BADA) revision 3.10. Atmosphere 2010, 2010, 001. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, W.; Chu, X.; Xu, Z.; Liu, Y.; Quan, Z. Aircraft 4D Trajectory Prediction in Civil Aviation: A Review. Aerospace 2022, 9, 91. https://doi.org/10.3390/aerospace9020091
Zeng W, Chu X, Xu Z, Liu Y, Quan Z. Aircraft 4D Trajectory Prediction in Civil Aviation: A Review. Aerospace. 2022; 9(2):91. https://doi.org/10.3390/aerospace9020091
Chicago/Turabian StyleZeng, Weili, Xiao Chu, Zhengfeng Xu, Yan Liu, and Zhibin Quan. 2022. "Aircraft 4D Trajectory Prediction in Civil Aviation: A Review" Aerospace 9, no. 2: 91. https://doi.org/10.3390/aerospace9020091
APA StyleZeng, W., Chu, X., Xu, Z., Liu, Y., & Quan, Z. (2022). Aircraft 4D Trajectory Prediction in Civil Aviation: A Review. Aerospace, 9(2), 91. https://doi.org/10.3390/aerospace9020091








