Sensitivity-Based Non-Linear Model Predictive Control for Aircraft Descent Operations Subject to Time Constraints
Abstract
:1. Introduction
2. Trajectory Management Using NMPC
2.1. Trajectory Planning
2.1.1. Optimal Control Problem Formulation in the Continuous Domain
2.1.2. Optimal Control Problem Discretization Using Direct Methods
2.1.3. Solution of the Direct Optimal Control Problem Using NLP Algorithms
2.2. Trajectory Guidance
2.2.1. Ideal NMPC (INMPC) Guidance
| Algorithm 1 Working principle of the ideal NMPC (INMPC) |
|
2.2.2. Sensitivity-Based NMPC (SbNMPC) Guidance
2.2.3. Advanced Step NMPC (AsNMPC) Guidance
| Algorithm 2 Working Principle of the Sensitivity-Based NMPC (SbNMPC) |
|
| Algorithm 3 Working principle of the advanced-step NMPC (AsNMPC) |
|
3. NMPC Guidance Strategies for a Time-Constrained CDO
3.1. Optimal Control Problem Formulation
3.2. On-Line Wind Profile Parameters Estimation
4. Experiment Setup
4.1. Arrival Route
4.2. Case Studies
4.3. Descent Simulation Workflow
5. Results
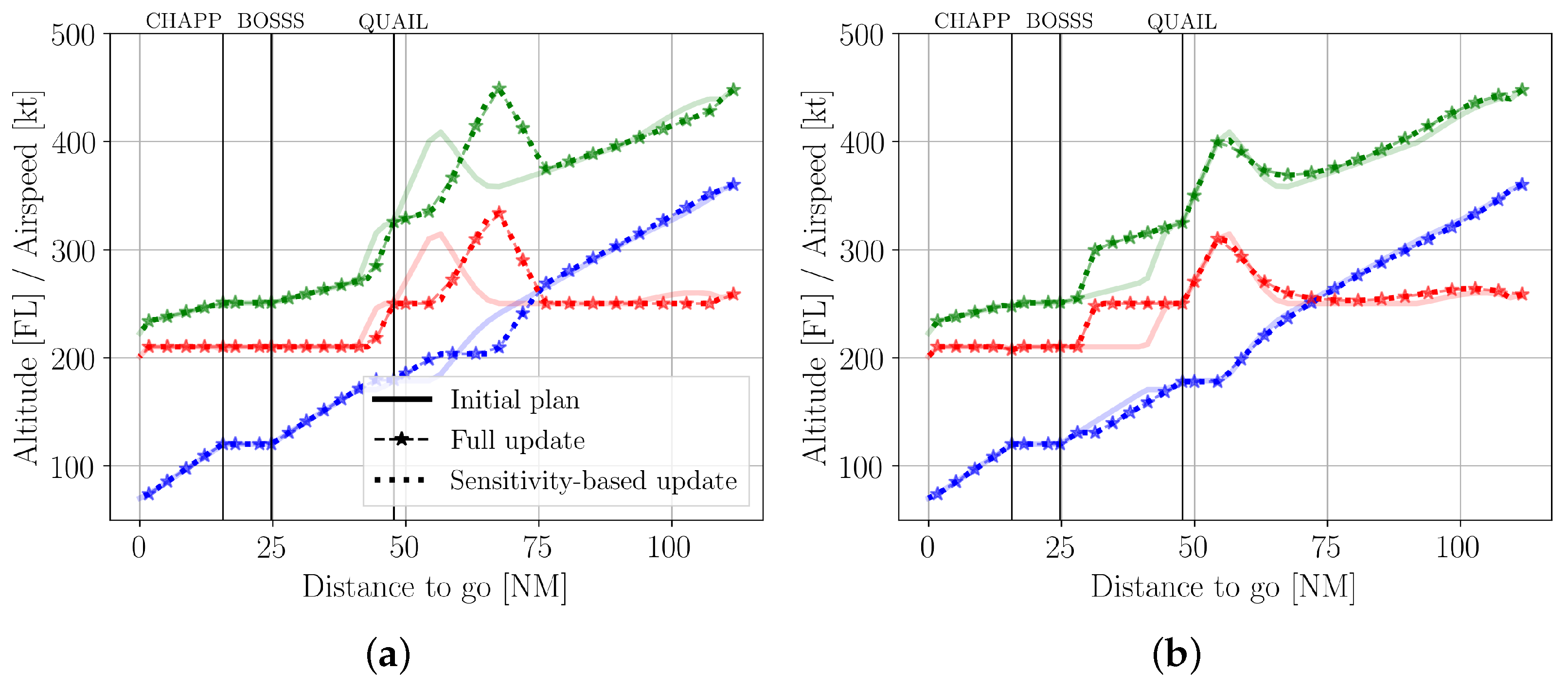
5.1. Illustrative Examples: Trajectory Updates
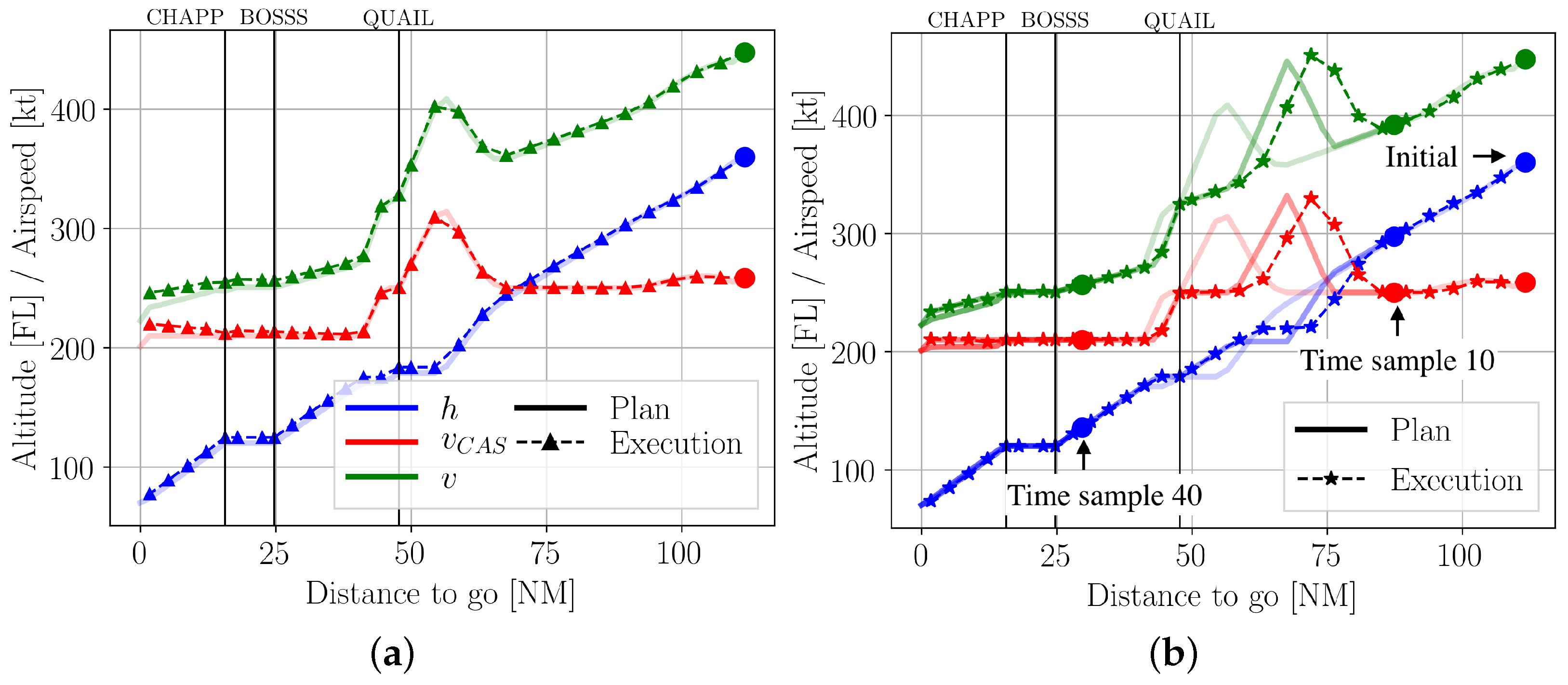
5.2. Illustrative Examples: Guidance Strategies
5.3. Aggregated Results
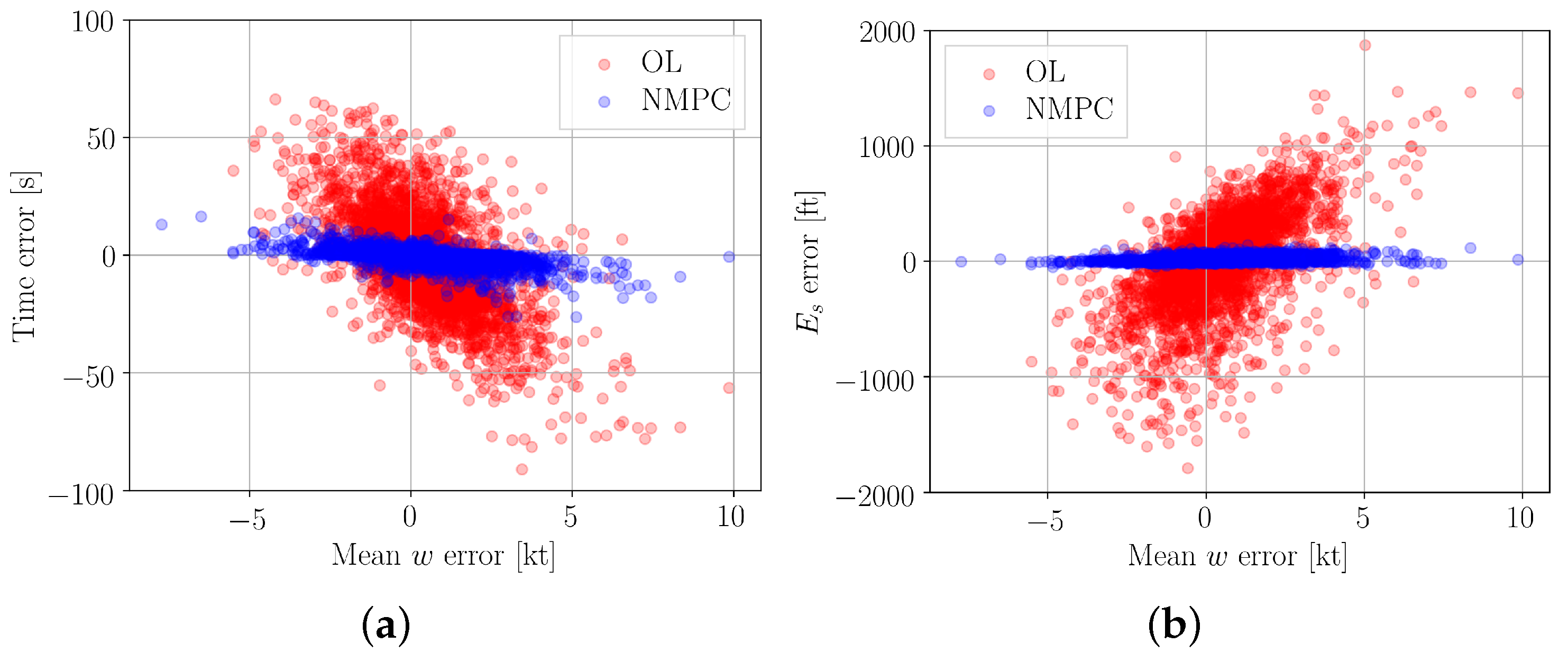
5.3.1. Time Error and Specific Energy Error Results
5.3.2. Speed Brakes, Throttle and Fuel Results
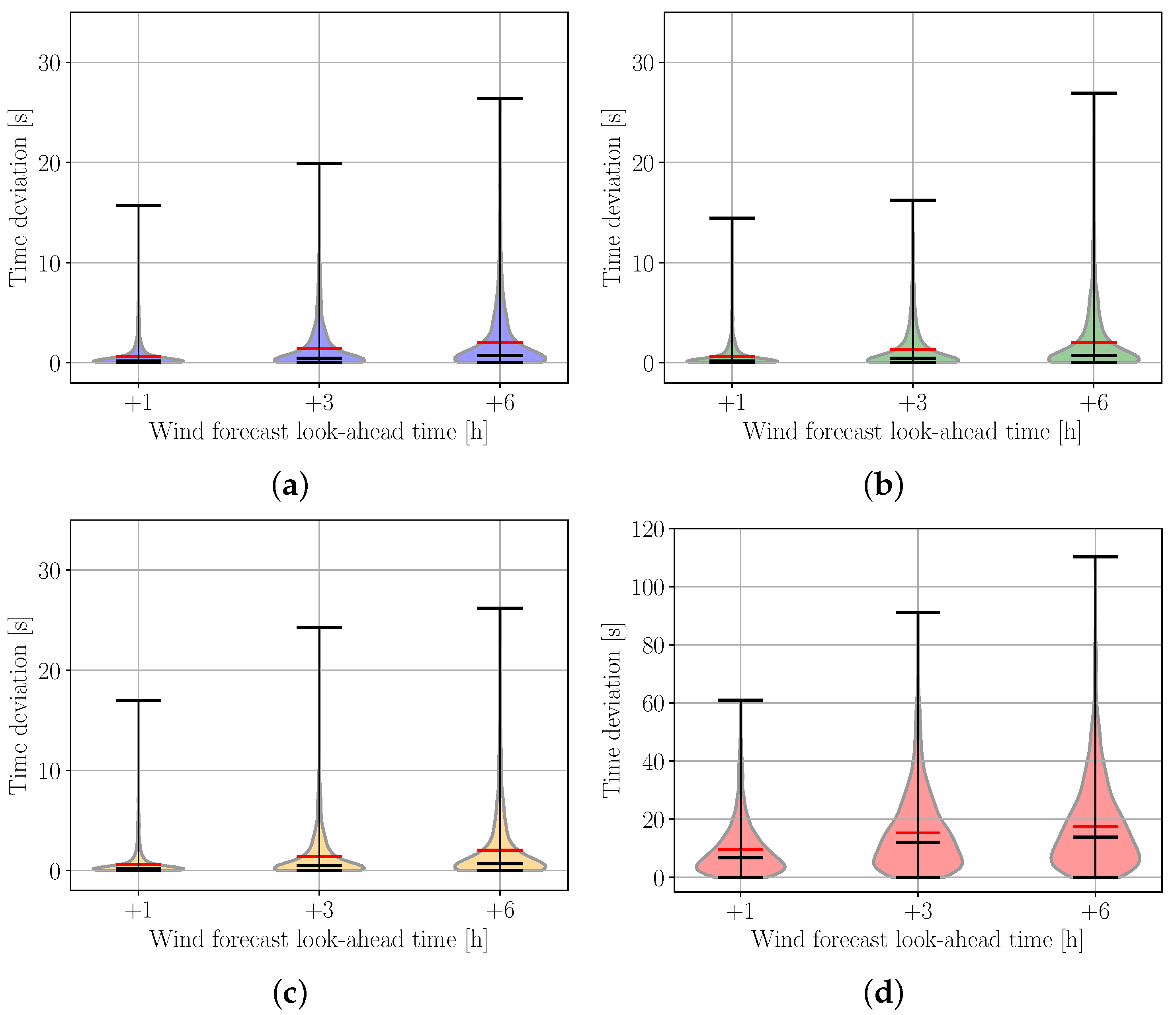
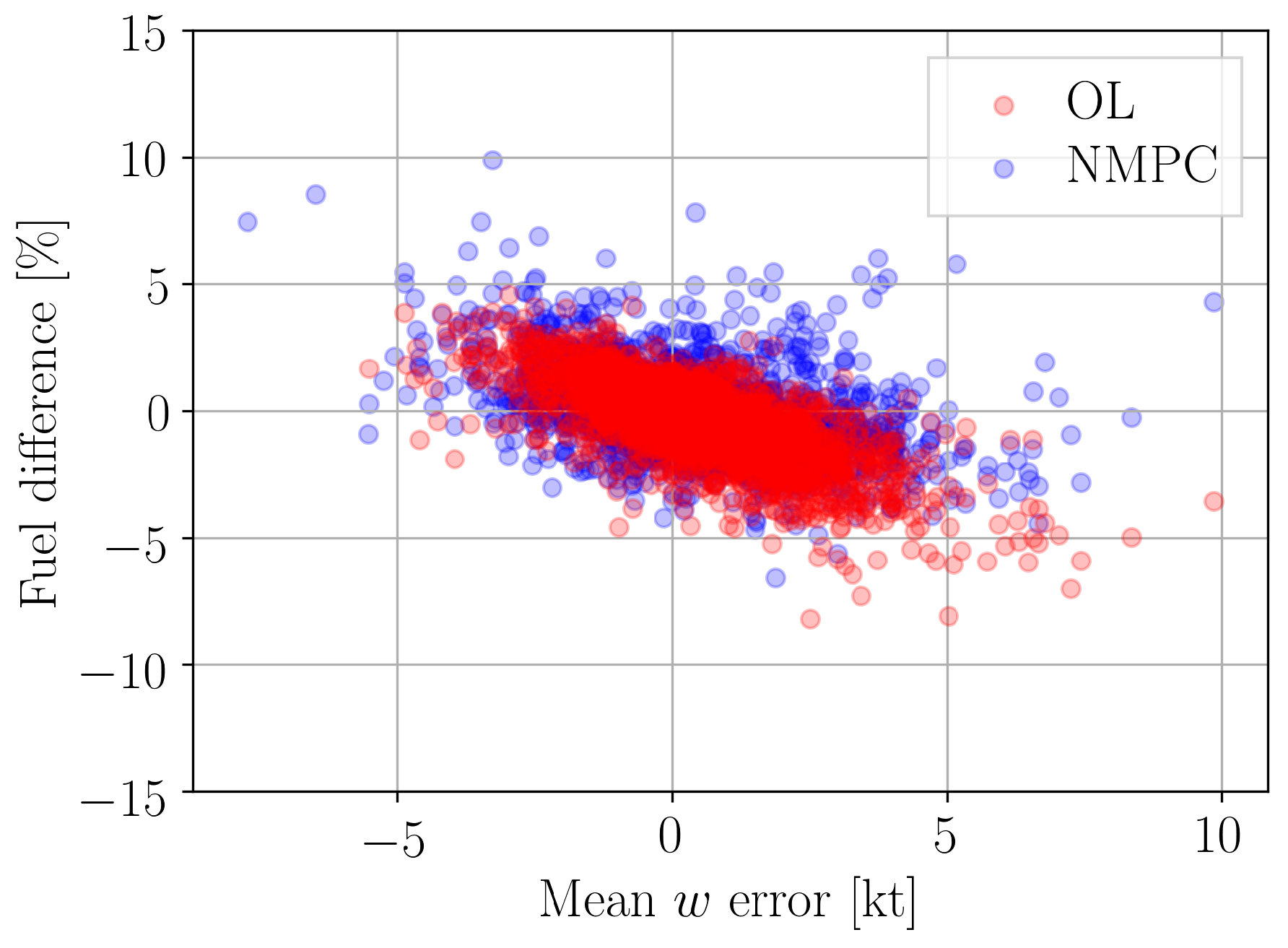
5.3.3. Sensitivity to Wind Error
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bryson, A.E.; Ho, Y. Applied Optimal Control: Optimization, Estimation, and Control; Taylor and Francis Group: New York, NY, USA, 1975. [Google Scholar]
- González-Arribas, D.; Soler, M.; Sanjurjo-Rivo, M. Robust Aircraft Trajectory Planning Under Wind Uncertainty Using Optimal Control. J. Guid. Control. Dyn. 2018, 41, 673–688. [Google Scholar] [CrossRef] [Green Version]
- Kamo, S.; Rosenow, J.; Fricke, H.; Soler, M. Robust CDO Trajectory Planning under Uncertainties in Weather Prediction. In Proceedings of the the 13th USA/Europe Air Traffic Management Research and Development Seminar, Saclay, France, 17–19 June 2019. [Google Scholar]
- Dalmau, R.; Prats, X.; Verhoeven, R.; Bussink, F.J.L.; Heesbeen, B. Performance comparison of guidance strategies to accomplish RTAs during a CDO. In Proceedings of the 36th AIAA/IEEE Digital Avionics Systems Conference (DASC), St. Petersburg, FL, USA, 17–21 September 2017. [Google Scholar] [CrossRef] [Green Version]
- de Jong, P.M.A.; de Gelder, N.; Verhoeven, R.; Bussink, F.J.L.; Kohrs, R.; van Paassen, M.M.; Mulder, M. Time and Energy Management During Descent and Approach: Batch Simulation Study. J. Aircr. 2014, 52, 190–203. [Google Scholar] [CrossRef]
- Diehl, M.; Ferreau, H.J.; Haverbeke, N. Efficient Numerical Methods for Nonlinear MPC and Moving Horizon Estimation Problem Formulation. In Nonlinear Model Predictive Control; Springer: Berlin/Heidelberg, Germany, 2008; pp. 391–417. [Google Scholar] [CrossRef] [Green Version]
- Dalmau, R.; Verhoeven, R.; De Gelder, N.; Prats, X. Performance comparison between TEMO and a typical FMS in presence of CTA and wind uncertainties. In Proceedings of the 35th AIAA/IEEE Digital Avionics Systems Conference (DASC), Sacramento, CA, USA, 25–29 September 2016. [Google Scholar] [CrossRef] [Green Version]
- Weitz, L.A.; Bai, X. Using Model Predictive Control for Trajectory Optimization and to Meet Spacing Objectives. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Ru, P.; Subbarao, K. Nonlinear Model Predictive Control for Unmanned Aerial Vehicles. Aerospace 2017, 4, 31. [Google Scholar] [CrossRef]
- Mothes, F. Trajectory Planning in Time-Varying Adverse Weather for Fixed-Wing Aircraft Using Robust Model Predictive Control. Aerospace 2019, 6, 68. [Google Scholar] [CrossRef] [Green Version]
- Suwartadi, E.; Kungurtsev, V.; Jäschke, J. Sensitivity-Based Economic NMPC with a Path-Following Approach. Processes 2017, 5, 8. [Google Scholar] [CrossRef] [Green Version]
- Kim, T.J.; Hull, D.G. Optimal control design that accounts for model mismatch errors. In Proceedings of the AAS/MAA Space Flight Mechanics Meeting, Albuquerque, New Mexico, 13–16 February 1995. [Google Scholar]
- Zavala, V.M.; Biegler, L.T. The advanced-step NMPC controller: Optimality, stability and robustness. Automatica 2009, 45, 86–93. [Google Scholar] [CrossRef]
- Wetzel, T.A. Development of a Finite Difference Neighboring Optimal Control Law and Application to the Optimal Landing of a Reusable Launch Vehicle. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 1996. [Google Scholar]
- Pesch, H.J. Numerical computation of neighboring optimum feedback control schemes in real-time. Appl. Math. Optim. 1979, 5, 231–252. [Google Scholar] [CrossRef]
- Würth, L.; Hannemann, R.; Marquardt, W. An Efficient Strategy for Real-Time Dynamic Optimization based on Parametric Sensitivities. IFAC Proc. Vol. 2008, 41, 1928–1933. [Google Scholar] [CrossRef] [Green Version]
- Würth, L.; Hannemann, R.; Marquardt, W. Neighboring-extremal updates for nonlinear model-predictive control and dynamic real-time optimization. J. Process. Control. 2009, 19, 1277–1288. [Google Scholar] [CrossRef]
- Wolf, I.J.; Marquardt, W. Fast NMPC schemes for regulatory and economic NMPC—A review. J. Process. Control. 2016, 44, 162–183. [Google Scholar] [CrossRef]
- Dalmau, R.; Baxley, B.; Prats, X. Fast sensitivity-based optimal trajectory updates for descent operations subject to time constraints. In Proceedings of the 37th IEEE/AIAA Digital Avionics Systems Conference (DASC), London, UK, 23–27 September 2018. [Google Scholar] [CrossRef] [Green Version]
- Betts, J.T. Practical Methods for Optimal Control and Estimation Using Nonlinear Programming, 2nd ed.; SIAM: Philadelphia, PA, USA, 2010; p. 434. [Google Scholar] [CrossRef]
- Dalmau, R. Optimal Trajectory Management for Aircraft Descent Operations Subject to Time Constraints. Ph.D. Thesis, Technical University of Catalonia (UPC), Barcelona, Spain, 2019. [Google Scholar]
- Jäschke, J.; Yang, X.; Biegler, L.T. Fast economic model predictive control based on NLP-sensitivities. J. Process. Control. 2014, 24, 1260–1272. [Google Scholar] [CrossRef]
- Kadam, J.V.; Marquardt, W. Sensitivity-Based Solution Updates in Closed-Loop Dynamic Optimization. IFAC Proc. Vol. 2004, 37, 947–952. [Google Scholar] [CrossRef]
- Gros, S.; Srinivasan, B.; Chachuat, B.; Bonvin, D. Neighbouring-extremal control for singular dynamic optimisation problems. Part I: Single-input systems. Int. J. Control. 2009, 82, 1099–1112. [Google Scholar] [CrossRef]
- Clarke, J.P.B.; Ho, N.T.; Ren, L.; Brown, J.A.; Elmer, K.R.; Zou, K.F.; Hunting, C.; McGregor, D.L.; Shivashankara, B.N.; Tong, K.; et al. Continuous descent approach: Design and flight test for Louisville international airport. J. Aircr. 2004, 41, 1054–1066. [Google Scholar] [CrossRef]
- de Boor, C. On calculating with B-splines. J. Approx. Theory 1972, 6, 50–62. [Google Scholar] [CrossRef] [Green Version]
- de Jong, P.M.A.; van der Laan, J.J.; Veld, A.C.; van Paassen, M.M.; Mulder, M. Wind-Profile Estimation Using Airborne Sensors. J. Aircr. 2014, 51, 1852–1863. [Google Scholar] [CrossRef]
- Poles, D.; Nuic, A.; Mouillet, V. Advanced aircraft performance modelling for ATM: Analysis of BADA model capabilities. In Proceedings of the 29th Digital Avionics Systems Conference (DASC), Salt Lake City, UT, USA, 3–7 October 2010. [Google Scholar] [CrossRef]
- Hindmarsh, A.C.; Brown, P.N.; Grant, K.E.; Lee, S.L.; Serban, R.; Shumaker, D.E.; Woodward, C.S. SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. 2005, 31, 363–396. [Google Scholar] [CrossRef]
- Dalmau, R.; Melgosa, M.; Prats, X. pyBADA: Easy BADA integration in python for rapid prototyping. In Proceedings of the 8th SESAR Innovation Days (SID), Salzburg, Austria, 3–6 December 2018. [Google Scholar]
- Airbus. Getting to Grips with the Cost Index; Technical Report; Airbus Flight Operations Support & Line Assistance: Blagnac, France, 1998. [Google Scholar]
- Dalmau, R.; Prats, X. Controlled time of arrival windows for already initiated energy-neutral continuous descent operations. Transp. Res. Part C 2017, 85, 334–347. [Google Scholar] [CrossRef] [Green Version]
- Andersson, J.; Akesson, J.; Diehl, M. Dynamic optimization with CasADi. In Proceedings of the IEEE Conference on Decision and Control, Maui, HI, USA, 10–13 December 2012; pp. 681–686. [Google Scholar] [CrossRef]
- Andersson, J.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi—A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W.; Saunders, M.A. SNOPT: An SQP algorithm for large-scale constrained optimization. Soc. Ind. Appl. Math. 2005, 47, 99–131. [Google Scholar] [CrossRef]
- Sáez, R.; Prats, X.; Polishchuk, T.; Polishchuk, V. Traffic synchronization in terminal airspace to enable continuous descent operations in trombone sequencing and merging procedures: An implementation study for Frankfurt airport. Transp. Res. Part C 2020, 121, 102875. [Google Scholar] [CrossRef]
- Sáez, R.; Polishchuk, T.; Schmidt, C.; Hardell, H.; Smetanová, L.; Polishchuk, V.; Prats, X. Automated sequencing and merging with dynamic aircraft arrival routes and speed management for continuous descent operations. Transp. Res. Part C 2021, 132, 103402. [Google Scholar] [CrossRef]
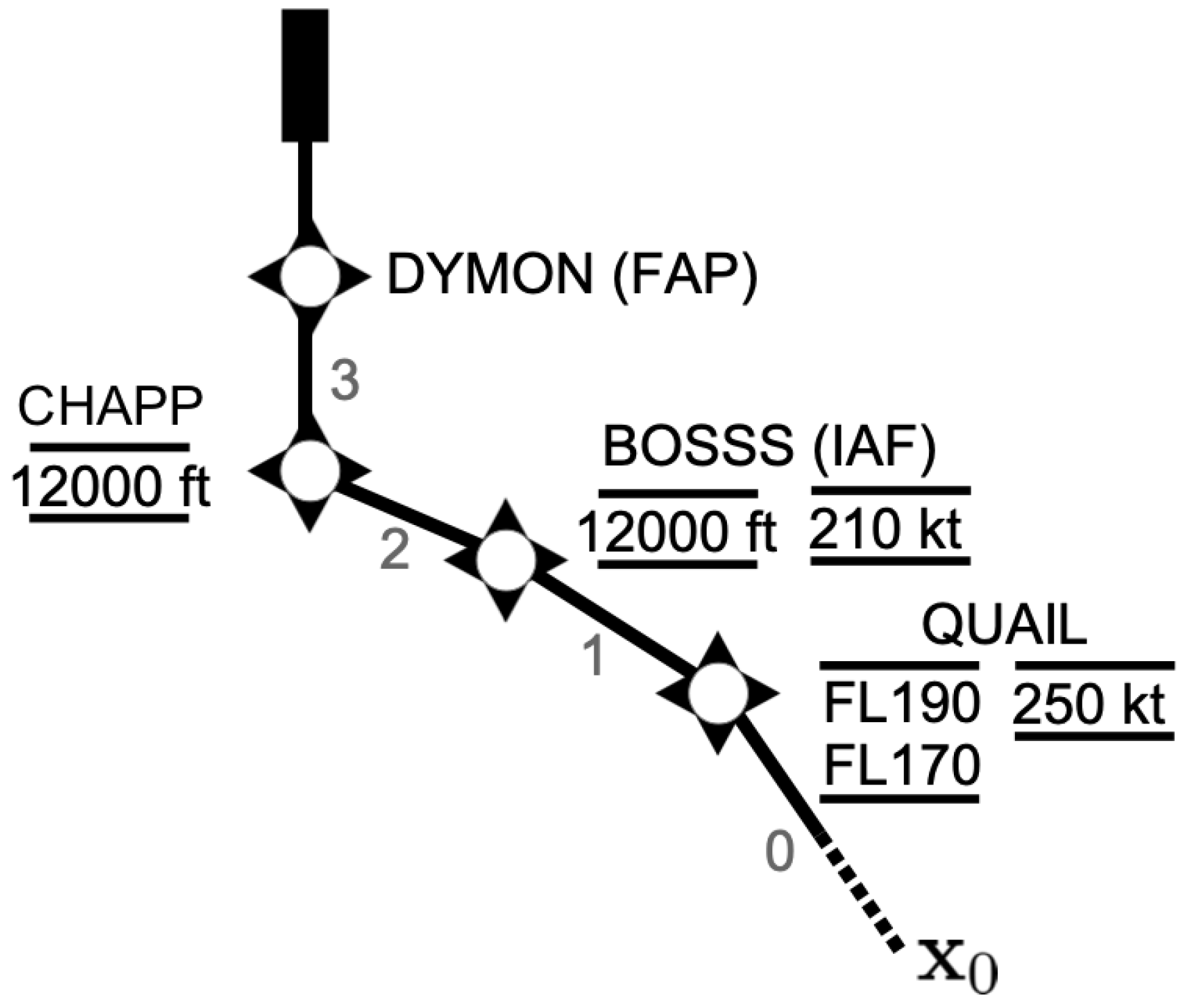


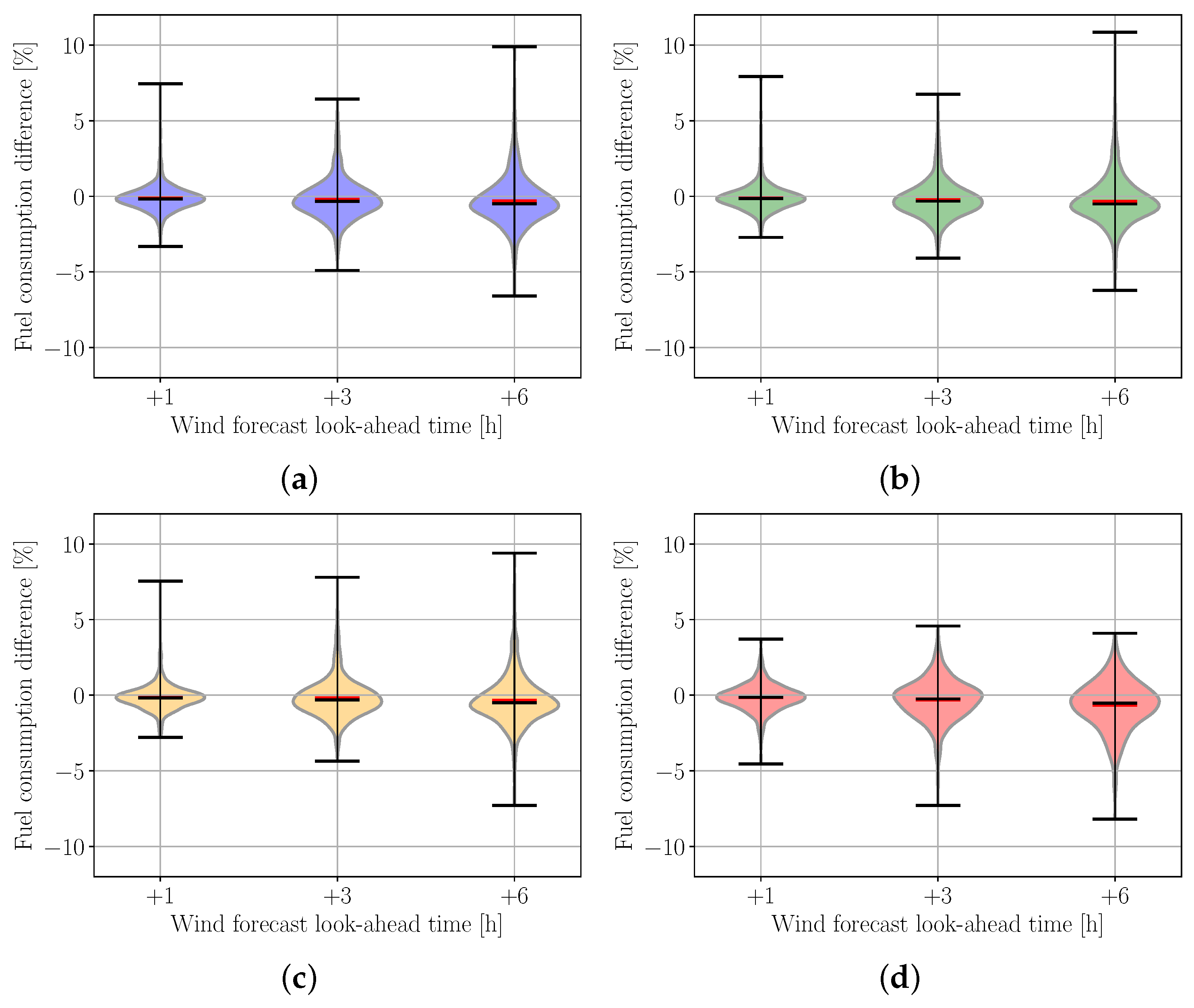
| j | Description | ||||
|---|---|---|---|---|---|
| 0 | TOD-QUAIL | - | |||
| 1 | QUAIL-BOSSS | - | - | ||
| 2 | BOSSS-CHAPP | - | - | ||
| 3 | CHAPP-DYMON | - | - |
| Guidance Strategy | Without Speed Brakes | Without Additional Thrust | Energy-Neutral | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| +1 | +3 | +6 | +1 | +3 | +6 | +1 | +3 | +6 | |||
| INMPC | 98.3 | 93.7 | 90.0 | 82.1 | 75.6 | 75.5 | 80.6 | 70.3 | 67.0 | ||
| SbNMPC | 98.3 | 93.2 | 89.2 | 81.9 | 77.4 | 76.6 | 80.5 | 71.3 | 67.4 | ||
| AsNMPC | 98.6 | 93.2 | 89.9 | 82.0 | 76.3 | 76.7 | 80.9 | 70.5 | 68.4 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dalmau, R.; Prats, X.; Baxley, B. Sensitivity-Based Non-Linear Model Predictive Control for Aircraft Descent Operations Subject to Time Constraints. Aerospace 2021, 8, 377. https://doi.org/10.3390/aerospace8120377
Dalmau R, Prats X, Baxley B. Sensitivity-Based Non-Linear Model Predictive Control for Aircraft Descent Operations Subject to Time Constraints. Aerospace. 2021; 8(12):377. https://doi.org/10.3390/aerospace8120377
Chicago/Turabian StyleDalmau, Ramon, Xavier Prats, and Brian Baxley. 2021. "Sensitivity-Based Non-Linear Model Predictive Control for Aircraft Descent Operations Subject to Time Constraints" Aerospace 8, no. 12: 377. https://doi.org/10.3390/aerospace8120377
APA StyleDalmau, R., Prats, X., & Baxley, B. (2021). Sensitivity-Based Non-Linear Model Predictive Control for Aircraft Descent Operations Subject to Time Constraints. Aerospace, 8(12), 377. https://doi.org/10.3390/aerospace8120377







