Multidisciplinary Optimization of Thermal Insulation Layer for Stratospheric Airship with a Solar Array

Abstract

Stratospheric airships with a solar array have demonstrated overwhelming superiority in many aspects, such as earth observation, meteorological survey, and communication relay. The solar array supplies sufficient power for the airship to be in flight for months, but excessive heat is also transferred to the airship, causing high overpressure of inner gas. However, the optimal arrangement of the insulation layer on the airship has not been investigated. The theoretical method, including the geometry, thermal, and energy models, is developed and validated. The distribution of the temperatures and power of the solar cells, with different installation angles on the curved surface, is investigated. The thickness of insulation layer has a significant effect on the solar output power and internal pressure of the airship. An optimized configuration of the insulation structure is proposed, in order to improve the total output energy of solar array. The optimized configuration of insulations helps to reduce the structural mass by 24.9% and increase the payload mass by 9%. Moreover, the optimized arrangement improves the output energy of solar array in a year, and the maximum improvement is 8.2% on the winter solstice. The work displays the optimization of the thermal insulation layer for the stratospheric airship with a solar array, in order to improve the everyday energy acquirement during flight in a year.

1. Introduction

A stratospheric airship, also known as a pseudo-satellite [1], is an ideal platform for high-resolution observation, atmospheric monitoring, and uninterrupted communication [2]. Long-term flight in the stratosphere for several months requires adequate energy. The development of flexible, thin-film materials and conversion efficiency makes solar cells an essential part of renewable energy system on this long endurance vehicle [3].

Research progress, regarding the utilization of the photovoltaic (PV) array on the stratospheric airship, has been spectacular during the past one or two decades [4,5]. Garg et al. [6] proposed a method to estimate the incident solar energy on the airship hull profiles. The arrangement and area of solar panel was designed based on required energy per day. Wang et al. [7] studied the variation of the output power of solar cells with the heading direction of airship on the summer and winter solstice. Appropriate flight directions, at different times of the day, were advised when the cell efficiency was low. Alam and Pant [8] developed a method to optimize the layout of the PV array in different seasons. The area of the solar cell array can be minimized on the premise of the energy requirements for specific days. Li et al. [9] presented a numerical model to simulate the output power of the solar array with the thermal effect. The output power of solar cells was overestimated when the excessively high temperatures of them were neglected. Du et al. [10] investigated the curve surface of the airship and optical paths on different solar cells. The output power and total energy were overestimated, without consideration of angular losses.

With the in-depth study on predicting the energy conversion of solar array on the stratospheric airship, scholars are conscious of the excessive rise in internal temperature, caused by the considerable irradiation absorbed by photovoltaic cells [11,12]. Wang and Yang [13] conducted steady and unsteady simulations of two stratospheric airships, developed in Japan. The temperatures of inner gas and upper film for the airship with PV array were higher than those of another airship. Li et al. [14] pointed out that the PV array may the aggravate superheat of the airship at noon because the solar absorptivity of the PV array was higher than that of the airship hull. They also stated that if the emissivity of the PV array was higher than that of the airship hull, the temperature of the upper part of the airship hull would be lower than the bottom part at night, which was called “supercool”. The variation scope of the temperature of lifting gas was expanded, so the structural strength of the airship was affected. Sun et al. [15] proposed a mathematical model to describe the solar radiation on the solar array. A three-dimensional temperature profile of airship with PV array was presented. The difference between the maximum and minimum film temperatures exceeded 20 K.

In order to reduce the significant impact of the PV array on airship temperature, a thermal insulation structure between cell units and outer film was adopted. The insulation structures of the solar array on the stratospheric airship refer to the same structure on the satellite [16]. Sun et al. [17] applied the honeycomb sandwich structure and analyzed its equivalent thermal conductivity. The temperature difference between the upper and lower surface was calculated and in good agreement with the experimental results. Li et al. [18] summarized the common layouts of the insulation structure. The temperature differences of insulation structure, with various combinations of parameters, under different irradiation conditions, were compared. Meng et al. [19] researched the optimal structural parameters of the photovoltaic module with the maximum temperature difference and output power. The independent variables were the thickness and interval of the insulation layer.

Up until now, the researches on insulation structure were concentrated on increasing the temperature difference between the flat solar module and airship film. Once the structural parameters were determined, they would be applied to the other hundreds of solar cell modules on the vehicle. The influence of different installation angles of solar cell units in the airship body reference frame was not considered [20]. Moreover, only the output power of a single solar cell, under different irradiation intensities, was studied. The distribution of output power of solar cell units with insulation layers during the flight process has not been evaluated. The output energy should be maximized by reasonable arrangement of the thermal insulation layers.

In this paper, the geometry model of the solar array on the curved surface of airship is firstly introduced. The thermal and power models of the solar powered airship with thermal insulation layer between photovoltaic array and film are developed and validated. The thickness of thermal insulation layer has a notable effect on the output energy of the solar array and maximum differential pressure of airship. The traditional and optimized configurations of the insulation layer are obtained. The results indicate that the optimized layout functions to decrease the structural weight of insulation layer and improve the capacity to accommodate payloads. The distributions of the temperature and output power of the solar cells with different configurations of insulations are analyzed and compared. The optimized arrangement of the insulation layer significantly increases the output energy throughout the whole year, without breaking the structural integrity of airship film. The multidisciplinary optimization study has valuable reference for reducing the structural weight and improving the everyday output energy of solar powered airships during flight in a year.

2. Theoretical Method

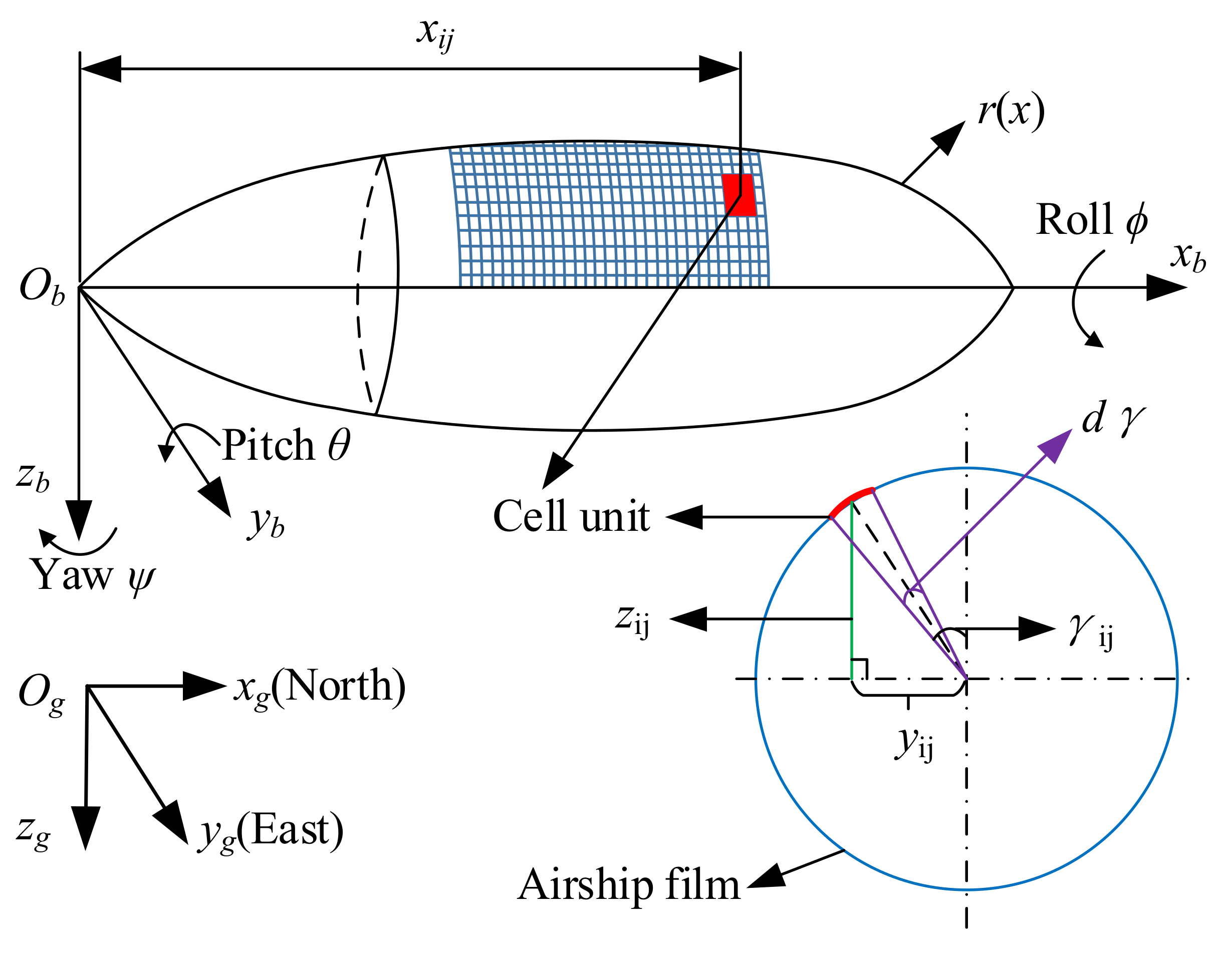
2.1. Spatial Geometry Model

Figure 1 shows the description of the spatial position and attitude of airship. The $O_g{x}_g{y}_g{z}_g$ and $O_b{x}_b{y}_b{z}_b$ are earth reference frame and body coordinate frame, respectively [21]. The axis $O_g{x}_g$ points to the north. The positive directions of axes $O_g{y}_g$ and $O_g{z}_g$ are east and downward perpendicular to the ground. As for the body reference system, the origin $O_b$ is located at the airship stern. The $O_b{x}_b$ axis coincides with the geometrical longitudinal axis of the airship, pointing to the nose of the airship. The $O_b{z}_b$ axis is in the symmetrical plane and directs downward. The $O_b{y}_b$ axis is perpendicular to the $x_b{O}_b{z}_b$ plane and points to the right. The positive yaw motion moves the nose of the airship to the right. The positive pitch motion raises the nose of the airship and lowers the stern. The positive roll motion lifts the left side of the airship and lowers the right side.

The surface equation of the airship in the body coordinate frame is:

$$F=y^2+z^2-r^2\left(x\right)$$

(1)

where $r$ is the rotation radius of the hull, according to standardization models, given by the National Physics Laboratory [22], and is written as:

$$r\left(x_b\right)=\left\{\begin{array}{l}\frac{b}{a_2}\sqrt{a_2^2-{\left(x-a_2\right)}^2}\hspace{1em}\hspace{1em}0\le x\le a_2\\ \frac{b}{a_1}\sqrt{a_1^2-{\left(x-a_2\right)}^2}\hspace{1em}\hspace{1em}{a}_2\le x\le a_1+a_2\end{array}\right.$$

(2)

where $a_1$ and $a_2$ are the lengths of the semi-major axis, and $a_2=\sqrt{2}{a}_1$. $b$ is the length of the semi-minor axis.

The upper limit of differential pressure is derived according to the mechanical property of the film of airship hull and can be calculated by:

$$\Delta P_{limit}=\frac{2\cdot d_f\cdot {\sigma }_f}{r_{max}}$$

(3)

where $d_f$ is the thickness of film, ${\sigma }_f$ is the tensile strength of film, and $r_{max}$ is the maximum radius of curvature of film.

The differential pressure of the airship is:

$$\Delta P=P_{he}-P_{atm}$$

(4)

where $P_{atm}$ is the pressure of ambient air at the flight altitude [23], and $P_{he}$ is the pressure of the buoyancy gas and can be obtained by:

$$P_{he}=\frac{m_{he}\cdot R\cdot T_{he}}{M_{he}\cdot V_{he}}$$

(5)

where $m_{he}$ is the mass of helium, $M_{he}$ is the molar mass of helium, $R$ is the ideal gas constant, $T_{he}$ is the temperature of helium, and $V_{he}$ is the volume of helium.

The installation of the solar cells on top of the airship is described by the central angle $\gamma$ and $x_{ij}$ coordinate [24]. The other two coordinates of the center point of the cell unit in the body reference system can be derived by:

$$y_{ij}=r\left(x_{ij}\right)\cdot \sin \left({\gamma }_{ij}\right)$$

(6)

$$z_{ij}=-r\left(x_{ij}\right)\cdot \cos \left({\gamma }_{ij}\right).$$

(7)

The area of the solar cell unit is:

$$A_{ij}=r\left(x_{ij}\right)\cdot d\gamma \cdot dx\cdot \sqrt{1+r^{\prime }{\left(x_{ij}\right)}^2}.$$

(8)

The normal vector of airship surface in the body reference frame is defined by:

$${\overrightarrow{n}}_{b,ij}=\left(\frac{\partial F}{\partial x_{ij}},\frac{\partial F}{\partial y_{ij}},\frac{\partial F}{\partial z_{ij}}\right)/\left(\sqrt{{\left(\frac{\partial F}{\partial x_{ij}}\right)}^2+{\left(\frac{\partial F}{\partial y_{ij}}\right)}^2+{\left(\frac{\partial F}{\partial z_{ij}}\right)}^2}\right)$$

(9)

where $\frac{\partial F}{\partial x_{ij}}$, $\frac{\partial F}{\partial y_{ij}}$ and $\frac{\partial F}{\partial z_{ij}}$ are calculated by:

$$\frac{\partial F}{\partial x_{ij}}=\left\{\begin{array}{l}\frac{2·b^2·\left(x_{ij}-a_2\right)}{a_2^2} 0\le x_b\le a_2\\ \frac{2\cdot b^2\cdot \left(x_{ij}-a_2\right)}{a_1^2} a_2\le x_b\le a_1+a_2\end{array}\right.$$

(10)

$$\frac{\partial F}{\partial y_{ij}}=2\cdot y_{ij}$$

(11)

$$\frac{\partial F}{\partial z_{ij}}=2\cdot z_{ij}$$

(12)

The normal vector of the cell unit in the earth coordinate frame is [25]:

$${\overrightarrow{n}}_{ij}=R_b^g\cdot {\overrightarrow{n}}_{b,ij}$$

(13)

where $R_b^g$ is the transformation matrix from the airship body coordinate system to the earth reference frame.

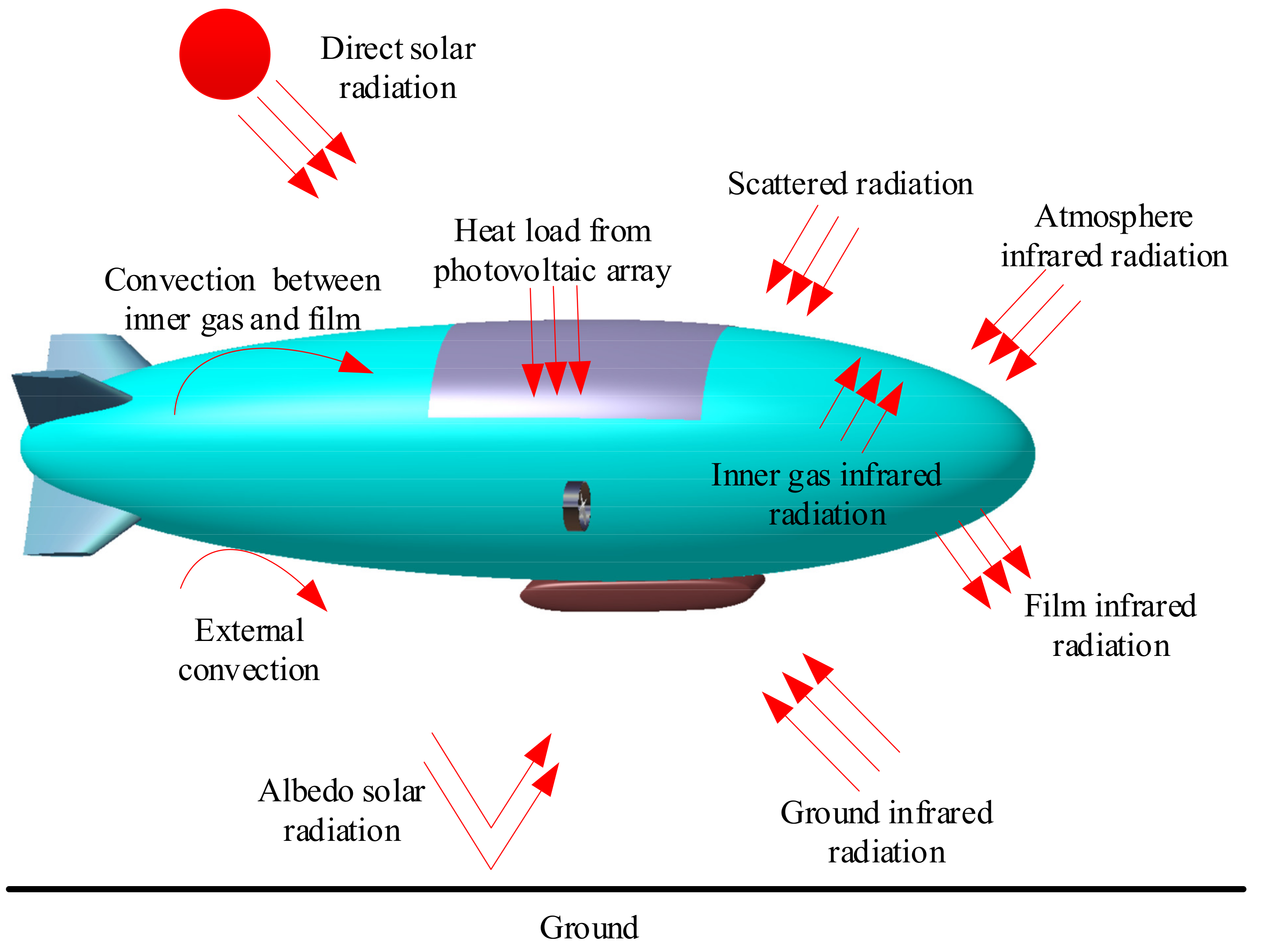
2.2. Thermal Environment

Figure 2 shows the thermal environment of the stratospheric airship with the solar array. The external solar radiation includes direct solar, diffuse solar, and albedo radiation. The external infrared radiation consists of atmosphere and ground infrared radiation [26]. A certain proportion of the solar irradiance can be converted to electrical power through the solar array, but the majority of the solar energy is transformed to heat as a thermal load on the airship. Convective heat transfer also exists between airship and external atmosphere [27]. The internal thermal environment is composed of infrared radiation of the film, inner gas infrared radiation, and convection between the film and internal gases [28].

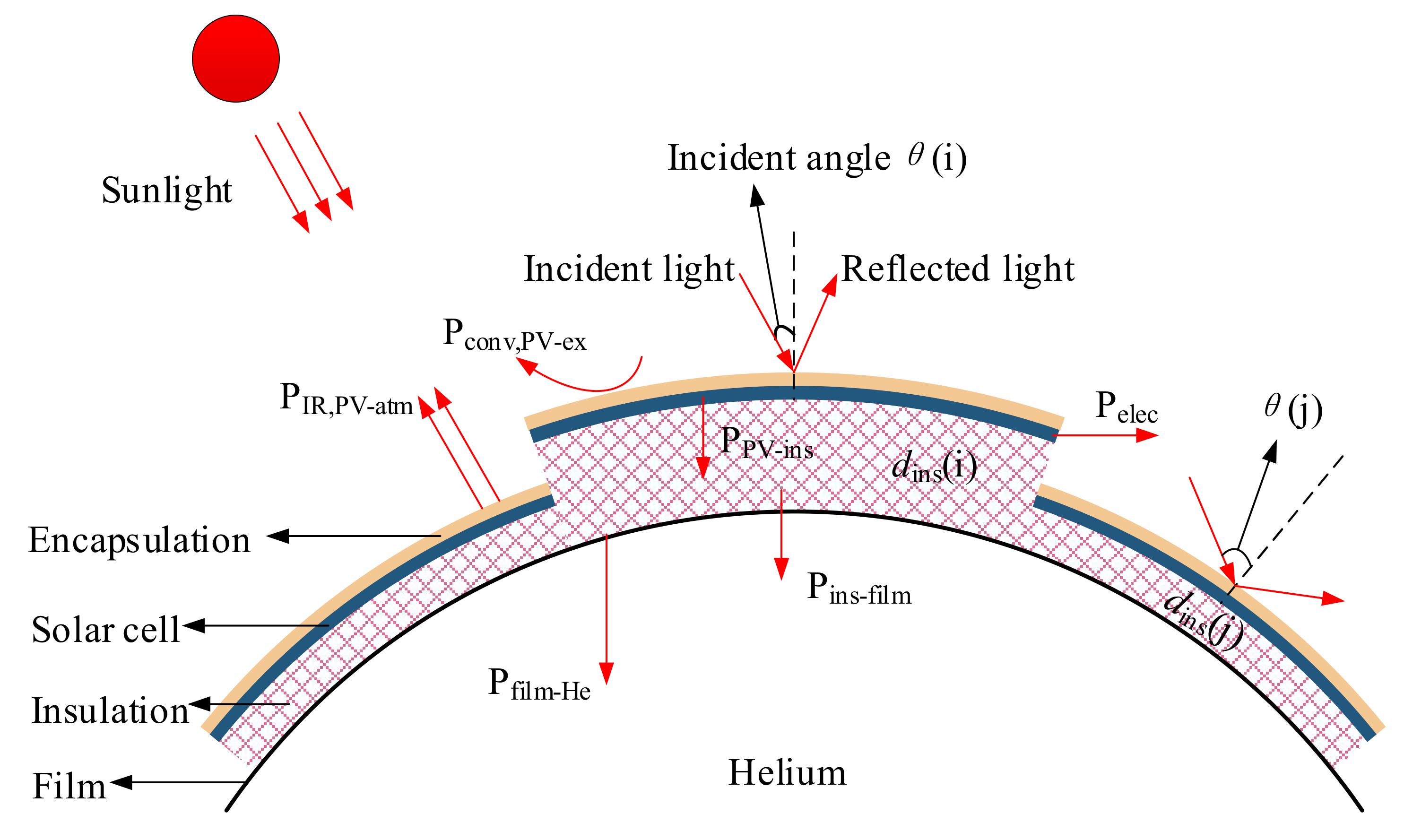
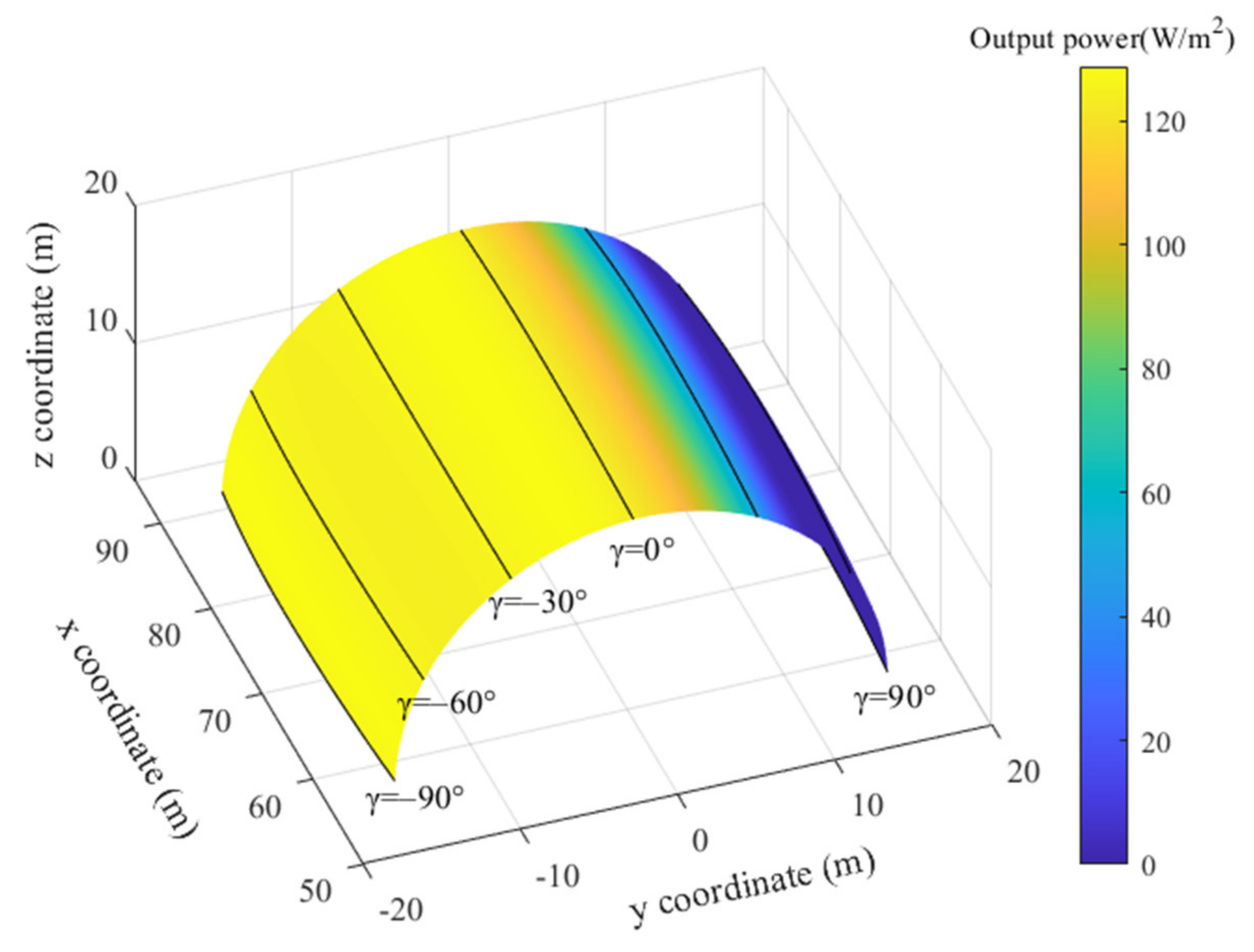
2.3. Power Model

Figure 3 shows the photoelectric process of solar array on the airship. The total output power of solar array is determined by [29]:

$$P_{PV}={\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{P}_{ij}}}$$

(14)

where $m$ and $n$ are the numbers of units in the axial and circumferential directions, respectively.

The output power of a single cell unit $P_{ij}$ is:

$$P_{ij}={\eta }_{ij}\cdot P_{eff,ij}$$

(15)

where ${\eta }_{ij}$ is the conversion efficiency of the solar cell, as a function of temperature [30], obtained by:

$${\eta }_{ij}={\eta }_0-\left|c_1\right|\cdot \left(T_{PV,ij}-T_0\right)$$

(16)

where ${\eta }_0$ is the conversion efficiency under standard test conditions, $T_0$ is the standard temperature of 298.15 K, and $c_1$ is the attenuation coefficient.

The effective incident radiation energy on the cell unit $P_{eff,ij}$ is:

$$P_{eff,ij}=\left(P_{D,ij}+P_{S,ij}+P_{R,ij}\right)\cdot \frac{{\tau }_{al}\left({\theta }_{ij}\right)}{{\tau }_{al}\left(0\right)}$$

(17)

where $P_{D,ij}$, $P_{S,ij}$, and $P_{R,ij}$ are direct, diffuse, and reflected radiation, and ${\tau }_{al}\left({\theta }_{ij}\right)$ and ${\tau }_{al}\left(0\right)$ are effective transmittance of encapsulation, with incident angles of ${\theta }_{ij}$ and 0°, respectively. ${\tau }_{al}\left({\theta }_{ij}\right)$ is calculated by:

$${\tau }_{al}\left({\theta }_{ij}\right)=1-\frac{1}{2}\cdot \left(r_s^2\left({\theta }_{ij}\right)+r_p^2\left({\theta }_{ij}\right)\right)$$

(18)

where $r_s\left({\theta }_{ij}\right)$ and $r_p\left({\theta }_{ij}\right)$ are the reflection coefficients of transverse-electric and transverse-magnetic [31].

The govern equation of the solar cell unit temperature $T_{PV,ij}$ is [32]:

$$m_{PV,ij}{c}_{PV}\cdot {\dot{T}}_{PV,ij}=P_{D,ij}+P_{S,ij}+P_{R,ij}-P_{ij}-P_{conv,PV-ex,ij}-P_{cond,PV-ins,ij}-P_{IR,PV-atm,ij}$$

(19)

where $m_{PV,ij}$ is the mass of photovoltaic array, $c_{PV}$ is the specific heat of the photovoltaic array, ${\dot{T}}_{PV,ij}$ is the change rates of the photovoltaic array temperature, $P_{conv\_PV\_ex,ij}$ is the external convection heat transfer of the unit, $P_{cond\_PV\_ins,ij}$ is the conduction heat transfer energy between the solar cell unit and insulation layer, and $P_{IR\_atm\_PV,ij}$ is the absorbed infrared radiation from the sky.

The direct solar radiation on the unit is:

$$P_{D,ij}={\mu }_{ij}\cdot {\alpha }_{PV}\cdot I_D\cdot A_{ij}$$

(20)

where ${\alpha }_{PV}$ is the absorptivity of solar cell, $A_{ij}$ is the unit area, and ${\mu }_{ij}$ is the discount factor of direct radiation, defined by:

$${\mu }_{ij}=\left\{\begin{array}{l}\left|{\overrightarrow{n}}_{ij}\cdot {\overrightarrow{n}}_S\right| {\overrightarrow{n}}_{ij}\cdot {\overrightarrow{n}}_S<0,-\arccos (\frac{R_{Earth}}{R_{Earth}+h})<{\theta }_h<\pi +\arccos (\frac{R_{Earth}}{R_{Earth}+h})\\ 0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}else\end{array}\right.$$

(21)

where $R_{Earth}$ is the radius of the Earth, and ${\overrightarrow{n}}_S$ is the direction vector of sunlight in the earth reference frame and can be expressed by:

$${\overrightarrow{n}}_S=\left(\cos {\theta }_h\cos {\theta }_{azi},\cos {\theta }_h\sin {\theta }_{azi},\sin {\theta }_h\right)$$

(22)

where ${\theta }_{azi}$ is the azimuth angle of sun.

The absorbed diffuse solar radiation from the sky of the cell unit is:

$$P_{S,ij}=\frac{1}{2}\cdot \left(1-\cos {\theta }_{z,ij}\right)\cdot {\alpha }_{PV}\cdot I_S\cdot A_{ij}$$

(23)

where ${\theta }_{z,ij}$ is the included angle between the normal vector and gravity acceleration direction ${\overrightarrow{n}}_z=\left(0,0,1\right)$ [33], calculated by:

$${\theta }_{z,ij}=\arccos \left(\frac{{\overrightarrow{n}}_{ij}\cdot {\overrightarrow{n}}_z}{\left|{\overrightarrow{n}}_{ij}\right|\cdot \left|{\overrightarrow{n}}_z\right|}\right).$$

(24)

The reflected radiation on the unit is:

$$P_{R,ij}={\theta }_{R,ij}\cdot {\alpha }_{PV}\cdot I_R\cdot A_{ij}$$

(25)

where ${\theta }_{R,ij}$ is the self-shadowing coefficient, defined by:

$${\theta }_{R,ij}=\left\{\begin{array}{l}1\hspace{1em}{\overrightarrow{n}}_{ij}\cdot {\overrightarrow{n}}_z\ge 0\\ 0\hspace{1em}{\overrightarrow{n}}_{ij}\cdot {\overrightarrow{n}}_z<0\end{array}\right..$$

(26)

The conductive heat transfer between PV unit and insulation structure is:

$$P_{cond,PV-ins,ij}=A_{ij}\cdot \left(\frac{T_{ij}-T_{ins,ij}}{d_{PV}/{\lambda }_{PV}+d_{ins,ij}/{\lambda }_{ins}}\right)$$

(27)

where ${\lambda }_{PV}$ and ${\lambda }_{ins}$ are the thermal conductivity of solar cell and insulation layer, and $d_{ins,ij}$ is the thickness of insulation layer. The conductive heat transfer between insulation structure and film obeys the same law as:

$$P_{cond,ins-film,ij}=A_{ij}\cdot \left(\frac{T_{ins,ij}-T_{film,ij}}{d_{ins,ij}/{\lambda }_{ins}+d_{film}/{\lambda }_{film}}\right).$$

(28)

The incident angle ${\theta }_{ij}$ for calculating the ${\tau }_{al}\left({\theta }_{ij}\right)$, considering angular loss, is:

$${\theta }_{ij}=\arccos \left(\frac{{\overrightarrow{n}}_{ij}\cdot {\overrightarrow{n}}_S}{\left|{\overrightarrow{n}}_{ij}\cdot {\overrightarrow{n}}_S\right|}\right)$$

(29)

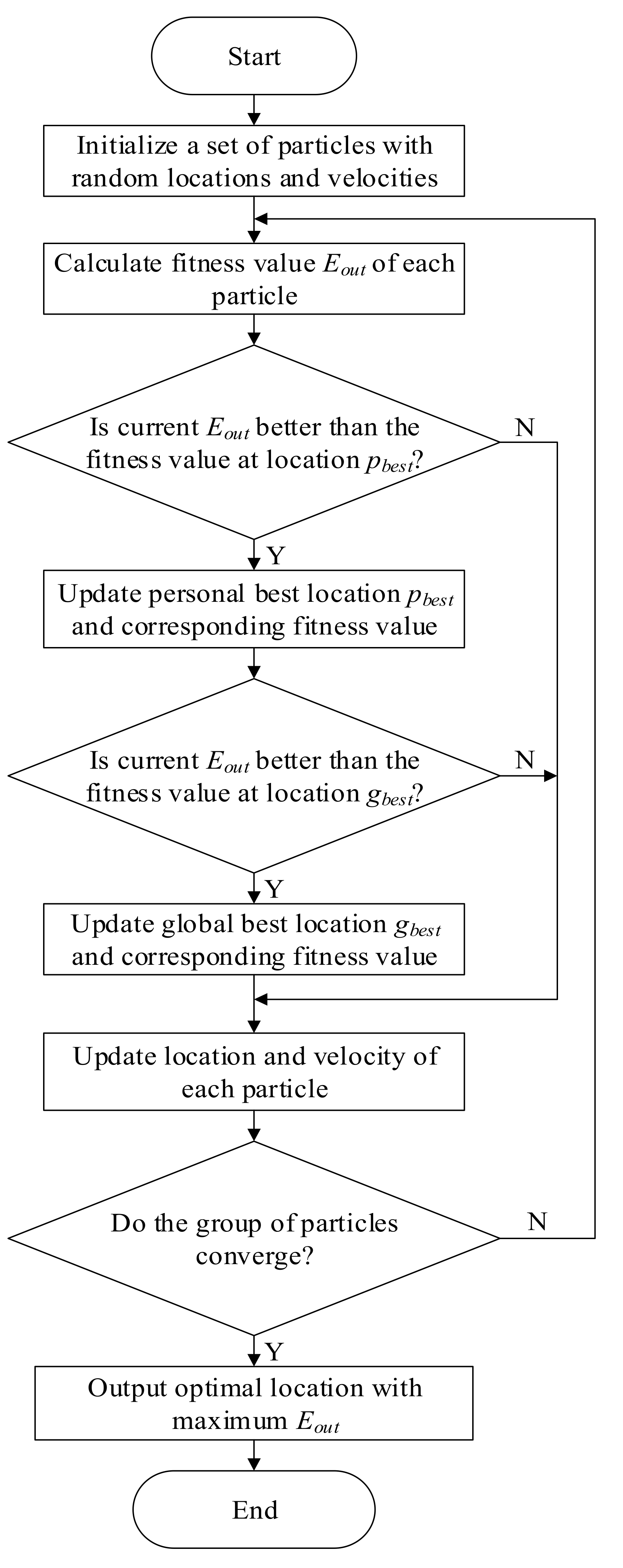
2.4. Optimization Method of Insulation Layer Configuration

The incident solar radiation and temperatures of solar cells vary with their positions on the airship film. Therefore, the thicknesses of thermal insulations under each solar cell should be optimized to increase the total output energy of the solar array, especially when the airship flights with insufficient solar irradiance. As shown in Figure 1 and Figure 3, the thicknesses of insulation layers $d_{ins}\left(\gamma ,x\right)$ are expressed as the function of central angle $\gamma$ and $x$ coordinate in the body reference system, $O_b{x}_b{y}_b{z}_b$, on the curved surface of the airship.

The objective of the optimization is to obtain maximum output energy of solar array during a day and can be written as:

$$\max \text{:} E_{out}={\displaystyle \underset{t=0}{\overset{t=t_{end}}{\int }}{P}_{PV}(t)}dt.$$

(30)

Considering the actual flight of stratospheric airship, four constraints are adopted, as follows:

Constraint I: Considering the carrying capacity of airship, the thicknesses of insulation layers cannot be infinity large, and the upper bound is determined as $d_{max}$.

$$d_{ins,ij}\le \hspace{1em}{d}_{max}$$

(31)

Constraint II: The maximum differential pressure of airship, $\Delta P_{max}$, during a day should not exceed the limit of differential pressure, $\Delta P_{limit}$. The maximum hoop stress of the airship film will be greater than the tensile strength when the $\Delta P_{max}$ is larger than $\Delta P_{limit}$.

$$\Delta P_{max}\le \Delta P_{limit}$$

(32)

Constraint III: The center of gravity should be kept in the $O_b{x}_b{z}_b$ plane to ensure the lateral static stability of the airship [34]. The thicknesses of the insulation structures, at the symmetrical position, relative to the $O_b{x}_b{z}_b$ plane, should be the same.

$$d_{ins}\left(\gamma ,x\right)=d_{ins}\left(-\gamma ,x\right)$$

(33)

Constraint IV: In order to prevent the array from being overturned, the thicknesses of the insulation structures should be uniform in the direction of flight.

$$d_{ins}\left(\gamma ,x_1\right)=d_{ins}\left(\gamma ,x_2\right)$$

(34)

Based on the above constraints, the optimization process is simplified to search for the optimal thicknesses of the insulation layers, $d_{ins}\left(\gamma \right)$, with different central angles, $\gamma$. The particle swarm optimization method [35] is adopted to solve the problem, which uses a set of particles with the properties of location, $l$, and velocity, $v$. The location space of particles, $L_m$, is $m$ dimensional and each dimension corresponds to $d_{ins}\left({\gamma }_1\right)$, $d_{ins}\left({\gamma }_2\right)$,…, $d_{ins}\left({\gamma }_m\right)$. The velocity space of particles, $V_m$, is $m$ dimensional and each dimension corresponds to the change rate of $d_{ins}\left({\gamma }_1\right)$, $d_{ins}\left({\gamma }_2\right)$,…, $d_{ins}\left({\gamma }_m\right)$. The fitness value of the particle is the output energy, $E_{out}$, during a day. The update equations of the location and velocity for each particle are written by [36]:

$$x_i^{k+1}=x_i^k+v_i^k$$

(35)

$$v_i^{k+1}=\omega \cdot v_i^k+c_1\cdot r_1\left(p_{best,i}^k-x_i^k\right)+c_2\cdot r_2\left(g_{best,i}^k-x_i^k\right)$$

(36)

where $k$ is the number of iterations in the range of $1,2,\dots ,k_{end}$, $\omega$ is inertia weight, $c_1$ and $c_2$ are learning factors, $r_1$ and $r_2$ are uniform random numbers in the range of $\left[0,1\right]$, $p_{best}$ is the personal best location, and $g_{best}$ is global best location. The optimization process of the insulation arrangement, using particle swarm optimization, is shown in Figure 4.

3. Results and Discussion

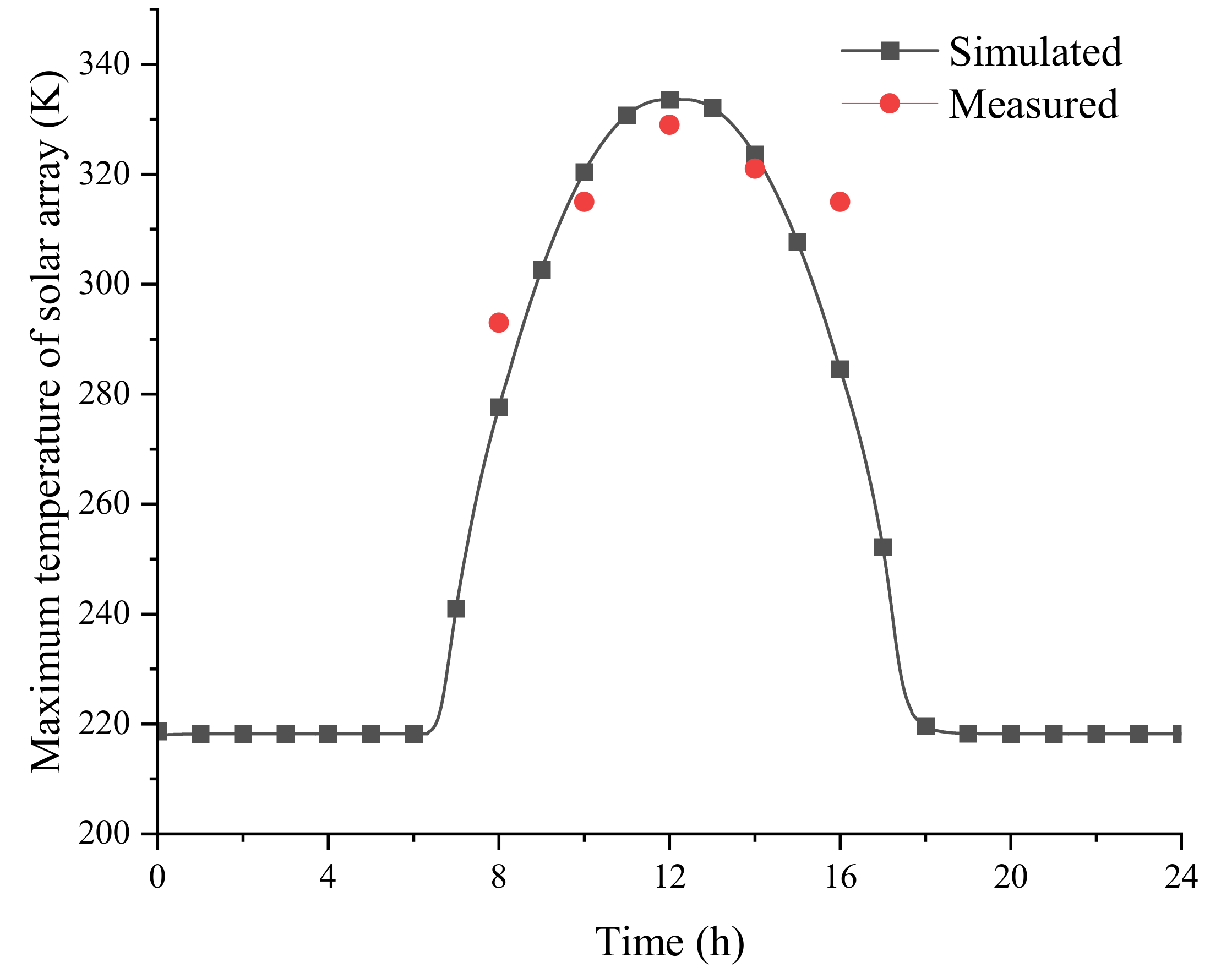
3.1. Model Validation

In order to verify the theoretical method, the experimental result, recorded by Harada et al. [37], is used. The measured points of the maximum temperature of the solar array was from 8:00 am to 16:00 pm in June 2003. The simulated results were obtained under the same conditions. The comparison of the simulated and measured values is presented in Figure 5. The simulated curve coincides with the measured points, and the deviations between them are less than 1.5%, from 10:00 a.m. to 14:00 p.m. The maximum deviation is below 9.7%. Therefore, it is valid to adopt the current method to predict the thermal performance of airship with solar array.

3.2. Simulation Condition

The flight requirements and overall design parameters of the solar powered airship are shown in

Table 1. Requirements and overall design parameters of airship.

Requirements	Value	Design Parameters	Value
Flight altitude, km	20	Volume of airship, m3	71,897
Location	Jiujiang (30° N, 116° E)	$\mathrm{Semi}-\mathrm{major}\mathrm{axis}\mathrm{length}{a}_1$, m	53.8
Working date	1 January~31 December	$\mathrm{Semi}-\mathrm{major}\mathrm{axis}\mathrm{length}{a}_2$, m	76.2
Flight direction	East–west	$\mathrm{Semi}-\mathrm{minor}\mathrm{axis}\mathrm{length}b$, m	16.3
Airspeed, m/s	15	Total mass, kg	6392
Payload capacity, kg	650	Film mass, kg	2140
Thickness range of insulation layers, mm	0.5~15	Helium mass, kg	882
Central angle range, °	−90~90	Propulsion system mass, kg	957
Allowable stress of skin, MPa	52.5	Storage battery mass, kg	1130
Limit of differential pressure, Pa	1254	Solar array mass, kg	398

. At the altitude of 20 km, the west–east component of the wind is greater than the north–south component, based on analysis of the six hourly interval wind data of Jiujiang (30° N, 116° E) in 2020 and 2021 [38]. Therefore, the flight direction of the airship is defined as east–west. The minimum change interval of the insulation thickness for the configuration optimization, with the proposed method, is 0.1 mm.

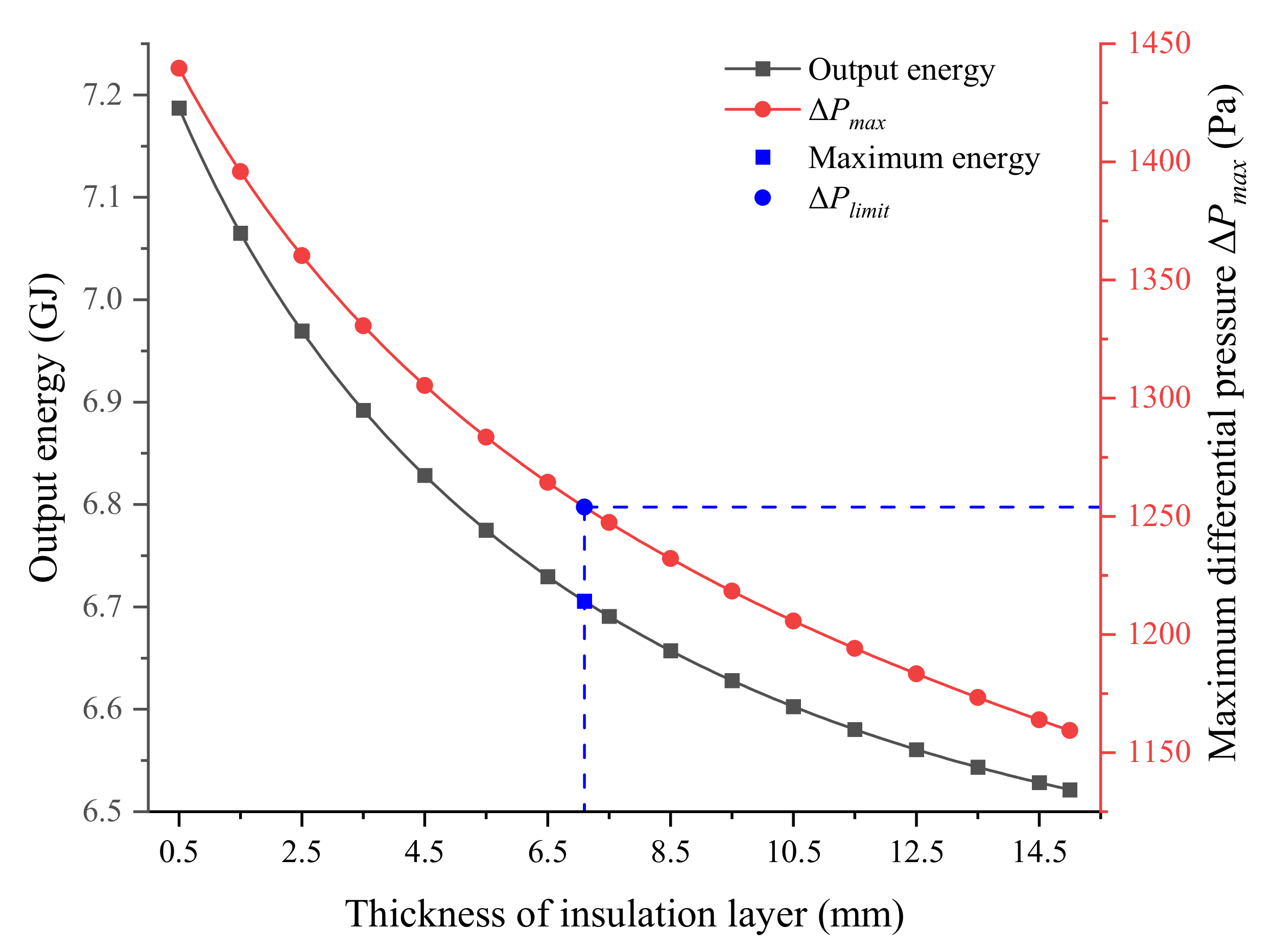
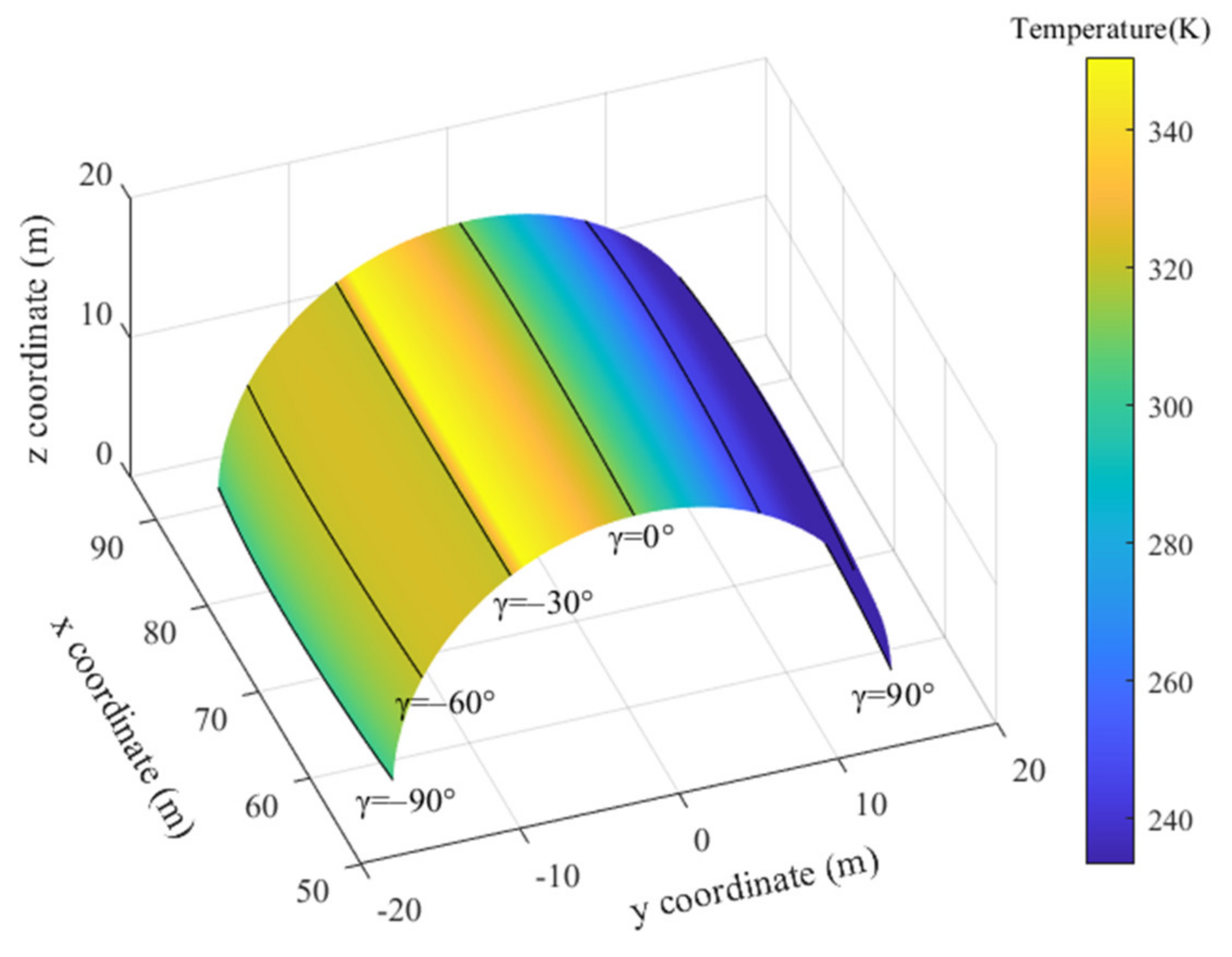
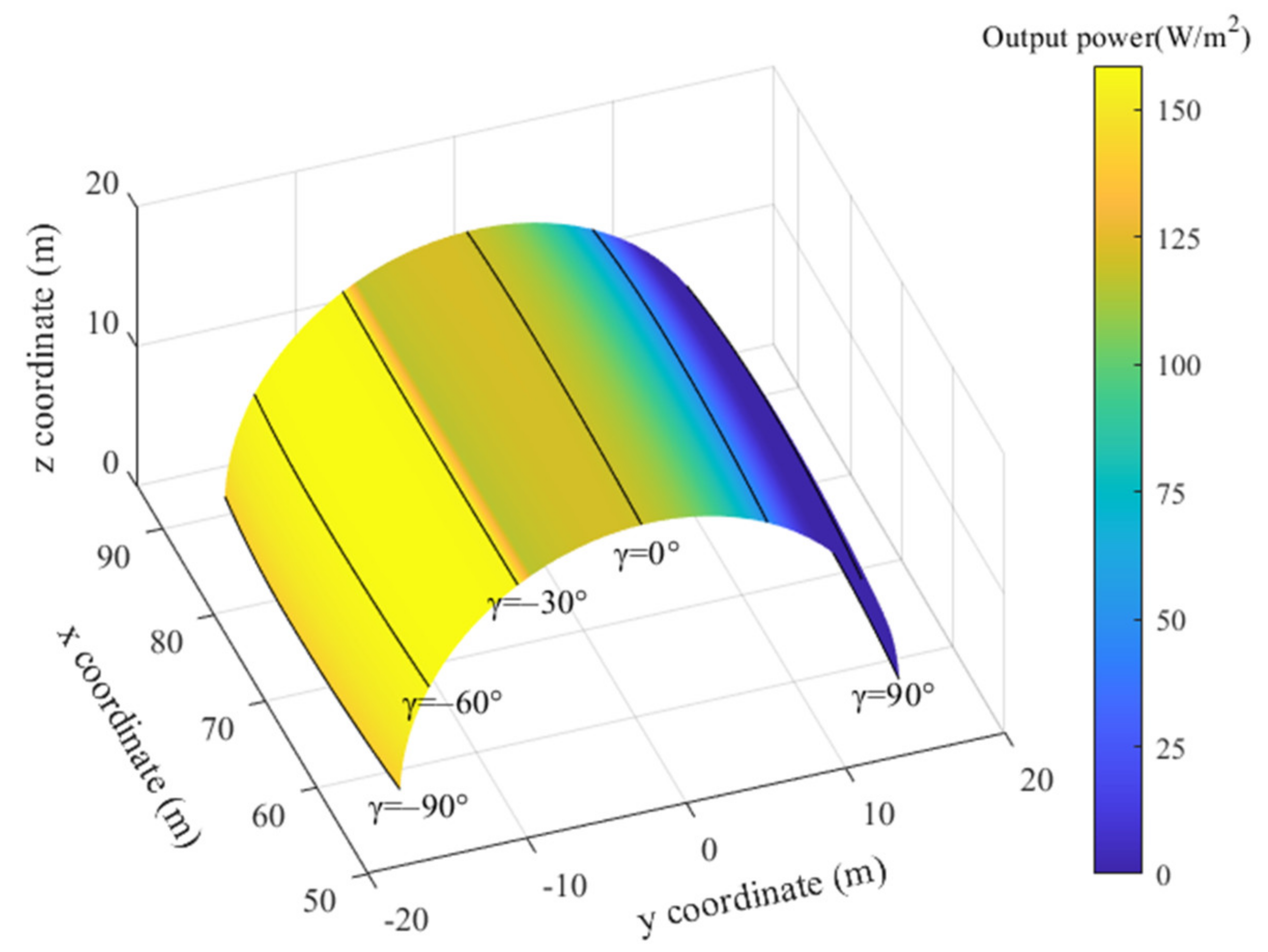
3.3. Effect of Insulation Configuration

As for Jiujiang (30° N, 116° E), the strongest solar irradiation occurs on the summer solstice, the 172nd day of 2021, and the airship has the highest overpressure. Figure 6 shows the variations of output energy and maximum differential pressure, $\Delta P_{max}$, and marks up the traditional configuration of the insulation, with a constant thickness of 7.1 mm. The total energy acquirement and maximum differential pressure, $\Delta P_{max}$, both increase when the thickness of insulation layer decreases. The small thickness of the insulation layer is beneficial for the solar array to transfer heat to the film and helium, so decreasing the thickness of the insulation layer functions to increase the average temperature of the inner gas. With the increase of the helium temperature, the differential pressure increases. As for the traditional configuration, the constant thickness of the insulation layer should not be less than 7.1 mm, in order to ensure that the $\Delta P_{max}$ does not exceed the limit of differential pressure, $\Delta P_{limit}$. In order to maximize the output energy and minimize the structural mass of the thermal insulation layers, a constant thickness of 7.1 mm is adopted as the traditional configuration for the solar powered airship.

Figure 7 depicts the configurations of the traditional and optimized thermal insulation layer. As for the traditional layout, the thicknesses of the insulation layers, under different solar cells, are the same as 7.1 mm. For the optimized layout, the thicknesses of the insulation layers, with the central angle, $\gamma$, from 0° to ±30°, are thickened to 15 mm, while the others are thinned to 0.5 mm. The parameters of the airships with the above two configurations of thermal insulation are displayed in

Table 2. Comparison of airships with traditional and optimized insulation layers.

Parameters	Traditional Layout	Optimized Layout
Insulation layer mass, kg	235	176.5
Limit of differential pressure, Pa	1254	1254
Maximum differential pressure, Pa	1253.9	1253.8

. For the airship with the optimized layout, the mass of the insulation structure is decreased by 58.5 kg, and the reduction rate is 24.9%, compared to the traditional arrangement. It is indicated that the payload mass of the airship can be increased by 58.5 kg.

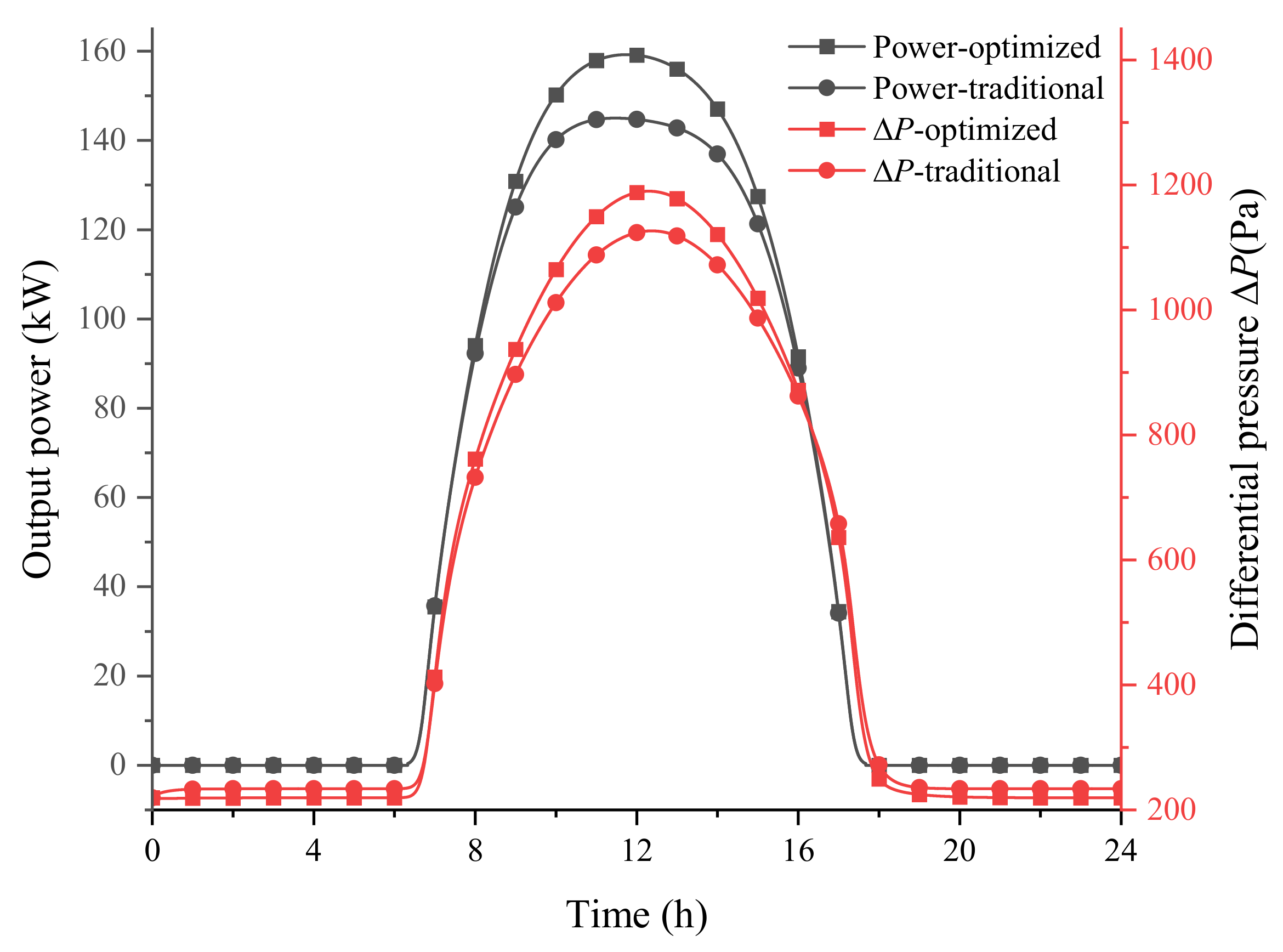
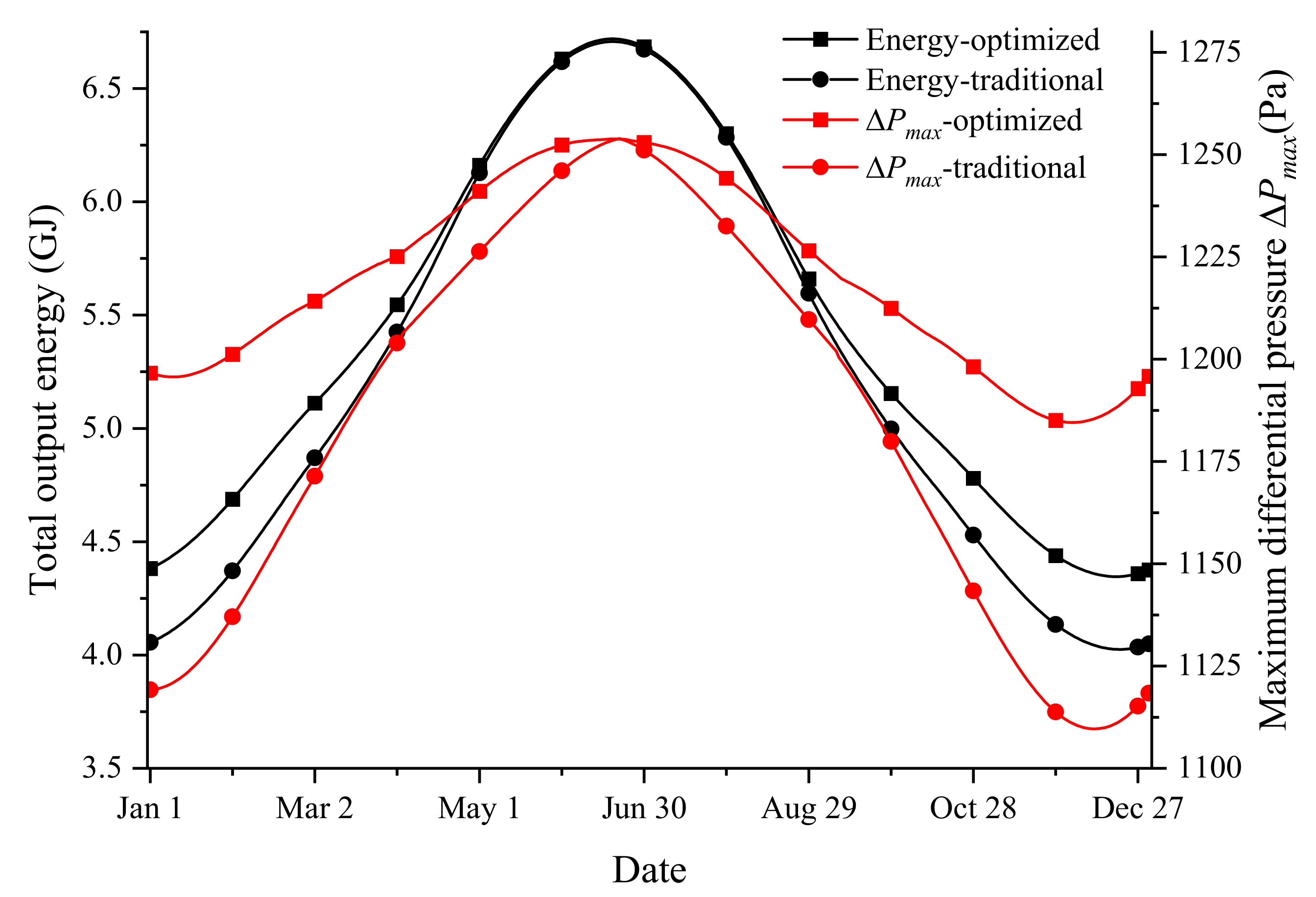
3.4. Comparative Analysis

Figure 8 describes the distribution of the incident solar irradiation intensity at 12:00 on 11 November 2021. The illumination intensity of the solar cells with the central angle, $\gamma$, of −47° is the highest. The incident solar irradiance decreases when $\gamma$ changes from −47° to ± 90°. However, the irradiation intensity of solar cells with $\gamma$ from −90° to 0° is higher than that of solar cells in a symmetrical position with $\gamma$ from 0° to 90°.

Figure 9 and Figure 10 show the distribution of solar cell temperature with the traditional and optimized configuration of the insulation layer at noon, respectively. The distribution of the cell temperature, with traditional layout insulations, shows the same trend with illumination intensity. Compared to the solar cells with the traditional configuration, the temperatures of the cells with the optimized layout of the thermal insulation layer decrease or increase to different degrees. The temperatures of solar cells with a central angle, $\gamma$, of −90° to −30° decrease by 14~26 K. The temperatures of solar cells with $\gamma$ of −30° to 0° increase by 4~9 K. The temperatures of cells with $\gamma$ of 0° to 30° have no obvious change. The temperatures of cells with $\gamma$ of 30° to 60° have a maximum increase of 7 K. The optimized configuration effectively influences the heat exchange process and, therefore, changes the distribution of the solar cell temperature.

Figure 11 displays the distribution of the solar cell output power, with the traditional configuration of the insulation layer, at 12:00. The output power of cells with the central angle, $\gamma$, of −90° to −6° is basically the same. The output power of solar cells with $\gamma$ of −47° is not significantly higher than that of the other cells with $\gamma$ of −90° to −6°, despite the maximum illumination intensity. The output power of cells decreases as the $\gamma$ changes from −6° to 90°.

Figure 12 demonstrates the distribution of the output power with the optimized configuration of insulations. The solar cells with a central angle $\gamma$ of −47° to −30° have the maximum increasement of output power. The output power of solar cells with $\gamma$ of −90° to −47° also increases. The output power cells with $\gamma$ of −30° to 0° decreases, but the magnitude of change is lower than that of the cells with $\gamma$ of −47° to −30°. The output power of the solar cells with $\gamma$ of 0° to 90° has no obvious change.

Figure 13 depicts the output power and differential pressure, $\Delta P$, during the day, with the traditional and optimized layouts of insulation layers. The output power of the solar array with optimized thermal insulations is higher than that of traditional insulations from 8:00 am to 16:00 pm. The maximum increase of the output power is 9.9% at 11:58 am. The values of the total energy of solar array with traditional and optimized configurations of insulations during the day are 4.32 and 4.60 GJ, respectively. The output energy is improved by 6.5%, with optimized layout of thermal insulations. The optimized configuration of the insulation layer results in the rise of differential pressure during the daytime, and the maximum differential pressure is 1190.2 Pa at 12:10 pm. The limit of differential pressure, $\Delta P_{limit}$, of the investigated airship is 1254 Pa, so the structural integrity is guaranteed.

Figure 14 compares the variation of output energy of solar array and maximum differential pressure, $\Delta P_{max}$, on different dates of a year, with the traditional and optimized configurations of the insulation layers. The maximum values of the energy acquirement and $\Delta P_{max}$ occur on 21 June, when the solar irradiation is highest at the investigated location. It is also indicated that the optimized insulation layer functions to improve the energy output throughout the year. The maximum increasement of the total output energy during a day is 8.2%, on 21 December, when the energy acquirements of the solar powered airship with traditional and optimized insulations are 4.02 and 4.35 GJ, respectively. The $\Delta P_{max}$ of the airship with an optimized layout of the insulations is higher than that of the airship with traditional layout on most dates of the year, and the maximum derivation is 77.6 Pa.

The results from the conducted analysis indicate that, compared with the traditional arrangement, with constant thickness of the insulation layer under each solar cell unit, the optimized configuration decides the thicknesses of the insulation layer under the solar cells according to their solar irradiation intensity. The thicknesses of the insulation layers under the solar cells with sufficient solar irradiation decrease, so as to improve the output power of the solar array. Meanwhile, the thicknesses under other cells increase to avoid an excessive rise of differential pressure of the airship. Based on the multidisciplinary optimization method, the everyday output energy of solar powered airships can be improved during flight in a year.

4. Conclusions

The arrangement of the insulation configuration plays an important role in the temperature and output power of solar array. This paper discusses an optimized layout of insulation to improve the total output energy of the solar array. The theoretical method, consisting of spatial geometry, thermal, and power models, is developed and validated. The optimized configuration of the insulation structure on the curved surface of the airship is obtained and compared with the traditional layout with constant thicknesses. The conclusions are drawn as follows:

1.

The thickness of the insulation layer has a significant influence on the output power of the solar array and maximum differential pressure of the airship. Decreasing thickness is beneficial for reducing the average temperatures of the solar cells, hence increasing energy acquisition. However, a thin thermal insulation layer results in the temperature rise of the inner gas of the airship, causing an increase of differential pressure, which could lead to structural failure of the airship film.

2.

The optimized configuration significantly reduces the total weight of the thermal insulation layers. Meanwhile, the limit of the maximum differential pressure is not exceeded. The thicknesses of the optimized insulation layers vary with the central angles. For the investigated airship, the thicknesses of the insulation layers with a central angle from 0° to ±30° are thickened, and the others are thinned. The decreased mass of insulations can be used to increase the capacity of carrying payload.

3.

The optimized layout of the insulations improves the output energy of the solar array throughout the entire year. In the long time period, the optimized arrangement functions to increase the energy acquirement and maximum differential pressure, especially on dates when the solar radiation are insufficient (before and after the winter solstice). The maximum increase of the total output energy during a day is 8.2% on the winter solstice. The proposed method plays an essential role in the long endurance mission of stratospheric airships.