Hierarchical Optimization Algorithm and Applications of Spacecraft Trajectory Optimization
Abstract
1. Introduction
2. Optimization Problem Formulation
3. Hierarchical Optimization Algorithm
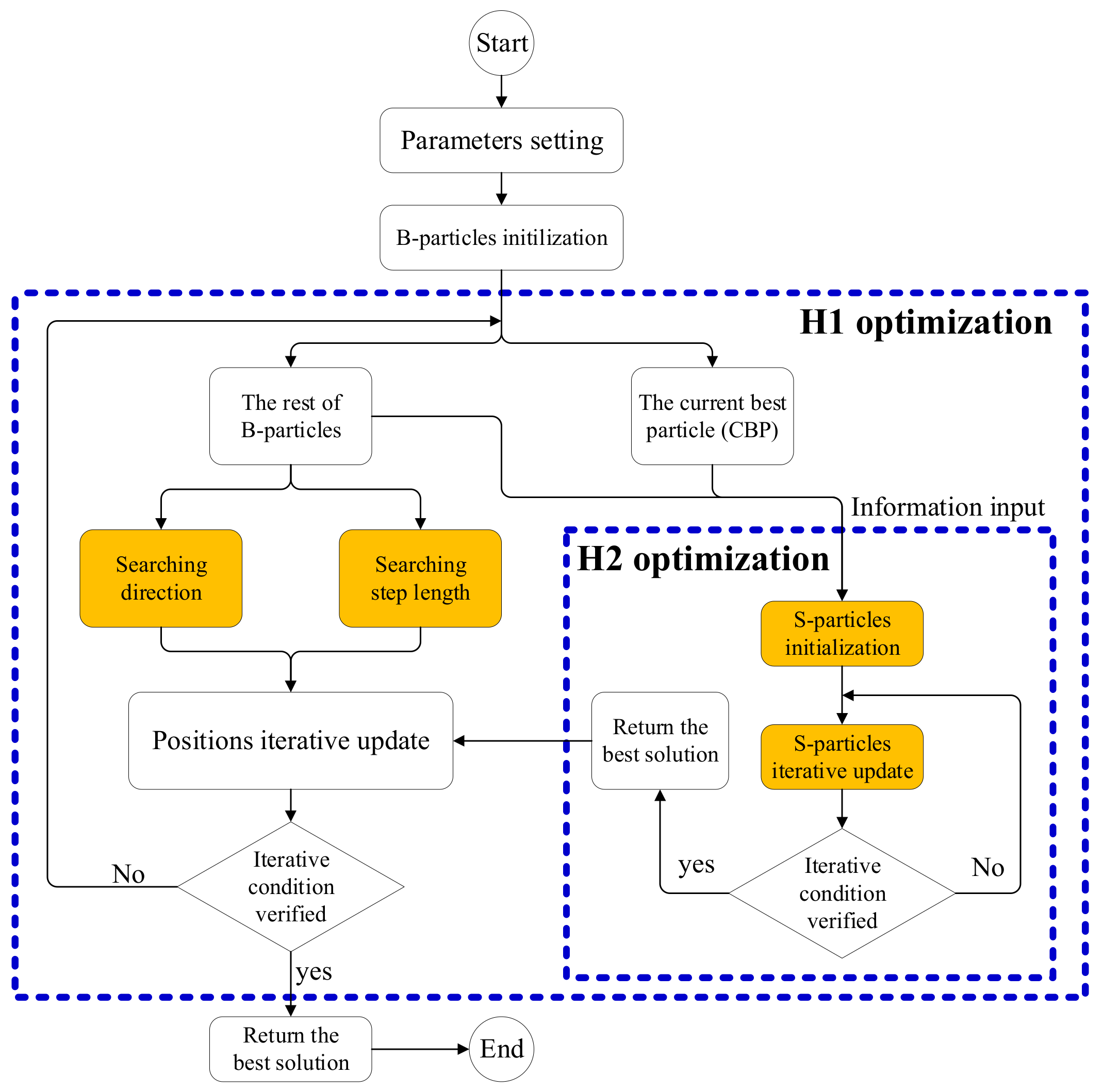
3.1. Hierarchical Optimization Frame
3.2. Two Hierarchical Optimization Algorithms
3.2.1. Formula of HOA-1
| Algorithm 1 Pseudo code of HOA-1. |
| Generate initial Bi1 (i = 1, 2, …, p) Calculate the fitness of each B-particle f(Bi1) Choose L1 and L2 Starting H1 iterations: while 1 (n < Ib) for 1 Bin if 1 Bin doesn’t equal L1n Update the position by (5) else Starting H2 iterations: Input CBP’s position as Pr and fitness as fr and deltaSn by (6) while 2 (m < Is) for 2 Sjm(j = 1, 2, …, N) Generate Sjm by (8) if 2 f(Sim) < fr Pr = Sim end if 2 end for 2 end while 2 Output Pr as CBP’s updating position end if 1 end for 1 Update L1 and L2 according to f(Bin+1) end while 1 return the final L1 |
3.2.2. Formula of HOA-2
| Algorithm 2 Pseudo code of HOA-2. |
| Generate initial Bi1 (i = 1, 2, …, p) Calculate the fitness of each B-particle f(Bi1) Choose L1 and L2 Starting H1 iterations: while 1 (n < Ib) for 1 Bin if 1 Bin does not equal L1n Update the position by (5) else Starting H2 iterations: Input the position and fitness of L1 and L2 while 2 (m < Is) for 2 Sjm(j = 1, 2, …, q) Generate Sjm by (12) Update the position and fitness of SL1 and SL2 Update μ and σ by (9) and (11). end for 2 end while 2 Output SL1q as CBP’s updating position end if 1 end for 1 Update L1 and L2 according to f(Bin+1) end while 1 return the final L1 |
3.3. Comparison with Other Algorithms
4. Experiments on Benchmark Functions
4.1. Explanations of Performance Test
4.2. Results and Discussion
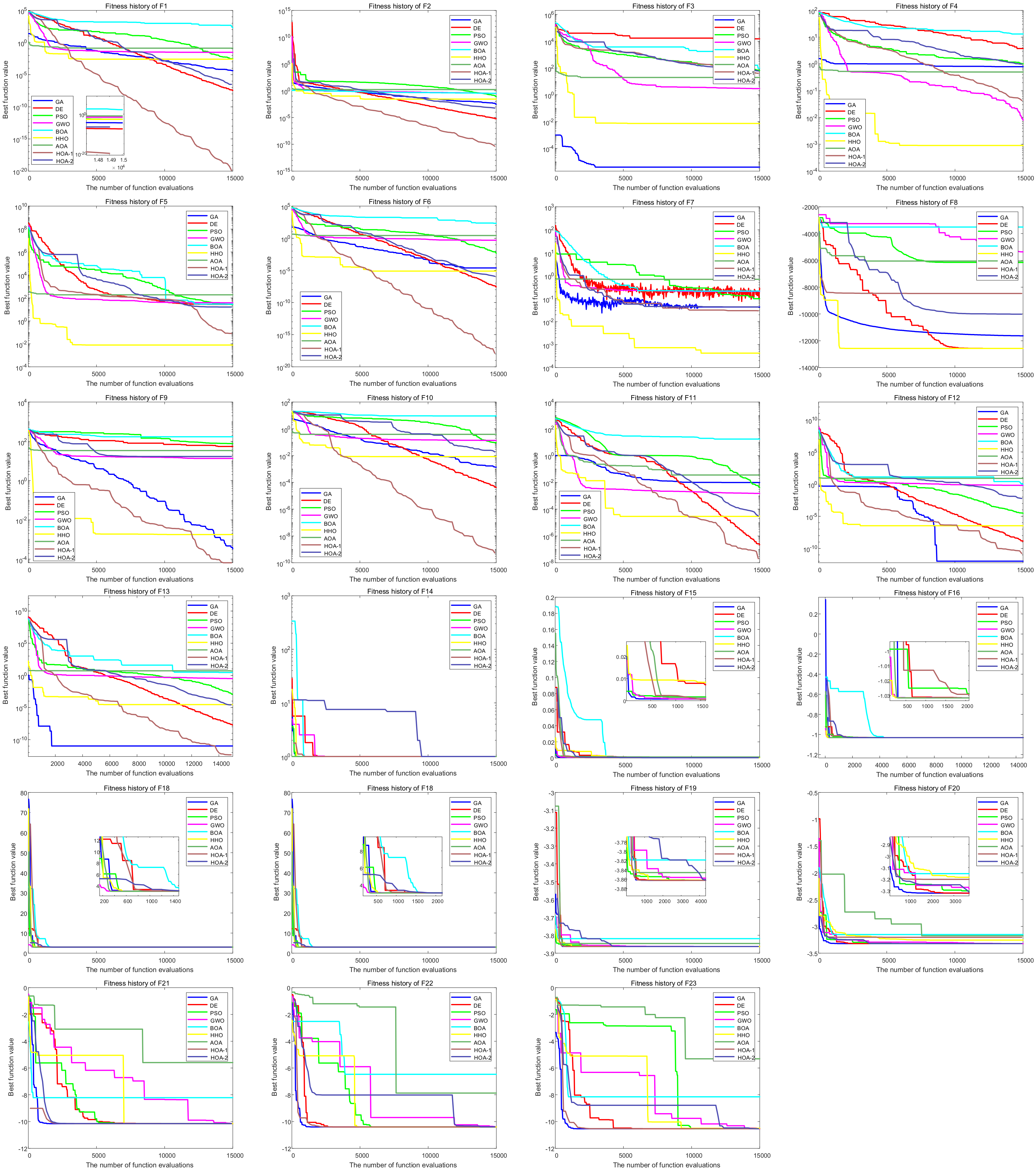
4.2.1. The Performance
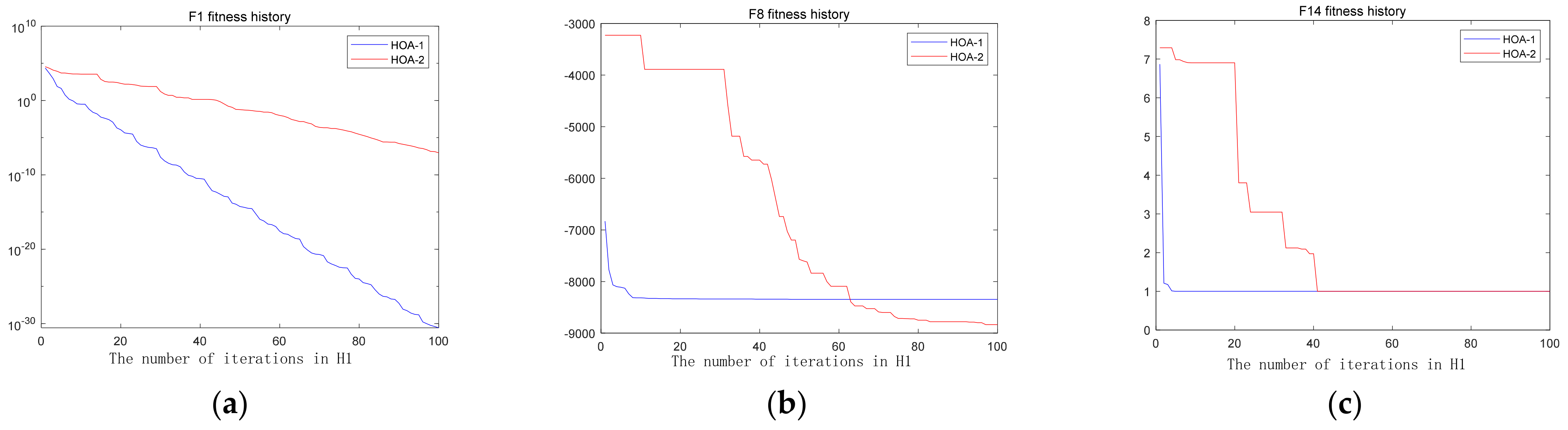
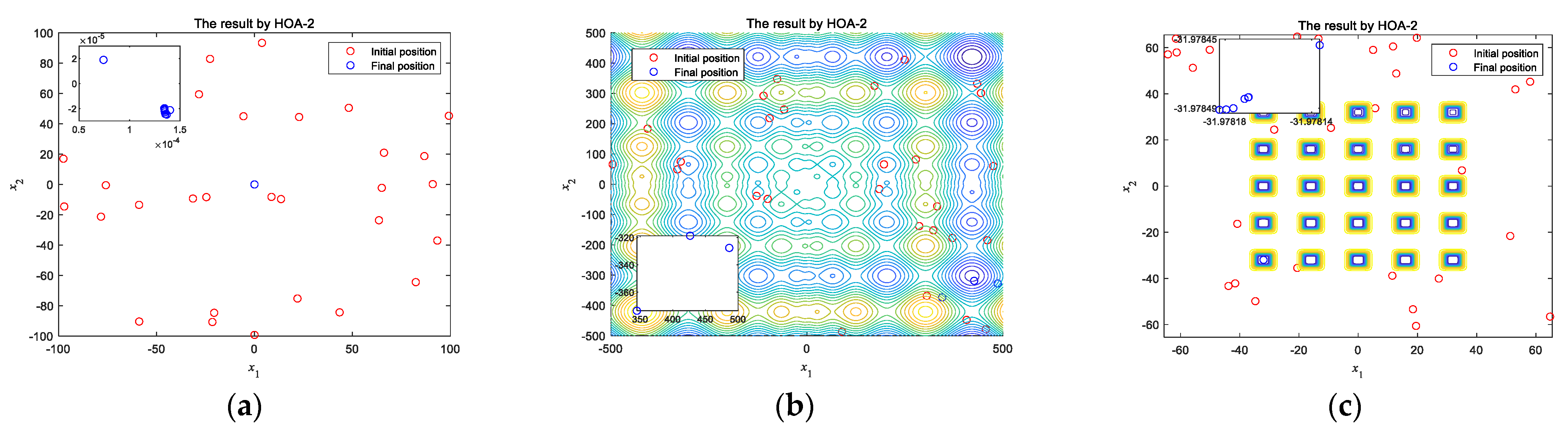
4.2.2. The Mechanism Explanation by Examples
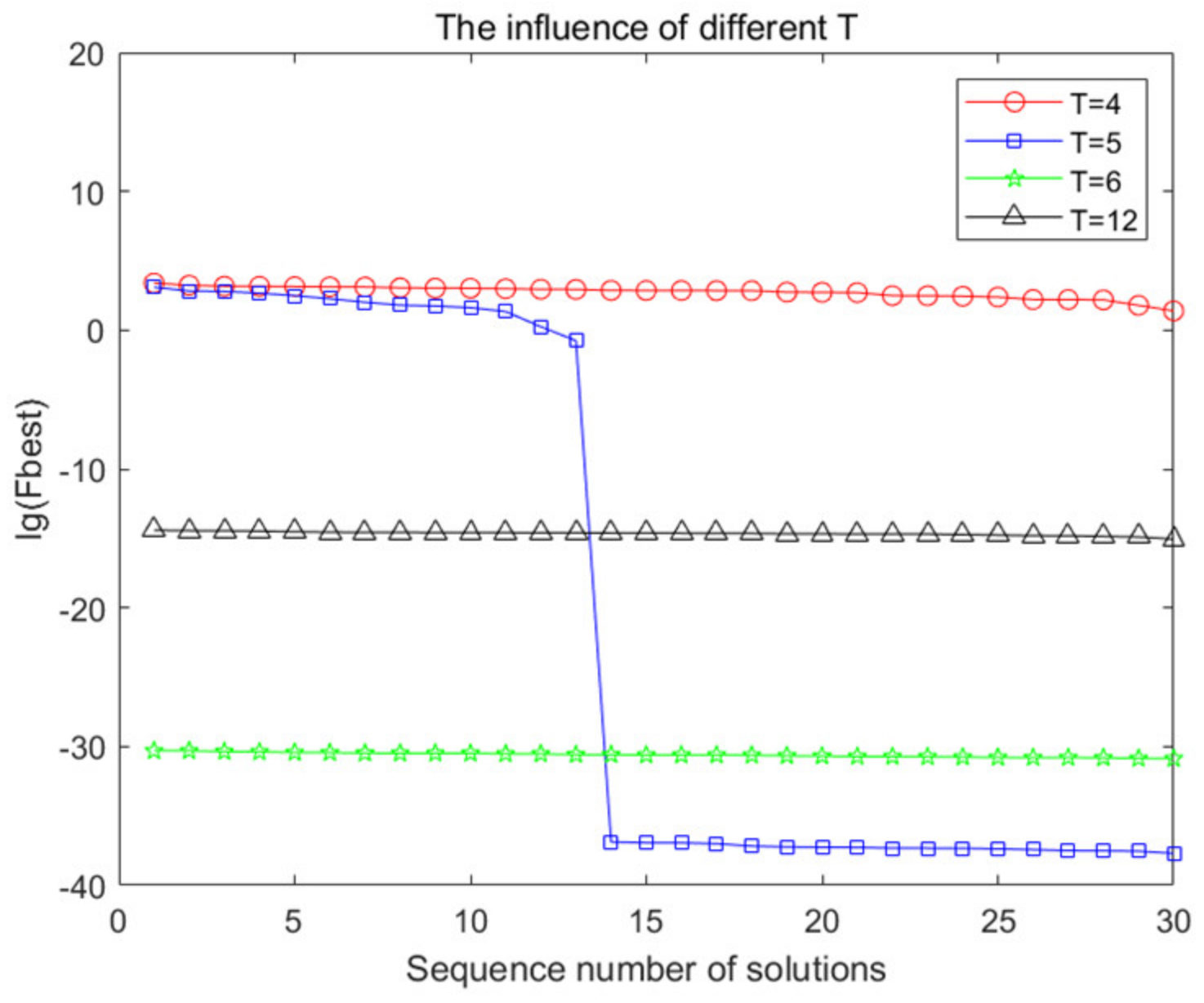
4.2.3. The Value of Parameter T
- A smaller T has the potential to make the algorithm find a better solution.
- A destabilization of the search may occur when the value of T varies.
- A T that is too small may impede the algorithm search for the optimal solution.
5. Applications of the Proposed Methods
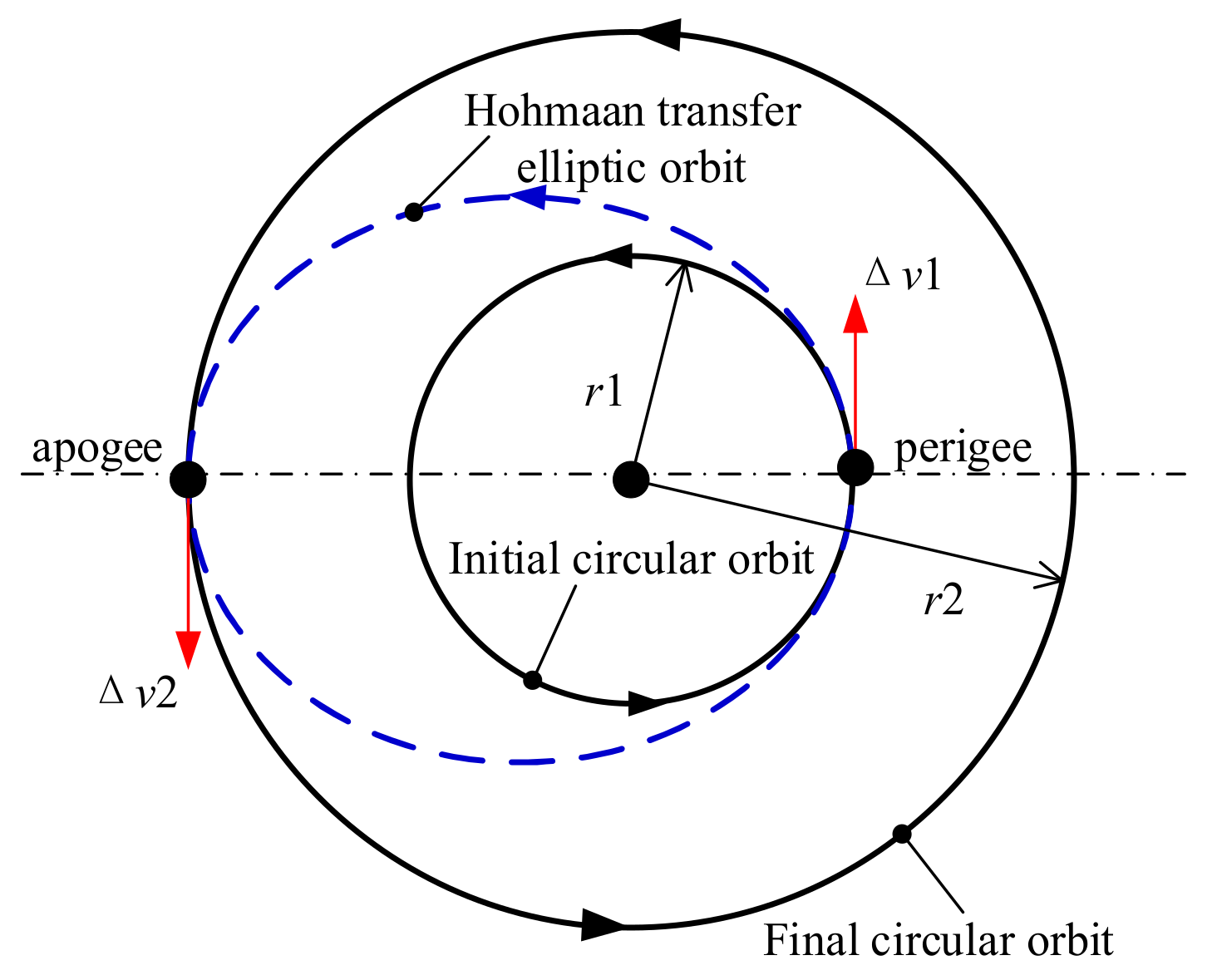
5.1. Multi-Impulse Minimum Fuel Orbit Transfer
5.1.1. Problem Formulation and Parameter Setting
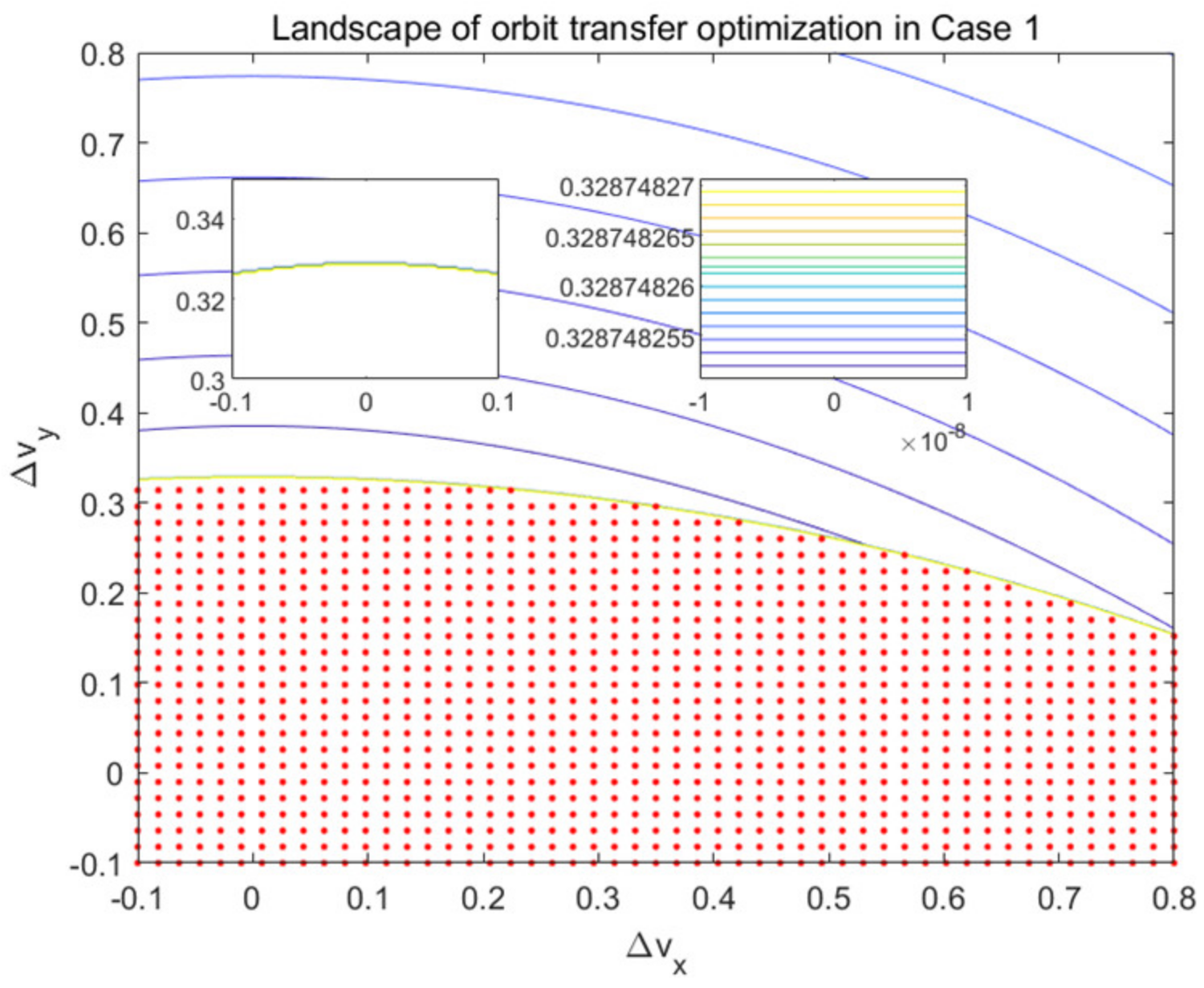
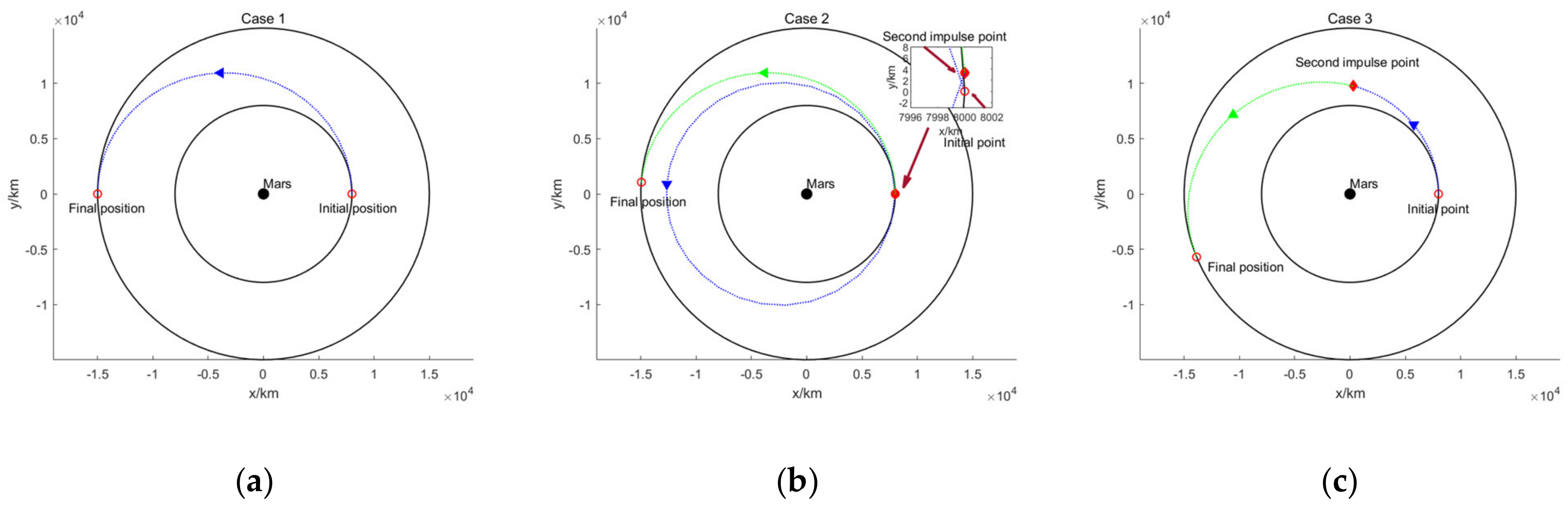
5.1.2. Results and Discussion
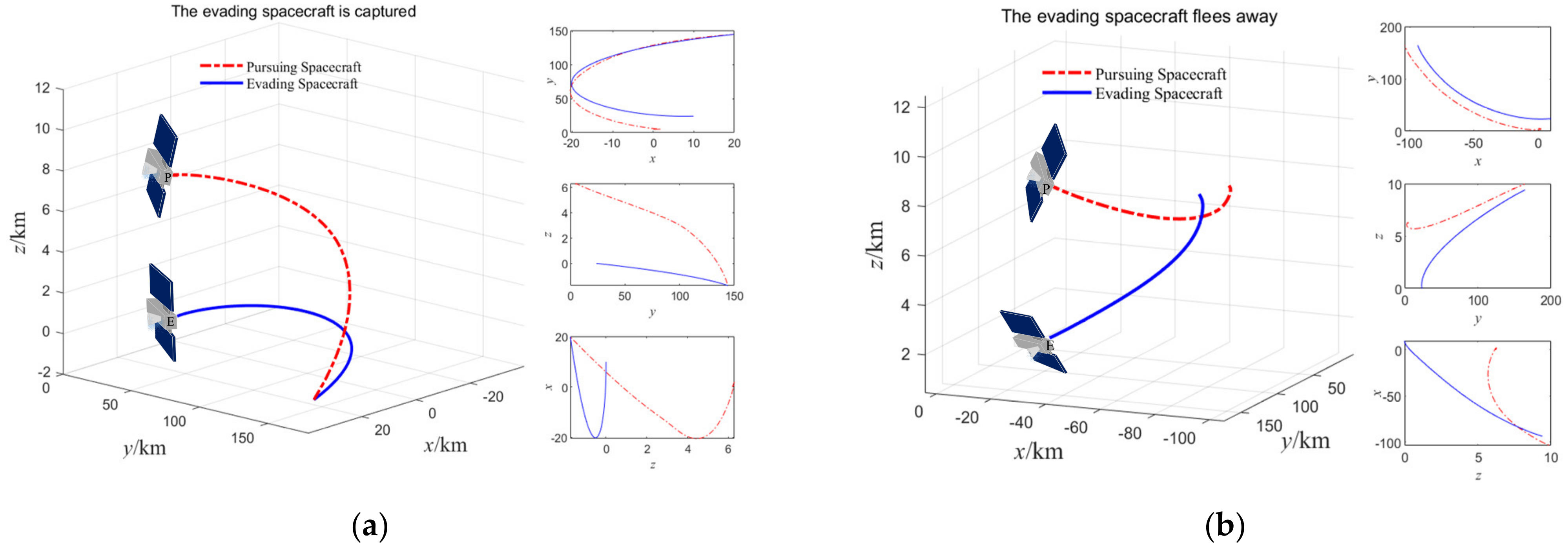
5.2. Pursuit-Evasion Game of Two Spacecraft
5.2.1. Problem Formulation and Parameters Setting
5.2.2. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Benchmark Functions
| Function | Dim | Range | fmin |
|---|---|---|---|
| 30 | [−100, 100] | 0 | |
| 30 | [−10, 10] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−30, 30] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−1.28, 1.28] | 0 |
| Function | Dim | Range | fmin |
|---|---|---|---|
| 30 | [−500, 500] | ||
| 30 | [−5.12, 5.12] | 0 | |
| 30 | [−32, 32] | 0 | |
| 30 | [−600, 600] | 0 | |
| 30 | [−50, 50] | 0 | |
| 30 | [−50, 50] | 0 |
| Function | Dim | Range | fmin |
|---|---|---|---|
| 2 | [−65, 65] | 0.998 | |
| 4 | [−5, 5] | 0.0003 | |
| 2 | [−5, 5] | −1.0316 | |
| 2 | [−5, 5] | 0.398 | |
| 2 | [−2, 2] | 3 | |
| 3 | [0, 1] | −3.86 | |
| 6 | [0, 1] | −3.32 | |
| 4 | [0, 10] | −10.1532 | |
| 4 | [0, 10] | −10.4028 | |
| 4 | [0, 10] | −10.5363 |
References
- Zhang, P.; Xu, Z.; Wang, Q.; Fan, S.; Cheng, W.; Wang, H.; Wu, Y. A novel variable selection method based on combined moving window and intelligent optimization algorithm for variable selection in chemical modeling. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 246, 118986. [Google Scholar] [CrossRef]
- Lin, C.; Wang, J.; Lee, C. Pattern recognition using neural-fuzzy networks based on improved particle swam optimization. Expert Syst. Appl. 2009, 36, 5402–5410. [Google Scholar] [CrossRef]
- Majeed, A.; Hwang, S. A Multi-Objective Coverage Path Planning Algorithm for UAVs to Cover Spatially Distributed Regions in Urban Environments. Aerospace 2021, 8, 343. [Google Scholar] [CrossRef]
- Gao, X.Z.; Nalluri, M.S.R.; Kannan, K.; Sinharoy, D. Multi-objective optimization of feature selection using hybrid cat swarm optimization. Sci. China Technol. Sci. 2021, 64, 508–520. [Google Scholar] [CrossRef]
- Singh, T. A novel data clustering approach based on whale optimization algorithm. Expert Syst. 2021, 38, e12657. [Google Scholar] [CrossRef]
- Pontani, M.; Ghosh, P.; Conway, B. Particle swarm optimization of multiple-burn rendezvous trajectories. J. Guid. Control Dyn. 2012, 35, 1192–1207. [Google Scholar] [CrossRef]
- Wagner, S.; Wie, B. Hybrid algorithm for multiple gravity-assist and impulsive delta-V maneuvers. J. Guid. Control Dyn. 2015, 38, 2096–2107. [Google Scholar] [CrossRef][Green Version]
- Wang, X.; Zhang, H.; Bai, S.; Yue, Y. Design of agile satellite constellation based on hybrid-resampling particle swarm optimization method. Acta Astronaut. 2021, 178, 595–605. [Google Scholar] [CrossRef]
- Wu, C.; Xu, R.; Zhu, S.; Cui, P. Time-optimal spacecraft attitude maneuver path planning under boundary and pointing constraints. Acta Astronaut. 2017, 137, 128–137. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–72. [Google Scholar] [CrossRef]
- Yao, X.; Liu, Y.; Lin, G. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 1999, 3, 82–102. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Juang, C. A hybrid of genetic algorithm and particle swarm optimization for recurrent network design. IEEE Trans. Syst. Man. Cybern. 2004, 34, 997–1006. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Zhang, H.; Gao, Y. Correlations between the scaling factor and fitness values in differential evolution. IEEE Access. 2020, 8, 32100–32120. [Google Scholar] [CrossRef]
- Smith, J. Coevolving memetic algorithms: A review and progress report. IEEE Trans. Syst. Man Cybern. Part B-Cybern. 2007, 37, 6–17. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.; Fogarty, T. Operator and parameter adaptation in genetic algorithms. Soft Comput. 1997, 1, 81–87. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, Perth, WA, USA, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE Word Congress on Computational Intelligence, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. A discrete binary version of the particle swarm algorithm. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics-Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; pp. 4104–4108. [Google Scholar] [CrossRef]
- Rana, S.; Jasola, S.; Kumar, R. A review on particle swarm optimization algorithms and their applications to data clustering. Artif. Intell. Rev. 2011, 35, 211–222. [Google Scholar] [CrossRef]
- Yang, X. Firefly algorithm, stochastic test functions and design optimization. Int. J. Bio-Inspired Comput. 2010, 2, 78–84. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Gao, K.; Cao, Z.; Zhang, L.; Han, Y.; Pan, Q. A review on swarm intelligence and evolutionary algorithms for solving flexible job shop scheduling problems. IEEE-CAA J. Autom. Sin. 2019, 6, 904–916. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Elaziz, M.A.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Engrgy 2021, 376, 113609. [Google Scholar] [CrossRef]
- Wolpert, D.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evolut. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Passino, K. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Syst. Mag. 2002, 22, 52–67. [Google Scholar] [CrossRef]
- Jin, M.; Lu, H. A multi-subgroup hierarchical hybrid of genetic algorithm and particle swarm optimization. Control Theory Appl. 2013, 30, 1231–1238. [Google Scholar] [CrossRef]
- Liu, L.; Guo, Y. Multi-objective optimization for attitude maneuver of liquid-filled flexible spacecraft based on improved hierarchical optimization algorithm. Appl. Soft Comput. 2020, 96, 106598. [Google Scholar] [CrossRef]
- Vasile, M.; Locatelli, M. A hybrid multiagent approach for global trajectory optimization. J. Glob. Optim. 2009, 44, 461–479. [Google Scholar] [CrossRef]
- Zuiani, F.; Vasile, M. Multi Agent Collaborative Search based on Tchebycheff decomposition. Comput. Optim. Appl. 2013, 56, 189–208. [Google Scholar] [CrossRef]
- Arab, A.; Alfi, A. An adaptive gradient descent-based local search in memetic algorithm applied to optimal controller design. Inf. Sci. 2015, 299, 117–142. [Google Scholar] [CrossRef]
- Bao, Y.; Hu, Z.; Xiong, T. A PSO and pattern search based memetic algorithm for SVMs parameters optimization. Neurocomputing 2013, 117, 98–106. [Google Scholar] [CrossRef]
- Lin, S. A parallel processing multi-coordinate descent method with line search for a class of large-scale optimization-algorithm and convergence. In Proceedings of the 30th IEEE Conference on Decision and Control, Brighton, UK, 11–13 December 1991. [Google Scholar] [CrossRef]
- Kennedy, J. Bare bones particle swarms. In Proceedings of the 2003 IEEE Swarm Intelligence Symposium, Indianapolis, IN, USA, 26 April 2003; pp. 80–87. [Google Scholar] [CrossRef]
- Zhang, E.; Wu, Y.; Chen, Q. A practical approach for solving multi-objective reliability redundancy allocation problems using extended bare-bones particle swarm optimization. Reliab. Eng. Syst. Saf. 2014, 127, 65–76. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.; Ding, Z. A bare-bones multi-objective particle swarm optimization algorithm for environmental/economic dispatch. Inf. Sci. 2012, 192, 213–227. [Google Scholar] [CrossRef]
- Hansen, N.; Muller, S.; Koumoutsakos, P. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evol. Comput. 2003, 11, 1–18. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Abdelkhalik, O.; Mortari, D. N-impulse orbit transfer using genetic algorithms. J. Spacecr. Rockets 2007, 44, 456–460. [Google Scholar] [CrossRef]
- Wang, X.; Shi, P.; Zhao, Y.; Sun, Y. A pre-trained fuzzy reinforcement learning method for the pursuing satellite in a one-to-one game in space. Sensors 2020, 20, 2253. [Google Scholar] [CrossRef]
- Hughes, S.; Mailhe, L.; Guzman, J. A comparison of trajectory optimization methods for the impulsive minimum fuel rendezvous problem. Adv. Astronaut. Sci. 2003, 113, 85–104. [Google Scholar]
- Curtis, H. Orbital Mechanics for Engineering Students; Elsevier Butterworth-Heinemann: Oxford, UK, 2010; pp. 257–264. [Google Scholar] [CrossRef]
- Yang, Z.; Luo, Y.; Zhang, J. Nonlinear semi-analytical uncertainty propagation of trajectory under impulsive maneuvers. Astrodynamics 2019, 3, 61–77. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, Q.; Loxton, R.; Li, B. Numerical solution of a pursuit-evasion differential game involving two spacecraft in low Earth orbit. J. Ind. Manag. Optim. 2015, 11, 1127–1147. [Google Scholar] [CrossRef]
- Clohessy, W.; Wiltshire, R. Terminal guidance system for satellite rendezvous. J. Aerosp. Sci. 1960, 11, 653–658. [Google Scholar] [CrossRef]




| Algorithm | Parameters |
|---|---|
| GA | Pc = 0.8, Pm = 0.2, Pr = 1.5 |
| DE | F = 0.3, CR = 0.2 |
| PSO | ωmax = 0.9, ωmin = 0.4, c1 = c2 = 2 |
| GWO | a = 2(1-i/Imax), i is the current iteration |
| BOA | a = 0.1 + 0.2 × i/Imax, i is the current iteration, c = 0.01, p = 0.8 |
| HHO | β = 1.5, J = 2(1-r5), r5~U(0,1) |
| AOA | = 5, μ = 0.5 |
| HOA-1 | = 0.3, c1 = 1, c2 = 0.3, c = 1 |
| HOA-2 | = 0.3, c1 = 1, c2 = 0.3, c = 1 |
| F | HOA-1 | HOA-2 | GA | DE | PSO | GWO | BOA | HHO | AOA | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | B | 3.28 × 10−16 | T = 6 | 3.16 × 10−7 | T = 15 | 6.73 × 10−9 | 1.12 × 10−8 | 1.13 × 10−3 | 1.88 × 10−6 | 68.0 | 2.43 × 10−6 | 0.134 |
| A | 8.87 × 10−16 | 9.34 × 10−6 | 1.33 × 10−8 | 1.13 × 10−2 | 0.0157 | 3.18 × 10−2 | 407 | 0.0106 | 0.172 | |||
| S | 3.28 × 10−16 | 8.63 × 10−6 | 3.78 × 10−9 | 0.0542 | 0.0127 | 0.0153 | 155 | 0.0241 | 0.0157 | |||
| F2 | B | 4.38 × 10−10 | T = 8 | 1.05 × 10−4 | T = 15 | 1.92 × 10−4 | 4.92 × 10−6 | 0.0568 | 0.174 | 0.225 | 9.46 × 10−3 | 1.65 |
| A | 0.237 | 5.21 × 10−4 | 3.74 × 10−4 | 8.67 × 10−6 | 0.175 | 0.417 | 2.39 | 0.0489 | 1.81 | |||
| S | 1.10 | 6.26 × 10−3 | 9.17 × 10−5 | 2.57 × 10−6 | 0.819 | 0.137 | 1.67 | 0.0368 | 0.0763 | |||
| F3 | B | 75.7 | T = 40 | 35.2 | T = 30 | 1.14 × 10−18 | 1.54 × 104 | 40.8 | 2.27 | 72.9 | 3.62 × 10−4 | 14.1 |
| A | 314 | 189 | 7.04 × 10−11 | 1.88 × 104 | 99.7 | 6.93 | 497 | 0.142 | 73.1 | |||
| S | 146 | 89.5 | 2.75 × 10−10 | 2.64 × 103 | 35.9 | 2.74 | 325 | 0.231 | 107 | |||
| F4 | B | 0.0302 | T = 35 | 0.664 | T = 30 | 0.804 | 3.59 | 0.931 | 5.38 × 10−3 | 12.2 | 1.52 × 10−5 | 0.500 |
| A | 0.136 | 2.39 | 1.76 | 6.26 | 1.35 | 0.274 | 16.0 | 4.94 × 10−3 | 0.504 | |||
| S | 0.191 | 1.24 | 0.547 | 3.15 | 0.240 | 0.212 | 1.33 | 3.78 × 10−3 | 6.63 × 10−3 | |||
| F5 | B | 0.173 | T = 40 | 14.7 | T = 30 | N/A | 21.8 | 33.3 | 36 | 29.0 | 5.76 × 10−4 | 183 |
| A | 52.6 | 41.1 | N/A | 112 | 190 | 64.1 | 29.1 | 0.0186 | 223 | |||
| S | 33.2 | 23.8 | N/A | 81.8 | 223 | 14.6 | 0.158 | 0.0256 | 15.0 | |||
| F6 | B | 1.36 × 10−18 | T = 10 | 3.35 × 10−7 | T = 15 | 1.55 × 10−5 | 5.82 × 10−9 | 3.59 × 10−3 | 5.80 × 10−5 | 140 | 3.37 × 10−8 | 2.57 |
| A | 2.82 × 10−18 | 3.51 × 10−5 | 4.93 × 10−5 | 6.82 × 10−4 | 0.0201 | 0.718 | 465 | 9.17 × 10−5 | 3.20 | |||
| S | 1.03 × 10−18 | 5.63 × 10−5 | 3.46 × 10−5 | 3.67 × 10−3 | 0.0217 | 0.365 | 162 | 1.29 × 10−4 | 0.286 | |||
| F7 | B | 0.0135 | T = 70 | 0.0329 | T = 25 | 0.0303 | 0.0818 | 0.168 | 0.0923 | 0.204 | 5.99 × 10−5 | 0.684 |
| A | 0.0480 | 0.0747 | 0.0916 | 0.198 | 0.377 | 0.191 | 0.299 | 9.79 × 10−4 | 0.724 | |||
| S | 0.0192 | 0.0228 | 0.0364 | 0.0572 | 0.147 | 0.0500 | 0.0691 | 1.11 × 10−3 | 0.0133 | |||
| F | HOA-1 | HOA-2 | GA | DE | PSO | GWO | BOA | HHO | AOA | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F8 | B | −9.19 × 103 | T = 40 | −10.0 × 104 | T = 25 | −1.21 × 104 | −1.26 × 104 | −8.23 × 103 | −7.51 × 103 | −3.53 × 103 | −1.26 × 104 | −6.21 × 103 |
| A | −7.40 × 103 | −7.83 × 103 | −1.13 × 104 | −1.24 × 104 | −5.56 × 103 | −5.95 × 103 | −2.67 × 103 | −1.26 × 104 | −5.44 × 103 | |||
| S | 604 | 924 | 399 | 142 | 1.53 × 103 | 924 | 372 | 0.941 | 405 | |||
| F9 | B | 1.99 × 10−6 | T = 40 | 10.9 | T = 10 | 6.51 × 10−5 | 53.7 | 39.3 | 5.77 | 177 | 4.19 × 10−5 | 33.9 |
| A | 1.02 × 10−4 | 39.0 | 2.34 × 10−1 | 65.0 | 68.5 | 19.3 | 210 | 0.0219 | 37.3 | |||
| S | 3.44 × 10−5 | 18.1 | 0.493 | 7.29 | 16.7 | 8.04 | 15.5 | 0.0238 | 1.46 | |||
| F10 | B | 4.21 × 10−7 | T = 7 | 0.0255 | T = 30 | 1.05 × 10−3 | 3.06 × 10−5 | 0.0380 | 1.36 × 10−3 | 9.13 | 2.90 × 10−4 | 0.379 |
| A | 0.211 | 1.54 | 2.73 × 10−3 | 0.0209 | 0.473 | 0.175 | 10.5 | 7.91 × 10−3 | 0.435 | |||
| S | 0.636 | 0.772 | 1.09 × 10−3 | 0.109 | 0.530 | 0.0738 | 0.557 | 6.15 × 10−3 | 0.0322 | |||
| F11 | B | 2.60 × 10−8 | T = 20 | 2.52 × 10−7 | T = 15 | 6.08 × 10−6 | 3.91 × 10−8 | 1.64 × 10−4 | 7.66 × 10−4 | 13.0 | 6.18 × 10−6 | 0.0324 |
| A | 0.0339 | 0.0106 | 3.81 × 10−3 | 1.02 × 10−3 | 0.0107 | 6.87 × 10−3 | 19.3 | 1.51 × 10−3 | 0.253 | |||
| S | 0.0276 | 0.0123 | 2.08 × 10−3 | 2.69 × 10−3 | 9.58 × 10−3 | 9.10 × 10−3 | 2.50 | 2.60 × 10−3 | 0.196 | |||
| F12 | B | 6.87 × 10−12 | T = 20 | 1.71 × 10−6 | T = 30 | 3.47 × 10−11 | 5.44 × 10−10 | 2.93 × 10−5 | 0.667 | 1.01 | 5.85 × 10−8 | 7.33 |
| A | 4.15 × 10−11 | 2.18 | 3.84 | 3.07 × 10−3 | 3.68 × 10−3 | 1.36 | 5.08 | 2.48 × 10−5 | 8.58 | |||
| S | 6.81 × 10−11 | 1.44 | 6.03 | 8.78 × 10−3 | 0.0186 | 0.408 | 5.27 | 3.43 × 10−5 | 0.412 | |||
| F13 | B | 8.78 × 10−14 | T = 15 | 1.92 × 10−6 | T = 20 | 3.41 × 10−13 | 3.27 × 10−9 | 5.68 × 10−4 | 0.346 | 2.85 | 2.21 × 10−6 | 4.76 |
| A | 3.67 × 10−13 | 0.0505 | 0.0549 | 0.151 | 9.20 × 10−3 | 0.999 | 3.03 | 3.92 × 10−4 | 5.27 | |||
| S | 2.04 × 10−13 | 0.137 | 0.236 | 0.523 | 7.49 × 10−3 | 0.367 | 0.0993 | 3.41 × 10−4 | 0.192 | |||
| F | HOA-1 | HOA-2 | GA | DE | PSO | GWO | BOA | HHO | AOA | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F14 | B | 0.998 | T = 25 | 0.998 | T = 25 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 |
| A | 8.04 | 2.71 | 7.51 | 1.16 | 3.13 | 3.58 | 3.13 | 1.097 | 6.47 | |||
| S | 0.0139 | 1.87 | 4.30 | 0.885 | 2.43 | 3.32 | 2.35 | 0.298 | 1.64 | |||
| F15 | B | 3.09 × 10−4 | T = 20 | 3.07 × 10−4 | T = 25 | 5.55 × 10−4 | 4.97 × 10−4 | 3.70 × 10−4 | 3.60 × 10−4 | 8.53 × 10−4 | 3.08 × 10−4 | 8.56 × 10−4 |
| A | 8.48 × 10−3 | 2.01 × 10−3 | 2.85 × 10−3 | 7.65 × 10−4 | 8.98 × 10−4 | 5.61 × 10−3 | 0.0173 | 4.03 × 10−4 | 0.0199 | |||
| S | 0.0139 | 4.92 × 10−3 | 5.08 × 10−3 | 2.03 × 10−4 | 2.64 × 10−4 | 7.04 × 10−3 | 0.0270 | 2.21 × 10−4 | 0.0207 | |||
| F16 | B | −1.03 | T = 20 | −1.03 | T = 30 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 |
| A | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.02 | −1.03 | −1.03 | |||
| S | 2.57 × 10−12 | 1.22 × 10−5 | 2.14 × 10−9 | 0 | 0 | 7.11 × 10−8 | 0.0120 | 1.24 × 10−7 | 1.56 × 10−7 | |||
| F17 | B | −0.398 | T = 20 | 0.398 | T = 30 | 0.398 | 0.398 | 0.398 | 0.398 | 0.398 | 0.398 | 0.398 |
| A | −0.398 | 0.398 | 0.398 | 0.398 | 0.398 | 0.398 | 0.937 | 0.398 | 0.411 | |||
| S | 1.83 × 10−12 | 1.89 × 10−8 | 1.65 × 10−9 | 2.66 × 10−15 | 1.11 × 10−16 | 1.50 × 10−4 | 1.41 | 4.84 × 10−5 | 7.51 × 10−3 | |||
| F18 | B | 3.00 | T = 20 | 3.00 | T = 40 | 3.00 | 3.00 | 3.00 | 3.00 | 3.02 | 3.00 | 3.00 |
| A | 3.00 | 3.00 | 3.00 | 3.90 | 3.00 | 5.70 | 10.7 | 3.00 | 23.3 | |||
| S | 9.42 × 10−11 | 1.78 × 10−5 | 1.60 × 10−7 | 4.85 | 4.40 × 10−15 | 14.5 | 7.62 | 2.06 × 10−8 | 21.1 | |||
| F19 | B | −3.86 | T = 20 | −3.86 | T = 40 | −3.86 | −3.86 | −3.86 | −3.86 | −3.84 | −3.86 | −3.86 |
| A | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.53 | −3.86 | −3.84 | |||
| S | 4.83 × 10−13 | 9.00 × 10−7 | 3.48 × 10−8 | 2.66 × 10−15 | 3.00 × 10−3 | 5.43 × 10−3 | 0.288 | 6.04 × 10−3 | 8.22 × 10−3 | |||
| F20 | B | −3.32 | T = 30 | −3.32 | T = 40 | −3.32 | −3.32 | −3.32 | −3.32 | −3.09 | −3.26 | −3.21 |
| A | −3.28 | −3.30 | −3.28 | −3.32 | −3.29 | −3.24 | −2.27 | −3.07 | −3.04 | |||
| S | 0.0573 | 0.0476 | 0.0573 | 1.68 × 10−6 | 0.0503 | 0.119 | 0.467 | 0.0997 | 0.119 | |||
| F21 | B | −10.1532 | T = 80 | −10.1489 | T = 80 | −10.1532 | −10.1532 | −10.1532 | −10.1529 | −6.11 | −10.1508 | −5.91 |
| A | −6.31 | −7.20 | −5.88 | −8.84 | −6.89 | −9.646 | −2.83 | −8.4191 | −3.20 | |||
| S | 3.46 | 3.41 | 2.97 | 2.43 | 3.37 | 1.516 | 1.49 | 2.2256 | 0.850 | |||
| F22 | B | −10.4029 | T = 80 | −10.3931 | T = 80 | −10.4029 | −10.4029 | −10.4029 | −10.4028 | −8.55 | −10.4028 | −7.87 |
| A | −5.98 | −7.29 | −5.76 | −10.002 | −9.52 | −10.225 | −2.91 | −8.7108 | −3.45 | |||
| S | 3.47 | 3.55 | 2.91 | 1.096 | 2.23 | 0.947 | 1.49 | 2.4287 | 0.971 | |||
| F23 | B | −10.5364 | T = 80 | −10.5318 | T = 80 | −10.5364 | −10.5364 | −10.5364 | −10.5357 | −6.97 | −10.5358 | −9.93 |
| A | −6.05 | −7.37 | −5.41 | −10.428 | −8.99 | −10.354 | −3.28 | −8.3461 | −4.42 | |||
| S | 3.74 | 3.81 | 3.46 | 0.379 | 2.81 | 0.970 | 1.69 | 2.4791 | 2.44 | |||
| F | HOA-1 | HOA-2 | GA | DE | PSO | GWO | BOA | HHO | AOA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 1 | 4 | 2 | 3 | 7 | 5 | 9 | 6 | 8 |
| F2 | 1 | 3 | 4 | 2 | 6 | 7 | 8 | 5 | 9 |
| F3 | 8 | 5 | 1 | 9 | 6 | 3 | 7 | 2 | 4 |
| F4 | 3 | 5 | 6 | 8 | 7 | 2 | 9 | 1 | 4 |
| F5 | 2 | 3 | 9 | 4 | 6 | 7 | 5 | 1 | 8 |
| F6 | 1 | 4 | 5 | 2 | 7 | 6 | 9 | 3 | 8 |
| F7 | 2 | 4 | 3 | 5 | 7 | 6 | 8 | 1 | 9 |
| F8 | 5 | 4 | 3 | 1.5 | 6 | 7 | 9 | 1.5 | 8 |
| F9 | 1 | 6 | 3 | 7 | 8 | 4 | 9 | 2 | 5 |
| F10 | 1 | 6 | 4 | 2 | 7 | 5 | 9 | 3 | 8 |
| F11 | 1 | 3 | 4 | 2 | 6 | 7 | 9 | 5 | 8 |
| F12 | 1 | 5 | 2 | 3 | 6 | 7 | 8 | 4 | 9 |
| F13 | 1 | 4 | 2 | 3 | 6 | 7 | 8 | 5 | 9 |
| F14 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| F15 | 3 | 1 | 7 | 6 | 5 | 4 | 8 | 2 | 9 |
| F16 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| F17 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| F18 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 9 | 4.5 | 4.5 |
| F19 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 4.5 | 9 | 4.5 | 4.5 |
| F20 | 3.5 | 3.5 | 3.5 | 3.5 | 3.5 | 3.5 | 9 | 7 | 8 |
| F21 | 2.5 | 7 | 2.5 | 2.5 | 2.5 | 5 | 8 | 6 | 9 |
| F22 | 2.5 | 7 | 2.5 | 2.5 | 2.5 | 5.5 | 8 | 5.5 | 9 |
| F23 | 2.5 | 7 | 2.5 | 2.5 | 2.5 | 6 | 9 | 5 | 8 |
| Mean Rank | 2.869565 | 4.586957 | 3.913043 | 4.021739 | 5.434783 | 5.26087 | 7.913043 | 3.869565 | 7.130435 |
| Case | Search Space |
|---|---|
| Case 1 | 2-dimension, Lb = [−0.1 −0.1]T and Ub = [0.8 0.8]T |
| Case 2 | 5-dimension, Lb = [0 0 5577 0 0]T and Ub = [0.25 0.25 33,465 0.25 0.25]T |
| Case 3 | 5-dimension, Lb = [0 0 5577 0 0]T and Ub = [0.25 0.25 16,733 0.25 0.25]T |
| Algorithms | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| DE | 0.609153269 | 0.609856799 | 0.616650300 |
| GA | 0.609154556 | 0.609274226 | 0.634113176 |
| PSO | 0.609155127 | 0.609163945 | 0.613222985 |
| HHO | 0.609158146 | 0.609227931 | 0.613319255 |
| AOA | 0.609333116 | 0.609173849 | 0.613235349 |
| GWO | 0.609156659 | 0.609232163 | 0.612584848 |
| HOA-1 | 0.609156393 (T = 10) | 0.609189193 (T = 15) | 0.613940295 (T = 15) |
| HOA-2 | 0.609153802 (T = 10) | 0.609153512 (T = 15) | 0.612572700 (T = 15) |
| Case | Search Space |
|---|---|
| Case 1 | |
| Case 2 |
| Algorithms | Case 1 | Case 2 |
|---|---|---|
| DE | 31.99873636 | 11.53267283 |
| GA | 38.30182027 | 7.804473121 |
| PSO | 9.975250323 | 13.99749289 |
| GWO | 9.945175394 | 1.523214099 |
| HHO | 27.19103058 | 2.48115544 |
| AOA | 26.93112607 | 10.05829695 |
| HOA-1 | 11.56198501 (T = 4) | 2.194148725 (T = 4) |
| HOA-2 | 7.148744461 (T = 4) | 1.032140678 (T = 5) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, H.; Shi, P.; Zhao, Y. Hierarchical Optimization Algorithm and Applications of Spacecraft Trajectory Optimization. Aerospace 2022, 9, 81. https://doi.org/10.3390/aerospace9020081
He H, Shi P, Zhao Y. Hierarchical Optimization Algorithm and Applications of Spacecraft Trajectory Optimization. Aerospace. 2022; 9(2):81. https://doi.org/10.3390/aerospace9020081
Chicago/Turabian StyleHe, Hanqing, Peng Shi, and Yushan Zhao. 2022. "Hierarchical Optimization Algorithm and Applications of Spacecraft Trajectory Optimization" Aerospace 9, no. 2: 81. https://doi.org/10.3390/aerospace9020081
APA StyleHe, H., Shi, P., & Zhao, Y. (2022). Hierarchical Optimization Algorithm and Applications of Spacecraft Trajectory Optimization. Aerospace, 9(2), 81. https://doi.org/10.3390/aerospace9020081






