Investigation on a Flow Coupling Rudder for Directional Control of a Low-Aspect Tailless Configuration with Diamond-Shaped Wing
Abstract
:1. Introduction
2. Numerical Method and Model
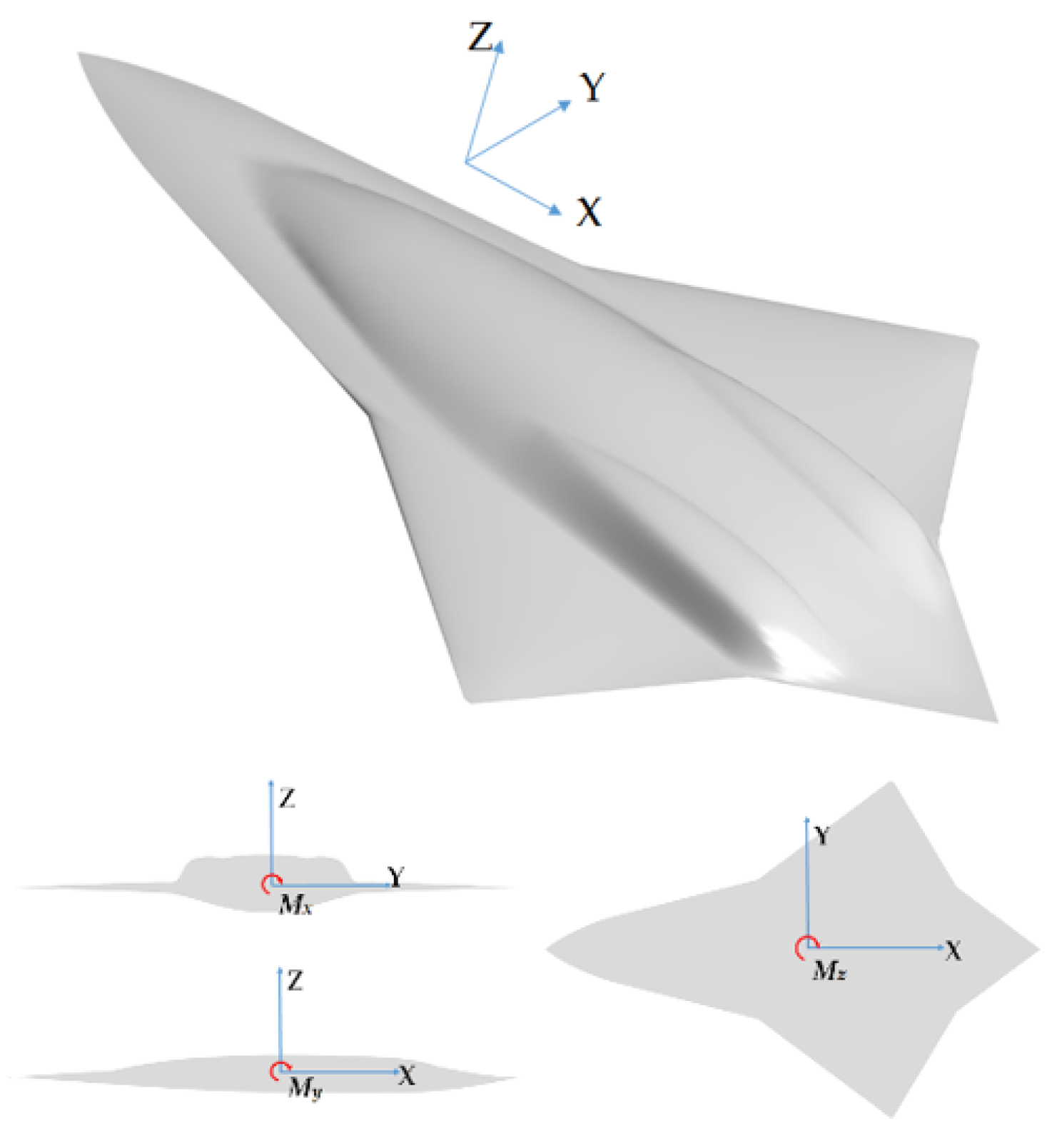
2.1. Research Model
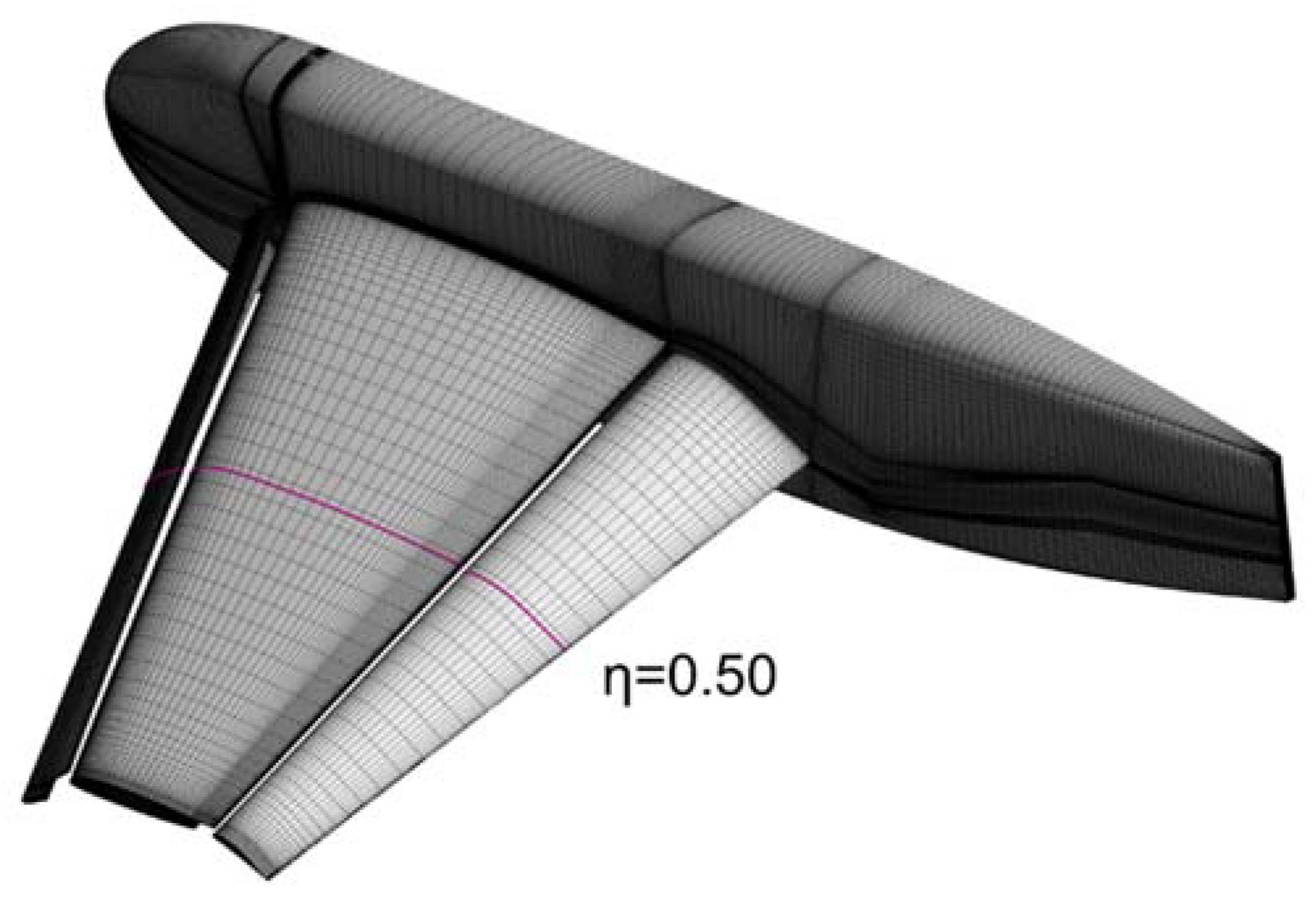
2.2. Numerical Method and Verification
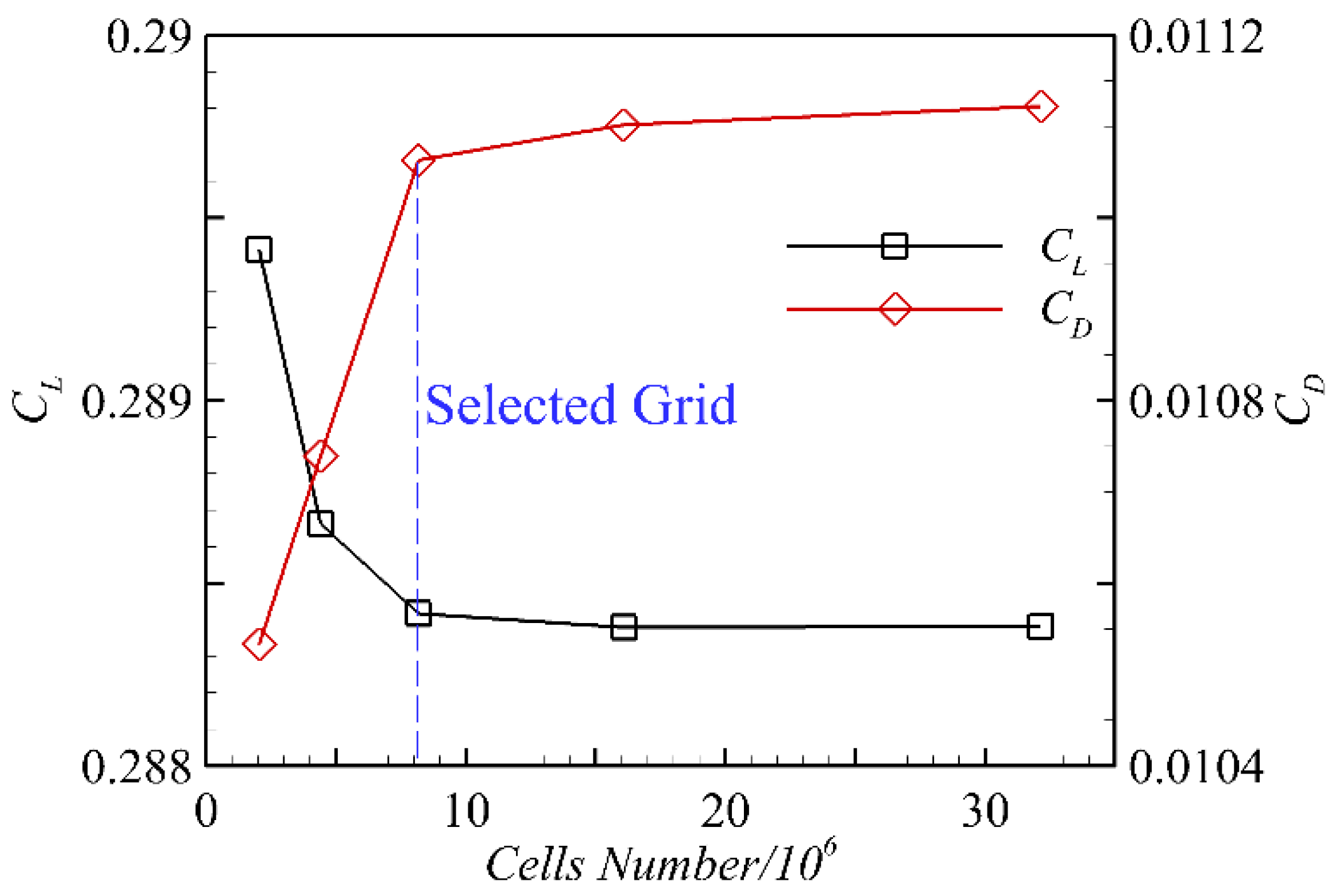
2.3. Grid Convergence Study
3. Control Characteristics of Single Rudder
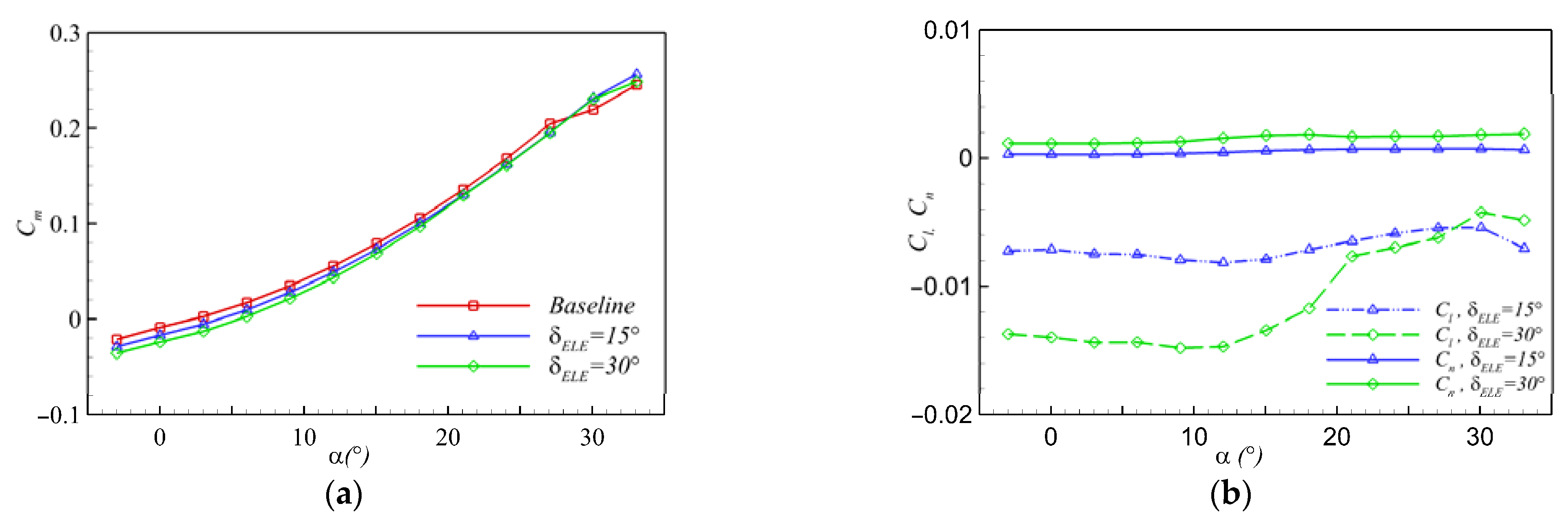
3.1. Elevon
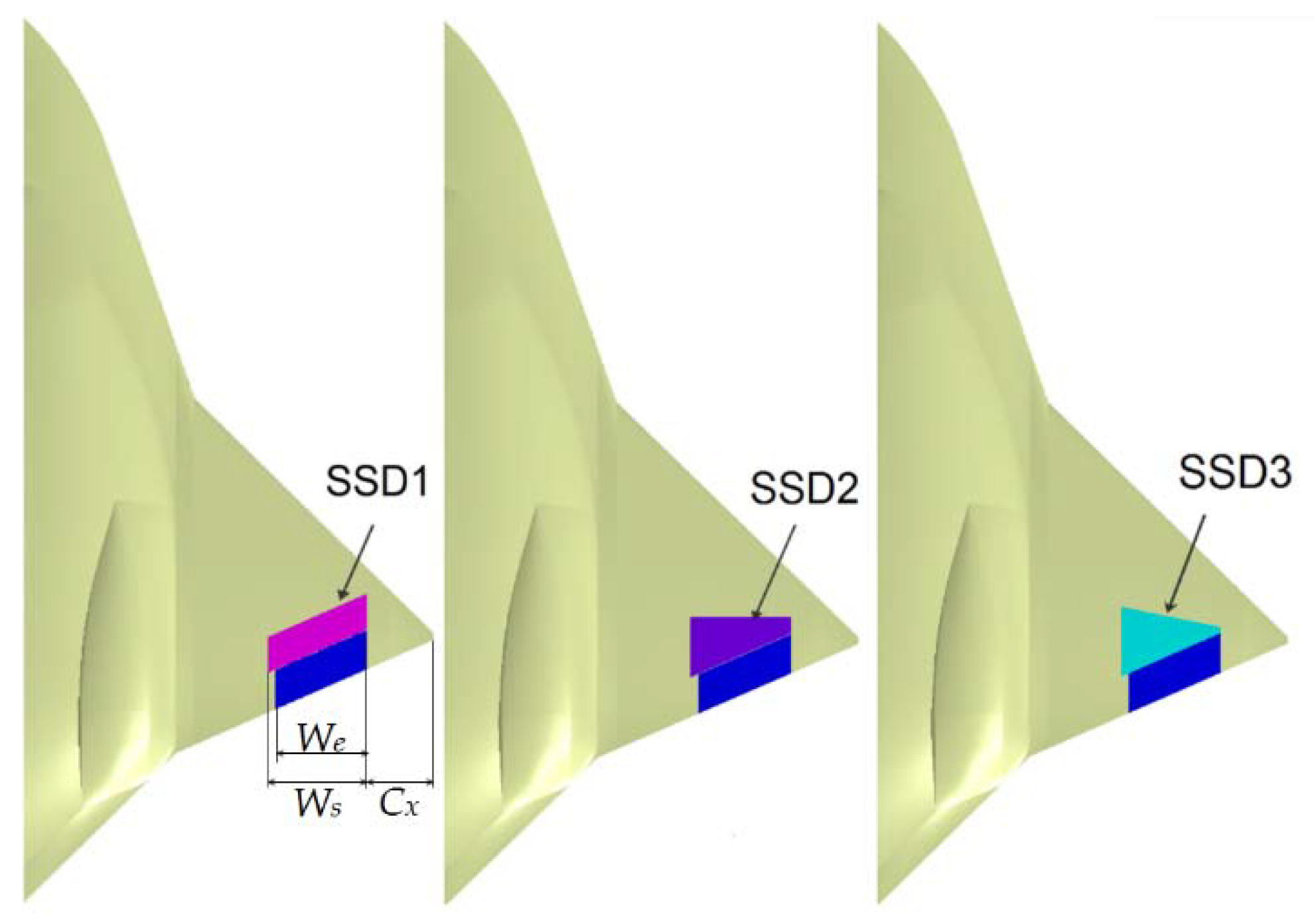
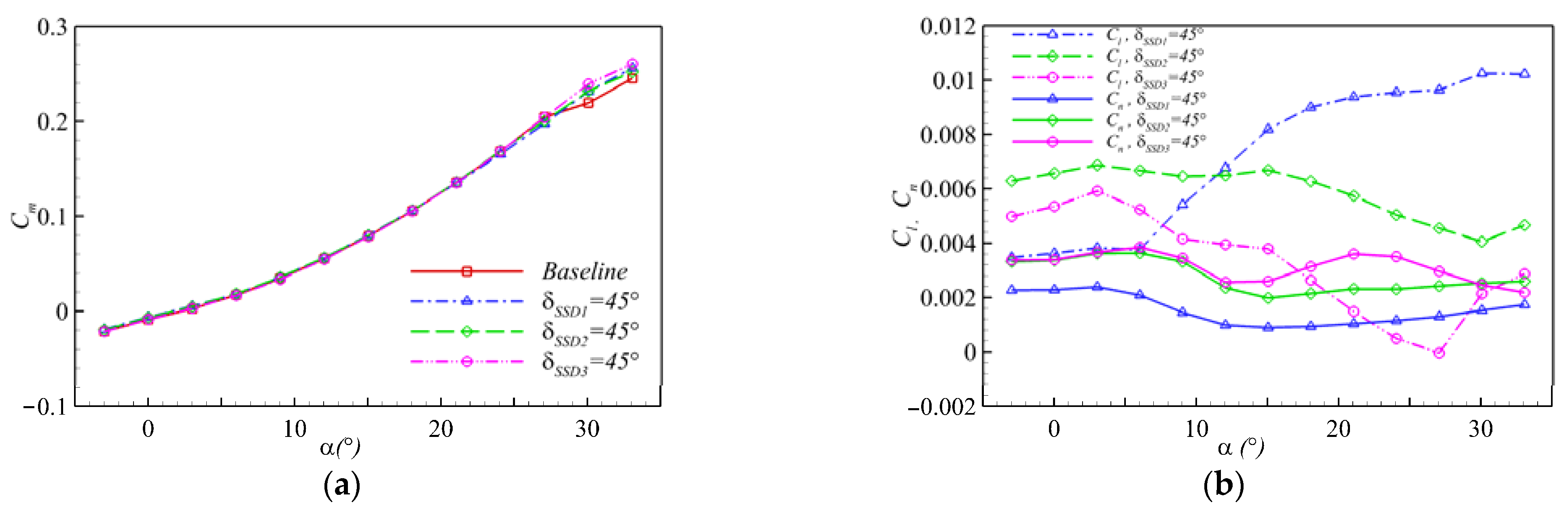
3.2. Spoiler Slot Deflector
4. Investigation on Flow Coupling Rudder
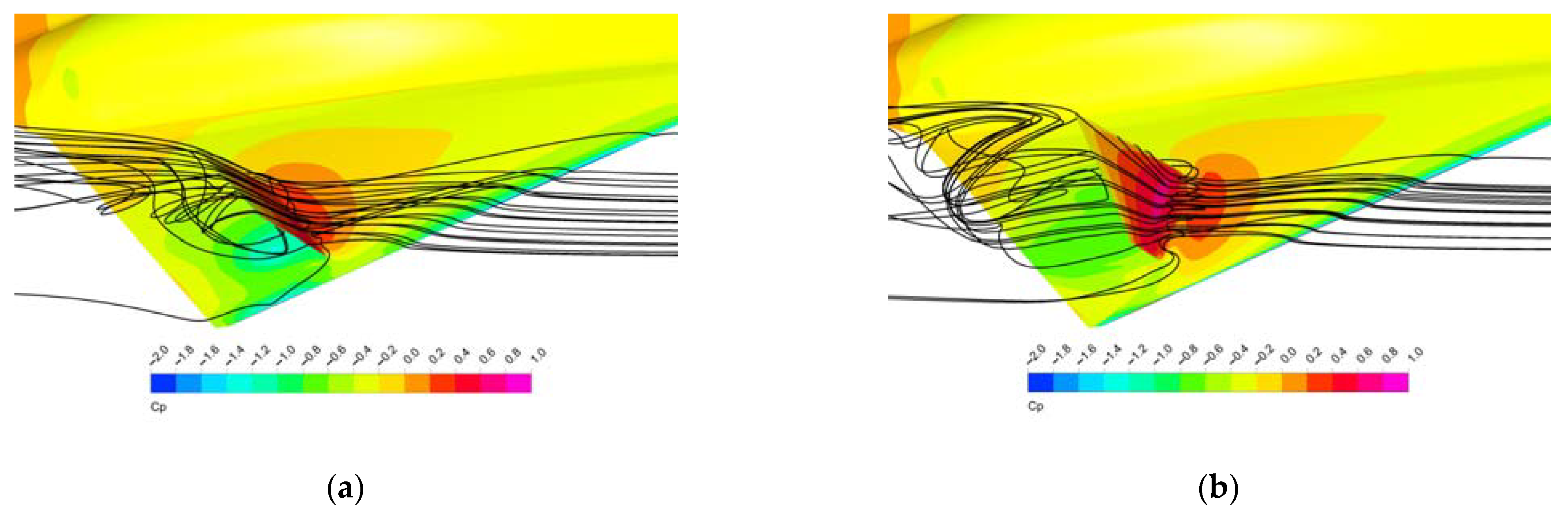
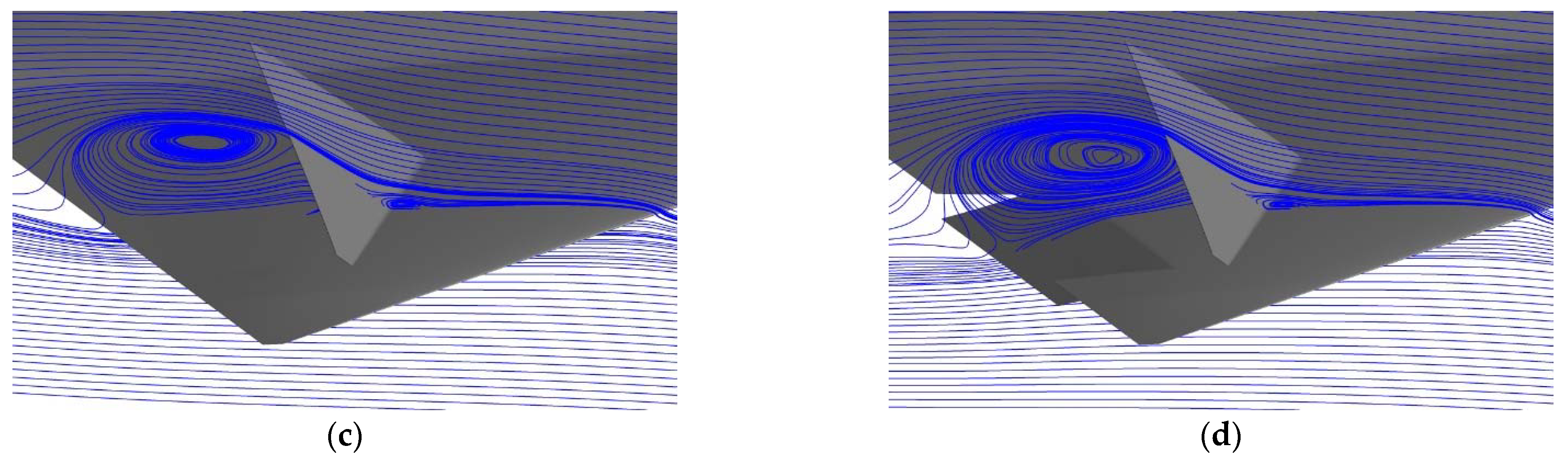
4.1. Flow Coupling Mechanism of FCR
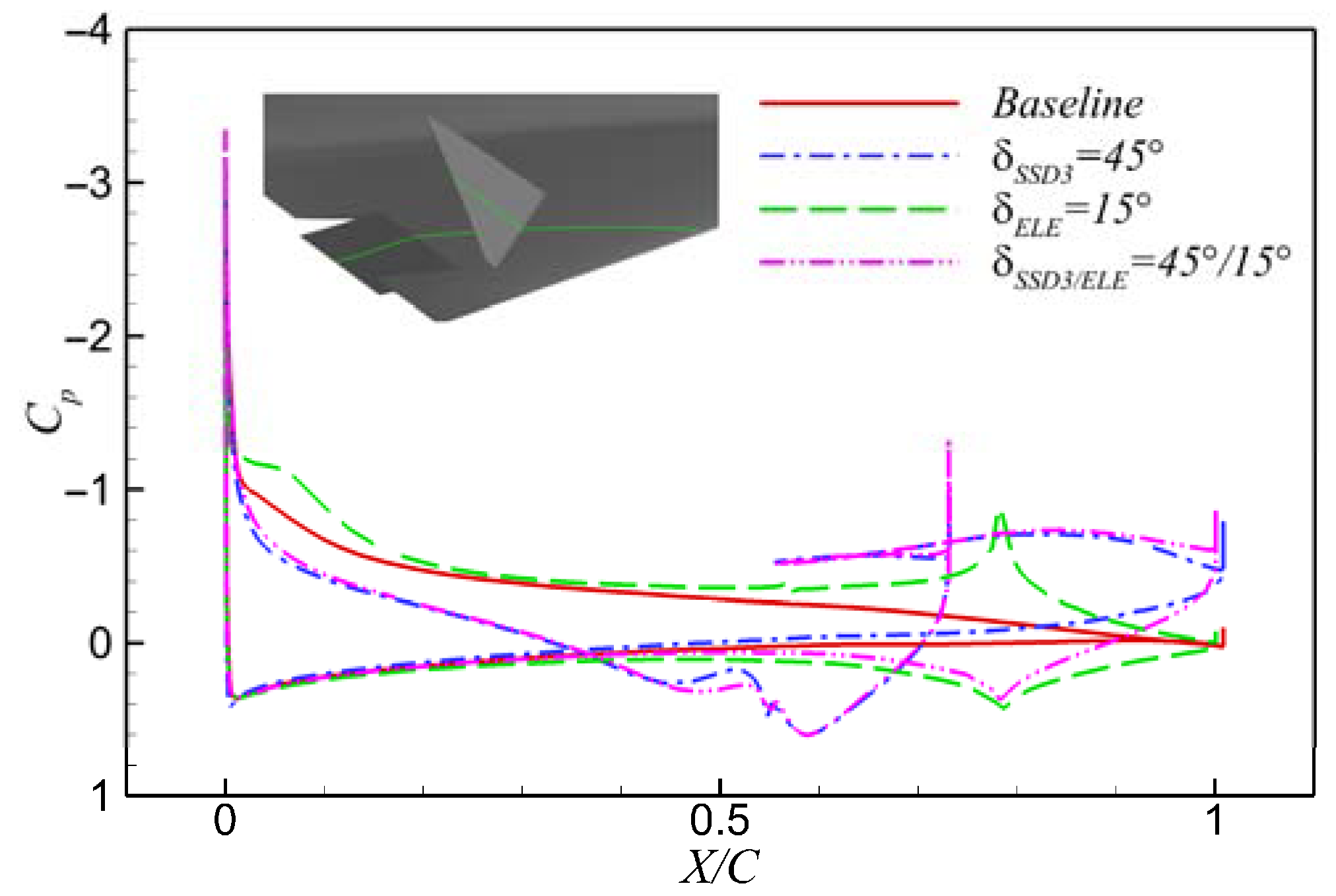
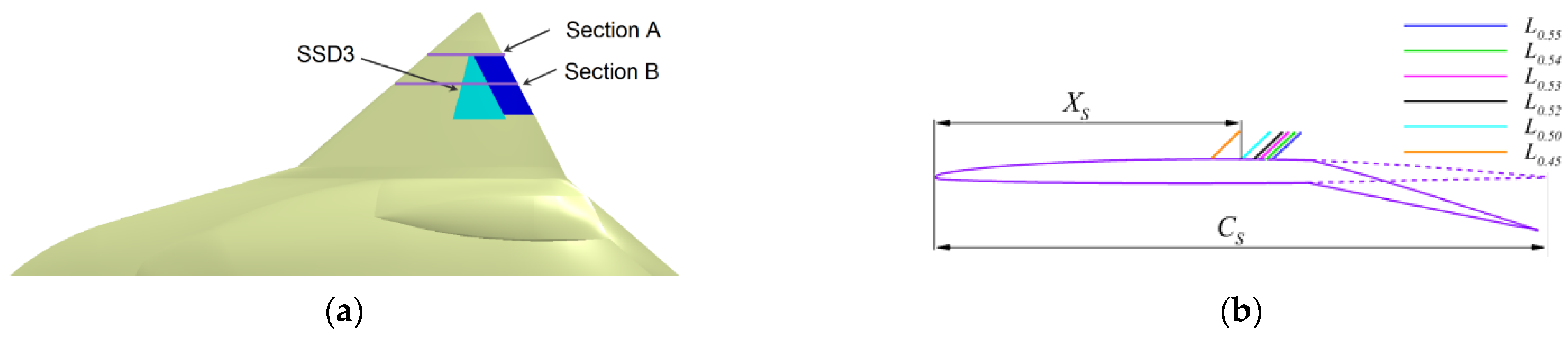
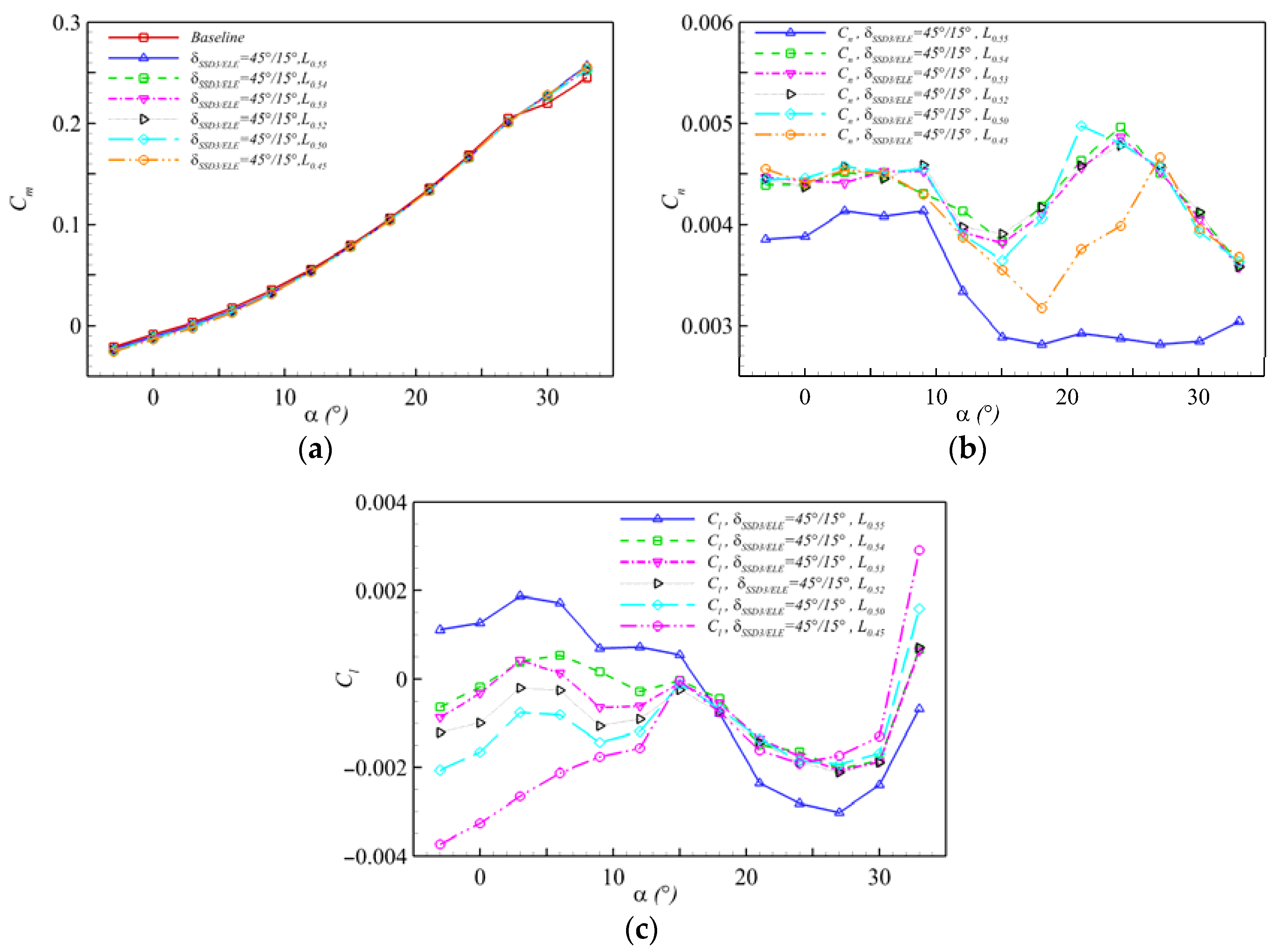
4.2. Location Effect of SSD3 of FCR
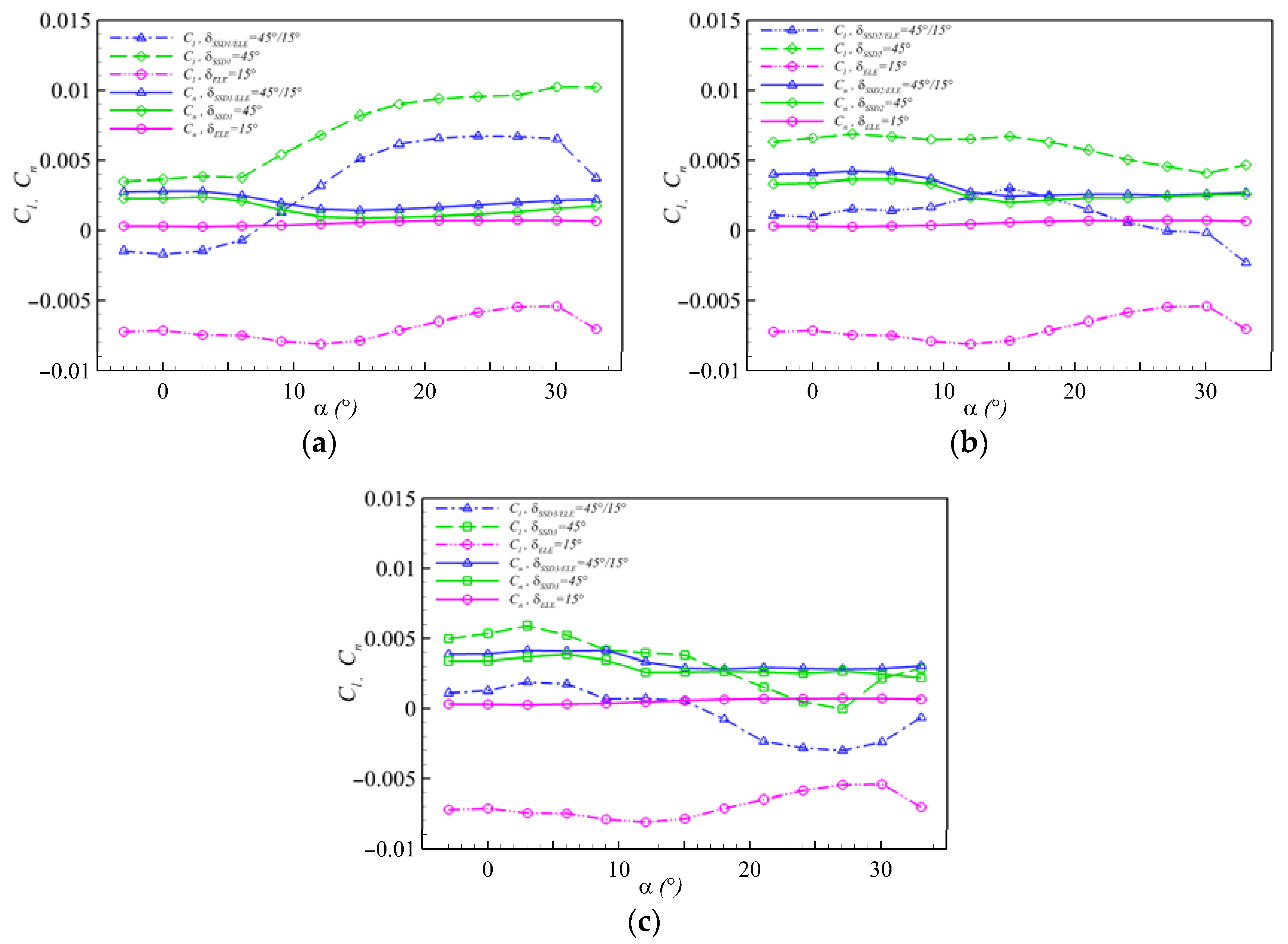
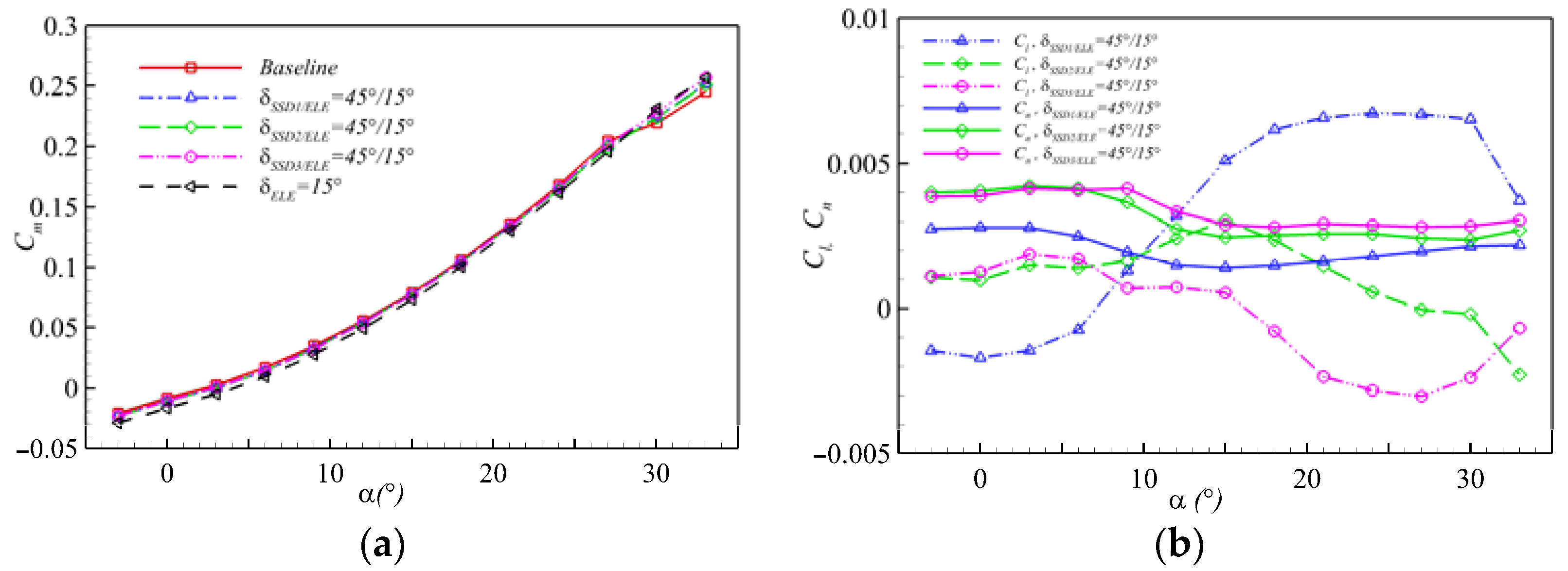
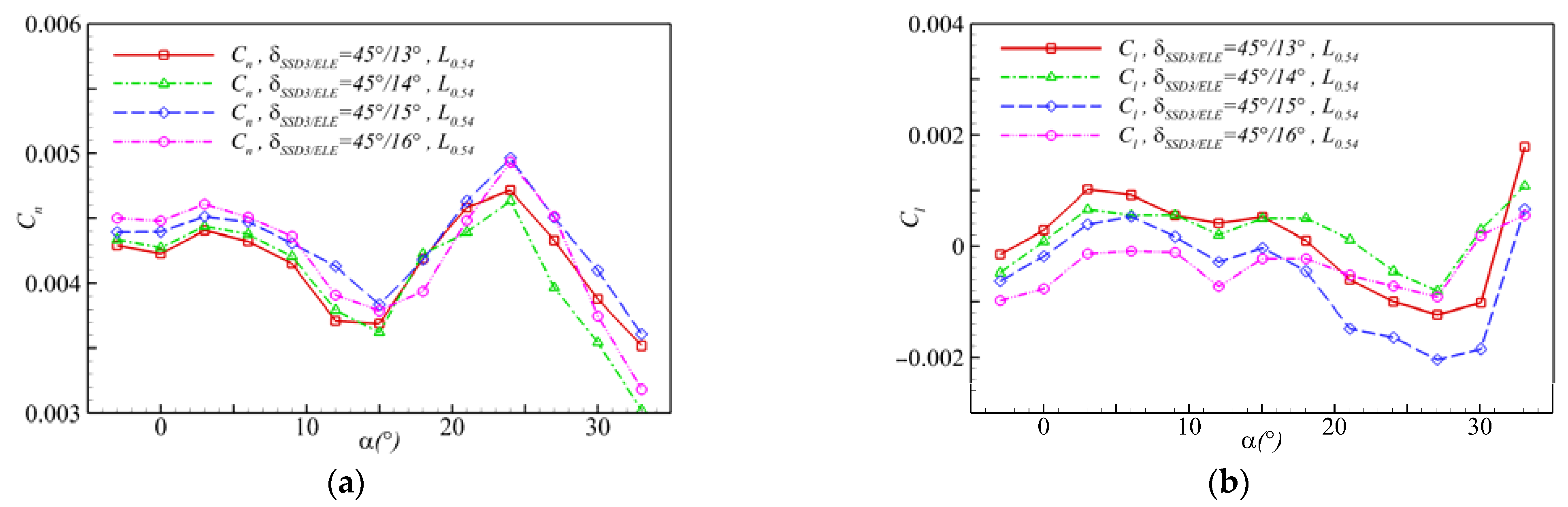
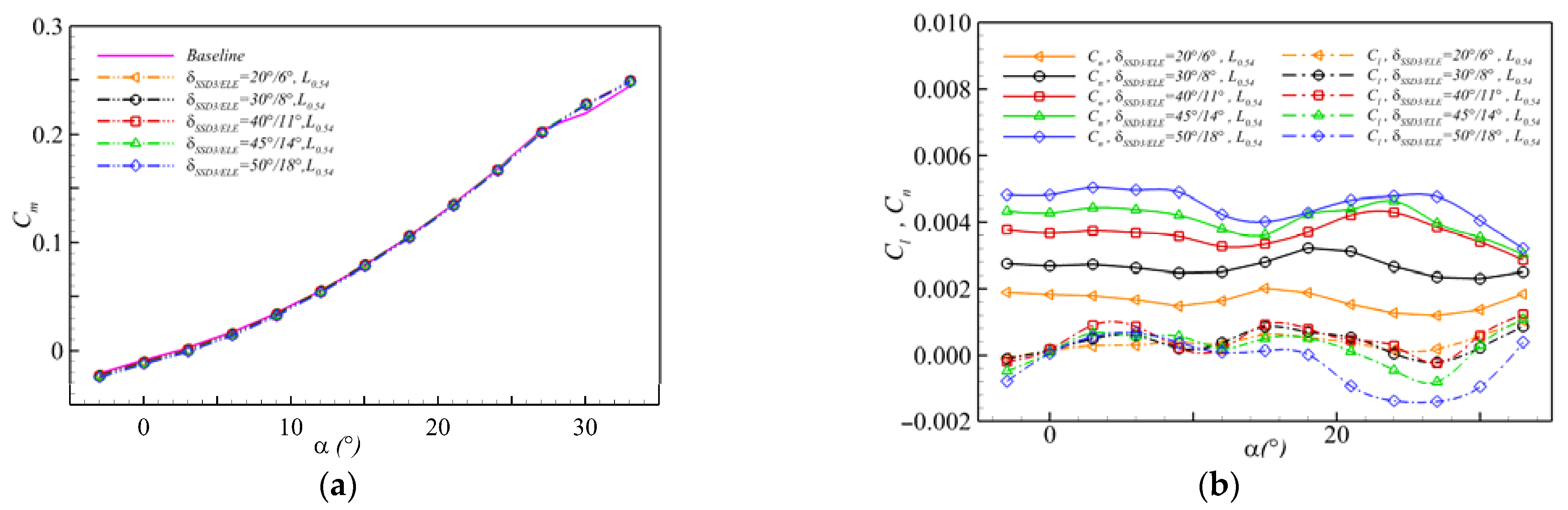
4.3. Effect of Collocating Deflection Angles of the FCR
4.4. Selection Principle of Key Parameters of FCR
5. Conclusions
- When adopting the elevon or SSD alone, it not only provides yawing but also couples the rolling and pitching moments. It requires the cooperation of other control surfaces to reduce or even eliminate coupled moments;
- For the configuration with a diamond-shaped wing, the SSD with an appropriate sweptback leading edge is more conducive to improving the directional control and providing more stable control than the SSD with the leading edge parallel to the trailing edge of the wing;
- In terms of the configuration studied herein, adjust collocating deflection angles of FCR reasonably, the directional stability of maneuvering flight state can be increased and the coupled rolling and pitching moments can be weakened or even be eliminated at small and medium angles of attack;
- The concept of FCR for the tailless configuration could provide a satisfactory yaw moment and weaken or even eliminate the coupling pitching and rolling moments. The FCR can improve the directional control and aerodynamic moment coupling issues by only one group of control surfaces, providing more options for the other side of the control surface to participate in other controls.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Küchemann, D. The Aerodynamic Design of Aircraft; AIAA: Reston, VA, USA, 2012; pp. 338–438. [Google Scholar]
- Raymer, D.P. Aircraft Design: A Conceptual Approach; AIAA: Washington, DC, USA, 1989; pp. 33–47. [Google Scholar]
- Sang, J.H. Low-Observable Technologies of Aircraft; Aviation Industry Press: Beijing, China, 2013; pp. 57–68. [Google Scholar]
- Fang, B.R. Aircraft Aerodynamic Configuration Design; Aviation Industry Press: Beijing, China, 1997; pp. 97–130. [Google Scholar]
- Bowlus, J.A.; Multhopp, D.; Banda, S.S. Challenges and opportunities in tailless aircraft stability and control. In Proceedings of the AIAA Guidance, Navigation and Control Conference, New Orleans, LA, USA, 11–13 August 1997. [Google Scholar] [CrossRef]
- Dorsett, K.M.; Mehl, D.R. Innovative Control Effectors (ICE); WPAFB: New Haven, CT, USA, 1996. [Google Scholar]
- Gillard, W.J. Innovative Control Effectors (Configuration 101) Dynamic Wind Tunnel Test Report; Air Force Research Laboratory, Wright-Patterson AFB: Dayton, OH, USA, 1998. [Google Scholar]
- Gillard, W.J.; Dorsett, K.M. Directional control for tailless aircraft using all moving wing tips. In Proceedings of the 22nd Atmospheric Flight Mechanics Conference, New Orleans, LA, USA, 11–13 August 1997. [Google Scholar] [CrossRef]
- Zuo, L.X.; Wang, J.J. Experimental study of the effect of AMT on aerodynamic performance of tailless flying wing aircraft. Acta Aerodyn. Sin. 2010, 28, 132–137. [Google Scholar]
- Ward, D.T.; Stout, L.J. Use of differential leading edge flaps for lateral control at high angle of attack. In Proceedings of the 24th Aerospace Sciences Meeting, Reno, NV, USA, 6–9 January 1986. [Google Scholar] [CrossRef]
- Li, Z.J.; Ma, D.L. Control Characteristics Analysis of Split-drag-rudder. Appl. Mech. Mater. 2014, 472, 185–190. [Google Scholar] [CrossRef]
- Smith, C.W.; Ralston, J.N.; Mann, H.W. Aerodynamic of Forebody and Nose Strakes Based on F-16 Wind Tunnel Test Experience; Langley Research Center: Fort Worth, TX, USA, 1979.
- Iwanski, K.P.; O’Rourke, M.J. F-15 forebody vortex flow control using jet nozzle blowing. J. Aircr. 1996, 33, 491–498. [Google Scholar] [CrossRef]
- Hunter, C.A.; Viken, S.A.; Wood, R.M.; Bauer, S.X.S. Advanced aerodynamic design of passive porosity control effectors. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001. [Google Scholar] [CrossRef] [Green Version]
- Stenfelt, G.; Ringertz, U. Lateral Stability and Control of a Tailless Aircraft Configuration. J. Aircr. 2009, 46, 2161–2163. [Google Scholar] [CrossRef]
- Zhou, Z.; Yu, Y.G.; Liu, G.; Chen, Z.B.; Heng, K.F. Comprehensive Study on yaw control characteristic of combined control surfaces of Flying wing configuration. Acta Aeronaut. Astronaut. Sin. 2020, 41, 523422. [Google Scholar] [CrossRef]
- Li, L.L.; Zhang, B.Q.; Li, P.F.; Zhang, M.H. Research on control technology of combined control surface for large tailless civil aircraft. Flight Dyn. 2013, 31, 450–454. [Google Scholar] [CrossRef]
- Zhang, B.Q.; Ma, Y.; Chu, H.B.; Chen, Z.L.; Chen, Y.C. Investigation on combined control surface for yaw control of low aspect ratio flying wing configuration. Acta Aeronaut. Astronaut. Sin. 2013, 34, 2435–2442. [Google Scholar] [CrossRef]
- Anderson, J.D. Fundamentals of Aerodynamics; McGraw-Hill Education: New York, NY, USA, 2005; pp. 19–26. [Google Scholar]
- ANSYS. ANSYS User Manual CFX-Solver Theory Guide; ANSYS Release 18.0; ANSYS, Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Rumsey, C.L.; Slotnick, J.P.; Long, M.; Stuever, R.A.; Wayman, T.R. Summary of the first AIAA CFD high lift prediction work shop. J. Aircr. 2011, 48, 2068–2079. [Google Scholar] [CrossRef]
- Rumsey, C.L.; Gatski, T.B.; Ying, S.X.; Bertelrud, A. Prediction of high-lift flows using turbulent closure models. AIAA J. 1998, 36, 765–774. [Google Scholar] [CrossRef] [Green Version]
- Sha, Z.P. Aircraft Design Manual Volume 4: Conceptual Design of Military Aircraft; Aviation Industry Press: Beijing, China, 2005; pp. 15–31. [Google Scholar]
- Eduardo, S.; Howard, S. Conceptual design of a fifth generation unmanned strike fighter. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef] [Green Version]






| Parameter | Value |
|---|---|
| Aspect ratio | 1.7 |
| Wingspan (m) | 12 |
| Total Length (m) | 18.9 |
| SSD Width We (m) | 1.6 |
| Elevon Width Ws (m) | 1.5 |
| Position Parameter Cx (m) | 1.1 |
| SSD Area (m2) | 1.33 |
| Elevon Area (m2) | 1.26 |
| Reference Area (m2) | 86 |
| Case | Moment | Value | γp or γr |
|---|---|---|---|
| δELE = 15° | Cn | 0.00032 | - |
| Cl | −0.00749 | 23.78 | |
| △Cm | −0.00761 | 23.40 | |
| δELE = 30° | Cn | 0.00120 | - |
| Cl | −0.01437 | 11.49 | |
| △Cm | −0.01463 | 12.19 |
| Case | Descriptions | ||
|---|---|---|---|
| Cn | Cl | γr | |
| SSD1 | α ≤ 3, increase slowly; 3° ≤ α ≤ 12°, decrease significantly; α ≥ 12°, increase slowly. | α ≤ 6, increase slowly; α ≥ 6, increase obviously. | >1. |
| SSD2 | Similar trendency with SSD1; Larger than Cn of SSD1. | α ≤ 12°, change slowly, α ≥ 12°, decrease obviously; α ≤ 9°, larger than Cl of SSD1, α ≥ 12°, less than Cl of SSD1. | >1. |
| SSD3 | Similar trendency with SSD1; α ≤ 9°, almost equivalent to Cn of SSD2, α ≥ 12°, Larger than Cn of SSD2. | α ≤ 3, increase slowly, α ≥ 3°, decrease obviously; less than Cl of SSD2. | A < 18°, >1; α ≥ 18°, <1. |
| Case | Moment | Value | γp or γr |
|---|---|---|---|
| δSSD1 = 45° | Cn | 0.00209 | - |
| Cl | 0.00378 | 1.80 | |
| △Cm | 0.00104 | 0.48 | |
| δSSD2 = 45° | Cn | 0.00364 | - |
| Cl | 0.00667 | 1.83 | |
| △Cm | 0.00130 | 0.36 | |
| δSSD3 = 45° | Cn | 0.00385 | - |
| Cl | 0.00524 | 1.36 | |
| △Cm | −0.00046 | 0.12 |
| Case | Cn | γp | γr |
|---|---|---|---|
| δELE = 15° | 0.00032 | 23.40 | 23.78 |
| δELE = 30° | 0.00120 | 12.19 | 11.49 |
| δSSD1 = 45° | 0.00209 | 0.48 | 1.80 |
| δSSD2 = 45° | 0.00364 | 0.36 | 1.83 |
| δSSD3 = 45° | 0.00385 | 0.12 | 1.36 |
| Case | Moment | Value | γp or γr |
|---|---|---|---|
| δSSD1/ELE = 45°/15° | Cn | 0.00249 | - |
| Cl | −0.00072 | 0.29 | |
| △Cm | −0.00228 | 0.92 | |
| δSSD2/ELE = 45°/15° | Cn | 0.00414 | - |
| Cl | 0.00139 | 0.70 | |
| △Cm | −0.00289 | 0.34 | |
| δSSD3/ELE = 45°/15° | Cn | 0.00408 | - |
| Cl | 0.00172 | 0.63 | |
| △Cm | −0.00254 | 0.42 |
| Case | Descriptions | |
|---|---|---|
| Cn | Cl | |
| SSD1/ELE | Similar trendency with SSD1 | α ≤ 6, reversed; α ≥ 6°, a nonlinear rise trendency (not conducive to turning control) |
| SSD2/ELE | Similar trendency with SSD1; higher than Cn of SSD1/ELE | α ≤ 9° or α ≥ 21°, small value, 9° ≤ α ≤ 21°, Cl ≥ Cn; |
| SSD3/ELE | α ≤ 9°, almost equivalent to Cn of SSD2/ELE, α ≥ 12°, Larger than Cn of SSD2/ELE. | A < 18°, small positive value |
| Case | γp | γr | ||
|---|---|---|---|---|
| Elevon | 11.00% | 14.49% | 23.40 | 23.78 |
| SSD | −9.01% | 27.85% | 0.12 | 1.36 |
| FCR | −1.53% | 38.60% | 0.42 | 0.63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Zhang, B. Investigation on a Flow Coupling Rudder for Directional Control of a Low-Aspect Tailless Configuration with Diamond-Shaped Wing. Aerospace 2022, 9, 79. https://doi.org/10.3390/aerospace9020079
Liu Z, Zhang B. Investigation on a Flow Coupling Rudder for Directional Control of a Low-Aspect Tailless Configuration with Diamond-Shaped Wing. Aerospace. 2022; 9(2):79. https://doi.org/10.3390/aerospace9020079
Chicago/Turabian StyleLiu, Zhongyuan, and Binqian Zhang. 2022. "Investigation on a Flow Coupling Rudder for Directional Control of a Low-Aspect Tailless Configuration with Diamond-Shaped Wing" Aerospace 9, no. 2: 79. https://doi.org/10.3390/aerospace9020079
APA StyleLiu, Z., & Zhang, B. (2022). Investigation on a Flow Coupling Rudder for Directional Control of a Low-Aspect Tailless Configuration with Diamond-Shaped Wing. Aerospace, 9(2), 79. https://doi.org/10.3390/aerospace9020079







