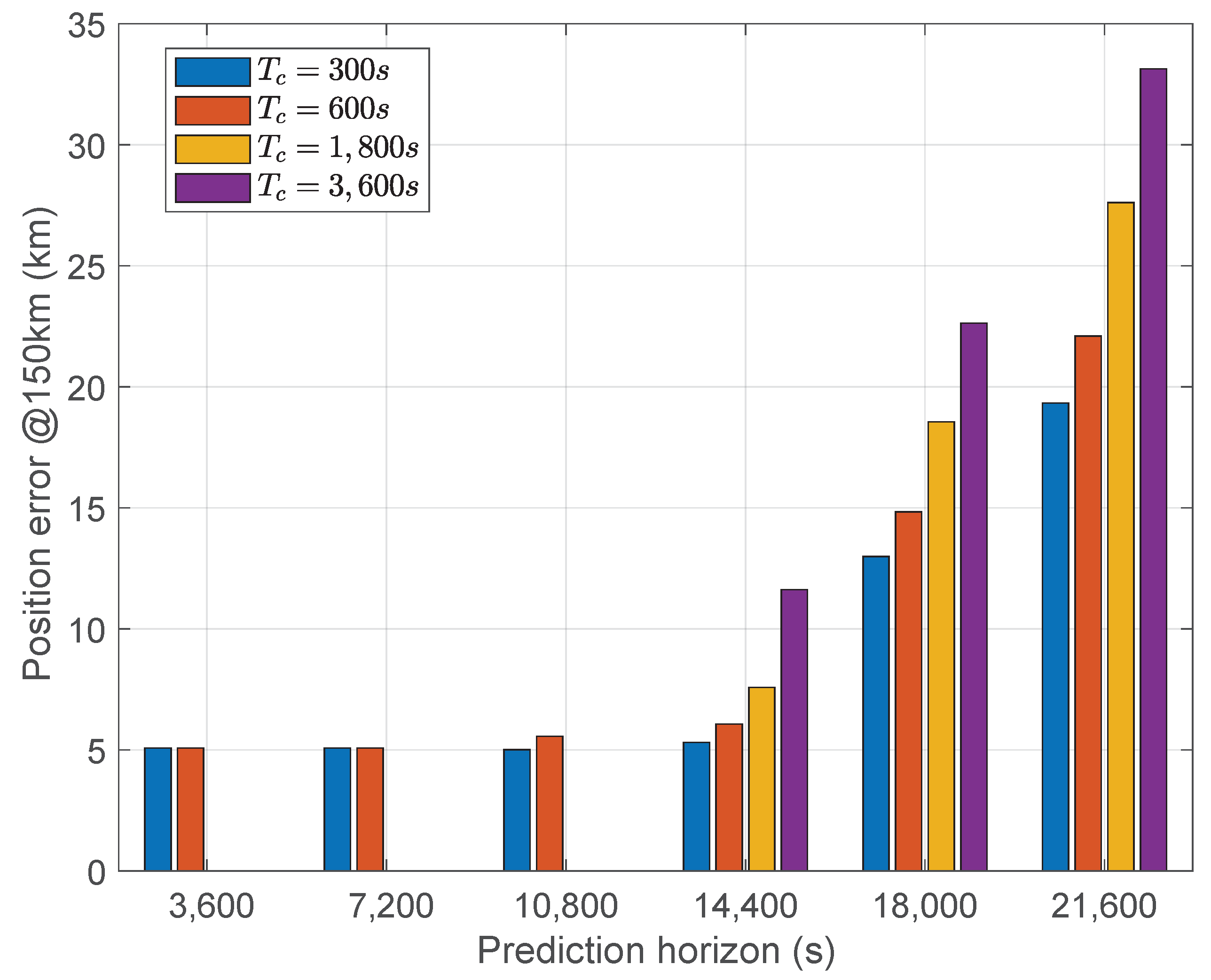Trajectory Planning and Tracking for a Re-Entry Capsule with a Deployable Aero-Brake

Abstract

In the last decade, the increasing use of NanoSats and CubeSats has made the re-entry capsule an emerging research field needing updates in configuration and technology. In particular, the door to advancements in terms of efficiency and re-usability has been opened by the introduction of inflatable and/or deployable aerodynamic brakes and the use of on-board electronics for active control. Such technologies allow smaller sizes at launch, controlled re-entries, and safe recovery. This paper deals with the design of a guidance and control algorithm for the re-entry of a capsule with a deployable aero-brake. A trajectory optimization model is used both in the mission planning phase to design the reference re-entry path and during the mission to update the trajectory in case of major deviations from the prescribed orbit, thanks to simplifications aimed at reducing the computational burden. Successively, a trajectory tracking controller, based on Nonlinear Model Predictive Control (NMPC), is able to modulate the opening of the aero-brake in order to follow the planned trajectory towards the target. A robustness analysis was carried out, via numerical simulations, to verify the reliability of the proposed controller in the presence of model uncertainties, orbital perturbations, and measurement noise.

1. Introduction

The reorientation of NASA’s priorities after shuttle retirement and the current increasing number of NanoSats and CubeSats have brought the re-entry vehicle technology back in the news. The decrease of size, mass, and power results in a reduction of the overall mission costs, increasing the accessibility to space [1]. However, despite the remarkable research and technology developments over time, re-entry capsules have been characterized by the same basic design concept. As a consequence of the miniaturization, more solutions are needed to offer the possibility to recover a payload and potential information for post-flight analyses coming from space [2,3].

Furthermore, several research projects have worked on the design of on-board electronics for small re-entry vehicles, increasing the efficiency and the re-usability, by enabling actively controlled re-entry and safe recovery [4].

To this purpose, inflatable and deployable aerodynamic brakes have been proposed and developed in the last few years. Umbrella-like or inflatable re-entry capsules are usually lighter and less expensive than conventional ones. They allow small sizes at launch and a sufficiently large surface area in re-entry. Thanks to their low ballistic coefficient, reducing the peak heat flux and the mechanical load, these kinds of capsule are usually based on commercial off-the-shelf (COTS) components and materials, minimizing development, building, and launching costs.

In the literature, several papers deal with inflatable or deployable aero-brake devices for capsule re-entry missions. Reference [5] introduced the concept of the parashield with application to a variety of capsules, including advanced manned spacecraft. In [6], the authors focused on the heat shield design, the flight dynamics, and the thermal loads in the re-entry mission of BREM-SAT 2, where the parashield resembles a reinforced umbrella, increasing the front area by a maximum factor of twelve. Reference [7] presented a drag device module, capable of de-orbiting a 15 kg CubeSat from a 700 km circular orbit in under 25 years. The geometry of such a drag device is also able to provide a three-axis attitude stabilization of the host CubeSat. Reference [8] focused on a flare-type membrane aeroshell sustained by an inflatable torus for an experimental vehicle of 15.6 kg. In [9], the authors analysed the aerodynamic longitudinal stability of a suborbital re-entry demonstrator in several conditions, in order to implement a proper re-entry strategy. Reference [10] showed the structural analysis and testing of the Inflatable Re-entry Vehicle Experiment (IRVE) [11] inflatable structure. In [12], the authors showed the design of a semi-rigid, deployable hypersonic decelerator system for heavy vehicles for manned missions on Mars. In this case, the architecture is similar to an umbrella, where the aerosurface is a flexible thin skin, used as thermal protection, which is draped over a structure of high-strength ribs.

Several challenges need to be addressed in guidance and control, due to the nonlinearity of the flight dynamics model, the constraints on the state and input variables, and the parametric uncertainties of the flight. Constraints about the heating rate and structural loads on the capsule can be considered in the optimal control problem as in [13]. Reference [14] considered flight time constraints and no-fly zones in the optimization problem, in order to propose an analytical solution for a formation of Hypersonic Glide Vehicles (HGVs). The guidance logic in [15] computes the bank reversals by evaluating information from the reference cross-range profile, current cross-range, and estimated actual lift-to-drag ratio; an noniterative numerical predictor, in the last phase of the trajectory, chooses whether a final bank reversal is needed to make null the heading error. In [16], the authors divided the re-entry mission into two phases and focused their attention on the second one, being the atmospheric re-entry, adding heating constraints to the trajectory optimization problem, where the design variable is the bank angle.

Optimal control methods were presented in [17,18]. More specifically, in [17], the author compared five different types of optimum guidance and control algorithms, while in [18], the Pontryagin principle was used to generate an autonomous slew trajectory, and its performance was compared with a sinusoidal approach, whereas in [19], the authors improved the previous trajectory planning algorithms, with autonomous collision avoidance schemes for the re-entry.

Indeed, the re-entry of a capsule is a critical phase of the mission, where model uncertainties and environment disturbances can strongly affect the landing point on the ground. Non-lifting vehicles go through a ballistic trajectory, where the only control ability is achieved by changing the drag coefficients, retracting or deployingthe aero-brake [20].

Usually, the re-entry phase is divided into two main phases: de-orbit at very high altitude and atmospheric entry. The former is a long stage in a low-density atmosphere, where the decaying trajectory planning is fundamental to find the right starting point, while the latter is the most critical stage for the structure, being stressed by very high thermal flows [8,21]. Therefore, in the atmospheric entry, the deployable aero-brake acts also as a thermal shield, resulting in reduced manoeuvring capabilities.

For all these reasons, trajectory tracking control becomes a challenging problem, and the uncertainties in air density and aerodynamic drag suggest the development of adaptive, parameter varying, or optimization-based closed-loop techniques aimed at minimizing the tracking error [22].

The actuated aero-brake has the ability to control the trajectory and eventually reaching a predetermined landing position by changing its shape, and consequently its wetted surface, during the descent flight [9,23,24]. Reference [25] presented a de-orbit and guidance scheme to control the trajectory of a vehicle with a passive drag-based system, defined as the Exo-brake. Reference [26] dealt with a method for drag-controlled re-entry, applying to a retractable drag de-orbit device that can be attached to CubeSats and larger satellite structures. In [27], the authors designed a simple Proportional–Integrative–Derivative (PID) controller for satellite formation keeping, modulating differential drag. The scope of [28] was to mitigate casualty risk due to an undesired re-entry, by modulating drag in the last orbit revolutions, with the objective of increasing the probability to impact in the Southern Hemisphere. Reference [29] proposed an algorithm that computes the drag profile needed to de-orbit in a desired location.

Unfortunately, although open-loop control techniques were used in successful missions, they cannot react to environmental unpredictable uncertainties, turning out to be often unreliable. The trajectory tracking performance can be strongly improved by means of a closed-loop control, in terms of both reliability and tracking error.

In the literature, several approaches can be found to address the problem. The most typical approach is based on PID trajectory tracking controllers [30] and the use of gain scheduling techniques, where the trajectory is computed in advance and controller parameters can change during the decay depending on the state of the capsule [31,32,33]. While [34] proposed a time-varying feedback controller, in [35,36,37], the re-entry strategy was based on fuzzy logic to track the drag reference profile. Gain scheduling was proposed also with optimal control techniques in [38,39,40].

Another approach to track the reference drag profile during the re-entry phase was proposed in [41] with a nonlinear PID control law able to guarantee, in the absence of control saturation, the global asymptotic stability. A sliding mode observer to estimate and track the variation of the drag coefficient was proposed in [42], while [43,44] was based on feedback linearization. The nonlinear dynamic inversion technique was used in [45,46].

In this paper, a unified approach to plan and control the re-entry mission of the capsule with a deployable aero-brake is proposed. This is based on an optimization strategy that covers both the off-line calculation of the optimal trajectory and the on-line possible path re-planning, taking into account the system dynamic response. The objective of the optimization is to find a (sub)optimal trajectory to reach a predefined target point at the Terminal Area Management (TAEM) fixed at an altitude around 30 km. The flight path must be compliant with the system dynamics and constraints, as well as the maximum admissible value of the heat flux, in order to guarantee a safe re-entry trajectory for the capsule.

While the off-line flight path planner relies on a Genetic Algorithm (GA) able to fully exploit the search domain, the on-line planner is based on a Sequential Quadratic Programming (SQP) algorithm to update the planned trajectory in case of deviation from the prescribed path computed off-line. SQP reduces the on-board computational burden and provides a sub-optimal solution in a finite and predictable time.

Once the re-entry has begun, the planned path is frozen and a Nonlinear-Model-Predictive-Control (NMPC)-based trajectory tracking algorithm modulates the aero-brake, to minimize the tracking error and reach the desired target position at a given altitude, ensuring the feasibility of the trajectory under suitable constraints [47,48].

The use of MPC is not new in the control of re-entry vehicles, and it was introduced in [49,50]. In [51], the authors presented preliminary results on an atmospheric re-entry MPC controller, which does not make use of any pre-computed nominal trajectory, focusing directly on the target point. The present paper extends the use of MPC to the whole descent phase, including de-orbiting and considering an adaptive objective function to be minimized, whose weights depend on the actual vehicle state.

To demonstrate the effectiveness of the proposed strategy, a campaign of numerical simulations was executed making a sensitivity analysis on the main parameters of the control system and, so, guiding the designer to their optimal selection for balancing performance and computational burden.

Once the parameters were chosen, an extensive robustness analysis was carried out in the presence of model uncertainties, orbital perturbations, and measurement noises, to test further the capabilities of the proposed control scheme.

The paper is structured as follows: Section 2 deals with the problem statement, with details about the mission and the model; in Section 3, the proposed guidance system is described, with details the path planning procedure, the NMPC-based control scheme, and the adaptive strategy in the different phases of the re-entry; Section 4 resumes results about the path planning, sensitivity, and robustness analysis to prove the effectiveness of the proposed controller.

2. Mathematical Model

The satellite configuration consists of a detachable capsule and a service module, containing every subsystem needed during the in-orbit operations. The main feature of the capsule is an umbrella-like front structure, which can be used both as an aero-braking device and as a thermal shield.

Such a design allows at the same time slowing down the satellite and protecting the capsule from the extremely high temperatures reached during the atmospheric entry.

The re-entry mission is made-up of four main phases:

• De-orbiting: At an altitude $H_1=300\mathrm{km}$, the satellite leaves its nominal orbit and begins the slow decay towards the Earth’s surface, modulating the aero-brake in order to control the trajectory of the satellite.
• Atmospheric approach: When the altitude $H_2=150\mathrm{km}$ is reached, the service module releases the capsule, which, after the separation, approaches the atmospheric entry through a ballistic trajectory, controlled by the modulation of the deployable front structure.
• Atmospheric entry: At the height $H_3=100\mathrm{km}$, the capsule enters the atmosphere and follows a purely ballistic path until the Terminal Area Energy Management (TAEM) interface at $H_4=30\mathrm{km}$.
• Terminal area phase: In this phase, the capsule follows an uncontrolled vertical descent path until $H_5=10\mathrm{km}$, when the parachute is deployed.

In the whole mission, mainly two kinds of forces act on the capsule: gravity and aerodynamics.

Usually, the gravity acceleration between Earth and the satellite is considered as the gradient (∇ operator) of the gravitational potential W [52]:

$${\mathit{a}}_g=\mathsf{\nabla }W$$

(1)

Let G be the universal gravitational constant and ${\mathcal{V}}_{\oplus }$ and ${\sigma }_{\oplus }$ the Earth’s volume and mass density, respectively. In the Earth-Centred Inertial (ECI) reference frame, the sum of the contributions of each element of the Earth’s mass $d{M}_{\oplus }$ is the gravitational potential:

$$W\left({\mathit{R}}_{ECI}\right)=-G{\int }_{{\mathcal{V}}_{\oplus }}\frac{{\sigma }_{\oplus }}{∥{\mathit{R}}_{ECI}-{\mathit{R}}_{\mathit{c}}∥}d\mathcal{V}$$

(2)

where the symbol $∥·∥$ is the Euclidean norm, ${\mathit{R}}_c$ is the position vector of the individual mass elements $d{M}_{\oplus }={\sigma }_{\oplus }d\mathcal{V}$ from the centre of the reference system, and ${\mathit{R}}_{ECI}={[X_{ECI},Y_{ECI},Z_{ECI}]}^T$ is the position vector of the satellite in the ECI frame.

Consider a spherical coordinate system $(r,\varphi ,\lambda )$ such that:

$$\begin{array}{c}{X}_{ECI}=rcos\left(\lambda \right)cos\left(\varphi \right)\\ Y_{ECI}=rsin\left(\lambda \right)cos\left(\varphi \right)\\ Z_{ECI}=rsin\left(\varphi \right)\end{array}$$

(3)

where $r=\parallel {\mathit{R}}_{ECI}\parallel$ is the distance of the capsule from the Earth’s centre, $\lambda$ (assumed positive towards the east) represents the longitude, and $\varphi$ is the geocentric latitude.

In empty space ($r>\parallel {\mathit{R}}_c\parallel )$, the gravity potential satisfies the Laplace equation; consequently, it can be expressed as an expansion in series of spherical harmonics:

$$W(r,\varphi ,\lambda )=\frac{G{M}_{\oplus }}{R_{\oplus }}\sum _{l=0}^{\infty }\sum _{m=0}^l\frac{R_{\oplus }^l}{r^l}{P}_{lm}\left[C_{lm}cos\left(m\lambda \right)+S_{lm}sin\left(m\lambda \right)\right]$$

(4)

where $R_{\oplus }$ is the Earth’s equatorial radius. $P_{lm}=$$P_{lm}\left(sin\varphi \right)$ are the associated Legendre functions of degree l and order m, and $C_{lm}$ and $S_{lm}$ are the Stokes coefficients [52] describing the dependence of gravity potential on the Earth’s shape.

Geopotential coefficients with $l=0$ are called zonal coefficients, since they describe the part of the potential that does not depend on the longitude. In this case, the coefficients $S_{l0}$ are equal to zero and the coefficients $C_{l0}$ are denoted as $-J_l$.

Sectoral coefficients are obtained with $m=l$. They describe the part of the gravity potential that depends only on the longitude.

$C_{lm}$ and $S_{lm}$ with $m\ne l$ are called tesseral coefficients and describe the part of the gravity potential that depends both on the longitude and latitude.

Equation (4) can be efficiently approximated by considering only the first four zonal coefficients:

$$W(r,\varphi ,\lambda )=-\frac{\mu }{∥{\mathit{R}}_{ECI}∥}+\frac{\mu }{R_{\oplus }}\sum _{l=1}^4\frac{J_l}{r^{l+1}}$$

(5)

with $\mu =G{M}_{\oplus }$. In (5), the dominating term related to the first zonal coefficient $J_1$ was extracted from the summation.

Considering the transformation from polar coordinates to ECI Cartesian coordinates and using (5), the gravity acceleration in the ECI frame can be approximated as follows:

$$\mathit{a}\left({\mathit{R}}_{ECI}\right)=-\mu \frac{{\mathit{R}}_{ECI}}{{∥{\mathit{R}}_{ECI}∥}^3}+{\mathit{a}}_{J_2}\left({\mathit{R}}_{ECI}\right)+{\mathit{a}}_{J_3}\left({\mathit{R}}_{ECI}\right)+{\mathit{a}}_{J_4}\left({\mathit{R}}_{ECI}\right)$$

(6)

where ${\mathit{a}}_{J_2}\left({\mathit{R}}_{\mathrm{ECI}}\right)$, ${\mathit{a}}_{J_3}\left({\mathit{R}}_{\mathrm{ECI}}\right)$, and ${\mathit{a}}_{J_4}\left({\mathit{R}}_{\mathrm{ECI}}\right)$ are the perturbation accelerations related to zonal harmonics $J_2$, $J_3$, and $J_4$.

The terms ${\mathit{a}}_{J_2}$, ${\mathit{a}}_{J_3}$, and ${\mathit{a}}_{J_4}$, as well as the other ones related to neglected zonal, tesseral, and sectoral coefficients are due to Earth’s shape: the oblateness causes an asymmetry of the gravitational field, which results in a variety of perturbations in the satellite orbit, affecting satellites at low altitudes more.

The atmospheric drag represents the largest non-gravitational perturbations acting on low-altitude satellites. The lift contribution of a blunt body is negligible, whereas the aerodynamic drag plays a significant role more so in the atmospheric entry, due to the presence of the Earth’s atmosphere. The drag force can be written as:

$$\mathit{D}=-\frac{1}{2}\rho \left(H\right)∥\mathit{V}∥\mathit{V}{C}_{D}S$$

(7)

where:

• $\rho$ is the air density, depending by the altitude H;
• $\mathit{V}={\mathit{V}}_{\mathrm{ECI}}-{\mathsf{\Omega }}_{\oplus }\times {\mathit{R}}_{\mathrm{ECI}}$ represents the Earth-relative speed of the satellite;
• ${\mathsf{\Omega }}_{\oplus }$ is the Earth rotational speed;
• ${\mathit{V}}_{\mathrm{ECI}}={\left[V_{X_{\mathrm{ECI}}},V_{Y_{\mathrm{ECI}}},V_{Z_{\mathrm{ECI}}}\right]}^T$ is the satellite velocity vector in the ECI reference frame;
• $C_D$ is the drag coefficient;
• S is the surface of the deployable aero-brake.

The drag coefficient $C_D$ describes the interaction of the atmospheric constituents with the satellite surface. More specifically, it depends on the satellite surface material, the chemical constituents of the atmosphere and the molecular weight and temperature of the impinging particles. In the free molecular flow regime, characterized by a Knudsen number greater than 1 ($Kn>1$), the particles re-emitted from the satellite do not interfere with the incident molecules. At lower altitudes, with $Kn<0.1$, the re-emitted molecules partially shield the satellite from the incident flow. This phenomena causes a drag decrease [52,53].

The model of the Earth’s atmosphere is not simple, and an accurate description would require many parameters.

The largest source of uncertainties in the evaluation of the atmospheric density at the highest altitudes is related to the solar activity. The Sun always emits a different amount of energy, changing the portion of energy penetrating and heating the atmosphere. The effect is a continuous change in density, extremely hard to predict, Solar activity being an almost unpredictable phenomenon.

In this paper, the USA Standard Atmosphere model was assumed [54]:

$$\rho ={\rho }_{0}exp\left(-\frac{H-H_0}{SH}\right)$$

(8)

where $\rho$ is the air density at any altitude above sea level H, ${\rho }_0$ is the air density at some specified reference altitude $H_0$, and $SH$ is the atmospheric scale height at $H_0$.

In the exponential model, the solar activity is approximately taken into account through the atmospheric scale height. In fact, the atmosphere can been divided into 28 sections, from 0 up to 1000 km, each having its adequate scale height [23].

Assuming an Earth-Centred Inertial (ECI) frame, the nonlinear motion equations are defined as follows:

$$\left\{\begin{array}{c}{\dot{\mathit{R}}}_{\mathrm{ECI}}\left(t\right)={\mathit{V}}_{\mathrm{ECI}}\left(t\right)\hfill \\ {\dot{\mathit{V}}}_{\mathrm{ECI}}\left(t\right)=-\mu \frac{{\mathit{R}}_{\mathrm{ECI}}\left(t\right)}{{\left|{\mathit{R}}_{\mathrm{ECI}}\left(t\right)\right|}^3}-\frac{1}{2}\rho \frac{C_{D}S}{M}∥\mathit{V}\left(t\right)∥\mathit{V}\left(t\right)+{\mathit{a}}_{J_2}\left(t\right)+{\mathit{a}}_{J_3}\left(t\right)+{\mathit{a}}_{J_4}\left(t\right)\hfill \end{array}\right.$$

(9)

where M is the satellite mass.

Equation (9) creates a relationship between the ballistic coefficient $C_b=\frac{M}{C_{D}S}$ and the velocity vector of the satellite; consequently, the control of the trajectory can then be achieved through the modulation of the aero-brake surface.

The aero-brake has also the role of a thermal shield in the hottest phase of re-entry.

Chapman’s and Sutton–Grave’s simplified methods allow computing the heating rate experienced by a re-entry vehicle [55]:

$$\dot{q}=K\left|\right|V_{ECI}{\left|\right|}^3\sqrt{\frac{\rho }{l_{\mathrm{nose}}}}$$

(10)

where K is a suitable constant, $\left|\right|V_{ECI}\left|\right|$ is the vehicle speed, and $l_{nose}$ is the capsule nose radius, which measures the “bluntness” of capsule’s shape.

The altitude where the maximum heating rate is reached can be found using the following relation [55]:

$$H_{{\dot{q}}_{max}}=\frac{1}{SH}ln\left(\frac{{\rho }_0}{3C_{b}sin\gamma SH}\right)$$

(11)

where $\gamma$ is the flight-path angle and $C_b=\frac{M}{C_{d}S}$ is the ballistic coefficient of the capsule.

3. Guidance System Design

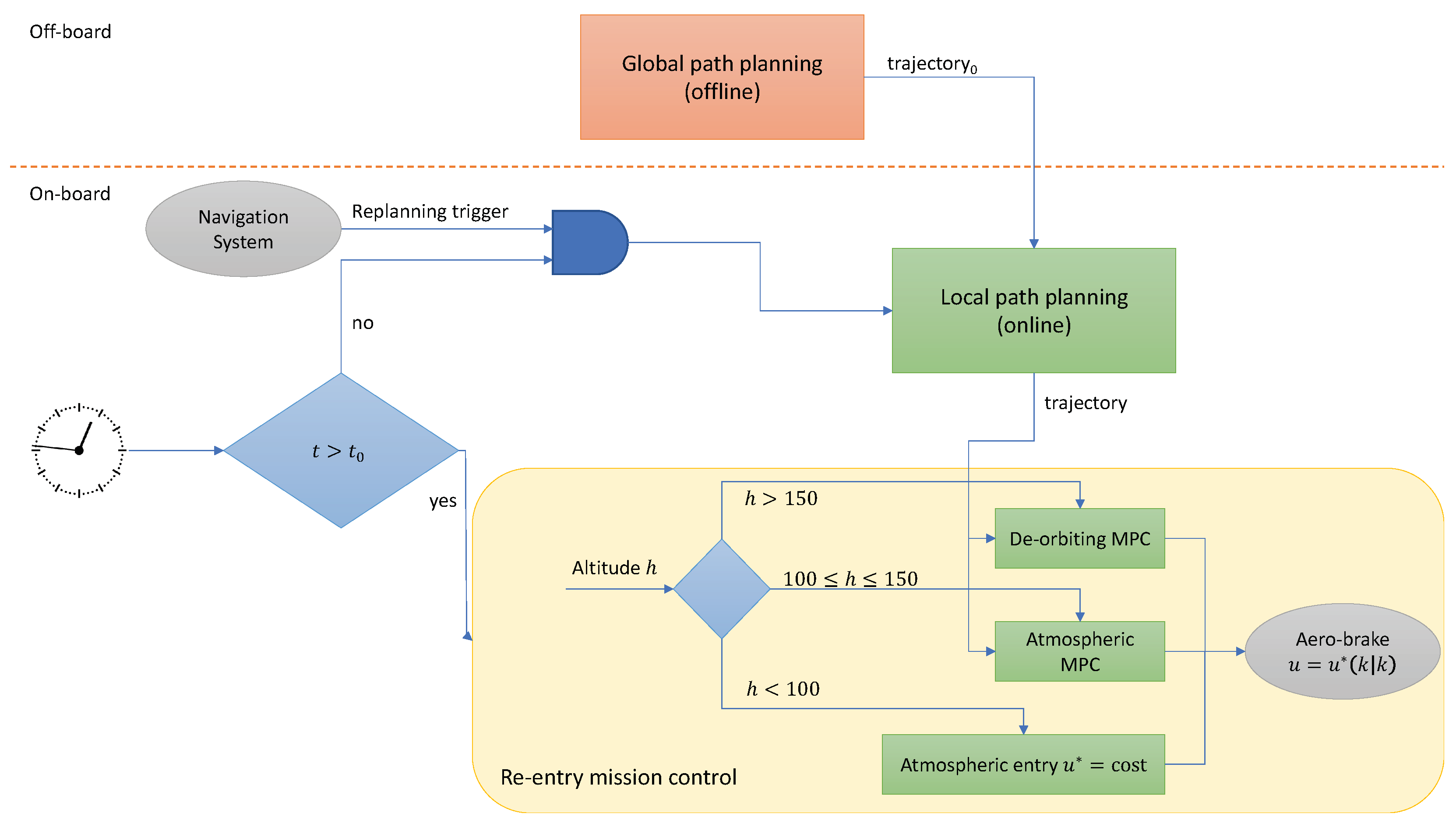
The scheme of the proposed guidance and control algorithm is shown in Figure 1, with the off-board and on-board parts. Before the whole mission, a path planning block is able to compute the optimal trajectory for the overall descent path. During the mission, before the de-orbiting phase, such a trajectory can be updated in order to take into account possible deviations from the prescribed orbital parameters by sending a replanning trigger to the local path planning subsystem. Once the re-entry has begun, the trajectory is considered frozen and the re-entry mission control block becomes active. Two MPC-based trajectory tracking algorithms are considered, with different optimization parameters fitting the model to the specific de-orbiting and atmospheric entry phases.

3.1. Path Planning

The goal of the path planning algorithm is to minimize the final position error with respect to a predefined target, by finding the optimal values of the control signal, i.e., the values assumed by the aero-brake surface along the trajectory, and the de-orbit point, i.e., the satellite on-orbit initial position, identified by the true anomaly.

The control signal, $S\left(t\right)$, is assumed piecewise constant to avoid damages of the aero-brake actuation system caused by overloads due to consecutive openings and closures.

Given $N_h$ time ranges during the re-entry, the design variable vector can be defined as follows:

$${\mathit{\zeta }}_{opt}={[\nu ,S_0,t_1,S_1,t_2,S_2,\cdots ,t_{N_h-3},S_{N_h-3},S_{N_h-2},S_{N_h-1}]}^T$$

(12)

where:

• $\nu$ is the true anomaly of satellite when the descent phase starts;
• $S_i$ with $i\in 1,2,\dots ,N_h-3$ is the aero-brake surface to be required by the control system in the time range $[t_i,t_{i+1}]$;
• $S_0,S_{N_h-2}$ and $S_{N_h-1}$ are the aero-brake surfaces at 300, 150, and 100 km.

The choice of relating the last two aero-brake surface values to the altitude in the atmospheric entry depends on the strong change in the drag coefficient and mass after the capsule leaves the hub.

The guidance algorithm is based on the following optimization problem:

$$\underset{{\mathit{\zeta }}_{opt}}{min}F\left({\mathit{\zeta }}_{opt}\right)$$

(13)

subject to:

$$\begin{array}{c}0\le \nu \le 2\pi \\ S_i\in \mathcal{S}\forall i=0,\cdots ,N_h-1\\ 0<t_1<t_2<\cdots <t_{N_h-3}<t_{max}\\ t_i-t_{i-1}>3\mathbb{P}\forall i=2,\cdots ,N_h-3\end{array}$$

(14)

with the orbital period $\mathbb{P}$ and a maximum descent time $t_{max}$, evaluated by Cowell’s method [56]. It is worth noting that, in order to avoid unrealistic values of the aero-brake surface, the constraint $S_i\in \mathcal{S}$ takes into account the mechanical limits and the quantization of the actuation system. Practically, such a set $\mathcal{S}$ is defined by loading a table containing all the values of the aero-brake surface actually achievable.

The objective function F to be minimized is:

$$\begin{array}{cc}\hfill F\left({\mathit{\zeta }}_{opt}\right)& \hfill ={\left({\overline{\mathit{R}}}_{ECEF}^{*}-{\mathit{R}}_{ECEF}^{*}\right)}^T{\mathit{Q}}_r\left({\overline{\mathit{R}}}_{ECEF}^{*}-{\mathit{R}}_{ECEF}^{*}\right)\hfill \\ \hfill & \hfill +{\left({\dot{\overline{q}}}_{max}-{\dot{q}}_{max}\right)}^T{Q}_q\left({\dot{\overline{q}}}_{max}-{\dot{q}}_{max}\right)\hfill \end{array}$$

(15)

where:

• ${\overline{\mathit{R}}}_{ECEF}^{*}$ is the desired position vector in the ECEF reference frame at the altitude $H^{*}=30\mathrm{km}$;
• ${\mathit{R}}_{ECEF}^{*}$ is the effective position in the ECEF reference frame at the altitude $H^{*}=30\mathrm{km}$;
• ${\dot{q}}_{max}$ is the value of the heat flux peak along the trajectory;
• ${\dot{\overline{q}}}_{max}$ is the maximum admissible value of the heat flux peak, assumed as 600 $\frac{\mathrm{kW}}{{\mathrm{m}}^2}$;
• ${\mathit{Q}}_r$ is a suitable definite positive weights matrix and $Q_q$ is a positive scalar.

The objective function essentially is the sum of two contributions. The former is the position error with respect to the target point at altitude $H^{*}=30\mathrm{km}$; the latter is a term assessing the difference between the heat flux peak reached along the trajectory and its maximum allowable value.

The defined optimization model is strongly nonlinear due to the capsule dynamics. However, the off-line path planning phase can trust on ground-based equipment, so, to achieve a global search of the optimum, a Genetic Algorithm (GA) procedure was implemented, with the integration of Equation (9) with a fixed step size solver to compute the objective function and solve the optimization problem (13).

The on-board guidance and control system is provided with a local path planning block to update the trajectory whenever the navigation system estimates a deviation from the prescribed mission orbital parameters, before the de-orbiting phase begins. In this case, a SQP-based nonlinear local search [57] is carried out, starting from the reference trajectory, leading to a new sub-optimal solution.

3.2. MPC-Based Trajectory Tracking

The goal of the control system is to minimize the tracking error of the reference trajectory, provided by the guidance system, for the whole descent phase. On the other hand, the control system must guarantee an error at the target landing point less than 250 km. Considering that the capsule follows a quasi-vertical path below the target altitude $H=30\mathrm{km}$, the requirement can be converted into a maximum admissible position error at the TAEM interface less than 200 km.

In the hottest phase, in order to mitigate the thermal stress on the capsule, the aero-brake surface is kept fixed equal to the reference value ${\overline{S}}_5=0.770{\mathrm{m}}^2$. Consequently, the optimal control law can only be calculated until the altitude $H=100\mathrm{km}$.

To achieve the above-defined goal, taking into account the control signals’ bounds, a Model Predictive Control (MPC) strategy is proposed. Following the MPC approach, the control law is computed by minimizing a given cost function, which weights the difference between the predicted state trajectory and the reference one. According to the Receding Horizon paradigm, only the first move of the discrete sequence is applied to the controlled system.

The predicted state trajectory is computed by using a discrete-time state space model by discretizing Equation (9) with a suitable sample time $T_c$.

Let k be the actual discrete time step, with $\mathit{x}\left(k\right)={\left[{\mathit{R}}_{ECI}^T\left(k\right),{\mathit{V}}_{ECI}^T\left(k\right)\right]}^T$ the state vector composed by the satellite position and velocity in ECI frame, and let $u\left(k\right)=S\left(k\right)$ be the control input equal to the aero-brake surface.

Consider a time window of amplitude ${\mathbb{T}}_p$ composed by $N_p$ steps. By using the mathematical model, it is possible to predict the future behaviour of the system. At each tome step k, the predicted state $\mathit{x}(k+i|k)$ ($i=1,\dots ,N_p$) depends on the control sequence $\mathit{U}\left(k\right)={[\mathit{u}\left(k|k\right),\dots ,\mathit{u}\left(k+N_p-1|k\right)]}^T$, which must be optimized, and by the initial state $\mathit{x}\left(k\right)$, which is measured or, at least, estimated. In order to reduce the computation burden, only $N_c$ (with $N_c\le N_p$) control moves are optimized by assuming that the last $N_p-N_c$ control moves are constant $\mathit{u}\left(k+i|k\right)=u(k+N_c-1|k)$ $\left(i=N_c,N_c+1,\dots ,N_p-1\right)$.

The cost function to be optimized is:

$$\begin{array}{cc}\hfill J\left(\mathit{x}\left(k\right|k),\mathit{U}(k),k\right)& =\sum _{i=0}^{N_p\left(k\right)-1}p\left(i\right){∥{\overline{\mathit{R}}}_{ECI}\left(k+i+1\right)-{\mathit{R}}_{ECI}\left(k+i+1|k\right)∥}^2+\hfill \\ \hfill & +q\left(i\right){∥{\overline{\mathit{V}}}_{ECI}\left(k+i+1\right)-{\mathit{V}}_{ECI}\left(k+i+1|k\right)∥}^2+\hfill \\ \hfill & +w\left(i\right){∥\overline{S}\left(k+i\right)-S\left(k+i|k\right)∥}^2\hfill \end{array}$$

(16)

where ${\mathit{R}}_{ECI}\left(k+i|k\right)$ and ${\mathit{V}}_{ECI}\left(k+i|k\right)$ are the predicted position and velocity vector, respectively, ${\overline{\mathit{R}}}_{ECI}\left(k+i\right)$ and ${\overline{\mathit{V}}}_{ECI}\left(k+i\right)$ are the reference position and velocity vectors, $\overline{S}\left(k+i\right)$ is the reference surface of the aero-brake, and $S\left(k+i|k\right)$ represents the predicted value of the control variable. The objective function is then composed of three parts, weighted by the scalar values $p\left(i\right)$, $q\left(i\right)$, and $w\left(i\right)$: the first two terms weight the error between the reference position and speed vectors and the predicted ones; the last term attempts to minimize the difference between the control variable and the reference one.

The optimal control law ${\mathit{U}}^{*}\left(k\right)$ is calculated by solving the following problem:

$${\mathit{U}}^{*}\left(k\right)=\mathrm{argmin}J\left(x\left(k|k\right),\mathit{U}\left(k\right),k\right)$$

(17)

subject to

$$\begin{array}{c}\hfill \mathit{\eta }\left(\mathit{x}\left(k+i|k\right),u\left(k+i|k\right)\right)\le 0\forall i=0,1,\dots ,N_p-1\end{array}$$

(18)

$$\begin{array}{c}\hfill \begin{array}{c}\mathit{x}\left(k+i+1|k\right)=\mathit{f}\left(\mathit{x}\left(k+i|k\right),\mathit{u}\left(k+i|k\right)\right)\forall i=0,\dots ,N_p-1\\ \mathit{x}\left(k|k\right)=\mathit{x}\left(k\right)\end{array}\end{array}$$

(19)

where $\mathit{x}\left(k\right)$ is the current measured state at discrete time k. Equation (19) takes into account the discrete-time implicit state space model defined by a suitable discretization of (9). Inequality constraints described by (18) allow taking into account the bounds of control signal and can be rewritten as follows:

$$S_{min}\le u\left(k+i|k\right)\le S_{max}\forall i=0,1,\dots ,N_p-1$$

(20)

Given the optimal control sequence, according to the Receding Horizon technique, only the first move $u^{*}\left(k\right|k)$ is applied. The reason is that the remaining sequence $u^{*}\left(k+i|k\right)$ (with $i=1,\dots ,N_c-1$), though based on a prediction of the system behaviour, is an open-loop control law, affected by disturbances and uncertainties.

At the next time step $k+1$, on the basis of a new current state measurement, new predictions and optimization can be performed. Hence, the optimization process can be iterated.

In order to minimize the computational burden and ensure the existence of a solution in a reasonable time, due to the nonlinear nature of the plant model, it is assumed that the control horizon is made up by a single time step $\left(N_c=1\right)$ so that, at each step, a single control move is optimized. In this case, the MPC problem can be numerically solved with the golden section method, which guarantees the convergence of the solution to a local minimum. The maximum number of iterations needed to achieve the solution can be evaluated on the basis of the requested resolution of the optimal control variable, which is related to the quantization of the deployable umbrella control command $\alpha$ [58].

In the proposed guidance and control scheme, two MPC-based trajectory tracking algorithms are considered, based on the same model, but using different weights for the objective function definition, in order to better suit the specific re-entry phases.

In particular, in the former phase, the controller objective is to minimize the error over a finite limited prediction horizon, in order to follow the planned path. During this long phase, the sampling frequency is low (<10${}^{-3}$ Hz) to minimize the computational burden. Under the altitude of 150 km, during the atmospheric approach, the sampling rate of the MPC-based controller must be increased to be effective (>10${}^{-2}$ Hz), and the objective of the optimization is the error in terms of position and velocity at TAEM. A shorter prediction horizon would make the control signal too sensitive to model uncertainties and atmospheric perturbations, resulting in a strong deviation from the trajectory and leading to an increase in the target error.

4. Results

4.1. Path Planning

In this section, the results of the path planning phase are shown. A number $N_h=5$ of altitude ranges was chosen, to reduce the computational burden, providing a good sub-optimal solution.

The orbital parameters used in the optimization are resumed in

Table 1. Orbital parameters.

Description	Value
Semimajor axis	6678 km
Eccentricity	0
Inclination	51.6 deg
RAAN	32.57 deg
Argument of perigee	0 deg

.

As a result, the guidance algorithm provides five constant values of the optimal aero-brake surface $S_i$ for the entire re-entry path, as described in

Table 2. Aero-brake surface deployment schedule along the re-entry path.

Aero-Brake Surface	Times/Range
$S_0$	1,328,400 s
$S_1$	2,301,310 s
$S_2$	2,314,950 s
$S_3$	150 km $\le h$ < 100 km
$S_4$	100 km $\le h$ < 30 km

.

In Figure 2, the trajectory provided by the guidance system is shown in terms of altitude variation during time. The target is located at an altitude of $30\mathrm{km}$, and its geographic position is above the Great Victoria Desert, Australia.

The main stage is the de-orbiting, whose length is 26 days, 19 h, 2 min, and 30 s. The atmospheric approach, together with the atmospheric entry phase, represents just a small piece of the entire path: the former takes 1 h, 12 min, and 19 s to go from 150 km to the altitude of 100 km; the latter takes just 6 min and 11 s to cover the last 70 km of the remaining height.

It is worth noting that the de-orbiting phase is characterized by oscillations (Figure 2), which are due to the perturbative phenomena caused by the asymmetry of the Earth’s gravity potential: indeed, the satellite, while descending towards the Earth’s surface, follows an orbit whose semimajor axis gradually reduces, and this results in a slightly elliptical spiral trajectory in which the position vector is no longer constant. As a matter of fact, the period of the single oscillation is comparable to the nominal orbital period ($\mathbb{P}=5431$ s).

The last portion of the trajectory, below 150 km, appears to be quasi-vertical, but a closer look (Figure 2) shows the typical ballistic re-entry path. At these heights, limiting thermal loads on the structure is of paramount importance.

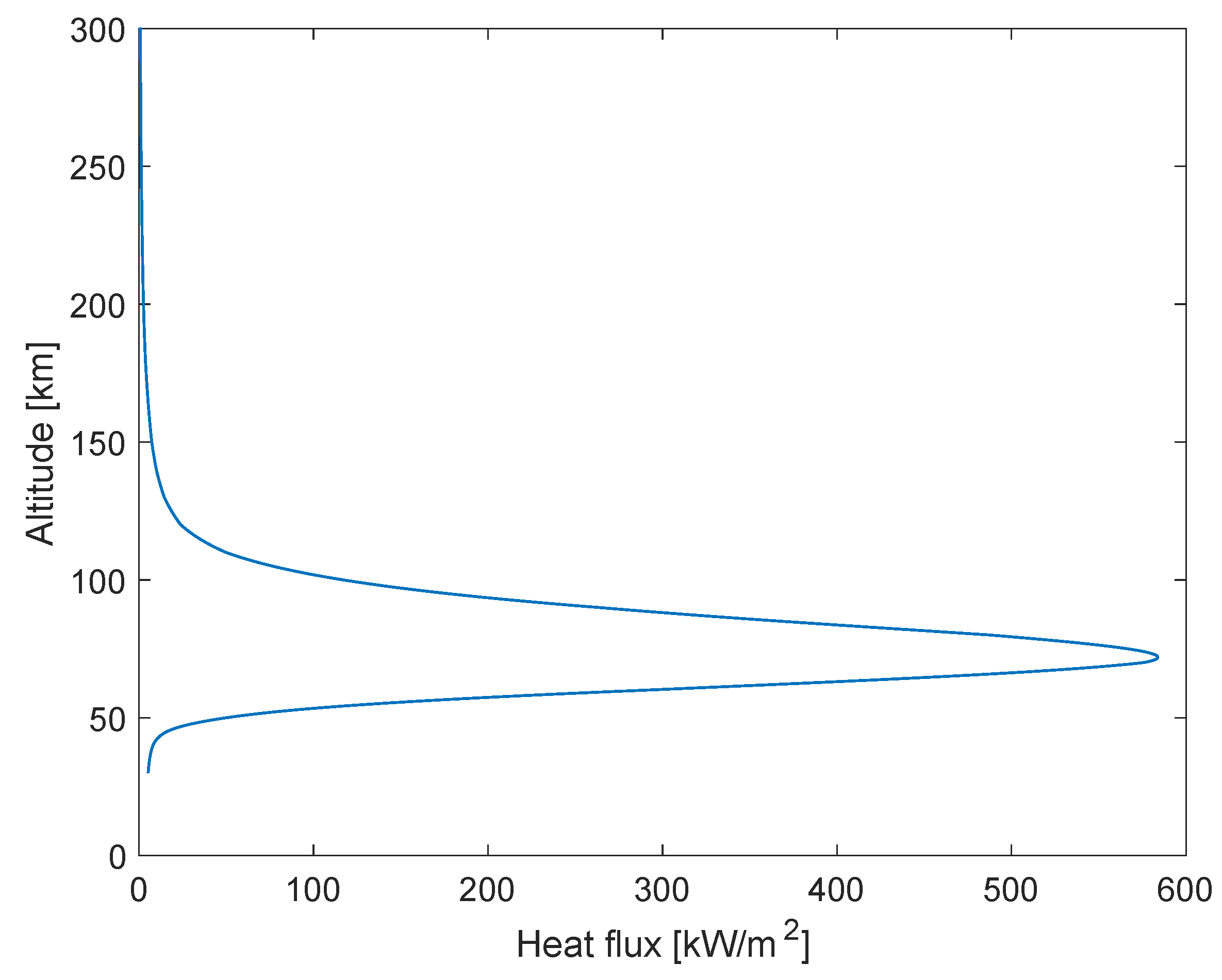
In Figure 3, the heating flux on the capsule for the whole descent phase is shown. As can be seen, the effect of the atmosphere is detectable from an altitude of 150 km, but becomes remarkable only below 100 km. This height marks the beginning of the atmospheric entry, in which the thermal flux on the capsule suddenly increases, reaching its peak value of about 584 ${\mathrm{kW}/\mathrm{m}}^2$ at an altitude of 72 km and then decreases.

4.2. Sensitivity Analysis

To provide a deeper understanding of the proposed strategy’s behaviour, a campaign of numerical simulations was carried out to evaluate the performance of the proposed control system, varying its main operating parameters.

In these simulations, no model uncertainties or initial condition perturbations were taken into account, except for the sensor noise and the quantization of control signals. More specifically, the GPS error is modelled as the sum of two contributions: a sinusoidally varying error with a frequency equal to the average orbital frequency and millimetre level amplitude for position error and ${10}^{-2}$ millimetre per second amplitude for velocity error and a Gaussian white noise with a standard deviation of $1.5/\sqrt{2}$ m for both horizontal and vertical error and standard deviation of $0.03/\sqrt{3}$ m/s for speed error. Those values were defined on the basis of the CubeSat kit GPSRM-1 GPS Receiver, which uses a OEM719 Multi-Frequency GNSS Receive (http://novatel.com/products/receivers/gnss-gps-receiver-boards/oem719) (accessed on 27 November 2022).

Since the controlled re-entry is composed of two different phases (de-orbiting and atmospheric approach), two NMPC-based schemes were implemented:

• The former must guarantee that the satellite follows the reference trajectory and reaches the transition point (H = 150 km) with a low tracking error;
• The latter has the goal of reaching the TAEM interface with a very small position error, in order to land near the desired point.

Both controllers are based on the same model, but with different configuration parameters, i.e., the weights of the objective function, the control frequency, and the length of the prediction horizon. In the atmospheric approach, due to its short time duration compared to the deorbiting phase, the controller must be faster, requiring a smaller prediction horizon and a greater control frequency.

Another important constraint to be taken into account is the duty cycle of the actuator moving the aero-brake surface. Usually, this kind of servo cannot be operating all the time, but needs to be stopped to avoid overheating. The characteristics of the deployable aero-brake system are summarized in

Table 3. Deployable aero-brake system characteristics.

Description	Value
Aero-brake surface $\left[S_{min},S_{max}\right]$	$\left[0.088,0.810\right]{\mathrm{m}}^2$
Actuator extension $\left[Y_{min},Y_{max}\right]$	$\left[0,30\right]\mathrm{mm}$
Actuation rate	3 mm/s
Duty cycle	10%

. As shown, the low actuation rate and the limited duty cycle suggest avoiding a too-high control frequency, which may be useless or even dangerous if not constrained, in particular, by considering the time to extend the actuator $t_{ext}$, given by the ratio between the extension and the actuation rate:

$$t_{ext}=0.03/0.003=10s$$

A 10% duty-cycle results in a minimum controller sample time of 100 s. During de-orbit, a slow control frequency becomes a safety constraint to cope with the presence of perturbations and uncertainties, which could lead to strong variation in the aero-brake surface. On the other hand, in the atmospheric approach, the different objective makes the control signal smoother, enabling a higher control frequency to be used.

To highlight the effects of de-orbiting MPC parameters, Figure 4 shows the position error before the atmospheric approach at the altitude of 150 km, obtained by changing the length of the prediction horizon and the controller sample time. As can be noticed, some combinations of the parameter values are not allowable: by reducing the length of the prediction horizon, the sample time must be decreased as well; otherwise, the controller is unable to bring the capsule towards the target. Moreover, looking at a prediction horizon smaller than 14,400 s (4 h), the results are quite similar and the increased computational burden is not compensated by an increased level of performance. The effect of sample time becomes more significant as the prediction horizon length increases; in this case, as expected, a higher controller frequency leads to better results. Obviously, the computational burden increases linearly with frequency; therefore, a trade-off between performance and sample time must be found with respect to the specific on-board computational power.

Starting from the de-orbiting results, a sensitivity analysis on the atmospheric approach controller was conducted, as shown in Figure 5. It is worth noticing that, with a sample time of 300 s, sometimes, the capsule is unable to arrive at the destination. As expected, the MPC frequency must be higher in the last phase to guide the capsule towards the target. However, below a sample time threshold of 300 s, the results are very similar, depending on the specific values selected for $T_c$ and ${\mathbb{T}}_p$, giving the opportunity to obtain a lower computational burden and avoid higher actuator duty cycles.

In the de-orbiting phase, the weights $p\left(i\right)$, $q\left(i\right)$, and $w\left(i\right)$ of the objective function can be modulated to obtain different results. Figure 6 shows the results in terms of position and velocity error obtained by considering:

$$\begin{array}{cc}p\left(i\right)=p_0& i=0,\cdots ,N_p-1\\ q\left(i\right)=q_0& i=0,\cdots ,N_p-1\\ w\left(i\right)=w_0& i=0,\cdots ,N_p-1\end{array}$$

(21)

To reduce the dimensionality of the figure, on the abscissa, the ratio $q_0/p_0$ between two weights is highlighted. The sensitivity analysis suggests that the weight on the control signal is almost useless, without a significant change in the final position error. The best ratio $q_0/p_0$ is equal to unity, advising that the position and the velocity error must be balanced.

4.3. Robustness Analysis

To assess the effectiveness of the proposed MPC-based trajectory tracking technique, a campaign of numerical simulations was carried out in the presence of model uncertainties, initial state perturbations, and measurement noise.

The simulation scenarios are summarized in

Table 4. Robustness analysis: simulation scenarios.

Simulation	CD Uncertainty	Density Uncertainty	Initial State Perturbation
sim1	+10%	/	/
sim2	+10%	/	Active
sim3	+10%	Active	/
sim4	+10%	Active	Active
sim5	−10%	/	/
sim6	−10%	/	Active
sim7	−10%	Active	/
sim8	−10%	Active	Active

. A maximum initial error of $-500$ m on the semi-major axis combined with an error on the true anomaly of $0.1$ deg was taken as the initial state perturbation. The initial velocity error is related to the position error, because of the satellite’s kinetic energy: a reduction in the semi-major axis leads to a rise in the kinetic energy of the satellite, thus resulting in an initial velocity error.

The model uncertainties were defined in terms of variations in the ballistic coefficient and air density values. In particular, the following was assumed:

• A ± 10% uncertainty on the nominal value of the aerodynamic drag coefficient $C_D$;
• Air density uncertainty defined by a time-dependent perturbative model (NASA/MSFC Global Reference Atmospheric Model) in which the perturbation depends on four random variables.

The number of time steps for the prediction horizon of the de-orbiting phase was set equal to 5 h, i.e., ${\mathbb{T}}_p$ = 18,000 s. The control system sampling time, for this stage, was set equal to $T_{c,d}=3600$ s, whereas it was set equal to $T_{c,r}=10$ s for the atmospheric approach.

Table 5. Robustness analysis: ECEF tracking error at altitude $H=30\mathrm{km}$.

Simulation	Position Error (km)	Velocity Error (m/s)	Time Error (s)
sim1	46.699	11.947	−5
sim2	46.695	11.973	−5
sim3	76.607	21.705	−8
sim4	77.073	21.906	−8
sim5	107.681	15.332	13
sim6	107.921	15.455	13
sim7	23.585	19.448	0
sim8	23.584	19.457	0

shows the results in terms of position and velocity errors in the ECEF reference frame. The initial state perturbation barely affects the final result. The most important sources of errors come from the uncertainties on drag and air density, but the maximum error at TAEM is always under the prescribed objective. The worst situation is the case with a drag coefficient under the nominal value, and an interesting result is shown in sim7 and sim8, where the density uncertainty compensates the decrease of the drag coefficient, improving the final result.

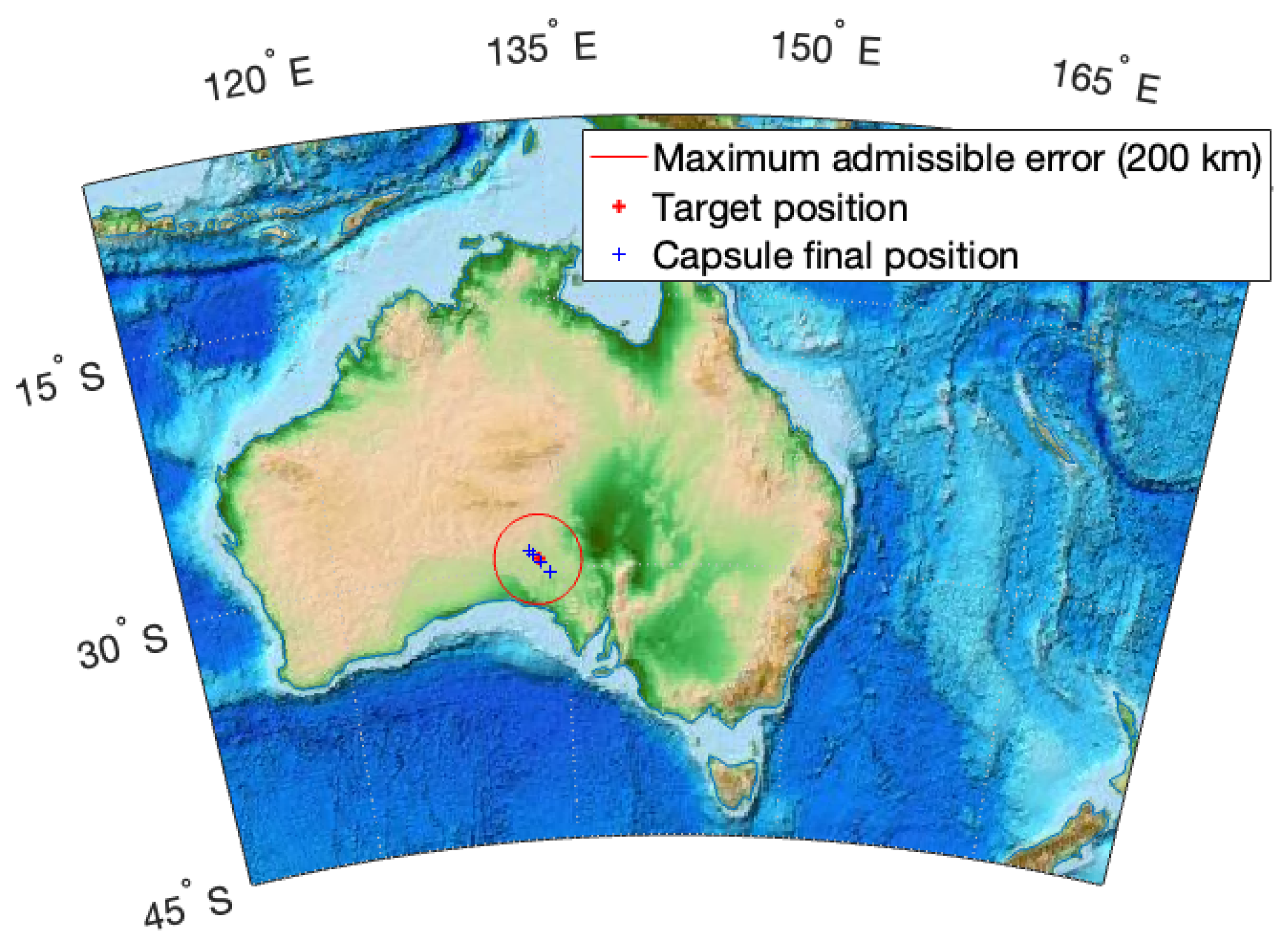
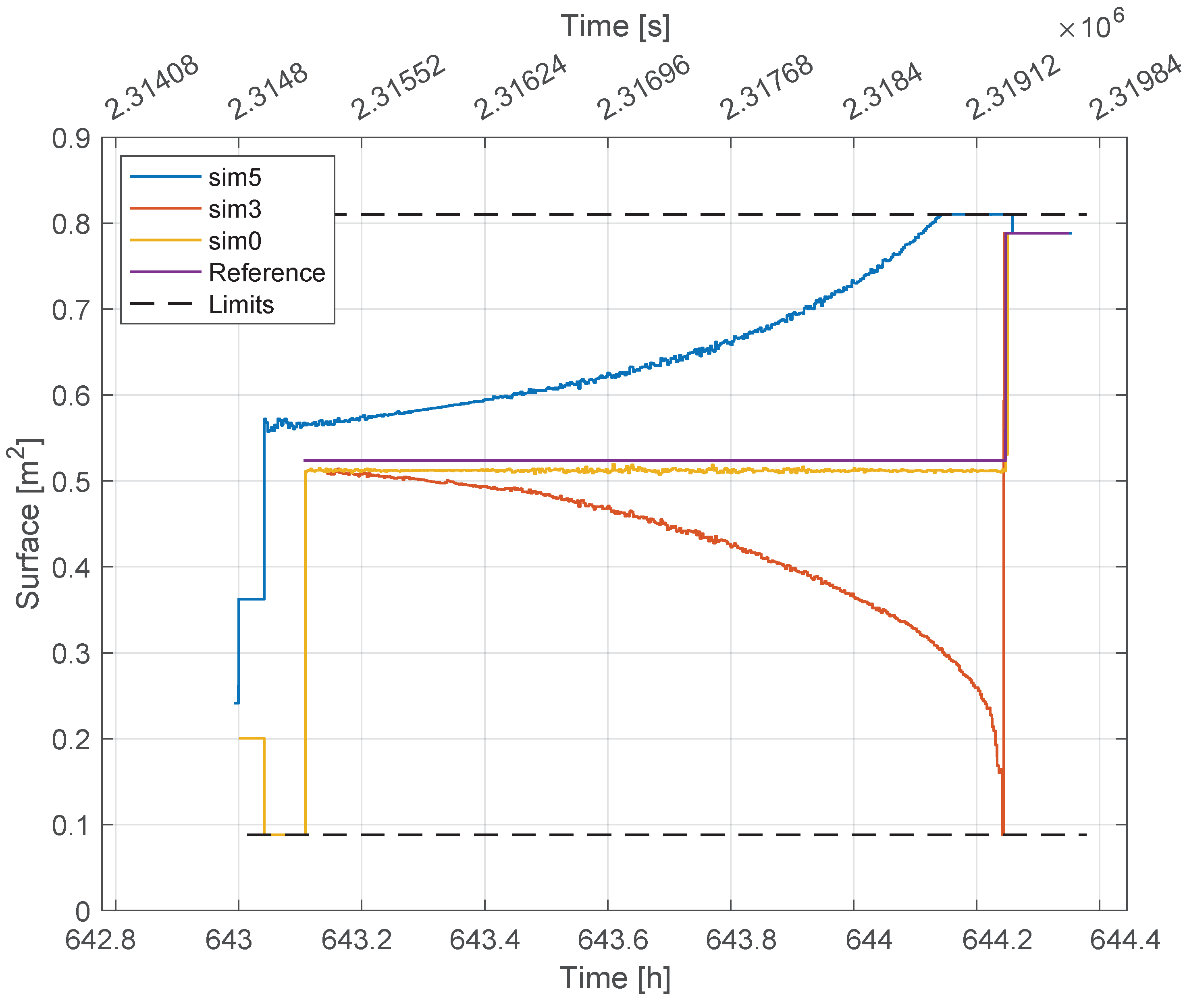
Figure 7 shows the capsule final position (marked with a blue cross) compared with the target location (marked with a red cross). It can be seen that, even in the worst case (highest position error), the maximum allowable error of $200\mathrm{km}$ at TAEM is always satisfied. Figure 8 and Figure 9 show the control signals, i.e., the time variation of the aero-brake surface, for the de-orbiting and atmospheric approach, respectively. It must be noted that sim0 denotes the nominal case, i.e., absence of disturbances.

Despite the control law for the first stage of the mission (Figure 8) seeming to be very noisy, it is important to clarify that the control system has a frequency of $2.78\times {10}^{-4}\mathrm{Hz}$, thus leading to a variation in the control law every 3600 s for almost 27 days.

The atmospheric approach (Figure 9) is characterized by a much more regular control law, though the optimal surface looks quite different from the reference one in the presence of uncertainties.

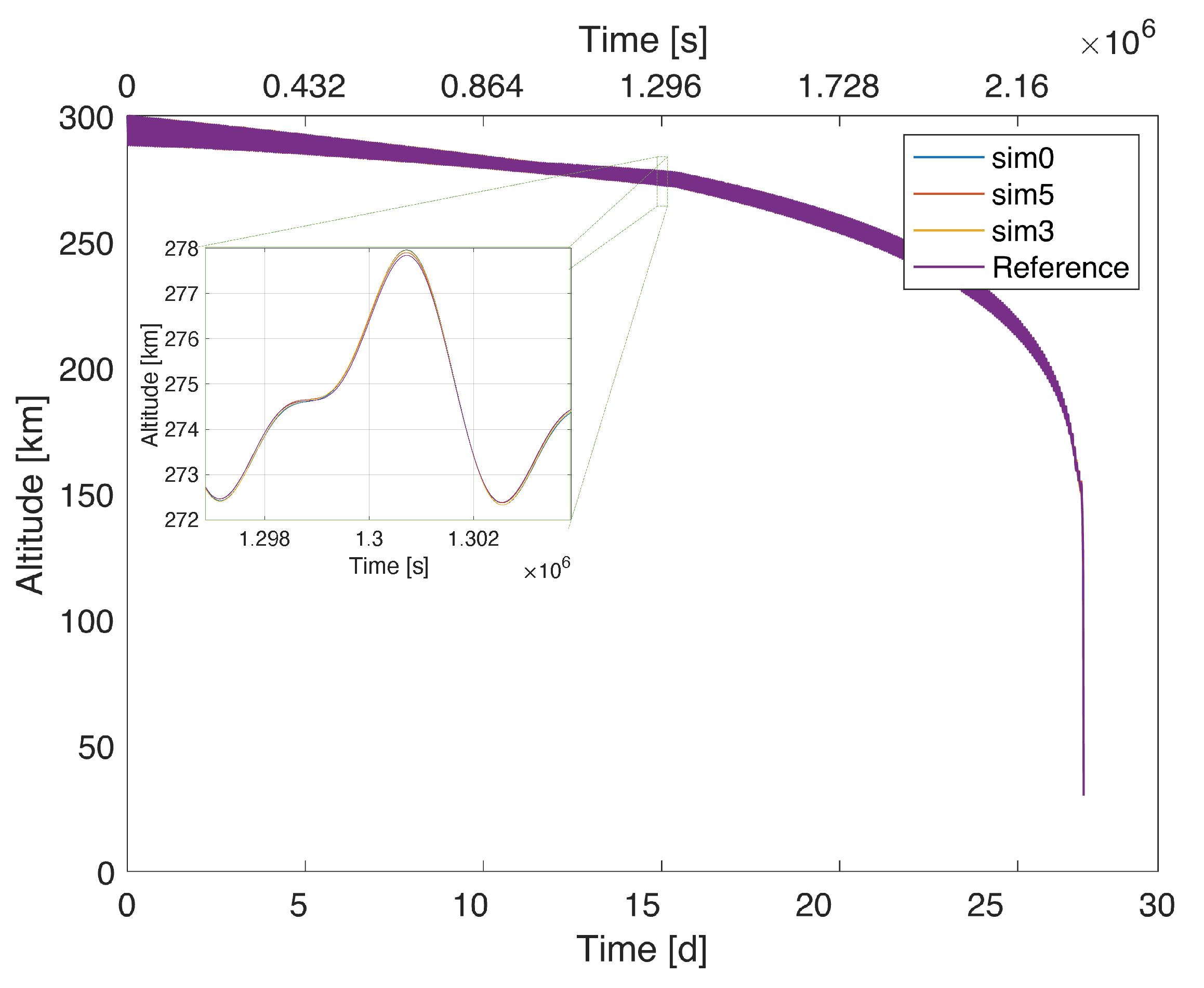
In Figure 10, the actual trajectories obtained in some simulation scenarios are shown, to highlight the difference between the reference trajectory provided by the path planner and the tracked trajectory in the absence of uncertainties and noise. As can be seen in the zoomed-in detail, the trajectories are almost overlapped in all the test cases shown in the figure.

Figure 11 shows the same trajectories, focusing on the atmospheric approach. The starting times are not equal, because they depend on the de-orbiting phase, achieving the altitude of $150\mathrm{km}$ (corresponding to the separation of the capsule from the main body) in different time instants. However, each trajectory reaches the target at TAEM with an acceptable tracking error.

5. Conclusions

In this paper, the design of a guidance and control algorithm for the re-entry of an orbiting capsule is described. The capsule is equipped with a deployable aero-brake system in order to increase the efficiency and re-usability of this kind of vehicle. The algorithm implements both off-board and on-board path planners to design the re-entry reference trajectory before the mission and locally update it in case of deviations from the prescribed orbit.

The trajectory optimization model is designed to minimize position and velocity error at TAEM, by considering several constraints: the discrete control signal of the aero-brake surface, the maximum admissible value of the heat flux, and the nonlinear dynamic model.

Once the re-entry begins, NMPC is able to modulate the aero-brake surface deployment to minimize position and speed errors. Such an NMPC uses different parameters depending on the specific phase of the re-entry mission. During the long de-orbiting phase, a greater sample time is selected to reduce the high computational burden that would result due to the long prediction horizon. In the atmospheric approach, the sample time can be decreased, because the prediction horizon is bounded by the proximity with the target, resulting in a lower computational burden.

A sensitivity analysis on the parameters of the NMPC was performed, in order to help designers in their proper selection for balancing performance and computational burden.

A numerical robustness analysis was carried out by simulating the re-entry mission in the presence of model uncertainties, initial state perturbations, and measurement noise. The position error at the target is always compliant with the maximum allowable error at TAEM in all the simulations presented.