Reynolds Number Effect on Aerodynamic and Starting Characteristics of a Two-Dimensional Hypersonic Inlet
Abstract
1. Introduction
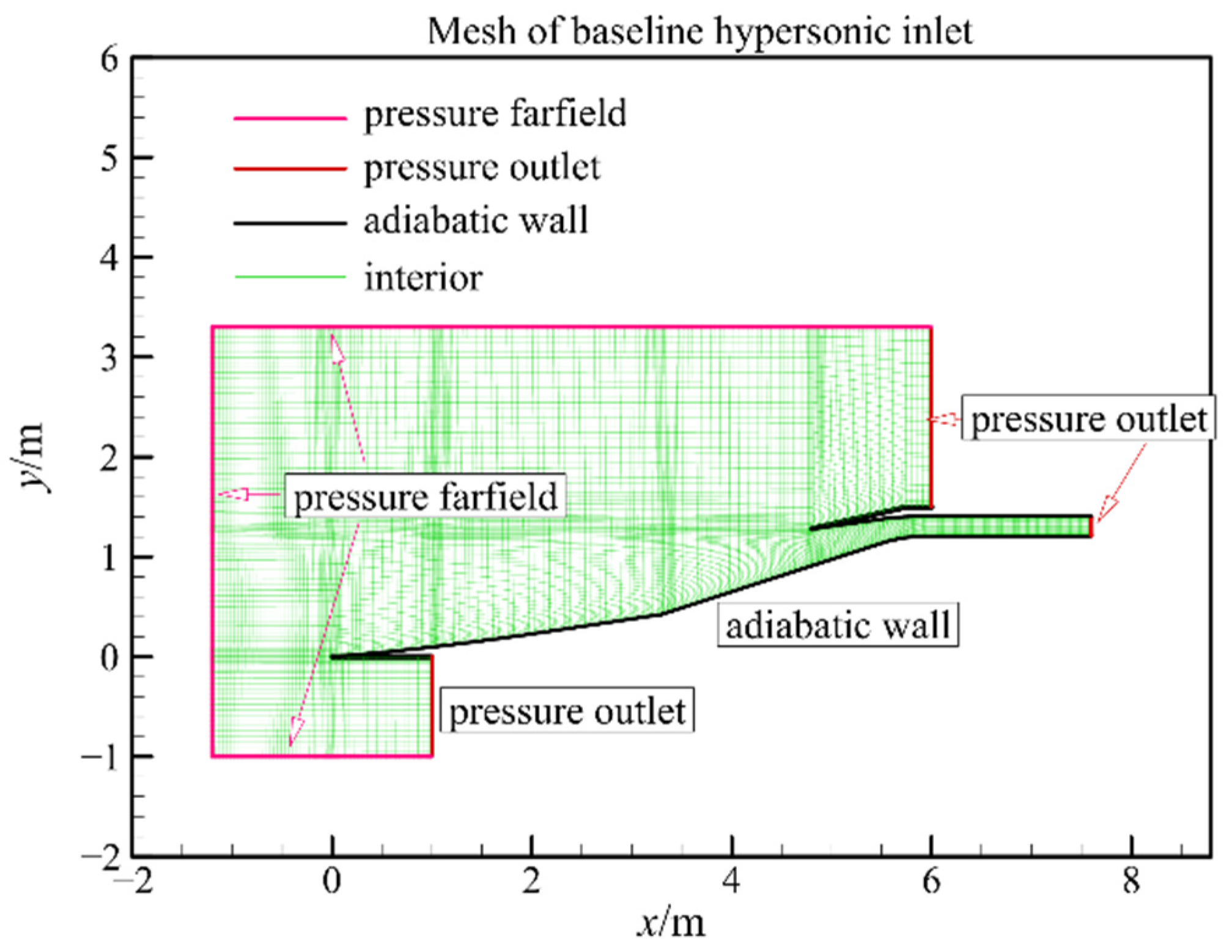
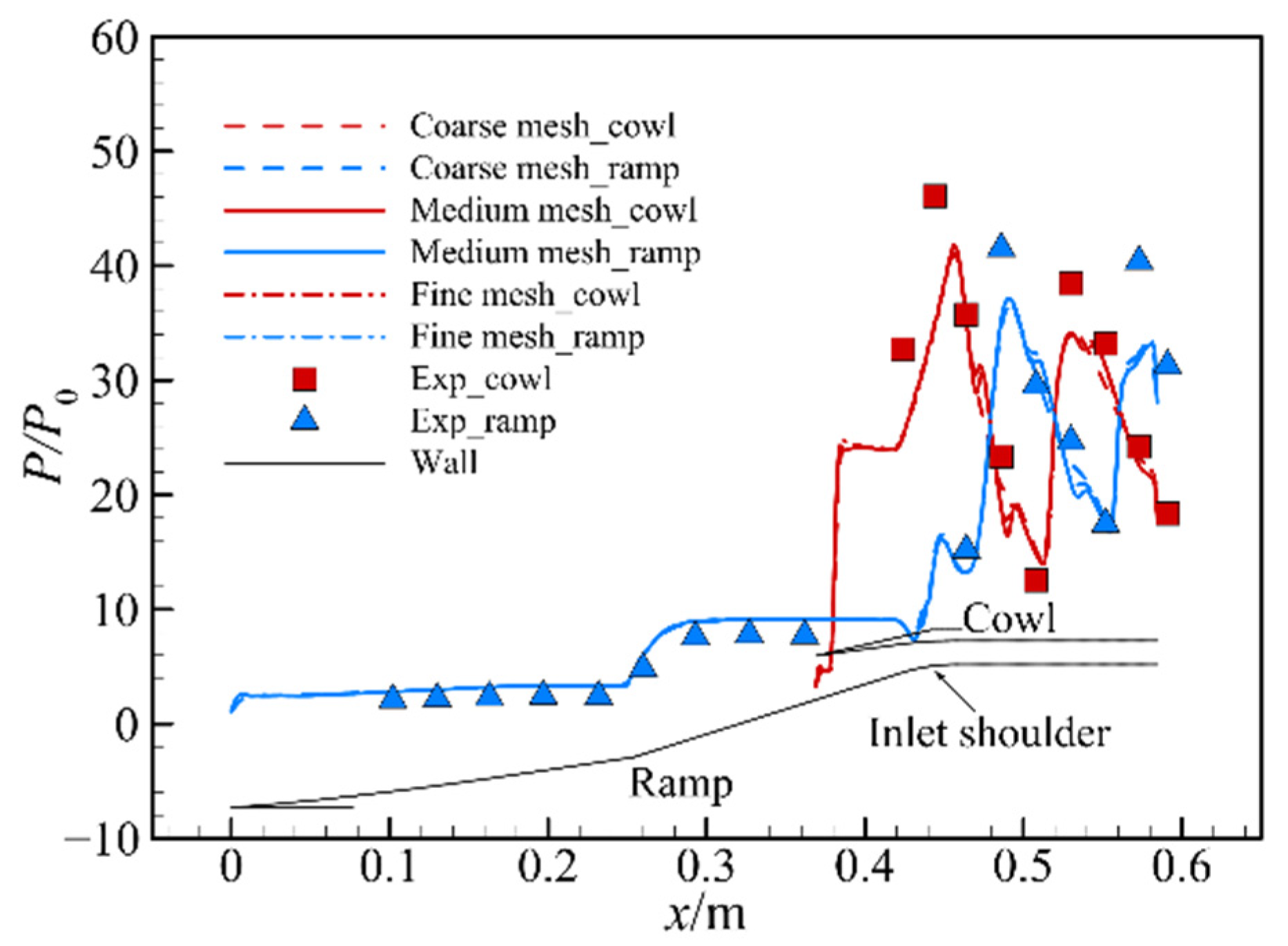
2. Methods
3. Results
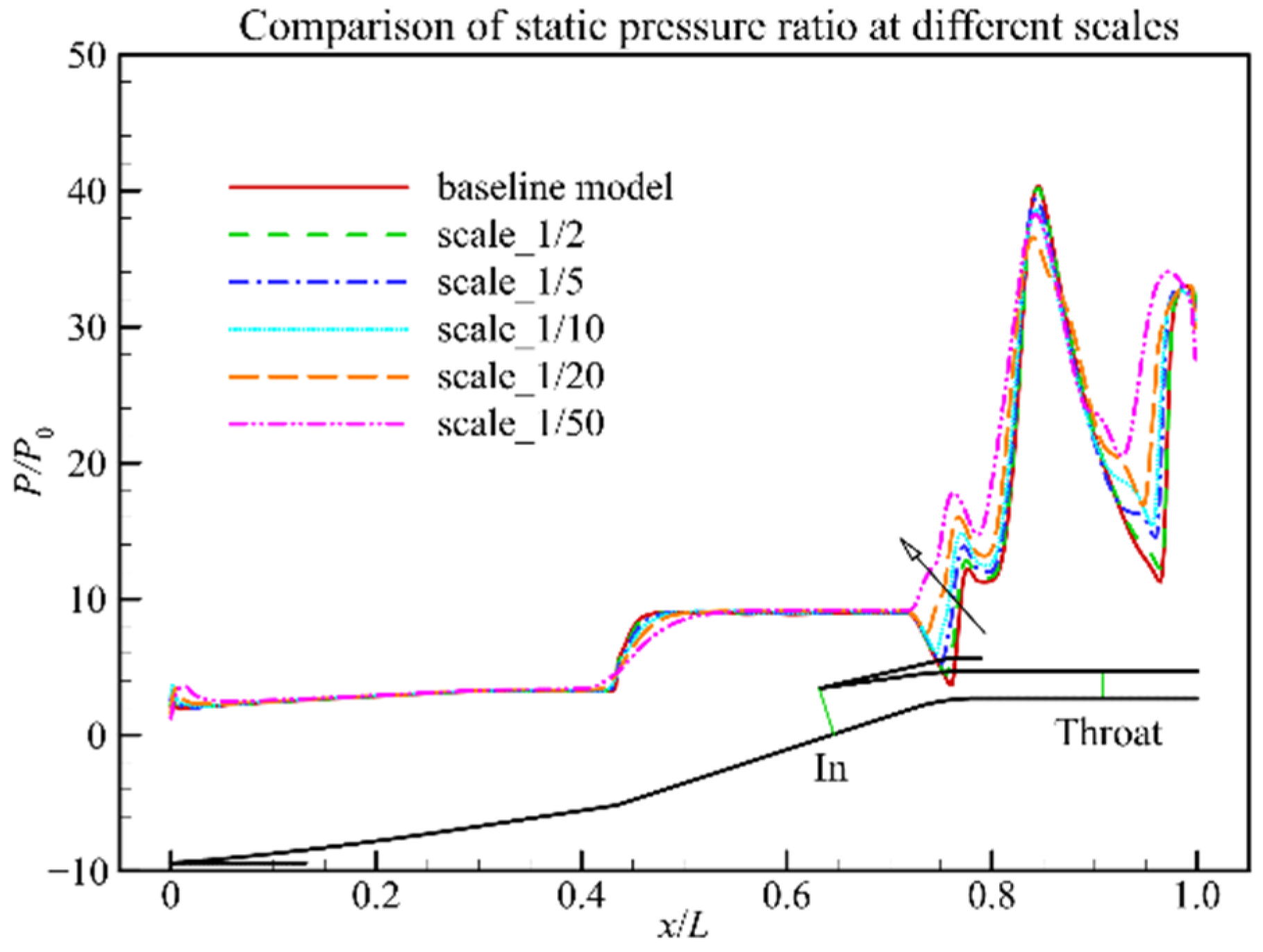
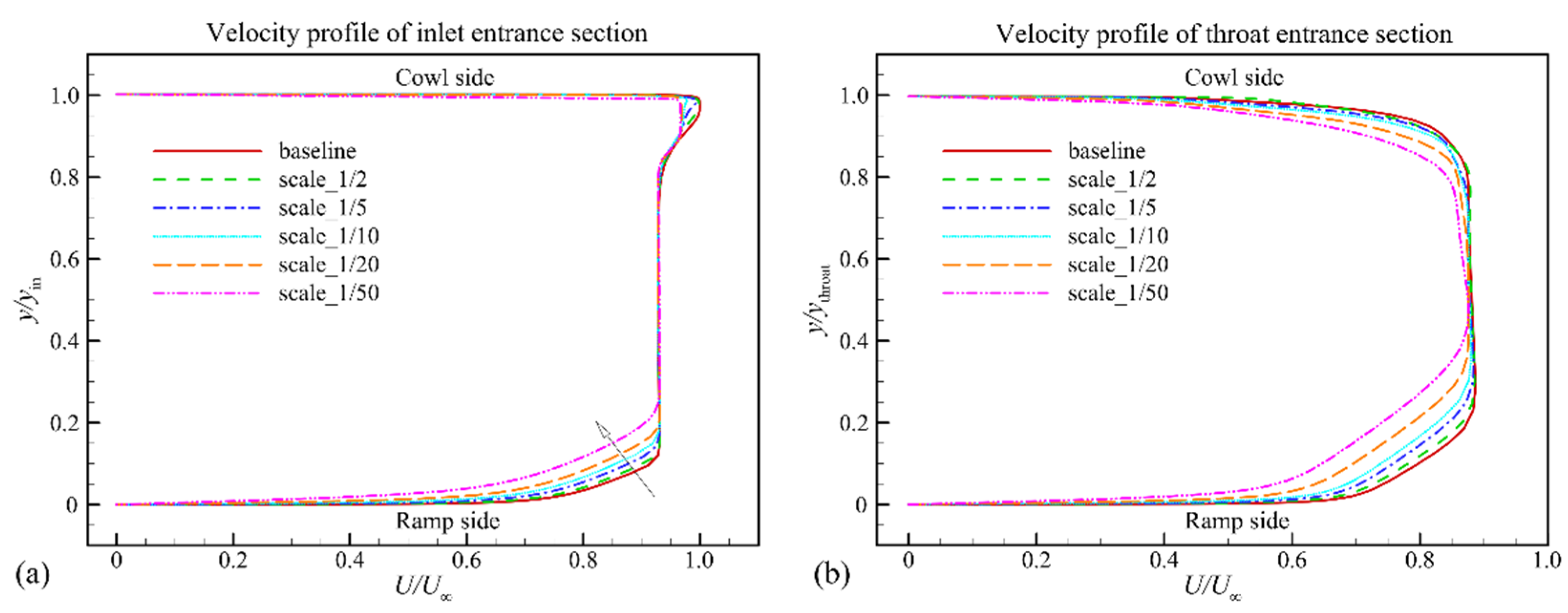
3.1. Model Scaling on Two-Dimensional Hypersonic Inlet Aerodynamic Characteristics
3.2. Inflow Conditions on Two-Dimensional Hypersonic Inlet Aerodynamic Characteristics
4. Discussion
5. Conclusions
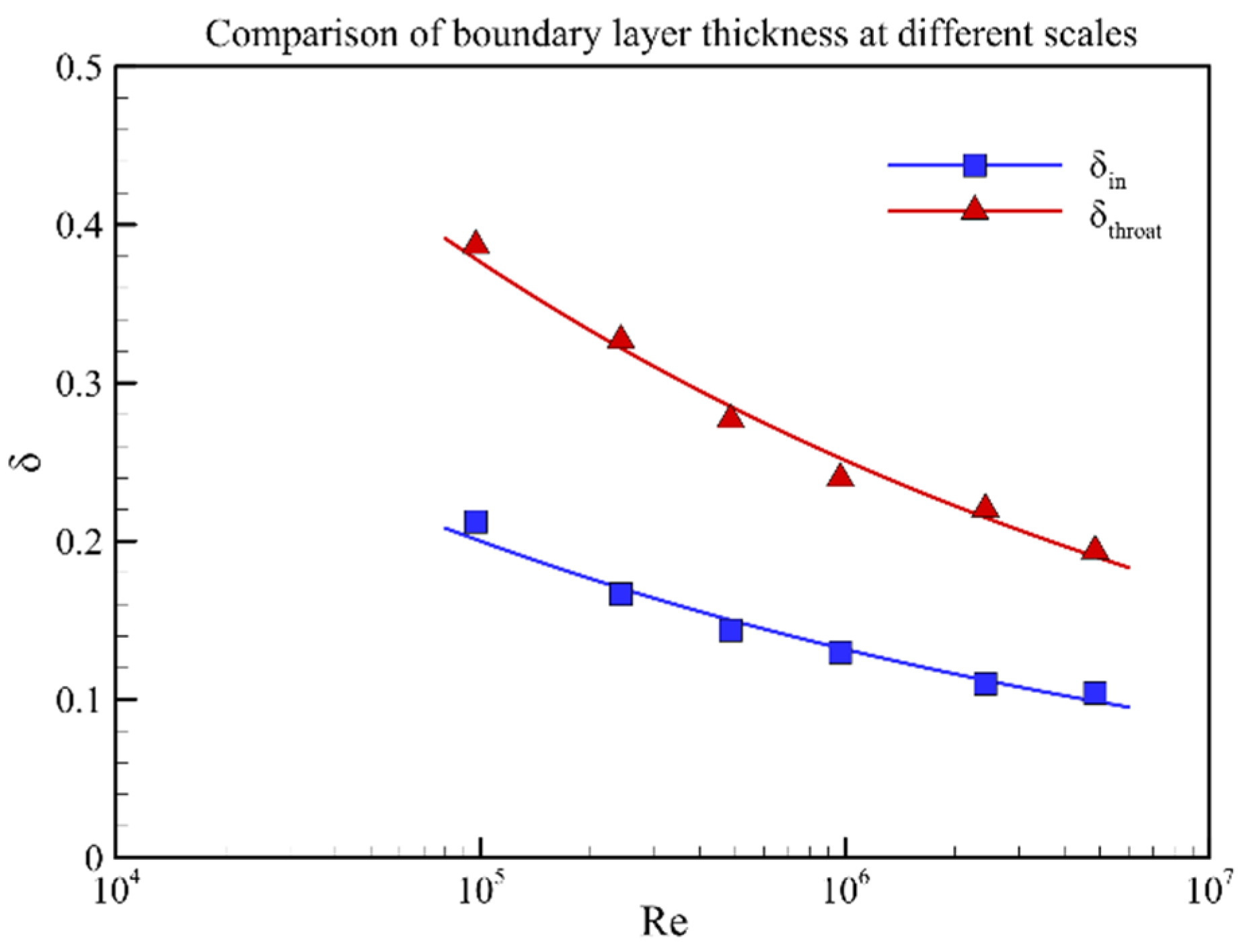
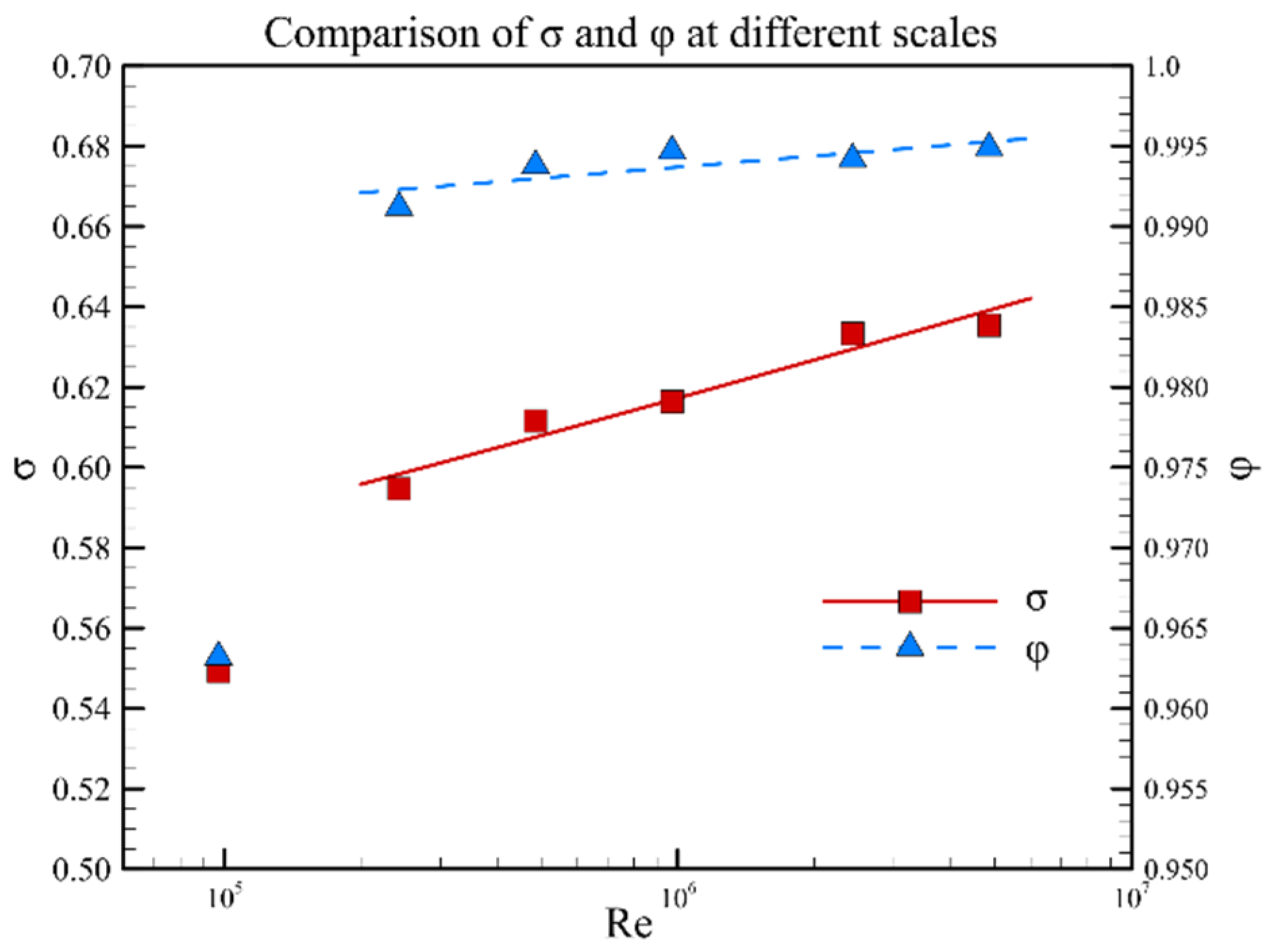
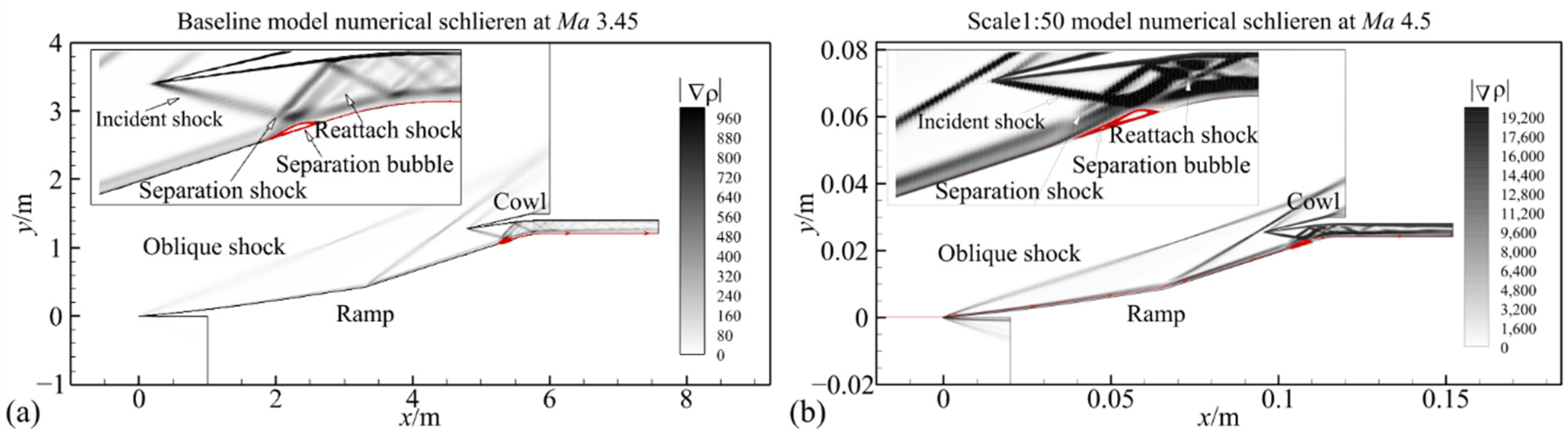
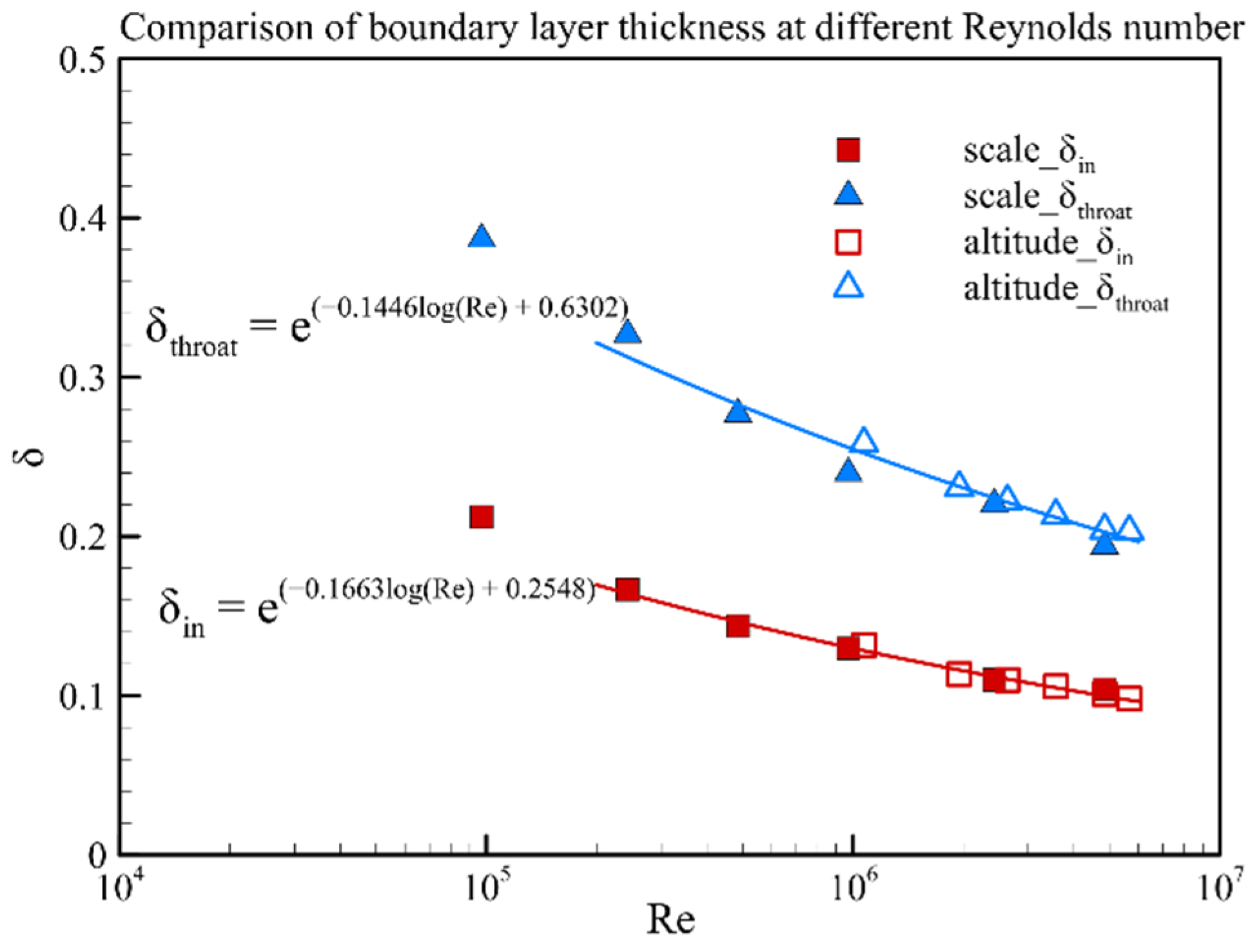
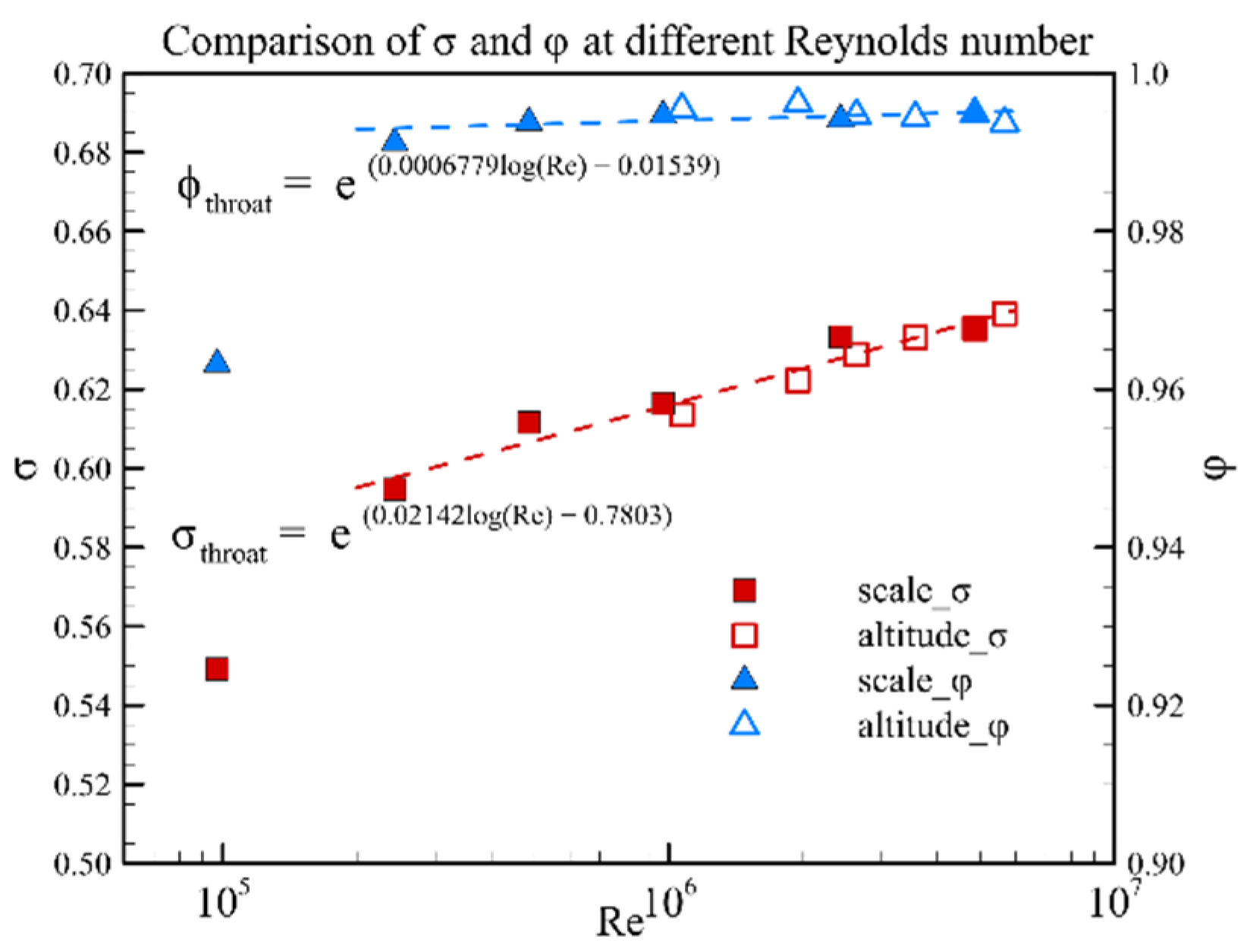
- The inflow Reynolds number decreased from 4.86 × 106 to 9.71 × 104 as the model scaling increased from 1 to 1/50. This resulted in an increase in the relative boundary layer thickness of the inlet entrance section from 10.4% to 21.2%. Thus, the inlet shoulder separation bubble size increased gradually, and the total pressure recovery at the inlet throat section decreased from 0.64 to 0.55. The starting Mach number increased from 3.45 to 4.50 with model scaling.
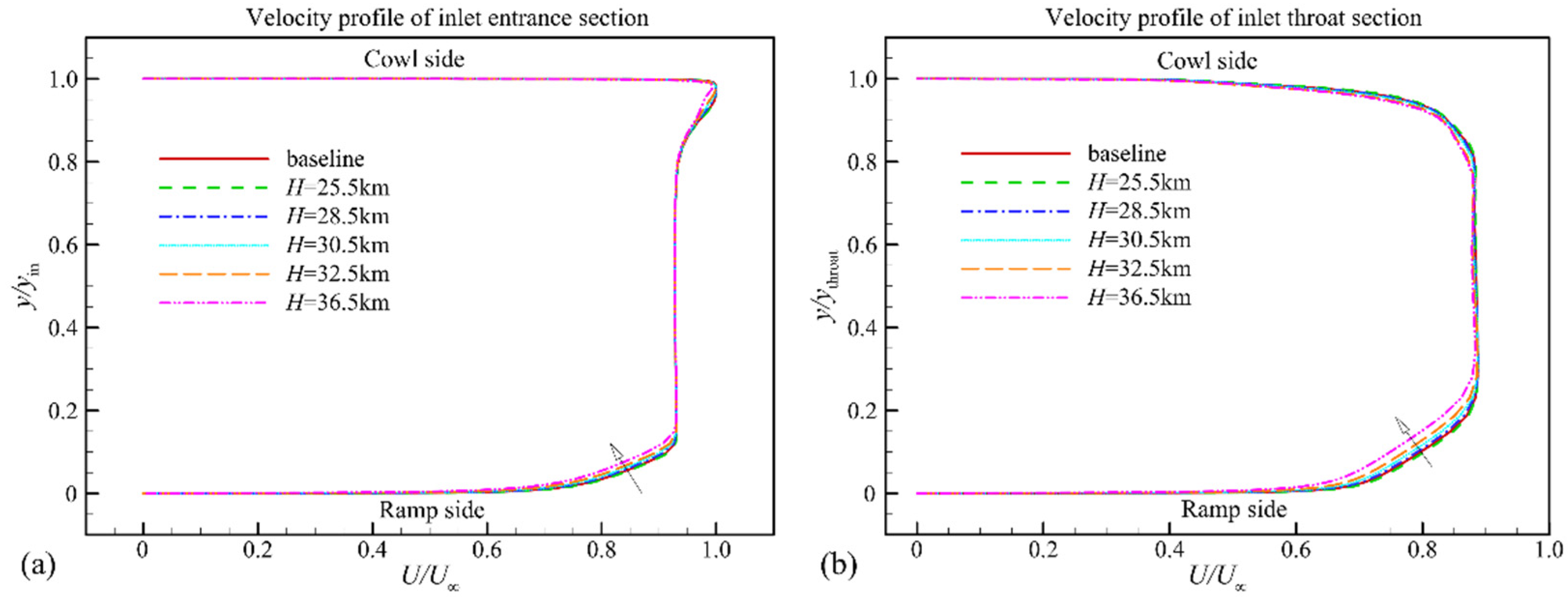
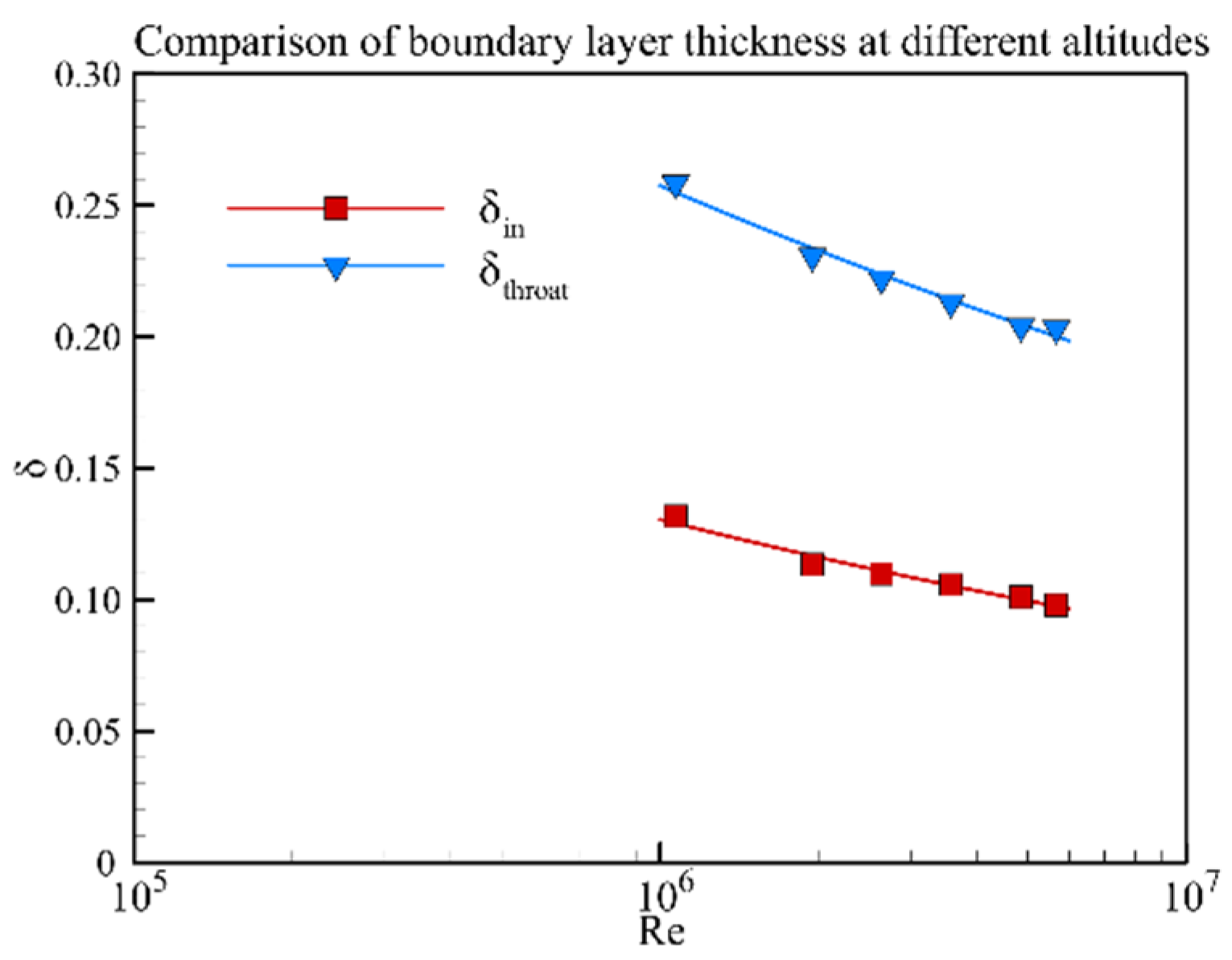
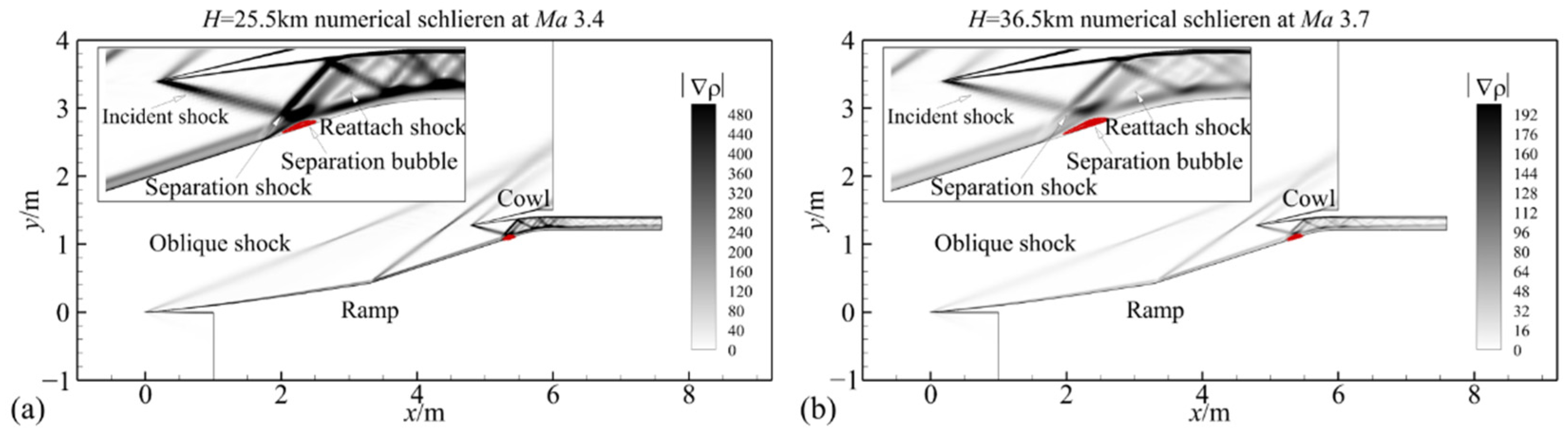
- The inflow Reynolds number decreased from 5.67 × 106 to 1.07 × 106 as the flight altitude increased from 25.5 km to 36.5 km. This resulted in an increase in the relative boundary layer thickness of the entrance section from 9.8% to 13.2%. Thus, the inlet shoulder separation bubble size increased gradually, and the total pressure recovery at the inlet throat section decreased from 0.64 to 0.61. The starting Mach number increased from 3.40 to 3.70 with flight altitude.
- The effect of the Reynolds number effect caused by the model scaling and flight altitude on the aerodynamic characteristics of the hypersonic inlet has been compared. The results show that the relative boundary layer thickness at the entrance section, mass flow ratio, total pressure recovery coefficient at the throat section and starting Mach number are almost the same under the same Reynolds number.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pettersson, K.; Rizzi, A. Aerodynamic scaling to free flight conditions: Past and present. Prog. Aerosp. Sci. 2008, 44, 295–313. [Google Scholar]
- Hitzel, S.; Zimper, D. Wind tunnel, simulation, and “real” flight of advanced combat aircraft: Industrial perspective. J. Aircr. 2018, 55, 587–602. [Google Scholar]
- Chen, M. How to determine the scale ratio of wind tunnel test models by CFD—A leap in the design standard of wind tunnel test models from the perception to the reason. J. Astronaut. 2007, 28, 594–597. (In Chinese) [Google Scholar]
- Bushnell, D.M. Scaling: Wind tunnel to flight. Annu. Rev. Fluid Mech. 2006, 38, 111–128. [Google Scholar] [CrossRef]
- Gong, A.L.; Xie, J.; Liu, X.W.; Liu, Z.; Yang, Y.J.; Zhou, W.J. Study on ground-to-flight extrapolation of near space hypersonic aerodynamic data. Eng. Mech. 2017, 34, 229–238. (In Chinese) [Google Scholar]
- Yamazaki, W.; Yamagishi, S.; Ueno, M. Investigation of indirect Reynolds number effect via computational fluid dynamics simulations. J. Aircr. 2018, 55, 1805–1816. [Google Scholar]
- Jouhaud, J.C.; Sagaut, P.; Labeyrie, B. A kriging approach for CFD/wind-tunnel data comparison. J. Fluids Eng. 2006, 128, 847–855. [Google Scholar] [CrossRef][Green Version]
- Jia, Q.; Yang, Y.; Chen, N. The influence of Reynolds number on dynamic aerodynamics correlation between real flight and wind tunnel. J. Exp. Fluid Mech. 2007, 21, 91–96. (In Chinese) [Google Scholar]
- Mani, M.; Rider, B.J.; Sclafani, A.J.; Winkler, C.; Vassberg, J.; Dorgan, A.J.; Cary, A.; Tinoco, E.N. Reynolds-averaged Navier–Stokes technology for transonic drag prediction: A Boeing perspective. J. Aircr. 2014, 51, 1118–1134. [Google Scholar] [CrossRef]
- Fukushima, Y.; Tamaki, Y.; Kawai, S. Predictability of wall-modeled LES for Reynolds number effects of airfoil flows at transonic buffet and near-stall conditions. In Proceedings of the AIAA SciTech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Liu, J.; Yuan, H.; Zhang, J.; Kuang, Z. A multifidelity simulation method for internal and external flow of a hypersonic airbreathing propulsion system. Aerospace 2022, 9, 685. [Google Scholar] [CrossRef]
- Bahm, C.; Baumann, E.; Martin, J.; Bose, D.; Strovers, B. The X-43A Hyper-X Mach 7 flight 2 guidance, navigation, and control overview and flight test results. In Proceedings of the AIAA/CIRA 13th International Space Planes and Hypersonics Systems and Technologies Conference, Capua, Italy, 16–20 May 2005. [Google Scholar]
- Imfeld, W.F. Development program for the F-15 inlet. J. Aircr. 1976, 13, 286–291. [Google Scholar] [CrossRef]
- Lin, G.; Li, Z.; Xiao, F.; Jiang, H.; Liu, K.; Gao, W.; Yang, Z. Scale effects of the starting characteristics of a 2D hypersonic inlet. J. Exp. Fluid Mech. 2014, 28, 26–31. (In Chinese) [Google Scholar]
- Wang, Y.; Yuan, H.; Guo, R. Effect of geometry dimensions on aerodynamic performance of hypersonic inlet. Acta Aeronaut. Astronaut. Sin. 2014, 35, 1893–1901. (In Chinese) [Google Scholar]
- Liu, J.; Yuan, H.; Yao, M.; Ge, N. Numerical simulation of terminal shock oscillation in over/under turbine-based combined-cycle inlet. Int. J. Turbo Jet Eng. 2021, 38, 73–83. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, H.; Chen, W.; Guo, R. Investigation of translation scheme turbine-based combined-cycle inlet mode transition. Aerosp. Sci. Technol. 2021, 116, 106894. [Google Scholar]
- Liu, F.; Yuan, H. Experimental Test of a Two-Dimensional Hypersonic Inlet; Technical Report: Nanjing, China, 2021. (In Chinese) [Google Scholar]
- Baldwin, A.; Mears, L.J.; Kumar, R.; Farrukh, S.A. Effects of Reynolds number on swept shock-wave/boundary-layer interactions. AIAA J. 2021, 59, 3883–3899. [Google Scholar]
- Seddon, J.; Goldsmith, E.L. Intake Aerodynamics, 2nd ed.; AIAA Education Series; Blackwell Science Ltd.: Hoboken, NJ, USA, 1999. [Google Scholar]
- Tan, H.J.; Guo, R.W. Experimental study of the unstable-unstarted condition of a hypersonic inlet at Mach 6. J. Propuls. Power 2007, 23, 783–788. [Google Scholar] [CrossRef]






| Scale | Re |
|---|---|
| 1 | 4.86 × 106 |
| 1/2 | 2.43 × 106 |
| 1/5 | 9.71 × 105 |
| 1/10 | 4.86 × 105 |
| 1/20 | 2.43 × 105 |
| 1/50 | 9.71 × 104 |
| Scale | Starting Mach Number |
|---|---|
| 1 | 3.45 |
| 1/2 | 3.55 |
| 1/5 | 3.70 |
| 1/10 | 3.85 |
| 1/20 | 4.05 |
| 1/50 | 4.50 |
| Altitude (km) | Starting Mach Number |
|---|---|
| 25.5 | 3.40 |
| 26.5 | 3.45 |
| 28.5 | 3.50 |
| 30.5 | 3.55 |
| 32.5 | 3.60 |
| 36.5 | 3.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Chen, J.; Yuan, H. Reynolds Number Effect on Aerodynamic and Starting Characteristics of a Two-Dimensional Hypersonic Inlet. Aerospace 2022, 9, 811. https://doi.org/10.3390/aerospace9120811
Liu J, Chen J, Yuan H. Reynolds Number Effect on Aerodynamic and Starting Characteristics of a Two-Dimensional Hypersonic Inlet. Aerospace. 2022; 9(12):811. https://doi.org/10.3390/aerospace9120811
Chicago/Turabian StyleLiu, Jun, Jingzhe Chen, and Huacheng Yuan. 2022. "Reynolds Number Effect on Aerodynamic and Starting Characteristics of a Two-Dimensional Hypersonic Inlet" Aerospace 9, no. 12: 811. https://doi.org/10.3390/aerospace9120811
APA StyleLiu, J., Chen, J., & Yuan, H. (2022). Reynolds Number Effect on Aerodynamic and Starting Characteristics of a Two-Dimensional Hypersonic Inlet. Aerospace, 9(12), 811. https://doi.org/10.3390/aerospace9120811






