Mesh Adaptation for Simulating Lateral Jet Interaction Flow
Abstract
:1. Introduction
2. Hybrid Mesh Adaptive Method
2.1. Numerical Simulation Method
2.2. Adaptation Strategy
2.3. Adaptive Criteria
2.3.1. Quasi-Gradient-Based Adaptation Criterion
2.3.2. Adaptation Criterion Based on Curl and Gradient of Velocity
2.3.3. Adaptation Criterion Based on Vortex Vector
2.4. Combined Adaptation Criteria
- (1)
- If a mesh cell satisfies and , then it needs to be refined. This identifies shock waves in the flow field.
- (2)
- If a mesh cell satisfies or , then it needs to be refined. This identifies vortex structures in the flow field.
- (3)
- If a mesh cell satisfies or , then it needs to be coarsened. This identifies absence of shock waves in the flow field.
- (4)
- If a mesh cell satisfies and , then it needs to be coarsened. This identifies absence of a vortex in the flow field.
2.5. Frequency Selection for Dynamic Grid Adaptation
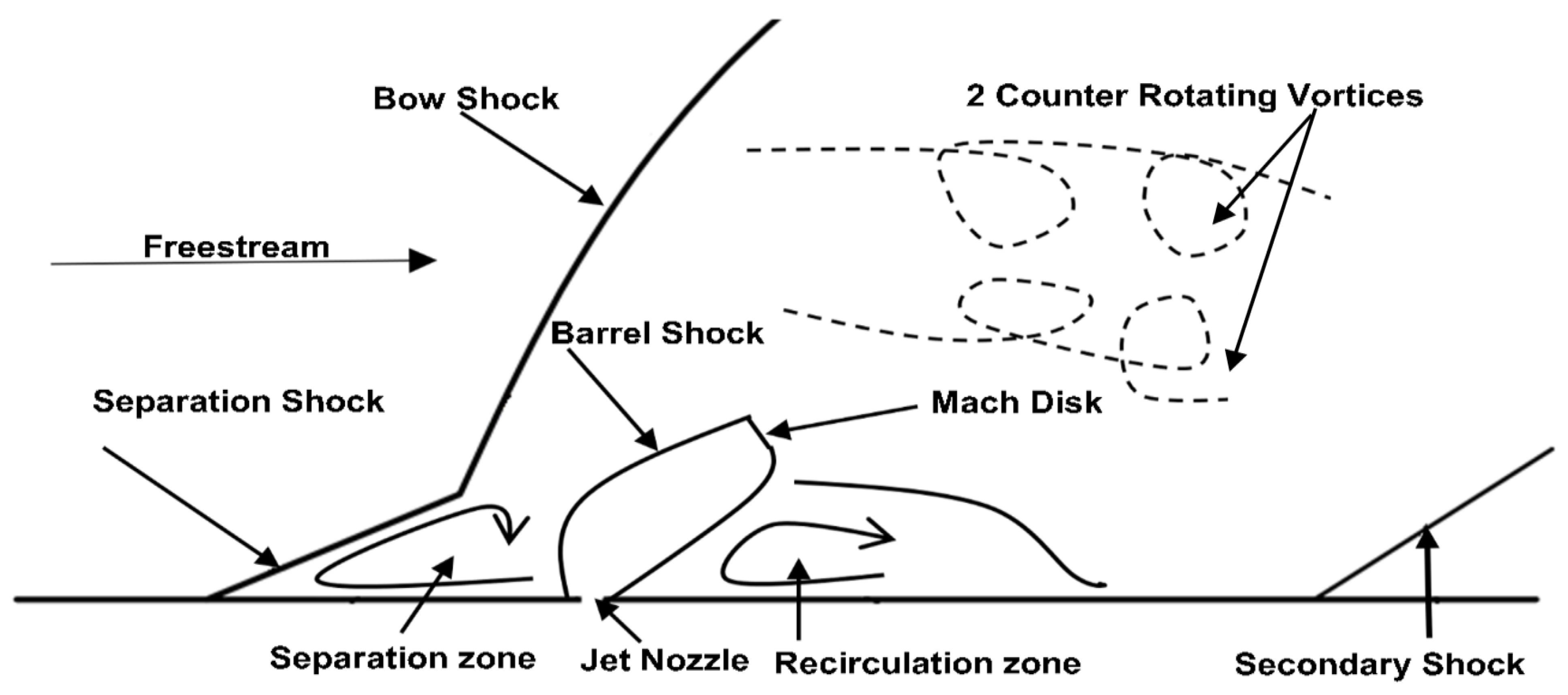
3. Adaptive Simulation of Lateral Jet Interaction Flow Field
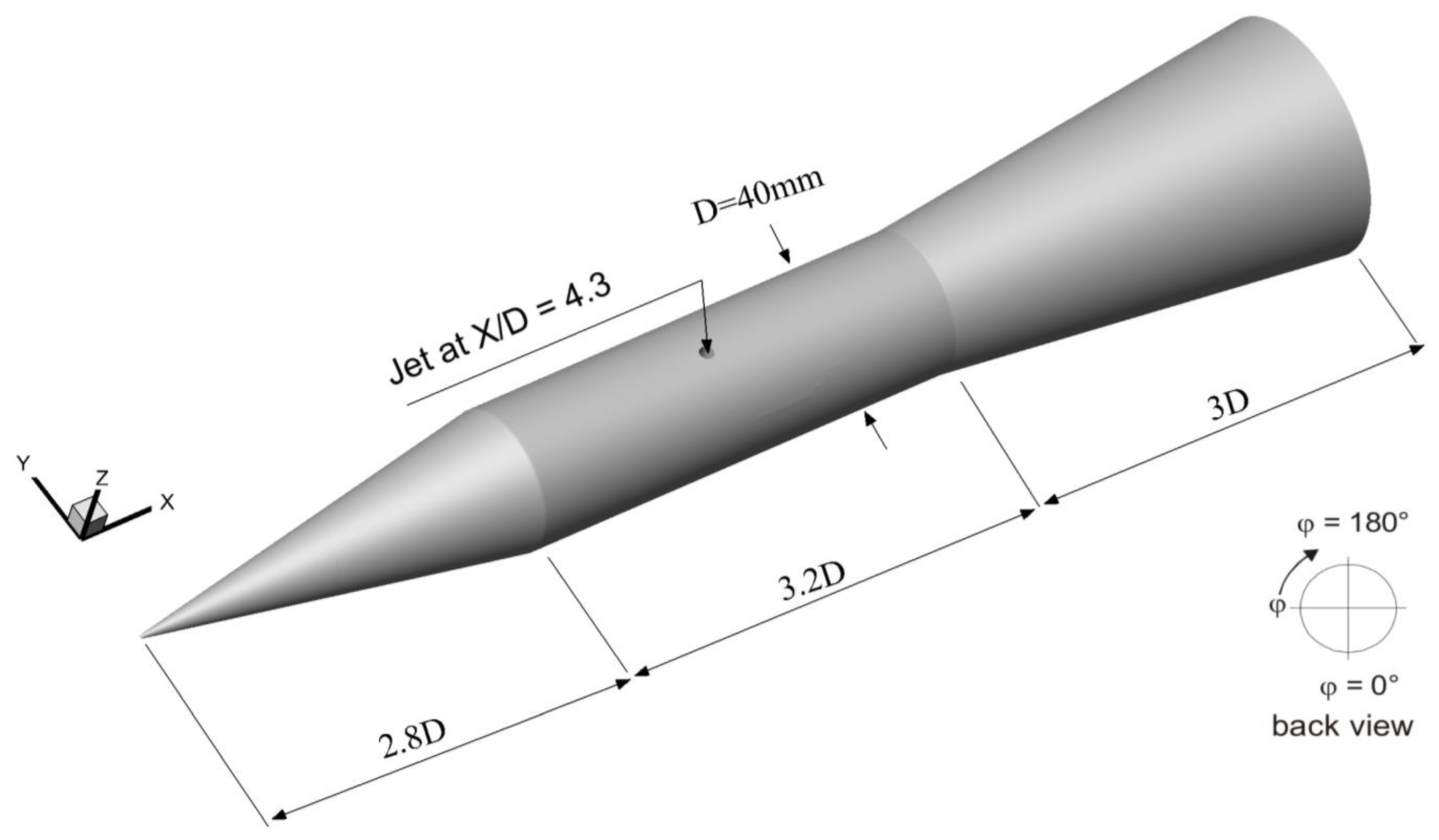
3.1. Generic Missile Model and Flow Conditions
3.2. Transverse Jet Efficiency
3.3. Simulation of a Steady Flow
3.4. Simulation of an Unsteady Flow
4. Summary
- (1)
- A combined adaptation criterion for unstructured hybrid mesh is proposed for simulating lateral jet interaction flows. This can effectively capture complex structures in the lateral jet interaction flow field, such as shock waves and vortices.
- (2)
- The proposed adaptation criterion can significantly improve convergence of flow computation and resolution of flow structures. It also plays an important role in numerical simulation of lateral jet interaction flows and improves prediction accuracy of the aerodynamic characteristics of a missile.
- (3)
- Compared to the uniformly refined mesh, the adaptive mesh had a similar resolution to the flow field, while the total number of mesh cells was much smaller. Additionally, in this way, computational efficiency can be improved greatly.
- (4)
- The present adaptation criteria can identify characteristic structures in the unsteady flow field and effectively improve resolution of flow and accuracy of aerodynamic calculation.
- (5)
- In parallel computing, adaptive refined mesh may be concentrated in one processor in such a way that seriously imbalanced distributed mesh cannot reduce computational cost effectively. Implementation of dynamic load balancing in the solver for parallel computing will be the focus of future research.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.J.; LI, S.H.; Zhu, H.B. Research on Modeling and Simulation of Optimal Search of Multifunction Phased Array Radar. J. Syst. Simul. 2008, 20, 4248–4251. [Google Scholar]
- Saif, U.K.; Saqib, H.; Ali, H.M.; Shehar, B.; Muhammad, A.N.; Naseem, A. Experimental investigation of aluminum fins on relative thermal performance of sintered copper wicked and grooved heat pipes. Prog. Nucl. Energy 2022, 152, 104374. [Google Scholar] [CrossRef]
- Siddiqi, H.-U.; Qamar, A.; Shaukat, R.; Anwar, Z.; Amjad, M.; Farooq, M.; Abbas, M.M.; Imran, S.; Ali, H.; Khan, T.; et al. Heat transfer and pressure drop characteristics of ZnO/DIW based nanofluids in small diameter compact channels: An experimental study. Case Stud. Therm. Eng. 2022, 39, 102441. [Google Scholar] [CrossRef]
- Lee, J.W.; Min, B.Y.; Byun, Y.H.; Lee, C. Numerical Analysis and Design Optimization of Lateral Jet Controlled Missile. In Proceedings of the 21st International Congress of Theoretical and Applied Mechanics, Warsaw, Poland, 5–21 August 2004. [Google Scholar]
- Gnemmi, P.; Schäfer, H.J. Experimental and Numerical Investigations of a Transverse Jet Interaction on a Missile Body. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Christie, R. Lateral Jet Interaction with a Supersonic Crossflow. Master’s Thesis, University of Cranfield, Cranfield, UK, October 2010. [Google Scholar]
- Alqahtani, S.; Ali, H.M.; Farukh, F.; Kandan, K. Experimental and computational analysis of polymeric lattice structure for efficient building materials. Appl. Therm. Eng. 2023, 218, 119366. [Google Scholar] [CrossRef]
- Zawawi, N.N.M.; Azmi, W.H.; Ghazali, M.F.; Ali, H.M. Performance of Air-Conditioning System with Different Nanoparticle Composition Ratio of Hybrid Nanolubricant. Micromachines 2022, 13, 1871. [Google Scholar] [CrossRef] [PubMed]
- Lawag, R.A.; Ali, H.M. Phase change materials for thermal management and energy storage: A review. J. Energy Storage 2022, 55, 105602. [Google Scholar] [CrossRef]
- Baker, T.J. Mesh generation: Art or science? Prog. Aerosp. Sci. 2005, 41, 29–63. [Google Scholar] [CrossRef]
- Baker, T.J. Mesh adaption strategies for problems in fluid dynamics. Finite Elem. Anal. Des. 1997, 25, 243–273. [Google Scholar] [CrossRef]
- Mavriplis, D.J. Unstructured Mesh Generation and Adaptivity: NASA-CR-195069; NASA: Washington, DC, USA, 1995.
- Lohner, R. Adaptive h-refinement on 3D unstructured grids for transient problems. Int. J. Numer. Methods Fluids 1992, 14, 1407–1419. [Google Scholar] [CrossRef]
- Roe, P.L. Approximate Riemann solvers, parameter vectors and different schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Yoon, S.; Jameson, A. Lower-upper Symmetric Gauss Sediel method for the Euler and Navier-Stokers equations. AIAA J. 1988, 26, 1025–1026. [Google Scholar] [CrossRef]
- Spalart, P.R.; Allmaras, S.R. A one-equation turbulence model for aerodynamic flows. In Proceedings of the AIAA the Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. [Google Scholar]
- Lai, J.; Zhao, Z.; Wang, X.; Li, H.; Li, Y. Uniform pitching motion and angular rate effects on transverse jet interaction. Acta Aeronaut. Astronaut. Sin. 2019, 40, 122866. (In Chinese) [Google Scholar] [CrossRef]
- Tang, J.; Zheng, M.; Deng, Y.Q.; Li, B. Grid adaption for flow simulation of complicated configuration. Chin. J. Comput. Mech. 2015, 32, 752–757. [Google Scholar]
- Zhang, P.H.; Tang, Y.; Tang, J.; Luo, L.; Jia, H.Y.; Zhang, Y.B. High Mach number cavity flow simulation based on adaptive unstructured hybrid mesh. J. Beijing Univ. Aeronaut. Astronaut. 2022, 1–12. [Google Scholar] [CrossRef]
- Fluent2020r2/Fluent Theory Guide/Hanging Node Adaption. Available online: https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v202/en/flu_th/flu_th_sec_adapt_hanging.html?q=Figure%2029.3 (accessed on 15 September 2022).
- Daunenhofer, J.F.; Baron, J.R. Grid Adaption for the 2D Euler Equations. In Technical Report AIAA-85-0484; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1985. [Google Scholar]
- De Zeeuw, D.L. A Quadtree Based Adaptively Refined Cartesian-Grid Algorithm for Solution of the Euler Equations. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1993. [Google Scholar]
- Hu, O. Development of Cartesian Grid Method for Complex Compressible Flows and its Applications. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2013. [Google Scholar]
- Tian, S.; Gao, Y.; Dong, X.; Liu, C. Definitions of vortex vector and vortex. J. Fluid Mech. 2018, 849, 312–339. [Google Scholar] [CrossRef] [Green Version]
- Tian, S.; Fu, H.; Xia, J.; Yang, Y. A vortex identification method based on local fluid rotation. Phys. Fluids 2020, 32, 015104. [Google Scholar] [CrossRef]
- Gnemmi, P.; Adeli, R.; Longo, J. Computational Comparisons of the Interaction of a Lateral Jet on a Supersonic Generic Missile. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar] [CrossRef]
- Geng, Y.F. Numerical Simulation of the New Methods of Drag Reduction and Thermal Protection in the Hypersonic Vehicle Design. Master’s Thesis, Beihang University, Beijing, China, 2011. [Google Scholar]
- Zhao, H.Y.; Liu, W.; Ren, B. Numerical simulation of lateral jets with forced pitching oscillation. Chin. Q. Mech. 2007, 28, 363–368. [Google Scholar]











| Mesh Adaptation | Total Number of Mesh Cells | Growth Rate |
|---|---|---|
| Base mesh | 1.71 million | / |
| Once-adapted | 4.32 million | 155.5% |
| Twice-adapted | 14.22 million | 731.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, S.; Peng, Z. Mesh Adaptation for Simulating Lateral Jet Interaction Flow. Aerospace 2022, 9, 781. https://doi.org/10.3390/aerospace9120781
Tian S, Peng Z. Mesh Adaptation for Simulating Lateral Jet Interaction Flow. Aerospace. 2022; 9(12):781. https://doi.org/10.3390/aerospace9120781
Chicago/Turabian StyleTian, Shuling, and Zongzi Peng. 2022. "Mesh Adaptation for Simulating Lateral Jet Interaction Flow" Aerospace 9, no. 12: 781. https://doi.org/10.3390/aerospace9120781
APA StyleTian, S., & Peng, Z. (2022). Mesh Adaptation for Simulating Lateral Jet Interaction Flow. Aerospace, 9(12), 781. https://doi.org/10.3390/aerospace9120781






