Abstract
Analytical target cascading (ATC) is a method for coordinating hierarchical system design optimization with a decomposition-based framework. Since a launch vehicle (LV) is usually powered by two or more stages of rocket motors, the overall design of the LV clearly has a hierarchical structure, including system level (conducted by the general design department) and subsystem level (conducted by the motor stage design department). In particular, the subsystem level contains stage-divided elements rather than discipline-divided elements. Therefore, ATC is inherently suitable for the overall design of the LV. This paper presents an ATC decomposition framework for LV design according to practical engineering. The feasibility of the multi-island genetic algorithm (MIGA) used in the ATC decomposition is verified by a mathematical programming test, in which non-linear programming with the quadratic Lagrangian (NLPQL) algorithm is set as a comparison. The multi-disciplinary analysis modules of a hybrid rocket motor (HRM) propelled LV, including propulsion, structure, aerodynamics and trajectory, are established. A hierarchical decomposition is proposed for this multi-level design with a multi-disciplinary model. The application and optimization results verify the feasibility of the ATC decomposition framework with MIGA in the preliminary design of the LV and the final orbit accuracy is better than that of the MDF method. In addition, the final design schemes also prove that HRMs can be considered as a feasible choice of propulsion system for a small payload at low earth orbit.
1. Introduction
With the increasing demand for small and micro satellites in commercial and military use, small launch vehicles (LVs) with high safety, low cost and fast response ability are flourishing. Hybrid rocket motors (HRMs) use liquid oxidizer and solid fuel, and have the inherent advantages of simple structure; restart and thrust throttling capabilities; and reserving safety for the separating of oxidizer and fuel [1,2]. Many numerical studies and experimental investigations of HRM have been carried out around the world [3,4,5,6] and its propulsion performance has been proven to be suitable for aerospace transport [7,8,9]. Thus, HRM is considered a suitable propulsion system for small LVs, and many studies of small LVs powered by HRMs have been conducted [10,11,12].
The overall design of an LV is a complex problem and contains several physical disciplines, including propulsion, structure, aerodynamics and trajectory [13]. Therefore, multi-disciplinary design optimization (MDO) is always applied to fully consider interdisciplinary interactions [14]. MDO methods were firstly proposed in the area of structural optimization more than 30 years ago. The multiple discipline feasible (MDF) method, as a basic MDO method which is widely used in the area of industrial application, considers the model as a “design black box”. Obviously, the MDF process has the advantages of intuitiveness and comprehensibility. However, when it comes to engineering problems with a complex coupling relationship, the application of the MDF method results in huge computational complexity. Thus, multi-level MDO methods are proposed in order to realize subspace decoupling and parallel optimization [14].
The frameworks of traditional multi-level MDO methods, including concurrent subspace optimization (CSSO), collaborative optimization (CO) and bi-level integrated system synthesis (BLISS), are shown in Figure 1. However, CSSO carries the risk of iteration oscillation without convergence and, moreover, one variable is not able to appear in another subsystem; thus, it is not adapted to industrial application [15]. CO only adapts to the system with loose coupling and analyzes the elements at a low level many times, which results in a significant computing burden [16]. The effectiveness of BLISS directly relies on the degree of system non-linearity and the global derivative needed in BLISS is difficult to obtain [17]. These three MDO methods are mainly developed to solve the design problems of multi-discipline systems more than multi-level systems. Even though traditional MDOs for hierarchical problems have been verified, they cannot be expanded to the design problems with more than two levels, and also have respective disadvantages. Thus, an optimization approach is needed to solve complex problems with large-scale design variables and hierarchical structure.
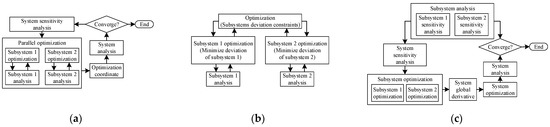
Figure 1.
Frameworks of traditional multi-level MDO methods: (a) CSSO; (b) CO; (c) BLISS.
The analytical target cascading (ATC) method was firstly proposed by Kim et al. in 2003 for multi-level systems with coupling variables [18], which can solve the problem that only double levels are concerned (such as CO) or decomposed only by disciplines (such as CSSO and BLISS). Since then, many relevant theoretical studies of ATC have been carried out in regard to response/linking deviation weighting coefficients, convergence properties and so on [19,20,21,22]. For application, the ATC method in automotive vehicle design was also firstly carried out by Kim et al. in 2003 and provides a framework for addressing large-scale and multi-disciplinary system design problems with a multi-level structure [18]. ATC is also used in simulation-based building design, demonstrating its potential for lending clarity and tractability to the typically complex decision-making problems [23]. A supersonic business jet design problem is developed to demonstrate the flexibility and effectiveness of an ATC formulation presented by Tosserams et al. [24]. ATC is also used in the design of commercial vehicle systems and the results provide useful insight into the feasibility of a target at the upper level and the adequacy of the design space at lower levels [25]. An application of trajectory optimal design has shown that ATC is effective in the nonlinear programming problem with sparse matrix of functional dependence table, and ATC can be combined with integrated design to solve a large-scale optimization problem [26]. A survey of MDO methods in LV design has been carried out and the characteristics of different MDO methods were compared; it was found that ATC is a generic formulation adapted to large-scale problems which can be solved with a multi-level structure [27].
The LV is a typical hierarchical system with 2–4 substages generally. The overall design of the LV is a system level work and the stage designs are subsystem level works. Ref. [28] reported a series of MDO decomposition frameworks based on the LV flight stage, dividing a large and complex optimization problem into multiple single-stage LV optimizations for an elementary trajectory. The design variables of propulsion, aerodynamics, structure and trajectory disciplines and the coupling relationship among the multi-disciplines are fully considered in the subsystem, which provides accurate optimal results of LV design. This paper presents a different decomposition framework based on each HRM stage, including the propulsion calculation and structure estimation of the HRM in the subsystem level and the trajectory and aerodynamics disciplines in the system level. Thus, the design process of each HRM stage is independent and only relative and responsive to the overall design. This characteristic represents the hierarchical relationships in the preliminary design of LV obviously. Therefore, it is potentially suitable for ATC methodology to be used in the design optimization of LV in the preliminary design phase.
In this paper, the ATC method is adopted in the design optimization of the LV powered by three stages of HRMs. An ATC code is developed and the multi-island genetic algorithm (MIGA) is selected as an optimizer in Section 2. The feasibility and properties of MIGA used in ATC-decomposition are also verified using a classic mathematical problem in this section. Section 3 provides a detailed description of the design problem in this study and the discipline analysis mathematical models of propulsion, structure, aerodynamics and trajectory are established. In Section 4, a multi-level and multi-discipline decomposition based on ATC is attempted and the design optimization of a three-stage LV is carried out based on a two-phase optimization strategy. Section 5 reports and discusses the results of the present study.
2. The ATC Method with MIGA
2.1. ATC Method
As mentioned above, ATC is a promising approach to solving complex hierarchical MDO problems [18]. Figure 2 provides the organization of an ATC problem containing N levels, where Pij is the problem of the jth element at the ith level. Each element contains its own target and passes the value of the optimal solution up and down. Therefore, an inner optimization occurs in every single element. Equation (1) shows the set of all ATC variables of the current element; x is the local input variable, t is the target, r is the response, f is the local objective function, π is the relaxation function, Cij is the collection of inferior elements decomposed and based on the current element, g is the local inequality constraint, h is the local equality constraint, xmin and xmax are the minimum value and maximum value of x, respectively, and ε is the number of elements in the same level. A hierarchical organization with elements is created as one outer loop for calculation. The consistency requirements of linking variables are satisfied after several cycles. Thus, the ATC method achieves a final optimal solution of the problem. Figure 3 provides the information communication of one element.
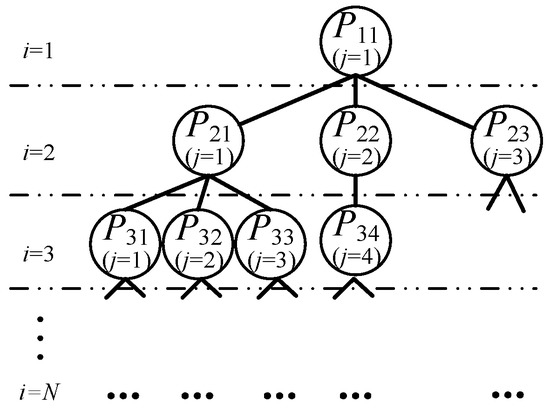
Figure 2.
Organization of an ATC problem.
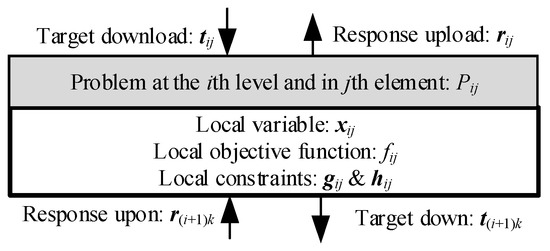
Figure 3.
Information communication of ATC method in one element.
One noteworthy point of ATC is the convergence of system deviation (also called consistency constraint) between elements (not only in two adjacent hierarchies but also in the same level) [29]. The system deviation is caused by independent design in different elements with the same variables (named coupling variables). Different methods are introduced to minimize these deviations [20,21,22], making ATC a feasible methodology with convergence results for a hierarchical multi-disciplinary design. In this paper, we adopt the quadratic penalty function to satisfy consistency constraints, which are described as:
where the weight coefficient wij is updated by:
where k is the iteration number and β is the step size.
2.2. Mathematical Test
A geometrical problem [30] which has the characteristics of multiple dimension and high non-linearity is used to test the ATC code developed in this study. The MDF method is also used as a comparison. In terms of the optimization method, the non-linear programming by quadratic Lagrangian (NLPQL) algorithm is a good choice for the optimization of this problem and has accurate results. However, when it comes to the problem with a complex and hierarchical non-linear system, such as the overall design of LV, the heuristic optimization method is more widely applied [14]. In this study, MIGA is considered as a feasible choice of optimization method with its good global search and quick convergence ability. Therefore, in this section, each MDO method (MDF/ATC) is applied with two different optimization algorithms, including MIGA and NLPQL and the performance of different methods is compared and discussed. Equation (4) shows the original mathematical test containing six inequality constraints and four equality constraints.
The design variables of the MDF method are selected as x4, x5, x7, x8, x9, x10, x11, x12, x13, x14 and the target f is calculated with the MDF analysis model. For the ATC method, the problem is decomposed into two levels (the parent level and the child level) and each element at each level contains its own mathematical model. Figure 4 shows the framework of the ATC decomposition, where superscript L is the abbreviation of ‘from lower level’, superscript U is the abbreviation of ‘from upper level’, subscript ss1 is the abbreviation of ‘from subsystem1′ and subscript ss2 is the abbreviation of ‘from subsystem2′. For both methods, the iteration is regarded as being convergent when the deviation of the objective function value is under 10−3 at continuous five times. Furthermore, all of the system deviations of the ATC model need to be less than 5 × 10−4 for a consistency of linking variables between each element.
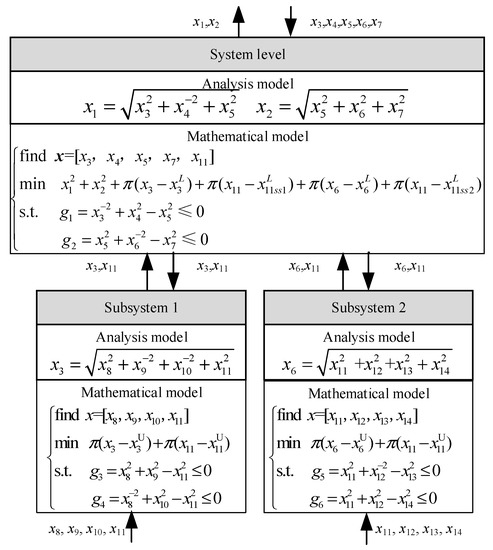
Figure 4.
ATC decomposition framework of the example.
The initialization of NLPQL is given in the form of a vector of variables as Table 1 shows, and the search starts at 0.001 steps from the initial point. In terms of the algorithm settings of MIGA, the number of islands is set as 15, the size of each subpopulation is 15, the mutation rate is set as 0.01 and the crossing-over rate is 1.0. The penalty function takes the form of external penalty function, including the setting of penalty multiplier and penalty index.

Table 1.
The initialization of NLPQL.
2.3. Discussion of the Mathematical Test
2.3.1. Statement of Calculation
Table 2 shows all of the results which keep four digits after the decimal point; the positive sign ‘+’ in Table 2 refers to the value above zero while the minus sign ‘−’ means the value is below zero. It needs to be emphasized that the original results of the ATC method contain system deviations, which are caused by linking variables (x11) and the targets and responses at neighboring levels (x3, x6, x11). However, the non-closure of variables is inadmissible in industrial applications. To thoroughly eliminate the system deviations, we recalculated the results of the ATC method through the MDF integral model with their local design variables in each element. The values of the variables which lead to system deviations are selected according to two principles. For the linking variables, the values at the lower level (refer to bigger i) and at the previous element (refer to smaller j) are prioritized. For the targets and responses between the neighboring levels, the local values are not adopted while the values are calculated by the related elements at lower level.

Table 2.
Results of the mathematical test.
2.3.2. Algorithm Comparison: MIGA and NLPQL
In terms of the MDF method, MIGA achieves a smaller objective function while the constraint values of NLPQL have smaller distance (less than −0.0001) away from the boundary (0.0000), which indicates that MIGA represents more effectiveness in global searching. Since the problem of LV design has a much higher non-linear degree than this example, MIGA is considered a better optimization method to be applied. For the ATC method, MIGA acquires only 0.32% increment compared to the NLPQL algorithm, which also proves the feasibility of MIGA as an algorithm on a multi-level system with ATC decomposition.
2.3.3. Comparison of MDO Methods: ATC and MDF
Based on the reasonable results produced by MIGA and NLPQL, the quadratic penalty function is proved to be suitable for ATC consistency constraints. At the same convergence precision of optimization and consistency constraints, the results of ATC obtain proper optimal targets (17.5898 with NLPQL and 17.6457 with MIGA), both of which have less than 3% difference from the theoretical value (17.5887). As mentioned above, the recalculation thoroughly eliminates the system deviations and obtains results slightly different from the original results of ATC. Another obvious effect of recalculation is that the original ATC results are well satisfied with the constraints, while parts of the constraints slightly overflow (but no more than +0.0002) because of the recalculation. The dissatisfaction can be tolerated in engineering design when these constraints are weak constraints, allowing exceeding of the boundary slightly after recalculation.
2.3.4. Efficiency of ATC Method
Figure 5 shows the convergence iterations of the ATC cycle with MIGA. Fourteen cycles proceed with ATC decomposition, which increases the calculation burden of global optimization. However, the application of the ATC method can realize parallel calculation of elements at a lower level at the same time. Each element has a smaller analysis scale (one formula at the child level and two formulas at the parent level) than the entire MDF analysis scale (four formulas). Thus, the model with a smaller scale enables the optimization of each element (at each level) to be simpler in ATC elements than that in MDF, which means that the calculation burden from ATC decomposition may be solved through the small element scale and the parallel calculation. This implies that when the system hierarchy and discipline structure become more complex, ATC is a possible method to solve the multi-level MDO problem and MIGA is an effective and precision-acceptable algorithm for both MDF and ATC methods.
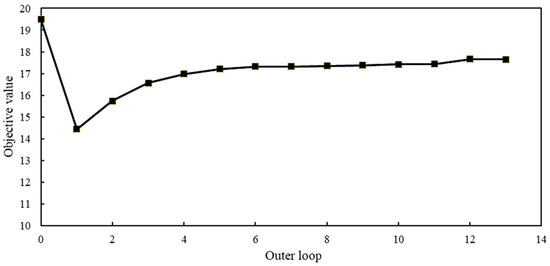
Figure 5.
Iterative curve of ATC cycle with MIGA.
3. Analysis Modules for the Overall Design of LV Powered by HRMs
3.1. LV Configuration
Figure 6 illustrates the baseline configuration of LV powered by three stages of HRMs [13]. A no-wing aerodynamic shape is selected. Two inter stage cabins are used to connect the three HRMs. A payload and its adapter, electronic avionic devices and attitude control systems are installed in a head module. Advanced composite materials, such as carbon fiber composite, aluminum alloy and titanium alloy, are adopted to reduce the total structure weight.

Figure 6.
Typical HRM-powered LV configuration.
3.2. Multi-Level and Multi-Discipline Characteristic Analysis of LV Design
Three stages of HRMs constitute the LV’s main body structure. Different from the strong coupling between each body structure in the design of a single-stage aircraft or an automotive vehicle, LV joins each motor stage with inter-stage sections, which have loose restrictions in size and other coupled parameters. In particular, all motor stages have the same design logic when the propulsion systems are of the same type. Accordingly, in the practical design process, with the technical requirements given by the overall design results, the three stages will be designed and then their performances will be returned to overall design as feedback, as shown in Figure 7, where Ri means the requirement with regard to the subsystem, and Pi is the performance of the subsystem. Therefore, the LV design shows obvious multi-level characteristics, in which the overall design is a system level process while the motor stage designs are subsystem level processes.
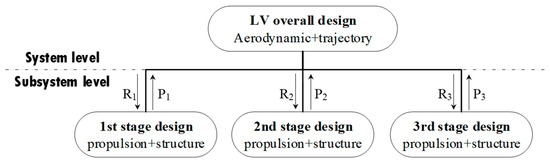
Figure 7.
Flowchart of LV design.
Apart from the multi-level characteristic, the design of LV also involves many disciplines. In the system level, the overall mass, size and trajectory parameters are required to obtain the final orbit parameters; thus, the aerodynamic performance estimation and trajectory simulation are needed. In the subsystem level, the propulsion performance and the mass of the stage are more concerned; thus, the propulsion and stage structure design are needed. Therefore, the discipline analysis model, including propulsion, structure, aerodynamic and trajectory, are established as the basis of the design optimization.
3.3. Propulsion
The propulsion model for the HRM design includes three main modules: the grain design, the preliminary design of the thrust chamber and the interior ballistic simulation according to Ref. [12]. Figure 8 shows the general process of HRM design. Through the propulsion model, the average chamber pressure pc, the average specific impulse Isp, the average thrust F, the motor operating time tmotor and the other propulsion performance parameters are computed from the initial design parameters, including initial thrust Fini, initial oxidizer to fuel ratio OFini, nozzle expansion ratio ε and initial grain shape parameters, such as the diameter of the grain Df and the thickness of the grain e.
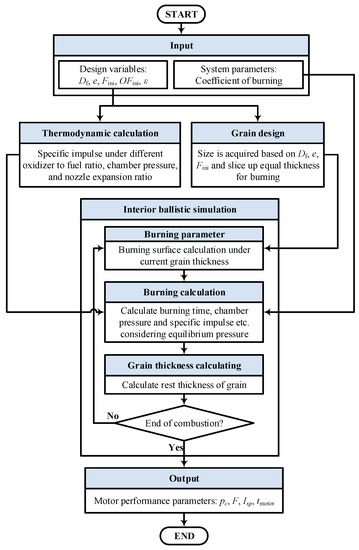
Figure 8.
Design process of HRM.
Specifically, a tube-shaped grain is chosen as the grain shape for its stably enlarging burning. As oxidizer and fuel, 98%H2O2 and HTPB, respectively, are used in this study because of their high specific impulse and non-toxicity. The equilibrium flow is considered in the interior ballistic simulation and the chamber pressure pc can be obtained as
where peq is the equilibrium pressure, is the regression rate of the fuel grain, c* is the characteristic velocity provided by thermodynamic calculation, Vc is the free volume of chamber (or chamber inflation volume), R is the specific gas constant, Tf is the propellant burning temperature, ṁo is the mass flow rate of the oxidizer, ṁf is the mass flow rate of the fuel and At is the nozzle throat area. While a design altitude is given to determine the external pressure of the nozzle, a reasonable average thrust is acquired at each stage of the HRM.
Further, Ref. [13] provides the validation of the internal ballistic simulation model of the HRM comparing with the data of HRM firing tests, which indicates that the model can be used as the basis for the overall design of HRM in the paper.
3.4. Structure
The baseline configuration of the LV is shown in Figure 6. Three HRMs make up the main structure of the LV. Apart from them, the mass and dimension of the other components, including payload adapters, electronic avionics device and attitude control equipment, inter-stages and tail cabin, are set as constant values based on engineering experience.
As Figure 9 shows, six components are concerned in a typical HRM system, including a gas bottle, an oxidizer tank, a set of connecting pipe and valve, a thrust chamber (including head, panel, fuel grain and chamber case), a nozzle and a skin [13]. The first and second stages adopt the tandem structure of gas bottle, oxidizer tank and chamber for a minor diameter, while the third stage adopts the parallel structure to reduce the length to the diameter ratio. The main dimension and mass parameters of the HRM components are deduced from the propellant mass and the pressure relationship among the chamber, the oxidizer tank and the gas bottle.
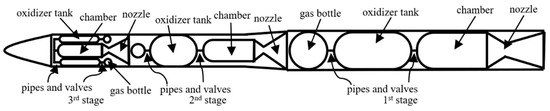
Figure 9.
Structure in detail of LV powered by three stages of HRMs.
3.5. Aerodynamics
The 1976 U.S. standard atmosphere model is coded in the aerodynamic module to obtain the atmosphere characteristics [31]. A small attack angle assumption is used to calculate the aerodynamic force, while the approximation aerodynamic formulas of “Titan II” rocket varying with the Mach number [32] are applied to acquire the drag coefficient CD and the lift coefficient CL.
3.6. Trajectory
A three-degrees-of-freedom (3DOF) point trajectory is implemented in the trajectory simulation. Until the payloads are released into the orbit, a four-phase flight strategy powered by HRM, including a vertical taking-off phase, a program turn phase, a zero-attack-angle flight phase and a program pitch phase, is adopted. The pitch angle φ, the attack angle α and the trajectory tilt angle ϑ of the four phases can be obtained with Equation (6).
where αmax is the maximum attack angle during the program turn phase, c is the control parameter of the attack angle during program turn phase, tendver is the end time of the vertical take-off phase, t is the flying time, vy is the velocity in the y-direction, vx is the velocity in the x-direction and ωφ is the pitch angular velocity during the program pitch phase.
Moreover, a free glide phase without power is considered after the second stage flight to turn the velocity direction from the radial direction to the tangential direction of the required orbit, and the control equation is
The state variables of the LV during the flight phase mainly include the time after launching, velocities in three directions, positions in three directions, attack angle, pitch angle, path angle, total mass and dynamic pressure. The 3DOF kinematical and dynamical differential equations are applied in trajectory simulation and the numerical solutions of the state variables at different times are acquired. Then, a feasible time-varying trajectory is generated.
Further, Refs. [12,13] provide more details about the analysis modules of the HRM and LV overall design and it should be noted that the analysis modules above are preliminary and generally sufficient in the LV early design phase.
4. Design Optimization
4.1. Target, Design Variables and Constraints
In this paper, the mission of the LV is to insert a 100 kg payload into a 300 km circle orbit. The overall take-off mass m0 is set as the optimal target since it is not only an important performance parameter of LV, but also has a direct effect on the total cost. The initial thrust to weight ratio FMi of each stage, length to diameter ratio LD, the relative error of orbit height ΔH and the eccentricity eorb are selected as constraints in order to comprehensively consider the requirements of acceleration performance, aerodynamic configuration, structural strength and orbit parameters. To protect the payload, the maximum lateral and longitudinal overload, Nxmax and Nymax, and the maximum dynamic pressure qmax are also considered as constraints. Therefore, the mathematical model of the design optimization is shown as Equation (8), where x is the vector of design variables.
According to Section 3.3, Table 3 shows the selected design variables of the LV design and their ranges, which are imported into the propulsion discipline to calculate the propulsion performance.

Table 3.
The range of design variables of LV design.
4.2. ATC Method
In this paper, the ATC design model of LV is decoupled hierarchically based on motor stages. This study also proposes two levels—a system level and a subsystem level—on the basis of the multi-level characteristic of LV design detailed in Section 3.1. As mentioned, ATC has been used in the design of single-stage aircraft such as supersonic business jets, where the ATC framework is decomposed by disciplines (one discipline in each element), as Figure 10 shows. However, multi-stage LV has the characteristic of containing several motor stages with the same design disciplines. In particular, all motor stages have the same design logic if the propulsion systems are of the same type. Moreover, different from strong coupling between each structure in the design of a single-stage aircraft or an automotive vehicle, the rocket joins each motor by inter-stage sections, which indicates that the coupling in size is relatively loose, and there are fewer other coupling relationships at the same time. Thus, a stage-divided ATC framework is established, as shown in Figure 11.
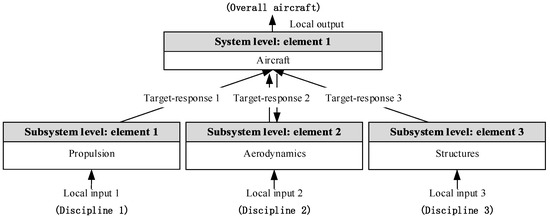
Figure 10.
ATC formulations without hierarchical coupling for single-stage aircraft.
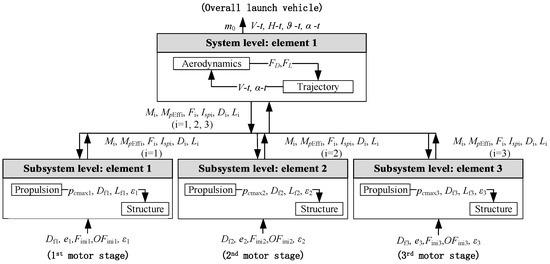
Figure 11.
ATC decomposition framework of LV design based on multi-stages.
4.2.1. Global Configuration
The hierarchically decomposed optimal framework of LV design includes the decomposed information of hierarchical relationships, element communications and interdisciplinary couplings. Specifically, in the system level, V is the actual velocity and H refers to the actual height. M, MpEff, F, Isp, D and L refer to the mass, effective propellant mass, average force, average specific impulse, diameter and length of each motor stage, respectively. Moreover, in the subsystem level, FD is the drag force, FL is the lift force, pcmax is the maximum chamber pressure, Lf is the length of the fuel grain and subscript i represents the stage number.
4.2.2. System Level
The multidisciplinary analysis indicates that a strong coupling happens between aerodynamics and trajectory, as well as between propulsion and structure. Moreover, trajectory is a discipline that requires the results of every other discipline as the inputs. The only element at the system level contains trajectory and aerodynamics and provides targets for elements at the subsystem level. The current attack angle and velocity are strong coupling between aerodynamics and trajectory and are provided in aerodynamics during the trajectory simulation. The drag force and the lift force are calculated and fed back into the trajectory. Moreover, Figure 11 demonstrates that no local variable is imported at the system level.
4.2.3. Subsystem Level
As Figure 11 shows, elements at the subsystem level are divided into three HRM stages. Each element has five local variables, including the outer diameter of the grain, the thickness of the grain, the initial force, the initial oxidizer to fuel ratio and the expansion ratio of the nozzle. Through propulsion discipline, the performance of the HRM is obtained and interdisciplinary variables are given into the structure discipline for mass and size calculation. At the subsystem level, the responses of each element for the upper level are the average specific impulse, the average force at design altitude, the total mass, the effective propellant mass, the outer diameter and the total length of each motor stage. The maximum values of the outer diameter and length of the LV at the current time are used for aerodynamic calculation.
4.2.4. System Deviations
System deviations derive from two aspects: the linking variables (referring to the same variable in different elements) at the same level and the responses and targets at neighboring levels. On account of the high independence degree between each HRM stage, there is no same design variable between two elements at the subsystem level. However, 18 coupling parameters between the system level and the subsystem level require consistency constraints. These coupling parameters are all responses at the subsystem level, which represent the results of the HRM design. Table 4 provides a reasonable deviation limit based on LV design experience. Percentage limits are applied to those parameters which have different orders of magnitude in different stages, while constant value limits are applied to other parameters with less variation in value in different stages. Under some circumstances, while the design of HRM is deemed a better result at the subsystem level than at the system level in terms of a specific parameter, the value of the deviation of the parameter is set to zero, which means it absolutely satisfies the deviation limits. For instance, the subsystem level provides a smaller total mass, a bigger effective propellant mass, a bigger average thrust and a bigger average specific impulse than that of the system level.

Table 4.
Parameter deviation limits of the LV design.
4.2.5. ATC Mathematical Model
Considering the calculation amount of the trajectory simulation, it is not cost-effective to search for a trajectory for every point during LV design iteration history. Therefore, some approaches are proposed to solve the problems of staging optimization and trajectory optimization separately [33,34]. In this context, a two-phase design optimization [13] is used to improve design efficiency under the ATC framework. In the first phase, the ATC decomposition and orbit capacity calculation (OCC)-based design optimization is carried out. The velocity increment of the LV is obtained with the Tsiolkovsky rocket equation considering velocity loss caused by air drag and gravity effect instead of the time-consuming trajectory simulation. The detailed structure parameters (including size and weight) and propulsion performance are acquired through the design optimization in this phase. However, an over-conservative or over-aggressive result will be produced if the estimated value of the velocity loss is too large or too small. Therefore, an extra trajectory optimization is needed to provide a feasible trajectory based on a given LV design. In the second phase, a scheme trajectory verification (STV)-based design optimization is applied to verify the feasibility of the velocity estimation at the OCC phase through a 3DOF trajectory simulation, where the detailed flight parameters are obtained.
- A.
- OCC-based design optimization phase
To achieve an adequate velocity for the required orbit, the actual velocity increment Vact at the shutdown point should be bigger than the theory velocity increment Vorb needed at the index orbit height and it is added to the constraints. Since there is no trajectory simulation in this phase, constraints of the trajectory are not considered. Figure 12 shows the mathematical model in each element both at the system level and at the subsystem level, where superscripts U and L refer to the contrast value from the upper and lower levels. For a better rocket motor, the objective of the element optimization at the system level is the minimization of the take-off mass as well as consistency in system parameter deviations, while the objective of each element optimization at the subsystem level is the minimization of the consistency deviation.
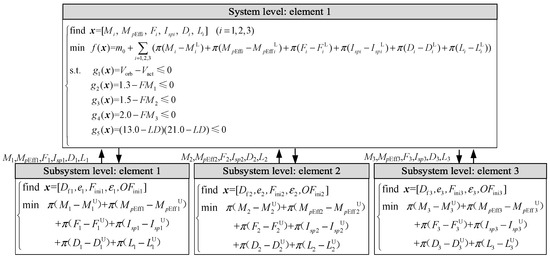
Figure 12.
ATC mathematical models at different levels.
- B.
- STV-based design optimization phase
Five design variables are chosen in the STV-based design optimization phase as Equation (9) shows, including the maximum attack angle during the program turn phase, the control parameter of attack angle during the program turn phase, the fixed pitch angular velocity during the second and third stage flight ωφ2 and ωφ3 and the free glide time tglide after the second HRM shutdown. The objective of the optimization is to minimize the final orbit eccentricity. To successfully enter the orbit, constraints of the trajectory are used in this phase as Equation (9) shows, where Horb corresponds to the target height of the orbit.
4.3. MDF Method
As a contrast, the two-phase design optimization strategy, as Section 4.2.5 shows, is also adopted in this part based on the MDF method. Moreover, the design variables, target and constraints of the optimization are exactly the same as the ATC method. At the first design phase (OCC-based design optimization phase), a serial design strategy is used as shown in Figure 13. The corresponding MDF mathematical model is shown in Equation (10). The mathematical model of the second phase (STV-based design optimization phase) is the same as the ATC one in Section 4.2.5.
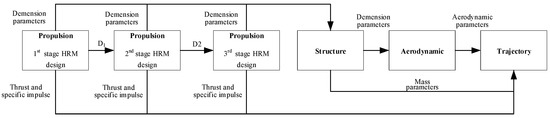
Figure 13.
Serial design strategy of LV design.
5. Results and Discussion
Both of the above methods are compared in terms of their performance in LV design optimization. Each stage of HRM is described in detail in order to investigate the performance of HRM. We also use the trajectory performance to verify each optimal design scheme. Relative difference (RD) is the most common measurement used in this section and the MDF results function as the control group, similar to the practice in Ref. [13].
5.1. Comparison of the Two MDO Methods
Table 5 shows the optimal results of the two methods, including MDF and ATC. To eliminate the system deviations, the design results of ATC are recalculated in the same way as in Section 2.3. Each method shows the feasibility by providing a reasonable solution and thus ATC is proved to be a feasible method applied to the LV overall design. The difference in target m0 between the two methods does not exceed 0.4%, which indicates that the ATC method also has the ability to provide an optimal LV design. The ATC solution achieves a value of actual velocity increment Vact 0.9% higher than that of the MDF solution, which indicates that the ATC method obtains a more conservative design. The results of FM using the ATC method show a better capacity of acceleration in the first and third stage flight, which is more beneficial for reducing the burning time of the motor. The results of LD prove that both solutions have a suitable geometrical profile for both structure and aerodynamics.

Table 5.
Optimal results of LV design using the two different methods.
Table 6 demonstrates the actual system deviation value of the ATC method, which satisfies all the convergence limits in Table 4. If the circumstances mentioned in Section 4.2.4 are satisfied, we label ‘0′ as the favorable deviation, which can be accepted because of the ‘better HRM performances’.

Table 6.
System deviation values of ATC method.
5.2. HRM Performance Analysis
Table 7 shows the main performance of the HRM at each stage using the two MDO methods separately. Each HRM in a different element at the subsystem level successfully realizes parallel calculation at the same time. As the optimal results show, the RDs of the mass and effective propellant mass at each stage do not exceed 2.5% and 3.2%, respectively. Moreover, the RDs of stage diameter at each stage do not exceed 2.8%. In addition, it is obvious that all the RDs of stage length and stage diameter have negative correlations, which implies that the optimal designs using the same MDO method have a similar scale variation trend. By using the definite propellant formulation and at the same design altitude, nearly the same average specific impulses can be achieved and it is also close to the optimum value of 98%H2O2/HTPB combination. This verifies that the average specific impulse is a parameter related to the propellant physical properties, but not significantly related to the initial oxygen to fuel ratio, the expansion ratio of the nozzle and the chamber pressure. Moreover, the RDs of working time and the average force also have negative correlations, which reveals that the optimal designs of the two MDO methods tend to be the same scale in terms of the effective propellant mass and total mass at each stage, since the total impulse of the force and time tends to be constant.

Table 7.
HRM performance at each stage.
5.3. 3DOF Trajectory Verification
The 3DOF trajectory calculation is the second phase in the two-phase optimization strategy, which is also regarded as a reasonability verification of the velocity increment estimation. MIGA is also used in this verification to choose a suitable set of design variables. For the index of the 300 km circle orbit, the ranges of design variables and the optimal results are all shown in Table 8. According to the optimal results, the ATC method achieves a smaller error of orbit height (only 0.27%) compared with the MDF method (4.9%), while the orbit eccentricity of the ATC method is larger (3.12 × 10−4 compared with 1.22 × 10−5 for the MDF method). Considering both of the parameters, this indicates that the optimal results of the ATC method show higher orbit injection accuracy. In terms of the velocity increment Vact, the maximum error between the result of trajectory verification and the result of velocity estimation does not exceed 0.8%, which shows that the two-phase optimization strategy is feasible and efficient in the LV design process. Moreover, the difference in take-off mass m0 of the two methods is relatively small and the result corresponds to the lightest mass of the HRM-powered LV needed to enter the index orbit.

Table 8.
Ranges of design variables and optimal results of trajectory simulation.
Figure 14 reveals that both optimal designs of the MDF method and the ATC method process a feasible scheme trajectory. As Figure 14a shows, both designs need no more than 500 s to enter the orbit, while the ATC design needs more time to achieve the final velocity. For the first and second stage flight, ATC design reaches a faster speed within smaller flying time, proving a better acceleration quality than that of the MDF design. However, too fast acceleration performance in ATC design results in a lower height at the end of second stage flight, as shown in Figure 14b. Thus, this leads to the longer time at the free glide stage in the ATC design than in MDF design, which directly causes the longer time to reach the payload releasing point. Correspondingly, in terms of the distribution of velocity increment at each stage, the ATC method tends to allocate more velocity increment to the first and second stage flight. The velocity of ATC method when the first HRM shuts down is 8.7% higher than that of MDF method, while the value is 5.5% when the second HRM shuts down.
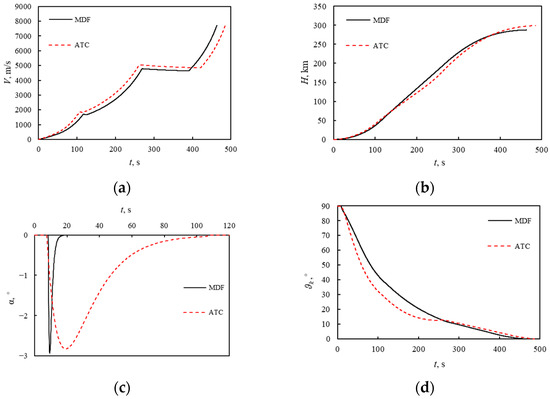
Figure 14.
Scheme trajectory curves: (a) Actual velocity; (b) Actual flight altitude; (c) Attack angle in program turn phase; (d) Tilt angle.
According to Figure 14c, ATC design processes a smoother turn in the program turn phase. Compared with the MDF method, the ATC method gives a longer turning time while the maximum angle of attack is similar, which leads to a rapid decline in tilt angle at the first stage flight, as Figure 14d shows. Thus, at the end of the first stage flight, the tilt angle of the ATC method is reduced to about 30°, while that of the MDF method is about 38°. At the same time, the angular rate of pitch angle at the second stage given by ATC method (0.04335°/s) is significantly smaller than that given by the MDF method (0.21604°/s), which slows down the downward trend of tilt angle. The tilt angle of the ATC method (12.8°) is similar to that of the MDF method (11.7°) when the second HRM shuts down. This difference in flight strategy leads to altitude of the ATC method being lower in the middle of the flight, which is consistent with the result presented in Figure 14b. ϑk-t curves in Figure 14d also indicate that both designs process a good performance for the smooth injection, based on a similar third HRM design.
6. Conclusions
In this paper, the ATC methodology was successfully applied to the LV overall design. A mathematical example was used to verify the feasibility of MIGA in non-linear multi-level design optimization. The present study established an ATC-decomposed multi-level and multi-disciplinary framework for LV overall design and this hierarchical framework was calculated using a two-phase design optimization strategy.
The optimization performance of ATC with MIGA was verified through the mathematical example and the quadratic penalty function method and recalculation was feasible for the ATC methodology. The ATC system decomposition was based on the interactive design mode of the aerospace department and provides complete digital design at the preliminary phase. The proposed hierarchical ATC framework decomposed according to the rocket stage was feasible for the multi-stage LV design problem and the optimization process was effective. The two-phase design optimization strategy, including an OCC phase and an STV phase, was proven to be feasible when considering the ATC process. The results show that HRMs have the potential to be applied as the propulsion system for a small payload at low earth orbit. Compared with the MDF method, the ATC method shows a capacity of parallel computing without nonhierarchical target–response coupling. Thus, the ATC method possesses the potential ability of efficiency improvement through reasonable system decomposition.
However, further study is still needed to solve the rational consistency constraints in the ATC method, which will cause convergence difficulty if it is too small or will cause too large an error by recalculating (in order to completely eliminate deviations of linking variables) if it is too big. Moreover, as the above research focuses on the preliminary design phase of the LV, the applicability of the methodology above in a high fidelity analysis model also needs further exploration.
Author Contributions
Conceptualization, P.W. and H.Z.; methodology, P.W. and W.X.; software, P.W.; validation, P.W.; investigation, P.W. and W.X.; resources, H.T. and G.C.; data curation, P.W. and W.X.; writing—original draft preparation, P.W. and W.X.; writing—review and editing, H.Z. and H.T.; supervision, G.C.; project administration, G.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Funds for the Central Universities.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Altman, D. Hybrid rocket development history. In Proceedings of the 27th AIAA/SAE/ASME/ASEE Joint Propulsion Conference, Sacramento, CA, USA, 24–26 June 1991. [Google Scholar]
- Davydenko, N.A.; Gollender, R.G.; Gubertov, A.M.; Mironov, V.V.; Volkov, N.N. Hybrid rocket engines: The benefits and prospects. Aerosp. Sci. Technol. 2007, 11, 55–60. [Google Scholar] [CrossRef]
- Marquardt, T.; Majdalani, J. Review of Classical Diffusion-Limited Regression Rate Models in Hybrid Rockets. Aerospace 2019, 6, 75. [Google Scholar] [CrossRef]
- Okninski, A.; Surmacz, P.; Bartkowiak, B.; Mayer, T.; Sobczak, K.; Pakosz, M.; Kaniewski, D.; Matyszewski, J.; Rarata, G.; Wolanski, P. Development of Green Storable Hybrid Rocket Propulsion Technology Using 98% Hydrogen Peroxide as Oxidizer. Aerospace 2021, 8, 234. [Google Scholar] [CrossRef]
- Viscor, T.; Kamps, L.; Yonekura, K.; Isochi, H.; Nagata, H. Large-Scale CAMUI Type Hybrid Rocket Motor Scaling, Modeling, and Test Results. Aerospace 2022, 9, 1. [Google Scholar] [CrossRef]
- Zhu, H.; Xiao, M.Y.; Zhang, J.H.; Cai, G.B. Uncertainty design and optimization of a hybrid rocket motor with mixed random-interval uncertainties. Aerosp. Sci. Technol. 2022, 128, 107791. [Google Scholar] [CrossRef]
- Zhu, H.; Tian, H.; Cai, G.B.; Bao, W.M. Uncertainty analysis and design optimization of hybrid rocket motor powered vehicle for suborbital flight. Chin. J. Aeronaut. 2015, 28, 676–686. [Google Scholar] [CrossRef]
- Zhu, H.; Tian, H.; Cai, G.B. Hybrid uncertainty-based design optimization and its application to hybrid rocket motors for manned lunar landing. Chin. J. Aeronaut. 2017, 30, 719–725. [Google Scholar] [CrossRef]
- Casalino, L.; Masseni, F.; Pastrone, D. Optimal Design of Electrically Fed Hybrid Mars Ascent Vehicle. Aerospace 2021, 8, 181. [Google Scholar] [CrossRef]
- Kamps, L.; Hirai, S.; Nagata, H. Hybrid Rockets as Post-Boost Stages and Kick Motors. Aerospace 2021, 8, 253. [Google Scholar] [CrossRef]
- Casalino, L.; Masseni, F.; Pastrone, D. Hybrid Rocket Engine Design Optimization at Politecnico di Torino: A Review. Aerospace 2021, 8, 226. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, P.C.; Xu, W.L.; Zhang, Y.J.; Tian, H.; Cai, G.B. Design Optimization and Parameter Analysis of a Hybrid Rocket Motor-Powered Small LEO Launch Vehicle. Int. J. Aerosp. Eng. 2021, 2021, 5574436. [Google Scholar] [CrossRef]
- Wang, P.C.; Tian, H.; Zhu, H.; Cai, G.B. Multi-disciplinary design optimization with fuzzy uncertainties and its application in hybrid rocket motor powered launch vehicle. Chin. J. Aeronaut. 2019, 33, 1454–1467. [Google Scholar] [CrossRef]
- Yao, W.; Chen, X.Q.; Luo, W.; Tooren, M.V.; Guo, J. Review of uncertainty-based multidisciplinary design optimization methods for aerospace vehicles. Prog. Aerosp. Sci. 2011, 47, 450–479. [Google Scholar] [CrossRef]
- Yi, S.I.; Shin, J.K.; Park, G.J. Comparison of MDO methods with mathematical examples. Sruct. Multidiscip. Optim. 2008, 35, 391–402. [Google Scholar] [CrossRef]
- DeMiguel, V.; Murray, W. A local convergence analysis of bilevel decomposition algorithms. Optim. Eng. 2006, 7, 99–133. [Google Scholar] [CrossRef]
- Zhao, M.; Cui, W.C. On the development of Bi-Level Integrated System Collaborative Optimization. Sruct. Multidiscip. Optim. 2011, 43, 73–84. [Google Scholar] [CrossRef]
- Kim, H.M.; Michelena, N.F.; Papalambros, P.Y.; Jiang, T. Target cascading in optimal system design. J. Mech. Design. 2003, 125, 474–480. [Google Scholar] [CrossRef]
- Michalek, J.J.; Papalambros, P.Y. Weights, norms, and notation in analytical target cascading. J. Mech. Design. 2005, 127, 499–501. [Google Scholar] [CrossRef]
- Michelena, N.; Park, H.; Papalambros, P.Y. Convergence properties of analytical target cascading. AIAA J. 2003, 41, 297–905. [Google Scholar] [CrossRef]
- Zhang, X.L.; Jiang, P.; Zheng, J.; Li, Y. Analytical target cascading based on the quadratic exterior penalty method for complex system design. Adv. Mater. Res. 2012, 544, 164–169. [Google Scholar]
- Kim, H.M.; Wei, C.; Wiecek, M.M. Lagrangian coordination for enhancing the convergence of analytical target cascading. AIAA J. 2006, 44, 2197–2207. [Google Scholar] [CrossRef]
- Choudhary, R.; Malkawi, A.; Papalambros, P.Y. Analytic target cascading in simulation-based building design. Automat. Constr. 2005, 14, 551–568. [Google Scholar] [CrossRef]
- Tosserams, S.; Kokkolaras, M.; Etman, L.F.P.; Rooda, J.E. A nonhierarchical formulation of analytical target cascading. J. Mech. Design. 2010, 132, 051002. [Google Scholar] [CrossRef]
- Kang, N.; Kokkolaras, M.; Papalambros, P.Y.; Yoo, S.; Na, W.; Park, J.; Featherman, D. Optimal design of commercial vehicle systems using analytical target cascading. Sruct. Multidiscip. Optim. 2014, 50, 1103–1114. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.P.; Zhang, H.J.; Guo, Y.H. Trajectory optimization using analytical target cascading. J. Mech. Design. 2017, 139, 124501. [Google Scholar] [CrossRef]
- Balesdent, M.; Bérend, N.; Dépincé, P.; Chriette, A. A survey of multidisciplinary design optimization methods in launch vehicle design. Sruct. Multidiscip. Optim. 2012, 45, 619–642. [Google Scholar] [CrossRef]
- Balesdent, M.; Bérend, N.; Dépincé, P. Stagewise multidisciplinary design optimization formulation for optimal design of expendable launch vehicles. J. Spacecr. Rocket. 2012, 49, 720–730. [Google Scholar] [CrossRef]
- Han, J.; Papalambros, P.Y. A note on the convergence of analytical target cascading with infinite norms. J. Mech. Design 2010, 132, 034502. [Google Scholar] [CrossRef]
- Beightler, C.S.; Phillips, D.T. Applied Geometric Programming; John Wiley and Sons, Inc.: New York, NY, USA, 1976. [Google Scholar]
- Krueger, A.J.; Minzner, R.A. A mid-latitude ozone model for the 1976 U.S. Standard Atmosphere. J. Geophys. Res. 1976, 81, 4477–4481. [Google Scholar] [CrossRef]
- He, L.S.; Xu, D.J. Solid Ballistic Missile and Launch Vehicle Conceptual Design; Beihang University Press: Beijing, China, 2017. [Google Scholar]
- Jamilnia, R.; Naghash, A. Simultaneous optimization of staging and trajectory of launch vehicles using two different approaches. Aerosp. Sci. Technol. 2012, 23, 85–92. [Google Scholar] [CrossRef]
- Ullah, R.; Zhou, D.Q.; Zhou, P.; Hussain, M.; Sohail, M.A. An approach for space launch vehicle conceptual design and multi-attribute evaluation. Aerosp. Sci. Technol. 2013, 25, 65–74. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).