Mitigating Forced Shock-Wave Oscillation with Two-Dimensional Wavy Surface

Abstract

Oscillating flow is one challenge for wide-Mach-number-range flight with supersonic/hype-rsonic vehicles. Aiming to mitigate the large-amplitude forced shock-wave oscillation, a 2D wavy surface has been implemented onto the flat-bottomed wall of the Sajben diffuser under downstream pressure disturbance. The oscillating SBLI in the diffuser is captured using the finite volume method with the second-order implicit dual-time-stepping method. Impacts of the wavy surface on the forced shock-wave oscillation are numerically investigated. It is found that increasing the wavy surface’s depth benefits mitigation of the shock-wave oscillation amplitudes on the walls under the given conditions, but that decreasing the wavy surface’s length may increase or decrease the oscillation amplitudes, depending on the specific value. The mitigating mechanism is interpreted from two viewpoints, i.e., the shock-wave stability and the work performed by a moving shock-wave. The transient second shock-wave temporally appears in the flow field and can be explained by the post-shock expansion.

1. Introduction

Wide-Mach-number-range flight is one of the most important tendencies of supersonic/hypersonic aircraft. Challenges arise when the vehicles take off from ground with zero speed, and go through transonic and supersonic climb, up to hypersonic cruise, e.g., the oscillating flow in the supersonic inlet [1,2]. The undesirable unsteady flow is either due to the self-sustained shock-wave oscillation or the forced shock-wave oscillation. The self-sustained shock-wave oscillation occurs with constant inflow and outflow conditions [3]. For example, the “buzz” problem prevents the airflow from entering a supersonic intake of a ramjet engine and may disastrously trigger engine shut-off [4]. Fortunately, it can be eliminated from the aircraft using a delicate wall profile design or some flow control methods, e.g., periodic injection [5]. However, the forced shock-wave oscillation [6] cannot be easily cleared from the aircraft engine. This phenomenon mainly occurs under varying downstream flow conditions. The forced shock-wave oscillation may not cause an engine shut-off, but it leads to performance fluctuation. Meanwhile, excitation loads induced by the forced shock-wave oscillation pound on the structures and may give rise to a structural fatigue problem, or even structural failure. A typical source of the external disturbance is back-pressure perturbation due to unsteady downstream combustion [7] in a ramjet engine [8] or a pulse detonation engine [9]. Because the unsteady air–fuel mixing is crucial to a high-performance combustion chamber, the disturbance pressure wave cannot vanish, and the forced shock-wave oscillation lingers within the engine of a supersonic air-breathing aircraft.

Efforts have been devoted to restricting the forced shock-wave oscillation using many flow control methods. The active bleeding technique reported by Cohen and Valerino [10] is the first approved method for reducing the forced shock-wave oscillation amplitude, although its major applications for improving the boundary-layer flow near walls are here to stay [11]. However, the mass flow rate loss through suction holes may be unwelcome in specific cases, e.g., a Lockheed Martin Mach 5 hypersonic airplane [12]. Consequently, the passive bleeding method arises to withstand this disadvantage. Porous plates are arranged near the SBLI and allow the high-pressure air downstream of the shock-wave to convect naturally to its upstream low-pressure region through a cavity or a channel. This method is widely used in external and internal flow control applications. However, Galli et al. [13] find that it is no use for weakening the forced shock-wave oscillation in a channel flow. The third candidate is the vortex generator [14], which is widely accepted by engineers for mitigating the flow separation in the subsonic and transonic airfoil flows [15]. Bur et al. [16] explore the impacts of the conventional and micro-vortex generators on the forced shock-wave oscillation. Regrettably, the influence of the vortex generator is too weak and can be neglected. On the other hand, Herges et al. [17] find that passive bleeding and the vortex generator are efficient for reducing the self-sustained shock-wave oscillation amplitude. Depending on the fluid–structure interaction, the fourth method employing the flexible structure achieves a jaw-dropping result for mitigating the forced shock-wave oscillation. Liang et al. [18] apply a flexible wall to a rocket nozzle and obtain a wonderful amplitude reduction for the forced shock-wave oscillation. Yao et al. [19] apply a local flexible wall to a supersonic intake. The large-amplitude forced shock-wave oscillation trims down, and the structural vibration amplitude is not large as compared to the static deformation of the flexible wall. Therefore, the dynamic cavity due to the flexible wall approximates to a fixed wavy surface. However, the fluid–structure interaction-induced problems may lead to a potential structural fatigue problem or even engine failure. This disadvantage may be overcome if a variable geometry based on shape memory alloy replaces the flexible wall. The variable geometry based on shape memory alloy has been used by Zhang et al. [20] to regulate ramp shock-waves, which indicates a real application in the supersonic intake.

Typical steady-state flow patterns in a supersonic intake can be found in Figure 1, where the SBLI locates in the diffuser part. Undergoing the back-pressure disturbance, the shock-wave is forced to oscillate in the diffuser part, where the compression part is not disturbed. In the present work, we focus on the transient flow in a diffuser to determine the impacts of the variable wavy surface, as shown in Figure 2. The diffuser experiences a back-pressure perturbation with a frequency of 250 Hz and a relative amplitude of 8%. The variable wavy surface is implemented to the flat bottom wall of the diffuser. The variable wavy surface’s impact on the forced shock-wave oscillation is numerically investigated by varying the wavy surface depth and length. An optimal wavy surface is determined, and the mitigating mechanism is discussed in detail.

2. Numerical Models

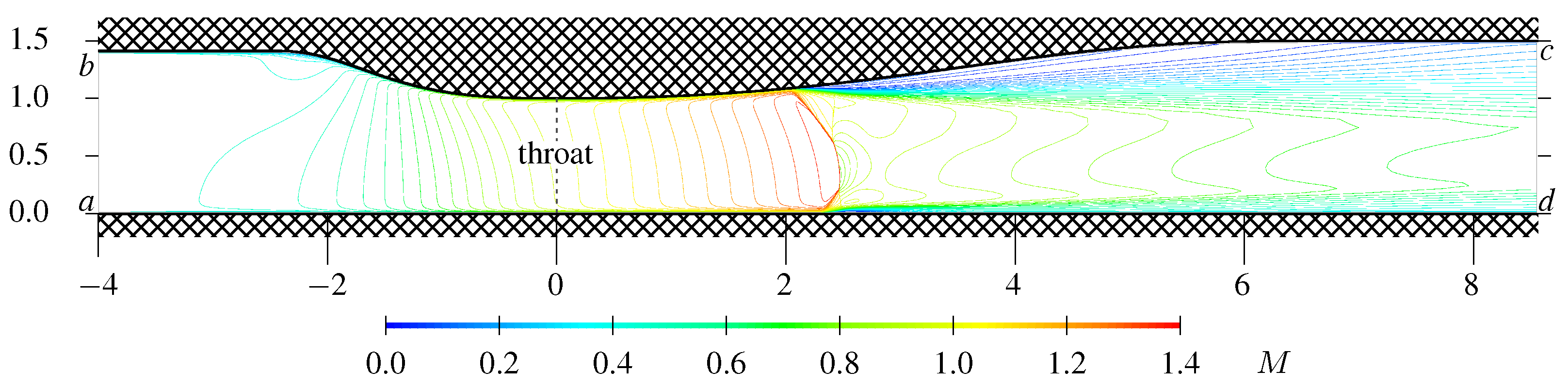
2.1. Sajben Diffuser

The transient flow of the Sajben diffuser [21] is chosen as the research object, where a simple $\lambda$-shaped shock-wave interacts with the separated boundary-layer. A schematic diagram of the Sajben diffuser is shown in Figure 2, where the surfaces a-b and c-d are the inlet and outlet of the diffuser, and the surfaces b-c and a-d are the top and bottom walls. The bottom wall is a flat surface, while the top wall is a curved surface. Detailed coordinate information can be found in Sajben’s work. This transonic diffuser consists of a convergent part on the left and a divergent part on the right, and the minimum flow path is the throat ($x=0$). The Mach number contour of the steady-state diffuser flow is given in Figure 2 as well, which clearly illustrates the shock/boundary-layer interaction near the walls. The coordinates are non-dimensionalized by the throat height $h_{th}=44$ mm.

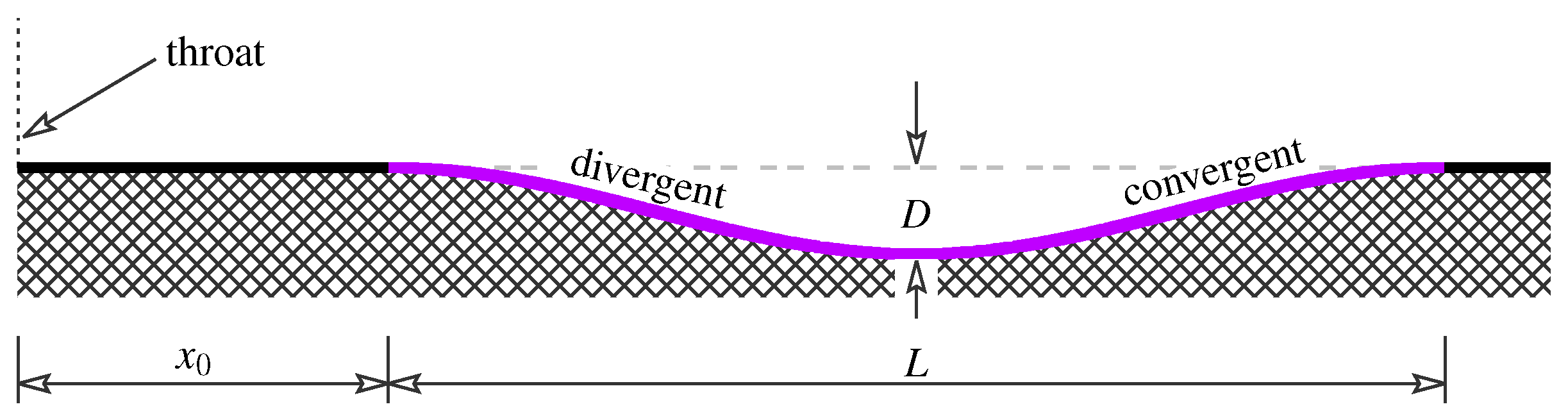
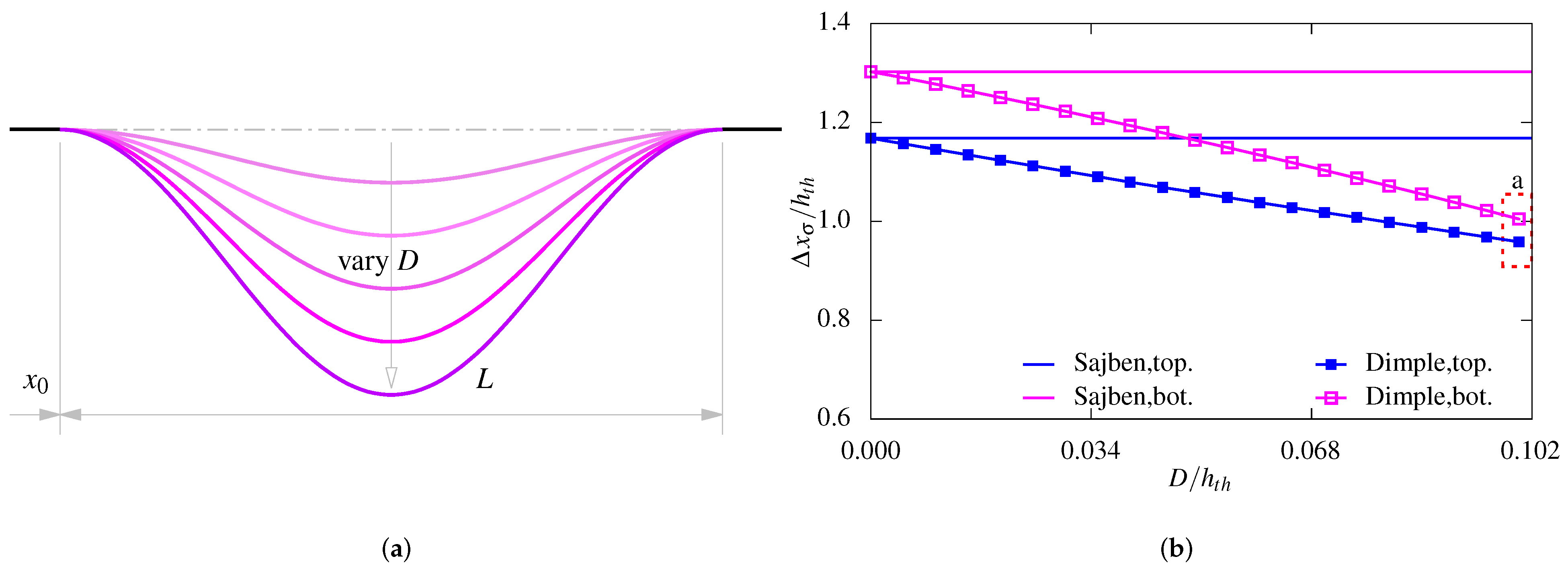
2.2. Geometry of a Wavy Surface

The whole prospect of this work is to apply variable wavy surfaces to a supersonic intake. However, the first step is to evaluate the wavy surface’s impact on the forced shock-wave oscillation. The variable wavy surface is applied to the flat bottom wall of the divergent part (i.e., $0<x<8h_{th}$) in Figure 2. The flat bottom wall is similar to the cowl wall of a supersonic intake, as shown in Figure 1. To prevent any sharp corner in the flow field, the wavy surface is smoothly connected to the flat bottom wall. A cosine-based curve with three parameters is implemented to describe the wavy surface, as shown in Figure 3. The cosine-based curve is governed by Equation (1), where $x_0$ is the x coordinate of the leading point, L is the wavy surface length, D is the wavy surface depth, and $x\in [x_0,x_0+L]$. The definitions of $x_0$, L, and D are shown in Figure 3. The wavy surface naturally divides into two parts: a divergent part ahead of the middle point and a convergent part behind. It should be noted that the convergent and divergent parts of the wavy surface should not be confused with those of the entire Sajben diffuser.

$$y={\displaystyle \frac{D}{2}}\left\{\cos \left[{\displaystyle \frac{2\pi }{L}}(x-x_0)\right]-1\right\}$$

(1)

2.3. Numerical Strategy

The steady-state viscous flow is solved with RANS-based techniques. Menter’s SST k-$\omega$ model [22] is applied to simulate the turbulence flow in the main stream domain of the diffuser. The enhanced near-wall treatment is implemented to predict the boundary-layer flow near the walls. The second-order upwind scheme with the Roe solver is used to capture the shock-wave. The ideal gas law is used to determine a compressible fluid density. For the transient flow solution, the URANS equations are computed to determine the oscillating behavior of the shock/boundary-layer interaction. The second-order implicit dual-time-stepping method is employed with a small time-step size of $1\times {10}^{-6}$ s, which is verified in Section 2.4.

The subsonic pressure–inflow boundary condition is applied to the inlet surface a-b in Figure 2, where the total temperature $T_0^{*}=300$ K and the total pressure $p_0^{*}=$ 135,000 Pa. The subsonic pressure–outflow boundary condition is implemented to the surface c-d, where a static pressure $p_e$ is given. For the steady-state diffuser flow simulation, the back-pressure $p_e=0.72p_0^{*}=$ 97,200 Pa. For the transient flow, a pressure disturbance is applied to the surface c-d to simulate the impact of the downstream perturbation from the unsteady combustion. Therefore, the static pressure at the outflow section varies with time. Generally, multiple frequency components exist on the pressure power spectrum of the combustion chamber, but only a single frequency component is discussed in most supersonic intake studies. Similarly, a simple harmonic disturbance is added to the static pressure $p_e$ in this work. For the transient diffuser flow, the back-pressure is described in Equation (2), where $f_e=250$ Hz and $A_e=8\%$ are the frequency and the relative amplitude of the back-pressure perturbation, respectively. The surfaces b-c and a-d are modeled with an adiabatic non-slip wall boundary condition, where the meshes near the walls satisfy the requirement of $y^{+}\le 1$.

$$p_e\left(t\right)=0.72\left[A_e\sin \left(2\pi f_{e}t\right)+1\right]p_0^{*}$$

(2)

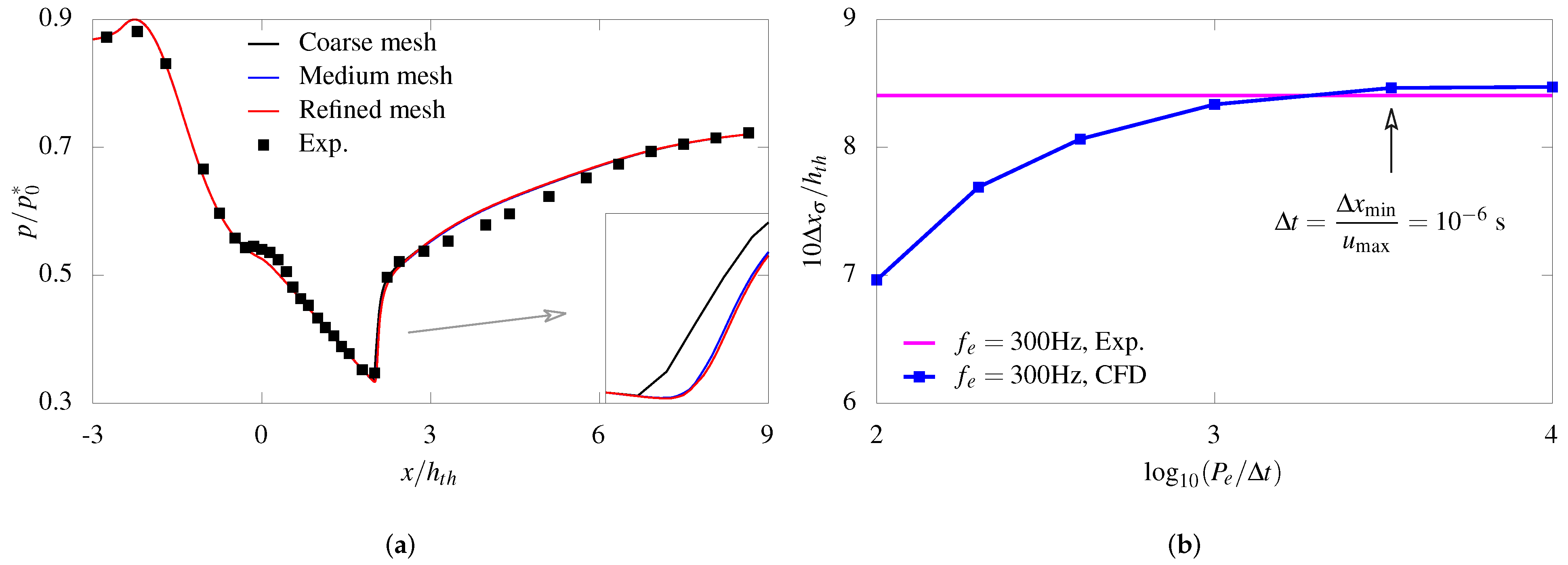
2.4. Verification and Validation

The steady-state flow is studied with different mesh strategies to verify the present numerical model. The steady-state solution refers to the flow without any downstream pressure perturbation on the Sajben diffuser. Numerical results are compared to the experiment data as well. Three mesh strategies are utilized for a mesh independence study, i.e., a coarse mesh with 500 × 120 cells along the x and y directions, a medium mesh with 1000 × 120 cells, and a fine mesh with 2000 × 400 cells. The static pressure distributions on the top wall for the steady-state flow with three different meshes are shown in Figure 4a, where Menter’s SST k-$\omega$ turbulence model is implemented. The results with the medium mesh and the fine mesh agree well with the experiment data [21]. The medium mesh is used in the present work.

The second-order implicit dual-time-stepping method is implemented for the transient flow simulation, which allows a larger time-step but may induce numerical damping. To verify the numerical scheme, a time-step-size check is performed for the perturbation condition with $f_e=$ 300 Hz, where the detailed back-pressure profile can be found in [23]. A forced shock-wave oscillation amplitude at the midstream position (i.e., $y=0.432h_{th}$) is illustrated in Figure 4b. The result with $\Delta t\le 3.333\times {10}^{-6}$ is close to the experiment data [24]. The time-step-size of $1\times {10}^{-6}$ s is chosen according to the CFL criterion, and is used for the transient simulation.

3. Numerical Results

3.1. Steady-State Flow

As described in Figure 4a, the steady-state pressure distributions on the walls agree well with the time-averaged experimental data. A further detailed Mach number contour for the steady-state diffuser flow solution is shown in Figure 2. The maximum Mach number is 1.4 in the diffuser under the given back-pressure condition. Turbulent flow separation occurs when $M_1$ reaches a limit that is close to 1.3 [25] for the transonic SBLI. The shock-wave in Figure 2 is strong enough to induce the flow separation bubble. Two shock-induced flow-separation bubbles are triggered on the top and bottom walls, which are indicated by the blue low-velocity regions.

To evaluate the performance, the total pressure loss parameter $\eta$ and the outflow distortion parameter $\xi$ are respectively defined in Equations (3) and (4) using the total pressure distributions at the inlet and outlet. The parameters $p_0^{*}\left(y\right)$ and $p_e^{*}\left(y\right)$ are the total pressures along the y-direction at the inflow and outflow sections. The performance parameters are ${\xi }_s=0.288$ and ${\eta }_s=0.086$ for the steady-state solution in the Sajben diffuser.

$$\begin{array}{cc}\hfill \eta & ={\displaystyle \frac{{\widehat{p}}_0^{*}\left(y\right)-{\widehat{p}}_e^{*}\left(y\right)}{{\widehat{p}}_0^{*}\left(y\right)}}\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \xi & ={\displaystyle \frac{p_e^{*}\left(y\right){{|}_{\max }-p_e^{*}\left(y\right)|}_{\min }}{{\widehat{p}}_e^{*}\left(y\right)}}\hfill \end{array}$$

(4)

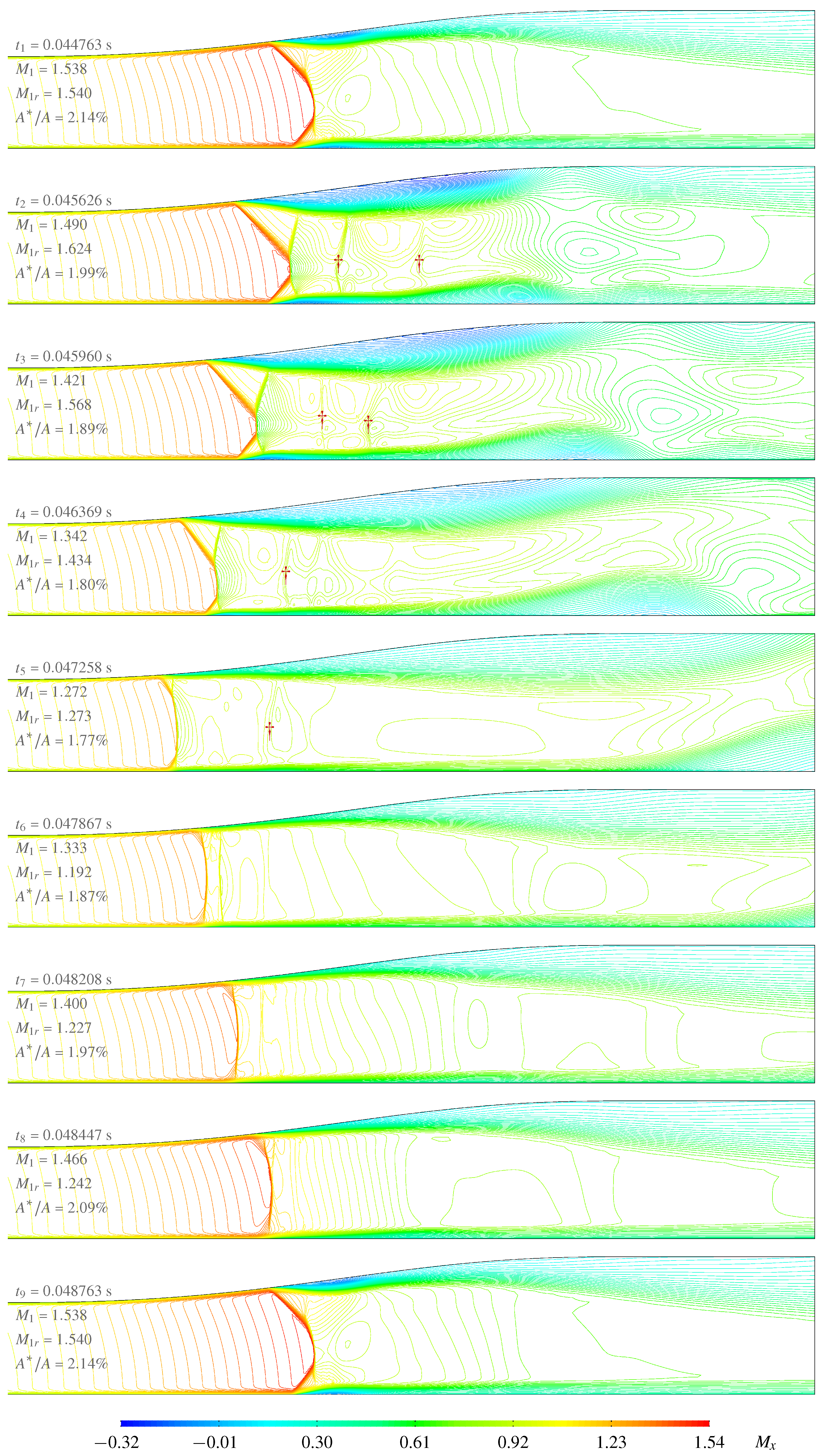
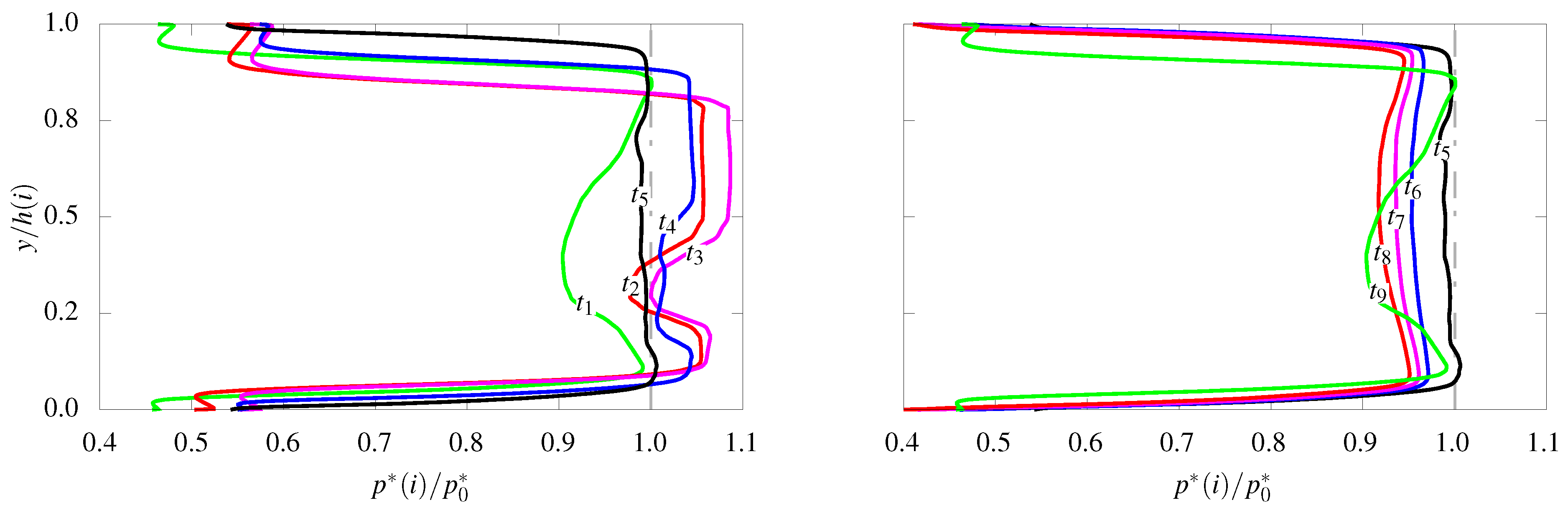
3.2. Oscillating Flow without Control

As described in Section 2.3, a downstream pressure perturbation is implemented to the outflow surface c-d of the Sajben diffuser within the transient flow analysis, i.e., a harmonic time-varying back-pressure with $f_e=250$ Hz and $A_e=8\%$. To achieve a good periodic transient solution stably and efficiently, the transient flow field is initialized with the steady-state flow solution in Section 3.1.

The oscillating shock-wave time histories on the top and bottom walls are shown in Figure 5a. They are achieved by searching for the minimum values of the static pressure distributions on the walls and choosing the x coordinates as the locations of the shock-wave on the top and bottom walls. Key features of the curves are shown in

Table 1. Fluctuations of key parameters for the forced shock-wave oscillation in Sajben diffuser without and with wavy surface.

Model	${\overline{\mathit{x}}}_{\mathit{\sigma }\mathit{t}}/{\mathit{h}}_{\mathit{th}}$	$\mathbf{\Delta }{\mathit{x}}_{\mathit{\sigma }\mathit{t}}/{\mathit{h}}_{\mathit{th}}$	${\overline{\mathit{x}}}_{\mathit{\sigma }\mathit{b}}/{\mathit{h}}_{\mathit{th}}$	$\mathbf{\Delta }{\mathit{x}}_{\mathit{\sigma }\mathit{b}}/{\mathit{h}}_{\mathit{th}}$	$\overline{\mathit{\xi }}$	$\mathbf{\Delta }\mathit{\xi }$	$\overline{\mathit{\eta }}$	$\mathbf{\Delta }\mathit{\eta }$
Sajben	$2.016$	$1.219$	$2.216$	$1.371$	0.282	0.169	0.089	0.089
Modified	$1.891$	$0.846$	$1.865$	$0.796$	0.274	0.136	0.098	0.083

, where the time-averaged positions on the walls are ${\overline{x}}_{\sigma t}\left(t\right)=2.016h_{th}$ and ${\overline{x}}_{\sigma b}\left(t\right)=2.216h_{th}$, and the peak-to-peak amplitudes are $\Delta x_{\sigma t}=1.219h_{th}$ and $\Delta x_{\sigma b}=1.371h_{th}$. Bruce and Babinsky [26] compare the forced shock-wave oscillation amplitudes in duct with different divergence, i.e., $\theta$ = 0°, 1°, 2°, 5°, 10°. The results show that increasing the wall-divergence helps to mitigate the forced shock-wave oscillation. In the present work, the divergence of the top wall varies along the streamwise direction, as shown in Figure 2. When the shock-wave oscillates on the top wall, the minimum local divergence is 4.8° (i.e., $t_5$ moment) and the maximum value is 7.6° (i.e., $t_1$ moment), as shown in the Mach number contour in Figure 6. The divergence of the bottom wall remains 0°. Consequently, the shock-wave oscillation amplitudes on the flat bottom wall are larger than those on the curved top wall.

A larger shock-wave oscillation amplitude on the flat wall compared to the divergent wall is not good for a supersonic intake of a ramjet engine. As shown in Figure 1, the supersonic intake is attached to the engine body through the ramp wall (i.e., a divergent wall), while the cowl wall is a free and flat surface. A larger shock-wave motion near the cowl wall generates a stronger exciting force and triggers a larger structural vibration amplitude on the free cowl wall than on the constrained ramp wall. The flat bottom wall in the present work is similar to the cowl wall of a supersonic intake. Therefore, the 2D wavy surface is implemented to the flat bottom wall of the present diffuser.

A transient Mach number contour within one perturbation period $P_e$ for the Sajben diffuser is shown in Figure 6, which clearly displays the forced shock-wave oscillation procedure. Only the region near the shock-wave and its downstream subsonic region are present in the figures because the upstream region is hardly changed by the disturbance pressure wave propagation. Nine sub-figures are determined by splitting the averaged shock-wave motion path $\left[x_{\sigma t}\left(t\right)+x_{\sigma b}\left(t\right)\right]/2$ with an equal streamwise distance, as shown by the nine green dots crossed by bars in Figure 5. Note that the flow result at $t_9$ is a repeat of that at $t_1$ for the periodic flow solution.

One obvious feature of the large-amplitude forced shock-wave oscillation is the second shock-wave, as indicated by the dagger symbol “†” in Figure 6. The primary shock-wave is formed by the $\lambda$-shaped shock-waves near the top and bottom walls. When the primary shock-wave moves upstream from $t_2$ to $t_5$, the second shock-wave appears downstream of it, and moves upstream with it. Similar to the shock-train, the flow pattern in the diffuser consists of an initial shock-wave and the second shock-wave. The gas decelerates and accelerates repeatedly in the shock train, which mainly occurs with an inflow Mach number beyond 1.6. However, the maximum Mach number is less than 1.6 in the present diffuser. The mechanism regarding the occurrence of second shock-wave is discussed in Section 4.2.

The other feature is the downstream-moving flow-separation bubble traveling downstream near the bottom wall. When the shock-wave moves upstream from $t_2$ to $t_5$, the flow-separation bubble appears on the bottom wall and travels downstream in the flow field, as indicated by a local low-velocity and high-pressure area with streamlines in Figure 6. One should distinguish it from the primary flow-separation bubble induced by shock-waves on the bottom wall. As discussed in Section 3.1, two flow-separation bubbles are triggered by the strong shock-wave in the steady-state flow solution. The primary flow-separation bubbles still exist under the shock-wave near the walls, but they move upstream with the shock-wave from $t_5$ to $t_9$.

In the work by Hsieh et al. [27], the downstream-moving flow-separation bubble is indicated by the “bifurcation of separation pocket” and a pressure peak. The downstream-moving pressure peak can be found in Sajben’s experiment [23] as well. A similar phenomenon can be found in a supersonic intake by Yao et al. [19]. When we decrease the perturbation amplitude, this feature weakens and disappears in the present diffuser, which agrees with the work by Hsieh et al. [28]. When we increase the back-pressure on the outlet, a pressure wave is generated and propagates upstream. The shock-wave is forced to move upstream when it is chased by the pressure wave. In addition, there is a local pressure increment; due to the pressure wave, a second pressure-increase across the flow rettachment point is added. If we keep increasing the perturbation pressure, the shock-wave, the flow separation bubble, and the pressure wave move upstream. However, the back-pressure has been reduced according to the sinusoidal function, i.e., Equation (2), when the shock-wave moves upstream. The local pressure increment is larger than its upstream and downstream pressure distributions, which show a local pressure peak in the static pressure distribution curve. The local pressure peak can not stay stably, but moves downstream in the form of a flow-separation bubble.

The performance parameters fluctuate as well, as shown by $\eta \left(t\right)$ and $\xi \left(t\right)$ in Figure 7. The time-averaged values and peak-to-peak amplitudes are listed in Table 1. A phase diagram is generated with $\eta \left(t\right)$ and $\xi \left(t\right)$. The performance parameters show a complicated phase trajectory that surrounds the steady-state phase point.

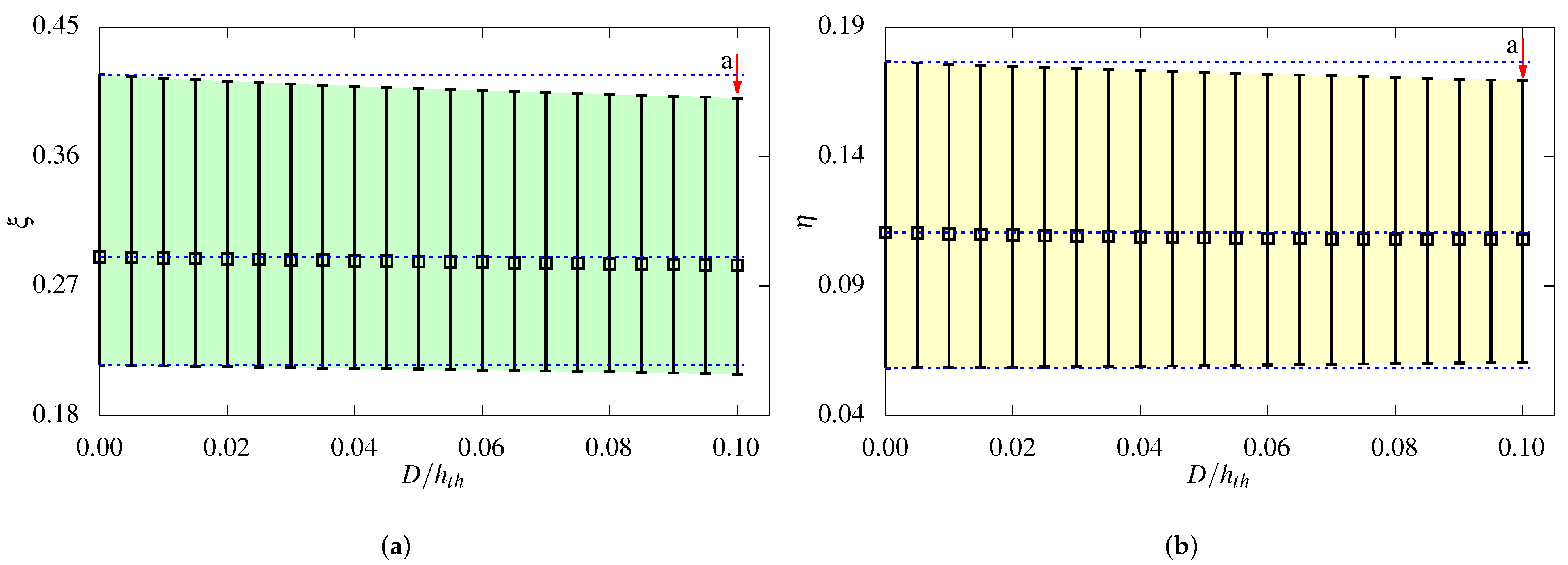
3.3. Impact of the Wavy Surface’s Depth

As described in Section 2.2, the parameters $x_0$, D, and L determine the shape of the 2D wavy surface. The impact of D is studied in this section, where $0<D\le h_{th}/10$. The other two parameters hold constant, where $x_0=h_{th}$ and $L=6h_{th}$. A schematic diagram of varying D is shown in Figure 8a, which is divided into 20 segments. The following results and discussion focus on the forced shock-wave oscillation amplitudes and the performance parameters for the transient results with 20 local wavy surfaces. Except for the wavy surface, all the other simulation parameters used in 20 CFD calculations are the same as those in the baseline-flow solution of the original Sajben diffuser in Section 3.2.

The variations of shock-wave oscillation amplitudes with the increasing D are shown in Figure 8b. The forced shock-wave oscillation amplitudes on the top and bottom walls both decrease with the wavy surface depth D until the design point “a”, where $x_0=h_{th}$, $L=6h_{th}$, and $D=h_{th}/10$. The forced shock-wave oscillation amplitudes on the walls at the design point “a” are, respectively, $\Delta x_{\sigma t}=0.958h_{th}$ and $\Delta x_{\sigma b}=1.005h_{th}$, while those of the baseline-flow are $1.219h_{th}$ and $1.371h_{th}$. The tendency indicates that a single wavy surface can be used to mitigate the forced shock-wave oscillation in the diffuser. Meanwhile, a strategy of increasing wavy surface depth benefits the mitigation of the shock-wave oscillation amplitudes.

The variations of $\xi \left(t\right)$ and $\eta \left(t\right)$ with increasing D are shown in Figure 9. The squares crossed by bars evaluate the fluctuations of $\xi \left(t\right)$ or $\eta \left(t\right)$ with different wavy surface depths, while the horizontal dashed lines indicate those of the baseline-flow in Section 3.2. The square indicates the time-averaged value of $\overline{\xi }\left(t\right)$ or $\overline{\eta }\left(t\right)$. The fluctuation amplitudes of $\xi$ and $\eta$ both shrink when the wavy surface depth D increases. The tendency is similar to that for the shock-wave oscillation amplitude. Meanwhile, the whole fluctuation range of $\xi$ decreases, and that of $\eta$ increases. A lower value of $\xi$ means a smoother outflow, and a higher $\eta$ means a lower total pressure loss for the diffuser. Consequently, increasing the wavy surface depth from zero to $h_{th}$ helps to provide a smooth and stable outflow, and is beneficial toward a stable performance for the Sajben diffuser.

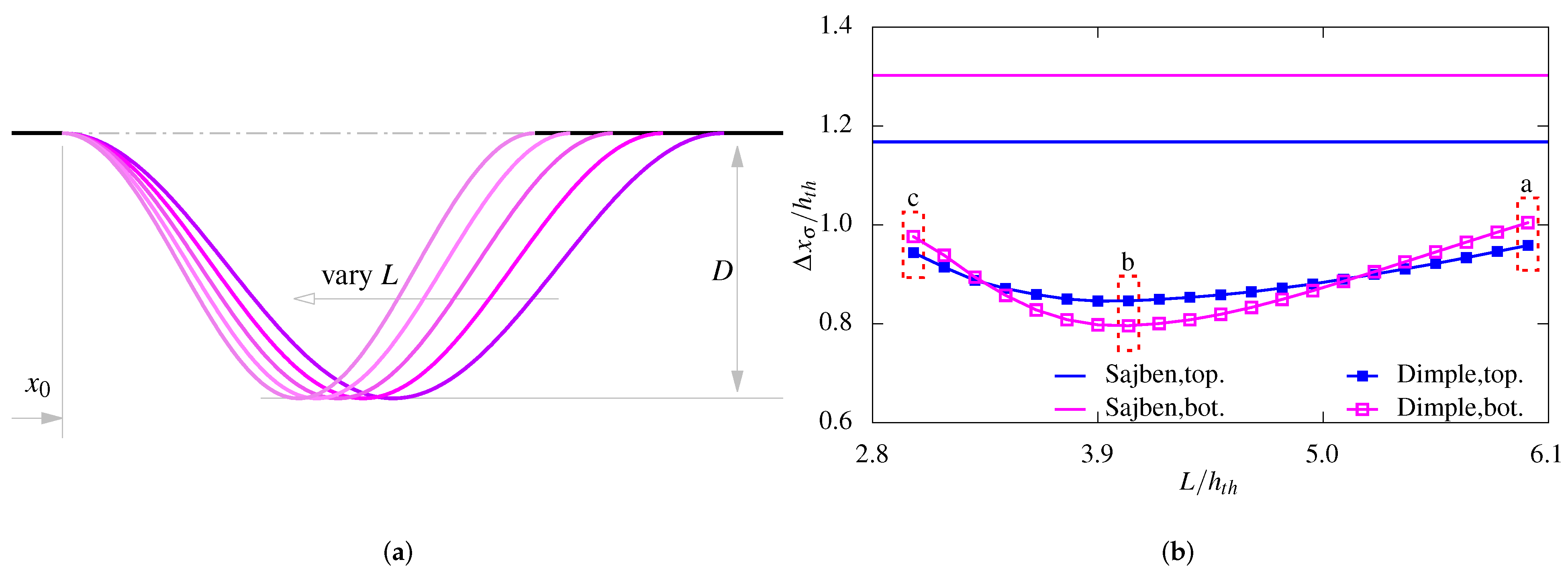
3.4. Impact of the Wavy Surface’s Length

A schematic diagram of decreasing L is shown in Figure 10a, where $x_0$ and D do not change. As discussed in Section 3.3, the design point “a” is the best wavy surface configuration for mitigating the shock-wave oscillation amplitudes. Based on the design point “a”, we vary the wavy surface length in this section, where $x_0=h_{th}$ and $D=h_{th}/10$. The length L decreases from $6h_{th}$ (i.e., the point “a”) to $3h_{th}$. The variation interval is divided into 20 segments.

The relationship between the forced shock-wave oscillation amplitudes on the top and bottom walls and the wavy surface length L is shown in Figure 10b. The point “a” indicates the best choice in Section 3.3, where $L=6h_{th}$. The wavy surface length decreases from point “a” to point “c”. The U-shaped curves can be found in Figure 10b. Dependent on the specific value, varying wavy surface lengths may mitigate or aggravate the shock-wave oscillation amplitudes. The local minimum oscillation amplitudes appear at the design point “b”, where $\Delta x_{\sigma t}=0.846h_{th}$ and $\Delta x_{\sigma b}=0.796h_{th}$. Therefore, the best choice for mitigating the shock-wave oscillation amplitudes is the point “b” when varying L in $[3h_{th},6h_{th}]$. The design parameters are $x_0=h_{th}$, $L=4.05h_{th}$, and $D=h_{th}/10$.

The variations of $\xi \left(t\right)$ and $\eta \left(t\right)$ with the wavy surface length L are shown in Figure 11. The fluctuation amplitudes $\Delta \xi$ and $\Delta \eta$ both gradually diminish when the wavy surface length decreases from $6h_{th}$ to $3h_{th}$. Consequently, the best result for $\xi$ and $\eta$ is the design point “c”. Therefore, decreasing the wavy surface length benefits toward the outflow distortion parameter and the total pressure loss parameter, under the given conditions.

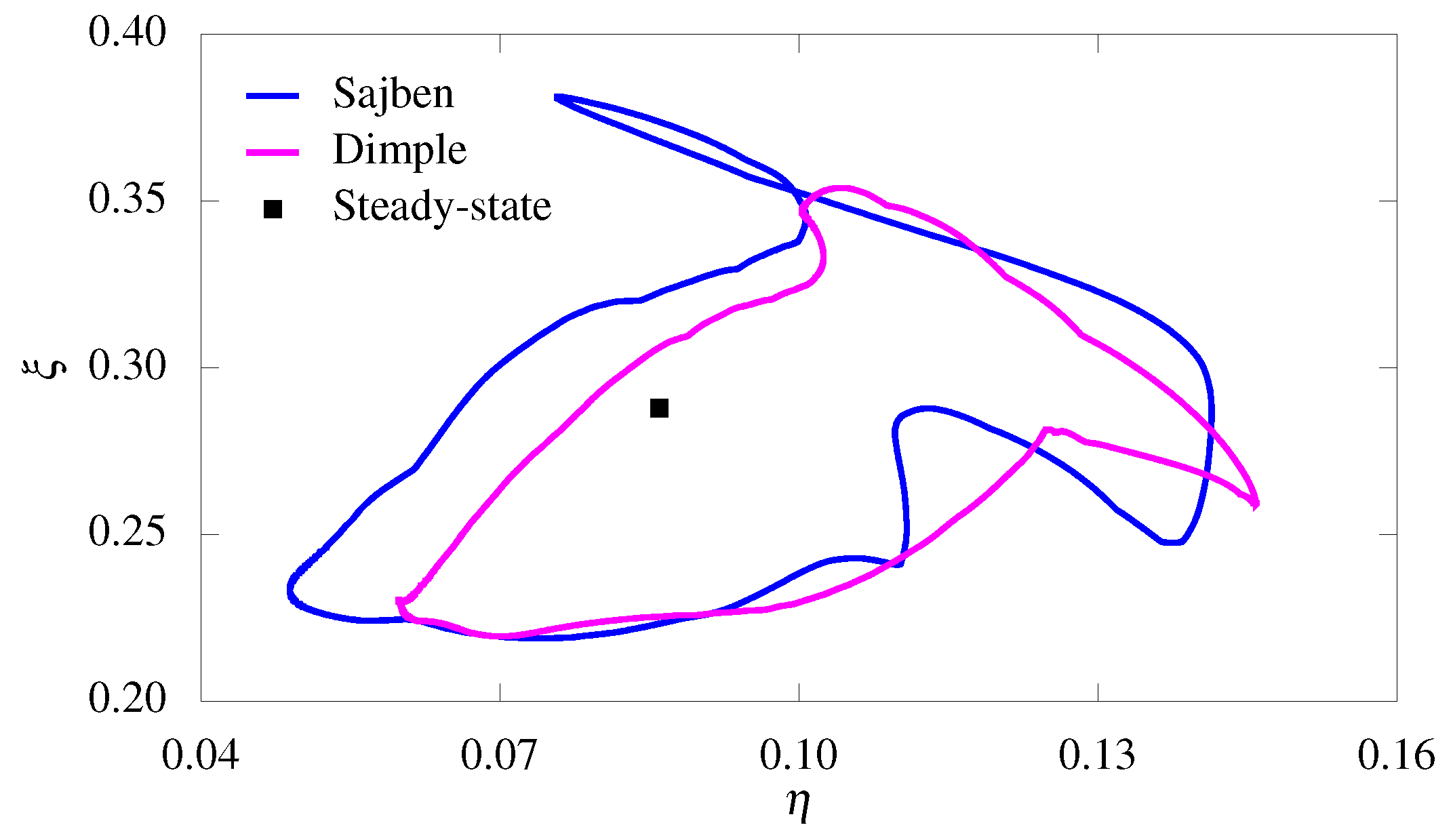
3.5. Mitigated Shock-Wave Oscillation

As discussed in Section 3.3 and Section 3.4, the best choices for mitigating the shock-wave oscillation amplitudes are the design points “a” and “b” when varying the wavy surface’s depth and length, respectively. Actually, the oscillation amplitudes of the point “b” are smaller than those of “a”, as shown in Figure 10. Therefore, the mitigated forced shock-wave oscillation at the point “b” is investigated in detail, where $x_0=h_{th}$, $D=h_{th}/10$, and $L=4.05h_{th}$.

The oscillating shock-wave time histories on the walls are shown in Figure 5b. The transient behavior of the shock-wave is dominated by the downstream pressure perturbation. The optimal wavy surface does not change the oscillation frequency. The dominant frequency of the shock-wave oscillation is same as the perturbation frequency, i.e., $f_e$ = 250 Hz. The time histories are close to each other, where the shock-wave oscillation amplitudes are $\Delta x_{\sigma t}=0.846h_{th}$ and $\Delta x_{\sigma b}=0.796h_{th}$. The relative reductions are 31% and 42% for the oscillation amplitudes on the top and bottom wall, respectively. According to the work by Bruce and Babinsky [26], increasing the wall-divergence helps to mitigate the shock-wave oscillation amplitude. The optimal wavy surface on the flat bottom wall increases the local wall-divergence near the shock-wave, and diminishes the shock-wave oscillation amplitude on the bottom wall. A detailed visualization can be found in the Mach number contours in Figure 12.

The optimal wavy surface does not eliminate the two obvious features in the flow field. The second shock-wave appears in the flow field when the primary shock-wave moves upstream, as shown in Figure 12. Meanwhile, the second flow-separation bubble near the bottom wall still moves downstream. The obvious features are discussed in detail in Section 4.2.

The variations of $\eta \left(t\right)$ and $\xi \left(t\right)$ are illustrated in the phase diagram of Figure 7. As compared with the original diffuser, the phase trajectory of the modified diffuser is shrunk in Figure 7. Therefore, the performance fluctuation is weakened by the optimal wavy surface. The relative reductions are 20% and 7% for $\Delta \xi$ and $\Delta \eta$, respectively. Detailed information can be found in Table 1.

4. Discussion

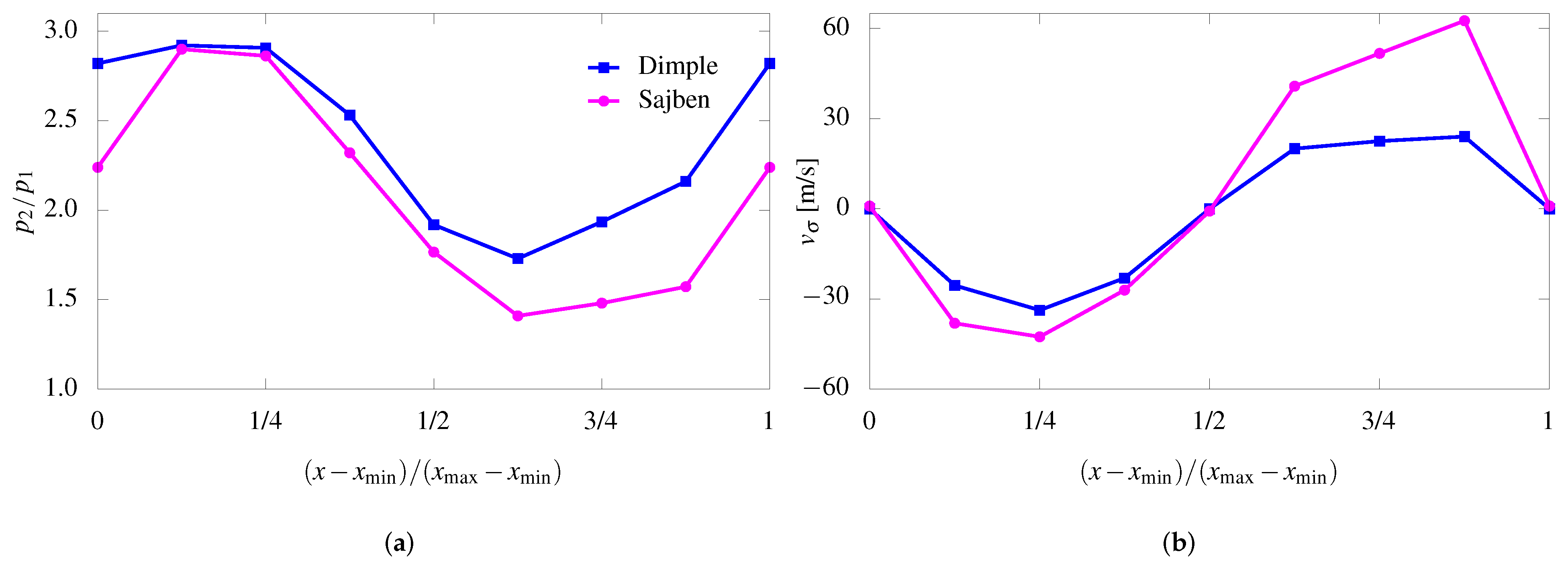
4.1. A Mechanism for Mitigating Shock-Wave Oscillation

The forced shock-wave oscillation is mitigated in the modified diffuser with the optimal wavy surface, as described in Section 3.5. The mitigating mechanism can be explained using two viewpoints.

The first one is the viewpoint of shock-wave stability. Culick and Rogers [29] associate the shock-wave oscillation amplitude with several parameters, e.g., the pressure ratio upstream and downstream, the local flow state, and the local flow passage geometry. Oh et al. [30] apply it to the forced shock oscillation in a supersonic intake. It is derived in Equations (5) and (6), where ${\overline{p}}_1$, ${\overline{c}}_1$ and ${\overline{M}}_1$ are, respectively, the time-mean static pressure, the sound speed, and the Mach number just upstream of the shock-wave, $\Delta p$ is the pressure oscillation amplitude behind the shock-wave, and A is the flow area at the shock-wave. Because the perturbation frequency $f_e$ and the perturbation amplitude $A_e$ do not change, $\Delta p$ is considered to be invariant in the present study. The static temperature changes slightly in the supersonic region, and the sound speed ${\overline{c}}_1$ is treated as the unchanged term. The other terms in Equation (5), i.e., ${\overline{p}}_1$, ${\overline{M}}_1$, A and $\mathrm{d}A/\mathrm{d}x$, vary when modifying the wavy surface, and their contributions are discussed as follows.

$$\begin{array}{cc}\hfill \Delta x_{\sigma }& ={\displaystyle \frac{\Delta p}{{\overline{p}}_1}}/\sqrt{{\left[{\displaystyle \frac{2\pi f}{{\overline{c}}_1}}{\displaystyle \frac{4\gamma {\overline{M}}_1}{\gamma +1}}\right]}^2+{\left[{\left({\displaystyle \frac{1}{A}}{\displaystyle \frac{\mathrm{d}A}{\mathrm{d}x}}\right)}_{\sigma }g\left({\overline{M}}_1\right)\right]}^2}\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill g\left({\overline{M}}_1\right)& =\left[\left({\gamma }^2+1\right){\overline{M}}_1^2+(\gamma -1)\right]/\left[{(\gamma +1)}^2/2\gamma \right]\hfill \end{array}$$

(6)

In the modified diffuser, the initial shock-wave oscillates in the divergent part of the wavy surface. The gradient $\mathrm{d}A/\mathrm{d}x$ is higher than that in the original diffuser. The time-mean shock-wave moves upstream in the modified diffuser, as shown in Figure 5. The time-mean shock-wave seeks for a location with a same flow area A as that in the original diffuser. Consequently, the term A slightly affects the forced shock-wave oscillation amplitude. Therefore, the Mach number ${\overline{M}}_1$ is higher and the static pressure ${\overline{p}}_1$ is lower in the modified diffuser. According to Equation (5), changes of $\mathrm{d}A/\mathrm{d}x$ and ${\overline{M}}_1$ in the modified diffuser benefit for mitigating the shock-wave oscillation, while ${\overline{p}}_1$ stimulates it. However, the contribution of ${\overline{p}}_1$ is less significant.

The other one is the viewpoint of the work performed by a moving shock-wave. A moving shock-wave does work to the gas, i.e., $W_{\sigma }$. A typical example is the transonic flow in the compressor of a modern gas turbine. The turbine drives the compressor with a blade-tip-speed of 400 m/s∼500 m/s. A local supersonic flow region is generated in the blade cascade where a shock-wave appears. The shock-wave rotates with the compressor, does work to the gas, and increases the total pressure of air-flow entering the combustor.

In the present work, the oscillating shock-wave does work in the diffuser as well. As a baseline for comparison, the post-shock total pressure distribution is evaluated in Figure 13 for the stationary shock-wave. One may find that the total pressure $p^{*}$ is smaller than the inflow value of $p_0^{*}$ = 135,000 Pa. In the rear shock-leg regions of b-c, d-e, b′-c′, and d′-e′, $p^{*}$ is nearly recovered to $p_0^{*}$ by the $\lambda$-shaped shock-wave. This feature is utilized for the shock-wave control with a contoured-surface bump, where a $\lambda$-shaped shock-wave structure is generated with a large rear shock-leg.

A significant difference appears in the post-shock total pressure distributions of a moving shock-wave in Figure 14. From the $t_2$ moment to the $t_4$ moment, the total pressure $p^{*}$ in the rear shock-leg region is greater than the inflow value $p_0^{*}$. The $\lambda$-shaped shock-wave only helps to recover $p^{*}$ to $p_0^{*}$ in the regions with a rear shock-leg, but they cannot stimulate it to be greater than $p_0^{*}$, as shown in Figure 13. The increased total pressure is due to the work performed by a moving shock-wave.

To evaluate the work performed by the shock-wave, the power of a micro-element area on the shock-wave surface is expressed by Equations (7) and (8), where $p_1$ and $p_2$ are the static pressures across the shock-wave, and $v_{\sigma }$ is the shock-wave traveling speed. The strong shock-wave generates a large pressure increment of $p_2-p_1$ in Equation (8). Suppose that the work capacity is constant. Accordingly, the shock-wave traveling speed $v_{\sigma }$ in Equation (7) is small for a strong shock-wave.

$$\mathrm{d}{\dot{W}}_{\sigma }=\mathrm{d}{F}_{\sigma }\times v_{\sigma }$$

(7)

$$\mathrm{d}{F}_{\sigma }=(p_2-p_1)\mathrm{d}A$$

(8)

In the modern compressor, the local shock-wave is actually driven by the gas turbine blades that determine the work capacity. In the present work, the oscillating shock-wave is driven by the perturbation pressure, which represents the combstor of a ramjet engine and determines the work capacity of the moving shock-wave. Because the perturbation pressure does not change, the work capacities of the moving shock-wave are identical for the original and the modified diffuser with a wavy surface.

The shock-wave strength $p_2/p_1$ and traveling speed $v_{\sigma }$ in the original and modified diffuser are illustrated in Figure 15. The independent variable $(x-x_{\min })/(x_{\max }-x_{\min })=0$ indicates the upstream-most position of the shock-wave, and $(x-x_{\min })/(x_{\max }-x_{\min })=1$ is the downstream-most position. The shock-wave strength in the modified diffuser is greater than that in the original diffuser, as shown in Figure 15. Note that the work capacity is constant due to the same pressure perturbation. The optimal wavy surface generates a stronger shock-wave with a larger pressure increment. Accordingly, the shock-wave traveling speed is limited and the forced shock-wave oscillation is mitigated.

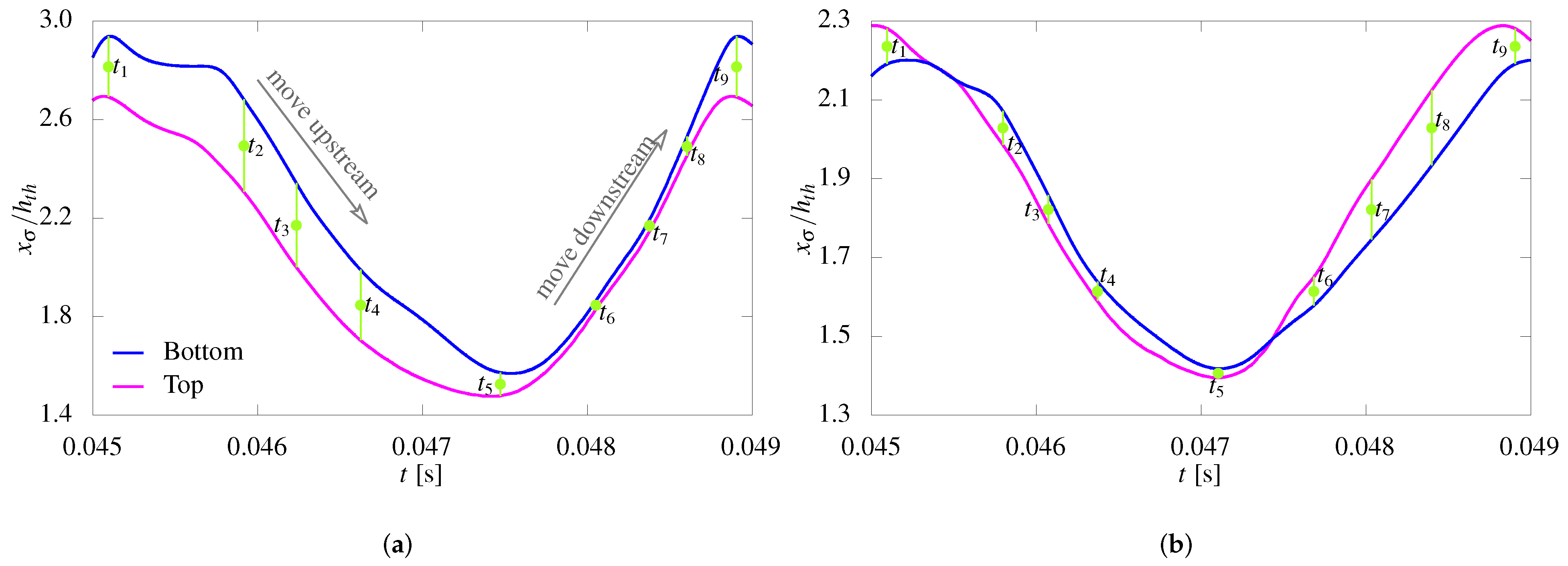
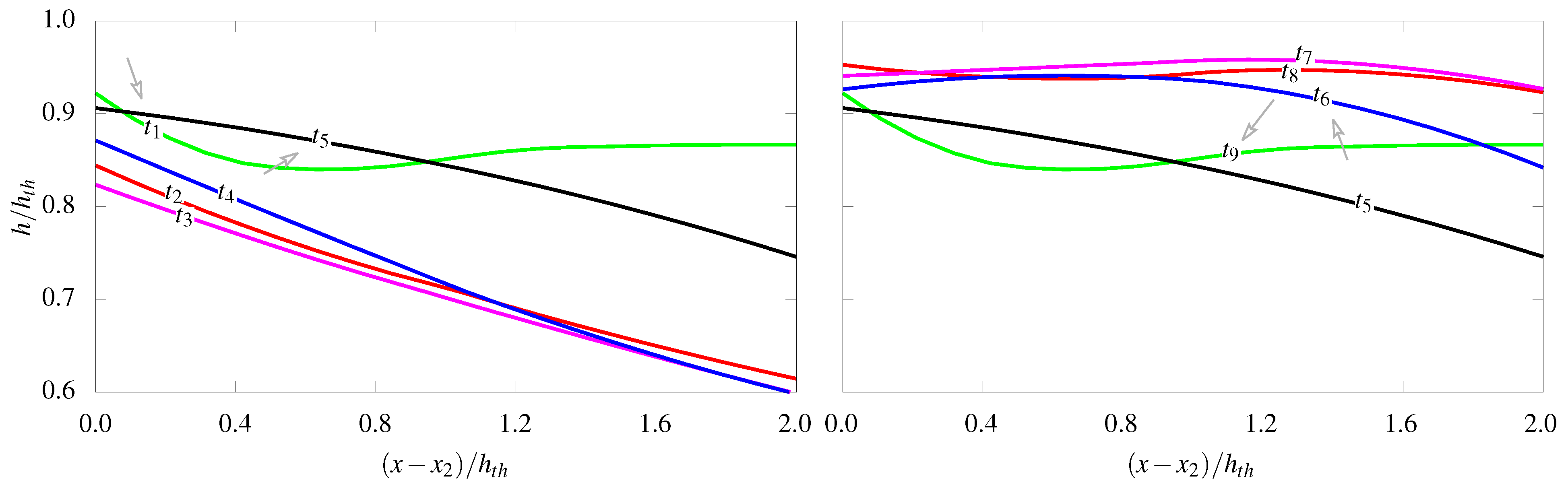
4.2. The Temporal Second Shock-Wave

The second shock-wave temporarily appears in the flow field, as indicated by the dagger symbols “†” in Figure 6 and Figure 12. The second shock-wave locates downstream of the primary shock-wave, and the size is smaller. The flow patterns, i.e., the initial and second shock-wave, are similar to the shock train. The occurrence is mainly due to the post-shock expansion phenomenon [31], which is associated with the inflow Mach number and the expansion wave downstream of the initial shock-wave. The factors do not affect the post-shock expansion separately, and are considered in combination as follows.

In Sajben’s steady-state flow experiment [32], the shock train occurs in the flow-field with $M_1>1.6$, and a normal shock-wave or $\lambda$-shaped shock-wave appears with $1<M_1<1.6$. The present numerical steady-state result satisfies this criterion, as shown in Figure 2. For the transient flow, the shock-wave traveling speed $v_{\sigma }$ should be considered for a moving shock-wave. $M_1$ is replaced by the relative Mach number $M_{1r}=M_1-v_{\sigma }/c_1$, The upstream-moving shock-wave faces an inflow with a greater relative Mach number. The second shock-wave appears with $M_{1r}=1.62$ in the original diffuser at the $t_2$ moment, as shown in Figure 6. This agrees with Sajben’s observation.

The expansion wave downstream of the initial shock-wave contributes to the second shock-wave in the moment between $t_2$ and $t_5$. The initial shock-induced separation bubble helps to understand the expansion wave’s effect. According to the criterion of predicting shock-induced separation in a supersonic flow [33], the onset of shock-induced separation is mainly associated with the Mach number $M_1$ upstream of the shock-wave. For the transonic SBLI, the turbulent flow separation occurs when $M_1$ reaches a limit close to 1.3 [25]. For a moving shock-wave, $M_1$ is replaced by the relative Mach number $M_{1r}$. From $t_1$ moment to $t_4$ moment, the flow separation bubbles are found in the original diffuser, and the Mach numbe $M_{1r}$ is greater than 1.3 in Figure 6. From $t_5$ moment to $t_8$ moment, shock-induced separation disappears in the flow field with $M_{1r}<1.3$. The same is true for the modified diffuser with an optimal wavy surface in Figure 12.

The flow-separation bubbles on the walls push the boundary layers to the main stream region of the flow field, and shrink the effective flow-passage downstream of the primary shock-wave. To take into account of the flow separation bubbles, the effective flow-passage height downstream of the primary shock-wave in the modified diffuser with an optimal wavy surface is shown in Figure 16, which is generated by subtracting the top and bottom wall boundary-layer thickness from the local height. The flow-passage starts from the downstream-most position $x_2$ of the primary shock-wave and stops with a length of $2h_{th}$. Two types of flow-passage could be found in Figure 16, i.e., the simple convergent flow-passage and the complex flow-passage. An obvious difference in height can be found between the two ends of a simple convergent flow-passage, e.g., a gap of $0.2h_{th}$ on the curve at $t_2$ moment in Figure 16. The second type may be a divergent–convergent or a convergent–divergent flow-passage, and the heights at the two ends are nearly the same, e.g., curves at $t_7$ moment in Figure 16.

With an obvious difference in height, the convergent flow-passage helps to accelerate the subsonic flow downstream of the initial shock-wave. The expansion wave becomes significantly strong enough to form the second shock-wave in the diffuser. For example, only one $\lambda$-shaped shock-wave is in Figure 12 at $t_1$ moment, and a convergent–divergent flow-passage locates downstream of the shock-wave in Figure 16. Suddenly, the main-stream flow is shrunk by the flow-separation bubbles at $t_2$ moment, and a simple convergent flow-passage is generated with an obvious difference in height. In the mean time, the subsonic flow accelerates and the second shock-wave emerges downstream of the primary shock-wave, as shown in Figure 12. The simple convergent flow-passage has been maintained until $t_6$ moment, and the second shock-wave is sustained in the diffuser as well. At $t_7$ moment, the flow-passage turns to a divergent–convergent shape, and the second shock-wave disappears from the flow field.

Overall, the back-pressure perturbation drives the shock-wave to depart from the time-averaged position. When it moves upstream from the downstream-most position, the shock-wave faces an inflow with a greater relative Mach number (i.e., $M_{1r}>1.3$), and induces flow-separation bubbles near the walls. The effective flow-passage downstream of the shock-wave is shrunk by the separation bubbles. The expansion wave becomes significantly strong in a simple convergent flow-passage, triggering the second shock-wave in the diffuser.

4.3. Limitation

The present wavy surface is fixed to the bottom wall of a diffuser. When applying to a real supersonic intake, three factors should be considered in the future work.

• More complicated perturbation pressure impacts should be studied. Harmonic components exit in the transient back-pressure of a real ramjet engine. For a wide-Mach-number-range flight, the combustor needs to work at several modes. The perturbation frequency will change when switching between the transonic and supersonic modes. An adaptive control strategy would be applied to the variable wavy surface.
• The fluid structure interaction’s impact should be evaluated. The variable wavy surface may vibrate due to the fluid–structure interaction. According to the work by Yao et al. [19], the flexible wavy surface will emulate the present wavy surface’s functions. However, the fatigue design would be implemented to prevent a potential fatigue failure of the wavy surface.
• Control over the effectiveness of the wavy surface should be verified for a real application. The present wavy surface works well for the simple flow-pattern in the diffuser. The control strategy would be evaluated for a different and complicated flow field, e.g., a real supersonic intake or an isolator of a ramjet engine. Meanwhile, the size of the wavy surface should be acceptable to the supersonic intake, and should not significantly change the whole geometry.

5. Conclusions

To mitigate the large-amplitude forced shock-wave oscillation, a variable 2D wavy surface has been numerically implemented to the Sajben diffuser. The impacts of the wavy surface on the oscillating shock-wave have been evaluated. Several interesting results emerge.

• The impacts of the wavy surface are investigated by increasing the depth D and decreasing the length L. Increasing the wavy surface depth D benefits toward mitigating the forced shock-wave oscillation. Decreasing the wavy surface length L may increase or decrease the oscillation amplitudes, dependent on the specific value.
• The mitigating mechanism of the optimal wavy surface on the forced shock-wave oscillation is interpreted from two viewpoints, i.e., the shock-wave stability and the work performed by a moving shock-wave. The second one is associated with the shock-wave traveling speed and the shock-wave strength. The work holds constant for a given pressure perturbation. The strong shock-wave induced by the optimal wavy surface gives rise to a small shock-wave traveling speed and a mitigated oscillation amplitude.
• The traveling second shock-wave temporarily appears in the diffuser, which is similar to the stationary shock-train. The occurrence can be interpreted with the post-shock expansion. The shock-induced flow-separation bubble generates a simple convergent effective flow-passage downstream of the initial shock-wave. The expansion wave becomes significantly strong in the flow-passage and triggers the second shock-wave.

The present work tries to illustrate the variable 2D wavy surface’s impact on the forced shock-wave oscillation. When applying it to a real supersonic intake, more complex flow patterns (e.g., the shock train) and complicated back-pressure perturbations (e.g., multi-frequency perturbation) need to be investigated. Further studies will be pursued in future research.