Quantitative Measurement Method for Ice Roughness on an Aircraft Surface
Abstract
1. Introduction
2. Theories and Methods
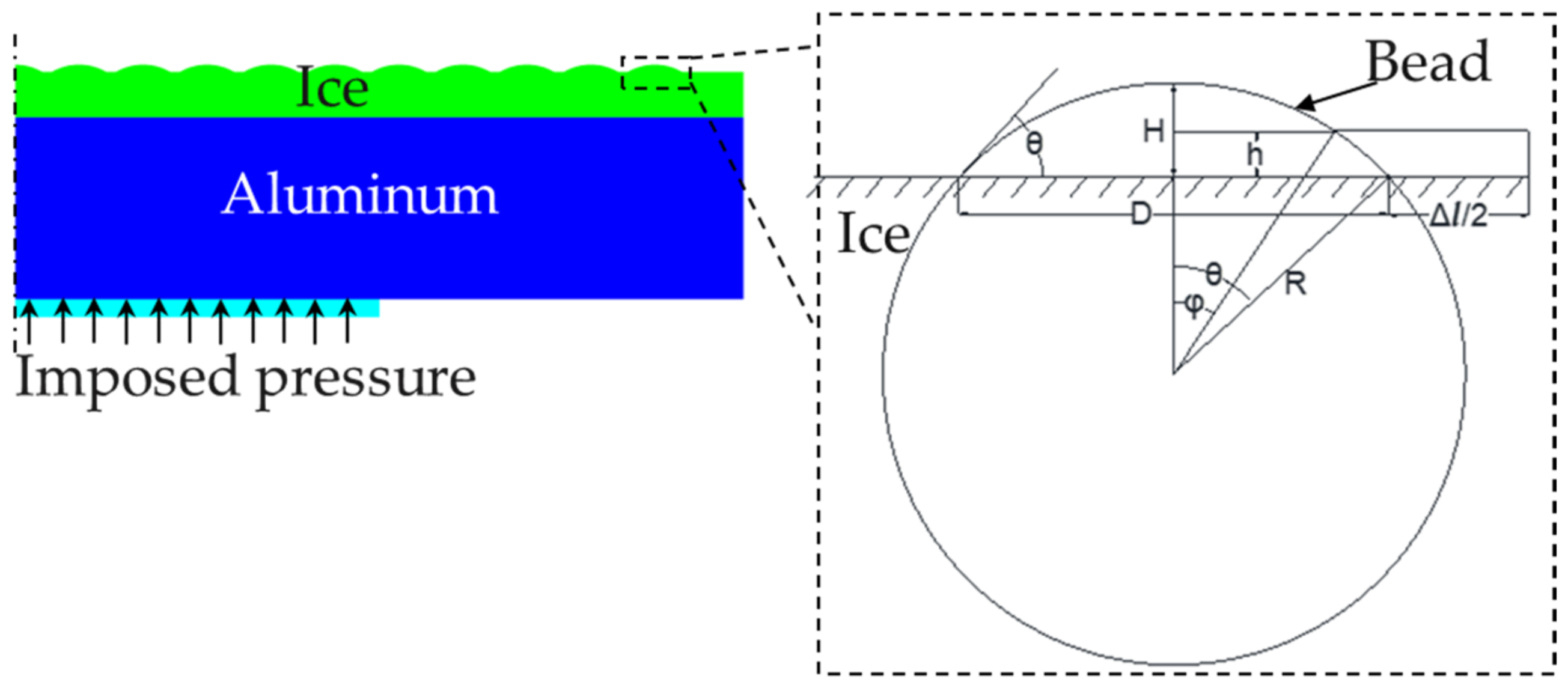
2.1. Description of the Numerical Model
2.2. Finite Element Simulation
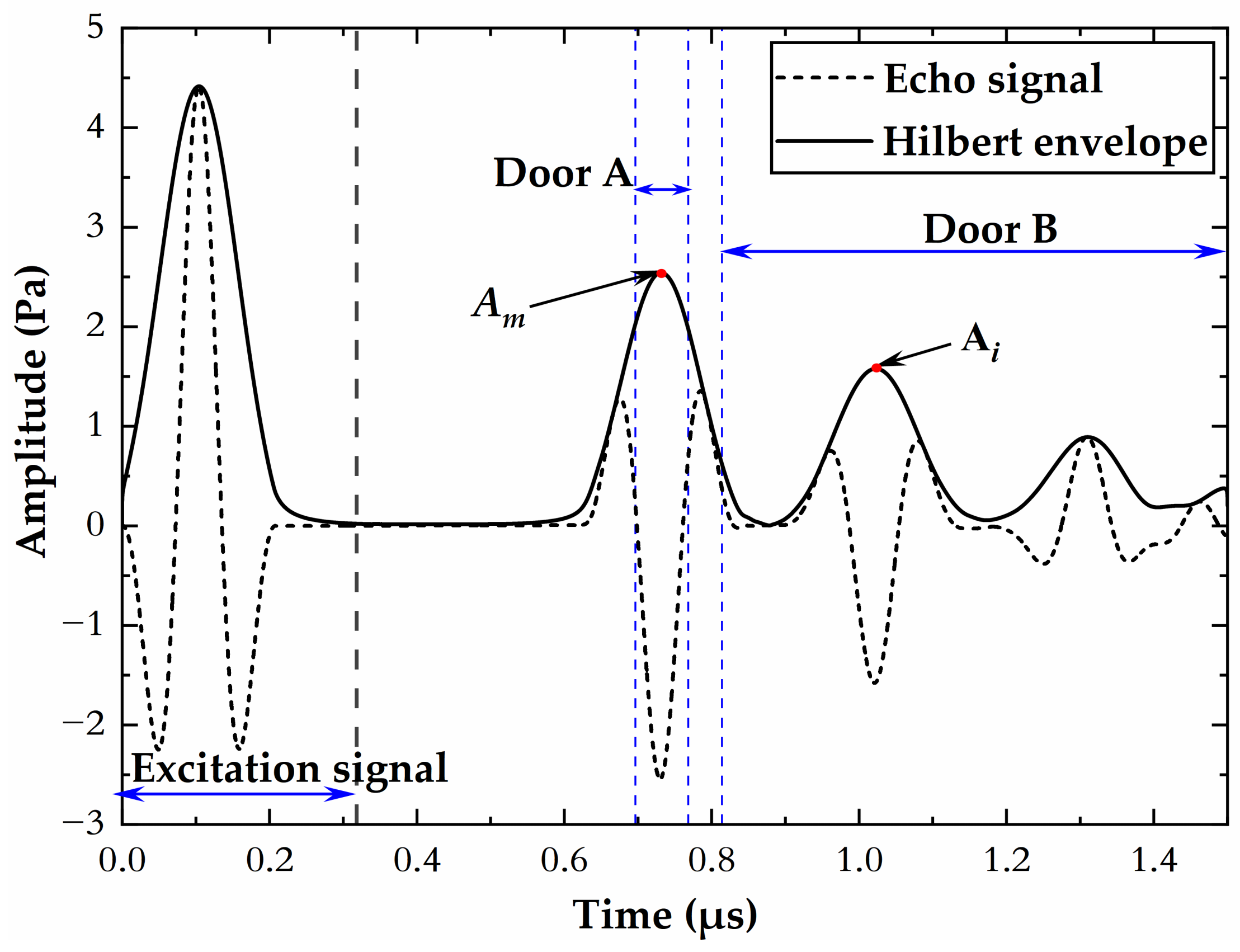
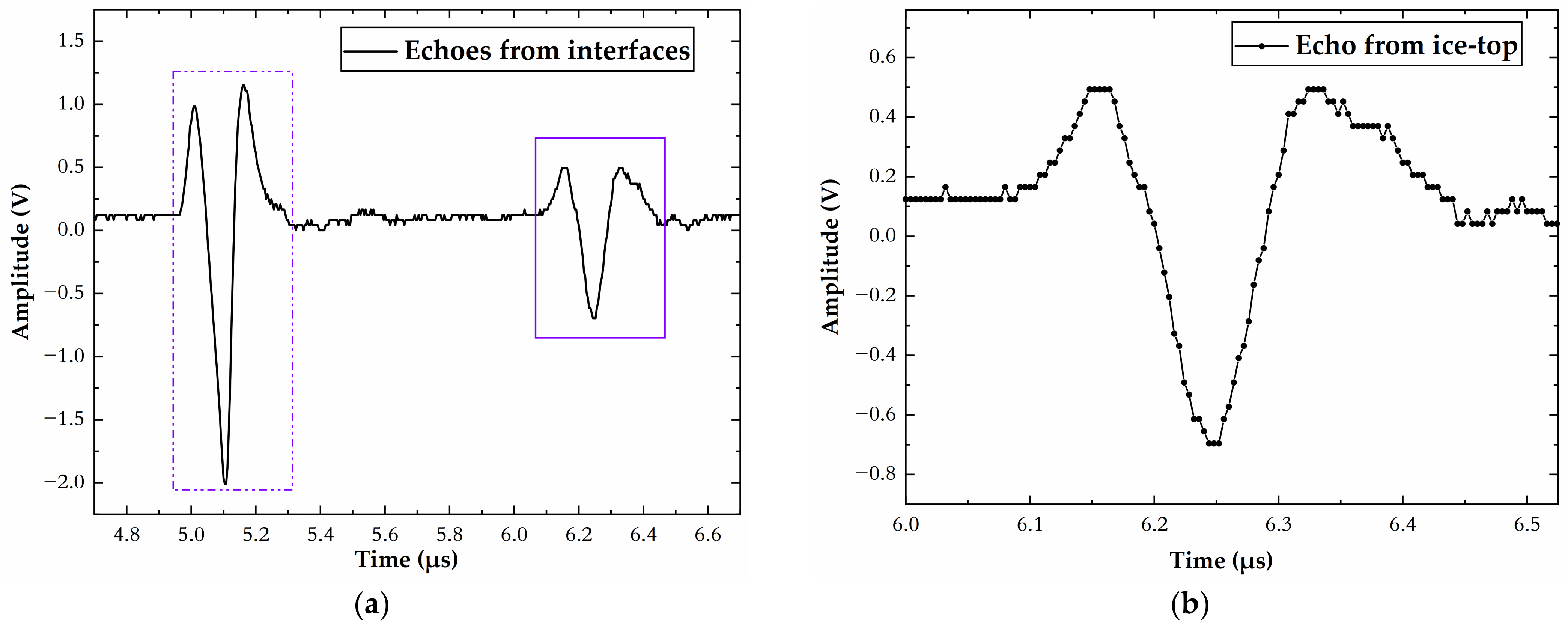
2.3. Signal Processing
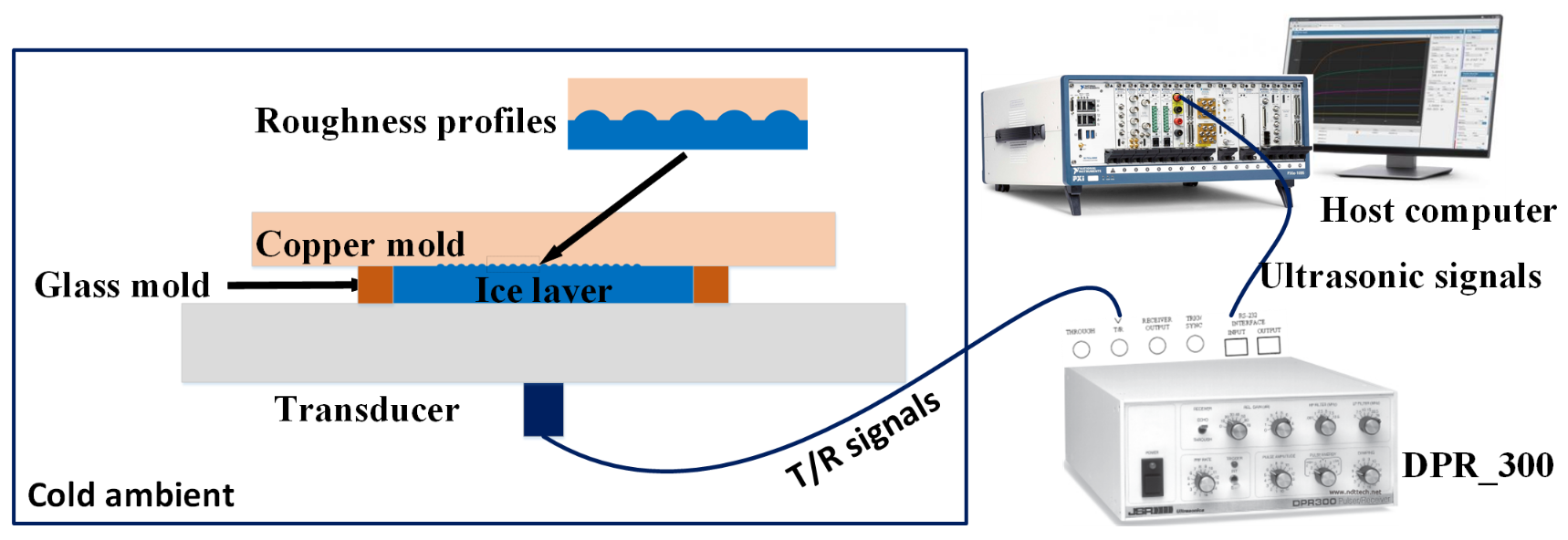
3. Experiment
3.1. Experimental Setup
3.2. Experimental Samples
3.3. Icing Wind Tunnel Research
3.4. Experimental Data Collection
4. Results and Discussion
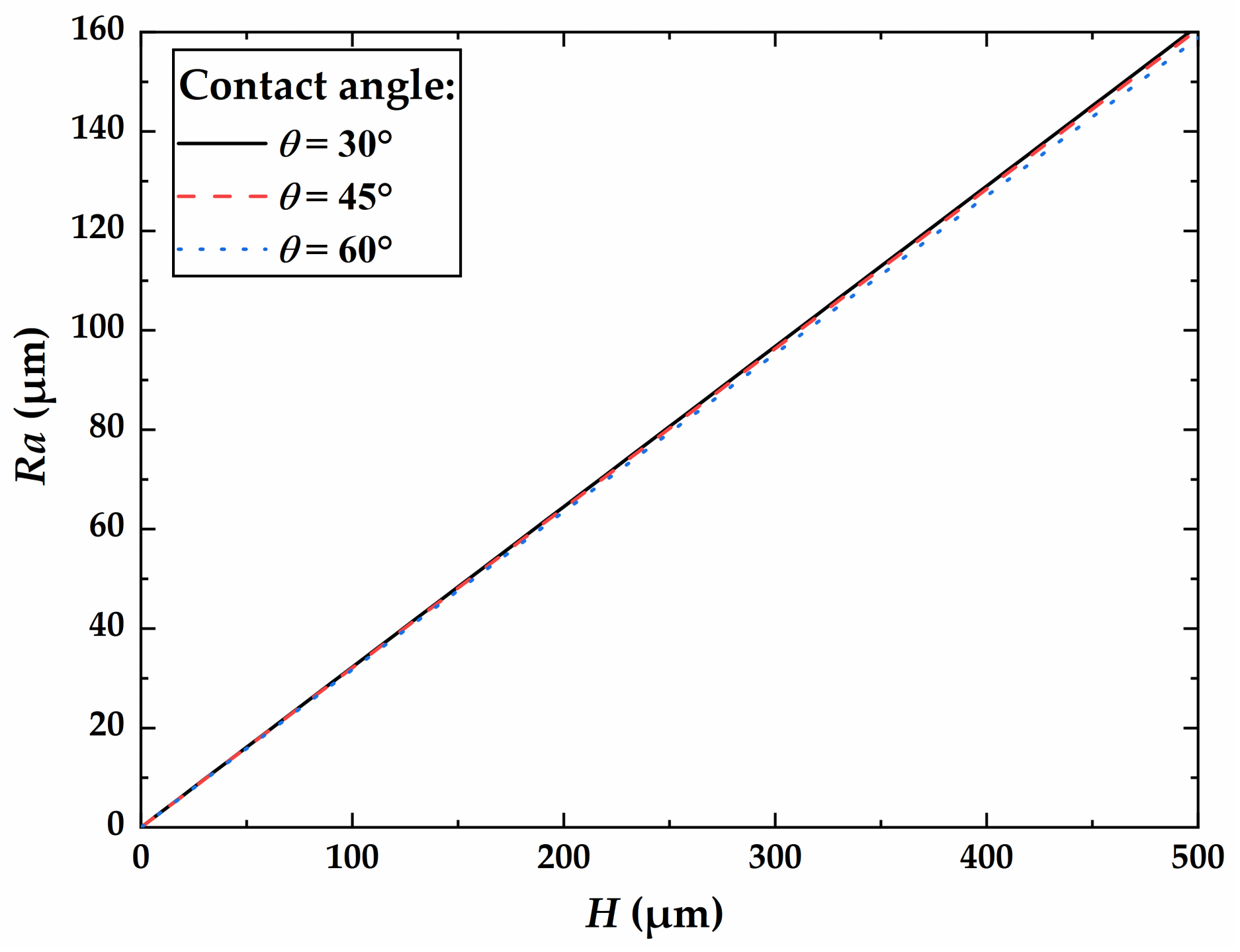
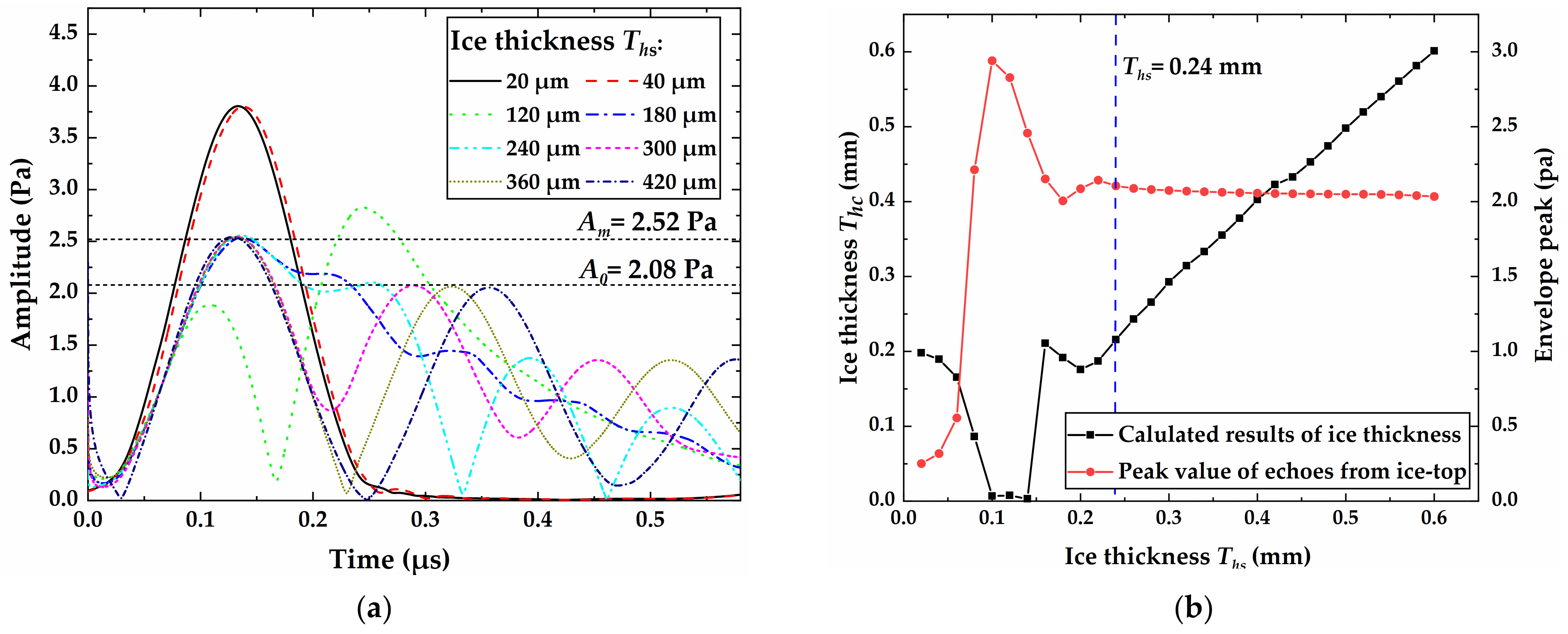
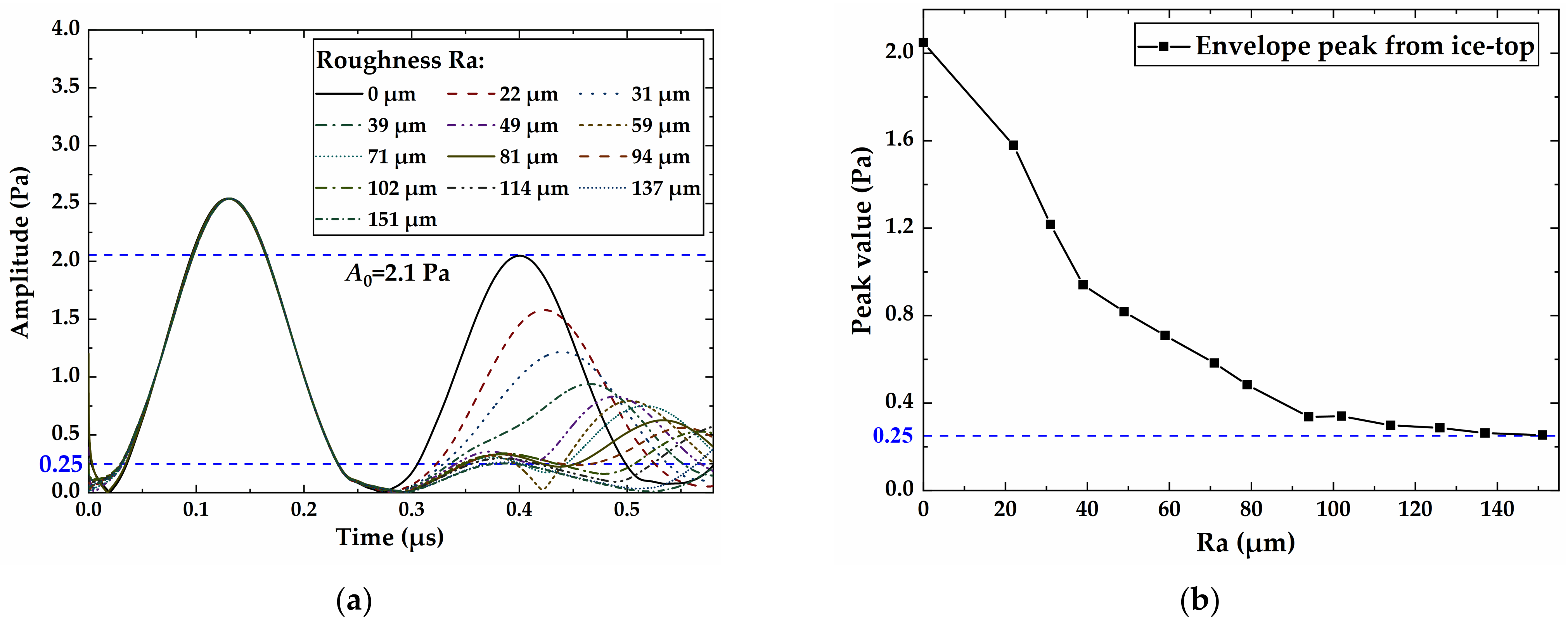
4.1. Measurement Sensitivity of Thickness and Roughness
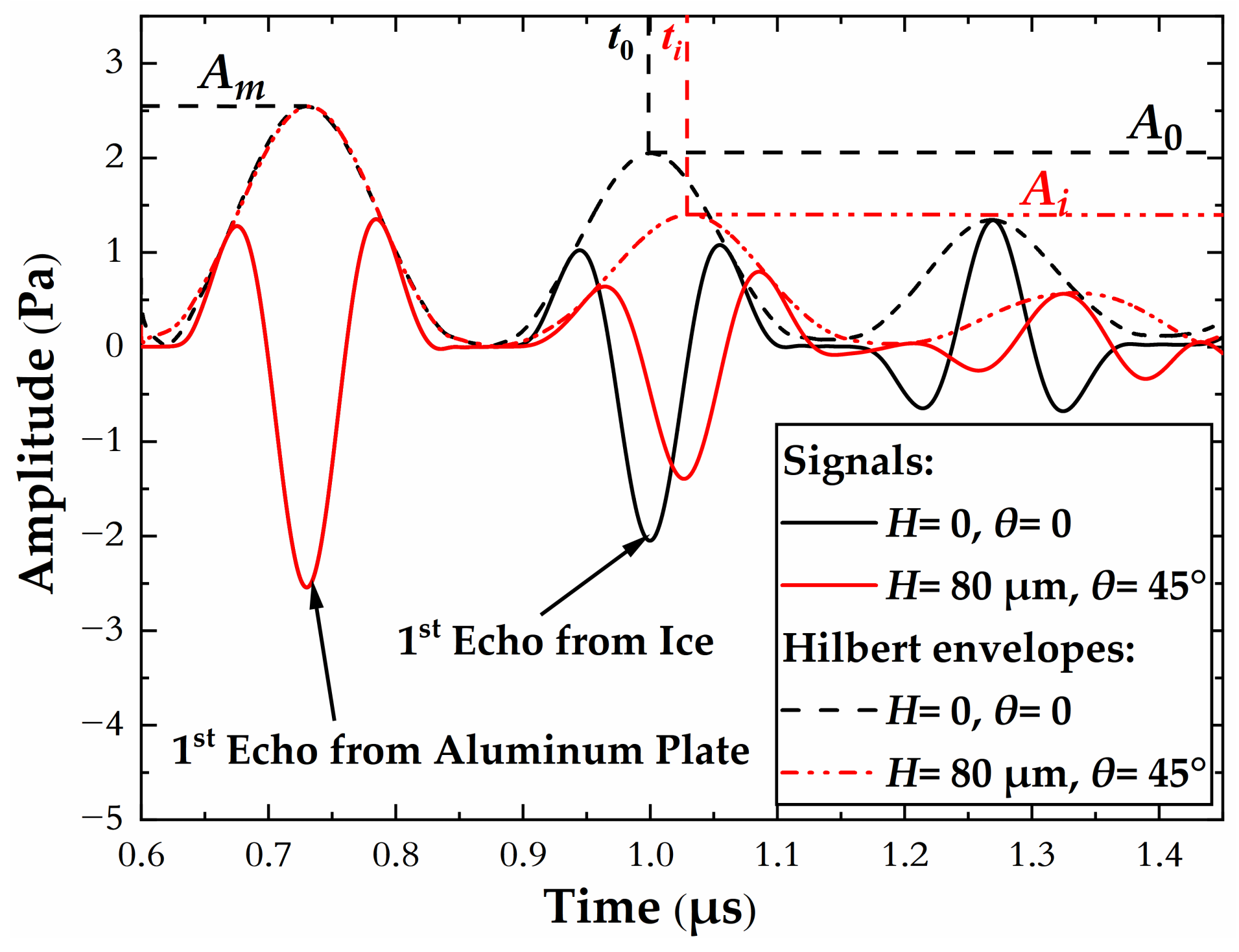
4.2. Effects of Ice Roughness on Ultrasonic Wave Propagation
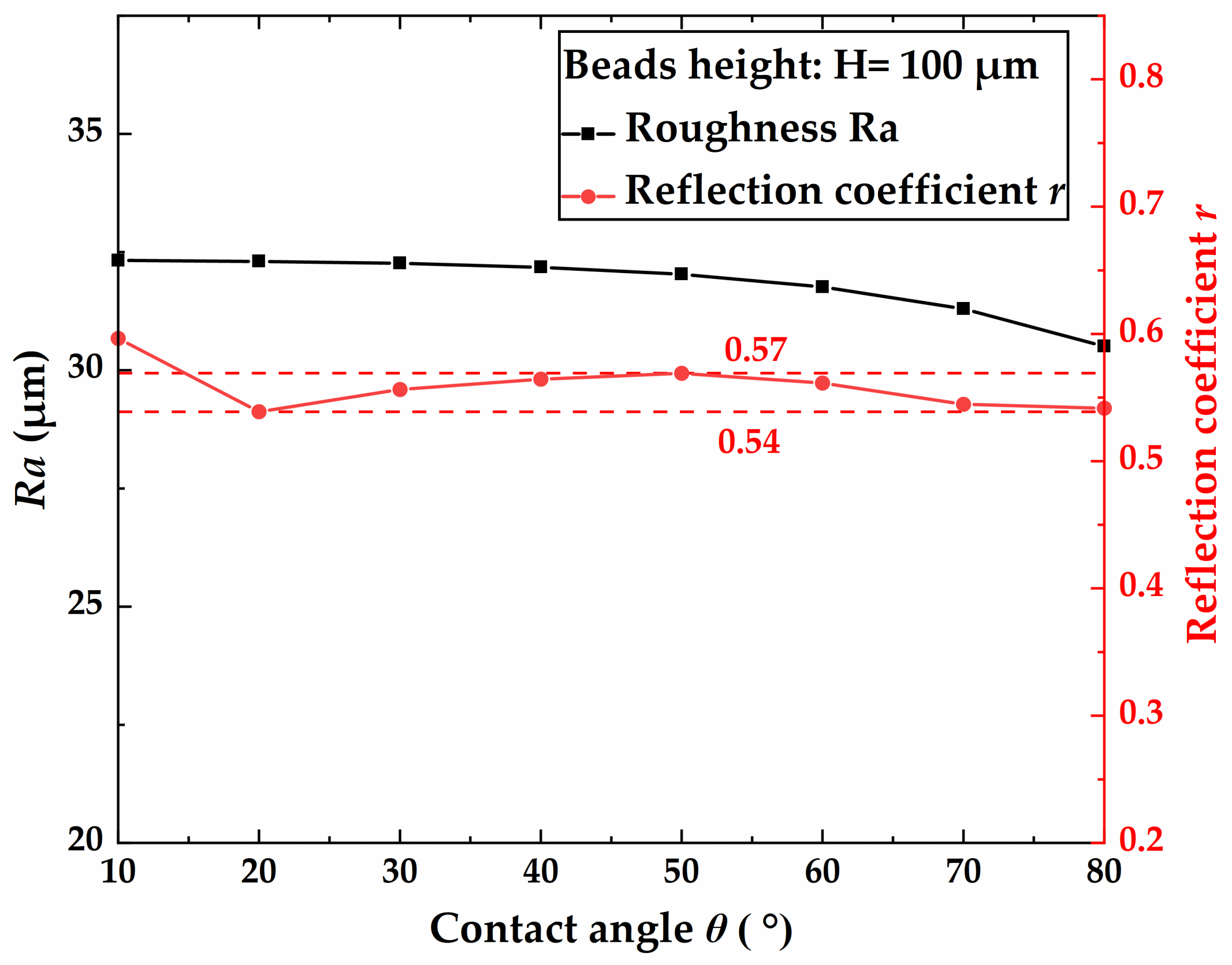
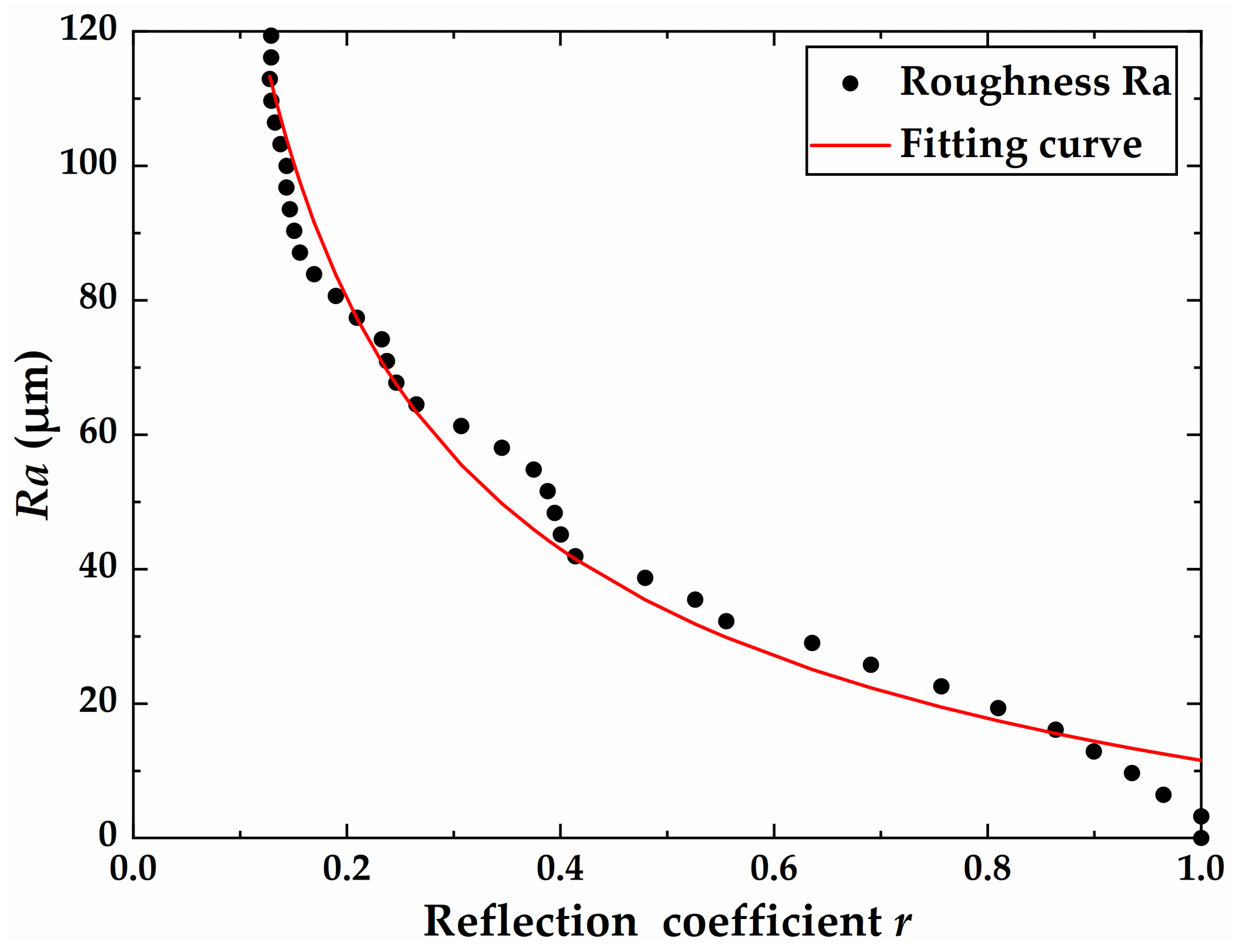
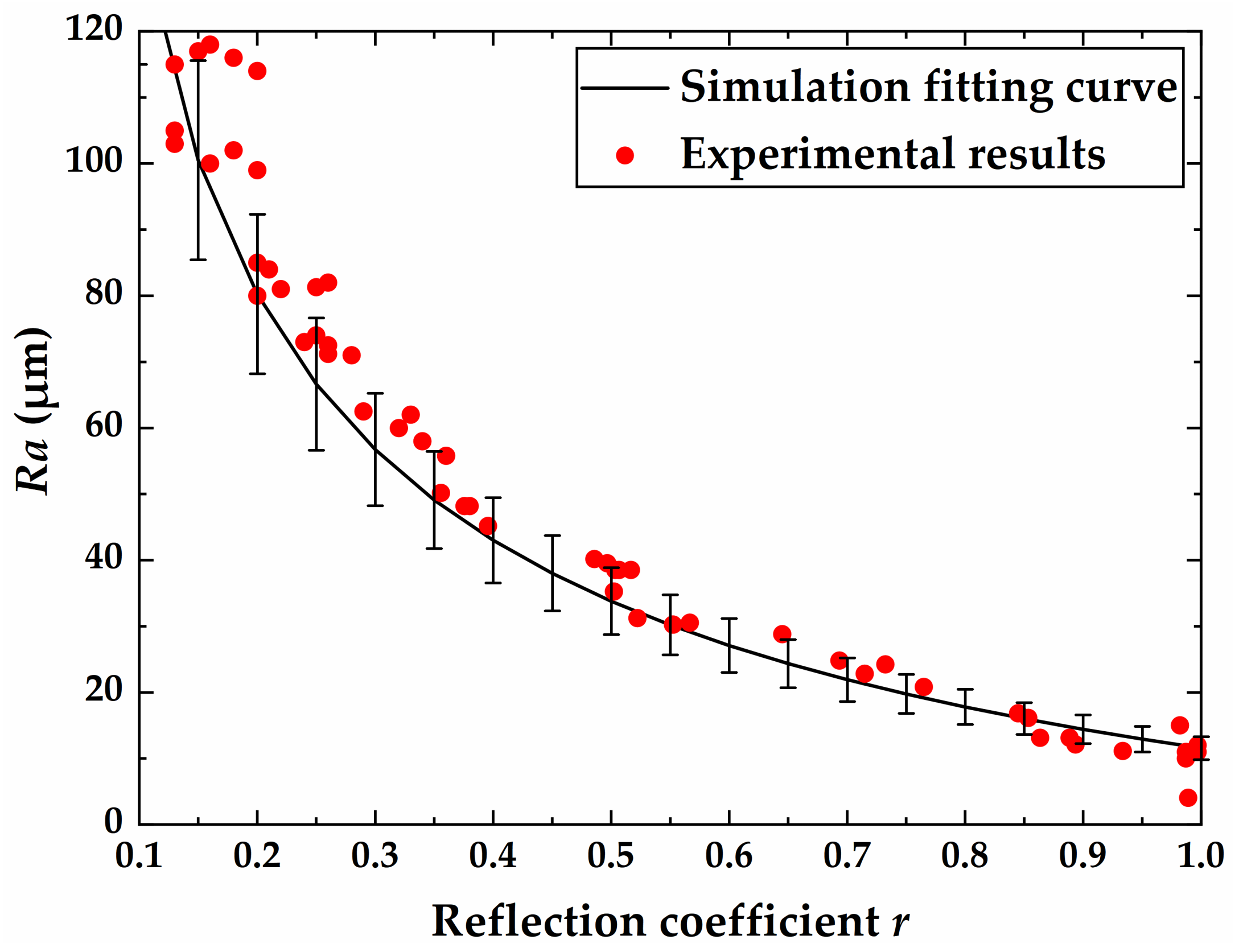
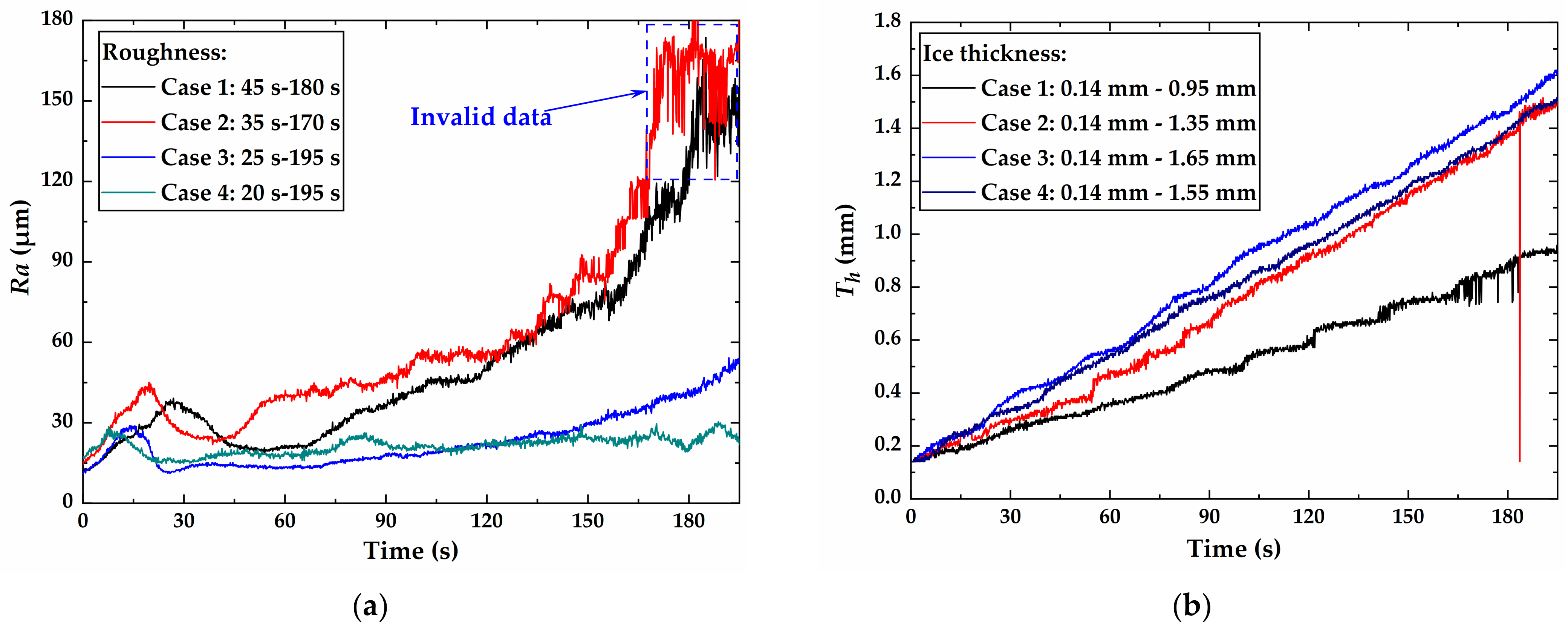
4.3. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cao, Y.H.; Tan, W.Y.; Wu, Z.L. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018, 75, 353–385. [Google Scholar] [CrossRef]
- Ozcer, I.A.; Baruzzi, G.S.; Reid, T.; Habashi, W.G.; Fossati, M.; Croce, G. FENSAP-ICE: Numerical prediction of ice roughness evolution, and its effects on ice shapes. SAE Tech. Pap. 2011. [Google Scholar] [CrossRef]
- McClain, S.T.; Vargas, M.M.; Tsao, J.-C. Ice roughness and thickness evolution on a swept NACA 0012 airfoil. In Proceedings of the 9th AIAA Atmospheric and Space Environments Conference, Denver, CO, USA, 5–9 June 2017; p. 1. [Google Scholar]
- Huebsch, W.W.; Rothmayer, A.P. Effects of surface ice roughness on dynamic stall. J. Aircr. 2002, 39, 945–953. [Google Scholar] [CrossRef]
- Tagawa, G.d.; Morency, F.; Beaugendre, H. CFD study of airfoil lift reduction caused by ice roughness. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018; p. 3010. [Google Scholar]
- Croce, G.; De Candido, E.; Habashi, W.; Aubé, M.; Baruzzi, G. FENSAP-ICE: Numerical prediction of in-flight icing roughness evolution. In Proceedings of the 1st AIAA Atmospheric and Space Environments Conference, San Antonio, TX, USA, 22–25 June 2009; p. 4126. [Google Scholar]
- Yoon, T.; Yee, K. Correction of local collection efficiency based on roughness element concept for glaze ice simulation. J. Mech. 2020, 36, 607–622. [Google Scholar] [CrossRef]
- Steiner, J.; Bansmer, S. Ice roughness and its impact on the ice accretion process. In Proceedings of the 8th AIAA Atmospheric and Space Environments Conference, Washington, DC, USA, 13–17 June 2016; p. 3591. [Google Scholar]
- Han, Y.; Palacios, J. Surface roughness and heat transfer improved predictions for aircraft ice-accretion modeling. AIAA J. 2017, 55, 1318–1331. [Google Scholar] [CrossRef]
- Shin, J. Characteristics of surface roughness associated with leading-edge ice accretion. J. Aircr. 1996, 33, 316–321. [Google Scholar] [CrossRef]
- McClain, S.T.; Vargas, M.; Kreeger, R.E.; Tsao, J. A reevaluation of appendix c ice roughness using laser scanning. SAE Tech. Pap. 2015. [Google Scholar] [CrossRef]
- Anderson, D.; Shin, J.; Anderson, D.; Shin, J. Characterization of ice roughness from simulated icing encounters. In Proceedings of the 35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1997; p. 52. [Google Scholar]
- Reehorst, A.L.; Richter, G.P. New Methods and Materials for Molding and Casting; NASA Technical Memorandum; NASA: Washington, DC, USA, 1987; p. 15.
- Collier, P.; Dixon, L.; Fontana, D.; Payne, D.; Pearson, A. The use of close range photogrammetry for studying ice accretion on aerofoil. Photogramm. Rec. 1999, 16, 671–684. [Google Scholar] [CrossRef]
- McKnight, R.; Palko, R.; Humes, R. In-flight photogrammetric measurement of wing ice accretions. In Proceedings of the 24th Aerospace Sciences Meeting, Reno, NV, USA, 6–9 January 1986; p. 483. [Google Scholar]
- McClain, S.T.; Vargas, M.; Tsao, J.-C.; Broeren, A.P.; Lee, S. Ice accretion roughness measurements and modeling. In Proceedings of the 7th European Conference for Aeronautics and Space Sciences (EUCASS), Milan, Italy, 3–6 July 2017; p. 555. [Google Scholar]
- Puffing, R.F.A.; Hassler, W.; Tramposch, A.; Peciar, M. Ice shape mapping by means of 4D-scans. In Proceedings of the SAE 2015 International Conference on Icing of Aircraft, Engines, and Structures, Prague, Czech Republic, 22–25 June 2015; p. 8. [Google Scholar]
- Neubauer, T.; Hassler, W.; Puffing, R. Ice shape roughness assessment based on a three-dimensional self-organizing map approach. In Proceedings of the Aiaa Aviation 2020 Forum, Virtual, 15–19 June 2020; p. 2805. [Google Scholar]
- Liu, Y.; Zhang, K.; Tian, W.; Hu, H. An experimental study to characterize the effects of initial ice roughness on the wind-driven water runback over an airfoil surface. Int. J. Multiph. Flow 2020, 126, 103254. [Google Scholar] [CrossRef]
- Cobbold, R.S. Foundations of Biomedical Ultrasound; Oxford University Press, Inc.: New York, NY, USA, 2007; Volume 9, pp. 609–620. [Google Scholar]
- Hansman, R.J., Jr.; Kirby, M.S. Measurement of ice accretion using ultrasonic pulse-echo techniques. J. Aircr. 1985, 22, 530–535. [Google Scholar] [CrossRef]
- Hansman, R.J., Jr.; Kirby, M.; Lichtenfelts, F. Ultrasonic techniques for aircraft ice accretion measurement. In Proceedings of the Sensor and Measurements Techniques for Aeronautical Applications, Atlanta, GA, USA, 1 March 1990; p. 4656. [Google Scholar]
- Liu, Y.; Bond, L.J.; Hu, H. Ultrasonic-attenuation-based technique for ice characterization pertinent to aircraft icing phenomena. AIAA J. 2017, 55, 1602–1609. [Google Scholar] [CrossRef]
- Heriveaux, Y.; Nguyen, V.H.; Brailovski, V.; Gorny, C.; Haiat, G. Reflection of an ultrasonic wave on the bone-implant interface: Effect of the roughness parameters. J. Acous. Soc. Am. 2019, 145, 3370. [Google Scholar] [CrossRef]
- Ma, Z.; Luo, Z.; Lin, L.; Krishnaswamy, S.; Lei, M. Quantitative characterization of the interfacial roughness and thickness of inhomogeneous coatings based on ultrasonic reflection coefficient phase spectrum. NDT E Int. 2019, 102, 16–25. [Google Scholar] [CrossRef]
- Okajima, K.; Nagaoka, S.; Islam, M.R.; Ito, R.; Watanabe, K. Development and testing of a surface roughness measurement device based on aerial ultrasonic reflections. Paddy Water Environ. 2019, 18, 345–353. [Google Scholar] [CrossRef]
- Shannon, T.A.; McClain, S.T. Convection from a simulated NACA 0012 airfoil with realistic ice accretion roughness variations. In Proceedings of the SAE International Conference on Icing of Aircraft, Engines, and Structures, Montreal, QC, Canada, 22–25 June 2015; p. 13. [Google Scholar]
- Anderson, D.; Hentschel, D.; Ruff, G. Measurement and correlation of ice accretion roughness. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998; p. 98. [Google Scholar]
- Zhang, K.; Liu, Y.; Rothmayer, A.P.; Hu, H. An experimental study of wind-driven water film flows over roughness array. In Proceedings of the 6th AIAA Atmospheric and Space Environments Conference, Atlanta, GA, USA, 16–20 June 2014; p. 2326. [Google Scholar]
- Berezovski, A.; Engelbrecht, J.; Maugin, G.A. Numerical simulation of two-dimensional wave propagation in functionally graded materials. Eur. J. Mech. 2003, 22, 257–265. [Google Scholar] [CrossRef]
- Senthil, K.; Iqbal, M.A.; Chandel, P.S.; Gupta, N.K. Study of the constitutive behavior of 7075-T651 aluminum alloy. Int. J. Impact Eng. 2017, 108, 171–190. [Google Scholar] [CrossRef]
- Petrenko, V.F.; Whitworth, R.W. The Physics of Ice; Elsevier: New York, NY, USA, 1999; Volume 6. [Google Scholar]
- Gadelmawla, E.; Koura, M.M.; Maksoud, T.M.; Elewa, I.M.; Soliman, H. Roughness parameters. J. Mater. Process. Technol. 2002, 123, 133–145. [Google Scholar] [CrossRef]
- Harris, F.J. On the use of windows for harmonic analysis with the discrete fourier transform. Proc. IEEE 1978, 66, 51–83. [Google Scholar] [CrossRef]
- Al-Aufi, Y.A.; Hewakandamby, B.N.; Dimitrakis, G.; Holmes, M.; Hasan, A.; Watson, N.J. Thin film thickness measurements in two phase annular flows using ultrasonic pulse echo techniques. Flow Meas. Instrum. 2019, 66, 67–78. [Google Scholar] [CrossRef]
- Shpigler, A.; Mor, E.; Bar-Hillel, A. Detection of overlapping ultrasonic echoes with deep neural networks. Ultrasonics 2022, 119, 106598. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Li, W.; Wu, D.; Zhao, N.; Zhu, C. Study on freezing characteristics of the surface water film over glaze ice by using an ultrasonic pulse-echo technique. Ultrasonics 2022, 126, 106804. [Google Scholar] [CrossRef]
- Madu, I.E.; Madu, C.N. Design optimization using signal-to-noise ratio. Simul. Pract. Theory 1999, 7, 349–372. [Google Scholar] [CrossRef]





| Material | Mass Density , kg m−3 | Longitudinal Velocity , m s−1 | Shear Velocity , m s−1 | Data Source |
|---|---|---|---|---|
| Aluminum | 2690 | 6297.4 | 3172.1 | Senthil et al. [31] |
| Ice | 917.6 | 3713.4 | 1869.3 | Pounder [32] |
| Sample Number | Bead Radius R, μm | Height H, μm | Contact Angle , ° | 2D Roughness Ra, μm | 3D Roughness Sa1, μm | Measurement by Microscopic Sa2, μm |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 4.0 |
| 2 | 500 | 67 | 30 | 23 | 24 | 18.2 |
| 3 | 500 | 95 | 36 | 26 | 27 | 27.5 |
| 4 | 500 | 123 | 41 | 33 | 36 | 31.2 |
| 5 | 500 | 153 | 46 | 46 | 50 | 39.5 |
| 6 | 500 | 185 | 51 | 59 | 63 | 62.5 |
| 7 | 500 | 217 | 56 | 71 | 74 | 71.3 |
| 8 | 500 | 250 | 60 | 79 | 84 | 83.9 |
| 9 | 1250 | 252 | 37 | 81 | 85 | 82.5 |
| 10 | 1250 | 292 | 40 | 94 | 99 | 93.6 |
| 11 | 1500 | 287 | 36 | 92 | 97 | 96.7 |
| 12 | 1500 | 318 | 38 | 102 | 108 | 106.5 |
| 13 | 1750 | 352 | 37 | 114 | 120 | 111.3 |
| 14 | 1750 | 390 | 39 | 126 | 133 | 132.2 |
| 15 | 2000 | 424 | 38 | 137 | 144 | 140.3 |
| 16 | 2000 | 468 | 40 | 151 | 159 | 140.0 |
| 17 | Irregular sample | 108.8 | ||||
| Case Number | Freestream Velocity, V (m/s) | Total Temperature (°C) |
|---|---|---|
| Case 1 | 24.8 | −5.4 |
| Case 2 | 33.0 | −6.8 |
| Case 3 | 41.2 | −5.5 |
| Case 4 | 49.5 | −4.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, Y.; Wang, Y.; Zhu, D.; Zhao, N.; Zhu, C. Quantitative Measurement Method for Ice Roughness on an Aircraft Surface. Aerospace 2022, 9, 739. https://doi.org/10.3390/aerospace9120739
Wang Y, Zhang Y, Wang Y, Zhu D, Zhao N, Zhu C. Quantitative Measurement Method for Ice Roughness on an Aircraft Surface. Aerospace. 2022; 9(12):739. https://doi.org/10.3390/aerospace9120739
Chicago/Turabian StyleWang, Yuan, Yang Zhang, Yan Wang, Dongyu Zhu, Ning Zhao, and Chunling Zhu. 2022. "Quantitative Measurement Method for Ice Roughness on an Aircraft Surface" Aerospace 9, no. 12: 739. https://doi.org/10.3390/aerospace9120739
APA StyleWang, Y., Zhang, Y., Wang, Y., Zhu, D., Zhao, N., & Zhu, C. (2022). Quantitative Measurement Method for Ice Roughness on an Aircraft Surface. Aerospace, 9(12), 739. https://doi.org/10.3390/aerospace9120739








