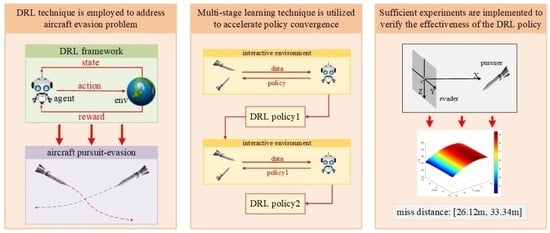
High-Speed Three-Dimensional Aerial Vehicle Evasion Based on a Multi-Stage Dueling Deep Q-Network
Abstract
1. Introduction
- An MS-DDQN algorithm is proposed to improve the typical DQN algorithm to accelerate the convergence process and modify the quality of training data;
- An adaptive iterative learning framework is implemented for high-speed aerial vehicle evasion problems;
- Adequate comparative simulation experiments are implemented to verify the effectiveness and robustness of the proposed MS-DDQN algorithm.
2. Fundamental and Problem Formulation
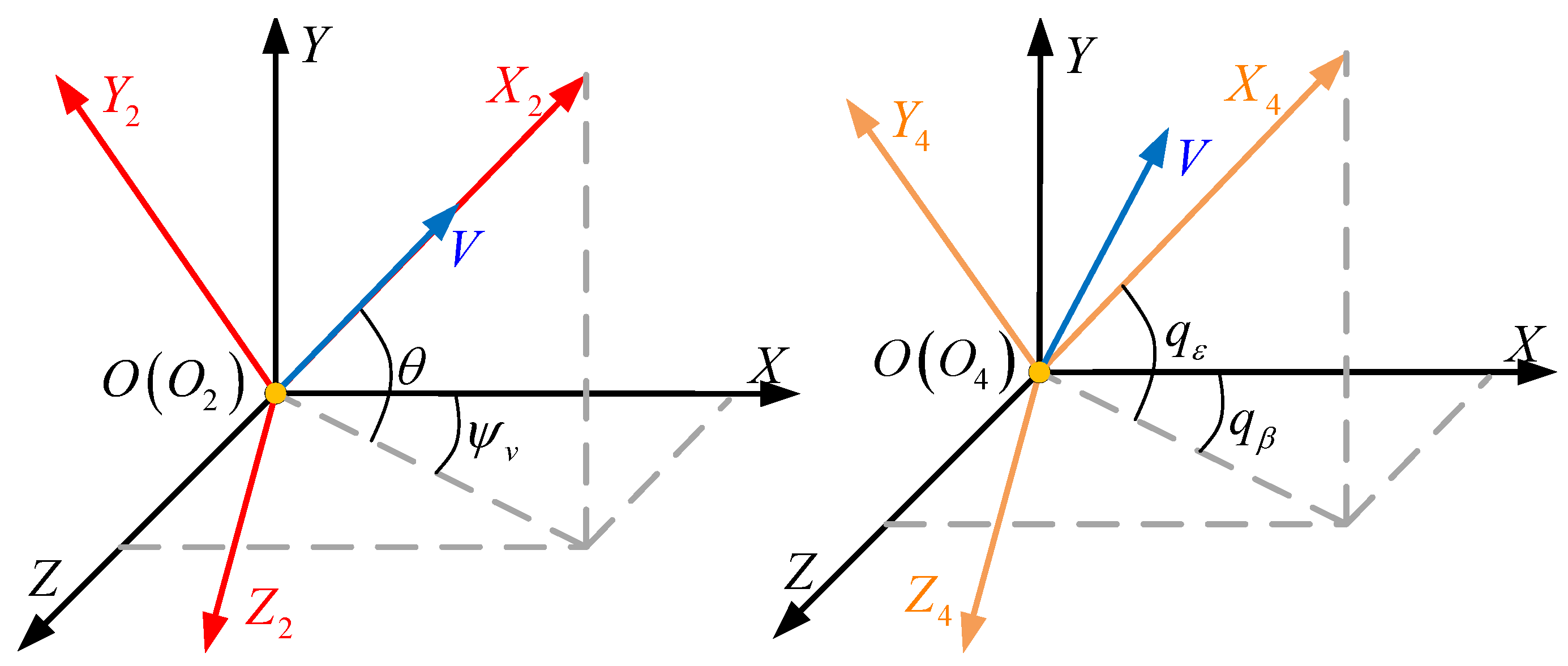
2.1. Aerial Vehicle Pursuit–Evasion Model
2.2. Value-Based Reinforcement Learning
- The evader is successfully intercepted by the pursuer, which is called failure evasion;
- The evader escapes from the attack of the pursuer successfully, which is called a successful evasion.
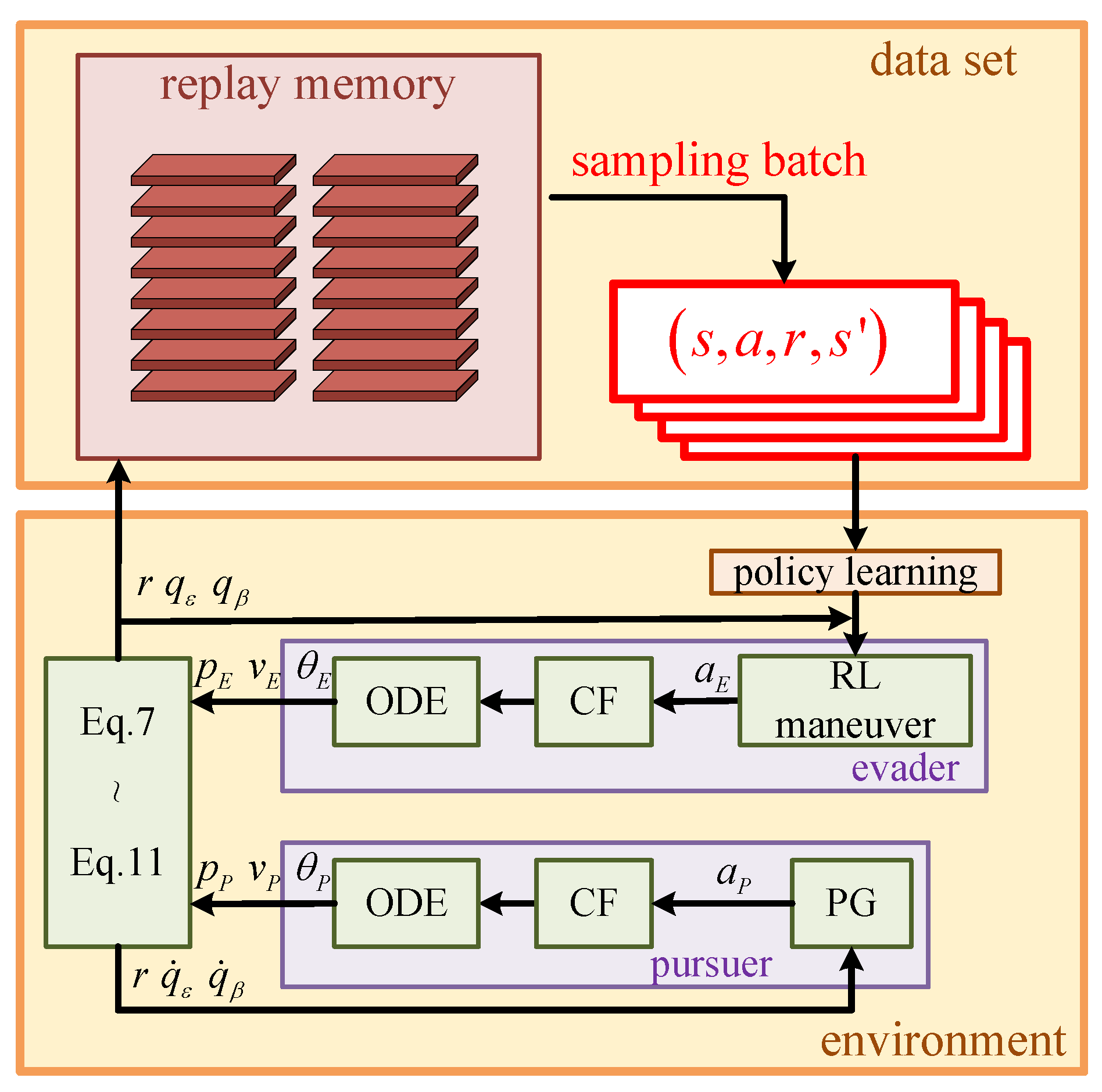
3. MS-DDQN Algorithm Design
3.1. Dueling DQN Framework
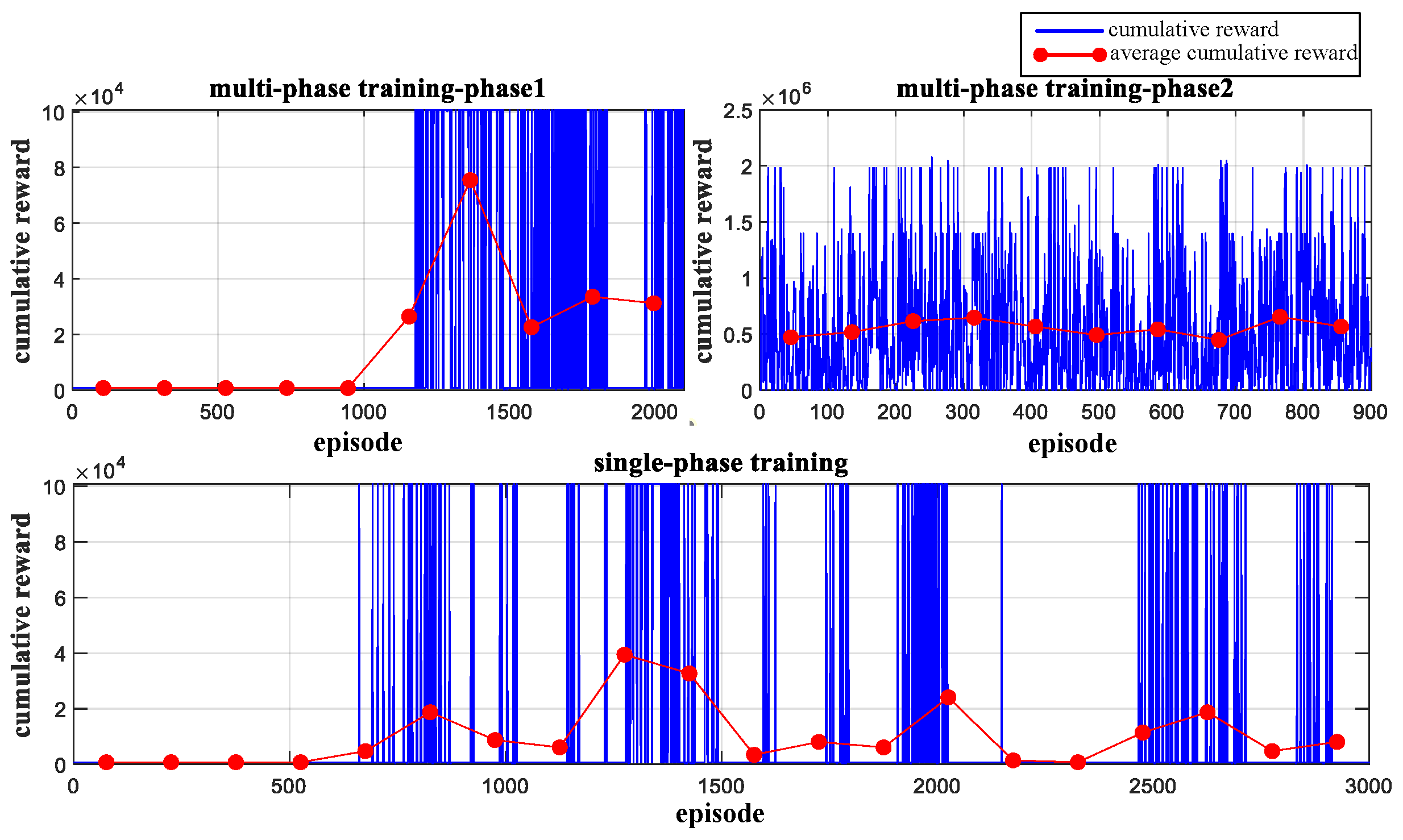
3.2. Multi-Stage Learning
| Algorithm 1 A multi-stage training framework with N sub-missions. |
|
3.3. Complete Learning Framework
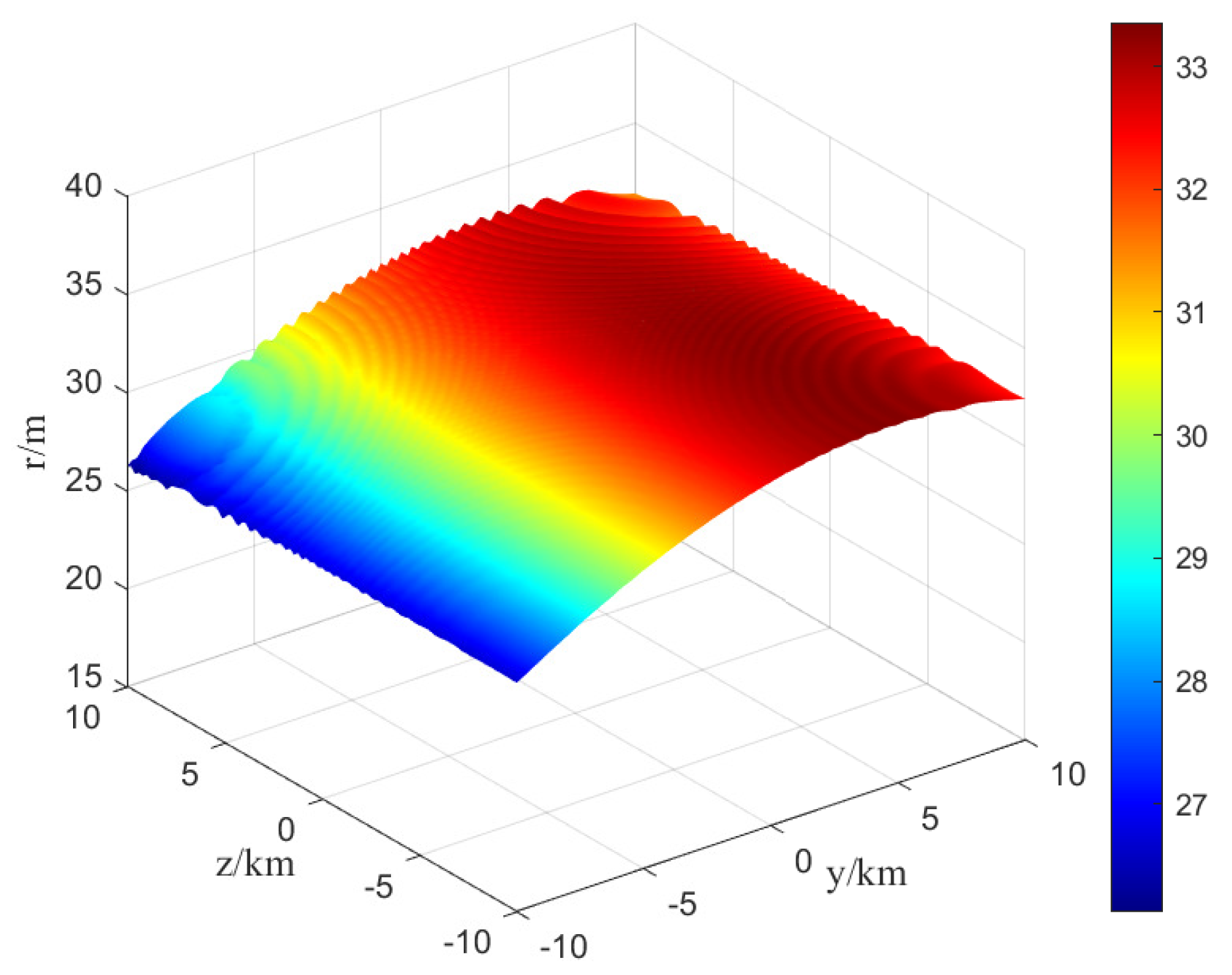
4. Simulation Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zeng, X.; Yang, L.; Zhu, Y.; Yang, F. Comparison of Two Optimal Guidance Methods for the Long-Distance Orbital Pursuit-Evasion Game. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 521–539. [Google Scholar] [CrossRef]
- Lee, J.; Ryoo, C. Impact Angle Control Law with Sinusoidal Evasive Maneuver for Survivability Enhancement. Int. J. Aeronaut. Space Sci. 2018, 19, 433–442. [Google Scholar] [CrossRef]
- Si, Y.; Song, S. Three-dimensional adaptive finite-time guidance law for intercepting maneuvering targets. Chin. J. Aeronaut. 2017, 30, 1985–2003. [Google Scholar] [CrossRef]
- Song, J.; Song, S. Three-dimensional guidance law based on adaptive integral sliding mode control. Chin. J. Aeronaut. 2016, 29, 202–214. [Google Scholar] [CrossRef]
- He, L.; Yan, X. Adaptive terminal guidance law for spiral-diving maneuver based on virtual sliding targets. J. Guid. Control Dynam. 2018, 41, 1591–1601. [Google Scholar] [CrossRef]
- Xu, X.; Cai, Y. Design and numerical simulation of a differential game guidance law. In Proceedings of the 2016 IEEE International Conference on Information and Automation (ICIA), Ningbo, China, 31 July–4 August 2016; pp. 314–318. [Google Scholar]
- Alias, I.; Ibragimov, G.; Rakhmanov, A. Evasion differential game of infinitely many evaders from infinitely many pursuers in Hilbert space. Dyn. Games Appl. 2017, 7, 347–359. [Google Scholar] [CrossRef]
- Liang, L.; Deng, F.; Peng, Z.; Li, X.; Zha, W. A differential game for cooperative target defense. Automatica 2019, 102, 58–71. [Google Scholar] [CrossRef]
- Ibragimov, G.; Ferrara, M.; Kuchkarov, A.; Pansera, B.A. Simple motion evasion differential game of many pursuers and evaders with integral constraints. Dyn. Games Appl. 2018, 8, 352–378. [Google Scholar] [CrossRef]
- Rilwan, J.; Kumam, P.; Badakaya, A.J.; Ahmed, I. A Modified Dynamic Equation of Evasion Differential Game Problem in a Hilbert space. Thai J. Math. 2020, 18, 199–211. [Google Scholar]
- Jagat, A.; Sinclair, A.J. Nonlinear Control for Spacecraft Pursuit-Evasion Game Using the State-Dependent Riccati Equation Method. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 3032–3042. [Google Scholar] [CrossRef]
- Asadi, M.M.; Gianoli, L.G.; Saussie, D. Optimal Vehicle-Target Assignment: A Swarm of Pursuers to Intercept Maneuvering Evaders based on Ideal Proportional Navigation. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 1316–1332. [Google Scholar] [CrossRef]
- Waxenegger-Wilfing, G.; Dresia, K.; Deeken, J.; Oschwald, M. A Reinforcement Learning Approach for Transient Control of Liquid Rocket Engines. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2938–2952. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, L.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Sun, J.; Liu, C.; Ye, Q. Robust differential game guidance laws design for uncertain interceptor-target engagement via adaptive dynamic programming. Int. J. Control 2016, 90, 990–1004. [Google Scholar] [CrossRef]
- Gaudet, B.; Furfaro, R.; Linares, R. Reinforcement learning for angle-only intercept guidance of maneuvering targets. Aerosp. Sci. Technol. 2020, 99, 105746. [Google Scholar] [CrossRef]
- Zhu, J.; Zou, W.; Zhu, Z. Learning Evasion Strategy in Pursuit-Evasion by Deep Q-network. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 67–72. [Google Scholar]
- Li, C.; Deng, B.; Zhang, T. Terminal guidance law of small anti-ship missile based on DDPG. In Proceedings of the International Conference on Image, Video Processing and Artificial Intelligence, Shanghai, China, 21 August 2020; Volume 11584. [Google Scholar]
- Shalumov, V. Cooperative online Guide-Launch-Guide policy in a target-missile-defender engagement using deep reinforcement learning. Aerosp. Sci. Technol. 2020, 104, 105996. [Google Scholar] [CrossRef]
- Souza, C.; Nwebury, R.; Cosgun, A.; Castillo, P.; Vidolov, B.; Kulić, D. Decentralized Multi-Agent Pursuit Using Deep Reinforcement Learning. IEEE Robot. Autom. Let. 2021, 6, 4552–4559. [Google Scholar] [CrossRef]
- Tipaldi, M.; Iervoline, R.; Massenio, P.R. Reinforcement learning in spacecraft control applications: Advances, prospects, and challenges. Annu. Rev. Control 2022, in press. [CrossRef]
- Selvi, E.; Buehrer, R.M.; Martone, A.; Sherbondy, K. Reinforcement Learning for Adaptable Bandwidth Tracking Radars. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3904–3921. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Ahmad, A.A.; Fortunati, S.; Sezgin, A.; Greco, M.S.; Gini, F. A Reinforcement Learning Based Approach for Multitarget Detection in Massive MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2622–2636. [Google Scholar] [CrossRef]
- Hu, Q.; Yang, H.; Dong, H.; Zhao, X. Learning-Based 6-DOF Control for Autonomous Proximity Operations Under Motion Constraints. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 4097–4109. [Google Scholar] [CrossRef]
- Elhaki, O.; Shojaei, K. A novel model-free robust saturated reinforcement learning-based controller for quadrotors guaranteeing prescribed transient and steady state performance. Aerosp. Sci. Technol. 2021, 119, 107128. [Google Scholar] [CrossRef]
- Volodymyr, M.; Koray, K.; David, S.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar]
- Wang, Z.; Schaul, T.; Hessel, M.; Hasselt, H.; Lanctot, M.; Freitas, N. Dueling network architectures for deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, San Francisco, CA, USA, 14 August 2016; Volume 48, pp. 1995–2003. [Google Scholar]
- Wang, C.; Wang, J.; Wang, J.; Zhang, X. Deep-Reinforcement-Learning-Based Autonomous UAV Navigation with Sparse Rewards. IEEE Internet Things J. 2020, 7, 6180–6190. [Google Scholar] [CrossRef]
- Huang, T.; Liang, Y.; Ban, X.; Zhang, J.; Huang, X. The Control of Magnetic Levitation System Based on Improved Q-network. In Proceedings of the Symposium Series on Computational Intelligence, Xiamen, China, 6–9 December 2019; pp. 191–197. [Google Scholar]
- Fan, J.; Wang, Z.; Xie, Y.; Yang, Z. A Theoretical Analysis of Deep Q-Learning. In Proceedings of the Learning for Dynamics and Control, PMLR, Online, 11–12 June 2020; pp. 486–489. [Google Scholar]
- Razzaghi, P.; Khatib, E.A.; Bakhtiari, S.; Hurmuzlu, Y. Real time control of tethered satellite systems to de-orbit space debris. Aerosp. Sci. Technol. 2021, 109, 106379. [Google Scholar] [CrossRef]




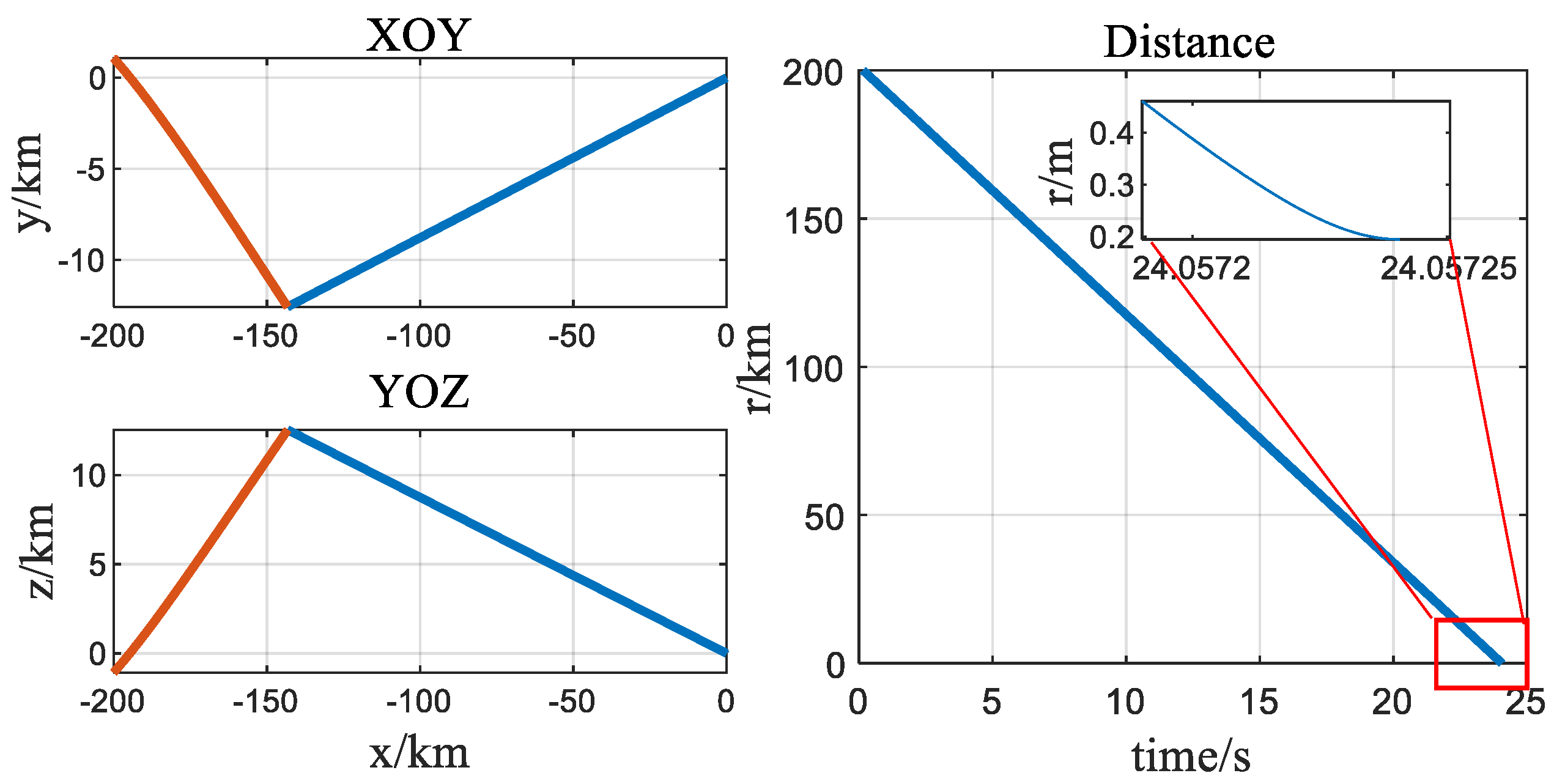
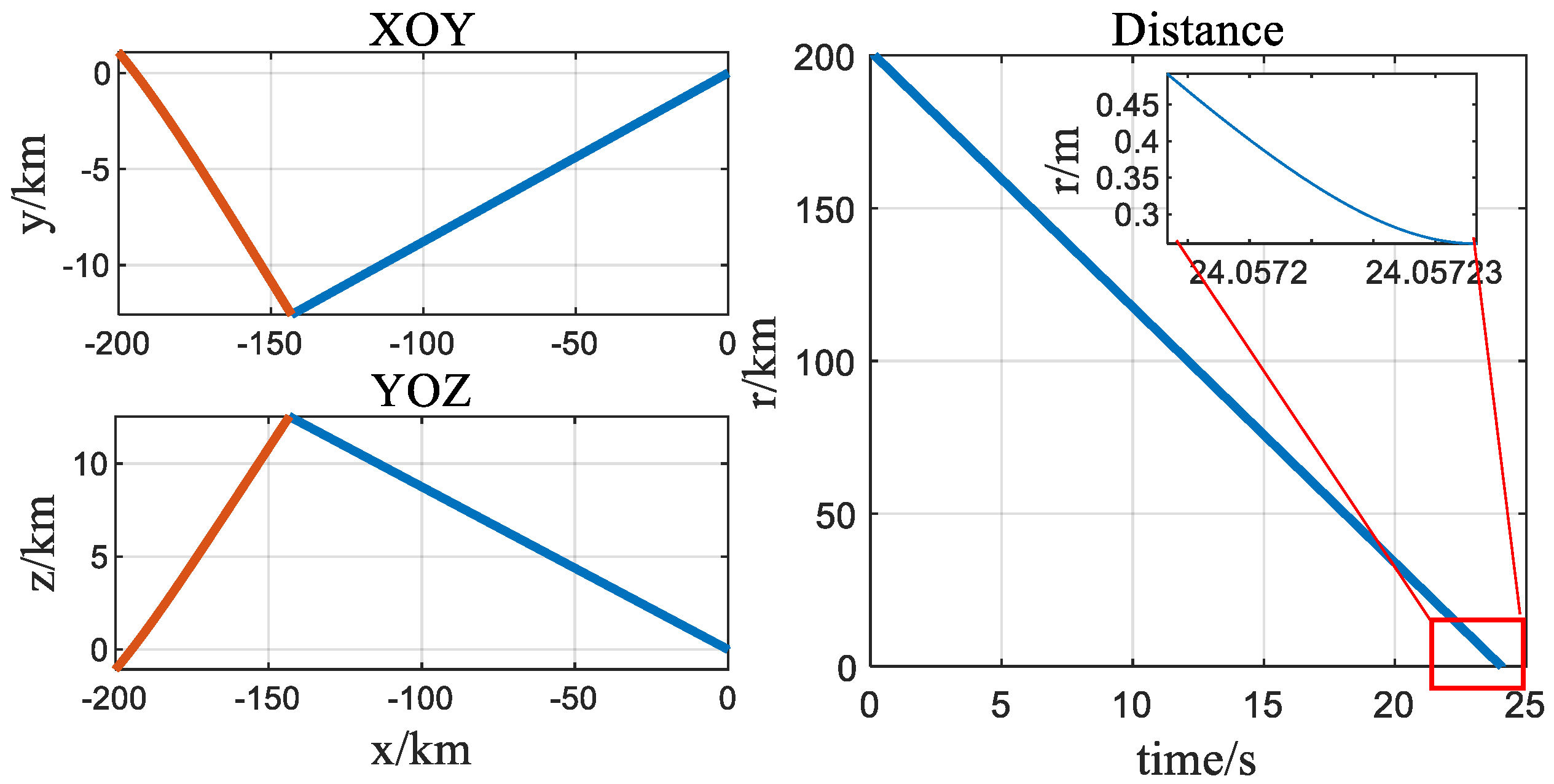
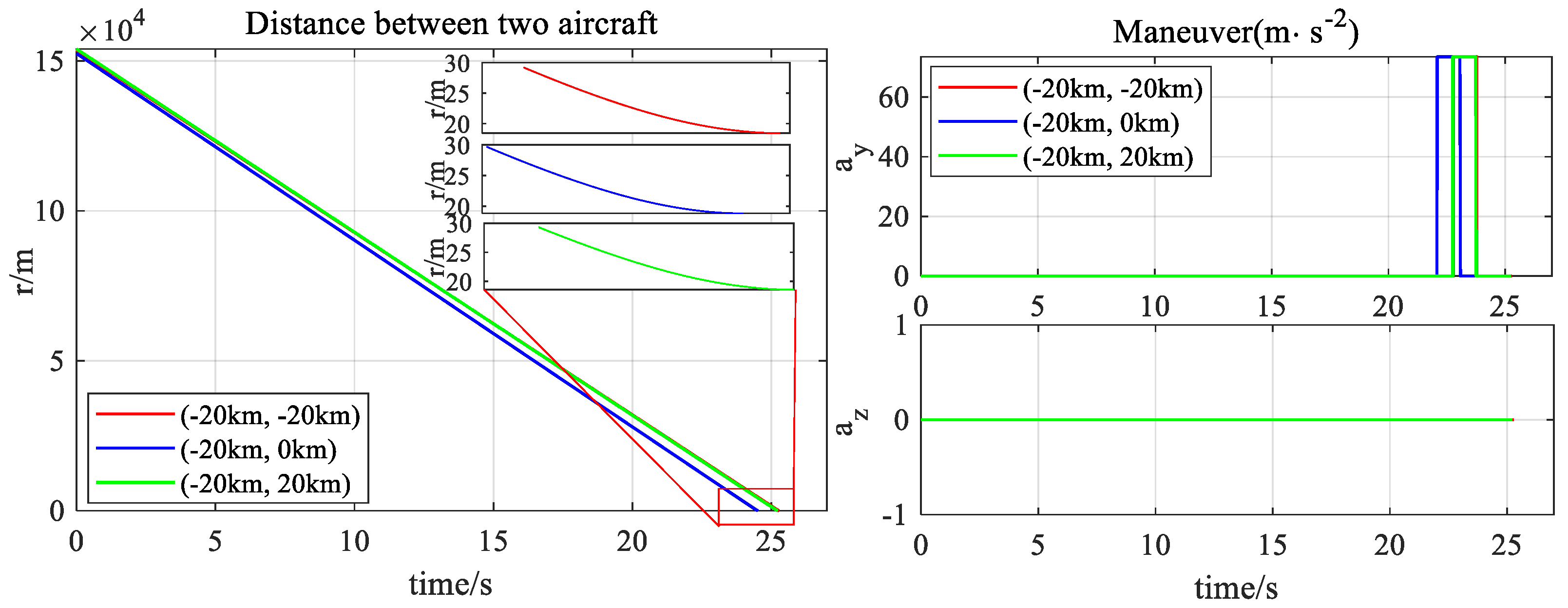

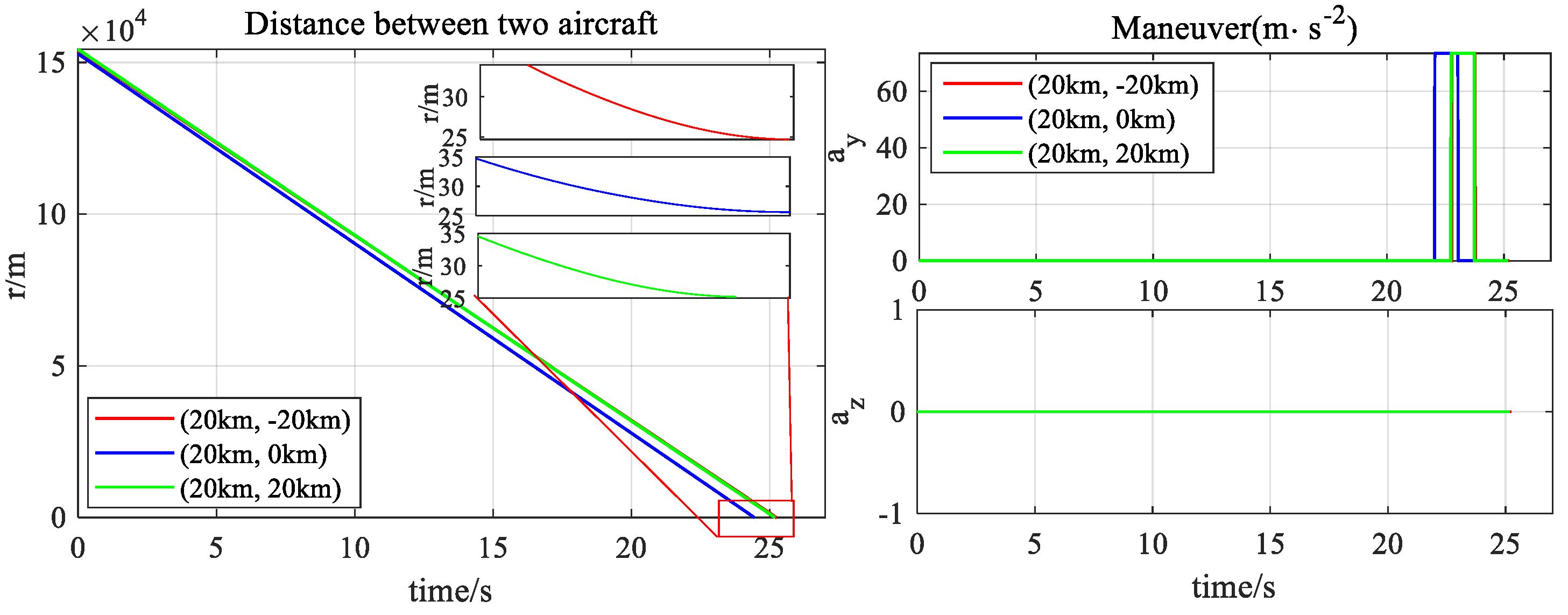
| Action | Acceleration | Action | Acceleration | Action | Acceleration |
|---|---|---|---|---|---|
| 0 | 3 | 6 | |||
| 1 | 4 | 7 | |||
| 2 | 5 | 8 |
| Layer | Input | Output | Activation Function |
|---|---|---|---|
| 1 | 3 | 20 | |
| 2 | 20 | 20 | |
| 3V | 20 | 9 | |
| 3A | 20 | 9 |
| Phase | Phase1-a | Phase1-b | Phase2 | |
|---|---|---|---|---|
| Parameter | ||||
| 0.9 | 0.9 | 0.9 | ||
| 0.9 | 0.9 | 0.9 | ||
| 0.01 | 0.01 | 0.01 | ||
| M | 5000 | 5000 | 2000 | |
| 64 | 64 | 64 | ||
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| g | |||
| Initial Relative Distance (km) | Heading Angle | ||||
|---|---|---|---|---|---|
| 10 | 5 | 0 | |||
| 19.81 | 23.25 | 25.17 | 25.36 | 25.45 | |
| 23.87 | 25.41 | 25.61 | 25.43 | 24.21 | |
| 25.69 | 25.53 | 24.90 | 23.12 | 18.80 | |
| 24.11 | 28.97 | 29.90 | 30.50 | 30.69 | |
| 30.29 | 30.71 | 30.75 | 30.48 | 29.71 | |
| 30.93 | 30.49 | 29.76 | 28.32 | 23.92 | |
| 13.71 | 9.79 | 13.15 | 13.79 | 14.19 | |
| 13.08 | 13.82 | 13.82 | 13.5 | 12.50 | |
| 14.38 | 13.71 | 12.56 | 9.79 | 6.67 | |
| Initial Relative Distance (km) | Heading Angle | ||||
|---|---|---|---|---|---|
| 10 | 5 | 0 | |||
| 20.17 | 23.30 | 25.63 | 26.21 | 26.13 | |
| 24.64 | 26.02 | 26.25 | 25.56 | 24.02 | |
| 25.83 | 25.98 | 25.26 | 23.60 | 19.21 | |
| 28.93 | 31.25 | 31.93 | 32.21 | 32.42 | |
| 32.44 | 32.56 | 32.44 | 32.22 | 31.72 | |
| 32.67 | 32.22 | 31.64 | 30.49 | 28.12 | |
| 14.14 | 17.39 | 16.93 | 17.36 | 17.90 | |
| 17.97 | 17.34 | 17.18 | 17.20 | 16.87 | |
| 17.99 | 17.21 | 16.69 | 15.18 | 13.66 | |
| Initial Relative Distance (km) | Heading Angle | ||||
|---|---|---|---|---|---|
| 10 | 5 | 0 | |||
| 16.61 | 22.12 | 25.19 | 25.47 | 25.37 | |
| 23.82 | 25.14 | 25.63 | 25.36 | 23.65 | |
| 25.59 | 25.72 | 24.68 | 22.12 | 17.41 | |
| 30.45 | 32.10 | 32.80 | 33.01 | 33.24 | |
| 33.33 | 33.39 | 33.23 | 33.07 | 32.54 | |
| 33.48 | 33.02 | 32.53 | 31.22 | 29.00 | |
| 16.69 | 19.12 | 18.57 | 19.06 | 19.64 | |
| 19.22 | 19.18 | 18.81 | 18.83 | 19.49 | |
| 19.68 | 18.96 | 18.42 | 18.07 | 18.27 | |
| Initial Relative Distance (km) | Heading Angle | ||||
|---|---|---|---|---|---|
| 10 | 5 | 0 | |||
| 11.14 | 19.92 | 23.16 | 24.21 | 24.17 | |
| 21.31 | 23.43 | 23.98 | 23.69 | 21.08 | |
| 23.91 | 24.24 | 22.84 | 19.07 | 10.31 | |
| 29.11 | 32.27 | 32.85 | 33.12 | 33.36 | |
| 33.25 | 33.49 | 33.35 | 33.15 | 32.52 | |
| 33.55 | 33.12 | 32.59 | 31.56 | 29.19 | |
| 18.55 | 19.65 | 19.73 | 19.85 | 20.47 | |
| 20.68 | 19.68 | 19.52 | 19.70 | 19.96 | |
| 20.45 | 19.77 | 19.47 | 18.48 | 18.74 | |
| Initial Relative Distance (km) | Heading Angle | ||||
|---|---|---|---|---|---|
| 10 | 5 | 0 | |||
| 8.70 | 15.98 | 20.88 | 22.21 | 22.31 | |
| 20.50 | 21.60 | 22.12 | 21.51 | 18.47 | |
| 22.51 | 22.22 | 20.22 | 15.94 | 6.58 | |
| 26.72 | 30.83 | 31.92 | 32.34 | 32.54 | |
| 32.15 | 32.53 | 32.59 | 32.34 | 31.37 | |
| 32.79 | 32.32 | 31.61 | 29.97 | 25.76 | |
| 19.89 | 19.79 | 19.68 | 20.15 | 20.72 | |
| 20.69 | 20.15 | 19.81 | 19.90 | 20.54 | |
| 20.72 | 20.10 | 19.54 | 19.46 | 17.85 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Huang, T.; Wang, X.; Wen, C.-Y.; Huang, X. High-Speed Three-Dimensional Aerial Vehicle Evasion Based on a Multi-Stage Dueling Deep Q-Network. Aerospace 2022, 9, 673. https://doi.org/10.3390/aerospace9110673
Yang Y, Huang T, Wang X, Wen C-Y, Huang X. High-Speed Three-Dimensional Aerial Vehicle Evasion Based on a Multi-Stage Dueling Deep Q-Network. Aerospace. 2022; 9(11):673. https://doi.org/10.3390/aerospace9110673
Chicago/Turabian StyleYang, Yefeng, Tao Huang, Xinxin Wang, Chih-Yung Wen, and Xianlin Huang. 2022. "High-Speed Three-Dimensional Aerial Vehicle Evasion Based on a Multi-Stage Dueling Deep Q-Network" Aerospace 9, no. 11: 673. https://doi.org/10.3390/aerospace9110673
APA StyleYang, Y., Huang, T., Wang, X., Wen, C.-Y., & Huang, X. (2022). High-Speed Three-Dimensional Aerial Vehicle Evasion Based on a Multi-Stage Dueling Deep Q-Network. Aerospace, 9(11), 673. https://doi.org/10.3390/aerospace9110673