Finite-Time Tracking Control Based on Immersion and Invariance with Dynamically Scaling Factor for Agile Missiles

Abstract

A novel finite-time tracking control algorithm with disturbances observer is investigated for agile missiles in the presence of mismatched and matched disturbances. A finite-time disturbance observer with the continuous super-twisting algorithm is designed to quickly estimate the mismatched and matched disturbances. An adaptive law on the basis of immersion and invariance theory (I&I) is proposed to estimate the uncertainty of aerodynamics and compensate for the inaccuracy of modeling. An adaptive dynamic scaling factor supervised by a designed supervision factor is implemented. Moreover, a novel sliding mode controller is designed, and a barrier Lyapunov function (CTV-BLF) containing the system state constraints is constructed, which can guarantee that the violation of the constraint will not appear. The finite-time stability of the new proposition is proven via Lyapunov-based analysis. Comparative simulation results illustrate the effectiveness of the proposed scheme.

1. Introduction

Compared with traditional missiles, agile missiles possess higher maneuverability and have great advantages in intercepting the target, which has the characteristics of high velocity, large maneuverability, and intelligent avoidance. During a high maneuver turning, the angle of attack inevitably increases to a high level. In such conditions, aerodynamic control is ineffective and cannot be in charge of missile control. Hence the most common method for maneuverability supply is the use of an additional actuator, such as Reaction-jet Control System (RCS) or Thrust Vector Control (TVC) [1].

Due to the complex battlefield environment and the presence of a high angle of attack flight domain, external disturbances and aerodynamic uncertainties frequently appear, which bring a challenge to the control design. A lot of control methods with strong robustness were exploited to address system disturbances, such as adaptive [2], sliding mode controls (SMC) [3,4,5], $H_{\infty }$control [6], and so on. In Ref. [7], the designed pitch channel autopilot based on SMC, which used Aero/RCS compound control, performed a high angle of attack maneuver including a 180° heading reversal. A new sliding mode control based on the second-order disturbance observer method is designed in Ref. [8] for integrated guidance and control (IGC) system which was considered as a mismatched uncertain linear system. The aerodynamic parameters in [8] were viewed as disturbances, which was similar to Ref. [9]. The aerodynamic uncertainties in [9] were regarded as external disturbances which were able to be online estimated by extended state observer (ESO). Moreover, the control method proposed by combining the back-stepping scheme with SMC was employed to track the angle of attack command.

Different from Refs. [7,8,9], this study introduces a parameter estimator to compensate for the inaccuracy of modeling and investigates the stability of the system in the presence of uncertain parameters under mismatched disturbance. Astolfi and Ortega in [10] developed a general nonlinear system observer, i.e., immersion and invariance (I&I) theory to solve the estimation of unknown parameters. They introduced an adjustable structure item for the estimation of unknown parameters, which enhanced the flexibility of the design process. For its outstanding characteristics, I&I theory was explored extensively [11,12,13]. To overcome the uncertainties in the flight vehicle model with internal moving massed, Ref. [11] designed an estimator based on I&I theory which has an additional nonlinear term to adjust the performance of the estimation error. Ref. [12] proposed an I&I-based adaptive controller for underactuated quadrotor systems with uncertain inertial parameters, which guaranteed the asymptotic convergence of the mass estimation to its actual value. In Ref. [13] a composite adaptive law based on I&I theory was proposed, which introduced tracking error-based estimation and prediction error-based estimation for the estimation of unknown parameters. In addition, I&I theory has received great achievements in air-breathing hypersonic vehicles (AHVs) control [14], robot manipulators [15], and spacecraft [16]. However, these works have no application in the control design of agile missiles.

Karagiannis et al. [17] creatively applied dynamic scaling techniques to the design of an I&I-based controller, which has been widely used in recent years. A modular dynamic scaling-based I&I theory adaptive control was proposed [18] for spacecraft with parametric uncertainties for the first time. The introduction of dynamic scaling factor design including saturation function was used to demonstrate the convergence of the additive disturbance brought by the matrix reconstruction and removed the requirement of scaling factor in the controller implementation. Ref. [19] proposed a novel non-certainty-equivalent adaptive control method in conjunction with a modified dynamic scaling factor for the attitude tracking control problem of spacecraft, which overcame the integrability obstacle caused by I&I theory. A lower dimensional I&I angular velocity observer with a dynamic scaling factor driven by quaternion filter error was designed in [20]. Although dynamic scaling technology can improve the accuracy of I&I-based estimators, the convergence speed of estimation error cannot be guaranteed. Thus, this study presents a supervision factor to accelerate the convergence of the estimated parameters.

Due to practical conditions, state constraints must be considered in the design of a missile control system. The normal method to handle state constraints is to transform the original constrained system into an equivalent unconstrained system [21]. In [22] Ngo et al. presented a continuous final control law for the Brunovsky standard-type system with state constraints which ensured that all specified states remain within certain bounds, and the control Lyapunov function they proposed is the first prototype for constructing the arctangent and logarithmic barrier functions. As an extension of the research, Tee et al. [23,24] employed a barrier Lyapunov function (BLF) for single-input single-output (SISO) nonlinear systems with an output constraint to prevent constraint violation. BLF was the control Lyapunov function based on the barrier function, which could grow to infinity when its arguments approach a certain limit. Therefore, the boundedness of BLF indicates that the system is stable and the violation of the constraint will not appear. The emergence of BLF provides greater design flexibility for the control system and relaxes the requirement on the initial conditions. In Refs. [25,26], an adaptive fault-tolerant control based on a symmetric BLF for hypersonic vehicles was investigated to overcome the effect of full-state constraints. Ref. [27] proposed a novel adaptive control scheme for nonlinear stochastic systems with full state constraints, which could guarantee that all the state constraints were not violated by introducing symmetric and asymmetric BLFs. Furthermore, the state constraint problem has been extended to spacecraft [28], quadrotors [29], and hypersonic flight vehicles [30]. However, the state constraint of BLFs in the above literature is constant rather than time-varying, which is inconsistent with many actual systems. In Refs. [31,32], time-varying BLFs were proposed for switched uncertain nonlinear systems with unknown dead-zone input to ensure that the constraint condition would not be violated. Ref. [33] developed a new form of composite time-varying BLF (CTV-BLF) which had a simple structure and was easy to solve. Motivated by the work in [33], this paper presents a novel CTV-BLF based on a sliding mode surface to deal with state constraints.

Furthermore, the finite-time controller which can improve the rapidity and stability of system state tracking has been widely used. In Refs. [34,35], an attitude controller based on SMC method was designed to guarantee the finite-time convergence of attitude to a region of zero in the presence of disturbances. Based on finite-time feedback control and disturbance feedforward compensation, Ref. [36] proposed a novel composite three-dimensional terminal guidance law for missile–target interception problem, which possessed finite-time convergence characteristics. In view of the advantages of finite time, the finite-time controller for agile missiles is one of the important contents of this paper.

Here, a finite-time tracking control scheme based on I&I theory and CTV-BLF is proposed to solve the problems of external disturbances and aerodynamic uncertainties of agile missiles with state constraints. The major contributions of this study are as follows.

(1)

A finite-time disturbance observer is used to solve the command tracking control of agile missiles with external disturbances. The designed finite-time disturbance observer with the continuous super-twisting algorithm can accurately estimate and compensate for mismatched and matched disturbances.

(2)

A novel adaptive law for the parameter uncertainties is proposed in combination with I&I theory. The dynamic scaling factor is developed to enhance the accuracy of the uncertain parameter convergence. Moreover, a new form of the supervision factor is introduced for the first time to achieve adaptive adjustment of the scaling error and considerably accelerate the convergence of the estimated parameters.

(3)

A novel sliding mode controller and a CTV-BLF based on the non-singular dynamic sliding mode surface are presented. In order to reduce the vibration of controller and bound the sliding mode surface, the hyperbolic tangent function is introduced into the virtual control variable and the sliding mode surface. The constructed CTV-BLF is adapted in logarithmic form, which can guarantee that the system state constraints will not be violated.

(4)

The finite-time stability proof of the closed-loop system via Lyapunov-based analysis demonstrates the superiority of the proposed controller, which is further illustrated by comparative simulation results.

The paper is organized as follows. A description of the issues and mathematical modeling of the agile missile is presented in Section 2. In Section 3, the finite-time disturbance observer and the stable proof are introduced. Section 4 shows the angle of attack tracking control using I&I and SMC method in conjunction with the constructed CTV-BLF which can deal with state constraints, and then the stability analysis of the closed-loop system is studied. Numerical simulations are performed in Section 5 to demonstrate the effectiveness of the proposed scheme. Finally, the study is concluded by providing comments.

2. Materials and Methods

2.1. Notations

The notations in this paper are defined as follow. ${ℝ}^n$ denotes the n-dimensional Euclidean space, $|•|$ denotes the absolute value of a scalar, and $\Vert •\Vert$ denotes the Euclidean norm of a vector or the 2-norm of a matrix. Moreover, we define a function as ${[•]}^{\nu }={|•|}^{\nu }\mathit{sgn}(•)$, where $\nu \in ℝ$ and $\mathit{sgn}(•)=\frac{(•)}{|•|}$.

2.2. Definitions and Lemmas

Lemma 1.

([37]). Consider the following system:

$$\left\{\begin{array}{l}{\dot{\zeta }}_0=-{\lambda }_0{\left[{\zeta }_0\right]}^{\frac{n}{n+1}}-{\rho }_0{\zeta }_0+{\zeta }_1\\ {\dot{\zeta }}_1=-{\lambda }_1{\left[{\zeta }_1-{\dot{\zeta }}_0\right]}^{\frac{n-1}{n}}-{\rho }_1\left({\zeta }_1-{\dot{\zeta }}_0\right)+{\zeta }_2\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮\\ {\dot{\zeta }}_{n-1}=-{\lambda }_{n-1}{\left[{\zeta }_{n-1}-{\dot{\zeta }}_{n-2}\right]}^{\frac{1}{2}}-{\rho }_{n-1}\left({\zeta }_{n-1}-{\dot{\zeta }}_{n-2}\right)+{\zeta }_n\\ {\dot{\zeta }}_n=-{\lambda }_n\mathit{sgn}\left({\zeta }_n-{\dot{\zeta }}_{n-1}\right)-{\rho }_n\left({\zeta }_n-{\dot{\zeta }}_{n-1}\right)-\frac{1}{L_0}f\left(t\right)\end{array}\right.$$

(1)

where${\zeta }_0,\dots ,{\zeta }_n$are the scalar state variables,${\lambda }_0,\dots ,{\lambda }_n$and${\rho }_0,\dots ,{\rho }_n$are appropriate positive constants,$L_0$is a proper positive constant, and the perturbation term$f\left(t\right)$satisfies$\left|f\left(t\right)\right|\le L_0$. Then, the system converges to the origin in finite time, i.e., it is finite-time stable.

Lemma 2.

([13]). Consider the system$\dot{x}=f\left(x\right)$, where$f\left(0\right)=0$and$x\in {ℝ}^n$. If a positive finite continuous function$V\left(x\right):U\to {ℝ}^n$, positive constants$c>0$and$\alpha \in \left(0,1\right)$, and open neighborhood$U_0\in U$of the origin exist, such that$\dot{V}\left(x\right)+c{V}^{\alpha }\left(x\right)\le 0$and$\forall x\in U_0\backslash \left\{0\right\}$, then the solution to$\dot{x}=f\left(x\right)$approaches zero in finite time$T\le \frac{V{\left(x_0\right)}^{1-\alpha }}{c\left(1-\alpha \right)}$, and the origin of system$\dot{x}=f\left(x\right)$is finite-time stable.

Lemma 3.

([33]). Suppose that function$V\left(x\right)$is a type of function with respect to system$\dot{x}=f\left(x,t\right)$and defined in open region$D$containing the origin. If$V\left(x\right)$satisfies the following properties, namely, (1) it is continuously differentiable and positive definite in region$D$, (2)$V\left(x\right)\to \infty$when x approaches the boundary of region$D$, and (3) a positive constant b exists for$\forall t\ge 0$and$x\left(0\right)\in D$such that$V\left(x\right)\le b$can be obtained along the solution of$\dot{x}=f\left(x,t\right)$, then function$V\left(x\right)$is a BLF. If domain$D$changes with time$t$, then function$V\left(x\right)$is a time-varying BLF.

2.3. Problem Statement

A specific illusion of the agile missile with the RCS system and aerodynamic surfaces is shown in Figure 1. The RCS system is installed in front of the mass center of the missile. $O{x}_1{y}_1{z}_1$ is the body coordinate system. $L_{RCS}$ represents the distance between the point of RCS action and the centroid of the missile. $P$ and $T_{RCS}$ represent the thrust force of the main engine and lateral force respectively.

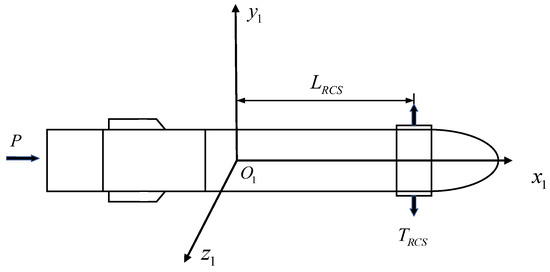
Figure 1. Sketch map of the agile missile.

High angle of attack flight is inevitable for agile turn. In this situation, the aerodynamic surfaces are inefficient, and the RCS in the forebody of the missile is the main source of control force and moment. Hence the RCS is the only actuator considered in this paper.

The longitudinal dynamics of an agile missile can be given as follows:

$$\{\begin{array}{l}\dot{\alpha }={\omega }_z-\frac{P\mathit{sin}\alpha +T_{RCS}\mathit{cos}\alpha +Y-mg\mathit{cos}\gamma }{mV}+d_{\alpha }\\ {\dot{\omega }}_z=\frac{M_{y,aero}+M_{y,u}}{J_z}+d_{{\omega }_z}\end{array}$$

(2)

where $\alpha$ is the angle of attack, ${\omega }_z$ is the pitch rate, $\gamma$ is the pitch angle, $Y$ is the aerodynamic lift, $P$ is the thrust force of main engine, $M_{y,aero}$ is the aerodynamic pitching moment, $M_{y,u}$ elevator deflection angle, $V$ is the missile velocity, $g$ is the gravitational acceleration, $m$ is the mass of missile, $J_z$ is the pitching moment of inertia, $d_{\alpha }$ and $d_{{\omega }_z}$ represent external disturbances in the missile, respectively.

The control force and moment are given as

$$\{\begin{array}{c}{T}_{RCS}=T_{max}{u}_{RCS}\\ M_{y,u}=T_{RCS}{L}_{RCS}\end{array}$$

(3)

where $T_{max}$ is the maximum thrust of RCS, $u_{RCS}$ is the control input which satisfies $u_{RCS}\in \left[-1,1\right]$.

While flying at high angle of attack, the aerodynamic model of the missile is different from that at small angle of attack. The agile missile discussed in this paper can be considered as a smooth cylinder, whose aerodynamic coefficients can be calculated by the cross-flow principle [38]. According to the cross-flow principle, a force normal to the cylindrical axis forms the aerodynamic force, which is defined as

$$N=0.5\rho V^{2}S{C}_N$$

(4)

where $\rho$ is the air density, $C_N$ is the normal force coefficient.

By converting the angle of attack varying within $\left[0^{°},{180}^{°}\right]$ into the equivalent angle of attack varying within $\left[-{90}^{°},{90}^{°}\right]$, the aerodynamic coefficient can be calculated as follows:

$$\{\begin{array}{c}{C}_N=C_{db}{\mathit{sin}}^2\alpha \\ C_L=C_N\mathit{cos}\alpha \end{array}\begin{array}{c}\\ \end{array}$$

(5)

where $C_L$ is the aerodynamic lift coefficient, the calculation method of $C_{db}$ can be found in [39].

Relatively, the missile aerodynamic force and moment at high angle of attack can be expressed as

$$\{\begin{array}{l}Y=0.5\rho V^{2}S{C}_L\\ M_{y,aero}=0.5\rho V^{2}S{C}_N{L}_{st}\end{array}$$

(6)

where $L_{st}$ is the distance between the centroid of missile and the pressure center of aerodynamic force.

To summarize, the missile dynamics with mismatched and matched disturbances that concern us are written as

$$\{\begin{array}{l}\dot{\alpha }={\omega }_z-\frac{P\mathit{sin}\alpha +T_{max}{u}_{RCS}cos\alpha +0.5\rho V^{2}S{C}_{db}{\mathit{sin}}^2\alpha \mathit{cos}\alpha -mg\mathit{cos}\gamma }{mV}+d_{\alpha }\\ {\dot{\omega }}_z=\frac{0.5C_{db}\rho V^{2}S{L}_{st}{\mathit{sin}}^2\alpha }{J_z}+\frac{T_{max}{u}_{RCS}}{J_z}+d_{{\omega }_z}\end{array}$$

(7)

Assumption 1.

The external disturbances$d_{\alpha }$,$d_{{\omega }_z}$are assumed to be continuous and differentiable, which satisfy$\left|d_{\alpha }\right|\le {\Delta }_1$,$\left|{\dot{d}}_{\alpha }\right|\le {\Lambda }_1$and$\left|d_{{\omega }_z}\right|\le {\Delta }_2$,$\left|{\dot{d}}_{{\omega }_z}\right|\le {\Lambda }_2$.

Due to the limited missile capability in practical work, the constraint set of the angle of attack and pitch rate is set as

$$\{\begin{array}{c}{\mathbb{Z}}_{\alpha }=\left\{\left|\alpha \right|\le {\alpha }_{max}\right\}\\ {\mathbb{Z}}_{{\omega }_z}=\{\left|{\omega }_z\right|\le {\omega }_z{}_{max}\}\end{array}$$

(8)

where ${\alpha }_{max}$ and ${\omega }_z{}_{max}$ are the set boundary values.

Assumption 2.

Positive constants${\Delta }_{\alpha }$and${\Delta }_{\omega }$exist and satisfy the constraint conditions (8). They limit the boundaries of the command angle of attack${\alpha }_c$and its differential term${\dot{\alpha }}_c$, which meet$\left|{\alpha }_c\right|\le {\Delta }_{\alpha }<{\alpha }_{max}$,$\left|{\dot{\alpha }}_c\right|\le {\Delta }_{\omega }<{\omega }_{zmax}$.

3. Finite-Time Disturbance Observer Design

A finite-time disturbance observer for agile missiles is designed in this section, wherein the objective is to estimate the external mismatched and matched disturbances. Ref. [37] proposed a new globally convergent differentiator based on robust exact sliding mode (SM). The output of the differentiator can quickly converge to the first $n$ exact derivatives of the input $f\left(t\right)$ in finite time. Inspired by the differentiator in Ref. [37], a finite-time disturbance observer for agile missiles is proposed in this study.

For the sake of clarity, the missile dynamics that concern us are rewritten as

$$\{\begin{array}{l}{\dot{x}}_1=x_2+d_1\\ {\dot{x}}_2=\theta g\left(x\right)+K_{u}u+d_2\end{array}$$

(9)

where $x_1$ and $x_2$ represent $\alpha$ and ${\omega }_z$, $\theta$ represents the unknown parameters $C_{db}$, and $g\left(x\right)=\frac{0.5\rho V^{2}S{L}_{st}{\mathit{sin}}^2\alpha }{J_z}, f=\frac{0.5\rho V^{2}S{L}_{st}{\mathit{sin}}^2\alpha }{J_z}$ $b=\frac{T_{max}{u}_{RCS}}{J_z}$ $d_1$ and $d_2$ represent mismatched and matched disturbances and $d_1=-\frac{P\mathit{sin}\alpha +T_{max}{u}_{RCS}cos\alpha +0.5\rho V^{2}S{C}_{db}{\mathit{sin}}^2\alpha \mathit{cos}\alpha -mg\mathit{cos}\gamma }{mV}+d_{\alpha }$, $d_2=d_{{\omega }_z}$.

The finite-time observer of mismatched disturbance is designed as follows:

$$\left\{\begin{array}{l}{\dot{\widehat{x}}}_1=v_1+x_2\\ v_1=-{\lambda }_1{H}_1^{-\frac{1}{3}}{\left[{\widehat{x}}_1-x_1\right]}^{\frac{2}{3}}-{\rho }_1\left({\widehat{x}}_1-x_1\right)+{\widehat{d}}_1\\ {\dot{\widehat{d}}}_1=v_2 \\ v_2=-{\lambda }_2{H}_1^{-\frac{1}{2}}{\left[{\widehat{d}}_1-v_1\right]}^{\frac{1}{2}}-{\rho }_2\left({\widehat{d}}_1-v_1\right)+{\widehat{D}}_1\\ {\dot{\widehat{D}}}_1=v_3\\ v_3=-{\lambda }_3{H}_1^{-1}\mathit{sgn}\left({\widehat{D}}_1-v_2\right)-{\rho }_3\left({\widehat{D}}_1-v_2\right)\end{array}\right.$$

(10)

where ${\lambda }_1,{\lambda }_2,{\lambda }_3$ and ${\rho }_1,{\rho }_2,{\rho }_3$ represent the observer coefficients, ${\widehat{d}}_1,{\widehat{D}}_1$ are the estimation of $d_1,{\dot{d}}_1$.

Theorem 1.

Consider the system (9), the finite-time disturbance observer given in Equation (10) with the appreciate observer gains can transform the estimation of external disturbances into the form of system (1). Then, the error of system converges to 0 in finite time.

Proof. 

First, the errors between the estimated external disturbances and the real external disturbances are designed as follows:

$$\{\begin{array}{l}{\zeta }_1=H_1\left({\widehat{x}}_1-x_1\right)\\ {\zeta }_2=H_1\left({\widehat{d}}_1-d_1\right)\\ {\zeta }_3=H_1\left({\widehat{D}}_1-{\dot{d}}_1\right)\end{array}$$

(11)

Taking the derivative of Equation (11) and substituting Equation (10) results in

$$\begin{array}{ll}{\dot{\zeta }}_1& =H_1\left({\stackrel{\dot{^}}{x}}_1-{\dot{x}}_1\right)\\ & =H_1\left(-{\lambda }_1{H}_1^{-\frac{1}{3}}{\left[{\hat{x}}_1-x_1\right]}^{\frac{2}{3}}-{\rho }_1\left({\hat{x}}_1-x_1\right)+{\hat{d}}_1+x_2-x_2-d_1\right)\\ & =-{\lambda }_1{\left[{\zeta }_1\right]}^{\frac{2}{3}}-{\rho }_1{\zeta }_1+{\zeta }_2\end{array}$$

(12)

$$\begin{array}{ll}{\dot{\zeta }}_2& =H_1\left({\stackrel{\dot{^}}{d}}_1-{\dot{d}}_1\right)\\ & =H_1\left(-{\lambda }_2{H}_1^{-\frac{1}{2}}{\left[{\hat{d}}_1-v_1\right]}^{\frac{1}{2}}-{\rho }_2\left({\hat{d}}_1-v_1\right)+\widehat{D_1}-{\dot{d}}_1\right)\\ & =-{\lambda }_2{H}_1^{\frac{1}{2}}{\left[{\hat{d}}_1-v_1\right]}^{\frac{1}{2}}-{\rho }_2{H}_1\left({\hat{d}}_1-v_1\right)+{\zeta }_3\end{array}$$

(13)

$$\begin{array}{ll}{\dot{\zeta }}_3& =H_1\left({\stackrel{\dot{^}}{D}}_1-{\ddot{d}}_1\right)\\ & =H_1(-{\lambda }_3{H}_1^{-1}\mathit{sgn}({\hat{D}}_1-v_2)-{\rho }_3({\hat{D}}_1-v_2)-{\ddot{d}}_1)\\ & =-{\lambda }_3\mathit{sgn}({\hat{D}}_1-v_2)-{\rho }_3{H}_1({\hat{D}}_1-v_2)-H_1{\ddot{d}}_1\end{array}$$

(14)

It follows from Equation (12) that

$$\begin{array}{c}{\widehat{d}}_1-v_1={\lambda }_1{H}_1^{-\frac{1}{3}}{\left[{\widehat{x}}_1-x_1\right]}^{\frac{2}{3}}+{\rho }_1\left({\widehat{x}}_1-x_1\right)\\ =H_1^{-1}\left({\lambda }_1{\left[{\zeta }_1\right]}^{\frac{2}{3}}+{\rho }_1{\zeta }_1\right) \\ =H_1^{-1}\left({\zeta }_2-{\dot{\zeta }}_1\right) \end{array}$$

(15)

Then, by substituting Equation (15) into Equation (13), we can obtain

$${\dot{\zeta }}_2=-{\lambda }_2{\left[{\zeta }_2-{\dot{\zeta }}_1\right]}^{\frac{1}{2}}-{\rho }_2\left({\zeta }_2-{\dot{\zeta }}_1\right)+{\zeta }_3$$

(16)

Similarly, we can obtain from Equation (10) that

$$\begin{array}{c}{\widehat{D}}_1-v_2={\lambda }_2{H}_1^{-\frac{1}{2}}{\left[{\widehat{d}}_1-v_1\right]}^{\frac{1}{2}}+{\rho }_2\left({\widehat{d}}_1-v_1\right)\\ =H_1^{-1}\left({\zeta }_3-{\dot{\zeta }}_2\right) \end{array}$$

(17)

and

$${\dot{\zeta }}_3=-{\lambda }_3\mathit{sgn}\left({\zeta }_3-{\dot{\zeta }}_2\right)-{\rho }_3\left({\zeta }_3-{\dot{\zeta }}_2\right)-H_1{\ddot{d}}_1$$

(18)

To summarize, the estimation errors can be formed as

$$\left\{\begin{array}{l}{\dot{\zeta }}_1=-{\lambda }_1{\left[{\zeta }_1\right]}^{\frac{2}{3}}-{\rho }_1{\zeta }_1+{\zeta }_2\\ {\dot{\zeta }}_2=-{\lambda }_2{\left[{\zeta }_2-{\dot{\zeta }}_1\right]}^{\frac{1}{2}}-{\rho }_2\left({\zeta }_2-{\dot{\zeta }}_1\right)+{\zeta }_3 \\ {\dot{\zeta }}_3=-{\lambda }_3\mathit{sgn}\left({\zeta }_3-{\dot{\zeta }}_2\right)-{\rho }_3\left({\zeta }_3-{\dot{\zeta }}_2\right)-H_1{\ddot{d}}_1\end{array}\right.$$

(19)

It follows from Lemma 1 that the error of system can converge to the origin in finite time. The proof is therefore complete. □

Following the same procedure shown in Equations (12)–(19), the finite-time observer of matched disturbance is designed as follows:

$$\left\{\begin{array}{l}{\dot{\widehat{x}}}_2=\theta g\left(x\right)+K_{u}u+l_1 \\ l_1=-{\lambda }_4{H}_2^{-\frac{1}{3}}{\left|{\widehat{x}}_2-x_2\right|}^{\frac{2}{3}}\mathit{sgn}\left({\widehat{x}}_2-x_2\right)-{\rho }_4\left({\widehat{x}}_2-x_2\right)+{\widehat{d}}_2\\ {\dot{\widehat{d}}}_2=l_2 \\ l_2=-{\lambda }_5{H}_2^{-\frac{1}{2}}{\left|{\widehat{d}}_2-l_1\right|}^{\frac{1}{2}}\mathit{sgn}\left({\widehat{d}}_2-l_1\right)-{\rho }_5\left({\widehat{d}}_2-l_1\right)+{\widehat{D}}_2\\ {\dot{\widehat{D}}}_2=l_3\\ l_3=-{\lambda }_6{H}_2^{-1}\mathit{sgn}\left({\widehat{D}}_2-l_2\right)-{\rho }_6\left({\widehat{D}}_2-l_2\right) \end{array}\right.$$

(20)

where ${\lambda }_4,{\lambda }_5,{\lambda }_6$ and ${\rho }_4,{\rho }_5,{\rho }_6$ represent the observer coefficients, ${\widehat{d}}_2,{\widehat{D}}_2$ are the estimation of $d_2,{\dot{d}}_2$.

4. Adaptive and Control Law

This section firstly presents an adaptive law based on I&I theory for an agile missile equipped with RCS, which introduces a supervision factor $a$ and a new scaling factor $r$. Then a second-order sliding mode controller and the CTV-BLF containing the system state constraint information are designed. Finally, the finite-time stability of the above system is proven.

4.1. Adaptive Law Based on I&I Theory

Let ${\alpha }_d=\alpha {\alpha }_{max}$ and define the command tracking error as $e_1=x_1-x_c$. If $\left|e_1\right|<{\alpha }_d$, then $\left|x_1\right|\le \left|{\alpha }_d\right|+\left|x_c\right|<{\alpha }_{max}$. For the command tracking error dynamics, a virtual control variable is developed as ${\hslash }_1=-l_c\mathit{tanh}\left(e_1\right)$, $l_c>0$, and $e_2={\dot{e}}_1-{\hslash }_1$. Let ${\omega }_d={\omega }_{zmax}-{\Delta }_{\omega }-{\Delta }_1$. If $\left|x_2+d_1-{\dot{x}}_c\right|<{\omega }_d$, we can deduce that $\left|x_2\right|\le \left|d_1\right|+\left|{\dot{x}}_c\right|+{\omega }_d<{\omega }_{zmax}$. Given that ${\hslash }_1<l_c\mathit{tan}h\left({\alpha }_d\right)$, it can be proven that $\left|e_2\right|<\sigma$, where $\sigma ={\omega }_d+l_c\mathit{tan}h\left({\alpha }_d\right)$.

Hence, we can obtain the system error dynamics as follows

$$\{\begin{array}{c}{\dot{e}}_1=x_2+d_1-{\dot{x}}_c \\ {\dot{e}}_2=\theta g\left(x\right)+K_{u}u+\rho \end{array}$$

(21)

where $\rho =d_2+{\dot{d}}_1-{\ddot{x}}_c-{\dot{\hslash }}_1$, ${\dot{\hslash }}_1=-l_{c}sec{h}^2\left(e_1\right){\dot{e}}_1$.

One of the most challenging problems in the controller design of agile missiles is to surmount the negative effect of severe aerodynamic uncertainty. Many researchers regard aerodynamic uncertainties as external disturbances which can be estimated by the designed observer. For example, [9] proposed an extended state observer (ESO) for agile missiles to online estimate the system disturbances which contain aerodynamic uncertainties. In contrast, this paper utilizes I&I theory to estimate the uncertain aerodynamic parameters $C_{db}$ and obtain approximate aerodynamics.

Considering system (9), the estimation error manifold of the uncertain parameter is designed as follows:

$$\tilde{\theta }=\widehat{\theta }-\kappa \theta$$

(22)

where $\kappa ={\kappa }_0\mathit{exp}\left(a{e}_1\right)$ is the compensation function between $\widehat{\theta }$ and $\theta$, $a>0$ is the supervision factor to be designed.

To guarantee that the error manifold is attractive and invariant, the I&I-based adaptive law is designed as

$$\dot{\widehat{\theta }}=a\widehat{\theta }{\dot{e}}_1-a\mathit{exp}\left({\dot{e}}_1\right){\dot{e}}_1\tilde{\theta }$$

(23)

Taking the time derivative of $\tilde{\theta }$ and substituting Equation (23) into Equation (22) yield

$$\begin{array}{ll}\dot{\tilde{\theta }}& =\dot{\widehat{\theta }}-\dot{\kappa }\theta \\ & =\dot{\widehat{\theta }}-\dot{\kappa }\left(\frac{\widehat{\theta }-\tilde{\theta }}{\kappa }\right)\\ & =a\widehat{\theta }{\dot{e}}_1-a\mathit{exp}\left({\dot{e}}_1\right){\dot{e}}_1\tilde{\theta }-a{\dot{e}}_1\left(\widehat{\theta }-\tilde{\theta }\right)\\ & =a\left(1-\mathit{exp}\left({\dot{e}}_1\right)\right){\dot{e}}_1\tilde{\theta }\end{array}$$

(24)

To improve the error accuracy of parameter estimation, a dynamic scale factor is introduced. The scaling estimation error can be written as

$$z=\frac{\tilde{\theta }}{r}=\frac{\widehat{\theta }-\kappa \theta }{r}$$

(25)

Thus, the dynamics along Equation (25) can be obtained as

$$\dot{z}=\frac{1}{r}\dot{\tilde{\theta }}-\frac{\dot{r}}{r}z=a\left(1-\mathit{exp}\left({\dot{e}}_1\right)\right){\dot{e}}_{1}z-\frac{\dot{r}}{r}z$$

(26)

where the supervision factor $a$ is active, and the dynamic scaling factor $r$ is passive. The combination of $a$ and $r$ can ensure the rapid convergence of the estimation error and the accuracy of estimation.

The dynamic form of $r$ is proposed as follows:

$$\dot{r}=\frac{a_r{\left|e_2\right|}^{v-1}}{\left(h_e-\lceil e_2\rceil {}^v\right)\left(h_e+\lceil e_2\rceil {}^v\right)}r$$

(27)

where $a_r$ is a positive constant, $\nu$ and $h_e$ are self-designed parameters in control law design in the next section. $r\left(0\right)\ge 1$, and $\dot{r}\ge 0$. So, the value range of $r$ meets $\left\{r\in ℝ|r\ge 1\right\}$ for $t\ge 0$.

To verify the stability of scaling estimation error $z$, considering the Lyapunov function $V_z=\frac{1}{2}{z}^2$ and taking the time derivative of $V_z$ yield

$${\dot{V}}_z=a\left(1-\mathit{exp}\left({\dot{e}}_1\right)\right){\dot{e}}_1{z}^2-\frac{a_r{\left|e_2\right|}^{v-1}}{\left(h_e-\lceil e_2\rceil {}^v\right)\left(h_e+\lceil e_2\rceil {}^v\right)}{z}^2$$

(28)

where $a>0$, and $r\ge 1$. Thus, ${\dot{V}}_z\le 0$ and the estimation error $z$ is stable.

To ensure the boundedness of the dynamic scaling factor $r$, we select the Lyapunov function as follows.

$$V_r=r{e}^{-r}$$

(29)

where $V_r$ meets $\left\{V_r\in ℝ|V_r\ge 0\right\}$ for $r\ge 1$.

The derivative of $V_r$ along Equation (29) can be written as

$${\dot{V}}_r=\left(1-r\right)e^{-r}\dot{r}=\frac{a_{r}r\left(1-r\right)e^{-r}{\left|e_2\right|}^{v-1}}{\left(h_e-\lceil e_2\rceil {}^v\right)\left(h_e+\lceil e_2\rceil {}^v\right)}$$

(30)

where $a_r>0$ and $r\left(1-r\right)\le 0$. Hence, $V_r\le 0$.

Equation (30) shows that the dynamic scaling factor $r$ is bounded. Thus, the estimation errors convergence to the origin asymptotically.

4.2. Control Law Design

A sliding mode surface is proposed as

$$s={\left[e_2\right]}^{\nu }+h_e\mathit{tanh}\left(e_1\right)$$

(31)

where $h_e={\sigma }^{\nu }$, $1<\nu <2$. From $\left|e_2\right|<\sigma$, we get ${\left|e_2\right|}^{\nu }<h_e$, such that

$$\left|s\right|<h_e+h_e\mathit{tanh}\left(\left|e_1\right|\right)$$

Taking the derivative of Equation (25) along Equation (13) yields

$$\begin{array}{c}\dot{s}=v{\left|e_2\right|}^{v-1}{\dot{e}}_2+h_e\mathit{sec}{h}^2\left(e_1\right){\dot{e}}_1 \\ =v{\left|e_2\right|}^{v-1}\left(\theta g\left(x\right)+K_{u}u+\rho \right)+h_e\mathit{sec}{h}^2\left(e_1\right)\left(x_2+d_1-{\dot{x}}_c\right)\end{array}$$

(32)

The controller is designed as

$$u=\frac{1}{K_u}\left(-\rho -\frac{\widehat{\theta }g\left(x\right)}{\kappa }-\frac{h_{e}sec{h}^2\left(e_1\right)\left(x_2+d_1-{\dot{x}}_c\right)}{v{\left|e_2\right|}^{v-1}}+\frac{sec{h}^2\left(e_1\right)\mathit{sgn}\left(e_1\right){\dot{e}}_{1}s}{v{\left|e_2\right|}^{v-1}\left(1+\mathit{tanh}\left(\left|e_1\right|\right)\right)}-\left(c_{1}s+c_2{\left[s\right]}^{\eta }\right)\right)$$

(33)

where $c_1>0$, $c_2>0$ and $0<\eta <1$.

Substituting Equation (33) into Equation (32) yields

$$\dot{s}=v{\left|e_2\right|}^{v-1}\left(-\varsigma zg\left(x\right)+\frac{1}{v{\left|e_2\right|}^{v-1}}\frac{sec{h}^2\left(e_1\right)\mathit{sgn}\left(e_1\right){\dot{e}}_{1}s}{1+\mathit{tanh}\left(\left|e_1\right|\right)}-c_{1}s-c_2{\lceil s\rceil }^{\eta }\right)$$

(34)

where $\varsigma =\frac{r}{\kappa }$.

Theorem 2.

The error system as described in Equation (21) with Assumption 1 and the finite-time disturbance observer in Equation (10) is considered. Given the sliding mode surface in Equation (31) and the controller with proper control gains in Equation (33), the tracking errors$e_1$and$e_2$can converge to zero in finite time, and the closed-loop system is finite-time stable.

Proof. 

Let the CTV-BLF $V_s$ be defined as

$$V_s=\frac{1}{2}\mathit{log}\frac{1}{1-{\varphi }^2}$$

(35)

where $\varphi =\frac{s}{h_e+h_e\mathit{tanh}\left(\left|e_1\right|\right)}$. Taking the time derivative of $V_s$ yields

$$\begin{array}{ll}{\dot{V}}_s& =\frac{\varphi }{1-{\varphi }^2}\dot{\varphi } \\ & =\frac{\varphi }{1-{\varphi }^2}\left(\frac{\dot{s}}{h_e+h_e\mathit{tanh}\left(\left|e_1\right|\right)}-\frac{sec{h}^2\left(\left|e_1\right|\right)\mathit{sgn}\left(e_1\right){\dot{e}}_{1}s}{\left(h_e+h_e\mathit{tanh}\left(\left|e_1\right|\right)\right)\left(1+\mathit{tanh}\left(\left|e_1\right|\right)\right)}\right)\end{array}$$

(36)

By substituting Equation (29) into Equation (34), we obtain

$$\begin{array}{c}{\dot{V}}_s=\frac{v\varphi {\left|e_2\right|}^{v-1}}{\left(1-{\varphi }^2\right)\left(h_e+h_e\mathit{tanh}\left(\left|e_1\right|\right)\right)}\left(-\varsigma zg\left(x\right)-c_{1}s-c_2{\lceil s\rceil }^{\eta }\right) \\ =\frac{v{\left|e_2\right|}^{v-1}}{{\left(h_e+h_e\mathit{tanh}\left(\left|e_1\right|\right)\right)}^2-s^2}\left(-\varsigma zsg\left(x\right)-c_1{s}^2-c_2{\lceil s\rceil }^{\eta +1}\right)\end{array}$$

(37)

Let the Lyapunov function $L_1$ be defined as

$$L_1=V_s+V_z$$

(38)

Taking the time derivative of Equation (38) yields

$$\begin{array}{l}{\dot{L}}_1=\frac{v{\left|e_2\right|}^{v-1}}{{\left(h_e+h_e\mathit{tanh}\left(\left|e_1\right|\right)\right)}^2-s^2}\left(-\varsigma zsg\left(x\right)-c_1{s}^2-c_2{\lceil s\rceil }^{\eta +1}\right)+a\left(1-\mathit{exp}\left({\dot{e}}_1\right)\right){\dot{e}}_1{z}^2 \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{a_r{\left|e_2\right|}^{v-1}}{\left(h_e-\lceil e_2\rceil {}^v\right)\left(h_e+\lceil e_2\rceil {}^v\right)}{z}^2\\ <\frac{v{\left|e_2\right|}^{v-1}}{{\left(h_e+h_e\mathit{tanh}\left(\left|e_1\right|\right)\right)}^2-s^2}\left(-\varsigma zsg\left(x\right)-c_1{s}^2-c_2{\lceil s\rceil }^{\eta +1}\right)-\frac{a_r{\left|e_2\right|}^{v-1}}{\left(h_e-\lceil e_2\rceil {}^v\right)\left(h_e+\lceil e_2\rceil {}^v\right)}{z}^2\end{array}$$

(39)

Considering that

$$\{\begin{array}{c}{h}_e+h_e\mathit{tanh}\left(\left|e_1\right|\right)-s=h_e-\lceil e_2\rceil {}^v+h_e\mathit{tanh}\left(\left|e_2\right|\right)-h_e\mathit{tanh}\left(e_2\right)\ge h_e-\lceil e_2\rceil {}^v\\ h_e+h_e\mathit{tanh}\left(\left|e_1\right|\right)+s=h_e+\lceil e_2\rceil {}^v+h_e\mathit{tanh}\left(\left|e_2\right|\right)+h_e\mathit{tanh}\left(e_2\right)\ge h_e+\lceil e_2\rceil {}^v\end{array}$$

(40)

We acquire

$$\frac{1}{{\left(h_e+h_e\mathit{tanh}\left(\left|e_1\right|\right)\right)}^2-s^2}\le \frac{1}{\left(h_e-\lceil e_2\rceil {}^v\right)\left(h_e+\lceil e_2\rceil {}^v\right)}$$

(41)

Thus, it follows from Equation (39) that

$$\begin{array}{l}\begin{array}{c}{\dot{L}}_1<\frac{v{\left|e_2\right|}^{v-1}}{{\left(h_e+h_e\mathit{tanh}\left(\left|e_1\right|\right)\right)}^2-s^2}\left(-\varsigma zsg\left(x\right)-c_1{s}^2-c_2{\lceil s\rceil }^{\eta +1}\right)-\frac{a_r{\left|e_2\right|}^{v-1}}{\left(h_e-\lceil e_2\rceil {}^v\right)\left(h_e+\lceil e_2\rceil {}^v\right)}{z}^2\\ \end{array}\\ \le \frac{v{\left|e_2\right|}^{v-1}}{\left(h_e-\lceil e_2\rceil {}^v\right)\left(h_e+\lceil e_2\rceil {}^v\right)}\left(-\left[\begin{array}{cc}s& z\end{array}\right]R\left[\begin{array}{c}s\\ z\end{array}\right]-c_2{\lceil s\rceil }^{\eta +1}\right)\end{array}$$

(42)

where

$$R=\left[\begin{array}{cc}{c}_1& \frac{1}{2}\varsigma g\left(x\right)\\ \frac{1}{2}\varsigma g\left(x\right)& \frac{a_r}{v}\end{array}\right]$$

(43)

is a positive definite matrix. Thus, the sliding mode variable $s$ is asymptotically stable.

We consider the Lyapunov function as follows:

$$L_2=\frac{1}{2}{e}_1^2$$

(44)

When the system errors reach the sliding mode surface and $s=0$, we can infer that $\left|e_2\right|={\left|h_e\mathit{tanh}\left(e_1\right)\right|}^{\frac{1}{v}}$ and $e_1{e}_2<0$.

Taking the time derivative of $L_2$ yields

$$\begin{array}{c}{\dot{L}}_2=e_1\left(e_2-l_c\mathit{tanh}\left(e_1\right)\right) \\ =-\left|e_1{e}_2\right|-l_c\left|e_1\mathit{tanh}\left(e_1\right)\right|\\ <0 \end{array}$$

(45)

Considering $\left|\mathit{tanh}\left(e_1\right)\right|\le \left|e_1\right|$ we acquire

$$\begin{array}{ll}{\dot{L}}_2& =-h_e{\left|e_1\mathit{tan}h\right(e_1\left)\right|}^{\frac{1}{v}}-l_c\left|e_1\mathit{tan}h\right(e_1\left)\right|\\ & \le -{h_e}^{\frac{1}{v}}{\left|e_1\right|}^{1+\frac{1}{v}}-l_c{\left|e_1\right|}^2\\ & \le -2^{\frac{1+v}{2v}{h_e}^{\frac{1}{v}}{L}_2^{\frac{1+v}{2v}}}\end{array}$$

(46)

Hence, the state errors $e_1$ and $e_2$ can converge to zero in finite time. The proof is therefore completed. □

5. Results

In this section, numerical simulation is performed to demonstrate the effectiveness of the proposed approach. The initial parameters of the agile missile are set as follows: $m=6 \mathrm{kg}$, $L_{RCS}=0.143 \mathrm{m}$, $L_{st}=0.05 \mathrm{m}$, $P=300 \mathrm{N}$, $T_{max}=120\mathrm{N}$, $S=0.0086546 {\mathrm{m}}^2$, $V_0=60 \frac{\mathrm{m}}{\mathrm{s}}$, ${\gamma }_0=0°$, ${\alpha }_0=0°$, ${\omega }_{z0}=0\frac{°}{\mathrm{s}}$. Considering the small variety of airspace and velocity domains in this simulation, the aerodynamic coefficient $C_{db}$ is set as a constant value of 10.

Assume that the agile missile is launched on the aircraft, and the starting point is $\left(0,0\right)$. With the aim of achieving an agile turn, the missile needs to track the open-loop angle of attack command ${\alpha }_c=80°\mathit{cos}(\frac{\pi t}{8})$. Meanwhile, it is assumed that the agile missile maneuvers in the vertical plane. The external time-varying disturbances are expressed as $d_{\alpha }=0.1\mathit{sin}(2t)$ and $d_{{\omega }_z}=0.1\mathit{sin}(2t)$. The parameters of the control scheme are shown in Table 1 and Table 2.

Figure 2 depicts the command tracking performance of the missile. The curve of the angle of attack is shown in Figure 2a. It is seen that the angle of attack can increase rapidly and track the commands precisely. The missile trajectory and the relevant angle are shown in Figure 2b–d, which note that the missile is able to achieve agile turning in a short time following the given open-loop angle of attack command. The velocity and pitch rate are plotted in Figure 2e,f the large pitch rate in the initial period leads to the high angle of attack, which is responsible for the decrease in velocity. The curves of the sliding mode surface and the continuous control input $u_{RCS}$ are illustrated in Figure 2g,h.

The online estimation results of mismatched and matched disturbances are illustrated in Figure 3. It can be seen that the designed disturbance observer is qualified to be used in the presence of mismatched and matched disturbances. The slight estimation error shows the excellent performance of the proposed observer.

Table 1. Design parameters of disturbances observer.

Signal	Values	Signal	Values
$H_1$	1	$H_2$	1
${\lambda }_1$	5	${\rho }_1$	1
${\lambda }_2$	10	${\rho }_2$	1
${\lambda }_3$	10	${\rho }_3$	1
${\lambda }_4$	1	${\rho }_4$	1
${\lambda }_5$	10	${\rho }_5$	1
${\lambda }_6$	1	${\rho }_6$	1

Table 1. Design parameters of disturbances observer.

Signal	Values	Signal	Values
$H_1$	1	$H_2$	1
${\lambda }_1$	5	${\rho }_1$	1
${\lambda }_2$	10	${\rho }_2$	1
${\lambda }_3$	10	${\rho }_3$	1
${\lambda }_4$	1	${\rho }_4$	1
${\lambda }_5$	10	${\rho }_5$	1
${\lambda }_6$	1	${\rho }_6$	1

Figure 4 shows the dynamic scaling factor and scaling estimation error with different supervision factors in the proposed method. The dynamic scaling factor in Figure 4a adaptively converges to a stable state which can be verified to be bound. The responses to scaling estimation error $z$ are plotted in Figure 4b. while setting different supervision factors $a$. The value of $a$ varies between 0.2 and 5, and correspondingly, the convergence speed of $z$ increases, which can prove that the developed supervision factor can directly accelerate the convergence.

Table 2. Design parameters of control laws.

Signal	Values
$l_c$	5
$\nu$	1.9
$h_e$	10
$c_1$	2
$c_2$	2
$\eta$	5
$l_c$	1.5

Table 2. Design parameters of control laws.

Signal	Values
$l_c$	5
$\nu$	1.9
$h_e$	10
$c_1$	2
$c_2$	2
$\eta$	5
$l_c$	1.5

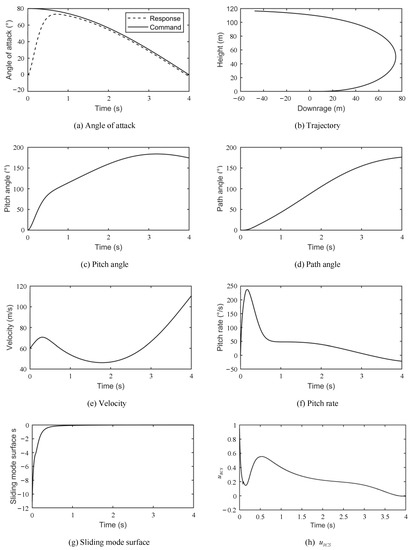
Figure 2. Responses for a command tracking scenario.

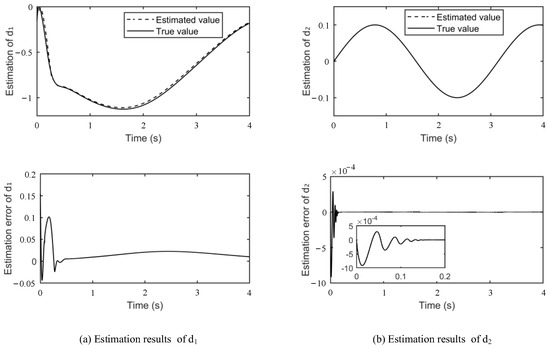
Figure 3. Estimation results of mismatched and matched disturbances.

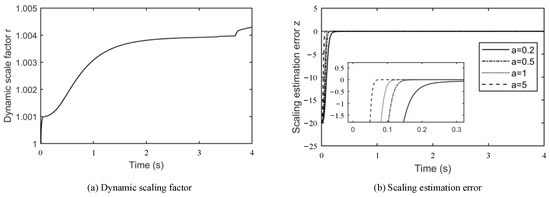
Figure 4. Dynamic scaling factor and scaling estimation error with different supervision factors.

The traditional I&I method and SMC method with extended state observer (ESO) in Ref. [9] are selected for comparison to verify the effect of the proposed scheme. Responses under the traditional I&I method are illustrated in Figure 5. As seen in Figure 5a, the traditional I&I method has lower tracking accuracy compared to the proposed approach in this paper, and the overshoot of angle of attack appears. The estimation error is shown in Figure 5c, which converges more slowly in comparison with the proposed method. In addition, the convergence speed cannot be adjusted actively.

Based on the sliding mode control, responses under ESO are shown in Figure 6. In the absence of the parameter estimator, the aerodynamic uncertainties are regarded as external disturbances, which can bring a great burden to the disturbance observer. As shown in Figure 6a, an obvious chattering phenomenon occurs in the angle of attack, which comes to be a poor performance compared with that seen in Figure 2a and Figure 6c,d illustrate the estimation of mismatched and matched disturbance, respectively, from which it can see that the method in Ref. [9] has a slower estimation and lower accuracy especially when disturbances vary dramatically. So, in contrast with the traditional I&I method and SMC method with ESO, the new method has better performances on the rate of convergence and tracking precision.

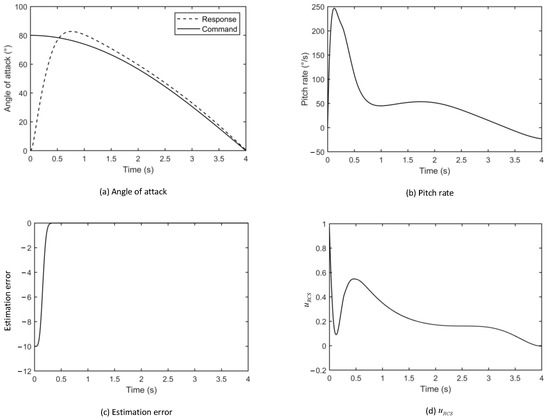
Figure 5. Responses under traditional I&I method.

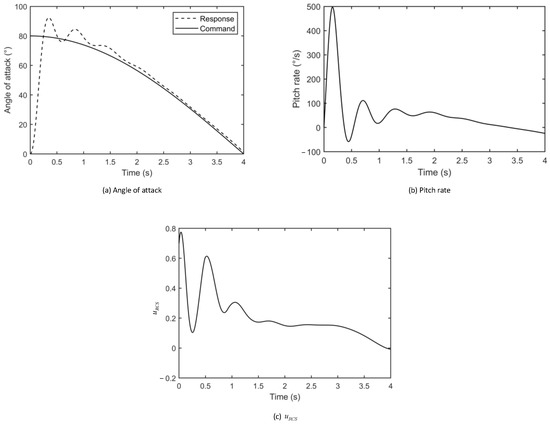
Figure 6. Responses under sliding mode control with ESO.

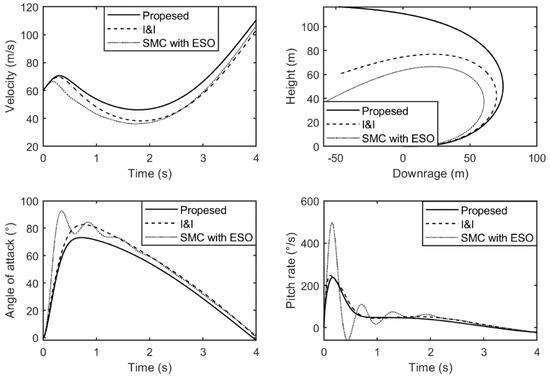
Figure 7. The comparison curves under three methods.

Figure 7 shows the comparison curves of velocity, trajectory, angle of attack and pitch rate under three methods. Compared with the proposed method, the angles of attack under traditional I&I method and SMC method with ESO increase too fast at the beginning, which induce a rapid speed decay. The comparison curves of pitch rate under three methods illustrate that, compared with the other methods, the proposed method can achieve agile turn at a lower pitch rate, which further proves the effectiveness of the proposed controller. Although it seems from the comparison curves of trajectory that the turning radius under the two other methods is smaller, it is actually a sacrifice of speed and a waste of control energy. Furthermore, Figure 2g shows that the sliding mode surface $s$ is maintained within the time-varying constraints in CTV-BLF.

The above simulation results show that the proposed method has significant advantages over other control methods for agile missiles, especially in terms of tracking accuracy, energy consumption, and robustness to external complex disturbances.

6. Conclusions

A finite-time control scheme based on I&I and CTV-BLF was developed for agile missiles with external disturbances and aerodynamic uncertainties. Firstly, a finite-time observer with the continuous super-twisting algorithm was improved, and its convergence was proven. Then, the I&I-based adaptive law for estimating the aerodynamic uncertainties was proposed and an adaptive dynamic scaling factor supervised by a designed supervision factor was introduced. A novel CTV-BLF sliding mode controller was designed to ensure that the state constraints would not be violated. The global stability of the proposed proposition was validated. Lastly, comparative experiments were conducted to illustrate the effectiveness and superiority of the proposed scheme.

The main contribution of this study is to provide a new reference for agile missile control methods and fills in the blank of the domestic in relevant field. However, the current work has a lack of a more accurate aerodynamic model for agile missiles. On the basis of an accurate aerodynamic model, further work will focus on the execution of the practical application of agile missiles, such as over-the-shoulder and rear-firing and maneuvering penetration.