In-Flight Radome Slope Estimation for Homing Guidance Using Bearing-Only Measurement via Gaussian Process Regression
Abstract
1. Introduction
2. Problem Formulation
3. Radome Slope Estimation and Compensation
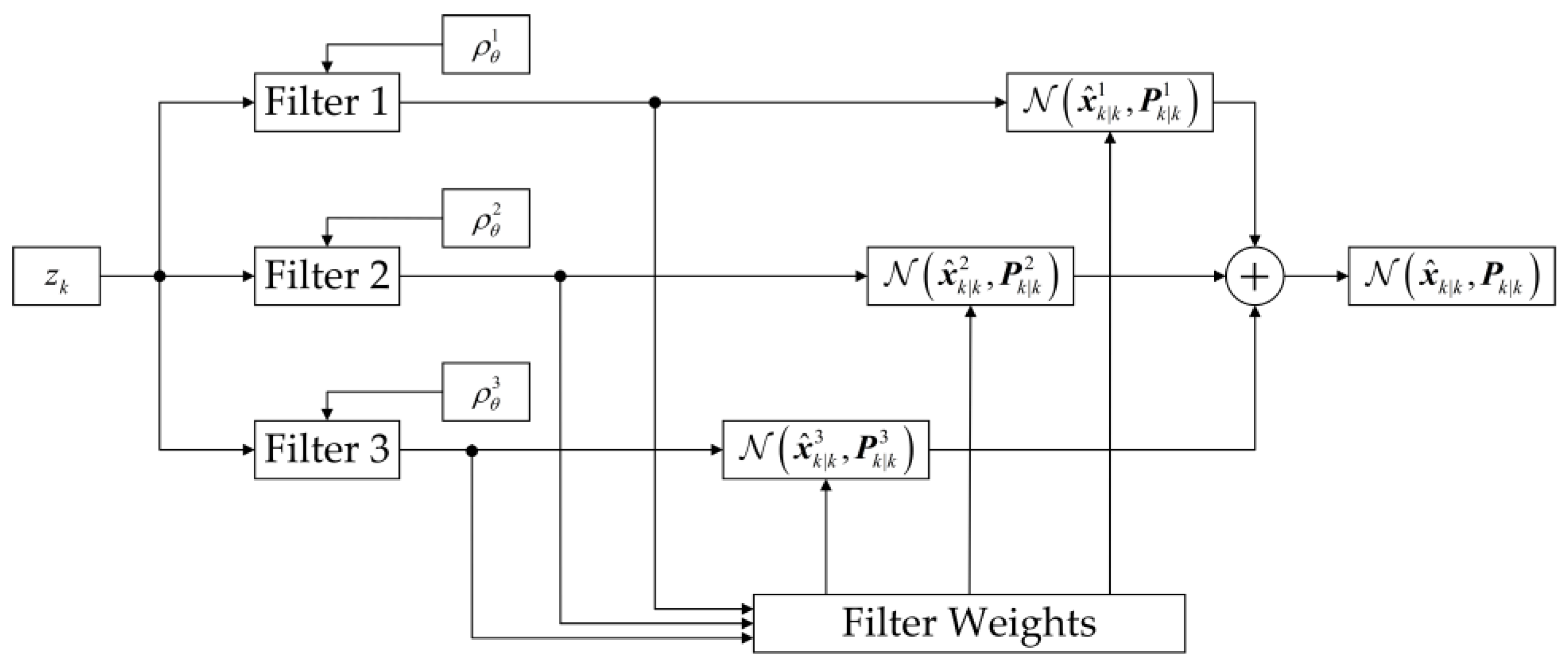
3.1. Guidance Information Estimation Using IMM Filter
3.2. Radome Slope Estimation via Gaussian Process Regression
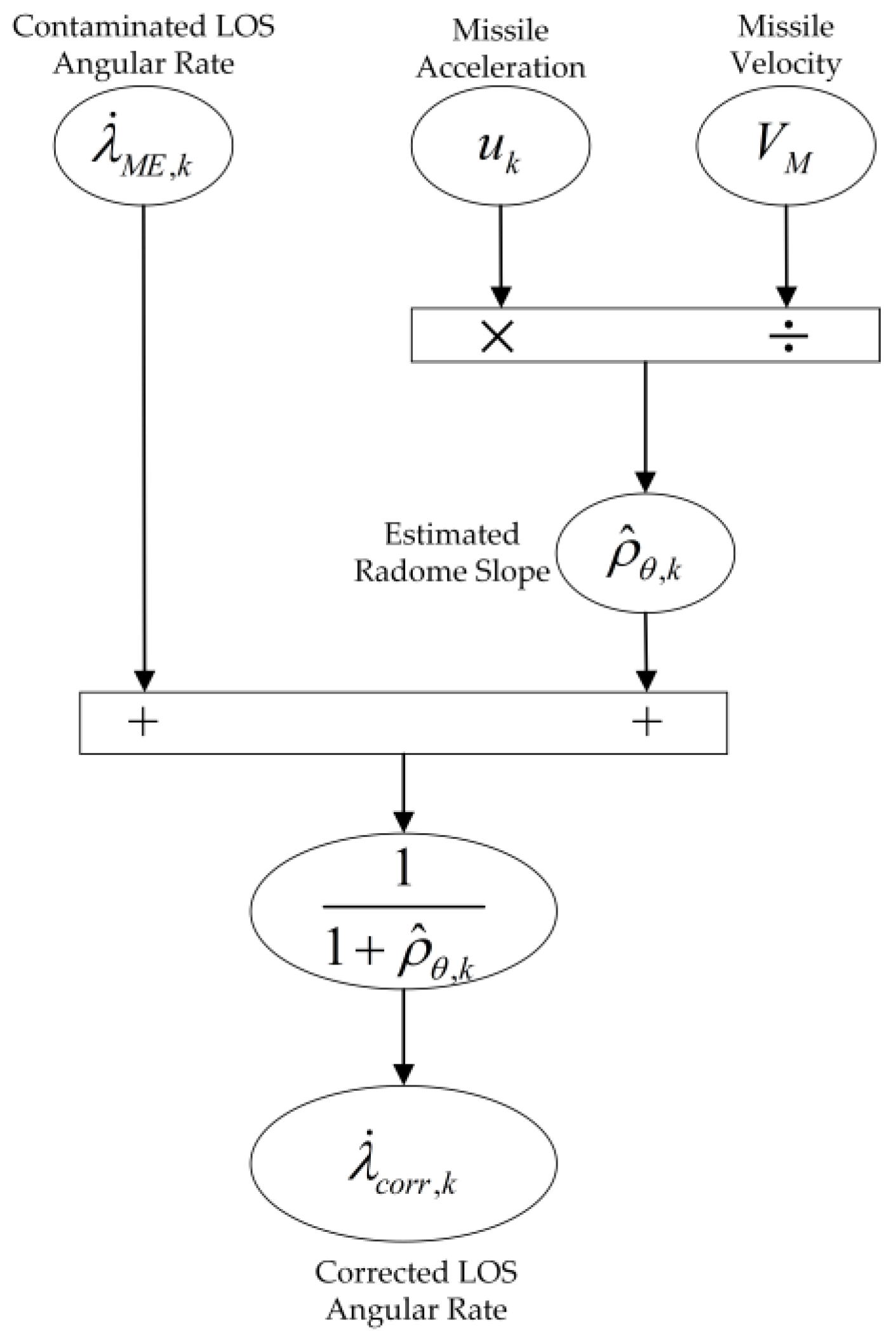
3.3. Implementation of the LOS Angular Rate Corrector
| Algorithm 1: Pseudo code for the proposed LOS angular rate corrector at the kth time step. |
| Inputs: the contaminated LOS angle , the contaminated LOS angular rate |
| 1: calculate the estimated LOS angle and the estimated flight path angle via Equation (31) |
| 2: calculate the estimated radome error via Equation (32) |
| 3: calculate the estimated look angle via Equation (33) |
| 4: calculate the estimated radome slope via Equation (54) |
| 5: calculate the corrected LOS angular rate via Equation (59) |
| Output: the corrected LOS angular rate |
4. Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gong, Z.; Zhou, Z.; Wang, Z.; Lv, Q.; Xu, J.; Jiang, Y. Coordinated Formation Guidance Law for Fixed-Wing UAVs Based on Missile Parallel Approach Method. Aerospace 2022, 9, 272. [Google Scholar] [CrossRef]
- Gurfil, P.; Kasdin, J.N. Improving Missile Guidance Performance by In-Flight Two-Step Nonlinear Estimation of Radome Aberration. IEEE Trans. Control Syst. Technol. 2004, 12, 532–541. [Google Scholar] [CrossRef]
- Ra, W.; Ahn, S.; Lee, Y.; Whang, I. Time-Varying Radome Slope Estimation for Passive Homing Anti-Ship Missiles. In Proceedings of the IEEE 58th Conference on Decision and Control, Nice, France, 11–13 December 2019; pp. 4940–4945. [Google Scholar]
- Seo, M.-G.; Tahk, M.-J. Observability Analysis and Enhancement of Radome Aberration Estimation with Line-of-Sight Angle-Only Measurement. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 3321–3331. [Google Scholar]
- Palumbo, N.F.; Blauwkamp, R.A.; Lloyd, J.M. Basic Principles of Homing Guidance. Johns Hopkins APL Tech. Dig. 2010, 29, 25–41. [Google Scholar]
- Han, S.; Ahn, S.; Ra, W.; Park, J.B. Missile Radome Error Compensation using Modified Interacting Multiple Model Kalman Filter. In Proceedings of the 14th International Conference on Control, Automation and Systems, Gyeonggi-do, Korea, 22–25 October 2014; pp. 391–395. [Google Scholar]
- Jalali-Naini, S.H. Normalized Miss Distance Analysis of Single-Lag Optimal Guidance Lawwith Radome Effect, Saturation and Fifth-Order Control System. Sci. Iran. 2014, 21, 1683–1692. [Google Scholar]
- Zarchan, P. Tactical and Strategic Missile Guidance, 6th ed.; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2012; p. 555. [Google Scholar]
- Li, C.; Wang, J.; Huang, P. Optimal Cooperative Line-of-Sight Guidance for Defending a Guided Missile. Aerospace 2022, 9, 232. [Google Scholar] [CrossRef]
- Nesline, F.; Zarchan, P. Radome Induced Miss Distance in Aerodynamically Controlled Homing Missiles. In Proceedings of the 17th Fluid Dynamics, Plasma Dynamics and Lasers Conference, Snowmass, CO, USA, 25–27 June 1984; p. 84-1845. [Google Scholar]
- Li, B.; Tang, P.; Xu, H.; Zheng, D. Terminal Impact Angle Control Guidance Law Considering Target Observability. Aerospace 2022, 9, 193. [Google Scholar] [CrossRef]
- Yueh, W.; Lin, C.-F. Guidance Performance Analysis with In-Flight Radome Error Calibration. J. Guid. Control Dyn. 1985, 8, 666–669. [Google Scholar] [CrossRef]
- Klein, I.; Rusnak, I. Loop-Shaping Approach to Mitigate Radome Effects in Homing Missiles. J. Guid. Control Dyn. 2017, 40, 1789–1795. [Google Scholar] [CrossRef]
- Deng, Y.; Ren, J.; Wang, X.; Cai, Y. Midcourse Iterative Guidance Method for the Impact Time and Angle Control of Two-Pulse Interceptors. Aerospace 2022, 9, 323. [Google Scholar] [CrossRef]
- Bai, R.; Xia, Q.; Du, X. The Study of Guidance Performance of a Phased Array Seeker with Platform. Optik 2017, 132, 9–23. [Google Scholar] [CrossRef]
- Zheng, D.; Lin, D.; Wang, J.; Xu, X. Dynamic Stability of Rolling Missiles Employing a Two-Loop Autopilot with Consideration for the Radome Aberration Parasitic Feedback Loop. Aerosp. Sci. Technol. 2017, 61, 1–10. [Google Scholar] [CrossRef]
- Nesline, F.W. Missile Guidance for Low-Altitude Air Defense. J. Guid. Control 1979, 2, 283–289. [Google Scholar] [CrossRef]
- Lin, S.; Lin, D.; Wang, W. A Novel Online Estimation and Compensation Method for Strapdown Phased Array Seeker Disturbance Rejection Effect Using Extended State Kalman Filter. IEEE Access 2019, 7, 172330–172340. [Google Scholar] [CrossRef]
- Das, R. Advances in Active Radar Seeker Technology. Def. Sci. J. 2005, 55, 329. [Google Scholar] [CrossRef][Green Version]
- Tiwari, P.; Vora, P.; Bhattacharjee, R. In Flight Radome Error Compensation through Simulated Test Data. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005; p. 6454. [Google Scholar]
- Lin, C.-L. Stability Analysis of Radome Error and Calibration Using Neural Networks. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 1442–1450. [Google Scholar]
- Kang, J.; Xiong, Z.; Wang, R.; Zhang, L. Multi-Layer Fault-Tolerant Robust Filter for Integrated Navigation in Launch Inertial Coordinate System. Aerospace 2022, 9, 282. [Google Scholar] [CrossRef]
- Paris, D. Computer-Aided Radome Analysis. IEEE Trans. Antennas Propag. 1970, 18, 7–15. [Google Scholar] [CrossRef]
- Jeng-Hwa, C.; Kuan-Kin, C. Analysis of A Two-Dimensional Radome of Arbitrarily Curved Surface. IEEE Trans. Antennas Propag. 1990, 38, 1565–1568. [Google Scholar] [CrossRef]
- Lee, H.-S.; Park, H. Prediction of Radome Bore-sight Errors using a Projected Image of Source Distributions. Prog. Electromagn. Res. 2009, 92, 181–194. [Google Scholar] [CrossRef]
- Asad, M.; Khan, S.; Ihsanullah; Mehmood, Z.; Shi, Y.; Memon, S.A.; Khan, U. A split target detection and tracking algorithm for ballistic missile tracking during the re-entry phase. Def. Technol. 2020, 16, 1142–1150. [Google Scholar] [CrossRef]
- Hu, Y.; Gao, C.; Jing, W. Joint State and Parameter Estimation for Hypersonic Glide Vehicles Based on Moving Horizon Estimation via Carleman Linearization. Aerospace 2022, 9, 217. [Google Scholar] [CrossRef]
- Zarchan, P.; Gratt, H. Adaptive Radome Compensation using Dither. J. Guid. Control Dyn. 1999, 22, 51–57. [Google Scholar] [CrossRef]
- Han, S.S.; Jang, S.K.; Lee, S.J. Radome Compensation using Adaptive Particle Filter. IFAC Proc. Vol. 2007, 40, 43–48. [Google Scholar] [CrossRef]
- Yueh, W.R. Adaptive Estimation Scheme for Radome Error Calibration. In Proceedings of the 22nd IEEE Conference on Decision and Control, San Antonio, TX, USA, 14–16 December 1983; pp. 546–551. [Google Scholar]
- Lin, J.-M.; Chau, Y.-F. Radome Slope Compensation using Multiple-model Kalman Filters. J. Guid. Control Dyn. 1995, 18, 637–640. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; He, S.; Shin, H.-S.; Tsourdos, A. Optimal Guidance with Active Observability Enhancement for Scale Factor Error Estimation of Strapdown Seeker. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 4347–4362. [Google Scholar] [CrossRef]
- Zheng, D.; Lin, D.; Xu, X.; Tian, S. Dynamic Stability of Rolling Missile with Proportional Navigation & PI Autopilot considering Parasitic Radome Loop. Aerosp. Sci. Technol. 2017, 67, 41–48. [Google Scholar]
- Süli, E.; Mayers, D.F. An Introduction to Numerical Analysis; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation, Theory, Algorithms and Software; Wiley-Interscience Publication: Hoboken, NJ, USA, 2008. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. Unscented Filtering and Nonlinear Estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2. [Google Scholar]
- Song, T.L.; Lee, D.; Shin, S.J. Active homing performance enhancement with multiple model radome slope estimation. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2005, 219, 217–224. [Google Scholar] [CrossRef]










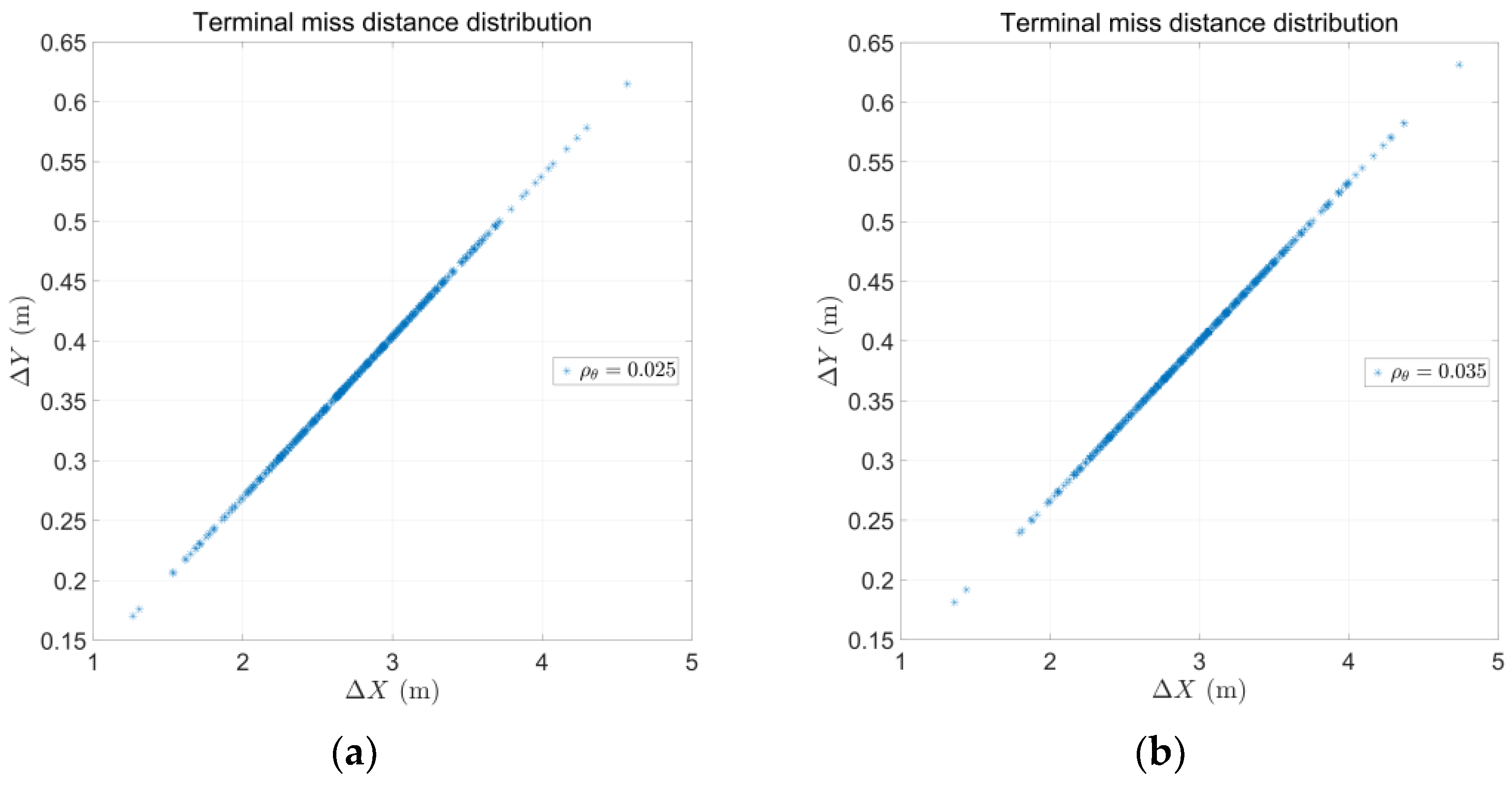
| Miss Distance (m) | ||||
|---|---|---|---|---|
| PNG with correction | 3.7803 | 3.1675 | 3.3914 | 3.5661 |
| PNG without correction | 6.8718 | 6.1265 | 6.4267 | 6.7251 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, K.; Jin, B.; Zhang, N. In-Flight Radome Slope Estimation for Homing Guidance Using Bearing-Only Measurement via Gaussian Process Regression. Aerospace 2022, 9, 626. https://doi.org/10.3390/aerospace9100626
Lu K, Jin B, Zhang N. In-Flight Radome Slope Estimation for Homing Guidance Using Bearing-Only Measurement via Gaussian Process Regression. Aerospace. 2022; 9(10):626. https://doi.org/10.3390/aerospace9100626
Chicago/Turabian StyleLu, Kelin, Bingyu Jin, and Ning Zhang. 2022. "In-Flight Radome Slope Estimation for Homing Guidance Using Bearing-Only Measurement via Gaussian Process Regression" Aerospace 9, no. 10: 626. https://doi.org/10.3390/aerospace9100626
APA StyleLu, K., Jin, B., & Zhang, N. (2022). In-Flight Radome Slope Estimation for Homing Guidance Using Bearing-Only Measurement via Gaussian Process Regression. Aerospace, 9(10), 626. https://doi.org/10.3390/aerospace9100626





