Heat Conduction and Microconvection in Nanofluids: Comparison between Theoretical Models and Experimental Results
Abstract
1. Introduction
2. Theoretical Models
2.1. Hamilton–Crosser Model
2.2. Nan Model
2.3. Modified Geometric Mean
- m = −1: the two components conduct the heat flow in series;
- m = 1: in this case, the two components conduct the heat flow in parallel.
2.4. Feng Model
2.5. Prasher Model
2.6. Corcione Model
3. Experimental Data Sets
3.1. SET-1
3.2. SET-2
- a.
- Type of nanofluid
- b.
- Realization of the nanofluid
- c.
- Samples
- d.
- Thermal conductivity measurements
- Shunt (S);
- Electrical generator (PS);
- Thermocouples;
- Data acquisition system: Keithley 2700 (DMM);
- Data converter: USB-6229 DAQ (DAC);
- Electronic calculator (PC);
- Platinum wire probe;
- Thermocouple on the wall of the measuring cell (to check the validity of the infinite medium hypothesis).
4. Discussion
4.1. SET-I
- , , T = 20 °C, interfacial thermal resistance in agreement with Buongiorno et al. [12].
- . In agreement with Liang et al. [31].
- minimum particle axis.
- ➢
- Geometric mean: this model was used in reverse (it allows the best estimate of m to be determined by the least-square regression).
- ➢
- The Prasher model can be used for spherical nanoparticles. Samples 5 and 6 have needle-like particles, so the Prasher model was not used for these samples.
- ➢
- The Prasher model was applied in direct and in reverse form. The inverse form is used, e.g., when the average number of particles per cluster Nint (or, alternatively, Rg/a) is the unknown parameter. In this case, the least-square regression allows the best Nint to be estimated. Direct use allows the thermal conductivity of the nanofluid to be determined once a value for Nint has been set.
- ➢
- The Feng model predicts the thermal conductivity of the spherical nanoparticles, but Samples 5 and 6 have particles, which can be approximated by an ellipsoid. The generalized Feng model described in Section 2 was used.
- ➢
- The Nan model gives a maximum error of 3.5% (Sample 4);
- ➢
- The Feng model makes fewer errors than the Nan model;
- ➢
- The generalized Feng model agrees with the experimental data. Its error is 0.38% for Sample 5 and 1.12% for Sample 6;
- ➢
- For the geometric mean, the values of “m” and a deviation from the zero value proposed by Turian [21] were collected. For the nanofluid couples (Samples 3–5 and 4–6), which have the same volumetric concentration, the shape of the nanoparticles is different. Homologous samples with spheroidal particles have a lower “m” than those with needle-like particles. The geometric mean model only explains the phenomenon related to volumetric concentration, temperature dependence on bulk thermal conductivity and particle size. Any other mechanism (microconvection, nanolayer, etc.) is considered within “m” if the choice of “m” accurately describes the experimental data.
- ➢
- Using the Prasher model, the number of particles for a cluster equal to 2 was determined indirectly. However, this value does not seem to be accurate, as nanofluids of this type usually consist of a larger number of particles per cluster. In this case, the Feng model leads to a lower error than the Nan model. The Nan and Feng models qualitatively show an opposite trend in thermal conductivity as a function of particle size. This trend can be explained by the fact that the thermal conductivity in the Nan model depends inversely on the Kapitza thermal resistance, which increases with smaller particles. On the other hand, the thermal conductivity in Feng’s model depends directly on the presence of aggregates, which increase as the particles become smaller. Nan’s and Feng’s models differ significantly both when the dimensions of the nanoparticles are very small and when the volumetric concentration increases significantly (as will be seen in the next section).
- ➢
- The formula for the geometric mean, Equation (10), used in an inverse mode, makes it possible to find the best estimate of m, which is closest to the experimental data. Such a procedure was not accurate in describing SET-1. Moreover, the procedure allows us to detect the effects of physical phenomena to be hidden in the variability of the parameter “m”. As a result, it is not possible to verify which phenomenon strongly influences the thermal conductivity of the nanofluid.
- ➢
- If a higher number of particles per cluster were taken into account, the thermal conductivity predicted by the Prasher model would significantly overestimate the measured one. That this model overestimates the thermal conductivity may be due to the approximation of the backbone structure as ellipsoidal particles with the same aspect ratio.
- ➢
- Nan’s and Feng’s models seem to be the simplest and give acceptable results. Problems arise when nanofluids have very small diameters of nanoparticles and very high volumetric concentrations. In the first case, the effect of particle size on thermal conductivity is uncertain. In the second case, the effect of volumetric concentration on thermal conductivity is well known. Although the tendency is the same for all models, the different models give different values for the thermal conductivity.
- ➢
- Since the Feng model has a smaller error compared to the Nan model, it can be concluded that the scattering is negligible with respect to the phenomena of the cluster and of the nanolayer, which are considered in the Feng model. It was important to also extend the Feng model to the case of ellipsoidal particles (see Appendix A). For spherical particles, it showed the worst prediction among the models considered. The prediction of Feng for Sample 5 was k/kbf = 1.034, and for Sample 6, k/kfb = 1.101.
- ➢
- Influence of microconvection: the tests were carried out at room temperature. With these values for temperature, particle diameter and concentration, microconvection is not significant.
- ➢
- Influence of temperature: the data given were determined at room temperature. It is not possible to evaluate the influence on thermal conductivity.
4.2. SET-II
- d = 50 nm.
- in agreement with Buongiorno et al. [12].
- h = 1 nm.
- in agreement with Liang et al. [24].
- in agreement with Prasher et al. [24].
- Electron density and Fermi velocity (relative to aluminum) equal to ne = 18.1∙1028 electrons/m3 and vf = 2.03∙106 m/s, respectively.
- The solidification temperature approximated to the scrolling point Tfr = −42 °C, in agreement with the technical data sheet of the base fluid Castrol Magnatec 10W40 A3/B4.
- ➢
- Geometric mean: as the analysis of SET-1 shows, the parameter “m” does not change significantly. m = 0 was assumed, in agreement with Turian et al. [21].
- ➢
- Prasher: the direct approach was chosen. A typical value for the number of particles per cluster was assumed, i.e., Nint = 10 particles/cluster.
- ➢
- Corcione: since the solidification temperature of the base fluid was not available, the temperature of the scrolling point was assumed.
- ➢
- The following values were used to calculate the Prandtl number of the base fluid in Equation (24) (Table 7).
- ➢
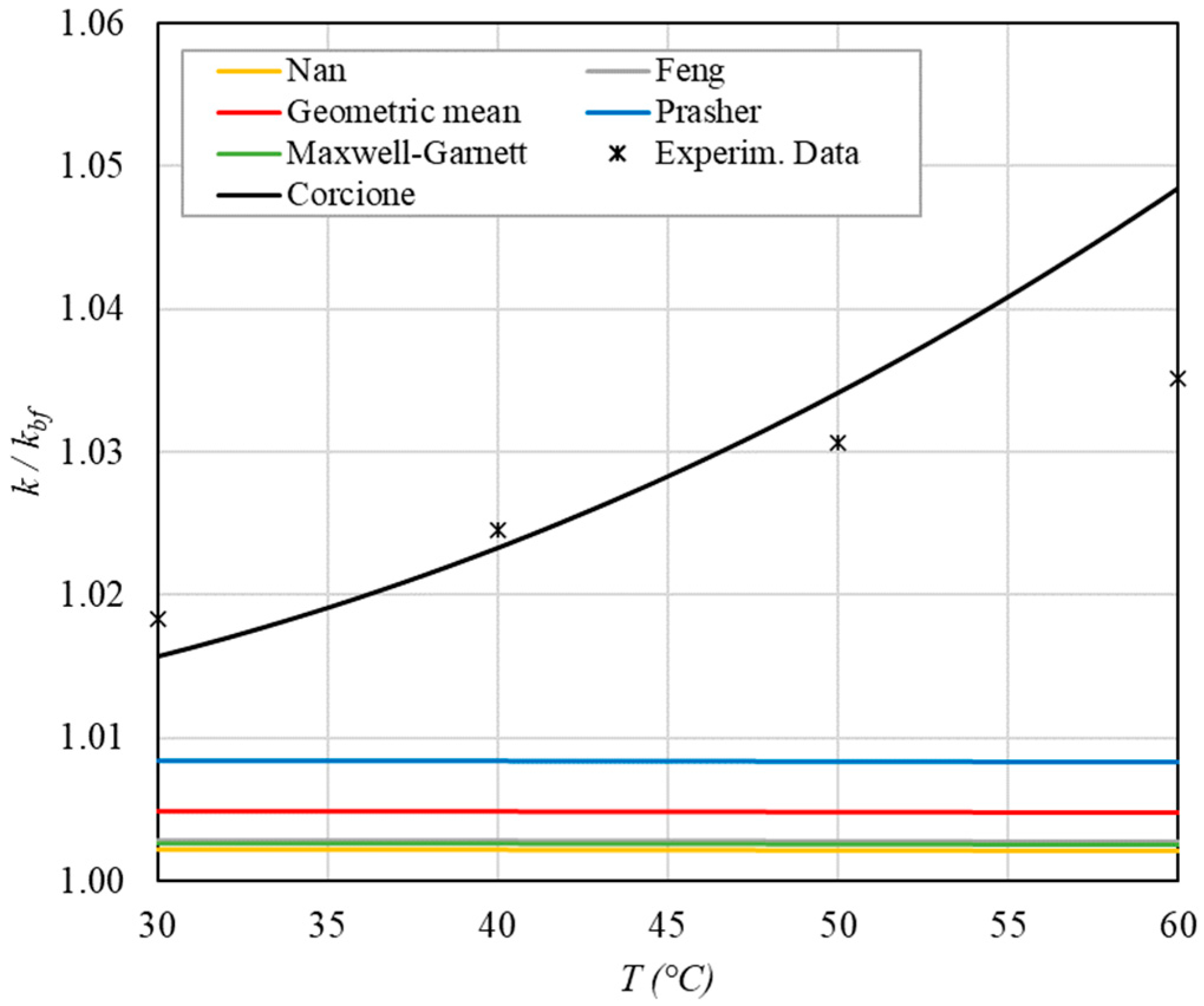
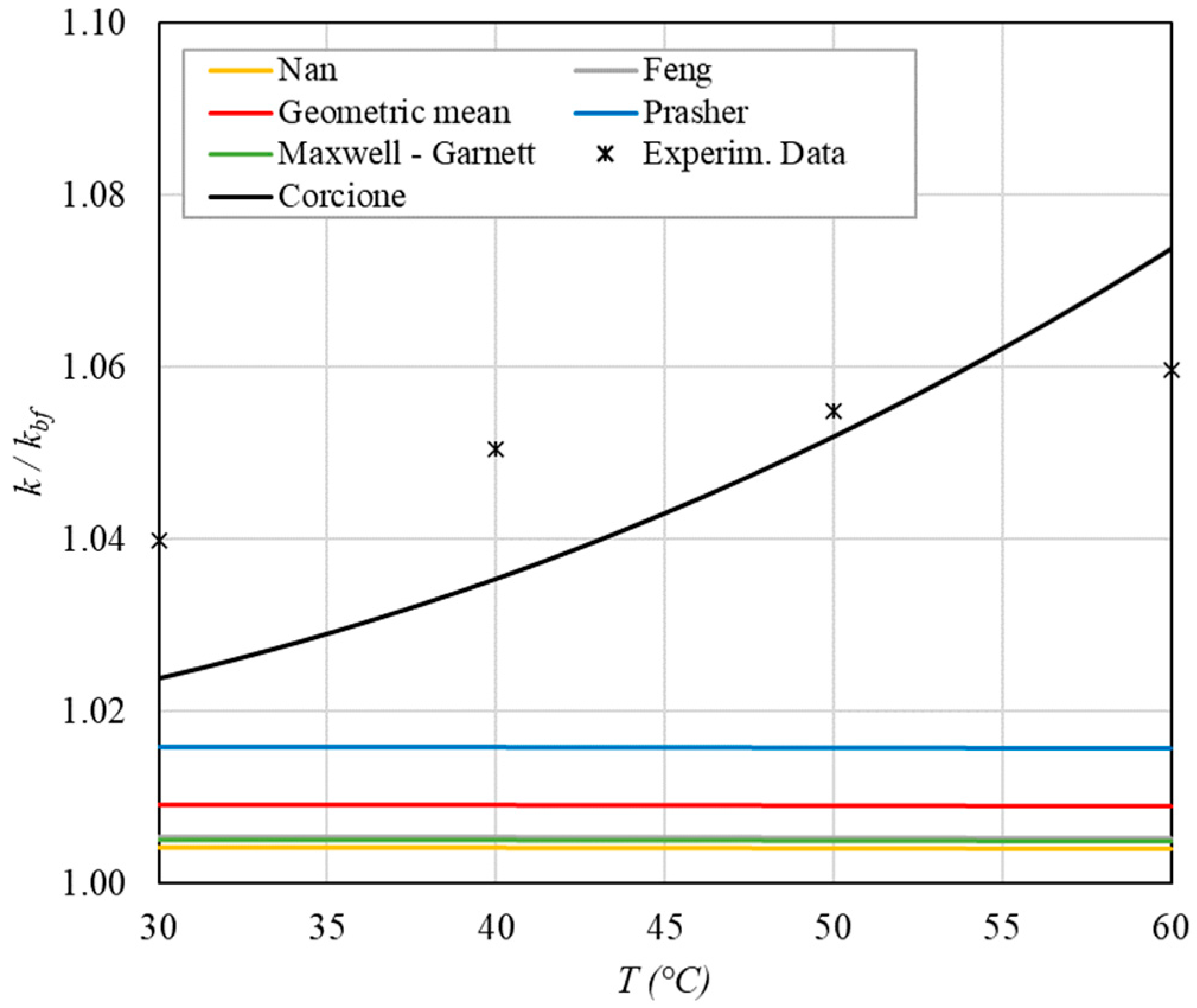
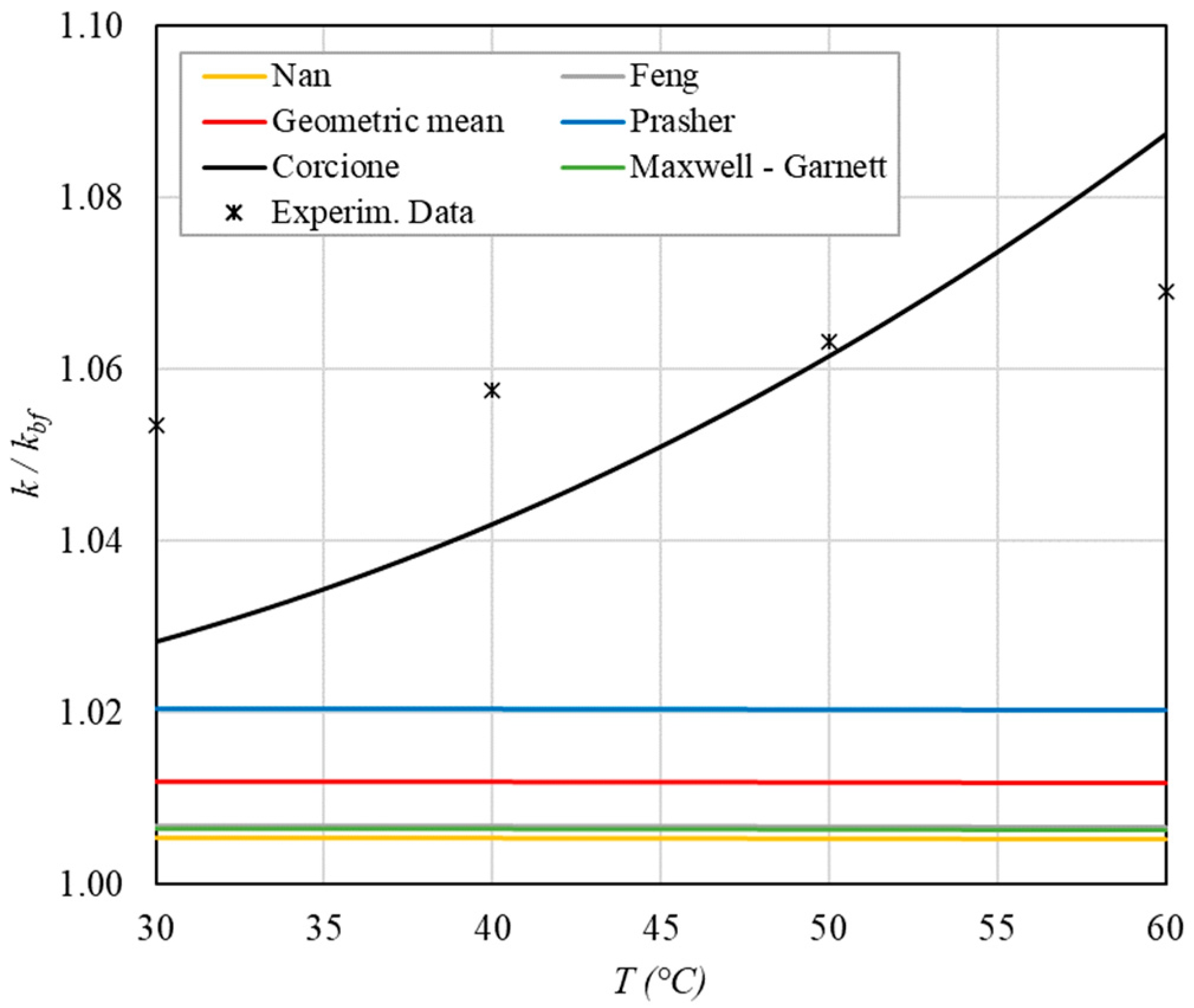
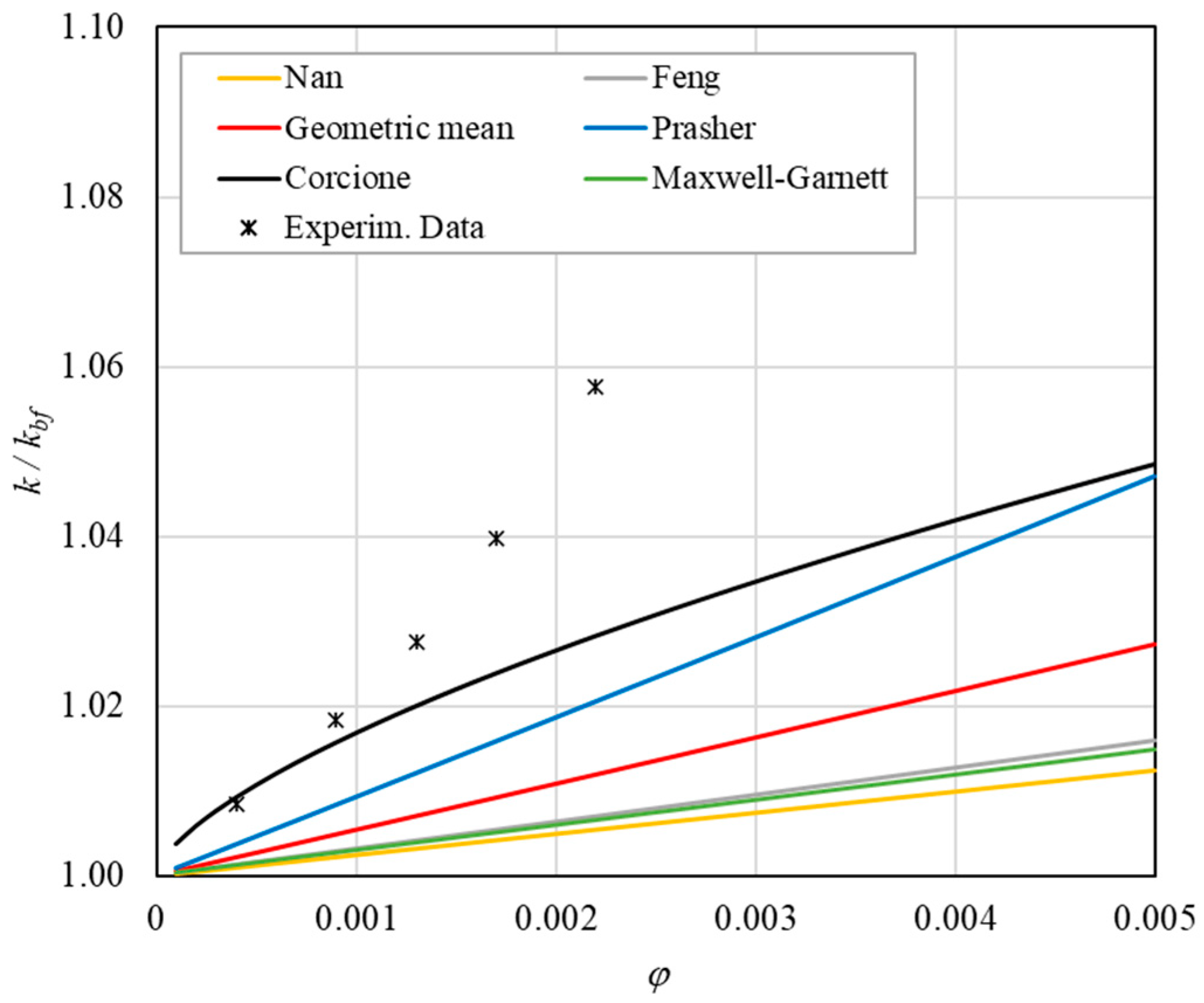
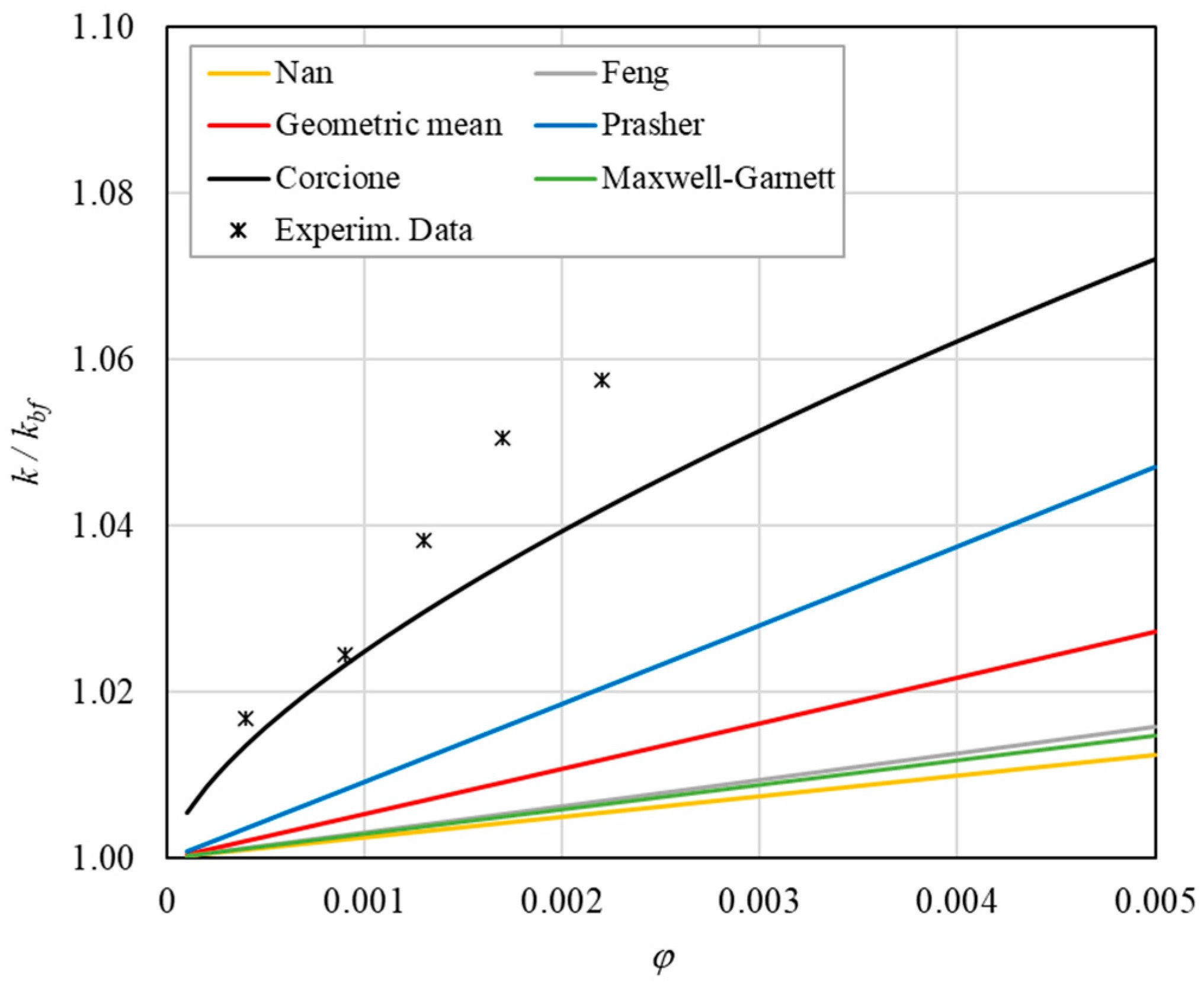
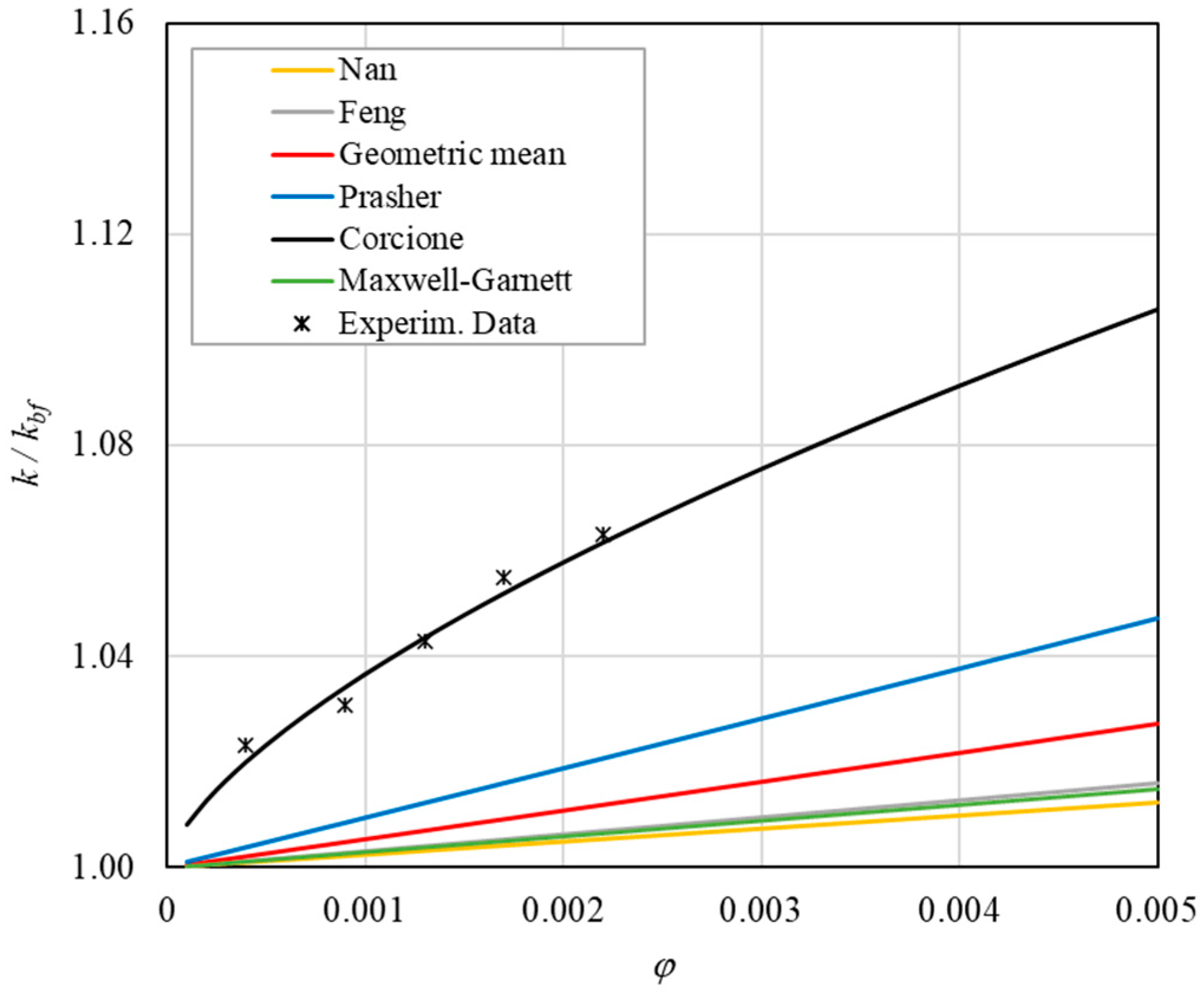
- The experimental enhancement in thermal conductivity ranges from a minimum of 0.8% to 6.9% as the volumetric concentration and temperature increase (Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13). All the models considered, with the exception of Corcione, do not take into account the Brownian motion. These models have an error ranging from a minimum of 0.46% to 6.4%. The error is comparable to thermal conductive enhancement; consequently, these predictions lose their meaning.
- ➢
- The Corcione model provides more accurate predictions. Its errors range from 0.13% to 2.2%.
- ➢
- If the temperatures are sufficiently high (T > 30 °C), the Brownian motion must be taken into account to obtain more accurate predictions. It is therefore advisable to use theoretical models that take such phenomena into account, such as Corcione.
- ➢
- When the volumetric concentration is very small (φ < 1%), the Nan, Feng, Prasher, the geometric mean (with n = 0) and H-C models underestimate the thermal conductivity acceptably at low temperatures, but at higher temperatures, the underestimation becomes non-negligible. The applicability of these models is limited to T ≤ 30 °C.
- ➢
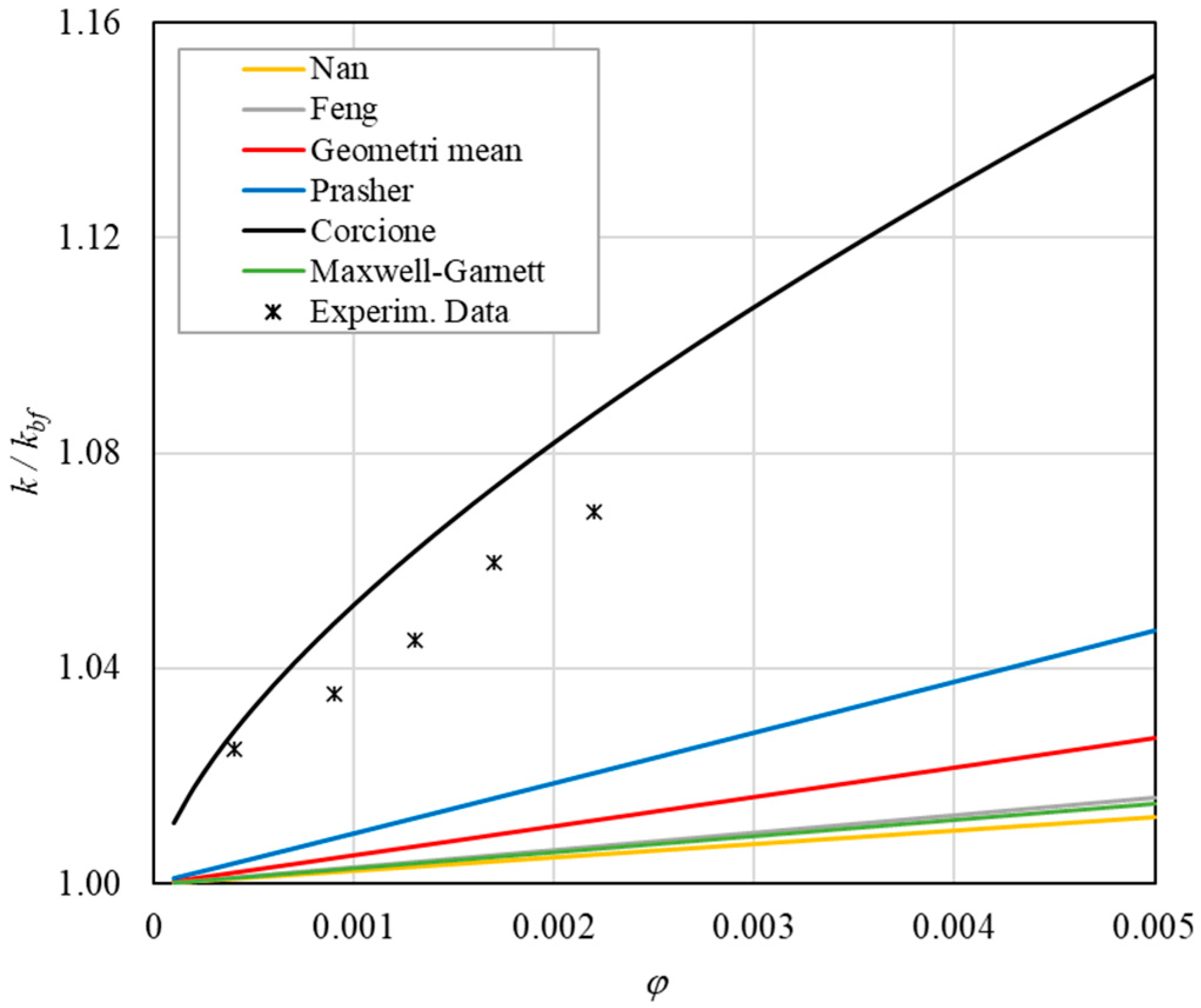
- Effect of volumetric content: it can be seen from Figure 10, Figure 11, Figure 12 and Figure 13 that the thermal conductivity at the same temperature increases by about 4–5% when the volumetric content is increased from 0.04 to 0.22%. However, from the experimental data, the growth rate is different at different temperatures. As the temperature is increased, the slope of the experimental data decreases from the case at T = 30 °C, where all the data are above the Corcione prediction, to the case at T = 60 °C, where all the data are below the Corcione prediction. In the middle case (T = 50 °C), the experimental data are almost perfectly described by the Corcione model. All the other models studied, i.e., Nan and Feng, show an average deviation of 3.61% and 3.51%, respectively, compared to the experimental results at the temperatures considered. This result shows that all the other theoretical models give results that are far from the experimental data. This result shows that there is a temperature range and a fraction value range where the microconvection effect is predominant compared to the other phenomena.
- ➢
- The experimental results show a non-linear trend (Figure 10). Unlike the other models, which predict a linear trend in the concentration range of 0.04–0.22%, the effect of microconvection shows a non-linear increase at low volumetric concentrations, as highlighted by the Corcione model.
- ➢
5. Conclusions
- ➢
- The comparison of SET-I with the models shows that clusters, the formation of the adsorbate nanolayer and the scattering of phonons at the solid–liquid interface are the most important phenomena to consider when φ = 1 ÷ 3. The Feng model is the most advisable model to use.
- ➢
- The shape of the particles also matters because the Feng model must be generalized for particles with an ellipsoidal shape. The generalized model reported in this paper agrees with the experimental data and has an error of 0.38% for Sample 5 and 1.12% for Sample 6.
- ➢
- The Feng model describes SET-I well, but not SET-II. This fact can be ascribed to the volume percentage of the nanoparticles and to the higher temperatures. SET-I has a volume percentage, which is an order of magnitude larger than SET-II. Consequently, microconvection at a very low percentage is significant for the phenomenon of clustering and the presence of the nanolayer. Indeed, the temperature is proportional to the Brownian motion. On the other hand, the volume percentage of the nanoparticle is proportional to the viscosity, and higher viscosity leads to a decrease in the Brownian motion.
- ➢
- The comparison of SET-II with the models showed a significant influence of microconvection in the range of the volumetric concentrations studied. Corcione’s model approximates the measured values better than the other models. If microconvection can be neglected for volumetric concentrations above 0.005, the models of Nan and Feng are the most accurate, as they take into account more significant phenomena in this range of volumetric fraction. At a temperature of 50 °C and in the range of the volume fraction (0.04–0.22%), the experimental data are well reproduced by the Corcione model. For the other conditions, where microconvection cannot be neglected, the Corcione model gives the best prediction compared to the other models used but not the best fit with the experimental values. This is probably due to the empirical nature of this formulation. The physical conditions under which microconvection prevails were defined.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ai | semiaxis in the “i” direction | [m] |
| ak | Kapitza radius | [m] |
| c | specific heat | [J·Kg−1·K−1] |
| cp | specific heat at constant pressure | [J·Kg−1·K−1] |
| d | nominal diameter | [m] |
| df | fractal dimension | |
| dl | chemical dimension | |
| h | layer thickness of adsorbate | [m] |
| k | thermal conductivity | [W·m−1·K−1] |
| thermal conductivity in “i” direction | [W·m−1·K−1] | |
| K | Boltzmann constant | [J·K−1] |
| Lii | geometrical factor in “i” direction | |
| me | electron mass | [Kg] |
| ne | electron density | [electrons·m−3] |
| Nint | number of particles for cluster | |
| p | aspect ratio | |
| specific heat flux | [W·m−2] | |
| heat flux | [W] | |
| Rbd | Kapitza thermal resistance | [m2·K·W−1] |
| t | time | [s] |
| T | temperature | [°C or K] |
| Tfr | solidification temperature | [K] |
| v | speed | [m·s−1] |
| vf | Fermi speed | [m·s−1] |
| Greek | ||
| φ | volumetric concentration of the nanoparticles | |
| Ψ | sphericity of the particle | |
| λ | average free path | [m] |
| βii | conductivity increase in direction “i” | |
| ρ | density | [Kg·m−3] |
| μ | dynamic viscosity | [Kg·m−1·s−1] |
| ν | kinematic viscosity | [m2·s−1] |
| Subscripts | ||
| p | nanoparticles | |
| bf | base fluid | |
| pe | equivalent particle | |
| e | electron equivalent | |
| b | bulk | |
| l | layer | |
| Dimensionless Numbers | ||
| Kn | Knudsen number | |
| Re | Reynolds number | |
| Pr | Prandtl number | |
Appendix A. Extension of the Feng Model



References
- Li, J.; Zhang, X.; Xu, B.; Yuan, M. Nanofluid research and applications: A review. Int. Commun. Heat Mass Transf. 2021, 127, 105543. [Google Scholar] [CrossRef]
- Sheremet, M.A. Applications of Nanofluids. Nanomaterials 2021, 11, 1716. [Google Scholar] [CrossRef] [PubMed]
- Sonawane, S.; Patankar, K.; Fogla, A.; Puranik, B.; Bhandarkar, U.; Kumar, S.S. An experimental investigation of thermophysical properties and heat transfer performance of Al2O3—Aviation Turbine Fuel nanofluids. Appl. Therm. Eng. 2011, 31, 2841–2849. [Google Scholar] [CrossRef]
- Li, Y.Y.; Lv, L.C.; Liu, Z.H. Influence of Nanofluids on the Operation Characteristics of Small Capillary Pumped Loop. Energy Convers. Manag. 2010, 51, 2312–2320. [Google Scholar] [CrossRef]
- Shukla, K.N. Heat Pipe for Aerospace Applications—An Overview. J. Electron. Cool. Therm. Control 2015, 5, 55065. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. In Developments and Applications of Non-Newtonian Flows; Singer, D.A., Wang, H.P., Eds.; American Society of Mechanical Engineers: New York, NY, USA, 1995; Volume 231, pp. 99–105. [Google Scholar]
- Lee, S.; Choi SU, S.; Li, S.; Eastman, J.A. Measuring Thermal Conductivity of Fluids Containing Oxide Nanoparticles. J. Heat Transf. 1999, 121, 280–289. [Google Scholar] [CrossRef]
- Beck, M.; Yuan, Y.; Warrier, P.; Teja, A. The effect of particle size on the thermal conductivity of nanofluids. J. Nanoparticle Res. 2009, 11, 1129–1136. [Google Scholar] [CrossRef]
- Kokate, Y.D.; Sonawane, S.B. Investigation of particle size effect on thermal conductivity enhancement of distilled water—Al2O3 nanofluids. Fluid Mech. Res. Int. J. 2019, 3, 55–59. [Google Scholar] [CrossRef]
- Al-Hossainy, A.F.; Eid, M.R. Structure, DFT calculations and heat transfer enhancement in [ZnO/PG + H2O] C hybrid nanofluid flow as a potential solar cell coolant application in a double-tube. J. Mater. Sci. Mater. Electron. 2020, 31, 15243–15257. [Google Scholar] [CrossRef]
- Eid, M.R.; Al-Hossainy, A.F. Synthesis, DFT calculations, and heat transfer performance large-surface TiO2: Ethylene glycol nanofluid and coolant applications. Eur. Phys. J. Plus 2020, 135, 596. [Google Scholar] [CrossRef]
- Buongiorno, J.; Venerus, D.; Prabhat, N.; McKrell, T.; Townsend, J.; Christianson, R.; Tolmachev, Y.V.; Keblinski, P.; Hu, L.; Alvarado, J.L.; et al. A benchmark study on the thermal conductivity of nanofluids. J. Appl. Phys. 2009, 106, 094312. [Google Scholar] [CrossRef]
- Nan, C.W.; Birringer, R.; Clarke, D.; Gleiter, H. The Effective Thermal Conductivity or Particular Composites with Interfacial Thermal Resistance. J. Appl. Phys. 1997, 81, 6692. [Google Scholar] [CrossRef]
- Hamilton, R.L.; Crosser, O.K. Thermal Conductivity of Heterogeneous Two-Component Systems. Ind. Eng. Chem. Fundam. 1962, 1, 187–191. [Google Scholar] [CrossRef]
- Warrier, P.; Teja, A. Effect of particle size on the thermal conductivity of nanofluids containing metallic nanoparticles. Nanoscale Res. Lett. 2011, 6, 247. [Google Scholar] [CrossRef] [PubMed]
- Chopkar, M.; Sudarshan, S.; Das, P.; Manna, I. Effect of Particle Size on Thermal Conductivity of Nanofluid. Metall. Mater. Trans. A 2008, 39, 1535–1542. [Google Scholar] [CrossRef]
- Lenin, R.; Joy, P.; Bera, C. A review of the recent progress on thermal conductivity of nanofluid. J. Mol. Liq. 2021, 338, 116929. [Google Scholar] [CrossRef]
- Maxwell Garnett, J.C. Colours in Metal Glasses and in Metallic Films. Philos. Trans. R. Soc. A 1904, 203, 385–420. [Google Scholar] [CrossRef]
- Maxwell Garnett, J.C. Colours in Metal Glasses, in Metallic Films, and in Metallic Solutions. Philos. Trans. R. Soc. A 1905, 76, 237–288. [Google Scholar] [CrossRef]
- Kapitza, P.L. Heat Transfer and Superfluidity of Helium II. Phys. Rev. 1941, 60, 354. [Google Scholar] [CrossRef]
- Turian, R.M.; Sung, D.J.; Hsu, F.L. Thermal conductivity of granular coals, coal-water mixtures and multi-solid/liquid suspensions. Fuel 1991, 70, 1157–1172. [Google Scholar] [CrossRef]
- Sommerfeld, A. Zur elektronentheorie der metalle auf grund der fermischen statistic. Z. Für Phys. 1928, 47, 1–32. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, B.; Zou, M. The effective thermal conductivity of nanofluids based on the nanolayer and the aggregation of nanoparticles. J. Phys. D Appl. Phys. 2007, 40, 3164. [Google Scholar] [CrossRef]
- Prasher, R.; Evans, W.; Meakin, P.; Fish, J.; Phelan, P.; Keblinski, P. Effect of aggregation on thermal conduction in colloidal nanofluids. Appl. Phys. Lett. 2006, 89, 143119. [Google Scholar] [CrossRef]
- Corcione, M. Empirical correlating equations for predicting the effective thermal conductivity and dynamic viscosity of nanofluids. Energy Convers. Manag. 2011, 52, 789–793. [Google Scholar] [CrossRef]
- Corasaniti, S.; Bovesecchi, G.; Gori, F. Experimental Thermal Conductivity of Alumina Nanoparticles in Water with and without Sonication. Int. J. Thermophys. 2021, 42, 23. [Google Scholar] [CrossRef]
- Bovesecchi, G.; Coppa, P. Basic Problems in Thermal-Conductivity Measurements of Soils. Int. J. Thermophys. 2013, 34, 1962–1974. [Google Scholar] [CrossRef]
- Coppa, P.; Pasquali, G. Thermal Conductivity of lipidic emulsions and its use for production and quality control. In Proceedings of the 2nd International Symposium on Instrumentation Science and Technology, Jinan, China, 20 August 2002; Volume 1, p. 486. [Google Scholar]
- Gori, F.; Corasaniti, S. Experimental Measurements and Theoretical Prediction of the Thermal Conductivity of Two- and Three-Phase Water/Olivine Systems. Int. J. Thermophys. 2003, 24, 1339–1353. [Google Scholar] [CrossRef]
- Bovesecchi, G.; Coppa, P.; Pistacchio, S. A new thermal conductivity probe for high temperature tests for the characterization of molten salts. Rev. Sci. Instrum. 2018, 89, 055107. [Google Scholar] [CrossRef]
- Liang, Z.; Tsai, H.L. Thermal conductivity of interfacial layers in nanofluids. Phys. Rev. E 2011, 83, 041602. [Google Scholar] [CrossRef]
- Wang, B.; Sheng, W.; Peng, X. A novel statistical clustering model for predicting thermal conductivity of nanofluid. Int. J. Thermophys. 2009, 30, 1992. [Google Scholar] [CrossRef]
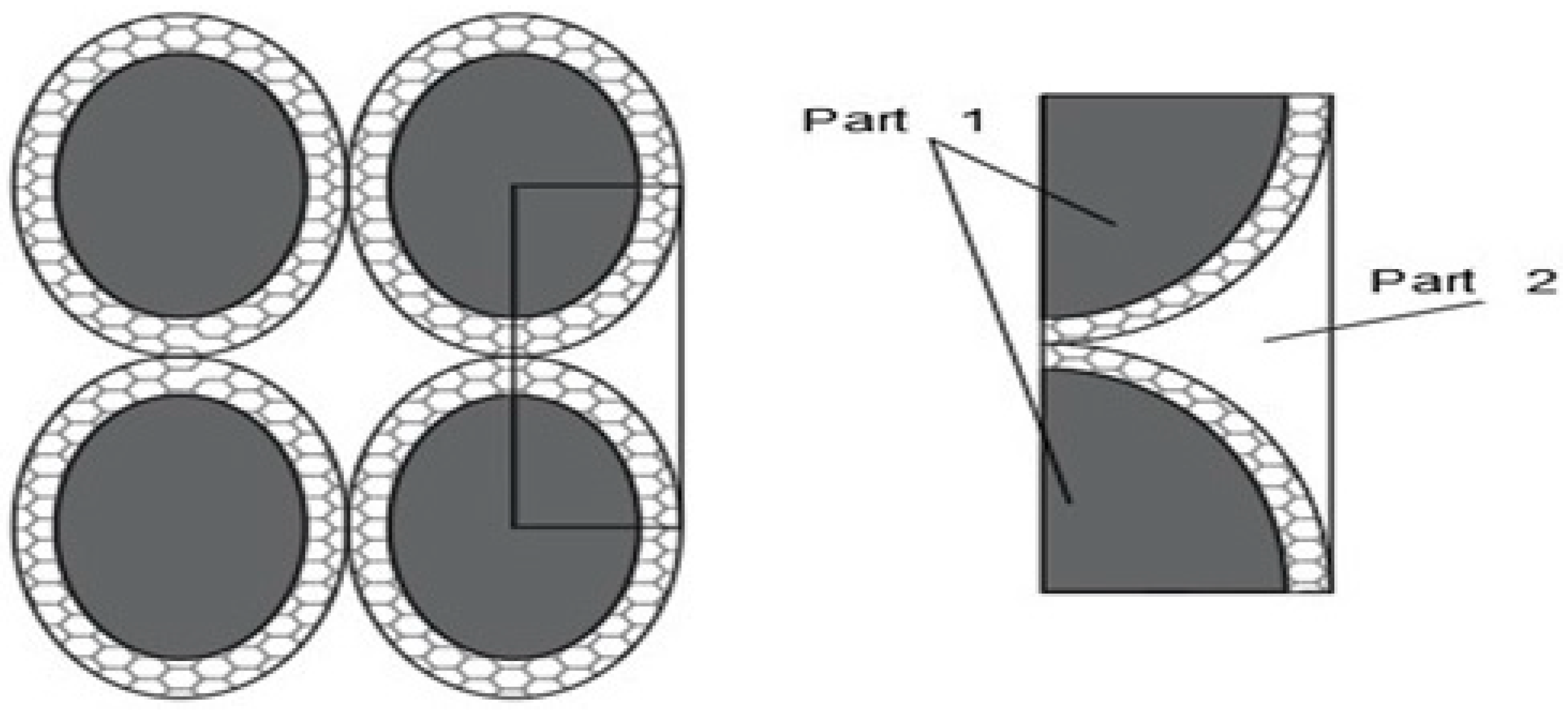




| SET-1 | k/kbf | |
|---|---|---|
| 3 | Alumina nanoparticles (81 nm) 1 vol% in PAO + surfactant | 1.039 ± 0.003 |
| 4 | Alumina nanoparticles (105 nm) 3 vol% in PAO + surfactant | 1.121 ± 0.004 |
| 5 | Alumina nanoneedles (80 nm × 10 nm) 1 vol% in PAO + surfactant | 1.051 ± 0.003 |
| 6 | Alumina nanoneedles (80 nm × 10 nm) 3 vol% in PAO + surfactant | 1.176 ± 0.005 |
| T (°C) | kbf (W·m−1·K−1) |
|---|---|
| 30 | 0.1530 ± 0.0006 |
| 40 | 0.1545 ± 0.0003 |
| 50 | 0.1567 ± 0.0002 |
| 60 | 0.1593 ± 0.0003 |
| φ (%) | T (°C) | k/kbf | φ (%) | T (°C) | k/kbf |
|---|---|---|---|---|---|
| 0.04 | 30 | 1.0084 | 0.13 | 30 | 1.0275 |
| 40 | 1.0168 | 40 | 1.0382 | ||
| 50 | 1.0230 | 50 | 1.0428 | ||
| 60 | 1.0251 | 60 | 1.0452 | ||
| 0.09 | 30 | 1.0183 | 0.17 | 30 | 1.0397 |
| 40 | 1.0246 | 40 | 1.0505 | ||
| 50 | 1.0306 | 50 | 1.0549 | ||
| 60 | 1.0352 | 60 | 1.0596 | ||
| 0.22 | 30 | 1.0536 | |||
| 40 | 1.0576 | ||||
| 50 | 1.0632 | ||||
| 60 | 1.0691 | ||||
| φ (%) | a11/2 (nm) | p = a3/a1 | |
|---|---|---|---|
| Sample 3 | 1 | 40.5 | 1 |
| Sample 4 | 3 | 52.5 | 1 |
| Sample 5 | 1 | 5.0 | 8 |
| Sample 6 | 3 | 5.0 | 8 |
| Sample | H-C | Nan | Feng | Geometric Mean | Prasher |
|---|---|---|---|---|---|
| 3 | 1.03 | 1.027 | 1.032 | 1.055 (m = 0) | 1.041 (Nint = 2) |
| 1.039 (m = −0.14) | 1.102 (Nint = 10) | ||||
| 4 | 1.091 | 1.083 | 1.1 | 1.1746 (m = 0) | 1.127 (Nint = 2) |
| 1.121 (m = −0.14) | 1.329 (Nint = 10) | ||||
| 5 | 1.047 * | 1.07 | 1.055 ** | 1.053 (m = 0) | n.a. |
| 1.051 (m = −0.015) | |||||
| 6 | 1.144 * | 1.211 | 1.163 * | 1.169 (m = 0) | n.a. |
| 1.176 (m = −0.015) |
| T (°C) | kbf-exp (W·m−1·K−1) | kp * (W·m−1·K−1) |
|---|---|---|
| 30 | 0.1530 ± 0.0006 | 33.4282 |
| 40 | 0.1545 ± 0.0003 | 33.4762 |
| 50 | 0.1567 ± 0.0002 | 33.5213 |
| 60 | 0.1593 ± 0.0003 | 33.5639 |
| T (°C) | cp (J·kg−1·K−1) | rbf (kg·m−3) | νbf·104 (m2·s−1) |
|---|---|---|---|
| 30 | 2000 | 860 | 151.50 |
| 40 | 2034 | 850 | 101.00 |
| 50 | 2067 | 845 | 67.33 |
| 60 | 2100 | 840 | 52.00 |
| φ (%) | T (°C) | k/kbf (exp.) | k/kbf (theor.) | ||||
|---|---|---|---|---|---|---|---|
| Nan | Feng | Geom. Mean (m = 0) | Prasher (Nint = 10) | Corcione | |||
| 0.04 | 30 | 1.0084 ± 0.0006 | 1.0009 | 1.0013 | 1.0022 | 1.0037 | 1.0085 |
| 40 | 1.0168 ± 0.0003 | 1.0009 | 1.0013 | 1.0022 | 1.0037 | 1.0149 | |
| 50 | 1.0230 ± 0.0002 | 1.0009 | 1.0013 | 1.0021 | 1.0037 | 1.0217 | |
| 60 | 1.0251 ± 0.0003 | 1.0009 | 1.0013 | 1.0021 | 1.0037 | 1.0310 | |
| 0.09 | 30 | 1.0183 ± 0.0006 | 1.0021 | 1.0029 | 1.0049 | 1.0083 | 1.0171 |
| 40 | 1.0246 ± 0.0003 | 1.0021 | 1.0029 | 1.0049 | 1.0083 | 1.0254 | |
| 50 | 1.0306 ± 0.0002 | 1.0021 | 1.0029 | 1.0048 | 1.0083 | 1.0373 | |
| 60 | 1.0352 ± 0.0003 | 1.0021 | 1.0029 | 1.0048 | 1.0083 | 1.0530 | |
| 0.13 | 30 | 1.0275 ± 0.0006 | 1.0031 | 1.0041 | 1.0070 | 1.0120 | 1.0218 |
| 40 | 1.0382 ± 0.0003 | 1.0031 | 1.0041 | 1.0070 | 1.0120 | 1.0324 | |
| 50 | 1.0428 ± 0.0002 | 1.0031 | 1.0041 | 1.0070 | 1.0120 | 1.0476 | |
| 60 | 1.0452 ± 0.0003 | 1.0031 | 1.0041 | 1.0070 | 1.0120 | 1.0675 | |
| 0.17 | 30 | 1.0397 ± 0.0006 | 1.0040 | 1.0054 | 1.0092 | 1.0158 | 1.0261 |
| 40 | 1.0505 ± 0.0003 | 1.0040 | 1.0054 | 1.0092 | 1.0158 | 1.0387 | |
| 50 | 1.0549 ± 0.0002 | 1.0040 | 1.0054 | 1.0092 | 1.0158 | 1.0568 | |
| 60 | 1.0596 ± 0.0003 | 1.0040 | 1.0054 | 1.0091 | 1.0158 | 1.0806 | |
| 0.22 | 30 | 1.0536 ± 0.0006 | 1.0052 | 1.0070 | 1.0119 | 1.0204 | 1.0309 |
| 40 | 1.0576 ± 0.0003 | 1.0052 | 1.0070 | 1.0119 | 1.0204 | 1.0459 | |
| 50 | 1.0632 ± 0.0002 | 1.0052 | 1.0070 | 1.0119 | 1.0204 | 1.0673 | |
| 60 | 1.0691 ± 0.0003 | 1.0052 | 1.0070 | 1.0118 | 1.0204 | 1.0956 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bovesecchi, G.; Corasaniti, S.; Costanza, G.; Piccotti, F.; Potenza, M.; Tata, M.E. Heat Conduction and Microconvection in Nanofluids: Comparison between Theoretical Models and Experimental Results. Aerospace 2022, 9, 608. https://doi.org/10.3390/aerospace9100608
Bovesecchi G, Corasaniti S, Costanza G, Piccotti F, Potenza M, Tata ME. Heat Conduction and Microconvection in Nanofluids: Comparison between Theoretical Models and Experimental Results. Aerospace. 2022; 9(10):608. https://doi.org/10.3390/aerospace9100608
Chicago/Turabian StyleBovesecchi, Gianluigi, Sandra Corasaniti, Girolamo Costanza, Fabio Piccotti, Michele Potenza, and Maria Elisa Tata. 2022. "Heat Conduction and Microconvection in Nanofluids: Comparison between Theoretical Models and Experimental Results" Aerospace 9, no. 10: 608. https://doi.org/10.3390/aerospace9100608
APA StyleBovesecchi, G., Corasaniti, S., Costanza, G., Piccotti, F., Potenza, M., & Tata, M. E. (2022). Heat Conduction and Microconvection in Nanofluids: Comparison between Theoretical Models and Experimental Results. Aerospace, 9(10), 608. https://doi.org/10.3390/aerospace9100608









