Manned Mars Mission Analysis Using Mission Architecture Matrix Method

Abstract

With the development of deep space exploration technology, manned missions to Mars are expected to be realized in the near future. However, the journey to Mars requires more supplies and fuel than near-Earth missions, including moon landings. Using the traditional Apollo-style mission method will result in the spacecraft reaching the LEO mass of 2000 tons, which is not easy to achieve. The use of the modular design method and multiple launches will significantly reduce the mass of a single launch. In addition, the use of nuclear power engines (Nuclear Thermal Propulsion, NTP, and Nuclear Electric Propulsion, NEP) can greatly improve propulsion efficiency, reducing the mass of the propellant. This paper uses the Mission Architecture Matrix (MAM) method to concisely and precisely analyze a series of mission architectures in the case of impulse maneuver transfer and low-thrust transfer. The results show that when only chemical propulsion (specific impulse is 440 s) is used, the maximum LEO launch mass in the optimal mission architecture is 325 tons, and the total LEO mass of the system is 1142 tons. With the usage of NTP (specific impulse is 900 s) and NEP (the specific impulse is 6000 s) technology, the maximum LEO launch mass in the optimal mission architecture is only 85 tons, and the total LEO mass of the system is only about 400 tons. Considering the current rocket technology, the total cost is about USD 1149 million US.

1. Introduction

1.1. Manned Mars Exploration: Setting Sail

As one of the planets closest to Earth, Mars has long been regarded as an extremely important goal in the process of human exploration of the universe.

After a series of spacecraft visited Mars [1,2,3,4,5,6,7,8,9], our astronauts are expected to land on Mars in the near future. Unlike manned near-Earth missions (including manned missions to the moon/NEO), manned Mars missions will greatly challenge our existing space technology in terms of mission duration and mass scale. The journey to Mars will consume a surprising amount of propellant and supplies, while landing/taking off on Mars and returning to Earth will also require more powerful (and heavier) landing vehicles.

Following the success of the Apollo mission to the moon, space agencies of several countries have been demonstrating plans for manned missions to Mars. The most direct method of manned Mars exploration (the basic profile) is to use chemical engines to implement several orbital shifts. The spacecraft is pushed from LEO to the Earth–Mars transfer orbit and accelerates into LMO when it reaches its rendezvous with Mars. When returning, the spacecraft accelerates from Mars into Mars–Earth transfer orbit and finally enters the atmosphere. Many researchers have estimated that the initial mass of the spacecraft in LEO reached thousands of tons in this profile. This is obviously difficult to achieve at present.

NASA proposed the NASA 90-day study [10] in the 1980s, aiming to use the framework of the Apollo mission to implement manned Mars exploration. The plan uses the opposition trajectory to shorten the mission time, and at the same time, the mission risk is low. However, a spacecraft with a large initial mass (thousands of tons) is required.

Clark et al. [11] proposed the straight arrow scheme based on the basic profile, which suggested collecting and producing part of the propellant for partial return on the surface of Mars, thereby reducing the initial mass of the spacecraft. Zubrin and Frenchs also proposed ‘Mars Direct’ and ‘Case for Mars’ [12,13], which need to collect and produce all the propellants for return on the surface of Mars. The concept of multiple functional modules and separate launches of modular spacecraft is explored in these two studies. NASA has also proposed a series of plans for manned Mars exploration missions [14,15,16,17,18].

In addition, Taraba et al. proposed a manned Mars exploration scheme based on the LMO space station and preliminarily estimated the mass scale and cost of the manned Mars exploration missions [19]. Salotti et al. first proposed a manned Mars exploration scheme that divides the return spacecraft into two parts, which can complete the mission requirements when carrying only three astronauts [20]. In another study of Salotti et al., a new roadmap for the preparation of the human mission to Mars based on the work of ISECG is proposed [21]. He also proposes using two Mars rovers to carry two astronauts to explore the surface of Mars [22]. Colombi et al. proposed a radiation environment warning system for manned Mars exploration missions, which can effectively ensure the safety of astronauts [23].

On the other hand, the development of propulsion technology has brought dawn to manned deep space exploration missions. At present, mature propulsion technologies include high specific impulse chemical propulsion technology, electric propulsion technology, and nuclear propulsion technology.

In terms of chemical propulsion, the propellant H₂/O₂ is widely used as the propellant with a high specific impulse of about 440 s [24]. This kind of engine can provide large thrust (1 KN∼100 kN) and can operate stably. It is suitable for manned deep space exploration missions [25,26].

Electric propulsion technology greatly reduces the propellant mass with extremely high propellant specific impulse, thereby significantly reducing the initial mass of the spacecraft [27,28,29]. At present, most electric propulsion engines are powered by solar panels, and their thrust is very small (mN magnitude) due to the low power. Thus, they can only be used for small probes.

The gradual maturity of nuclear electric propulsion (NEP) technology gives us the opportunity to use larger thrust engines for manned Mars exploration missions [30]. Konstantinov analyzed a 1000-day manned Mars exploration mission based on the use of nuclear power engines [31], reducing the initial mass of the spacecraft to 200 tons. Loeb et al. further used the Megawatt Type nuclear reactor and the clustered Ion Thruster RFIT-45 to design a technically feasible NEP device for a manned Mars mission with an impulse of about 6000 $\mathrm{s}$ [32]. Such megawatt nuclear reactors are similar to those carried by nuclear submarines, and their technical conditions are relatively mature.

In addition, the development of nuclear thermal propulsion (NTP) technology also provides more options for impulse maneuver. NTP can provide greater thrust with a higher specific impulse. At present, the mature nuclear fission thermal propulsion mainly focuses on the solid core type, which can provide 100–1000 kN thrust, and the specific impulse can reach about 1000 s [33,34,35,36]. This technology can be used as an alternative to chemical engines in manned Mars exploration missions.

In terms of spacecraft design, the Boeing Company proposed a design plan for the Spaceship Discovery in 2006 [37]. There are two types of landing modules used by the Discovery spacecraft for Mars exploration. One is a manned landing module called Landing Module No.2 (LM2); the other is an automatically controlled cargo landing model, which is called Landing Module No.3 (LM3) [38,39]. Boden et al. also gave the design scheme of manned spacecraft in the research of manned asteroid missions [40]. This provides viable vehicle systems for manned Mars missions.

1.2. Mission Architecture Analysis: The Mission Architecture Matrix (MAM) Method

Since the manned Mars exploration vehicle system is very complex, it is necessary to conduct a modular mission scale analysis. The Mission Architecture Matrix (MAM) method is a modular mission analysis method based on a series of studies of baseline mission design of human deep space exploration [41,42,43,44,45]. This method transforms the mission flow into Basic Operation Steps (BOS) according to the baseline design. Each BOS corresponds to a Basic State Vector (BSV) composed of the state values of all modules of the system. The Basic Step Matrix (BSM) can then be constructed based on the corresponding BOS with BSV and related velocity increment, specific impulse, and other mission parameters. The BSM is actually the parameter transfer matrix of the system, connecting the mission parameters (such as mass, reliability, etc.) before and after one BOS. The parameter transition matrix at any two moments can be obtained by matrix operation of all BSMs between the two moments. Therefore, this method can concisely and intuitively describe the state of the system at all moments, including the initial and the final moment. The fuel consumption can also be obtained from the matrix relationship between the initial and final states. The schematic diagram of the MAM method is shown in Figure 1.

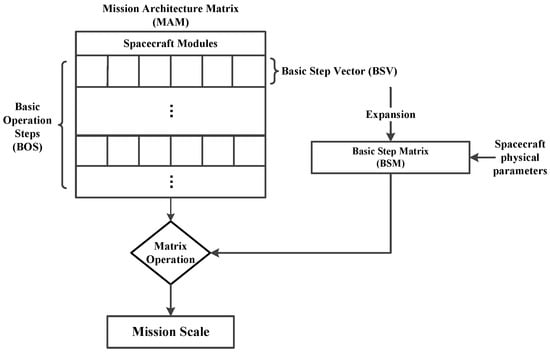
Figure 1. Schematic diagram of the MAM method.

This method has been detailed, introduced, and successfully used for manned Lunar/ near-Earth asteroid mission analysis in our previous work [46,47]. This paper presents several mission architectures of manned Mars missions and then uses the MAM method to analyze the corresponding mission scale in Section 4. Both chemical engines and nuclear propulsion engines (NTP and NEP) will be included.

2. Mission Profile Calculation and Spacecraft System Design

Taking into account the revolution period of Mars and Earth, a whole mission takes about 3 years. Considering the survival status of astronauts, the manned Mars mission time is limited to 1000 days, and the residence time on Mars is no less than 300 days. The launch time takes place 2035–2050. The spacecraft system must include at least the command module and the Mars Landing module (including the ascending rocket). The mission profiles are calculated based on the premise that all spacecraft modules are first launched to LEO.

2.1. Mission Profiles Calculation for Impulse Maneuver Transfers

2.1.1. Hohmann Transfer

For spacecraft using impulse engines (chemical engines and NTP engines are considered in this paper), we can use the Hohmann transfer to accomplish the Mars exploration trajectory as Figure 2 shows.

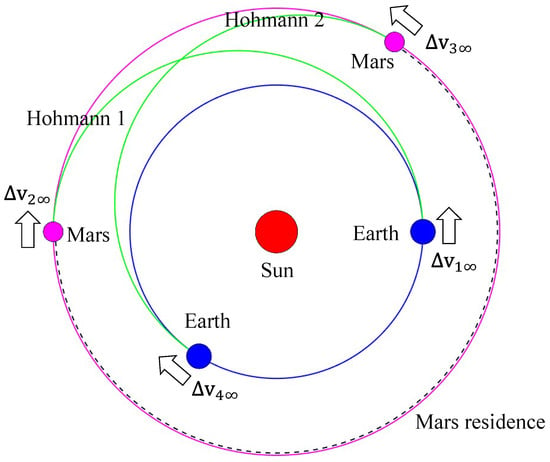
Figure 2. Mission profile for impulse maneuver transfers (Hohmann transfers) in heliocentric coordinate system.

Through the Hohmann transfer method, the velocity increments $\mathsf{\Delta }{v}_{1\infty }$∼$\mathsf{\Delta }{v}_{4\infty }$ in the heliocentric coordinate system could be calculated referring to the work of Howard D. Curtis [48].

Note that, considering departure from LEO, in order to escape the gravitational pull of Earth, the spacecraft needs to travel a hyperbolic trajectory relative to Earth, arriving at its sphere of influence with a relative velocity greater than zero, as Figure 3 shows [49]. As for velocity transformation into the sphere of Influence of Earth (reentry to Earth), the spacecraft will cross the sphere of influence behind Earth and then impact its atmosphere from the hyperbolic approach trajectory.

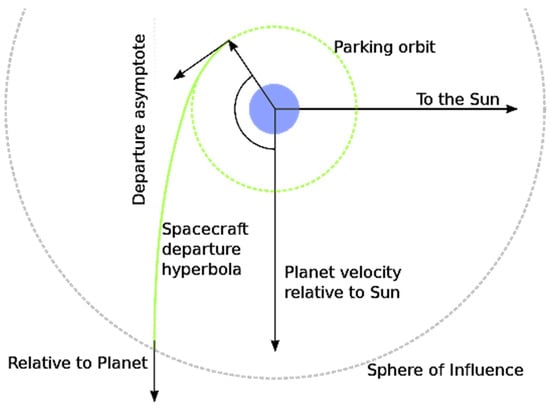
Figure 3. Departure of a spacecraft on a mission from an inner planet to an outer planet.

Thus, actual $\mathsf{\Delta }{v}_1$ and $\mathsf{\Delta }{v}_4$ for orbit maneuver must be conversed according to $v_{1\infty }$ and $v_{4\infty }$ [48,49]:

$$\mathsf{\Delta }{v}_1=\sqrt{{v_{1\infty }}^2+2{v_{LEO}}^2}-v_{LEO}$$

(1)

$$\mathsf{\Delta }{v}_4=\sqrt{{v_{4\infty }}^2+2{v_{EI}}^2}$$

(2)

In which $v_{LEO}$ is the orbit velocity of LEO (≈$7.7/\mathrm{s}$), and $v_{EI}$ is the orbit velocity at the Earth Entry Interface (EI, $130$) (≈$7.8/\mathrm{s}$) [50].

Similarly, actual $\mathsf{\Delta }{v}_2$ and $\mathsf{\Delta }{v}_3$ for orbit maneuver from LMO can be derived:

$$\mathsf{\Delta }{v}_2=\sqrt{{v_{2\infty }}^2+2{v_{LMO}}^2}-v_{LMO}$$

(3)

$$\mathsf{\Delta }{v}_3=\sqrt{{v_{3\infty }}^2+2{v_{LMO}}^2}-v_{LMO}$$

(4)

In which $v_{LMO}$ is the orbit velocity of LMO (≈3.5 km/s).

The total impulse $\mathsf{\Delta }v$ includes $\mathsf{\Delta }{v}_1$∼$\mathsf{\Delta }{v}_3$.

Calculated results of parameters of the Hohmann transfer for Earth–Mars (including mission duration and velocity increments) are listed in Table 1.

Table 1. Parameters ofthe Hohmann transfer for Earth–Mars and Mars–Earth. The velocity increments in this table are all actual $\mathsf{\Delta }v$ departure from LEO/LMO.

Mission Duration (Days)				Velocity Increments (km/s)
Total Duration	Earth-Mars	Mars Residence	Mars-Earth	Total Impulse $\mathsf{\Delta }\mathit{v}$	$\mathsf{\Delta }{\mathit{v}}_1$	$\mathsf{\Delta }{\mathit{v}}_2$	$\mathsf{\Delta }{\mathit{v}}_3$	$\mathsf{\Delta }{\mathit{v}}_4$
972.1	258.9	454.4	258.9	7.8	3.6	2.1	2.1	11.5

As seen in Table 1, the Hohmann transfer is indeed the most energy-efficient two-impulse maneuver for transferring between Earth and Mars or other two coplanar circular orbits sharing a common focus. However, it comes at the cost of excessive time consumption.

On the other hand, in the real situation, Mars and Earth orbits are not perfect circles. Consequently, there are a few differences in the transfer orbits in each rendezvous period, and the Hohmann transfer cannot accurately describe the Earth–Mars transfer opportunities with optimal energy in each rendezvous period. At this point, it comes down to solving Lambert’s problem.

2.1.2. Lambert Transfer

Concerned with the determination of an orbit from two position vectors and the time of flight, Lambert’s problem has important applications in the areas of rendezvous, targeting, guidance, and preliminary orbit determination. Thus, we can calculate the mission profiles and search their best launch/return windows based on the Lambert transfers.

Since the whole mission includes two Lambert transfers (Figure 4), it is necessary to calculate the velocity increments required for a series of Earth–Mars and Mars–Earth transfer orbits during 2035–2050, respectively, by providing the positions of Earth and Mars as well as the transfer times, and then selecting the appropriate launch window and return window according to the time constraints (mission time $<1000$ days). Figure 5 shows the Lambert transfer velocity increment from Earth to Mars from 2035 to 2050, and Figure 6 shows the Lambert transfer velocity increment from Mars to earth from 2035 to 2050. The calculation method of Lambert transfer refers to the work of Vallado [51].

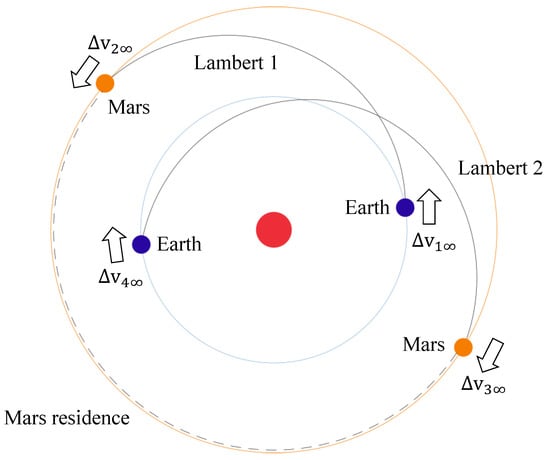
Figure 4. Mission profile for impulse maneuver transfers (Lambert transfers) in heliocentric coordinate system.

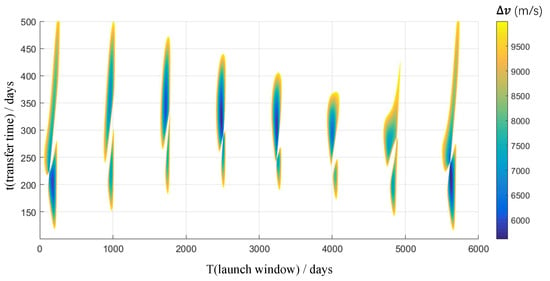
Figure 5. Total $\mathsf{\Delta }v$ for Earth-to-Mars Lambert transfer from 2035 to 2050. The horizontal axis is launch windows (in days after 1 January 2035), and the vertical axis is transfer time (in days).

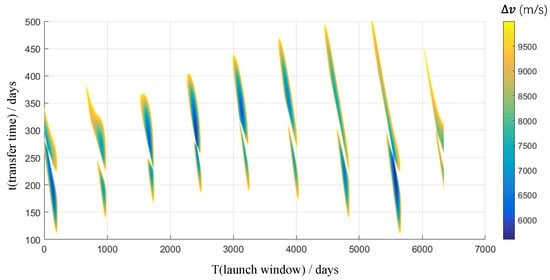
Figure 6. Total $\mathsf{\Delta }v$ for Mars-to-Earth Lambert transfer from 2035 to 2050. The horizontal axis is launch windows (in days after 1 January 2035), and the vertical axis is transfer time (in days).

The feasible mission profiles correspond to the minimum total transfer velocity increments and meet the time constraints. Therefore, the mission profiles are decided by four time variables (launch window $t_0$, transfer time from Earth to Mars $T_1=t_1-t_0$, return window $t_2$, and transfer time from Mars to Earth $T_2=t_3-t_2$):

$$\left\{\begin{array}{c}\left[V_{1\infty },V_{2\infty }\right]=Lambert\left(t_0,t_1,{Orbit}_{Earth},{Orbit}_{Mars}\right)\hfill \\ \left[V_{3\infty },V_{4\infty }\right]=Lambert\left(t_2,t_3,{Orbit}_{Earth},{Orbit}_{Mars}\right)\hfill \\ t_3-t_0\le 1000\hfill \\ t_2-t_1\ge 300\hfill \end{array}\right.$$

(5)

This optimization problem (minimum $\mathsf{\Delta }v$ can be solved using the Particle swarm optimization (PSO) method (searching optimal launch window in each local optimal region) [52]. The optimal profiles (with minimum local velocity increments) are shown in Table 2. Analogously, all actual $\mathsf{\Delta }v$ for orbit maneuver are conversed according to $v_{\infty }$.

Table 2. Optimal mission profiles for manned Mars mission using chemical engines. Time of expedition: <1000 days. The launch window is 2035–2050. The velocity increments in this table are all actual $\mathsf{\Delta }v$ departure from LEO/LMO.

Launch Date (dd.mm.yy)	Mission Duration (Days)				Velocity Increments (km/s)
	Total Duration	Earth–Mars	Mars Residence	Mars–Earth	Total Impulse $\mathsf{\Delta }\mathit{v}$	$\mathsf{\Delta }{\mathit{v}}_1$	$\mathsf{\Delta }{\mathit{v}}_2$	$\mathsf{\Delta }{\mathit{v}}_3$	$\mathsf{\Delta }{\mathit{v}}_4$
09.07.2035	928.2	184.3	544.1	199.7	8.4	3.6	2.1	2.7	11.9
05.09.2037	982.9	227.6	453.1	302.2	8.4	4.0	2.0	2.3	11.5
14.10.2039	974.0	224.2	433.1	316.8	8.6	4.0	2.4	2.2	11.6
24.11.2041	977.7	208.7	431.2	337.9	9.2	4.2	3.0	2.0	11.6
03.01.2044	987.3	185.6	481.2	320.6	9.9	4.2	3.7	2.0	12.1
12.02.2046	978.5	155.8	546.7	276.1	10.0	4.3	3.8	1.9	12.0
05.04.2048	988.4	151.1	598.4	238.9	8.7	3.9	3.0	1.9	11.6
06.06.2050	977.4	161.8	589.8	225.8	8.5	3.6	2.5	2.4	11.6

As can be seen in Table 2, the mission profile with the smallest total impulse is the bold line in this table, which can be considered an alternative mission profile for manned Mars mission.

2.1.3. Multi-Impulse Transfer

In addition to the two-impulse transfers, there are also multi-impulse transfers available for interplanetary trajectories, which may help reduce the velocity increments required for a mission so as to realize the minimal energy target.

Suppose there are n successive Lambert transfers that form an $n+1$ impulse transfer for a manned Mars mission. Let the initial conditions of the spacecraft for multi-impulse transfer be ${\mathit{r}}_{\mathbf{0}}$, ${\mathit{v}}_{\mathbf{0}}$, and $t_0$, and the terminal conditions are ${\mathit{r}}_{\mathit{f}}$, ${\mathit{v}}_{\mathit{f}}$, and $t_f$, in which $\mathit{r}$ is the position vector of the spacecraft, and $\mathit{v}$ is the velocity vector of the spacecraft. Assume that an impulsive $\mathsf{\Delta }{\mathit{v}}_i$ is applied; the conditions of the spacecraft before and after such impulse must satisfy

$$\left\{\begin{array}{c}{\mathit{r}}_i^{+}={\mathit{r}}_i^{-}\hfill \\ {\mathit{v}}_i^{+}={\mathit{v}}_i^{-}+\mathsf{\Delta }{\mathit{v}}_i\hfill \\ t_i^{+}=t_i^{-}\hfill \end{array}\right.$$

(6)

In which $i=0,1,\cdots ,n$.

Meanwhile, from the spacecraft orbital dynamic equation

$$\ddot{\mathit{r}}=-\mu \frac{\mathit{r}}{r^3}$$

(7)

In which r is the modulus of $\mathit{r}$. We can solve to get

$$\left\{\begin{array}{c}{\mathit{r}}_i={\mathit{f}}_1\left({\mathit{r}}_{i-1},{\mathit{v}}_{i-1}^{+},t_{i-1},t_i\right)\hfill \\ {\mathit{v}}_i^{-}={\mathit{f}}_2\left({\mathit{r}}_{i-1},{\mathit{v}}_{i-1}^{+},t_{i-1},t_i\right)\hfill \end{array}\right.$$

(8)

In which $i=0,1,\cdots ,n$.

According to the final conditions, using the above equations, we can obtain

$$\left\{\begin{array}{c}{\mathit{r}}_f={\mathit{f}}_1\left({\mathit{r}}_{n-1},{\mathit{v}}_{n-1}^{+},t_{n-1},t_f\right)\hfill \\ {\mathit{v}}_f={\mathit{v}}_n^{-}+\mathsf{\Delta }{\mathit{v}}_n={\mathit{f}}_2\left({\mathit{r}}_{n-1},{\mathit{v}}_{n-1}^{+},t_{n-1},t_f\right)+\mathsf{\Delta }{\mathit{v}}_n\hfill \end{array}\right.$$

(9)

Note that the transfer in every period between two consecutive impulses is the Lambert transfer, so we can obtain

$$\left({\mathit{v}}_{i-1}^{+},{\mathit{v}}_i^{-}\right)=\mathrm{Lambert}\left({\mathit{r}}_{i-1},{\mathit{r}}_i,t_{i-1},t_i\right)$$

(10)

In which $i=0,1,\cdots ,n$.

In summary, take three-impulse transfer as an instance. To minimize the total velocity increments, the following constraints must be satisfied for the manned Mars mission:

$$\left\{\begin{array}{c}minJ={\displaystyle \sum _{i=1}^n}\left|\mathsf{\Delta }{\mathit{v}}_i\right|\hfill \\ s.t.\left\{\begin{array}{c}{\mathit{v}}_i^{+}={\mathit{v}}_i^{-}+\mathsf{\Delta }{\mathit{v}}_i\hfill \\ {\mathit{r}}_j={\mathit{f}}_1\left({\mathit{r}}_{j-1},{\mathit{v}}_{j-1}^{+},t_{j-1},t_j\right)\hfill \\ {\mathit{v}}_j^{-}={\mathit{f}}_2\left({\mathit{r}}_{j-1},{\mathit{v}}_{j-1}^{+},t_{j-1},t_j\right)\hfill \\ {\mathit{r}}_f={\mathit{f}}_1\left({\mathit{r}}_1,{\mathit{v}}_1^{+},t_1,t_f\right)\hfill \\ {\mathit{v}}_f={\mathit{f}}_2\left({\mathit{r}}_1,{\mathit{v}}_1^{+},t_1,t_f\right)+\mathsf{\Delta }{\mathit{v}}_2\hfill \\ \left({\mathit{v}}_{j-1}^{+},{\mathit{v}}_j^{-}\right)=\mathrm{Lambert}\left({\mathit{r}}_{j-1},{\mathit{r}}_j,t_{j-1},t_j\right)\hfill \end{array}\right.\hfill \end{array}\right.$$

(11)

In which $i=0$∼2, $j=1$∼2.

Similar to two-impulse transfer using only one Lambert transfer, the optimization problem (minimum $\mathsf{\Delta }v$) can also be solved using the Particle swarm optimization (PSO) method by controlling the true anomaly $\theta$ or the transfer time $\mathsf{\Delta }t$ of each period between two consecutive impulses or another variable.

Meanwhile, as some researchers have pointed out, for the coplanar cases, the use of a minimum delta-V three-impulse transfer affords scant improvement in velocity penalty [53]. Thus, considering the reliability, it seems that two-impulse transfers are better than multi-transfers for manned Mars missions.

2.1.4. Summary

By comparing all the transfer trajectories from Section 2.1.2 and Section 2.1.3 together, in this study, the mission profile with the smallest total impulse is taken for research; that is, the bold line in Table 2. The launch date of the mission is 5 September 2037, and the arrival date at Mars is 21 April 2038. After 453 days’ stay on Mars, the crew leaves Mars on 18 July 2039, and finally returns back to Earth on 15 May 2040. The total duration of the mission is about 983 days.

2.2. Mission Profiles Calculation for Low-Thrust Transfers

In this paper, only electric engines are considered for low-thrust transfers.

While using low-thrust transfers, there are some characteristics of manned Mars missions which need to be taken into consideration as mission constraints, such as the launch date, the duration of transfer to Mars, the program of spacecraft transfer Earth–Mars and Mars–Earth, the duration of stay of spacecraft on Martian orbit (minimal time is fixed 30 days), as well as the launching costs, the vehicle initial mass and the risk of a mission failure, in which the main performance index is the mass of nuclear electric power and propulsion system [31,32].

Based on the above-listed mission constraints, article [31] established some constraints for manned Mars missions using low-thrust transfers: the duration of the crew stay in space is 1000 days; the power of a jet flow of the electric propulsion is $1853.457$ kW; the specific impulse of electric propulsion is 4500 s to 7500 s; the electric propulsion thrust is 50.4N to 84N; the specific mass of the system of Xenon storage (ratio of the mass of fuel compartment to Xenon mass $a_{tank}$) is equal to 0.1.

Furthermore, article [31] showed that at considered characteristics of a space transport system, the optimal magnitude of a specific impulse is equal to 7000 s. At an efficiency of electric propulsion 0.6, the specific mass of electric power and propulsion systems should not exceed $14.6$ kg/kW. If the efficiency of electric propulsion is equal to 0.7, the specific mass of electric power and propulsion systems should not exceed $17.0$ kg/kW.

Thus, as mentioned above, this research uses a nuclear power engine with a constant thrust of about 60 and a specific impulse of about 6000 $\mathrm{s}$, which can generate a thrust acceleration of about $3 \times {10}^{-4}$ m/s² for a 200 tons spacecraft (the mass is estimated according to the analysis in Section 3).

Note that electric engines generally work at their rated power. The bang–bang control theory based on Pontryagin’s maximum principle is widely used in this type of small thrust trajectory design [54,55,56].

To solve optimal bang–bang control for low-thrust orbital transfers considering the first-order necessary optimality conditions derived from Lawden’s primer vector theory, Chen Zhang and Yu-Shan Zhao presented an original, hybrid switching detection technique [54]. T. Haberkorn et al. used a homotopic approach combined with the single shooting method (based on Pontryagin’s maximum principle), which transforms an optimal control problem by solving an equation of the shooting function associated with the original problem [55]. Zhengfan Zhu et al. developed a novel continuation technique [56] and successfully found fuel-optimal orbital transfers with variable mission parameters via an automated algorithm.

In this research, the low-thrust mission profile is calculated according to David Eagle’s work [57], which optimizes the steering angle with a fixed thrust. Figure 7 shows one of the optimal trajectories 2035–2050 based on the 60 N nuclear thruster in the heliocentric coordinate system. Figure 8 shows the corresponding steering angle function. The parameter information of the entire mission profile (Earth-to-Mars and Mars-to-Earth) is listed in Table 3. The spacecraft is only driven by low-thrust engines outside the influence sphere of central planets, so impulse maneuvers (provided by upper stage rockets or orbit transfer stages) are still used to escape from LEO/LMO ($3.17$ km/s for LEO and $1.45$ km/s for LMO).

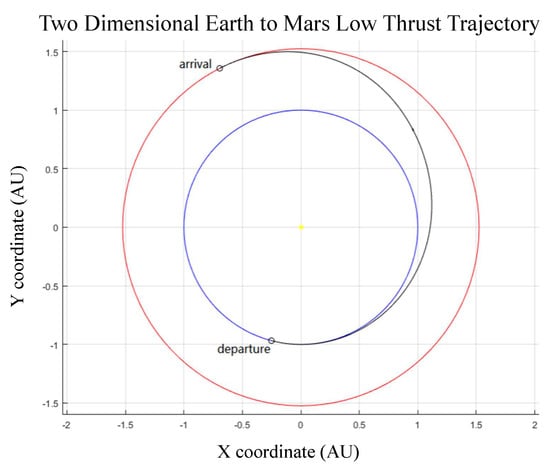
Figure 7. Heliocentric trajectories Earth to Mars (units in meters). This is one of the optimal mission profiles based on low-thrust orbital transfers using electric propulsion engines. The sun is at centre of the coordinate, the blue orbit is the Earth orbit, and the orange orbit is the Mars orbit. The black curve is the trajectory of the transfer.

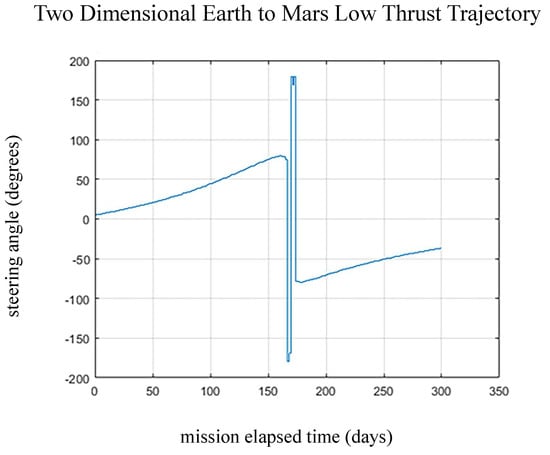
Figure 8. Steering angle (deg) for the mission profile in Figure 7. The horizontal axis is transfer time (in days).

Table 3. Parameters for one optimal mission profile for manned Mars mission using electric propulsion engines. Time of expedition: <1000 days. The launch window is 2035–2050.

	Transfer Duration	Start Time	End Time	Total $\mathsf{\Delta }\mathit{v}$ 1
Earth-to-Mars	300 days	7 June 2037	3 April 2038	6.1 km/s
Mars-to-Earth	300 days	11 August 2039	6 June 2040	9.4 km/s

¹ The total velocity increment is obtained by the propellant mass.

3. Spacecraft System Design

To reduce the mass of a single launch while ensuring the overall function of the spacecraft system, the modular spacecraft system design has been widely used in manned deep space exploration missions [58].

The spacecraft system in the manned Mars mission at least includes a manned module (command module) and a Mars lander. Extra propulsion modules, and sometimes an equipment module are also considered in the design of the mission.

B.D. Boden described a similar baseline spacecraft system including six modules for a manned Near Earth Objects (NEO) mission, but not considered a lander as NEOs always have a low-gravity environment [40]. A more complete spacecraft system for manned asteroid missions is concluded in the previous work [47] based on the modular spacecraft design method.

According to this method, spacecraft modules for manned Mars mission are then defined:

• The Crew Exploration Vehicle (CEV). It mainly consists of a Command Module (CM) and Habitation Module (HM). Sometimes, a Propulsion Module (PM) is also needed for orbit and attitude adjustment. The mass of CEV with a crew of four people is about 60 tons (full of supply).
• The Mars Lander (ML). This module may be similar to the Lander of Apollo, which contains a Descending Module (DM), and a separable Ascending Module (AM). Considering that the astronauts stay on the surface of Mars for a long time, a Long-term Mars Survival Cabin (MSC) is also necessary. The total mass of the Mars Lander is about 85 tons according to related research [31,32].
• The chemical propulsion modules, which are always referred to as Orbit Transfer Stages (OTS), can provide velocity increments for the manned module(s). One OTS usually has a dry mass ratio which is proportional to its fueled mass ($\eta =m_f/m_0$; $\eta$ is usually taken as 0.1). The most efficient specific impulse of OTS can reach about 440 s (liquid hydrogen–liquid oxygen engine, [24]).
• The Nuclear Thermal Propulsion (NTP) module is used to provide impulse maneuver. According to the data of solid core NFTP motor RD-0410 in [36], the dry mass of the engine (reaction part) is about 2 tons. The specific impulse of the NTP module is approximated as 900 s. The dry mass ratio $\eta$ is still $10\%$.
• The Nuclear Electric Propulsion (NEP) module is used to accelerate modules in the interplanetary journal. According to Leob’s research (Ion Thruster RFIT-45 with nuclear reactor), the dry mass of NEP is about 60 tons, and the specific impulse can reach about 6000 s [32].
• The Supply Module (SM). Due to the long mission duration to Mars, astronauts may need additional supplies to survive. The SM mainly carries food, water, air, and other essential supplies. It can be delivered to Mars separately in advance and docks with CEV when needed. Considering that the SM can provide replenishment for a long mission time after CEV reaches Mars, it can replace about 20t mass of CEV (i.e., a 60 tons CEV can be replaced by a 40 tons CEV together with a 20 tons SM).

The basic parameters of spacecraft modules are listed in Table 4.

Table 4. The basic parameters of all considered modules.

Modules	CEV	ML	OTS	NTP	NEP	SM
Dry mass (tons)	60	85	-	$2+x_{NTP}$1	60	20
Dry mass ratio	-	-	0.1	-	-
Specific impulse	-	-	440 s	900 s	6000 s	-

¹ The dry mass of NTP consists of the dry mass of nuclear engine (2 tons) and the propellant storage system (which can be estimated using dry mass ratio).

4. Mission Architectures Design and Mass Scale Analysis

This part will describe several mission architectures using chemical engines and NEP engines. The mission profiles (mainly transfer orbits and related delta-vs) in Section 2.1 and Section 2.2 are considered. For impulse maneuver engines (chemical engines and NTP engines), the launch date is 5 September 2037 (the second profile in Table 2, which has the smallest total velocity increment). For low-thrust (NEP) engines, the launch date is 7 June 2037.

There are four mission ‘nodes’ in a manned Mars mission including the Earth surface, the LEO, the LMO, and the Mars surface, thus dividing the manned Mars mission into seven successive mission ’phases’ (Figure 9). Therefore, the mission architectures are designed based on these four nodes and seven phases.

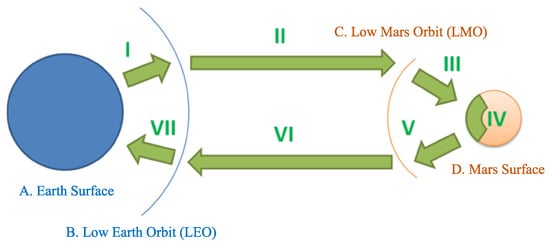
Figure 9. Four mission nodes and seven mission phases in manned Mars mission.

4.1. Architecture-1: The Basic Architecture

As described in Section 1.1, the basic profile for a manned Mars mission is a simple single process (similar to the Apollo mission), which contains launching from Earth, reaching LEO, accelerating twice to Mars ($\mathsf{\Delta }{v}_1+\mathsf{\Delta }{v}_2$), orbiting Mars on LMO, landing on Mars using ML, ML leaving Mars and back to LMO, accelerating from LEO to Earth and eventually re-entering the atmosphere. All spacecraft modules in this architecture are docked as one whole system at LEO and head to Mars together. The ML can be abandoned when returning from LMO to save propellant. The schematic of Architecture-1 is shown in Figure 10.

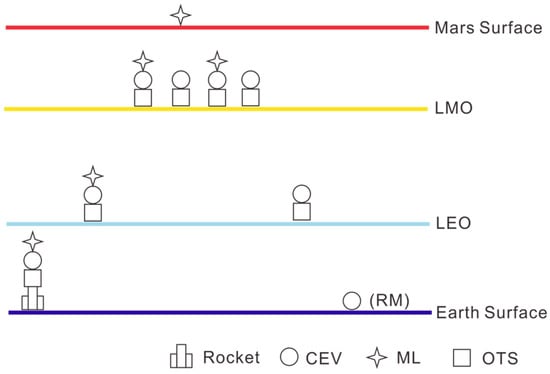
Figure 10. Schematic of Architecture-1.

According to the MAM calculation method in [47], the Mission Architecture Matrix can be listed according to the basic operation steps (BOS) of mission architecture and the corresponding parameters. Each BOS is used as a row vector in the MAM, and the elements of BOS are BOS number, RVD flag (rendezvous and docking flag; one represents yes, whereas zero represents no), the status value of each module (zero for not participating, one for participating but not providing velocity increment, and two for providing velocity increment), the number (IMV) of the module which provides velocity increment, and the velocity increment corresponding to this BOS. Table 5 shows the MAM corresponding to Architecture-1.

Table 5. Mission architecture matrix of Architecture-1.

(BOS)	No.	RVD 1	CEV	ML	OTS	IMV 1	$\mathsf{\Delta }\mathit{v}$ (m/s)
Launching to LEO	1	0	1	1	1	0	0
LEO accelerating (leaving) (dv1)	2	0	1	1	2	3	4011
Orbit Correction (OCC1) 2	3	0	1	1	2	3	302
LMO accelerating (reaching) (dv2)	4	0	1	1	2	3	2020
LMO stay	5	0	1	1	1	0	0
Landing/Launching on Mars	6	0	0	1	0	0	0
LMO docking 3	7	1	1	1	2	3	0.01
LMO accelerating (leaving) (dv3)	8	0	1	0	2	3	2334
Orbit Correction (OCC2)	9	0	1	0	2	3	117

¹ RVD: Rendezvous and docking flag; IMV: Number of the active module. ² OCC is considered about a 5% velocity increment of the entire transfer. ³ Orbit docking usually requires a 10 m/s velocity increment

Each BOS vector can be extended to an $N\times N$ state transition matrix (N is the number of modules), which is called the Basic Step Matrix (BSM). This matrix is used to connect the mass vectors (mass state of all modules) before and after BOS and generate them according to the following formula:

$$\mathbf{BSM}=I_{N\times N}-\mathbf{CMM}·\mathbf{FCM}$$

(12)

where $I_{N\times N}$ is the n th order identity matrix. CMM (carrying module matrix) is an $N\times N$ matrix, elements in the participating row (row number is the number of the module with the value of one or two in the BOS vector) in the active column (corresponding to the active module, the column number is IMV) is one, and the other elements are zero. FCM (fuel calculation matrix) is an $N\times N$ matrix, in which a diagonal element corresponds to the active module (both row and column numbers are IMV). The value is:

$${\mathbf{FCM}}_{IMV,IMV}=1-e^{-\frac{\mathsf{\Delta }v}{g{I}_{sp}}}$$

(13)

and the other elements are zero. In Formula (13), $\mathsf{\Delta }v$ is the velocity increment corresponding to this BOS, and $I_{sp}$ is the specific impulse corresponding to the active module. Take the second BOS of the MAM of Architecture-1 as an example, and its BSM is:

$$\begin{array}{cc}\hfill \mathbf{BSM}& =\left[\begin{array}{ccc}1& & \\ & 1& \\ & & 1\end{array}\right]-\left[\begin{array}{ccc}0& & 1\\ & 0& 1\\ & & 1\end{array}\right]·\left[\begin{array}{ccc}0& & \\ & 0& \\ & & 1-e^{-\frac{\mathsf{\Delta }v}{g{I}_{sp}}}\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{ccc}1& & \\ & 1& \\ & & 1\end{array}\right]-\left[\begin{array}{ccc}0& & 1-e^{-\frac{\mathsf{\Delta }v}{g{I}_{sp}}}\\ & 0& 1-e^{-\frac{\mathsf{\Delta }v}{g{I}_{sp}}}\\ & & 1-e^{-\frac{\mathsf{\Delta }v}{g{I}_{sp}}}\end{array}\right]=\left[\begin{array}{ccc}1& & e^{-\frac{\mathsf{\Delta }v}{g{I}_{sp}}}-1\\ & 1& e^{-\frac{\mathsf{\Delta }v}{g{I}_{sp}}}-1\\ & & e^{-\frac{\mathsf{\Delta }v}{g{I}_{sp}}}\end{array}\right]\hfill \end{array}$$

(14)

Then, for the initial mass vector $\left[m_1,m_2,m_3\right]$, there is:

$$\begin{array}{cc}\hfill \left[m_1^{{}^{\prime }},m_2^{{}^{\prime }},m_3^{{}^{\prime }}\right]& =\left[m_1,m_2,m_3\right]·\mathbf{BSM}=\left[m_1,m_2,m_3\right]·\left[\begin{array}{ccc}1& & e^{-\frac{\mathsf{\Delta }v}{g{I}_{sp}}}-1\\ & 1& e^{-\frac{\mathsf{\Delta }v}{g{I}_{sp}}}-1\\ & & e^{-\frac{\mathsf{\Delta }v}{g{I}_{sp}}}\end{array}\right]\hfill \\ \hfill & \hfill =\left[m_1,m_2,(m_1+m_2+m_3)·e^{-\frac{\mathsf{\Delta }v}{g{I}_{sp}}}-(m_1+m_2)\right]\hfill \end{array}$$

(15)

The final mass state exactly conforms to the Ziolkovsky formula.

Using the multiplicative property of matrix calculation, the Mass Transfer Matrix (MTM, which connects the initial and final mass status of the whole mission process) of Architecture-1, is:

$$\mathbf{MTM}=\prod _{i=1}^9{\mathbf{BSM}}_i=\left[\begin{array}{ccc}1& & -0.9\\ & 1& 0.4\\ & & 0.1\end{array}\right]$$

(16)

The mass of OTS can be then obtained:

$${\mathbf{M}}_f={\mathbf{M}}_0·\mathbf{MTM}$$

(17)

where

$${\mathbf{M}}_f=\left[m_{f\_CEV},m_{f\_ML},m_{f\_OTS}\right]=\left[60000,85000,m_{0\_OTS}\right]$$

(18)

$${\mathbf{M}}_0=\left[60000,85000,m_{0\_OTS}\right]$$

(19)

Formulas (16)∼(19) constitute matrix equations about $m_{0\_OTS}$. When the dry mass ratio $\eta$ is 0.1, the original mass of OTS is about 221 tons. Table 6 shows the mass scale of Architecture-1. Note, in Table 6, the minimum original mass has been bolded.

Table 6. Mass scale of Architecture-1.

Module	CEV	ML	OTS	Total	Max Mass
Original mass $m_0$ ($\mathrm{kg}$)	60,000	85,000	2,207,831	2,352,831	2,207,831
Final mass $m_f$ ($\mathrm{kg}$)	60,000	85,000	220,783	365,783	-

Obviously, Architecture-1 requires an LEO launch mass of up to 2200 tons, which is currently impossible for rockets. Therefore, mission architectures with more separate modules must be considered.

4.2. Architecture-2: Separate CEV and ML

Taking into account that ML only carries astronauts to perform landing operations after reaching Mars, CEV and ML can be launched to Mars separately as two parts, each carrying an OTS. This is described in Architecture-2. The schematic of Architecture-2 is shown in Figure 11. The mission architecture matrix of Architecture-2 is shown in Table 7.

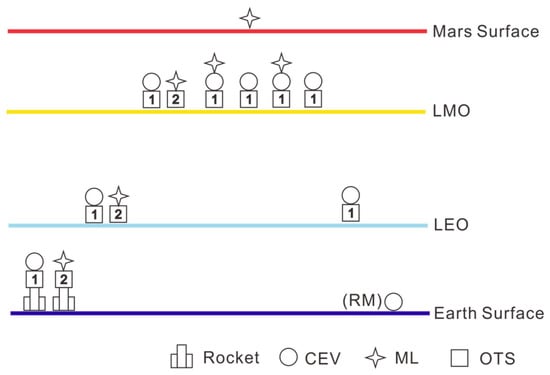
Figure 11. Schematic of Architecture-2.

Table 7. Mission architecture matrix of Architecture-2.

(BOS)	No.	RVD	CEV	ML	OTS1	OTS2	IMV	$\mathsf{\Delta }\mathit{v}$ (m/s)
LEO	1	0	1	1	1	1	0	0
dv1 (CEV)	2	0	1	0	2	0	3	4011
dv1 (ML)	3	0	0	1	0	2	4	4011
OCC1 (CEV)	4	0	1	0	2	0	3	302
OCC1 (ML)	5	0	0	1	0	2	4	302
dv2 (CEV)	6	0	1	0	2	0	3	2020
dv2 (ML)	7	0	0	1	0	2	4	2020
LMO stay	8	0	1	1	1	1	0	0.01
Landing	9	0	0	1	0	0	0	0
LMO docking	10	1	1	1	2	0	3	0.01
dv3	11	0	1	0	2	0	3	2334
OCC2	12	0	1	0	2	0	3	117

Similarly to Formulas (16)∼(19), the mass of OTS1 and OTS2 can be obtained via matrix calculation.

Table 8 shows the mass scale of Architecture-2. Also, in Table 8, the minimum original mass has been bolded.

Table 8. Mass scale of Architecture-2.

Module	CEV	ML	OTS1	OTS2	Total	Max Mass
$m_0$ ($\mathrm{kg}$)	60,000	85,000	1,715,989	502,438	2,363,427	1,715,989
$m_f$ ($\mathrm{kg}$)	60,000	85,000	171,599	50,244	366,843	-

Although the maximum LEO launch mass required by Architecture-2 is still as high as 1700 tons, it has been reduced by about 23% compared to the basic profile (Architecture-1). This shows that the separate orbit transfer of different modules is an effective way to reduce the maximum LEO launch mass.

4.3. Architecture-3: Additional SM and Additional OTS for Return

It is noticed that the module with the largest LEO mass in Architecture-2 comes from OTS1, the CEV propulsion module. As we mentioned in Section 3, a 20-ton SM can be used to reduce the mass of CEV. At the same time, an OTS used for return acceleration can also be transferred to Mars along with SM. In this way, OTS1 is only used to transfer 40 tons of CEV to LMO. This is the profile of Architecture-3, which includes three independent transfer systems (CEV+OTS1, ML+OTS2, SM+OTS3+OTS4).

The schematic of Architecture-3 is shown in Figure 12. The mission architecture matrix of Architecture-3 is shown in Table 9. Based on the matrix calculation, Table 10 shows the mass scale of Architecture-3, in which the minimum original mass has been bolded.

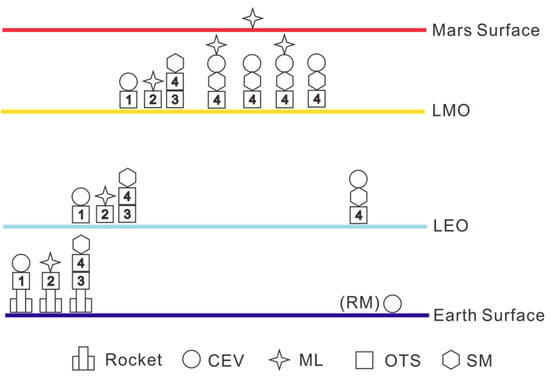
Figure 12. Schematic of Architecture-3.

Table 9. Mission architecture matrix of Architecture-3.

(BOS)	No.	RVD	CEV	ML	SM	OTS1	OTS2	OTS3	OTS4	IMV	$\mathsf{\Delta }\mathit{v}$ (m/s)
LEO	1	0	1	1	1	1	1	1	1	0	0
dv1 (CEV)	2	0	1	0	0	2	0	0	0	4	4011
dv1 (ML)	3	0	0	1	0	0	2	0	0	5	4011
dv1(SM)	4	0	0	0	1	0	0	2	1	6	4011
OCC1 (CEV)	5	0	1	0	0	2	0	0	0	4	302
OCC1 (ML)	6	0	0	1	0	0	2	0	0	5	302
OCC1 (SM)	7	0	0	0	1	0	0	2	1	6	302
dv2 (CEV)	8	0	1	0	0	2	0	0	0	4	2020
dv2 (ML)	9	0	0	1	0	0	2	0	0	5	2020
dv2 (SM)	10	0	0	0	1	0	0	2	1	6	2020
LMO stay	11	0	1	1	1	1	1	1	1	0	0
Landing	12	0	0	1	0	0	0	0	0	0	0
LMO docking	13	1	1	1	1	0	0	0	2	7	0.01
dv3	14	0	1	0	1	0	0	0	2	7	2334
OCC2	15	0	1	0	1	0	0	0	2	7	117

Table 10. Mass scale of Architecture-3.

Module	${\mathit{m}}_0$ kg	${\mathit{m}}_{\mathit{f}}$ (kg)	Module	${\mathit{m}}_0$ kg	${\mathit{m}}_{\mathit{f}}$ (kg)
CEV	40,000	40,000	OTS3	530,409	53,041
ML	85,000	85,000	OTS4	69,732	6973
SM	20,000	20,000	Total	1,484,021	278,902
OTS1	236,442	23,644	Max mass	530,409	-
OTS2	502,438	50,244

The use of an additional supply module and returning propulsion module (OTS4) further reduced the maximum launch mass of LEO to 530 tons. At this time, the module with the largest launch mass is OTS2, which transports ML to Mars, while the LEO launch mass of OTS3, which carries the supply module and returning propulsion module, is also larger. We will further reduce the mass of these modules in Architecture-4.

4.4. Architecture-4: Two-Stage OTS for Earth to Mars Transfer

In fact, the main reason for the large mass of the transfer OTS is the large velocity increment required in the Earth-to-Mars transfer. Considering that there are mainly two impulse maneuvers in this process, a two-level OTS system can be used to complete two impulse maneuvers (dv1 and dv2), respectively. The first OTS can be discarded after the first pulse is completed, and the subsequent OCC and the second pulse are completed by the second OTS. Considering the two-level OTS method, Architecture-4 is obtained, which is shown in Figure 13, Table 11 and Table 12. In Table 12, the minimum original mass has been bolded.

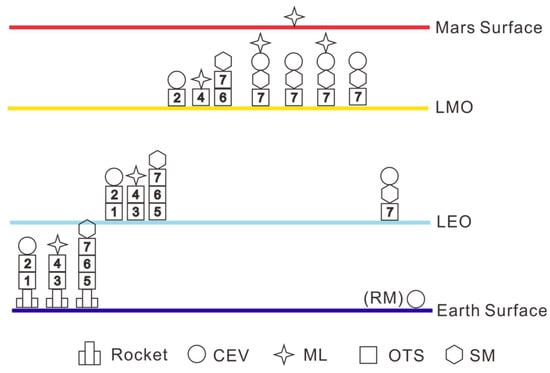
Figure 13. Schematic of Architecture-4.

Table 11. Mission architecture matrix of Architecture-4.

(BOS)	No.	RVD	CEV	ML	SM	OTS1	OTS2	OTS3	OTS4	OTS5	OTS6	OTS7	IMV	$\mathsf{\Delta }\mathit{v}$ (m/s)
LEO	1	0	1	1	1	1	1	1	1	1	1	1	0	0
dv1 (CEV)	2	0	1	0	0	2	1	0	0	0	0	0	4	4011
dv1 (ML)	3	0	0	1	0	0	0	2	1	0	0	0	6	4011
dv1(SM)	4	0	0	0	1	0	0	0	0	2	1	1	8	4011
OCC1 (CEV)	5	0	1	0	0	0	2	0	0	0	0	0	5	302
OCC1 (ML)	6	0	0	1	0	0	0	0	2	0	0	0	7	302
OCC1 (SM)	7	0	0	0	1	0	0	2	1	0	2	1	9	302
dv2 (CEV)	8	0	1	0	0	0	2	0	0	0	0	0	5	2020
dv2 (ML)	9	0	0	1	0	0	0	0	2	0	0	0	7	2020
dv2 (SM)	10	0	0	0	1	0	0	0	0	0	2	1	9	2020
LMO stay	11	0	1	1	1	0	1	0	1	0	1	1	0	0
Landing	12	0	0	1	0	0	0	0	0	0	0	0	0	0
LMO docking	13	1	1	1	1	0	0	0	0	0	0	2	10	0.01
dv3	14	0	1	0	1	0	0	0	0	0	0	2	10	2334
OCC2	15	0	1	0	1	0	0	0	0	0	0	2	10	117

Table 12. Mass scale of Architecture-4.

Module	${\mathit{m}}_0$ (kg)	${\mathit{m}}_{\mathit{f}}$ (kg)	Module	${\mathit{m}}_0$ (kg)	${\mathit{m}}_{\mathit{f}}$ (kg)
CEV	40,000	40,000	OTS4	73,181	7318
ML	85,000	85,000	OTS5	289,960	28,996
SM	20,000	20,000	OTS6	65,238	6524
OTS1	153,064	15,306	OTS7	55,774	5577
OTS2	34,438	3444	Total	1,141,917	244,692
OTS3	325,261	32,526	Max mass	325,261	-

In the case of a two-stage OTS design (one OTS for a single pulse), Architecture-4 is the profile with the lowest LEO mass requirement using chemical engines. At this time, we still need to launch an OTS weighing 325 tons to LEO, which is somewhat difficult with the current launch vehicle technology. The LEO carrying capacity of the Saturn V rocket with the largest thrust in human history is only about 140 tons. Therefore, it is necessary to use nuclear propulsion technology to send modules to Mars.

4.5. Architecture-5 8: Replace OTS with NTP Modules

According to the analysis in Section 3, NTP modules can actually be used in manned missions as OTS modules with higher specific impulses. Therefore, after replacing OTS in Architecture-1–4 with NTP without changing the basic architecture of the mission, the system mass scale can be significantly reduced. It is worth noting that the initial and final mass of one NTP module needs to meet:

$$m_{NTP,f}=2000 \mathrm{k}\mathrm{g}+\eta ·(m_{NTP,0}-m_{NTP,f})$$

(20)

where $m_{NTP,f}$ is the final mass, $m_{NTP,0}$ is the initial mass, $\eta$ is the dry mass ratio of the NTP propellant system. 2000 kg is the dry weight of the nuclear engine.

Therefore, the mass scale of Architecture-5–8 corresponding to Architecture-1–4 is shown in Table 13, Table 14, Table 15 and Table 16. Note, in Table 13, Table 14, Table 15 and Table 16, each minimum original mass has been bolded.

Table 13. Mass scale of Architecture-5.

Module	CEV	ML	NTP	Total	Max Mass
Original mass $m_0$ ($\mathrm{kg}$)	60,000	85,000	250,788	393,788	250,788
Final mass $m_f$ ($\mathrm{kg}$)	60,000	85,000	26,879	171,879	-

Table 14. Mass scale of Architecture-6.

Module	CEV	ML	NTP1	NTP2	Total	Max Mass
$m_0$ ($\mathrm{kg}$)	60,000	85,000	147,139	116,953	409,092	147,139
$m_f$ ($\mathrm{kg}$)	60,000	85,000	16,514	13,495	175,009	-

Table 15. Mass scale of Architecture-7.

Module	${\mathit{m}}_0$ (kg)	${\mathit{m}}_{\mathit{f}}$ (kg)	Module	${\mathit{m}}_0$ (kg)	${\mathit{m}}_{\mathit{f}}$ (kg)
CEV	40,000	40,000	NTP3	69,681	8768
ML	85,000	85,000	NTP4	31,223	4922
SM	20,000	20,000	Total	422,995	179,999
NTP1	60,137	7814	Max mass	116,953	-
NTP2	116,953	13,495

Table 16. Mass scale of Architecture-8.

Module	${\mathit{m}}_0$ (kg)	${\mathit{m}}_{\mathit{f}}$ (kg)	Module	${\mathit{m}}_0$ (kg)	${\mathit{m}}_{\mathit{f}}$ (kg)
CEV	40,000	40,000	NEP4	63,108	6311
ML	85,000	85,000	NTP5	49,695	6770
SM	20,000	20,000	NTP6	19,946	3795
NTP1	42,486	6049	NTP7	27,835	4584
NTP2	17,234	3523	Total	418,905	184,990
NTP3	83,893	10,189	Max mass	85,000	-

After using NTP instead of OTS, the overall mass scale of the mission decreased significantly. When the mission architecture similar to Architecture-4 is adopted (Figure 13, Table 11), the maximum LEO launch mass is reduced to 85 tons (the Mars Lander), which is expected to be realized in the next few decades.

4.6. Architecture-9: The Basic Architecture Using NTP + NEP

Although the maximum LEO launch mass can be reduced to about 84 tons by using NTP technology, there are still technical difficulties in such a heavy single LEO launch. In addition, the overall mass scale of the mission is still high, which will result in high costs. In fact, the simultaneous use of NTP and NEP technology can further reduce the mass scale and the cost of the mission [33].

According to the research of Konstantinov, the NEP module can be used on the manned Martian spacecraft, which is designed as a whole system. This profile is equivalent to replacing OTS in Architecture-1 with a NEP module. The high specific impulse characteristic of NEP will greatly reduce fuel consumption. In addition, the velocity increment of each transfer will be calculated according to the thrust impulse integral during the transfer. NTP modules mainly provide impulse maneuvers to escape or enter LEO/LMO (Section 2.2). Using this method, the profile of Architecture-9 uses both NTP and NEP is shown in Figure 14 and Table 17.

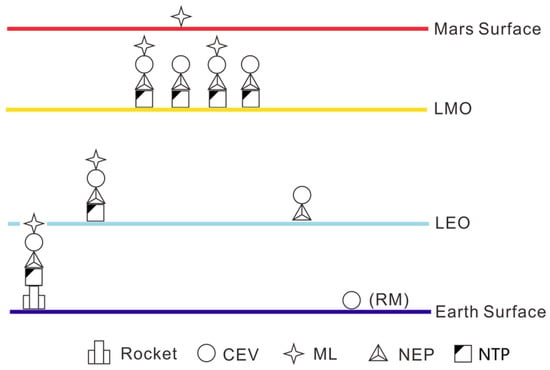
Figure 14. Schematic of Architecture-9.

Table 17. Mission architecture matrix of Architecture-9.

(BOS)	No.	RVD	CEV	ML	NEP	NTP	IMV	$\mathsf{\Delta }\mathit{v}$ (m/s)
Launching to LEO	1	0	1	1	1	1	0	0
LEO escape	2	0	1	1	1	2	4	3175
LEO-LMO transfer	3	0	1	1	2	1	3	6050
LMO entry	4	0	1	1	1	2	4	1449
LMO stay	5	0	1	1	1	1	0	0
Landing	6	0	0	1	0	0	0	0
LMO docking	7	1	1	1	2	1	3	0.01
LMO escape	8	0	1	0	1	2	4	1449
LMO-Earth transfer	9	0	1	0	2	1	3	5491

Considering that the dry mass of the NEP module is about 60 tons and its specific impulse is 6000 s, the relationship between the initial mass of NEP and its fuel mass (mp) is

$$m_{0\_NEP}-m_{p\_NEP}=m_{f\_NEP}=60tons$$

(21)

Using Formulas (20) and (21), the mass scale can be obtained in Table 18 (similarly, in Table 18, the minimum original mass has been bolded):

Table 18. Mass scale of Architecture-9.

Module	CEV	ML	NEP	NTP	Total	Max Mass
$m_0$ ($\mathrm{kg}$)	60,000	85,000	166,648	261,983	573,631	261,983
$m_f$ ($\mathrm{kg}$)	60,000	85,000	60,000	26,198	231,198	-

In Architecture-9, a 165-ton NEP module and a 262-ton NTP module are needed for the entire spacecraft system to complete the Mars exploration journey. Although it is still difficult to send such heavy modules to LEO, inspired by Architecture-4, we can send different module combinations to Mars separately.

4.7. Architecture-10: Separate Transfer Using NTP and NEP

Although NEP and NTP technologies have been applied in Architecture-9, the maximum single LEO launch mass is still difficult to achieve. Therefore, similar to the profile in Architecture-4/8, three module combinations can be transferred, respectively. It is noted that the only propulsion module that exceeds 50 tons in Architecture-8 is NTP-3, which sends ML to Mars. Therefore, we consider replacing it with NEP. Considering that ML can be launched to LMO for standby in advance, the launch time of the ML part can be advanced, and NEP can be used for LEO escape and LMO entry, which may take a long time due to its low thrust [31].

For the manned part (CEV), two orbital maneuvers at the time of Earth departure and Mars arrival are realized by using two NTP modules (NTP-1, NTP-2). For the supply part (SM+supply NTP for Mars-to-Earth transfer), two NTP modules are also used (NTP-3, NTP-4). For the LM part, it can gradually escape LEO or enter LMO through long-term orbit maneuver using NEP, and the interplanetary transfer is also conducted by the NEP module. The profile of Architecture-10 is shown in Figure 15 and Table 19.

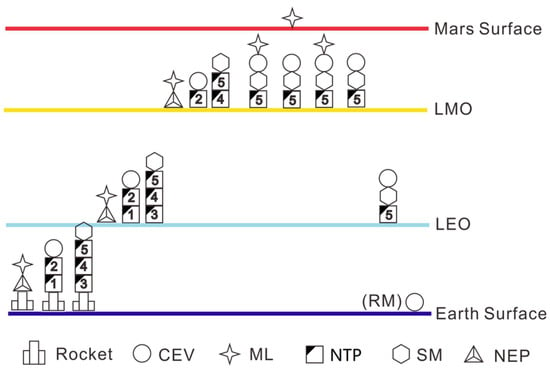
Figure 15. Schematic of Architecture-10.

Table 19. Mission architecture matrix of Architecture-10.

(BOS)	No.	RVD	CEV	ML	SM	NEP	NTP1	NTP2	NTP3	NTP4	NTP5	IMV	$\mathsf{\Delta }\mathit{v}$ (m/s)
LEO Launch	1	0	1	1	1	1	1	1	1	1	1	0	0
LEO escape (M)	2	0	0	1	0	2	0	0	0	0	0	4	3175
E-to-M (M)	3	0	0	1	0	2	0	0	0	0	0	4	6050
LMO entry (M)	4	0	0	1	0	2	0	0	0	0	0	4	1449
dv1 (C)	5	0	1	0	0	0	2	1	0	0	0	5	4011
OCC1 (C)	6	0	1	0	0	0	0	2	0	0	0	6	302
dv2 (C)	7	0	1	0	0	0	0	2	0	0	0	6	2020
dv1 (S)	8	0	1	0	0	0	0	0	2	1	1	7	4011
OCC1 (S)	9	0	1	0	0	0	0	0	0	2	1	8	302
dv2 (S)	10	0	1	0	0	0	0	0	0	2	1	8	2020
LMO stay	11	0	1	1	1	1	0	1	0	1	1	0	0
Landing	12	0	0	1	0	0	0	0	0	0	0	0	0
LMO docking	13	1	1	1	1	1	0	0	0	0	2	9	0.01
dv3 (C)	14	0	1	0	1	0	0	0	0	0	2	9	2334
OCC2 (C)	15	0	1	0	1	0	0	0	0	0	2	9	117

According to the MAM of this architecture, the mass scale of each module can be obtained (Table 20, in which the minimum original mass has been bolded):

Table 20. Mass scale of Architecture-10.

Module	${\mathit{m}}_0$ (kg)	${\mathit{m}}_{\mathit{f}}$ (kg)	Module	${\mathit{m}}_0$ (kg)	${\mathit{m}}_{\mathit{f}}$ (kg)
CEV	40,000	40,000	NTP3	49,695	6770
ML	85,000	85,000	NTP4	19,946	3795
SM	20,000	20,000	NTP5	27,835	4584
NEP	83,631	60,000	Total	385,827	229,721
NTP1	42,486	6049	Max mass	85,000	-
NTP2	17,234	3523

Compared with Architecture-8, which only uses NTP, the maximum LEO launch mass in the entire mission is still 85 tons (the Mars Lander), while the total LEO mass scale of Architecture-10 is about 8% lower than Architecture-8. On the other hand, Architecture-10 using NEP for low thrust transfer may require a more complex control system.

4.8. Total Cost

According to Aerospace Security’s statistics [59], considering the current rocket technology, the cost of a space launch to LEO is approximately USD 15,500 per 1 kg. As for spacecraft and launch vehicle system development and manufacturing, after comparing and analyzing the budgets of various programs, including the Artemis program, we estimate the cost to be approximately USD 500 million.

Hence, based on the above, the total cost of 10 mission architectures in Section 4.1, Section 4.2, Section 4.3, Section 4.4, Section 4.5, Section 4.6 and Section 4.7 can be calculated, as Figure 16 shows.

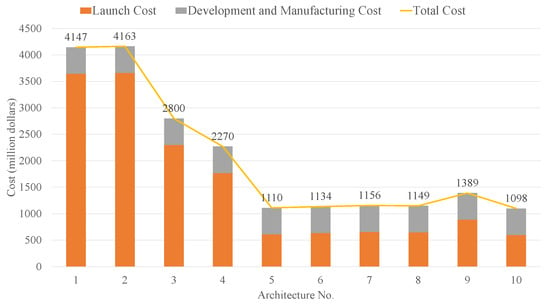
Figure 16. Total cost of 10 different architecture.

As can be seen from Figure 16, the total cost of 10 architectures approximately ranges from USD 1.1 billion to USD 4.2 billion. Among them, Architecture-10 enjoys the minimum total cost of USD 1.1 billion due to its low mass scale.

4.9. Summarize

We analyzed and calculated the mass scale of 10 mission architectures in Section 4.1, Section 4.2, Section 4.3, Section 4.4, Section 4.5, Section 4.6 and Section 4.7. The total mass scale and maximum LEO launch mass of 10 architectures are shown in Figure 17 and Figure 18.

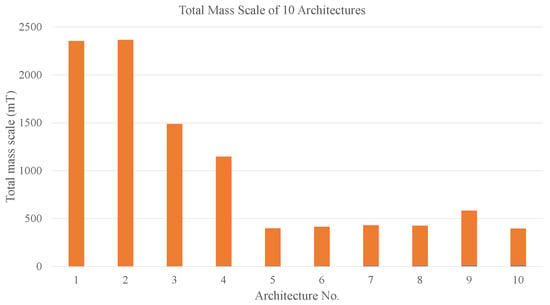
Figure 17. Total mass scale of 10 different architecture.

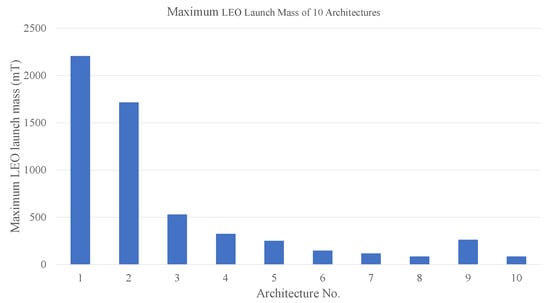
Figure 18. Maximum LEO launch mass of 10 different architecture.

As we can see from Figure 17 and Figure 18, the total mass scale of 10 architectures approximately ranges from 385 tons to 237 tons, while the maximum LEO launch mass ranges from 85 tons to about 2200 tons. Among them, the total mass scale of Architecture-10 is minimal, at around 385 tons, and the maximum LEO launch mass of Architecture-8 as well as Architecture-10 is minimal at 85 tons.

It is not difficult to find that the total mass scale and the maximum LEO launch mass of Architecture-1 and Architecture-2 are both excessively large and far beyond the other architectures due to their excessively low number of launches and modules. When using additional modules such as SM and OTS to reduce the transfer mass of every OTS, there exists a visible reduction in the mass scale, and the maximum LEO launch mass has dropped to 500 tons or below. Since the transfer mass of OTS is reduced, the required fuel mass is correspondingly reduced, resulting in an overall reduction in mission mass scale.

With the use of NTP and NEP, attributed to their higher specific impulse, the fuel mass required for the architecture is significantly reduced while the payload remains the same, greatly decreasing the total mass scale of Architecture-5–10 to less than 500 tons, except for Architecture-9 because of its Apollo style (a single launch and no additional module such as SM). As for the maximum LEO launch mass, the situation is similar.

Generally, the results show that the combined use of nuclear propulsion, the modular launch and separate transfer can greatly reduce the fuel mass required by the mission, to reduce the mass scale of the mission, as well as the maximum LEO launch mass.

Undoubtedly, the maximum LEO launch mass is a rather important evaluation factor for manned Mars mission architectures, as it involves the requirements for the carrying capacity of the launch vehicles. We can obtain the LEO carrying capacity (unit: $\mathrm{tons}$) of some large and heavy-lift launch vehicles (Figure 19) [60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76].

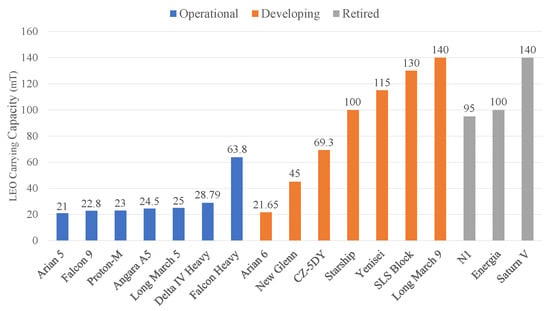
Figure 19. Current LEO carrying capacity of large and heavy-lift launch vehicles.

Let us take three heavy-lift launch vehicles under development, including Starship, SLS Block along with Long March 9, and compare their LEO carrying capacity to the maximum LEO launch mass of 10 architectures, as Figure 20 shows.

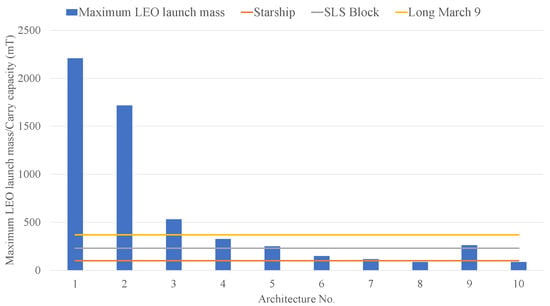
Figure 20. Comparison of the maximum LEO launch mass of 10 architectures with the LEO carrying capacity of selected launch vehicles.

After comparison, it can be found that with the exception of Architecture-8 and Architecture-10, the maximum LEO launch mass of nearly all architectures exceeds the LEO carrying capacity of Starship. The SLS Block is slightly better, and can meet the requirements of Architecture-6, 7, 8 and 10. Long March 9 can meet the launch quality requirements of other architectures except Architecture-1, 2, 3.

Note that although NTP and NEP both have a significant advantage in efficiency over traditional chemical rocket technologies, the nuclear reactors in NTP and NEP are more complex and have higher individual costs.

Moreover, as emerging aerospace propulsion systems undergo development, the reliability of NTP and NEP is relatively insufficient. As of today, no nuclear propulsion system has been officially put into service.

As the number of launches and the number of modules (especially for nuclear modules) increases, the complexity of an architecture increases, which in turn reduces the reliability of the architecture.

Clearly, a coordinated trade-off between cost and reliability is necessary.

According to the maximum LEO launch mass constraint (<100 tons), the total cost and the launch vehicle capacity limitations, two feasible architectures are selected, namely Architecture-8 and Architecture-10. Considering the technical maturity and control complexity, Architecture-8 is the best choice. Figure 21 shows the detailed mission profile of Architecture-8.

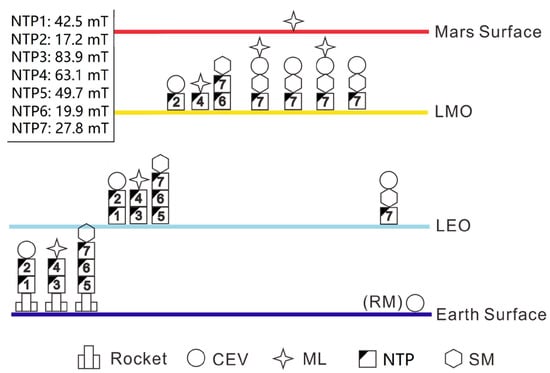
Figure 21. Mission profile of Architecture-8.

5. A Feasible Mission Profile

After considering modular launch, separate transfer, and use of NTP/NEP modules, we have obtained a feasible mission architecture (Architecture-8) in Section 4.9 (Figure 21, Table 16). This mission architecture includes 10 modules (CEV, ML, SM, and 7 NTP modules), with a total LEO launch mass of 419 tons and a maximum LEO launch mass of 85 tons (for ML). In order to reduce the number of ground launches as much as possible, the launches are planned in Table 21 according to the mass scale estimated in Table 16, where the maximum launch mass cannot exceed 100 tons.

Table 21. LEO Launch schedule.

LEO Launch No.	Module (s)	LEO Capacity Requirement (tons)
1	ML	85.0
2	NTP3	83.9
3	NTP1 + NTP2	59.7
4	NTP4	63.1
5	NTP5 + NTP6	69.6
6	NTP7 + SM	47.8
Total	All modules	418.9

According to Table 21 and Section 4.8, it can be estimated that the total cost of a manned Mars mission is about USD 1149 million.

Combined with the analysis of the launch window in Section 2.1.2, Table 22 shows a detailed flow-chart of the mission profile for manned Mars exploration.

Table 22. Detailed process of manned Mars exploration mission.

Time	Event
Before 5 September 2037	All modules are launched to LEO and docked as 3 transfer combinations.
5 September 2037	3 combinations start Earth-to-Mars transfer, and NTP-1, 3, and 5 are abandoned after the first maneuver.
21 April 2038	3 combinations arrive at LMO, and NTP-2, 4, and 6 are abandoned after the second maneuver. All modules start preparations for Mars landing.
21 April 2038–18 July 2039	CEV, ML, SM, and NTP-7 are docked together. The astronauts enter ML and then land on Mars, while the combination of CEV+SM+NTP-7 stays at LMO. After the landing mission, the astronauts go back to LMO using the upper stage and docking with CEV. Finally, the crew enters CEV and the upper stage is abandoned.
18 July 2039	The combination of CEV+SM+NTP-7 starts Mars-to-Earth transfer.
15 May 2040	The combination of CEV+SM+NTP-7 arrives at Earth. The astronauts enter the return cabin of CEV, re-enter the atmosphere and return to the ground.
Total mission time	983 days

6. Conclusions and Discussion

Using the modular design of the spacecraft system and the NTP/NEP technology, manned Mars exploration missions are expected to be realized in the near future. This paper uses the MAM method to analyze the mass scale of several multiple-mission architectures. Finally, the mission architecture using the NTP (Nuclear Thermal Propulsion) engines and the modular transfer method was determined (Figure 21). The Crew Exploration Vehicle, the Mars Lander, and the supply combination (the Supply Module and the supply NTP stage) is sent to Mars separately using two-stage NTP modules. All modules dock on the LMO, and then the Mars landing mission is executed. The return spacecraft system (the Crew Exploration Vehicle and the Supply module) finally flies back to Earth using the supply NTP stage.

The total LEO mass scale of the optimal architecture is about 419 tons, and its maximum LEO launch mass is only about 85 tons, which can be achieved by multiple launches by heavy launch vehicles. The total launch cost is about USD 1149 million.

According to this mission architecture, we designed a specific manned mission flow-chart to Mars. The three module combinations will be sent from LEO into the Earth–Mars transfer orbit on 5 September 2037, separately. The crew will stay on Mars from 21 April 2038, to 18 July 2039, and will return to Earth on 15 May 2040. The total mission duration is 983 days.

Throughout this paper, it is reasonable to assume that, compared with traditional research methods, the Mission Architecture Matrix method has the advantages of high efficiency and accuracy of calculation and analysis, conciseness, and strong flexibility. The method can be applied not only to the analysis of manned Mars missions, but also to the analysis of other space missions, including complex deep space exploration.

As seen in Section 4, the use of nuclear propulsion technology is a good option for manned deep space exploration missions with large mass scale and large velocity increments.

Of course, it must be acknowledged that nuclear propulsion technology is still immature. At present, as far as international research is concerned, there is more research on NEP technology, and NASA and Russia and so on have made progress. Regarding NTP, although related research has long been conducted to design and analyze a series of nuclear thermal propulsion engines, ranging from the solid reactor up to the gas core reactor, there still exist numerous problems and challenges to be solved. All early applications for NTP used fission processes; only in the last decade has there been a shift to fusion approaches.

As emerging aerospace propulsion systems undergo development, nuclear propulsion technology (especially for NTP) faces some risks, such as complex nuclear reactors, the dispersal of radioactive material into the environment resulting from an atmospheric or orbital rocket failure, the impact of cosmic ray particles on nuclear energy engines, and so forth, which needs further research in the future. We can believe that with the solution to these problems, nuclear propulsion technology will propel mankind into the vast universe.