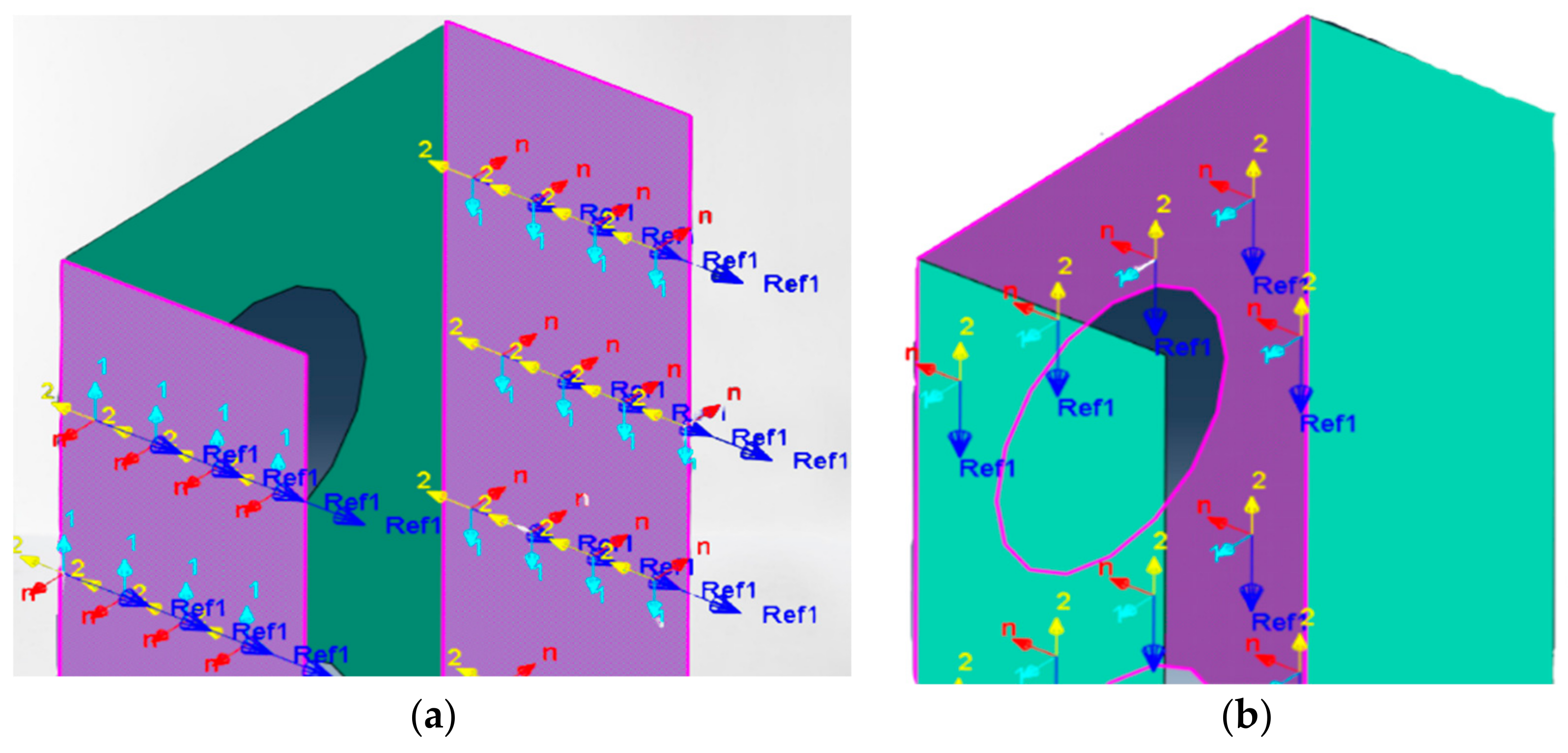
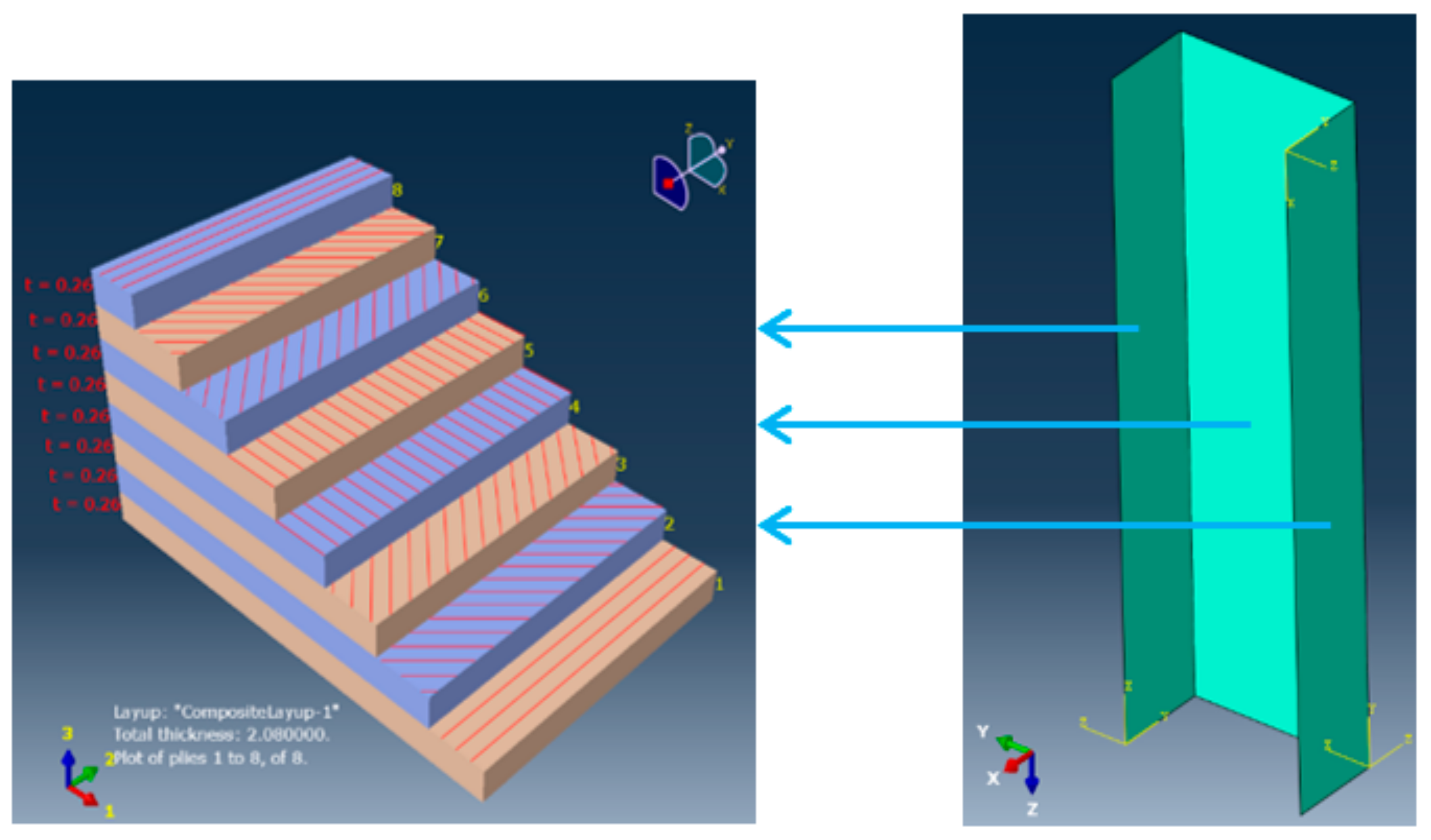
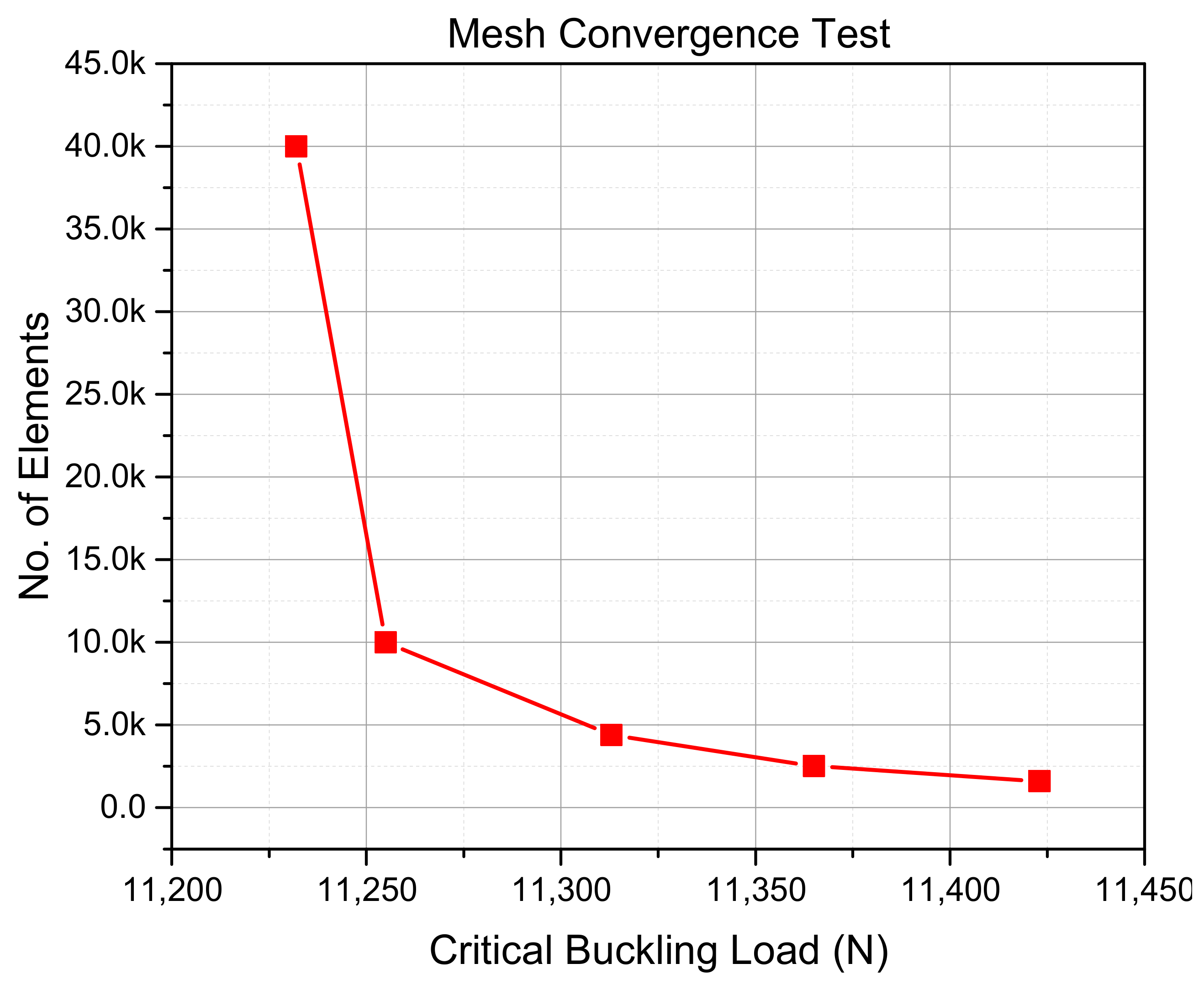
1. Introduction
Thin-walled structures are applicable for different engineering applications, such as in aerospace, automotive and construction industries, and they have played an important role in reducing the total weight of structures. One of the systems with the most efficient use of materials to prevent buckling is the thin-walled member because it is made up of several thin-walled parts. The thin-walled portion can easily be formed into various shapes with a high shape factor while using less material. However, the thin-walled member has significant disadvantages associated with its formed plates, such as local buckling. The composite plates of the member usually buckle before collapse when a thin-walled column is subjected to compressive loading [
1]. Various shapes of the thin-walled structure can be used to suit its application in the mentioned industries. For example, some studies have shown T-shaped thin-walled structures considering various geometries, which are used in aircraft as ribs [
2,
3,
4,
5]. Furthermore, Rozylo and Debski [
6] experimented on the Z shape of the thin-walled composite structure and showed the enhancement in improving the structural performance of the whole model.
Generally, buckling is a typical phenomenon in thin-walled structures. It is a term that refers to a component’s lack of stability caused by the lateral deflection on a member when an axial force is applied. The weakness of the column causes it to bend. This mode of failure is rapid and, therefore, risky. The length, strength, and other variables of a column determine whether or not it will buckle. Elastic buckling can occur in long columns relative to their thickness [
7]. It can also occur when an applied compressive load exceeds the critical allowable load of the thin-walled structure. Pre-buckling, critical buckling, and post-buckling are the three major states that describe a standard thin-walled composite structure. Buckling and carrying capacity determine the proper loading process of the structure. The structure can still function even after buckling because the post-critical equilibrium trend is stable, and the increasing compressive load increases the wall deflection [
8,
9].
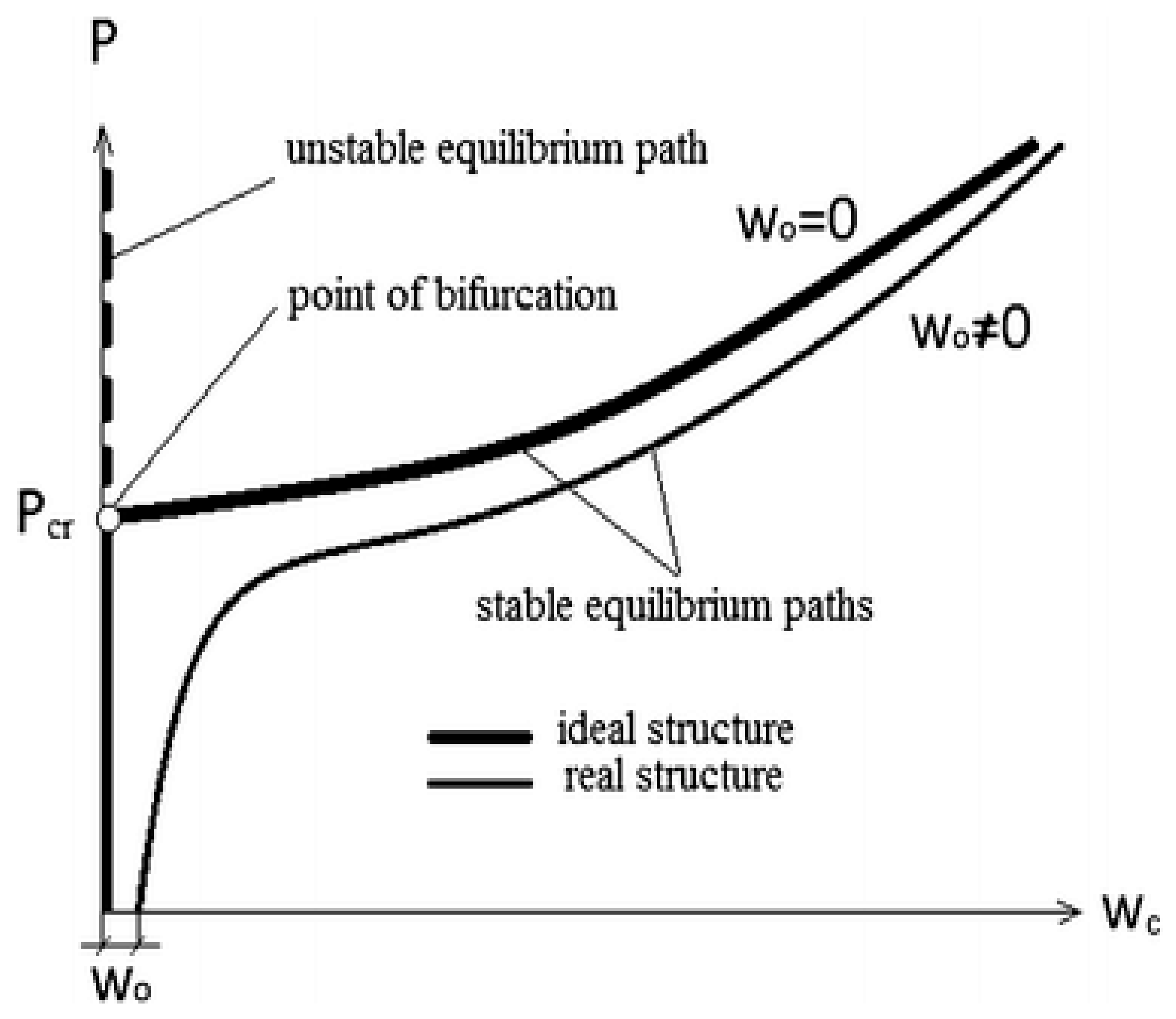
Figure 1 below shows the state of each operation for a thin-walled structure.
Figure 1.
Graph of load applied versus deflection [
9]. Reprinted under the Creative Commons (CC) License (CC BY 4.0).
Figure 1.
Graph of load applied versus deflection [
9]. Reprinted under the Creative Commons (CC) License (CC BY 4.0).
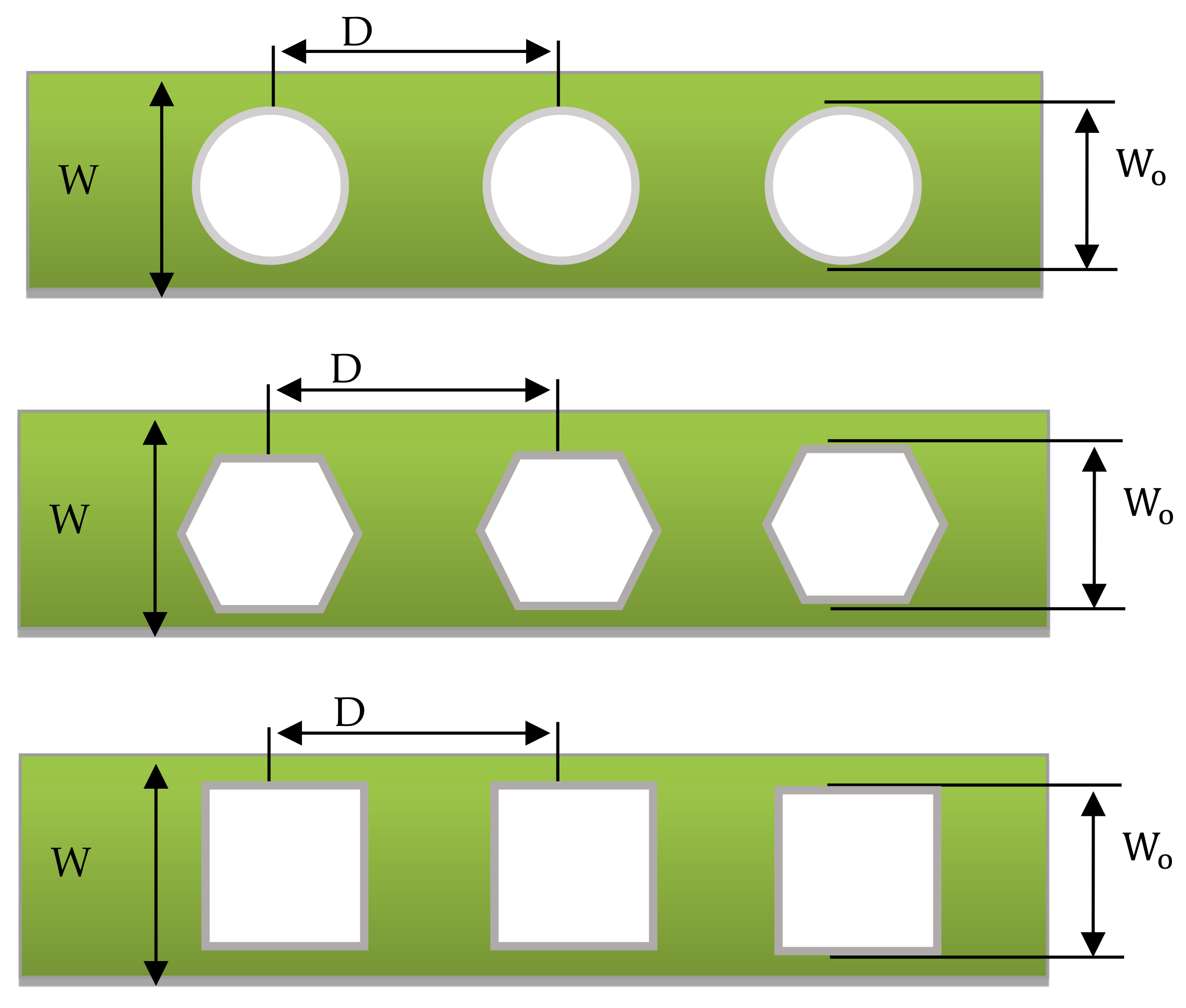
Damaged/holed thin-walled structures have become more prominent in recent investigations, and the reason for failure of the whole structure has been found. Composite materials are widely used in the aerospace and automotive industries due to their advantages, such as their lightweight nature and high strength ratio as compared to other types of materials. In recent investigations, composite materials have been utilized in a wide range of applications in response to the growing need for lightweight and efficient structures. Therefore, it is necessary to investigate the influence of the various sizes, shapes, and distances between cutouts of thin-walled composite structures on buckling and other behaviours. This study continued from the study conducted by Khazaal et al. [
10], in which the authors used aluminium alloys as the subject of the experiment. Three types of shapes, circular, hexagon, and rectangular, were chosen to optimize the results. They also studied the parameter that contributes most to the buckling behaviour of the aluminium alloy thin-walled structure.
The FE method was used to explore the stability properties of folded structures and analysed the buckling behaviour under a compression load, shear load, and combinations of both loads with varied boundary conditions. As a result, critical buckling loads for open- and closed-box structures with varying loading conditions were investigated [
11]. It has been stated that the newly proposed transverse extension modes have a practical advantage in that the increased artificial stiffness that results from constrained assessments of pure global and distortional deformations can be offset by taking into account the appropriate new transverse extension modes in thin-walled structures [
12]. For axial–flexural buckling, post-buckling, and geometrically nonlinear studies of thin-walled beams, an effective one-dimensional FE method using a novel structural concept known as equivalent layered composite cross-sectional modelling was proposed, in which nonclassical factors such as transverse shear and normal flexibilities are included in the formulation [
13]. A brand-new beam-type FE method has been developed that may be used for web distortion and elastic buckling analysis of thin-walled beams. Under the premise that there are no pre-buckling deformations, the buckling formulation was created based on nonlinear equilibrium equations [
14].
The load-bearing capability and involvement of stress components in the failure analysis of top-hat-shaped composite columns exposed to uniform compression and utilized a digital image correlation (DIC) technique to see the full-field displacements and strains, and failure tests were conducted across the whole load range [
15]. For the geometrically nonlinear analysis of thin-walled circular pipes, the formulation of generalized beam theory was used, and the complete geometrically nonlinear analysis was added to the existing generalized beam theory analysis of circular pipes, which is currently confined to buckling analysis [
16]. A new technique called the finite strip–Riccati transfer matrix method was established for buckling analysis of thin-walled components with a tree-branched cross-section. The procedure combines the semi-analytical finite strip approach with the Riccati transfer matrix method for a tree multi-body system [
17]. To calculate the changes in beam stiffness due to the decrease in thickness in the pre- and post-buckling stages, a nonlinear FE model of a thin-walled beam with variable thickness was introduced. The gauge sensitivity of the beam was then calculated using these stiffness values, and it changed as the beam thickness changed [
18]. Residual stresses in thin-walled structures manufactured by the directed energy deposition method were determined; additionally, in situ measurements, fast thermo-mechanical simulation, and buckling were investigated through the experimental and numerical approach [
19]. Buckling analysis of thin-walled metal liners of cylindrical composite overwrapped pressure vessels with depressions after autofrettage processing was investigated through the FE approach [
20]. Similarly, large deflection and post-buckling of thin-walled structures by finite elements with node-dependent kinematics [
21] were investigated.
Sudhirsastry et al. [
22] stated that composite materials have been widely used in the automotive and aircraft industries for plates and shells due to their high strength-to-weight ratio and stiffness-to-weight ratio. Due to the widespread usage of composite structures in the form of relatively thin plates, the load-carrying capacity of composite plates against buckling is crucial. Additionally, cutouts are frequently used in composite plates as part of the design of the structures. As a result, it is critical to have a firm grasp of the buckling properties of composite plates with cutouts. Erkliǧ and Yeter [
23] found that for composites with a thin-walled, fibre orientation, the angle of the cutouts, the plate size, and lastly the size of holes result in an effect on the buckling behaviour. Nevertheless, the parameter that contributes most towards the behaviour of the buckling of the holed composite plate is not identified. This, together with the work conducted by Khazaal et al. [
10], has ignited the motivation to carry out the present study to contribute to the knowledge on thin-walled structures with cutouts specifically for composite material.
The main objective of the current study was to use glass-fibre-reinforced polymer as a composite material. Different laminate types were tested using ABAQUS software upon verification of the work of [
24]. The laminates used were quasi-isotropic (0/90/45/−45)s, angle-ply (45/−45/45/−45)s, cross-ply (0/90/0/90/0/90/0/90), and balanced laminate (−45/30/60/30/−30/45/−60/−30). In this study, the implementation of the design of experiment (DOE) seemed necessary to ensure that all parameters affecting the buckling load were optimized. We began with identifying the factors and levels followed by selecting a suitable factorial design. This study used a full factorial L
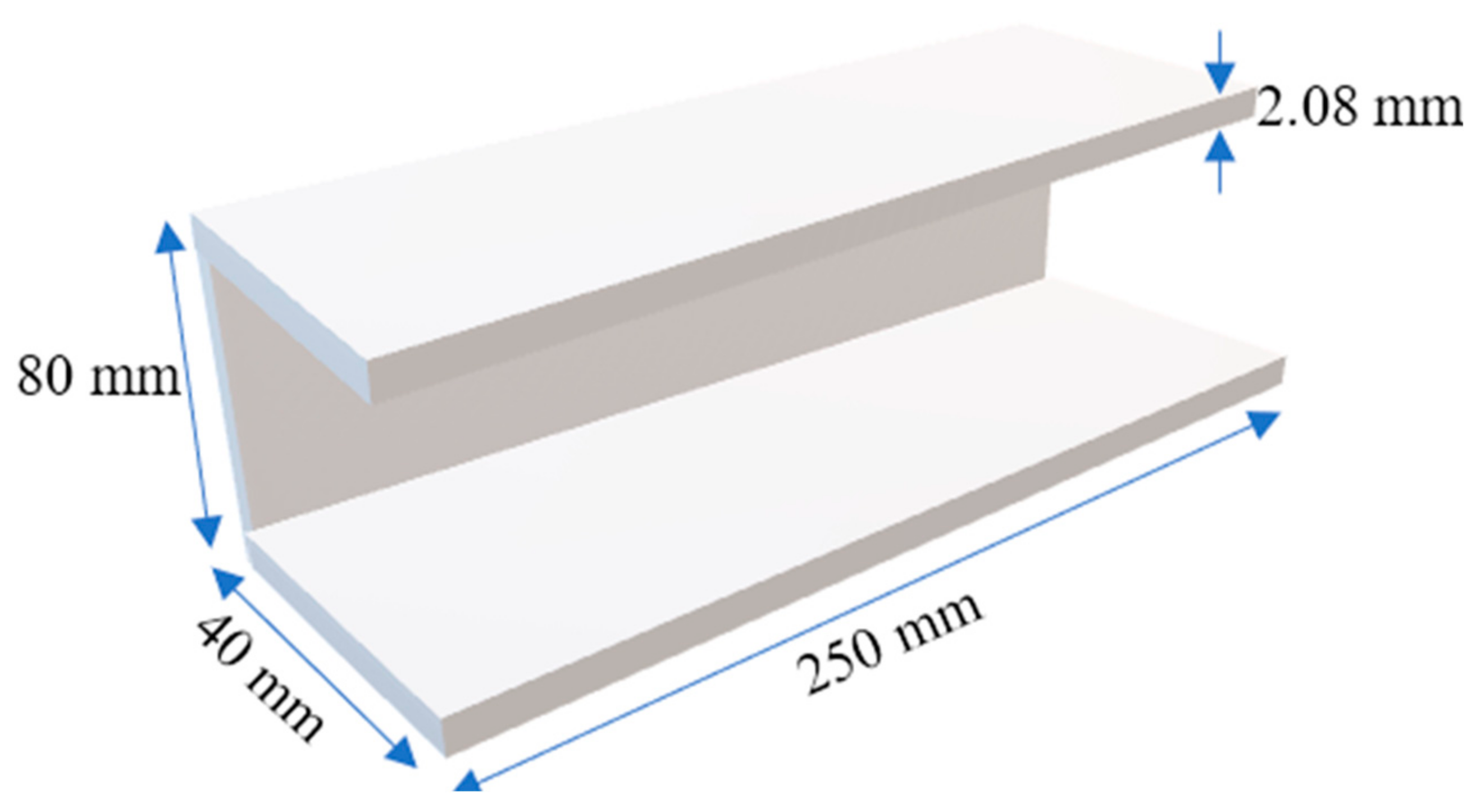
27 orthogonal array where 27 indicates the number of runs (simulation) required. Response surface methodology (RSM) was used to analyse the obtained data through the main effect plot, contour plot, regression, and analysis of variance (ANOVA). Additionally, the present study focused on perforated composite plates, and the supports were fixed at both ends and the orientation of the fibre was as mentioned. The cross-sectional shape considered was a C section. The novel work of this study focused on optimizing the parameters to achieve the highest probable critical buckling load for perforated composites and thin-walled members, through simulation using MINITAB and Design Epxert tools.
6. Conclusions
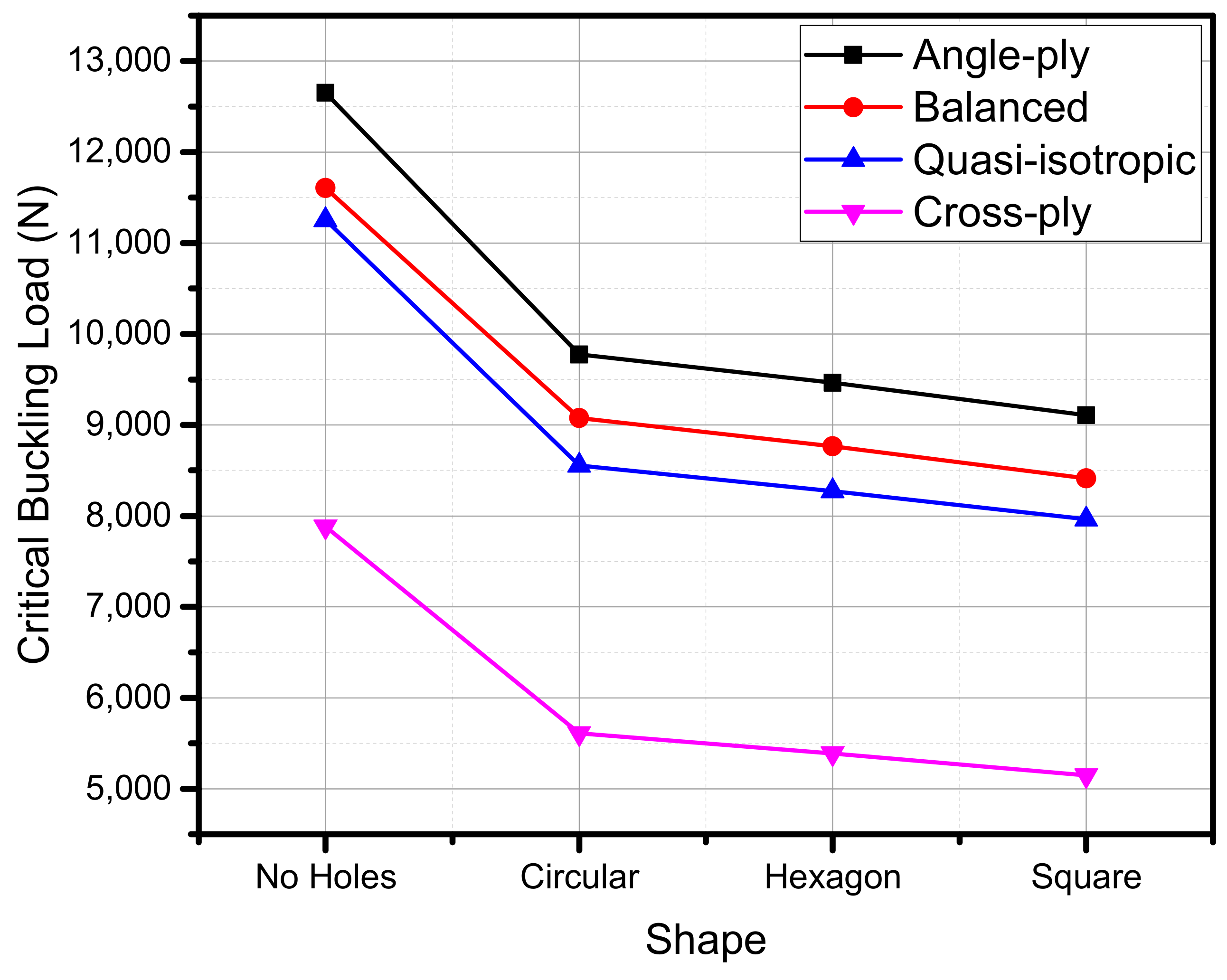
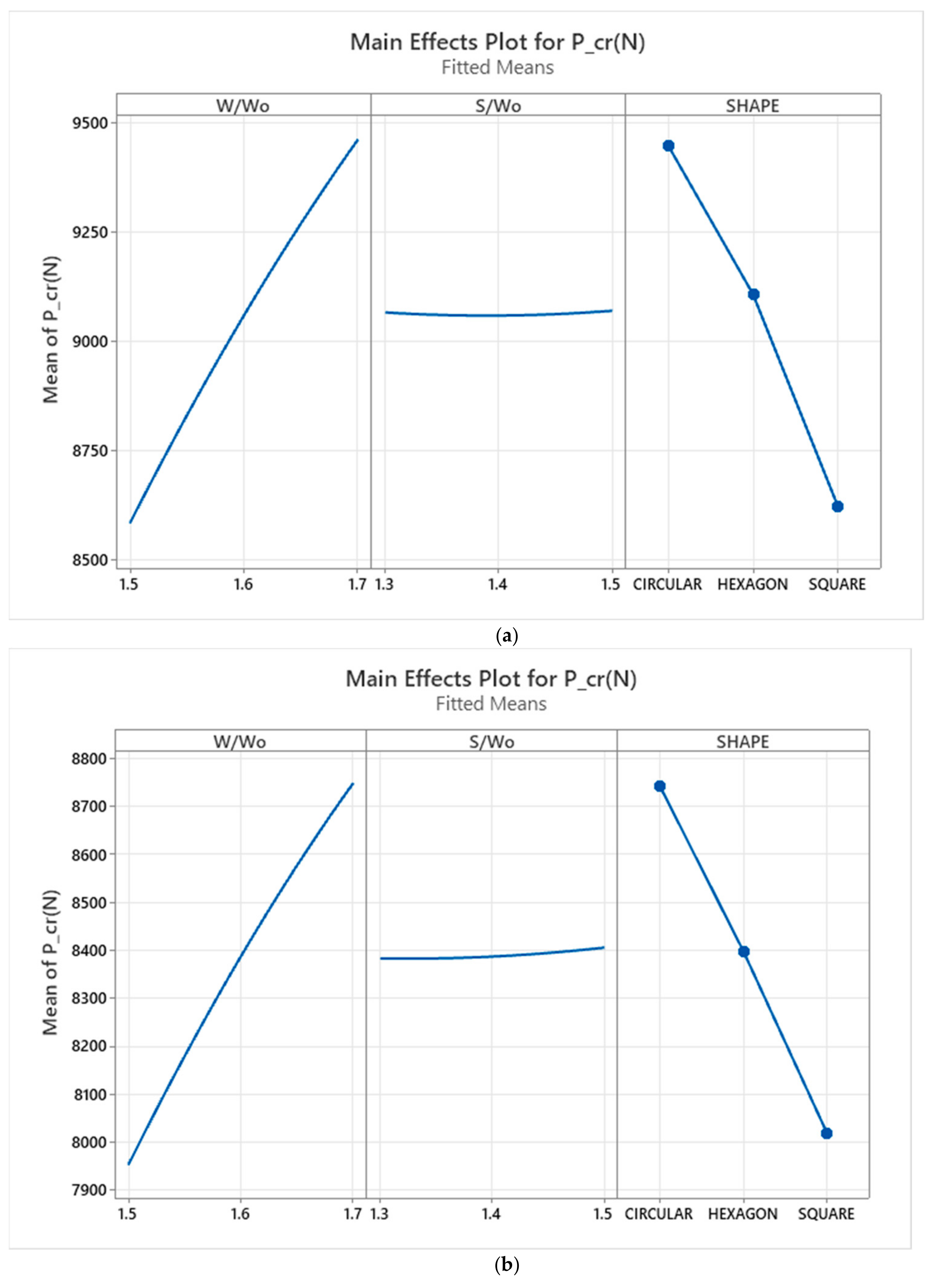
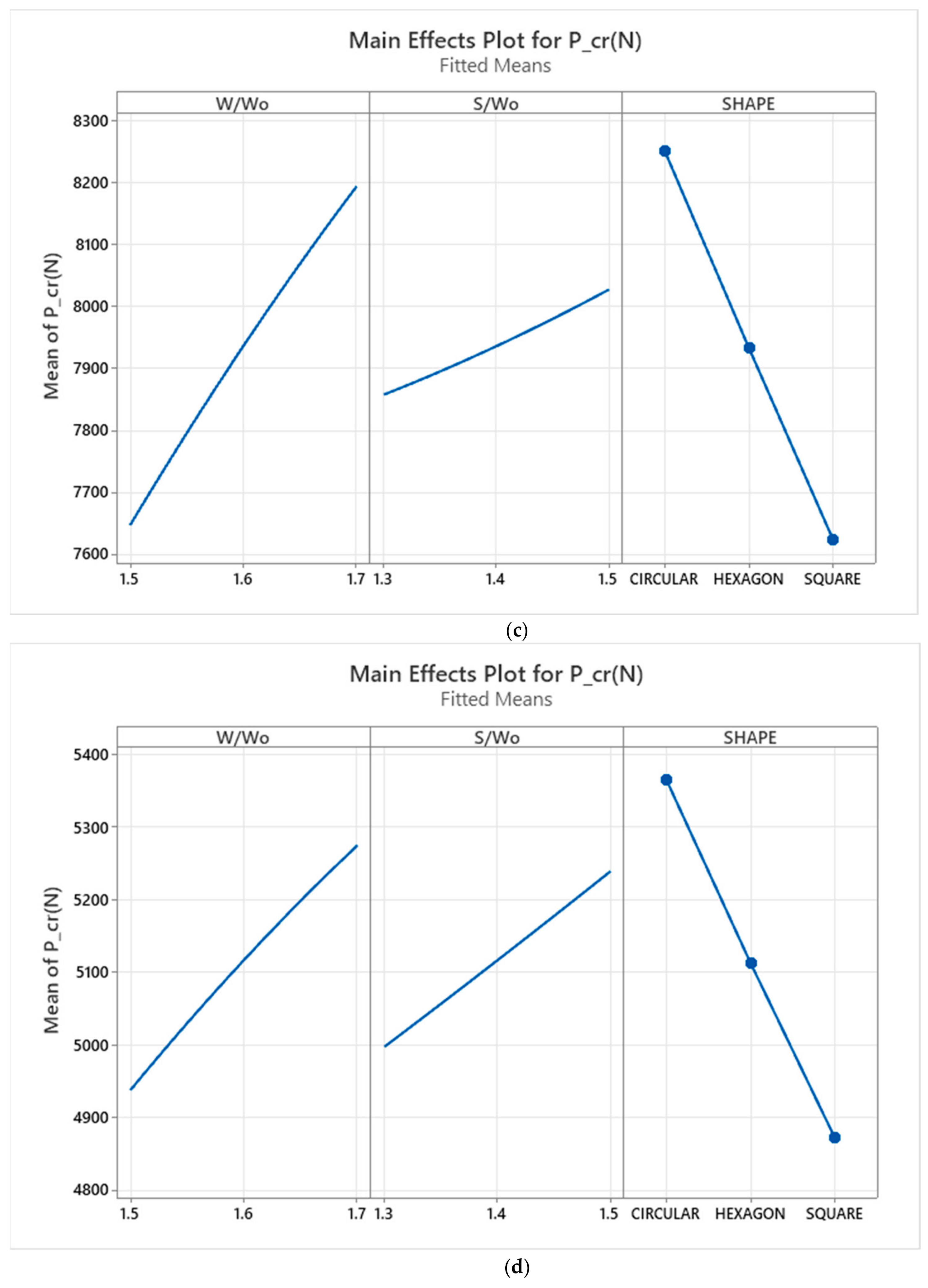
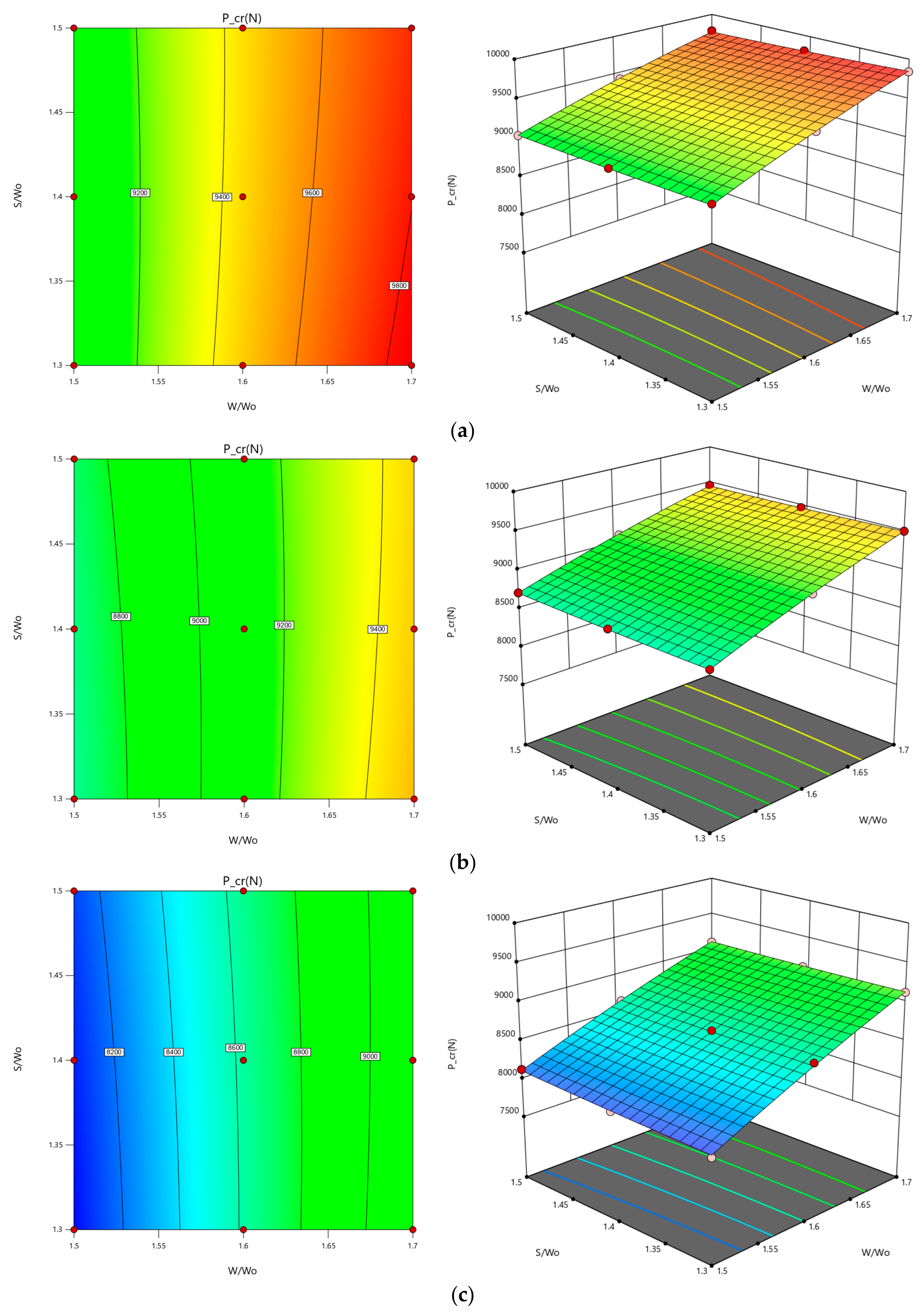
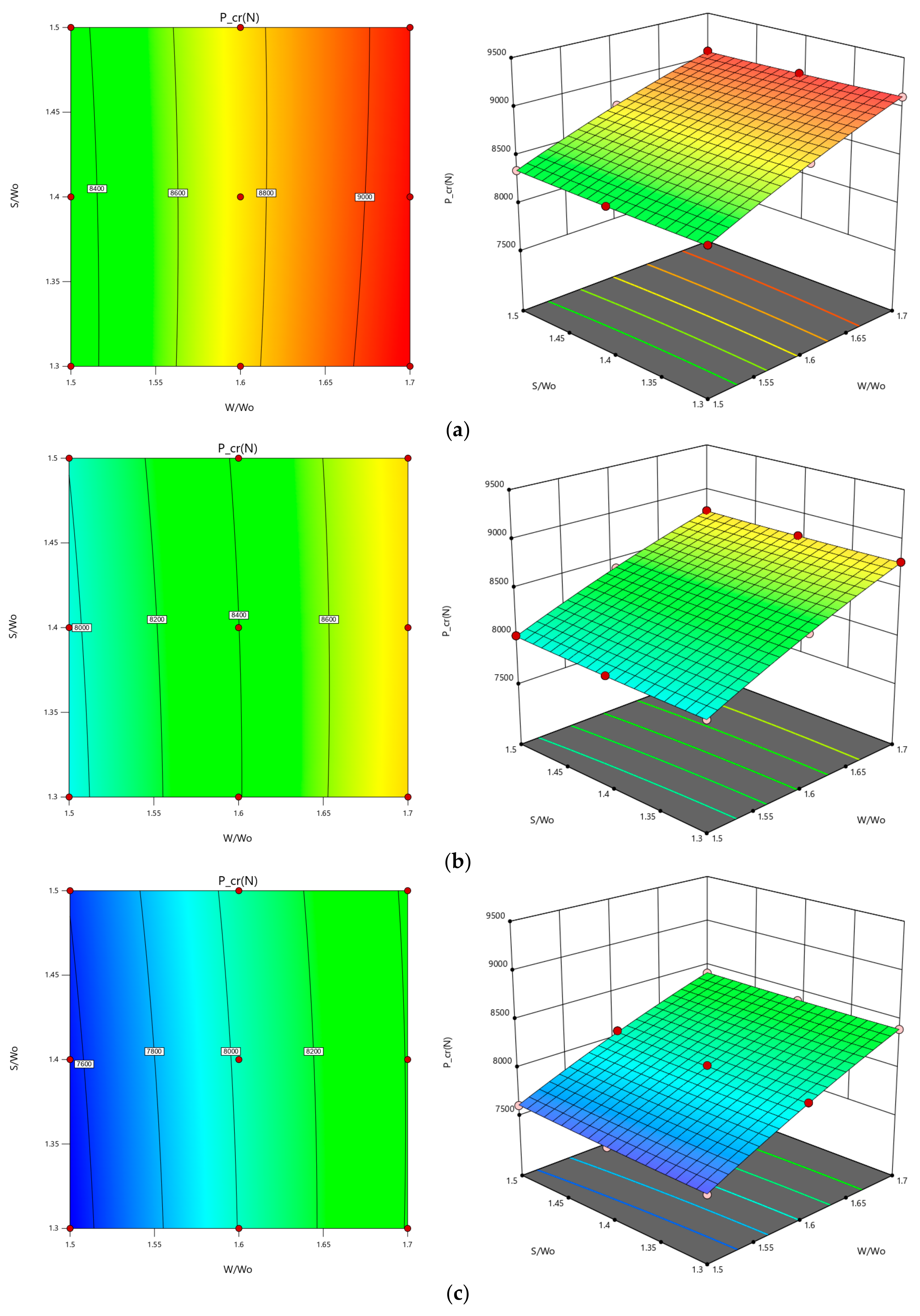
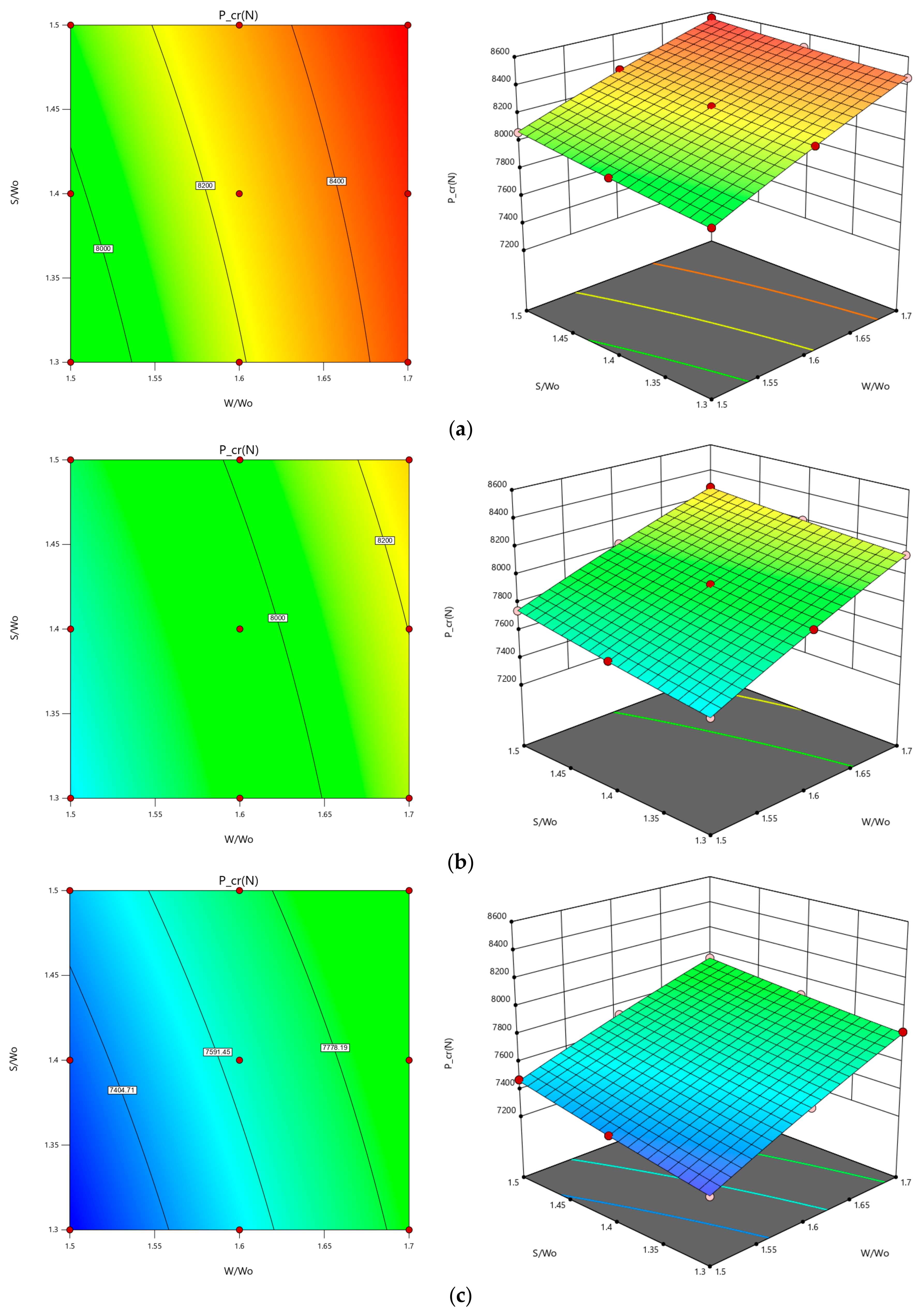
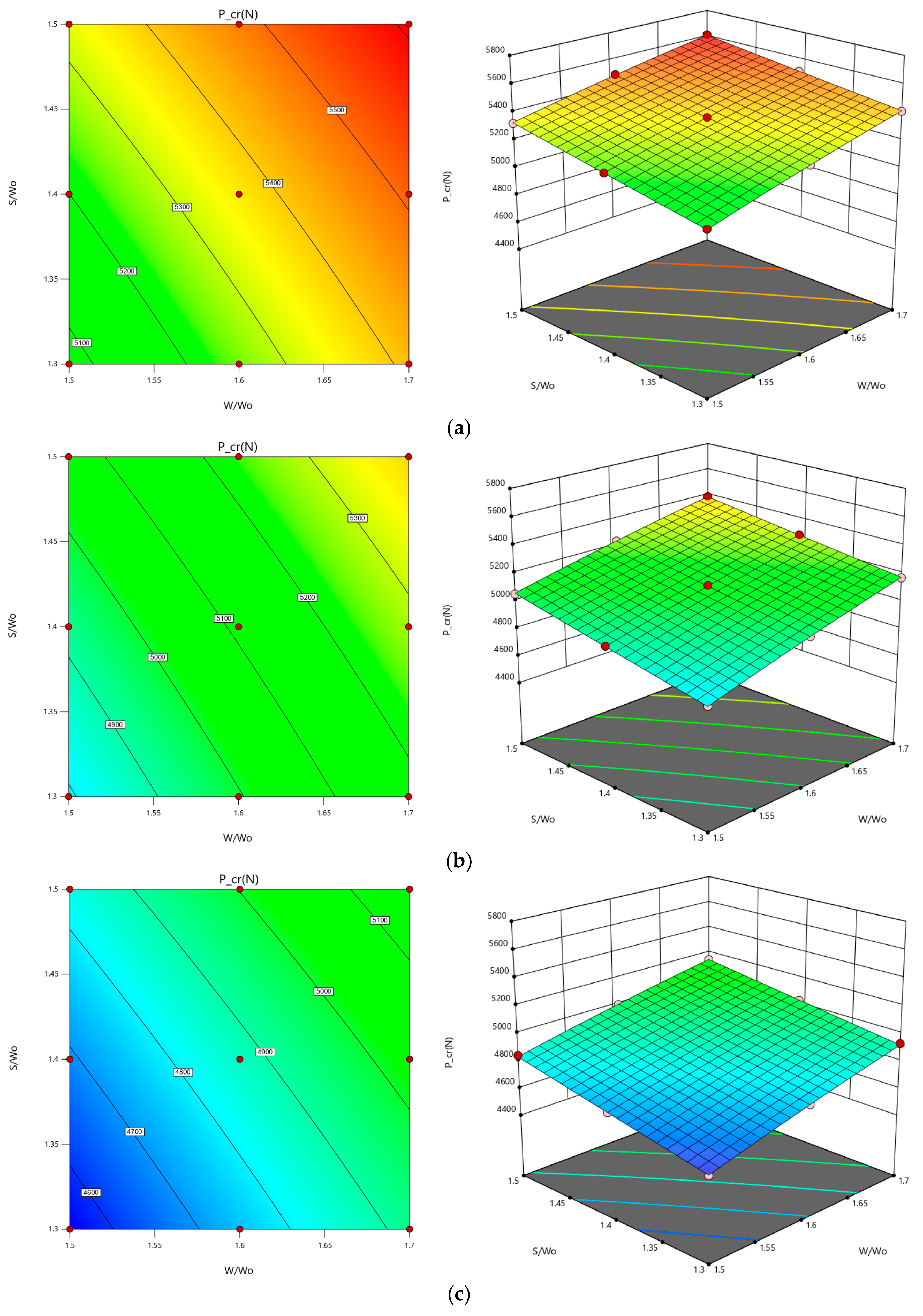
In short, ABAQUS software was used to numerically study thin-walled composite structure buckling. The critical buckling load was calculated using eigenvalue linear buckling. Four laminates were studied to see how parameters affect response and critical buckling load. Then, the results were optimized. This study used a full factorial orthogonal array first, then obtained eigenvalue buckling data for all cases to better understand the data. The obtained data were then analysed using MINITAB and Design Expert software using response surface methodologies to verify model estimation, graphs, and variable contours and levels. The W/Wo parameter had the highest F-value in all laminate types, indicating it is the most influential for one-way interaction. In quasi-isotropic, cross-ply, and balanced laminates, W/Wo and S/Wo had the highest F-value. The design of the composite thin-wall structure was influenced by these two combinations. Angle-ply can be combined in many ways. W/Wo and the cutout shape had the greatest impact on the buckling load. This study also found the best parameter combinations for different laminates in terms of critical buckling. An optimization analysis based on parameters showed that range changes affect buckling load values.
All laminates had an abrupt trend except the cross-ply laminate, which had a significant opening ratio. The opening ratio increased buckling loads, affecting response. Round laminates buckled more than hexagonal or square laminates, except for angle-ply, which had a closer margin between the circular and hexagonal shapes. The aspect ratio did not affect buckling load. Increased spacing ratio increased buckling load for quasi-isotropic and cross-ply laminates. The trend was almost flat for both angle-ply and balanced laminate, so the spacing ratio had little effect. Because both factors are steeper, the cross-ply laminate is adjustable. The QIS had a moderate effect on buckling load capacity as it increased gradually. These variables combine to determine a strut’s buckling load. A contour plot requires both parameters to work properly. These equations can be used to predict the response at any given point in the input parameters. To demonstrate this, all three equations for different shapes of angle-ply laminate cutouts were tested. The results were then compared to existing data. Finally, the response surface methodologies showed optimized results from the study’s analysis. As shown in the graph, the regression equation yielded an optimal response. It shows how the factors affect the critical buckling load and also shows the best combination for a higher critical buckling load.