Abstract
The leading edge is the critical portion for a gas turbine blade and is often insufficiently cooled due to the adverse effect of Crossflow in the cooling chamber. A novel internal cooling structure, wall jet cooling, can suppress Crossflow effect by changing the coolant flow direction. In this paper, the conjugate heat transfer and aerodynamic characteristics of blades with three different internal cooling structures, including impingement with a single row of jets, swirl cooling, and wall jet cooling, are investigated through RANS simulations. The results show that wall jet cooling combines the advantages of impingement cooling and swirl cooling, and has a 19–54% higher laterally-averaged overall cooling effectiveness than the conventional methods at different positions on the suction side. In the blade with wall jet cooling, the spent coolant at the leading edge is extracted away through the downstream channels so that the jet could accurately impinge the target surface without unnecessary mixing, and the high turbulence generated by the separation vortex enhances the heat transfer intensity. The Coriolis force induces the coolant air to adhere to the pressure side’s inner wall surface, preventing the jet from leaving the target surface. The parallel cooling channels eliminate the common Crossflow effect and make the flow distribution of the orifices more uniform. The trailing edge outlet reduces the entire cooling structure’s pressure to a low level, which means less penalty on power output and engine efficiency.
1. Introduction
Turbine blades work in extreme conditions, including high temperature, high pressure, and huge centrifugal force. The demand for increasing thermal efficiencies results in the sustaining improvement of turbine entry temperature and the requirement of advanced cooling technologies for turbine blades [1]. For the internal cooling of turbine blades, the most critical portion is the leading edge because that position is exposed to the highest heat flux and pressure with a narrow space and a high-curvature surface [2].
Although some potential internal cooling designs have been presented with the rise of casting technology, such as matrix cooling [3,4] and double-wall cooling [5], the conventional method, jet impingent cooling, is still the most widely used for the protection of blade leading edge because of its intense unsteady disturbance and high local heat transfer coefficient [6]. A vast number of reviews of impingement cooling exist, such as Refs. [7,8,9]. The heat transfer enhancement of impingement cooling is influenced by many factors such as jet Reynolds number, jetting hole diameter, jetting hole pitch [10], jet to plate distance [11] and target wall curvature [12]. With the development of additive manufacturing, more and more researchers are focusing on combining the target surface of impingement cooling with heat transfer enhancing features, including pin-fin [13,14], micro pin-fin [15], dimple [16,17], conical and ring protuberances [18]. The combination further improves the heat-dissipating rate of impingement cooling with a little increment of pressure penalty, but the manufacturing cost is still a problem.
Swirl cooling is another kind of cooling structure used at the leading edge of turbine blades. The swirl flow contributes to creating a thin boundary layer and high convective heat transfer coefficient, which was first demonstrated by Kreith et al. [19]. Qian et al. [20] found that the Görtler vortex pairs of swirl cooling lead to high turbulence and heat dissipation rate, which was also confirmed by the numerical simulations of Du et al. [21]. Liu et al. [22] investigated the effects of jet nozzle geometrical parameters and flow parameters on swirl cooling’s flow and heat transfer characteristics by a blade leading edge model. Kusterer et al. [23] developed a novel swirl cooling scheme, named double swirl cooling, by merging two swirl cooling cavities along the radial direction of blades. Some follow-up studies by Kusterer et al. [24,25] show that double swirl cooling is suitable for the blade leading edge and provides a higher local and average cooling performance than impingement cooling and single chamber swirl cooling.
In actual turbine blade cooling with radial cooling cavities, including jet impingement cooling and swirl cooling, the Crossflow of spent air exists and has a critical impact on the cooling performance. The interaction of the Crossflow and jets pushes the stagnation point away from the target surface and induces a thicker boundary layer, which negatively influences the heat transfer intensity and uniformity. The mass flux ratio of Crossflow to jets larger than 0.1 and a large impingement distance would dramatically undermine the cooling effectiveness of impingement cooling [26]. Several researchers [27,28,29] put forward some novel internal cooling schemes to reduce the adverse influence of Crossflow. Rekingen et al. [27] presented an impingement cooling scheme with a trapezoid corrugated target wall, which decreases the impingement distance and increases the Crossflow space to reduce the Crossflow influence. Hebert et al. [28] presented a “Zero-Crossflow” impingement scheme with a larger space between impingement holes to discharge spent air. Liu [29] proposed a multi-stage impingement concept, utilizing the spent air as the next impingement stage’s coolant source. However, the designs mentioned above are still too complicated to be accommodated in the leading edge of turbine blades and have additional flow loss penalty.
Unlike the radial internal cooling schemes, a design allowing coolant air to flow along the blade profile to avoid Crossflow was put forward by Zhang et al. [30] in 2017, named multi-channel wall cooling. As shown in Figure 1, the design is the combination of wall jet cooling and double-wall cooling, which are the leading-edge part and suction side part separately. The wall jet cooling chamber is separated by the ribs connecting the outer wall and inner wall into several parallel rectangular channels. After impinging the inner stagnation line, the wall jet flows along the target surface under the action of centrifugal force. Under the same flow mechanism with swirl cooling, the attaching-wall jet generates Görtler vortex pairs on the curvature’s surface, enhancing the target surface’s heat transfer. The spent coolant is extracted through the passage of the double-wall cooling to the exit at the trailing edge instead of mixed with the fresh jets. It was proposed based on the fugitive core casting technology, which could manufacture complicated structures by inserting tiny fugitive cores into ceramic cores and is a proven technology. Therefore, the multi-channel wall cooling design has great cooling air utilization and higher heat transfer enhancement with less manufacturing cost [30]. As the critical component, wall jet cooling maximizes the heat transfer performance of impingement cooling and is simple enough to be accommodated in blade leading edge.
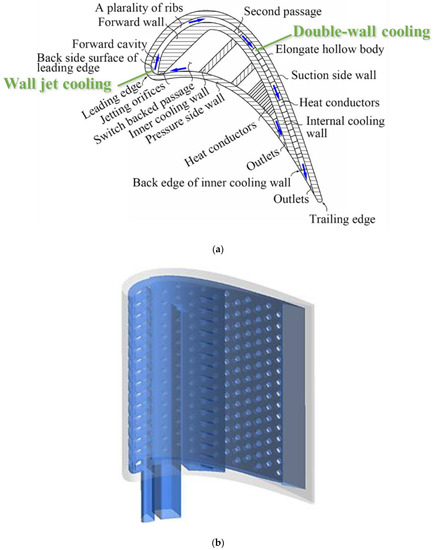
Figure 1.
The multi-channel wall cooling structure. (a) Section view [30]; (b) Overall structure.
Our previous work [31,32] has numerically studied the effects of several geometrical parameters, including orifice width, impingement distance, turning angle, turning internal radius and Reynolds number, on wall jet cooling performance. The results show that the vortex structure in the wall jet cooling channel depends on the orifice width and turning internal radius. As the width of the orifice and the jetting Reynolds number increase, the Nusselt number and pressure loss change drastically. Within the consideration of Ref. [29], the Nusselt number corresponding to the maximum jet Reynolds number is four times the Nusselt number corresponding to the minimum jet Reynolds number. However, the investigations were mainly based on simplified models. Many factors need to be considered, such as rotation, blade profile and Crossflow in the coolant plenum. The actual cooling performance of wall jet cooling is still insufficient in research.
In the current study, the numerical simulations with blade cascade models were carried out to compare the flow and heat transfer characteristics of wall jet cooling with impingement cooling and swirl cooling under operating conditions. The outlet position of wall jet cooling is different from the other two, which results in different flow parameters in the cooling chambers, so three kinds of coolant inlet boundary conditions were used: constant mass flow, constant jetting Reynolds number, and constant total pressure conditions. Steady conjugate heat transfer numerical method was utilized. The results, including inner heat transfer coefficient, overall cooling effectiveness, pressure distribution, velocity distribution, and temperature gradient, were compared and analyzed in detail.
2. Computational Model & Numerical Method
2.1. Computational Model
As shown in Figure 2, the simplified model of the first stage of GE-E3 turbine was simulated to conduct the study. The fluid domain contains the mainstream path (marked in red) and the internal cooling chambers at the leading edge of the blade (marked in blue), and the two regions are connected at the coolant outlet. In the passage with pin-fin rows in Figure 3, the solid domain is only the leading-edge part of the blade (marked in dark gray) to avoid the additional heat transfer of double-wall cooling. In other words, the region marked in light gray is not simulated. The periodic boundary condition was utilized in the study to reduce computational cost. Figure 3 illustrates the internal cooling structures investigated in the study, including the impingement cooling with a single row of jet (IC), swirl cooling (SC), and wall jet cooling (WJ). For the blades with impingement cooling and swirl cooling, the coolant and cooling chambers were designed based on the original design of GE-E3 turbine [33]. The film holes were ignored and the coolant outlet was at the tip clearance according to engineering practice, the height of which is 0.4 mm and 1% of the blade height.
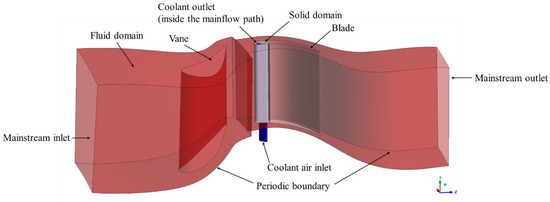
Figure 2.
Computational domain.
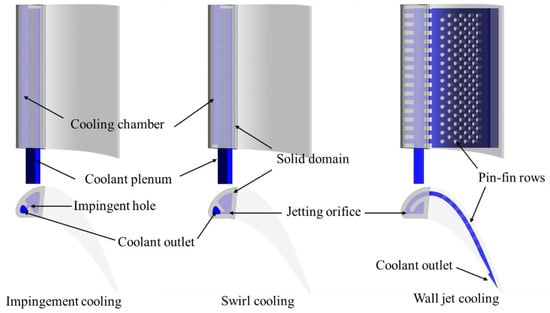
Figure 3.
Internal cooling structures at the leading edge.
For the blade with wall jet cooling, the cooling structure was designed according to the patent of Zhang et al. [30]. The coolant plenum size was decreased to make sure that the leading edge has the same cross-sectional area as that of the other two structures, and this may thus generate high radial velocity of the coolant. Eight rows of staggered pin-fins were set in the coolant passage between the out wall and inner wall. The coolant outlet was set at the trailing edge of the blade. More detailed parameters of the cooling channel were kept the same as those in Ref. [31], as shown in Figure 4. Due to the limitation of manufacturing, the inner wall thickness (tinner), channel width (Wch), and channel height (Hch) equal to the outer wall thickness (t). Hence, t was set as the characteristic length in the study, which is 1.2 mm according to Ref. [33]. The orifice width (Win) and turning internal radius (R) were set as 0.5t. The impingement distance is 0.63t.
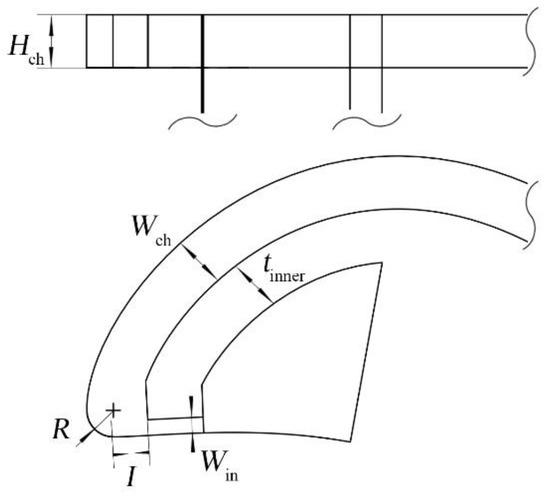
Figure 4.
Details of wall jet cooling structure.
The swirl cooling and wall jet cooling have the same jetting orifice size with the hydraulic diameter of 0.8 mm, the jetting hole diameter (Dj) of the impingement cooling. The pitches of the jetting holes and orifices (p) are all 2t. The geometrical parameters mentioned above are summarized in Table 1.

Table 1.
Detailed geometric parameters of the internal cooling structures.
2.2. Boundary Conditions
The commercial CFD software ANSYS CFX was utilized to solve the steady-state compressible Reynolds averaged Navier–Stokes (RANS) equations. The method is widely used for conjugate heat transfer (CHT) modeling and has enough prediction accuracy in the design of turbine blade cooling [34]. It is notable that the unsteady conjugate heat transfer simulation is very difficult at present because the time scale of solid conduction is about 10,000 times larger than that of fluid convection [35], so the unsteady calculation could not be carried out. The maximum iterations number was 1000, and the second-order accuracy was used with max RMS residual less than 0.0001.
The boundary conditions, referring to Ref. [31], are listed in Table 2. The fluid working medium is ideal air, and the solid domain material is DD6 alloy, a nickel-based superalloy for aero-engine. The property parameters of the two materials were the results of interpolated calculations. As mentioned above, the flow parameters between the conventional internal cooling methods and wall jet cooling vary greatly due to the different coolant outlets pressure. Hence, three kinds of boundary conditions at coolant inlets were adopted to systematically compare the cooling performance and aerodynamic characteristics of the cooling structures, including constant mass, constant total pressure, and constant jetting Reynolds number.

Table 2.
Detailed boundary conditions.
The jetting Reynolds number is defined as:
where ρ is the fluid density, U is the mean velocity of a jet emanating from the orifice/hole, and μ is the fluid dynamic viscosity.
2.3. Grid Independence
Given the complicated geometries, unstructured grids generated by Workbench Meshing were selected to conduct the study. As shown in Figure 5, the grids contain tetrahedron elements and prismatic boundary layer elements. To guarantee the requirement the of SST k-ω turbulence model that y+ is less than 1.0, the first layer grid height is 0.0005 mm, and the growth rate is 1.2. The blade model with wall jet cooling was utilized to perform the validation under the condition of the jetting Reynold number equals 20,000. Four sets of fluid domain grids with a size ranging from 5.5 to 20.1 million and four sets of solid domain grids with sizes of 3.5–10.5 million were adopted to carry the grid independence validation. Limited by the tip clearance, the minimum size of both fluid domain and solid domain grids were 0.2 mm. The grid size was adjusted by changing the maximal size. When the fluid domain grids were tested, the solid domain grids were set as 7.6 million, and the fluid domain grids of 20.1 million were used to test the solid domain grids. The Nusselt numbers at the target surfaces’ stagnation lines with fluid domain grids of different sizes are illustrated in Figure 6.
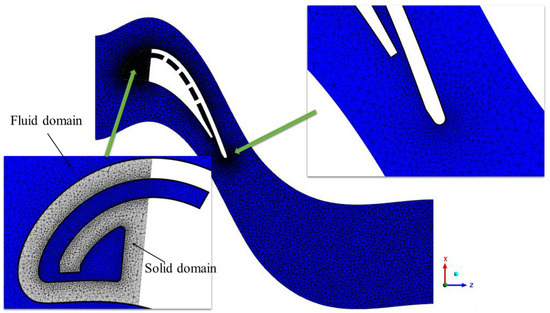
Figure 5.
Grid details of the internal cooling structure.
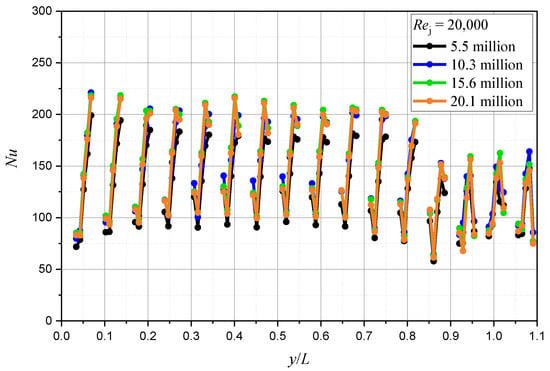
Figure 6.
Effect of fluid grids size on Nusselt number at the stagnation line of the target surface.
Nusselt number is commonly used for heat transfer investigations, which represents the dimensionless heat transfer coefficient. Equation (2) gives the definition:
where qw is the wall heat flux, Dhy is the hydraulic diameter of the jetting hole/orifice, Tc is the total temperature at the coolant plenum inlet, Tw is the target wall temperature, and is the cooling air thermal conductivity.
In Figure 6, y is the height direction coordinate and L is the chord length of the blade (35.21 mm). Due to the target surface of the wall jet cooling structure is divided by the ribs connecting the double walls into several pieces, the curves are discontinuous. It can be seen that the curves have the same tendency, and the results with a size over 10.3 million are nearly coincident. The maximum relative deviation between the results of 15.6 million and 20.1 million grids is 5.89%, which is at the penultimate peak. Therefore, a setting of the 15.6 million grids was selected to generate fluid domain grids. The solid domain grids’ testing results are all coincident with the maximum relative deviation of 0.94%. The results are ignored to avoid duplication of the curves. The girds of 3.5 million was selected as the solid domain for reducing the computational cost.
2.4. Turbulence Model Validation
The k-ε model, RNG k-ε model, k-ω model and SST k-ω model are adopted in the turbulence model validations, and the results are demonstrated in Figure 7, Figure 8 and Figure 9. In Figure 7, the experimental configuration was the plate jet impingement based on the geometry measured by Xing et al. [36]. From the comparison of numerical results and experimental data on the plate centerline, it can be concluded that SST k-ω model has the best prediction accuracy among the four broadly used models in simulating the heat transfer characteristics of impingement cooling under the Crossflow effect. In Figure 8, the swirl tube with two tangential inlets and a single outlet was firstly proposed and investigated by Ligrani et al. [37], and the heat transfer coefficient distribution and flow field of the structure was studied by Ling et al. [38]. In the paper, the experimental data in Ref. [38] was adopted to validate the turbulence model. In Figure 8, the x and r are the stream-wise distance and the pipe radius. The comparison of numerical results and experimental data also shows that the SST k-ω model is the optimal choice for simulating swirl cooling. To the author’s knowledge, there are little experimental data about wall jet cooling, and the flow structure of wall jet is the combination of the impingement jet and swirl jet. Therefore, we hold the opinion that the SST k-ω model is qualified for the prediction of wall jet cooling.
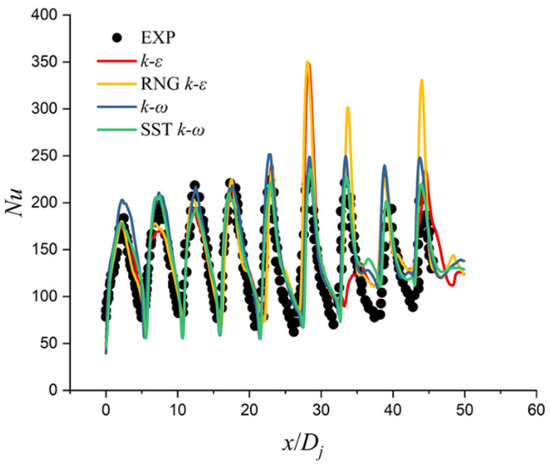
Figure 7.
Comparison of Nusselt number on the plate centerline at Rej = 35,000 and H/Dj = 3.
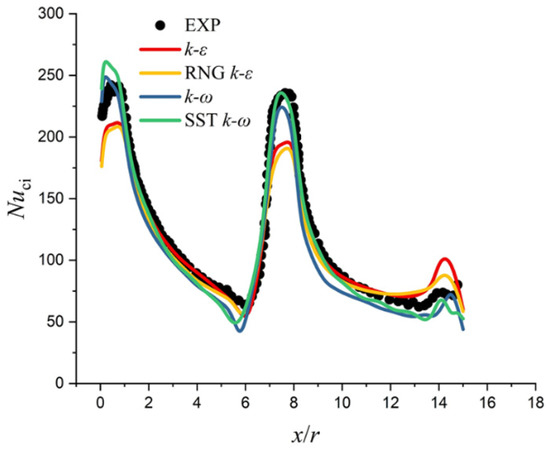
Figure 8.
Comparison of circumferentially averaged Nusselt number results at Re = 10,000 and temperature ratio = 0.83.
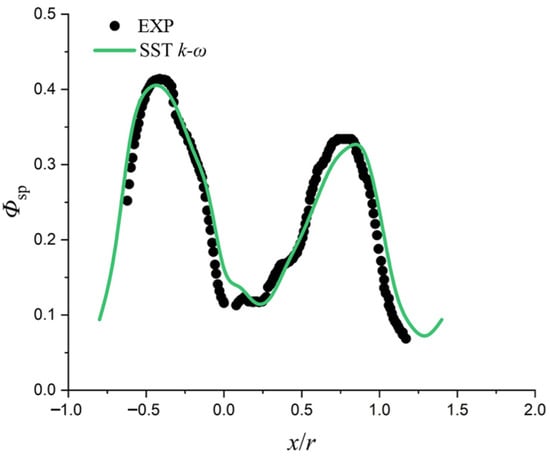
Figure 9.
Comparison of span-wise averaged overall cooling effectiveness at Tu = 0.5%.
In Figure 9, the experimental configuration was an internally cooled turbine vane based on the geometry measured by Dees et al. [39]. The figure also illustrates the comparison of numerical and experimental results on span-wise averaged overall cooling effectiveness under CHT conditions.
The definition of overall cooling effectiveness is given in Equation (3):
where Tew is the external surface temperature, Trec is the temperature of the blade wall without cooling, and Tc is the total temperature at the coolant inlet. The curve of simulation agrees well with that of the experimental data [39], which means that the SST k-ω model has enough prediction accuracy for the simulation of cascade model under conjugate heat transfer condition. According to the validation results above, the SST k-ω model was selected to conduct the simulations of all cases in this study.
3. Results and Discussion
3.1. Overall Performance Evaluations
Before the detailed mechanism study, the overall evaluations of flow and heat transfer characteristics are presented and analyzed in this section. According to different kinds of coolant inlet boundary conditions, Table 3, Table 4 and Table 5 list some parameters, respectively, including the static pressure of the cooling chamber outlet, area-averaged overall cooling efficiency on the pressure side, suction side and the leading edge of the solid domain, area-averaged Nusselt number on the target surface and the whole internal cooling surfaces of every single case. The important values are marked in bold.

Table 3.
Flow and heat transfer and parameters of the cases with the same coolant mass flow rate.

Table 4.
Flow and heat transfer and parameters of the cases with the same jetting Reynolds number.

Table 5.
Flow and heat transfer and parameters of the cases with the same coolant inlet total pressure.
Table 3 shows the results of the cases with the same coolant mass flow rate. Although the orifices of the impingement cooling, swirl cooling and wall-jet cooling structures have the same hydraulic diameters, the cylindrical shape holes of IC have a smaller flow area than the rectangular orifices of SC and WJ, which is 69.4% of the latter. Therefore, the jetting Reynolds number of IC is much higher than that of SC and WJ. As for the overall cooling performance, WJ is the optimal choice, obviously. No matter on which side of the solid domain outer surface, WJ has the highest overall cooling efficiency. It can be seen that WJ also has the highest area-averaged Nusselt number on the whole internal cooling surface, but the value of Nu on the target surface is the lowest. The reason is that the parallel channels of WJ have a larger target surface area, which will be discussed when comparing the internal cooling area of different internal cooling structures.
Table 4 depicts the parameters of the cases with the same jetting Reynolds number. The main difference between Table 3 and Table 4 is the values of IC. With Rej = 20,000, the coolant mass flow of IC is lower than that of SC and WJ, and the cooling performance of IC is also the worst.
Table 5 illustrates the parameter comparison of cases with the same coolant inlet total pressure (relative coordinate system). The flow resistance in the coolant chambers varies from structure to structure. The coolant outlet of IC (SC) is on the blade tip, and the pressure there is much higher than that on the blade trailing edge where the WJ outlet is. That explains why WJ has nearly three times as much coolant as IC or SC to adequately cool the leading edge and the whole suction side of the blade. It also means that the coolant supplied to WJ could be extracted from the compressor stage with lower pressure, reducing the aerodynamic loss of turbines. Besides, with the same cooling chamber and inlet total pressure, the higher outlet pressure indicates that IC has lower flow resistance than SC. According to the results under the above three different kinds of coolant inlet boundary conditions, wall jet cooling is the optimal structure in making full use of coolant under limited pressure penalty compared to impingement cooling and swirl cooling.
Although the preceding area-averaged parameters exhibit the heat transfer intensity in different structures, the overall cooling effectiveness also depends on the area of internal cooling surfaces. Based on positions, the surfaces are classified into target surfaces (tar), chamber surfaces (chm) and other cooling surfaces (ocs), which are shown in Figure 10. The target surfaces are the inner surfaces of the blade outer wall at the cooling chamber region, directly impacting the leading edge’s cooling performance and marked in gray with 20% transparency. The chamber surfaces are the coolant supply chamber’s inner surfaces in the blade and marked in blue. The other cooling surfaces include the jet holes or orifices surfaces and the cooling chamber surfaces except for the target surfaces marked in cyan.
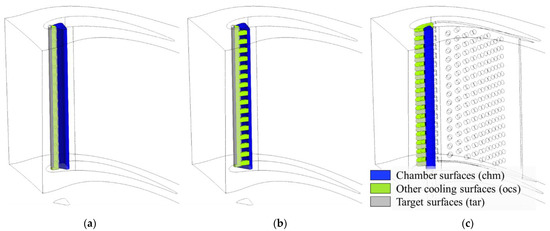
Figure 10.
Cooling surfaces among different internal cooling structures; (a) Impingement cooling; (b) Swirl cooling; (c) Wall jet cooling.
The internal cooling area comparisons among different internal cooling structures are illustrated in Figure 11. It can be seen that the target surfaces of the three structures almost have the same area, although those of wall jet cooling are discrete and parallel. For every single cooling channel of WJ, merely the outer surface is classified as the target surface; the other surfaces are all ‘other cooling surfaces’; hence, the ‘ocs’ of WJ has 6.4 times IC area and 3.5 times SC area. Regarding the chamber surfaces, the WJ area is nearly 67% of that of IC or SC. The reason is that the double-wall design of the wall jet cooling structure limits the size of the coolant supply chamber.
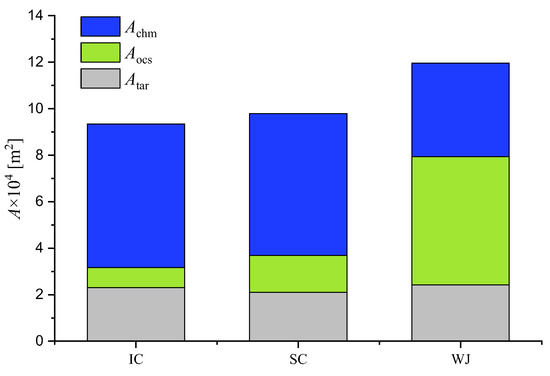
Figure 11.
Internal cooling area comparison among different internal cooling structures.
The total heat flux among different internal cooling structures is demonstrated in Figure 12 to contrast the cooling performance of the three designs and quantify the contributions of different surfaces. It is apparent that the heat flux of every part is directly proportional to its area for all the structures. Although the flow mechanism in the cooling chamber varies from that of cooling structures, the heat fluxes on the three structures’ target surfaces are nearly the same as the jetting Reynolds number of 20,000. The smallest area of the coolant chamber surface of wall jet cooling results in its lowest Qchm among all the cooling methods. However, the ‘ocs’ area’s huge preponderance ensures that WJ has the largest total heat flux compared with IC and SC, no matter under which coolant inlet boundary condition. Besides, WJ’s total heat flux in Figure 12c only increased 12% relative to that in Figure 12b, with a 154% gain in coolant mass flow rate. It means that the jetting Reynolds number of 20,000 might be close to an optimal value for WJ’s current design, and the Rej over 20,000 would lead to unnecessary flow resistance. If more coolant is needed to dissipate the suction side wall’s heat load in a real WJ design, the jetting orifice width should be increased to reduce the pressure loss.

Figure 12.
Total heat flux among different internal cooling structures; (a) Cases with the same ; (b) Cases with the same Rej; (c) Cases with the same Pt,cin.
3.2. Flow Characteristics
As previously described, the wall jet cooling structure has the highest overall cooling effectiveness, largest cooling area and maximal heat flux compared to impingement cooling and swirl cooling structures. The jet mass flow rate, cooling chamber pressure, and inner velocity distributions are investigated in detail in this section to identify the flow characteristics and cooling mechanisms of WJ.
The jet mass flow rate ratio is defined as follows:
where is the jet mass flow rate of one certain jetting orifice, and is the mass flow rate at the coolant chamber inlet.
The mass flow nonuniformity coefficient, , is a dimensionless parameter used to measure the uniformity of coolant distribution in the jet orifices. Equation (5) gives the definition:
where is the averaged mass flow rate in the jetting holes, and n is the total number of holes in one certain cooling structure.
Figure 13 depicts the two above parameters’ distributions and jetting Reynolds number under all the coolant inlet boundary conditions studied in this paper. It is evident that the jet mass flow rate rises with the blade height for all the cases, and the curves seem to be dominated by geometrical structures but not coolant boundary conditions. Besides, wall jet cooling has the most homogeneous coolant distribution in jetting orifices. Relative to the MR distributions of impingement cooling and swirl cooling, the curves of WJ are much more moderate from jetting hole 1 to jetting hole 16. The mass flow nonuniformity coefficients of wall jet cooling is 11–14%, which is nearly 30% and 50% lower than that of impingement cooling and swirl cooling structures. Additionally, the jetting Reynolds number distribution is generally in parallel with the curves of MR; however, the values of Rej would increase dramatically with coolant mass flow.
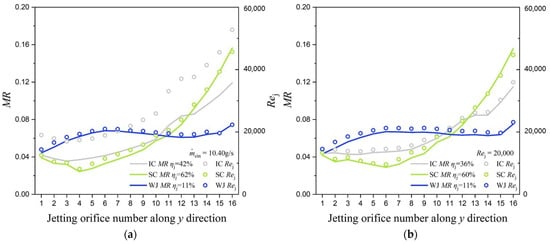
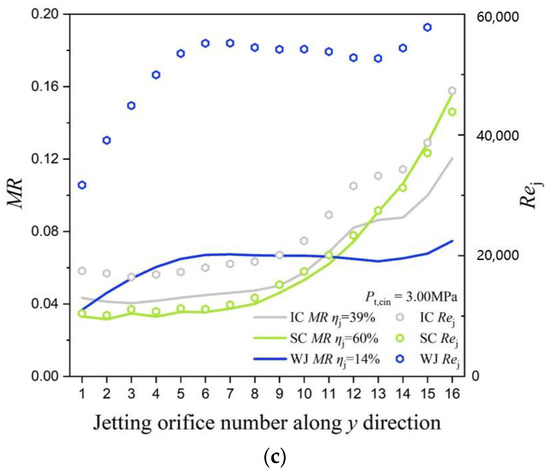
Figure 13.
Mass flow rate ratio and jetting Reynolds number comparison among different internal cooling structures; (a) Cases with the same ; (b) Cases with the same Rej; (c) Cases with the same Pt,cin.
Figure 14 illustrates the pressure ratio (PR) distribution of different internal cooling structures. Equation (6) gives the definition:
where P is the local static pressure and Pcou is the area-averaged static pressure at the outlet of the cooling chamber.
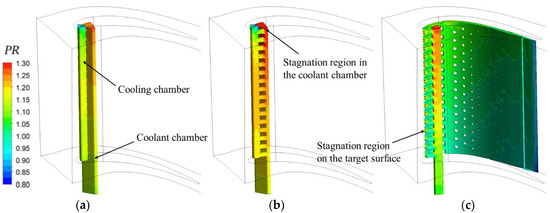
Figure 14.
Pressure ratio distribution of different internal cooling structures (Rej = 20,000); (a) Impingement cooling; (b) Swirl cooling; (c) Wall jet cooling.
The coolant chambers of all three cooling structures have a significant radial pressure gradient. The tip regions all have a high pressure ratio resulting from a centrifugal force and stagnation effect. Based on the same mechanisms, the pressure ratio distribution of cooling chambers of IC and SC are similar to those of their coolant chambers except for the outlet low pressure region. Therefore, the cooling holes at the top parts of IC and SC have a much higher pressure drop than those at the middle and bottom parts, leading to the high mass flow rate ratio of the top holes. However, the outlet of WJ is a rectangular slot at the blade trailing edge. There are many cylinder pins between the outer and inner walls on the suction side, so the effects of centrifugal force and tip stagnation are not that strong. The radial pressure gradient of the cooling channels is much less than that of the other two structures. It can be seen that the primary high pressure region in WJ is the stagnation regions on the target surfaces and in the coolant chamber. At the other regions in the wall jet structure, the pressure ratio is close to 1.05. Given that WJ’s outlet pressure is 50% lower than that of SC, the absolute value of the pressure drop between the coolant chamber and cooling chamber of WJ is inferior, contributing to its homogeneous coolant distribution in jetting orifices.
Figure 15 shows the internal streamlines of the three cooling structures viewed from three angles with the jetting Reynolds number of 20,000. In Figure 15a,b, it can be seen that the air in the coolant chamber is pushed to the pressure side by the Coriolis force, and the effect is more obvious with the height increases in the three structures. The radial velocity difference leads to the backflow in the coolant chamber, which would weaken the cooling of the suction side. The centrifugal force influences both the backflow and the swirl flow in the cooling chamber. Besides, the tip leakage flow produces additional cooling near the tip of the blade, which is not a designed function of the internal cooling structure. In Figure 15c, the Mach number inside the WJ is higher than 0.3. This is mainly because the cooling channels and inner wall limit the cross-section area of the coolant chamber. With a small coolant chamber, the flow in it is compressed and also pushed by the Coriolis force to attach to the pressure side of the blade inner surface. When the coolant’s mass flow rate is large, the pressure loss will increase dramatically, and the orifice should be wider.
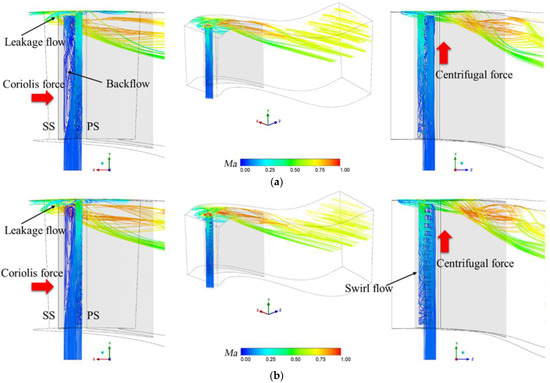
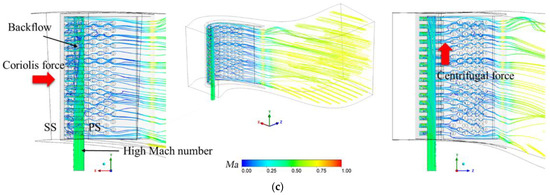
Figure 15.
Streamline comparison between different internal cooling structures (Rej = 20,000); (a) Impingement cooling; (b) Swirl cooling; (c) Wall jet impingement cooling.
Figure 16 demonstrates the streamlines and velocity contours on the sections at the middle height positions of orifices 1, 5, 9 and 13. The impinging jet inside IC forms a double swirl structure in the limited space of the cooling chamber, which helps to enhance the heat transfer on the pressure side and the suction side. However, the momentum exchange between the high- and low-velocity fluids would weaken the kinetic energy of the jet flow, which might reduce its resistance to the Crossflow in the cooling chamber and further deviate the jet from the stagnation line at the inner surface. In the SC structure, the jet flow attaches to the inner wall surface of the pressure side from the coolant chamber and forms an obvious swirling flow in the cooling chamber. With high turbulence, the swirl flow would break the boundary layer on the inner surface and enhance the cooling performance. For the WJ structure, the coolant with high radial velocity flows near orifice 1, so the jet in it would impinge the top surface of the orifice under the effect of inertial force, and the jet velocity in the middle height section of orifice 1 is low. As the radial height increases, the mass flow rate in the coolant chamber decreases, so the angle between the jet and the orifice direction decreases, maintaining a higher momentum for impinging the target surface. Under the effect of Coriolis force, the jet of WJ is always attached to the pressure side. There is an obvious separation vortex at the exit of the orifice. The sheer force of the attaching-wall jet would strengthen this separation vortex, further enhancing the heat transfer intensity at the leading edge region. This flow characteristic is the same in channels of different heights.
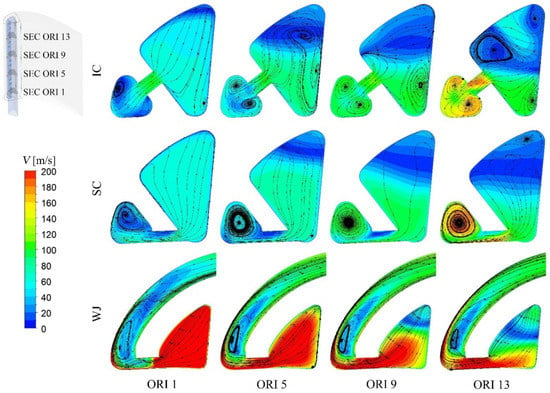
Figure 16.
Streamline and velocity contours in mid-span section with different internal cooling structures (Rej = 20,000).
In general, WJ combines the advantages of IC and SC. The spent coolant at the leading edge is extracted away through the downstream channels. The jet could impinge the target surface without unnecessary mixing, and the high turbulence generated by the separation vortex enhances the heat transfer intensity. The Coriolis force formed by the rotor’s rotation forces the coolant air to adhere to the inner wall surface on the pressure side, preventing the jet from leaving the target surface. The parallel cooling channels eliminate the common Crossflow effect and make the flow distribution of the orifices more even. The outlet at the trailing edge reduces the pressure in the entire cooling structure to a low level, which means the pressure of the incoming coolant could be lower to improve the efficiency of the turbine.
3.3. Heat Transfer Characteristics
In this section, the overall cooling effectiveness, blade temperature distribution, and internal heat transfer coefficient of IC, SC, and WJ are compared to study the heat transfer characteristics in detail. Figure 17 shows this span-wise averaged overall cooling effectiveness around the blade leading edge with three cooling structures. Since the tip leakage flows of IC and SC structures would provide additional cooling to the blade, the figure shows the average values of overall cooling effectiveness for two lateral ranges. The ‘sp’ represents the lateral average of the full blade height range, and the ‘msp’ represents the lateral average of the ‘main region’, which is 20–80% of the blade height. It can be found that the leakage flow mainly affects the downstream of the suction side and has little effect on WJ. The lateral average overall cooling effectiveness distribution trends of the three structures are similar. The Φsp on the suction side is low, on the pressure side is high, and there is a peak on each side. The WJ has significant advantages near the leading edge stagnation line and on the suction side. With the same jetting Reynolds number, the Φmsp value of WJ is 37.3% and 18.8% higher than that of IC and SC at the leading edge stagnation line, respectively, and 37–59% and 19–54% higher on the suction side, respectively. With the same total pressure at the coolant inlet, the Φmsp value of WJ is 54.5% and 41.4% higher than IC and SC at the stagnation line, respectively, and 30–80% and 20–90% higher, respectively, at the whole leading edge.
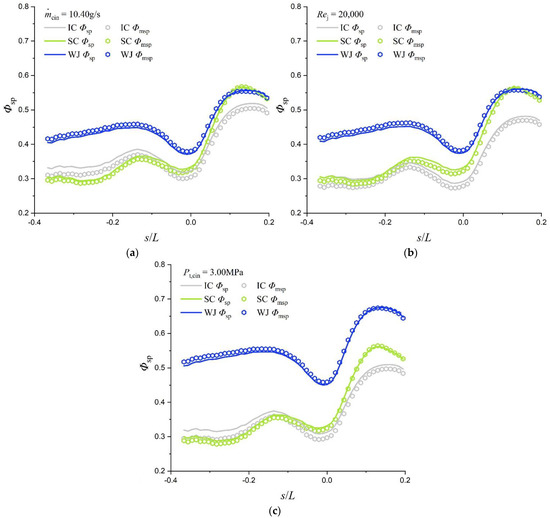
Figure 17.
Span-wise averaged overall cooling effectiveness around blade leading edge with three cooling structures; (a) Cases with the same ; (b) Cases with the same Rej; (c) Cases with the same Pt,cin.
Figure 18 shows the overall cooling effectiveness distribution of different internal cooling structures at the jetting Reynolds number of 20,000. The flow structures in the coolant chambers and cooling chambers of IC and SC are greatly affected by centrifugal force. The top jet holes’ mass flow rate is much higher than that of the bottom jet holes, which leads to the upper blade being cooler. The Coriolis force pushes the coolant to attach to the pressure side, resulting in higher cooling effectiveness than that of the suction side. The Crossflow destroys the jets’ strong cooling performance around the leading edge stagnation line and the heat load here is the highest, so the cooling in this area is insufficient. In the WJ structure, the influence of the centrifugal force in the cooling cavity is limited in each channel. Hence, the overall cooling effectiveness is relatively uniform along the blade span. Since the orifice is connected to the coolant chamber and cooling channels on the pressure side, the Coriolis force enhances the cooling effect of the wall jet and prevents the jet from leaving the inner surface. This generates sufficient cooling at the stagnation line.
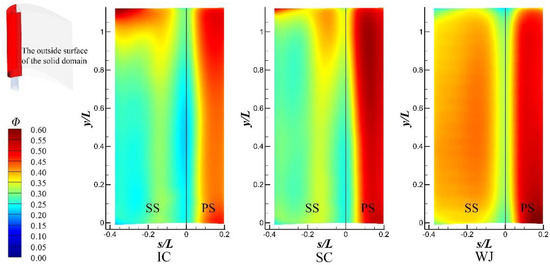
Figure 18.
Overall cooling effectiveness distribution of different internal cooling structures (Rej = 20,000).
Figure 19 exhibits the temperature distributions in sections with different heights of the studied internal cooling structures. In combination with Figure 18, it can be found that the heat transfer peak on the suction side of IC and SC is generated by the inner wall between the coolant chamber and the cooling chamber. In contrast, the pressure side peak is generated by the attaching-wall flow in the coolant chamber. Simultaneously, the cooling chamber has insufficient capacity to dissipate the high heat loads near the stagnation line. The jetting hole of IC is at the center of the inner wall, so the temperature distribution is relatively uniform.
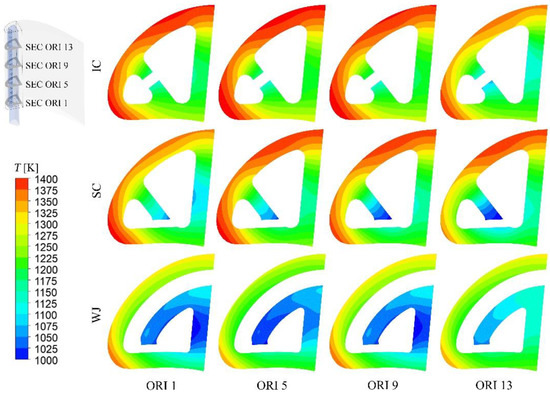
Figure 19.
Temperature distributions in sections with different heights of the studied internal cooling structures (Rej = 20,000).
In contrast, SC jetting hole is near the pressure side, resulting in an obvious temperature gradient in the inner wall. The suction side flow channel of WJ is continuous, leading to the small temperature gradient of the outer wall. Similar to SC, the pressure side of WJ has a high cooling performance. The only problem is that the inner wall of WJ is too long to reduce the temperature gradient in it, which means the structure needs to be further optimized.
To further analyze the inner heat transfer characteristics, the Nusselt number distribution on target surfaces of different internal cooling structures is illustrated in Figure 20. The data at the stagnation line of the target surfaces are listed in Figure 21. The results of IC show that the impingement cooling jet is seriously affected by the Crossflow. Except for orifice 1, the jet stagnation points of other orifices are located on the pressure side and the suction side, which cannot accurately cool the blade’s stagnation area. The performance of swirl cooling is not that bad. The swirl generated by the jet hole could accurately cool the stagnation line of the leading edge and has higher heat transfer intensity, but the Nusselt number distribution is uneven along with the height. By contrast, the high heat transfer region of WJ accurately and uniformly covers the stagnation and the pressure side of the blade without the effect of crossflow.
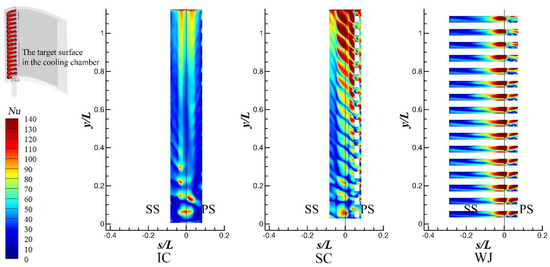
Figure 20.
Heat transfer coefficient distribution on target surfaces of different internal cooling structures (Rej = 20,000).
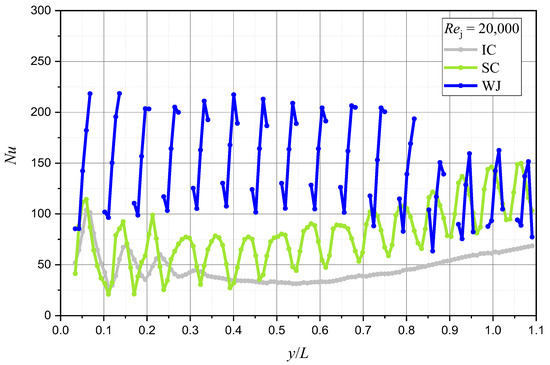
Figure 21.
Heat transfer coefficient distribution at the stagnation line of the target surfaces (Rej = 20,000).
The Nusselt number of WJ is around two to four times higher than that of IC and SC. Besides, the area of the region of wall jet cooling is significantly larger than the other two structures. Generally speaking, the wall jet cooling structure could better protect the blade.
4. Conclusions
A novel wall jet cooling scheme for the turbine blade leading edge is presented in this paper. The actual flow characteristic and cooling performance of a blade with wall jet cooling was studied numerically under turbine operating conditions. The wall jet cooling and two conventional cooling structures, including impingement with a single row of jets and swirl cooling, were compared with three different coolant inlet boundary conditions. The total heat flux, mass flow rate distribution, overall cooling effectiveness, pressure ratio and inner surface Nusselt number are analyzed in detail. The main conclusions are drawn as follows:
(1) The cooling surface area of wall jet cooling is larger than that of impingement cooling and swirl cooling due to the multi-channel design. Among the three cooling methods, wall jet cooling has the highest total heat flux, area-averaged overall cooling effectiveness no matter under which coolant inlet boundary condition studied.
(2) The coolant in wall jet cooling flows along the parallel channels on the suction side but not the radial direction, and the outlet of the design is set at the trailing edge of the blade, where the static pressure is lower than that of the leading edge. Therefore, wall jet cooling has a uniform radial pressure gradient and a moderate mass flow rate distribution of orifices. With the same jetting Reynolds number, the coolant inlet total pressure of wall jet cooling is much lower than that of conventional methods, which means less penalty on power output and engine efficiency.
(3) With the same jetting Reynolds number, the Φmsp (main region laterally-averaged overall cooling effectiveness) value of WJ is 37.3% and 18.8% higher than that of IC and SC at the leading edge stagnation line respectively, and 37–59% and 19–54% higher on the suction side. With the same total pressure at the coolant inlet, the Φmsp value of WJ is 54.5% and 41.4% higher than IC and SC at the stagnation line respectively, and 30–80% and 20–90% higher respectively at the whole leading edge.
(4) The suction side flow channel of wall jet cooling is continuous, leading to the small temperature gradient of the outer wall. The pressure side of WJ has high cooling performance, resulting from the attaching-wall jet under the effect of Coriolis force. The only problem is that the inner wall of the design is too long to reduce the temperature gradient in it, which needs to be further optimized.
(5) The high heat transfer region of wall jet cooling accurately and uniformly covers the stagnation and the pressure side of the blade without the influence of cross flow, and the area of the region is significantly larger than that of the single row jet impingement cooling and swirl cooling.
(6) By dividing the cooling chamber of jets into a plurality of channels, the Crossflow is thoroughly avoided and the cooling efficiency of jets with a short impingement distance is improved significantly under turbine operating conditions, which might be an enlightening concept for industrial designers.
Author Contributions
Conceptualization, Q.D.; methodology, W.H.; validation, W.H. and H.W.; writing—original draft preparation, W.H. and H.W.; writing—review and editing, Q.D.; supervision, Q.D.; project administration, Z.F. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Science and Technology Major Project (2017-III-0009-0035).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Symbols | |
| Achm | area of the coolant chamber surface, m2 |
| Aocs | area of the other cooling surface, m2 |
| Atar | area of the target surface, m2 |
| BR | blowing ratio |
| Dhy | hydraulic diameter, mm |
| Dim | diameter of impingement cooling hole, mm |
| Hch | height of bended channel, mm |
| h | heat transfer coefficient, W/(m2·K) |
| I | impingement distance, mm |
| Mais | isentropic Mach number |
| MR | ratio of jet mass to total coolant mass |
| mainstream mass flow rate, kg/s | |
| mideal | calculational mass flow rate in film hole with incompressible assumption, kg/s |
| mm | coolant air mass flow rate, kg/s |
| Nu | Nusselt number |
| Nua | area-averaged Nusselt number |
| Nuc | area-averaged Nusselt number on the whole internal cooling surfaces |
| Nuci | circumferentially-averaged Nusselt number |
| Nusp | span-wise averaged Nusselt number |
| Nutar | area-averaged Nusselt number on the target surface |
| qw | wall heat flux, W/m2 |
| P | static pressure, Pa |
| p | jetting orifice/hole pitch, mm |
| Pt,cin | total pressure at the coolant inlet, MPa |
| Pcou | total pressure at the coolant outlet, MPa |
| PR | pressure ratio |
| R | turning internal radius of the cooling channel, mm |
| Re | Reynolds number |
| Rej | Reynolds number based on the hydraulic diameter of the jetting orifice/hole |
| r | radius of swirl pipe, mm |
| s | stream-wise surface coordinate, mm |
| s’ | stream-wise surface coordinate on the target surface, mm |
| t | outer wall thickness of the blade, mm |
| tinner | inner cooling wall thickness of the blade, mm |
| Tew | external wall temperature, K |
| Tc | total temperature at coolant plenum inlet, K |
| Trec | uncooled blade wall temperature, K |
| Tw | target wall temperature, K |
| U | mean velocity, m/s |
| Wch | width of cooling channel, mm |
| Win | jetting orifice width, mm |
| x | stream-wise distance, mm |
| y | height direction coordinate, mm |
| Greek Symbols | |
| μ | fluid dynamic viscosity, kg/(m·s) |
| ρ | fluid density, kg/m3 |
| λ | fluid thermal conductivity, W/(m·K) |
| ηj | mass flow nonuniformity coefficient |
| Φ | overall cooling effectiveness |
| Φmsp | main region span-wise averaged overall cooling effectiveness |
| Φsp | span-wise averaged overall cooling effectiveness |
| Abbreviation | |
| CHT | Conjugate Heat Transfer |
| IC | Impingement Cooling |
| RANS | Reynolds-Averaged Navier-Stokes |
| SC | Swirl Cooling |
| WJ | Wall Jet cooling |
References
- Elnady, T.; Hassan, I.; Kadem, L.; Lucas, T. Cooling Effectiveness of Shaped Film Holes for Leading Edge. Exp. Therm. Fluid Sci. 2013, 44, 649–661. [Google Scholar] [CrossRef]
- Chowdhury, N.H.K.; Qureshi, S.A.; Zhang, M.J.; Han, J.C. Influence of Turbine Blade Leading Edge Shape on Film Cooling with Cylindrical Holes. Int. J. Heat Mass Transf. 2017, 115, 895–908. [Google Scholar] [CrossRef]
- Bu, S.; Yang, Z.; Zhang, W.; Liu, H.; Sun, H. Research on the Thermal Performance of Matrix Cooling Channel with Response Surface Methodology. Appl. Therm. Eng. 2016, 109, 75–86. [Google Scholar] [CrossRef]
- Sun, H.O.; Sun, T.; Yang, L.F.; Bu, S.; Luan, Y.G. Effect of Bleed Hole on Internal Flow and Heat Transfer in Matrix Cooling Channel. Appl. Therm. Eng. 2018, 136, 419–430. [Google Scholar] [CrossRef]
- Siw, S.C.; Chyu, M.K.; Karaivanov, V.G.; Slaughter, W.S.; Alvin, M.A. Influence of Internal Cooling Configuration on Metal Temperature Distributions of Future Coal-Fuel Based Turbine Airfoils; ASME Paper No. GT2009-59829; ASME: New York, NY, USA, 2009. [Google Scholar]
- Liu, L.L.; Zhu, X.C.; Liu, H.; Du, Z.H. Effect of Tangential Jet Impingement on Blade Leading Edge Impingement Heat Transfer. Appl. Therm. Eng. 2018, 130, 1380–1390. [Google Scholar] [CrossRef]
- Martin, H. Heat and Mass Transfer between Impinging Gas Jets and Solid Surfaces. Adv. Heat Transf. 1977, 13, 1–60. [Google Scholar]
- Zuckerman, N.; Lior, N. Jet Impingement Heat Transfer: Physics, Correlations, and Numerical Modeling. Adv. Heat Transf. 2006, 39, 565–631. [Google Scholar]
- Weigand, B.; Spring, S. Multiple Jet Impingement—A Review. Heat Transf. Res. 2011, 42, 101–142. [Google Scholar] [CrossRef]
- Chupp, R.E.; Helms, H.E.; Mcfadden, P.W. Evaluation of Internal Heat Transfer Coefficients for Impingement Cooled Turbine Airfoils. J. Aircr. 1969, 6, 203–208. [Google Scholar] [CrossRef]
- Taslim, M.E.; Setayeshgar, L.; Spring, S.D. An Experimental Evaluation of Advanced Leading Edge Impingement Cooling Concepts. J. Turbomach. 2000, 123, 147–153. [Google Scholar] [CrossRef]
- Ramakumar, B.V.N.; Joshi, D.S.; Sridhar, M.; Jong, S.; Liu, J.S.; Crites, D.C. Computational Investigation of Flow and Heat Transfer Characteristics of Impingement Cooling Channel. In Turbo Expo: Power for Land, Sea, and Air, Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013; ASME Paper No. GT2013-94553; ASME: New York, NY, USA, 2013. [Google Scholar]
- Parneix, S.; Behnia, M.; Durbin, P.A. Prediction of Turbulent Heat Transfer in an Axisymmetric Jet Impinging on a Heated Pedestal. J. Heat Transf. 1999, 121, 43–49. [Google Scholar] [CrossRef]
- Kondo, Y.; Matsushima, H.; Komatsu, T. Optimization of Pin-Fin Heat Sink for Impingement Cooling in Electronic Packaging. J. Electron. 2000, 122, 240–246. [Google Scholar]
- El-Gabry, L.A.; Kaminski, D.A. Experimental investigation of local heat transfer distribution on smooth and roughened surfaces under an array of angled impinging jets. J. Turbomach. 2005, 127, 532–544. [Google Scholar] [CrossRef]
- Kanokjaruvijit, K.; Martinezbotas, R.F. Heat Transfer Correlations of Perpendicularly Impinging Jets on a Hemispherical-Dimpled Surface. Int. J. Heat Mass Transf. 2010, 53, 3045–3056. [Google Scholar] [CrossRef]
- Xing, Y.; Weigand, B. Experimental Investigation of Impingement Heat Transfer on a Flat and Dimpled Plate with Different Crossflow Schemes. Int. J. Heat Mass Transf. 2010, 53, 3874–3886. [Google Scholar] [CrossRef]
- Hrycak, P. Heat Transfer from Impinging Jets to a Flat Plate with Conical and Ring Protuberances. Int. J. Heat Mass Transf. 1984, 27, 2145–2154. [Google Scholar] [CrossRef]
- Kreith, F.; Margolis, D. Heat Transfer and Friction in Turbulent Vortex Flow. Appl. Sci. Res. 1959, 8, 457–473. [Google Scholar] [CrossRef]
- Qian, C.; Flannery, K.; Saito, K.; Downs, J.; Soechting, F. Innovative Vortex Cooling Concept and Its Application to Turbine Airfoil Trailing Edge Cooling Design. In Proceedings of the Joint Propulsion Conference & Exhibit, Seattle, WA, USA, 6–9 July 1997; pp. 1997–3013. [Google Scholar]
- Du, C.H.; Li, L.; Wu, X.; Feng, Z.P. Effect of Jet Nozzle Geometry on Flow and Heat Transfer Performance of Vortex Cooling for Gas Turbine Blade Leading Edge. Appl. Therm. Eng. 2016, 93, 1020–1032. [Google Scholar] [CrossRef]
- Liu, Z.; Feng, Z.P. Numerical Simulation on the Effect of Jet Nozzle Position on the Impingement Cooling of Gas Turbine Blade Leading Edge. Int. J. Heat Mass Transf. 2011, 54, 4949–4959. [Google Scholar] [CrossRef]
- Kusterer, K.; Lin, G.; Bohn, D.; Sugimoto, T.; Tanaka, R.; Kazari, M. Heat Transfer Enhancement for Gas Turbine Internal Cooling by Application of Double Swirl Cooling Chambers. In Turbo Expo: Power for Land, Sea, and Air, Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013; ASME Paper No. GT2013-94774; ASME: New York, NY, USA, 2013. [Google Scholar]
- Lin, G.; Kusterer, K.; Bohn, D.; Sugimoto, T.; Tanaka, R.; Kazari, M. Investigation on Heat Transfer Enhancement and Pressure Loss of Double Swirl Chambers Cooling. Propuls. Power Res. 2013, 2, 177–187. [Google Scholar] [CrossRef] [Green Version]
- Kusterer, K.; Lin, G.; Bohn, D.; Sugimoto, T.; Tanaka, R.; Kazari, M. Leading Edge Cooling of a Gas Turbine Blade with Double Swirl Chambers. In Turbo Expo: Power for Land, Sea, and Air, Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014; ASME Paper No. GT2014-25851; ASME: New York, NY, USA, 2014. [Google Scholar]
- Han, J.C.; Dutta, S.; Ekkad, S. Gas Turbine Heat Transfer and Cooling Technology; Taylor & Francis: New York, NY, USA, 2000. [Google Scholar]
- Rekingen, J.H.; Othmarsingen, A.K.; Mandach, T.S.; Seon, R.T. Apparatus for Impingement Cooling. U.S. Patent No. 5467815, 8 June 1995. [Google Scholar]
- Hebert, R.; Ekkad, S.V.; Khanna, V.; Abreu, M.; Moon, H.K. Heat Transfer Study of a Novel Low-Crossflow Design for Jet Impingement. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Paper No. IMECE2004-60468. Anaheim, CA, USA, 13–19 November 2004; pp. 583–588. [Google Scholar]
- Liu, K. A Combustor Assembly with Impingement Plates for Redirecting Cooling Air Flow in Gas Turbine Engines. WO Patent No. 2017190967A1, 9 November 2017. [Google Scholar]
- Zhang, L.Z.; Yin, J.; Moon, H.K. Airfoil for Turbomachine and Airfoil Cooling Method. US Patent No. US 2017/0248022 A1, 19 February 2019. [Google Scholar]
- He, W.; Deng, Q.H.; He, J.; Gao, T.Y.; Feng, Z.P. Effects of Jetting Orifice Geometry Parameters and Channel Reynolds Number on Bended Channel Cooling for a Novel Internal Cooling Structure. In Turbo Expo: Power for Land, Sea, and Air, Proceedings of the ASME Turbo Expo 2019: Turbine Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019; ASME Paper No. GT2019-90421; ASME: New York, NY, USA, 2019. [Google Scholar]
- He, W.; Deng, Q.H.; Yang, G.Y.; Feng, Z.P. Effects of Turning Angle and Turning Internal Radius on Channel Impingement Cooling for a Novel Internal Cooling Structure. In Turbo Expo: Power for Land, Sea, and Air, Proceedings of the ASME Turbo Expo 2020: Turbine Technical Conference and Exposition, Online, 21–25 September 2020; ASME Paper No. GT2020-16115; ASME: New York, NY, USA, 2020. [Google Scholar]
- Timko, L.P. Energy Efficient Engine High Pressure Turbine Component Test Performance Report; NASA Contractor Report 168289; NASA: Washington, DC, USA, 1984.
- Takeshi, H.; Tomoki, T.; Ryozo, T.; Masanori, R.; Masahide, K. Application of Conjugate Heat Transfer Analysis to Improvement of Cooled Turbine Vane and Blade for Industrial Gas Turbine. In Turbo Expo: Power for Land, Sea, and Air, Proceedings of the ASME Turbo Expo 2018: Turbine Technical Conference and Exposition, Oslo Norway, 11–15 June 2018; ASME Paper No. GT2018-75669; ASME: New York, NY, USA, 2018. [Google Scholar]
- He, L.; Oldfield, M.L.G. Unsteady Conjugate Heat Transfer Modeling. J. Turbomach. 2011, 133, 031022. [Google Scholar] [CrossRef]
- Xing, Y.F.; Spring, S.; Weigand, B. Experimental and Numerical Investigation of Heat Transfer Characteristics of Inline and Staggered Arrays of Impinging Jets. J. Heat Transf. 2010, 132, 53–58. [Google Scholar] [CrossRef]
- Ligrani, P.M.; Hedlund, C.R.; Babinchak, B.T.; Thambu, R.; Moon, H.K.; Glezer, B. Flow Phenomena in Swirl Chambers. Exp. Fluids 1998, 24, 254–264. [Google Scholar] [CrossRef]
- Ling, J.P.C.W.; Ireland, P.T.; Harvey, N.W. Measurement of Heat Transfer Coefficient Distributions and Flow Field in a Model of a Turbine Blade Cooling Passage with Tangential Injection. In Turbo Expo: Power for Land, Sea, and Air, Proceedings of the ASME Turbo Expo 2006: Turbine Technical Conference and Exposition, Barcelona, Spain, 8–11 May 2006; ASME Paper No. GT2006-90352; ASME: New York, NY, USA, 2006. [Google Scholar]
- Dees, J.E.; Bogard, D.G.; Ledezma, G.A.; Laskowski, G.M.; Tolpadi, A.K. Experimental Measurements and Computational Predictions for an Internally Cooled Simulated Turbine Vane with 90 Degree Rib Turbulators. In Turbo Expo: Power for Land, Sea, and Air, Proceedings of the ASME Turbo Expo 2010: Turbine Technical Conference and Exposition, Glasgow, UK, 14–18 June 2010; ASME Paper No. GT2010-23004; ASME: New York, NY, USA, 2010. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).