Mechanism and Performance Differences between the SSG/LRR-ω and SST Turbulence Models in Separated Flows
Abstract
:1. Introduction
2. Turbulence Models
3. Case Descriptions and Calculation Results
3.1. Two-Dimensional NASA Wall-Mounted Hump Separated Flow
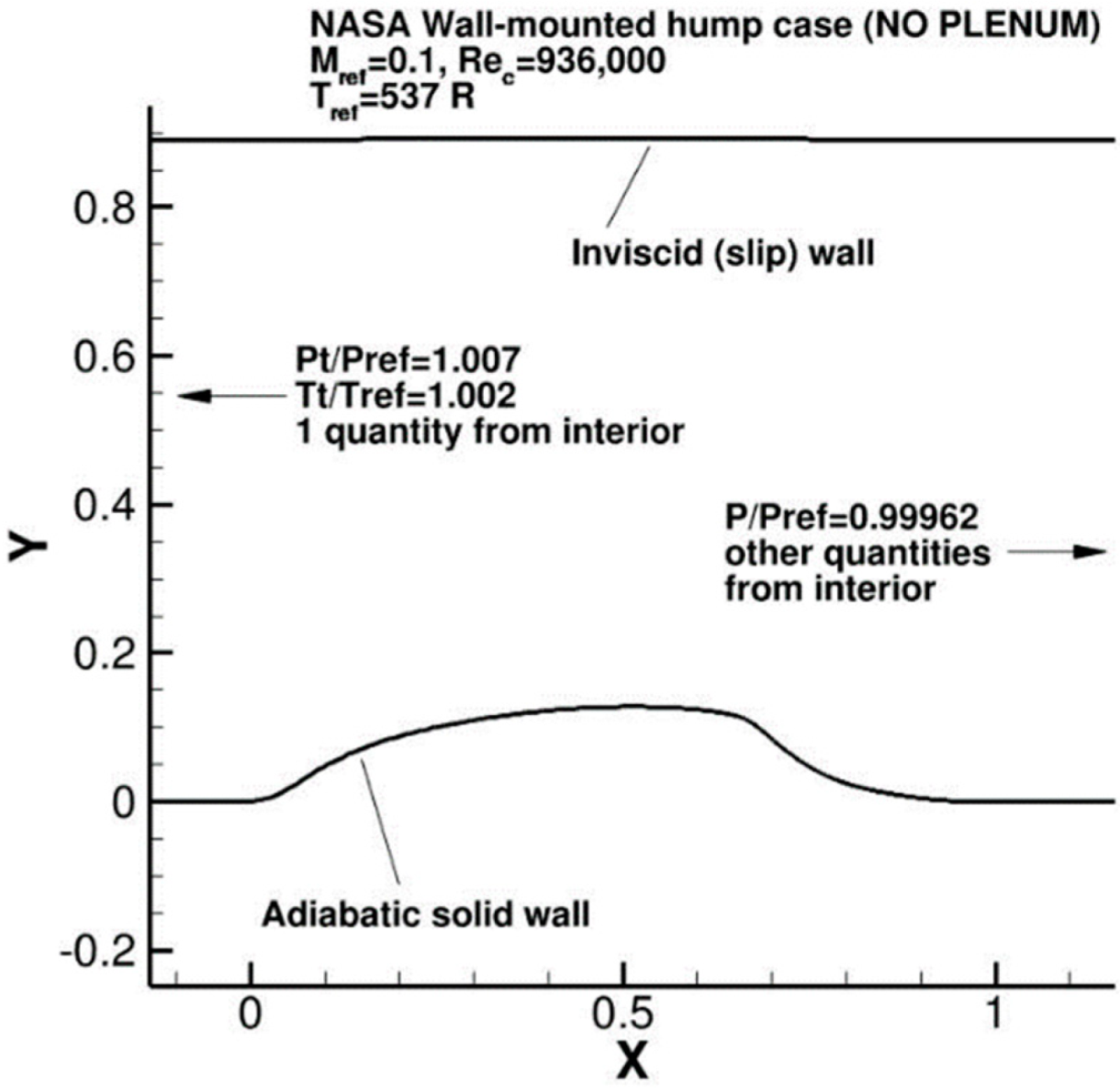
3.1.1. Case Description
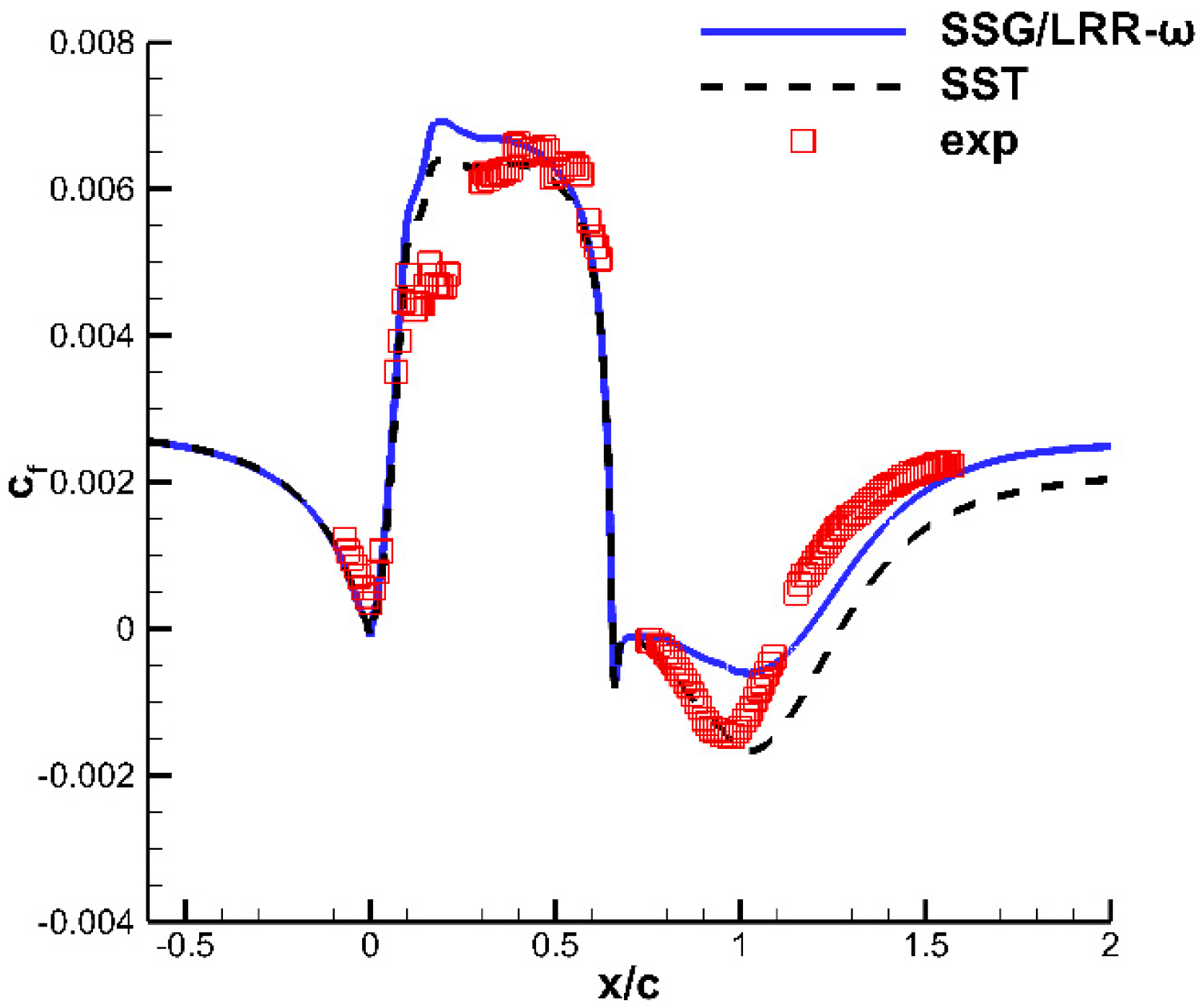
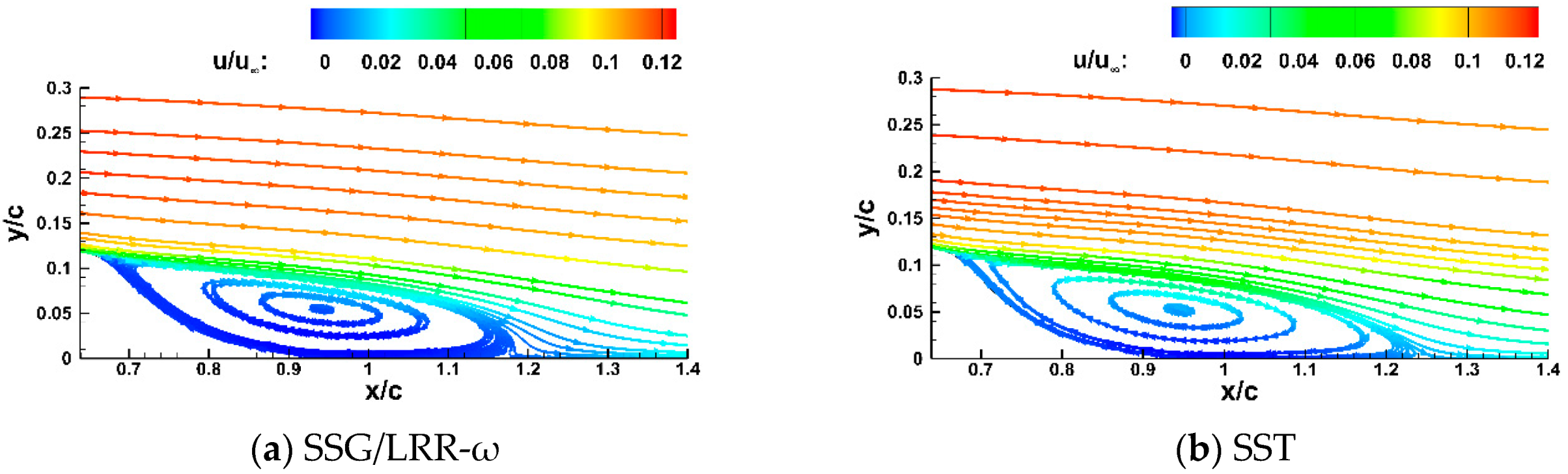
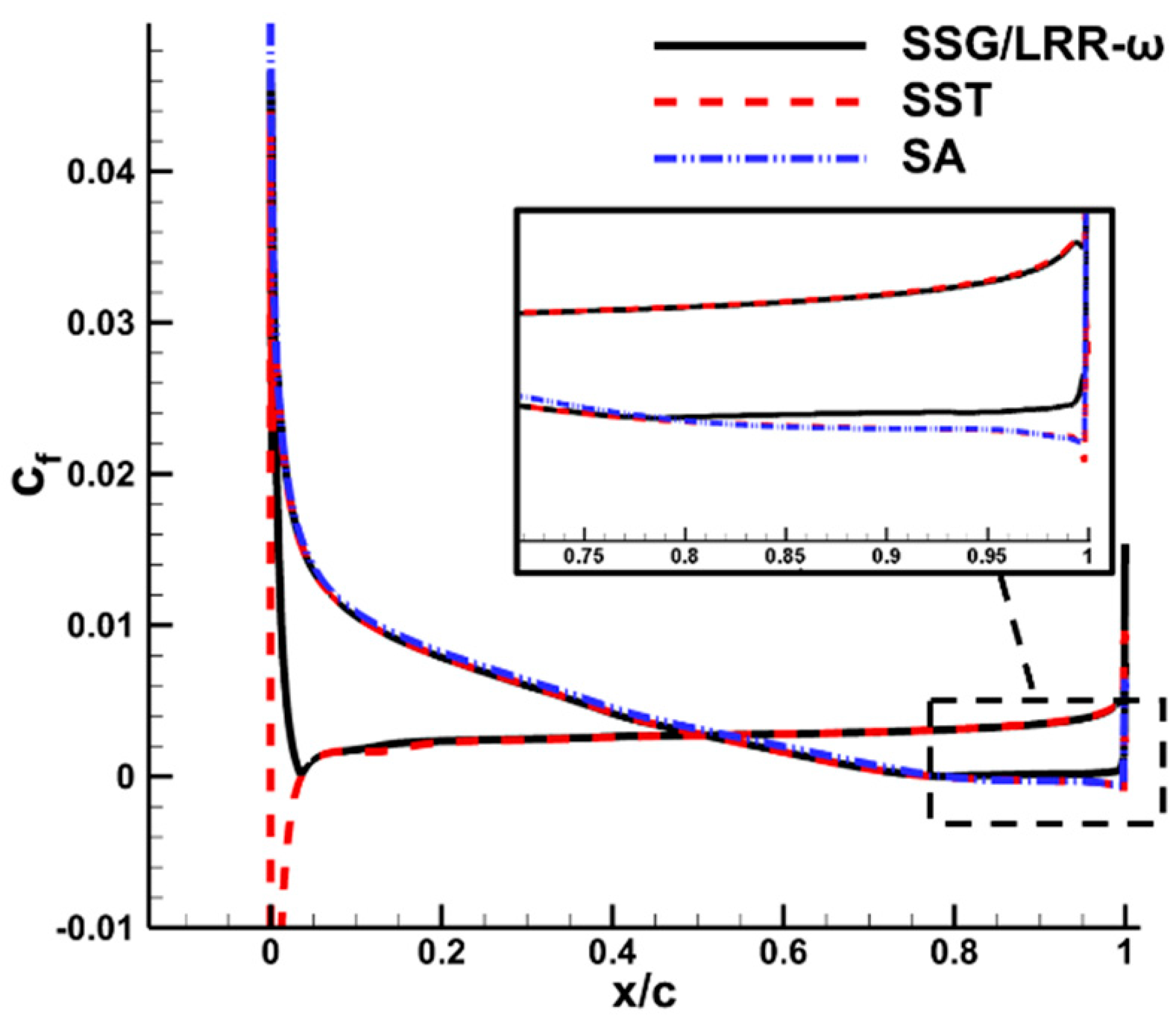
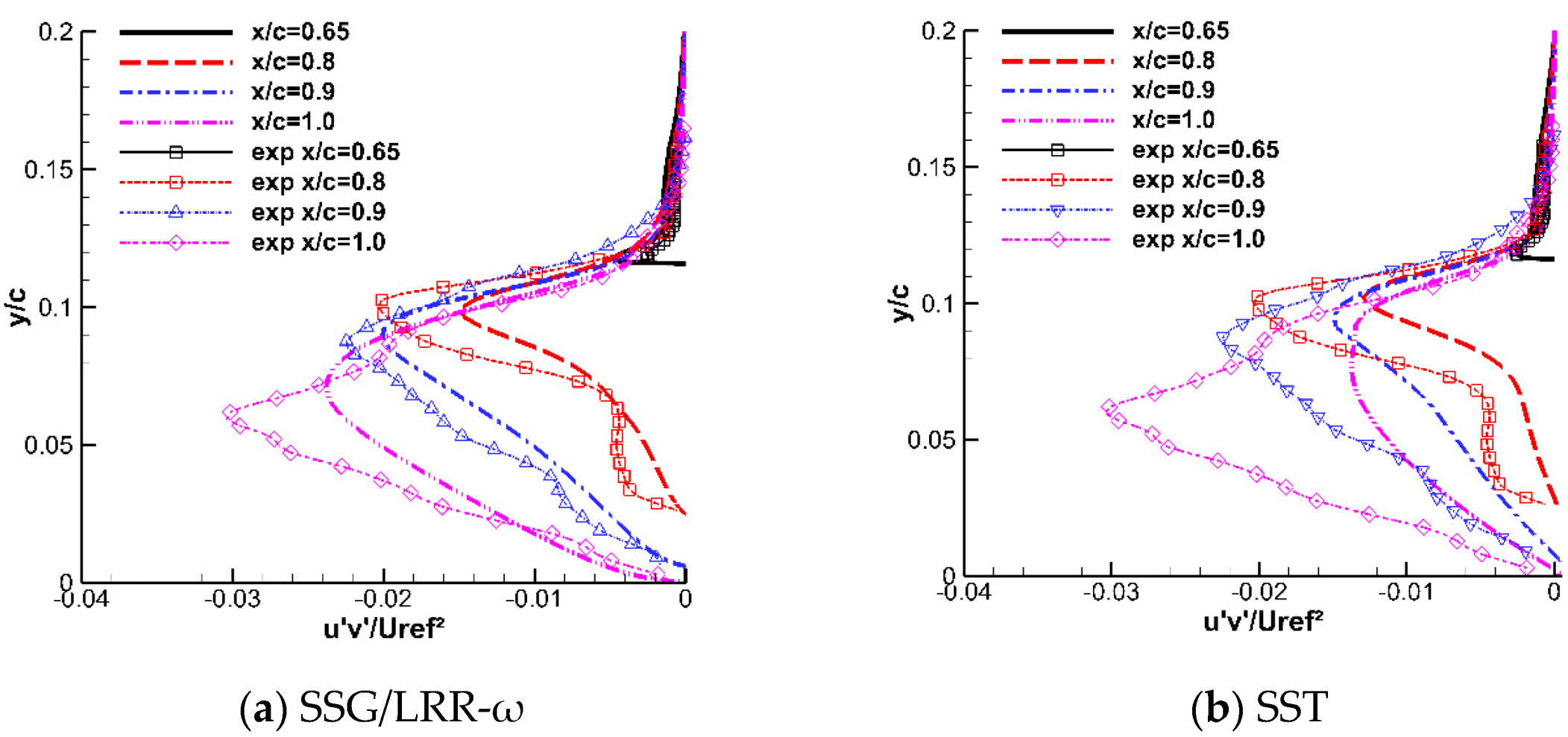
3.1.2. Calculation Results
3.2. Subsonic Flow around the NACA 4412 Airfoil
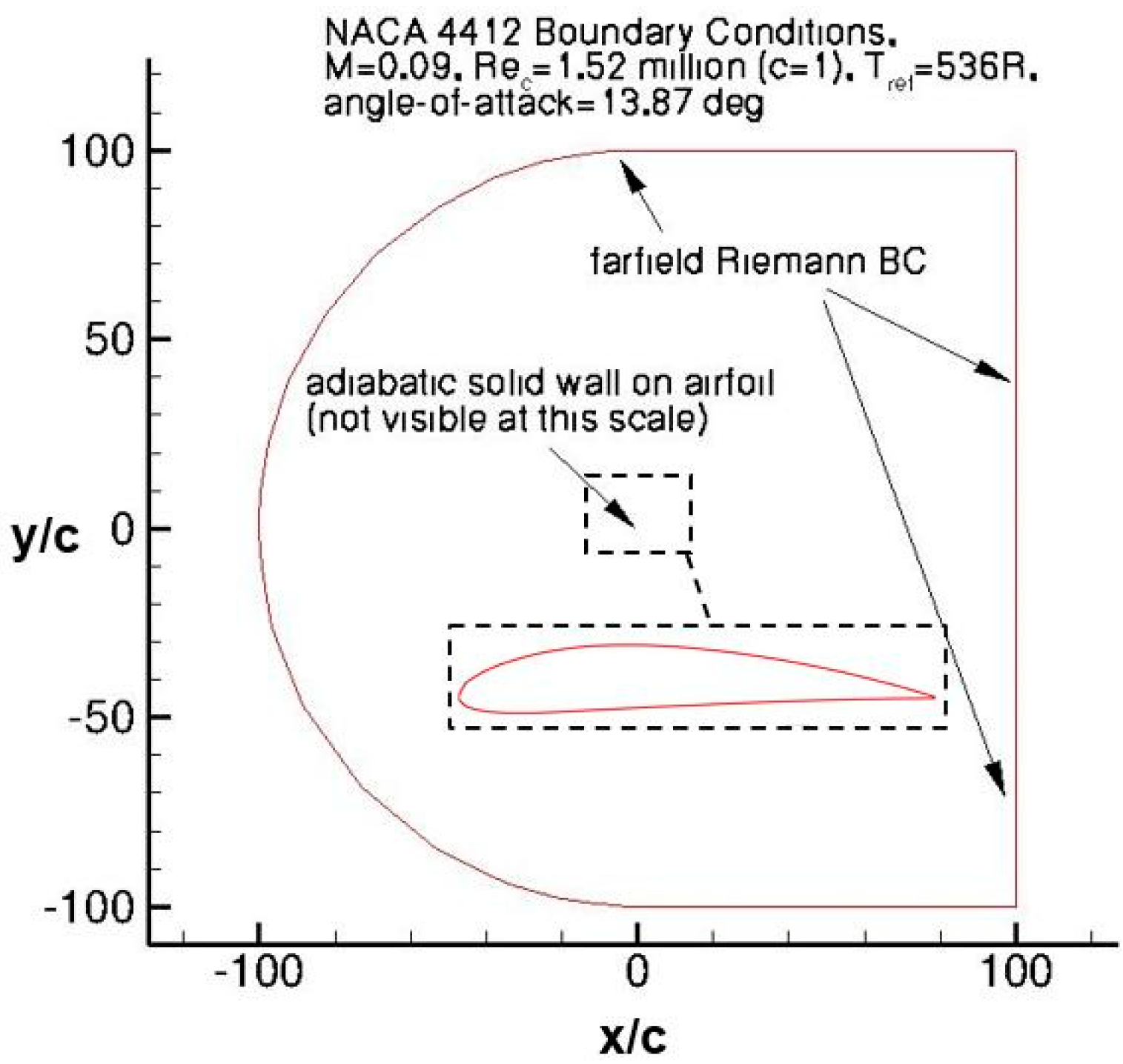
3.2.1. Case Description
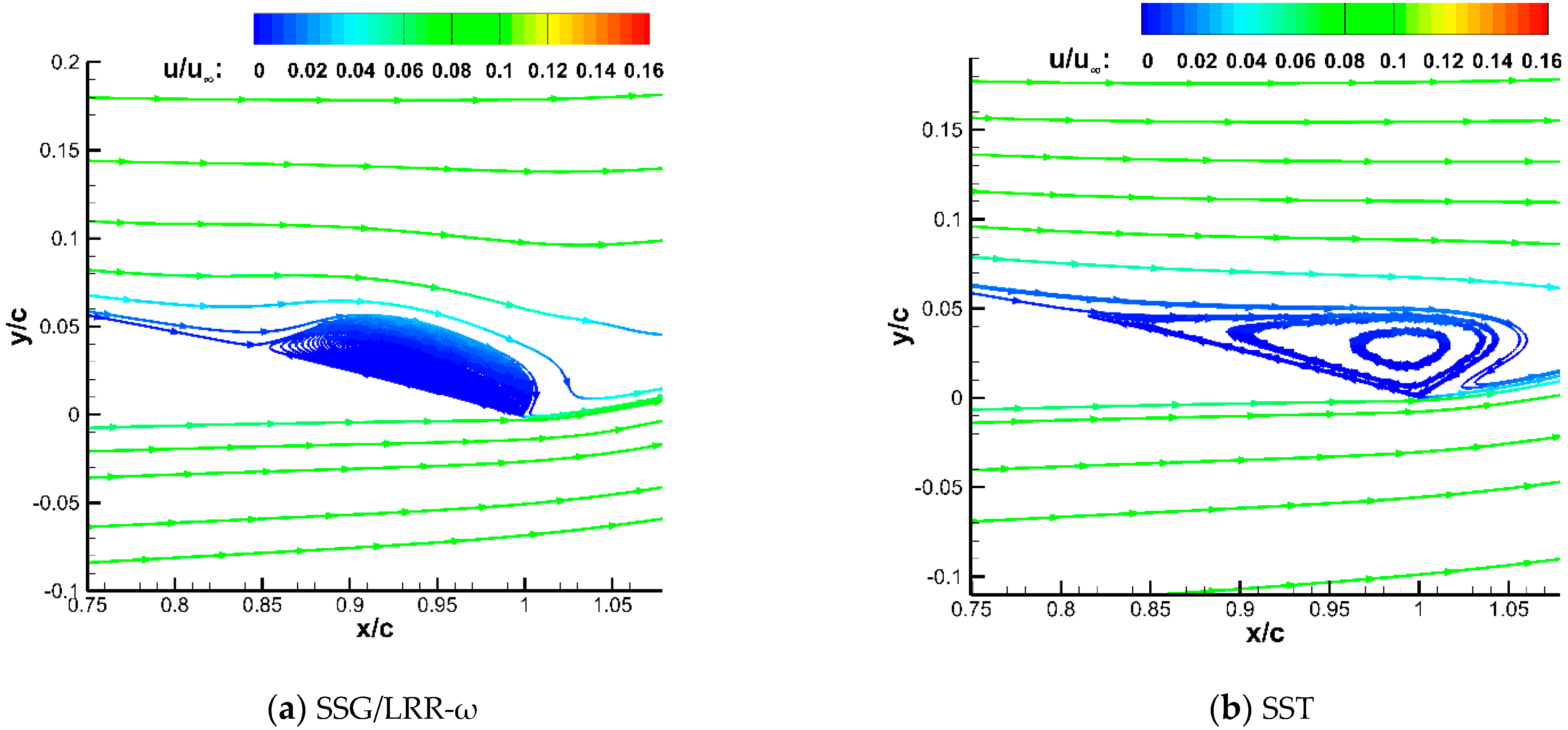
3.2.2. Calculation Results
3.3. Axisymmetric Transonic Bump
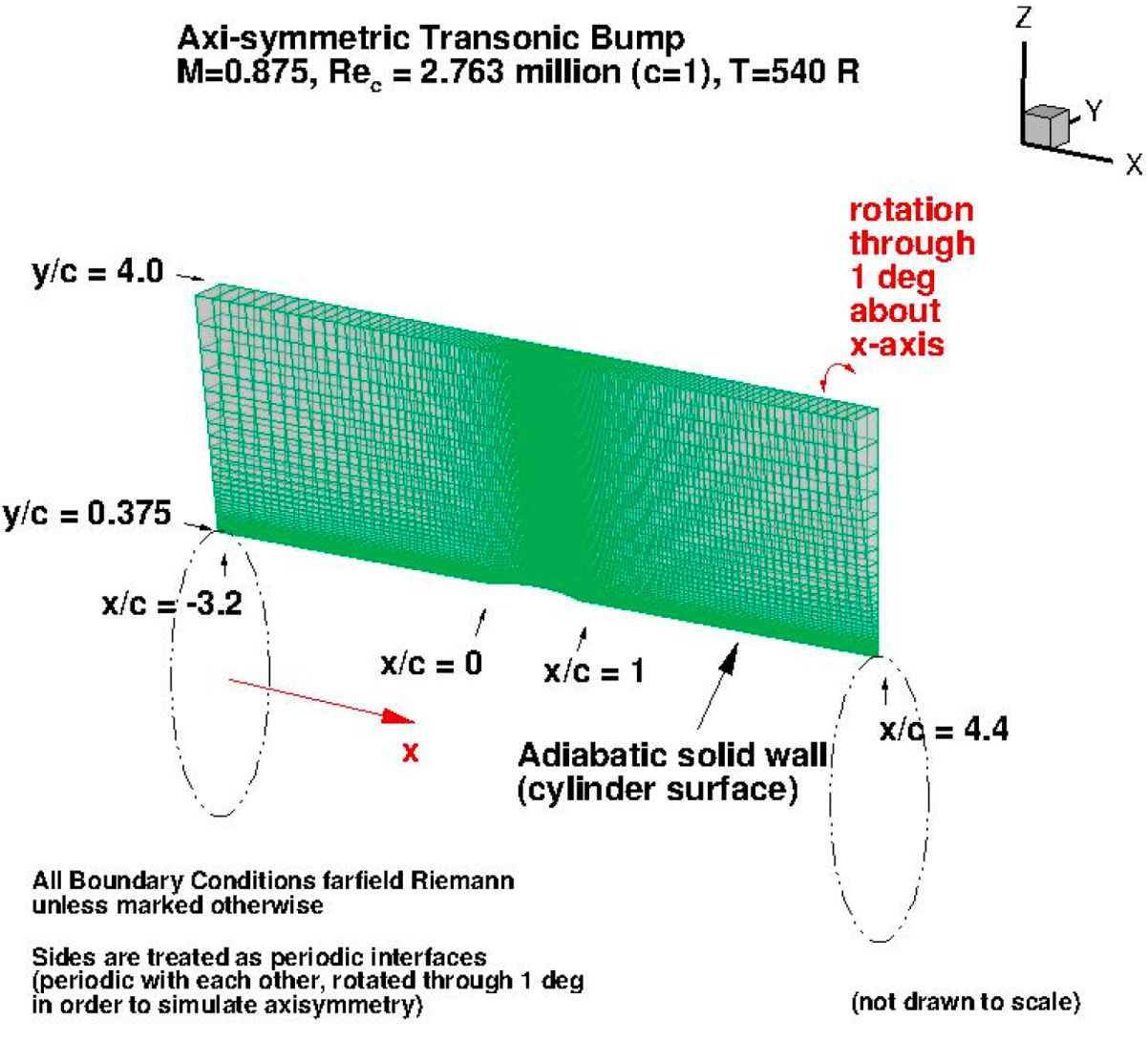
3.3.1. Case Description
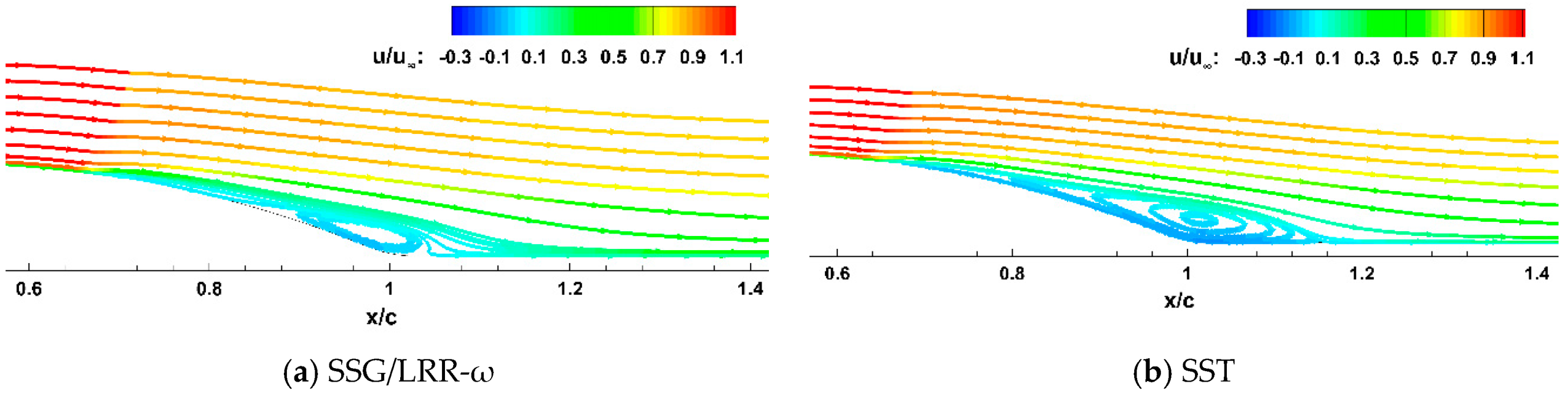
3.3.2. Calculation Results
4. Analysis of Differences in Model Performance and Mechanism Exploration
4.1. Advanced Separation
4.1.1. Separation Mechanism and Critical Physical Properties
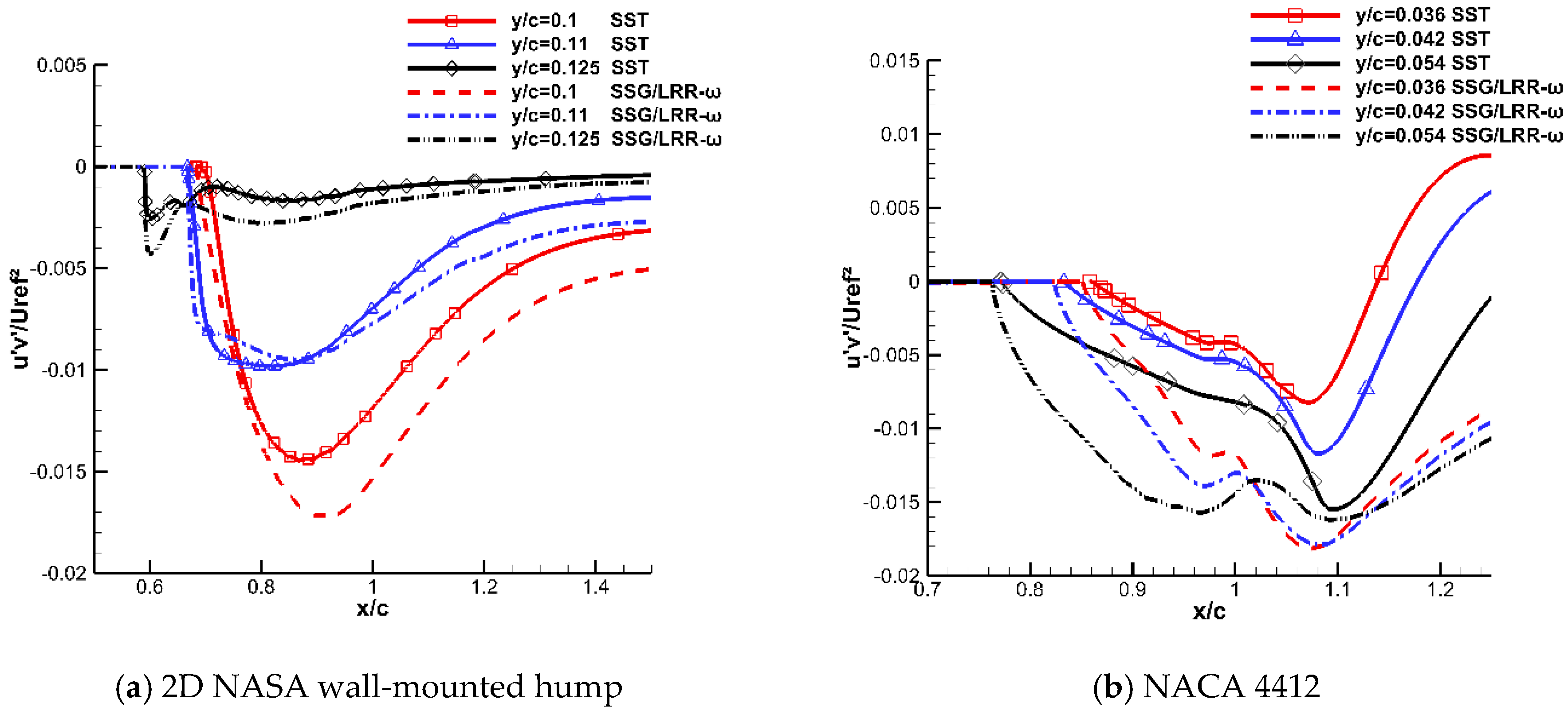
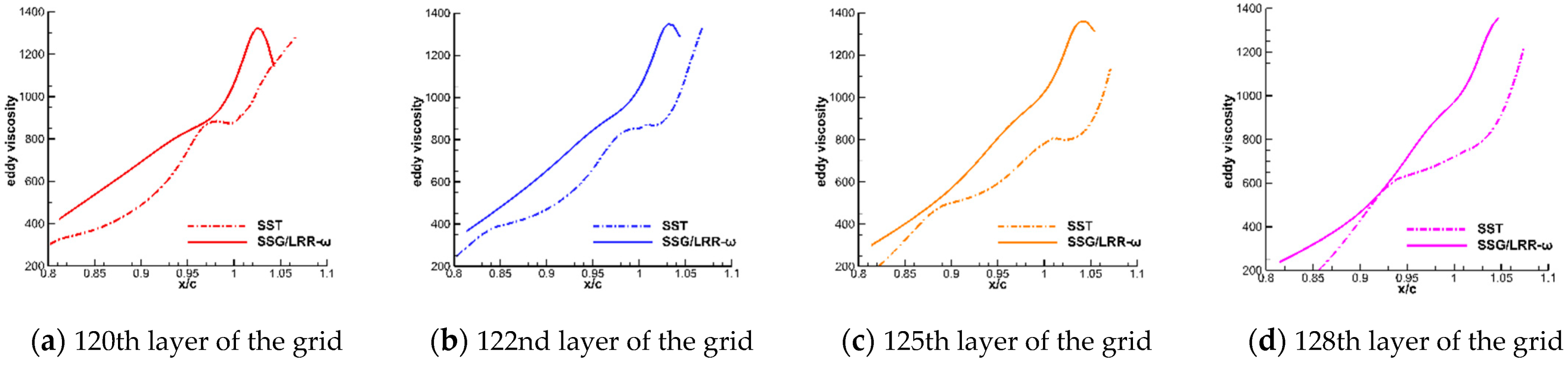
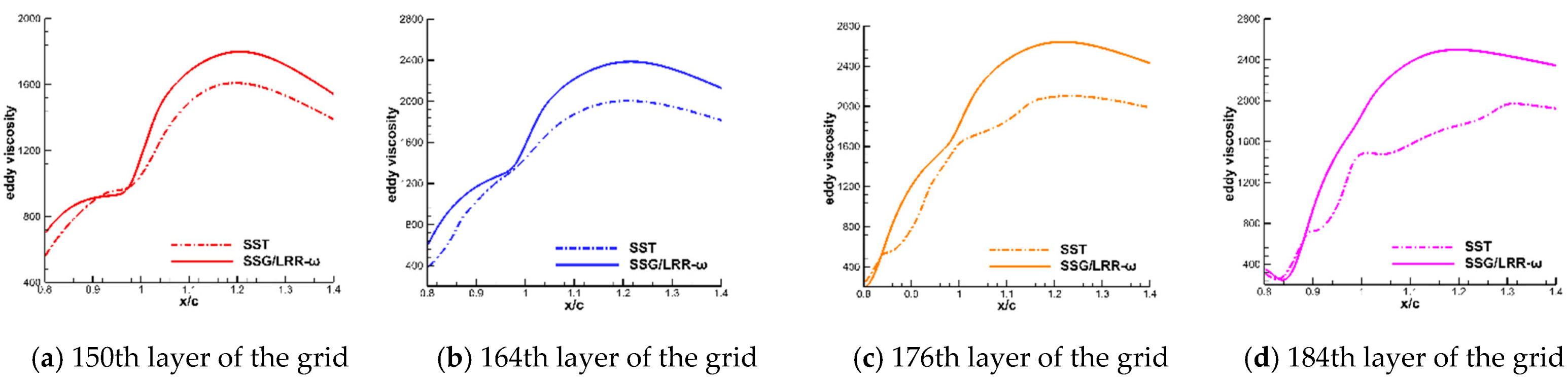
4.1.2. Reasons for Underestimating Shear Stress in the SST Model
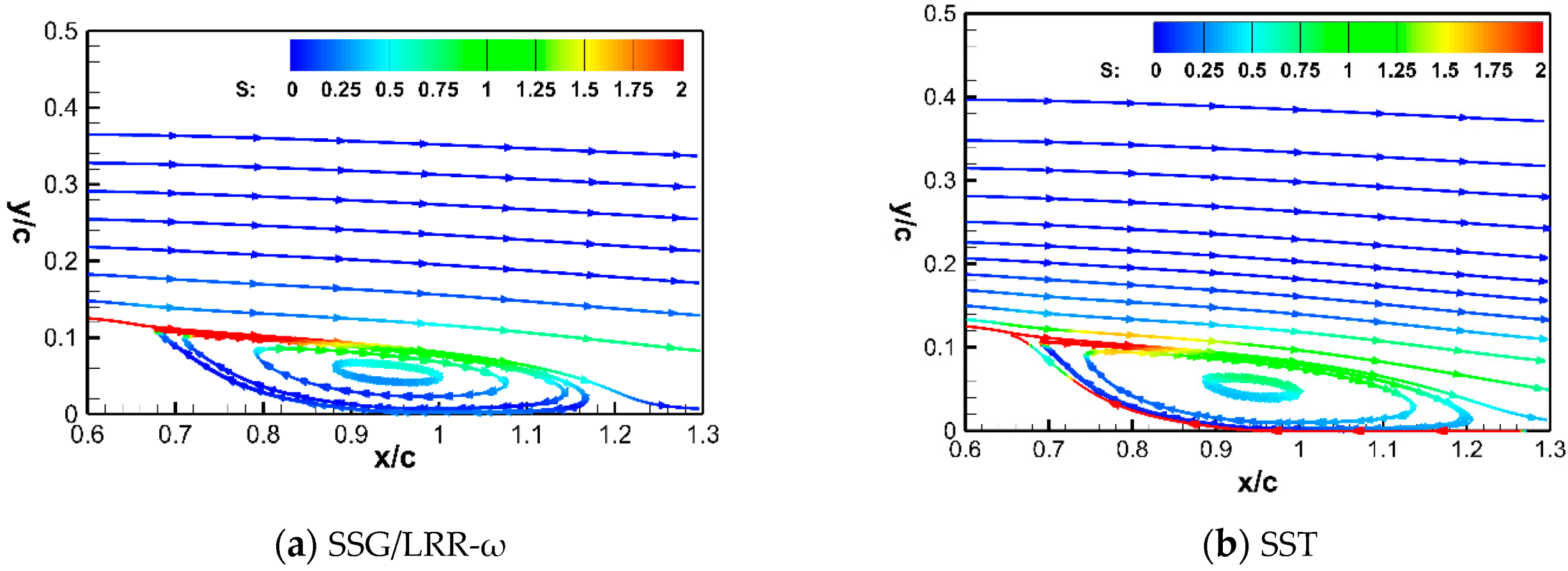
4.2. Lagging Reattachment
4.3. Difficulties of the Reynolds Stress Model
5. Conclusions
- The SST model underestimates the Reynolds stress upstream of the separation onset in the actual flows, leading to advanced separation. This phenomenon occurs because the SST model imposes [20] as a result of Menter’s modification of the eddy–viscosity coefficient by introducing Bradshaw’s relation (). However, this condition is strictly valid only in the log layer. When it is extrapolated to other areas or encounters a large adverse pressure gradient in the separated flow, the equilibrium condition cannot be satisfied, and the coefficient in Bradshaw’s relation needs to be corrected. Although the SST model noticeably enhances the prediction of the separated flows using Menter’s modified eddy–viscosity coefficient, the relation is too harsh, causing the phenomenon of separation to occur in advance.
- The SST model underestimates the Reynolds stress in the developing shear layer above the separation bubble, resulting in reattachment too far downstream. The reason for this phenomenon is different from that of the advanced separation. The modeling error of the eddy–viscosity coefficient and the calculation error of the average strain rate both introduce losses to the calculation accuracy of Reynolds stress. According to our analysis, the main effect on the Reynolds stress is caused by the underestimation of the eddy–viscosity coefficient, with relatively little effect caused by the average strain rate. In addition, the eddy–viscosity coefficient contains turbulent kinetic energy and dissipation. These components affect and restrict each other. Thus, the specific mechanism is very complex.
- The SSG/LRR-ω model obtains the Reynolds stress directly by solving the Reynolds stress transport equation. Most of the errors come from the modeling of the closure term, especially the modeling of the pressure–strain term. The inability to obtain accurate experimental data limits the accuracy with which the pressure–strain term can be modeled, but the redistribution of the pressure–strain term plays a decisive role in the production of Reynolds shear stress.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| a1 | coefficient of Bradshaw’s relation |
| c | chord |
| local skin-friction coefficient | |
| CP | pressure coefficient |
| turbulent-viscosity constant | |
| destruction term of ε transport equation | |
| F2 | Menter’s blending function |
| k | turbulent kinetic energy |
| pressure | |
| Pk | production term of k transport equation |
| Pε | production term of ε transport equation |
| Rec | Reynolds number based on c |
| Sij | mean rate-of-strain tensor, | Sij | |
| t | time |
| diffusive transport term of ε equation | |
| fluctuating velocity | |
| Reynolds shear stress | |
| U | mean velocity |
| U∞ | freestream velocity |
| rectangular Cartesian coordinates | |
| dimensionless, sublayer-scaled, distance | |
| specific Reynolds stress tensor | |
| Kronecker delta function | |
| e | rate of dissipation of turbulent kinetic energy |
| ρ | density |
| μ | molecular viscosity |
| kinematic molecular viscosity | |
| kinematic eddy viscosity | |
| ω | specific dissipation rate |
References
- Chen, M.Z. Fundamentals of Viscous Fluid Dynamics; Higher Education Press: Beijing, China, 2004. [Google Scholar]
- Pla, B.; Jp, B. On the modelling turbulent transition in turbine cascades with flow separation. Comput. Fluids 2019, 181, 160–172. [Google Scholar]
- Yan, C.; Qu, F.; Zhao, Y.T.; Yu, J.; Wu, C.H.; Zhang, S.H. Review of development and challenges for physical modeling and numerical scheme of CFD in aeronautics and astronautics. Acta Aerodyn. Sin. 2020, 38, 829–857. [Google Scholar]
- Slotnick, J.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences, Mchenry County Natural Hazards Mitigation Plan; NASA: Hampton, VA, USA, 2014. [Google Scholar]
- Driver, D.M.; Seegmiller, H.L. Features of a reattaching turbulent shear layer in divergent channel flow. AIAA J. 1984, 23, 163–171. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, C. Evaluation of engineering turbulence models for complex supersonic flows. J. Beijing Univ. Aeronaut. Astronaut. 2011, 37, 202–205+215. [Google Scholar]
- Eisfeld, B.; Rumsey, C.; Togiti, V. Verification and Validation of a Second-Moment-Closure Model. AIAA J. 2016, 54, 1524–1541. [Google Scholar] [CrossRef]
- Bush, R.H.; Chyczewski, T.S.; Duraisamy, K.; Eisfeld, B.; Rumsey, C.L.; Smith, B.R. Recommendations for Future Efforts in RANS Modeling and Simulation. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Rumsey, C.L. Application of Reynolds Stress Models to Separated Aerodynamic Flows. In Differential Reynolds Stress Modeling for Separating Flows in Industrial Aerodynamics; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Menter, F.R. Zonal Two Equation k-w Turbulence Models for Aerodynamic Flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993. [Google Scholar]
- Rodriguez, S. Applied Computational Fluid Dynamics and Turbulence Modeling: Practical Tools, Tips and Techniques; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Raje, P.; Sinha, K. Anisotropic SST turbulence model for shock-boundary layer interaction. Comput. Fluids 2021, 228, 105072. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Eisfeld, B.; Brodersen, O. Advanced Turbulence Modelling and Stress Analysis for the DLR-F6 Configuration. In Proceedings of the 23rd AIAA Applied Aerodynamics Conference, Toronto, ON, Canada, 6–9 June 2005. [Google Scholar]
- Rumsey, C.L. Turbulence Modeling Resource. Available online: http://turbmodels.larc.nasa.gov (accessed on 13 November 2021).
- Rumsey, C.L. Turbulence Modeling Verification and Validation (Invited). In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Krist, S.L.; Biedron, R.T.; Rumsey, C.L. CFL3D User’s Manual; (Version 5.0); NASA Langley Technical Report Server: Hampton, VA, USA, 1998. [Google Scholar]
- Greenblatt, D.; Paschal, K.B.; Yao, C.S.; Harris, J.; Schaeffler, N.W.; Washburn, A.E. Experimental Investigation of Separation Control Part 1: Baseline and Steady Suction. AIAA J. 2006, 44, 2820–2830. [Google Scholar] [CrossRef]
- Alber, I.E.; Bacon, J.W.; Masson, B.S.; Collins, D.J. An Experimental Investigation of Turbulent Transonic Viscous-Inviscid Interactions. AIAA J. 2015, 11, 620–627. [Google Scholar] [CrossRef]
- Leschziner, M. Statistical Turbulence Modelling for Fluid Dynamics-Demystified: An Introductory Text for Graduate Engineering Students; Imperial College Press: London, UK, 2015. [Google Scholar]
- Zhu, K.Q.; Xu, C.X. Viscous Fluid Mechanics; Higher Education Press: Beijing, China, 2009. [Google Scholar]
- Bertelrud, A.; Nordstrom, J. Experimental and computational investigation of the flow in the leading edge region of a swept wing. In Proceedings of the AIAA 16th Fluid and Plasmadynamics Conference, Danvers, MA, USA, 12–14 July 1983. [Google Scholar]
- Liou, W.W.; Huang, G.; Shih, T.H. Turbulence model assessment for shock wave/turbulent boundary-layer interaction in transonic and supersonic flows. Comput. Fluids 2000, 29, 275–299. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Cañada Flintridge, CA, USA, 2006. [Google Scholar]


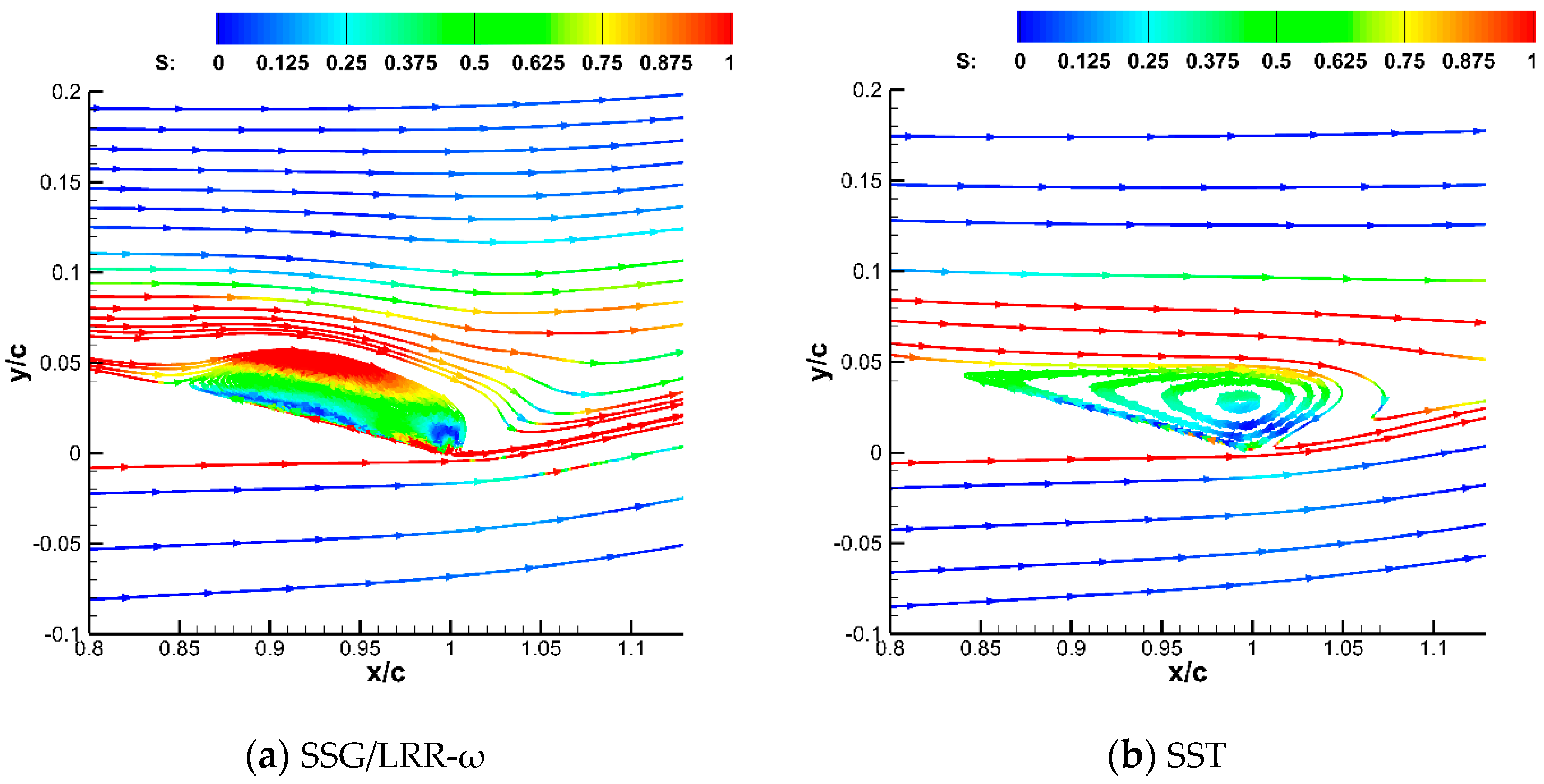
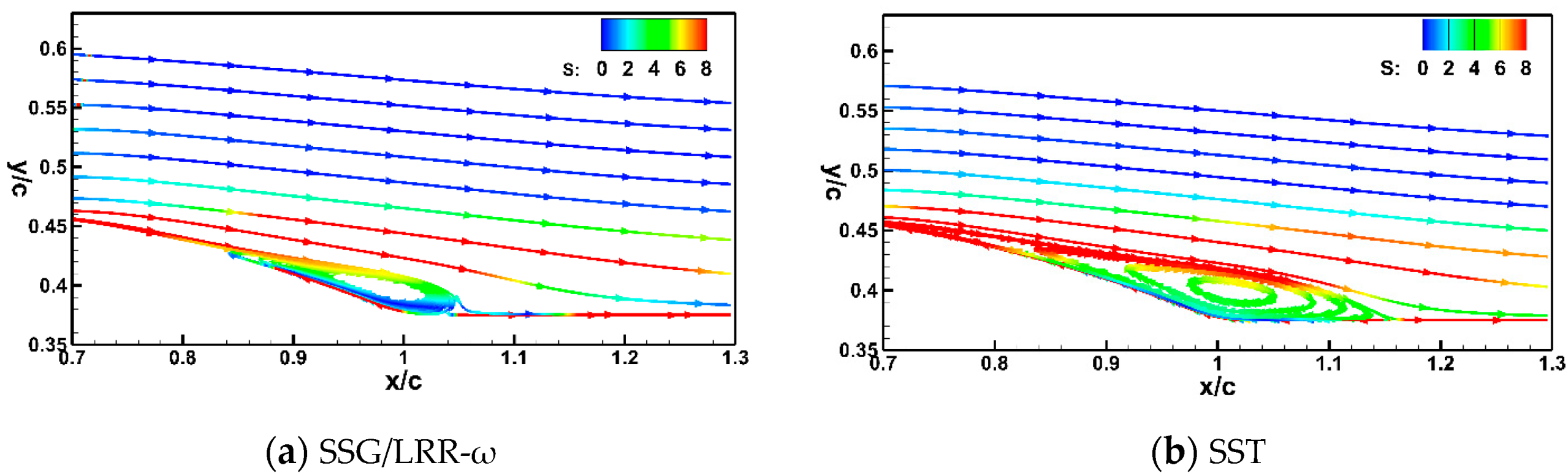
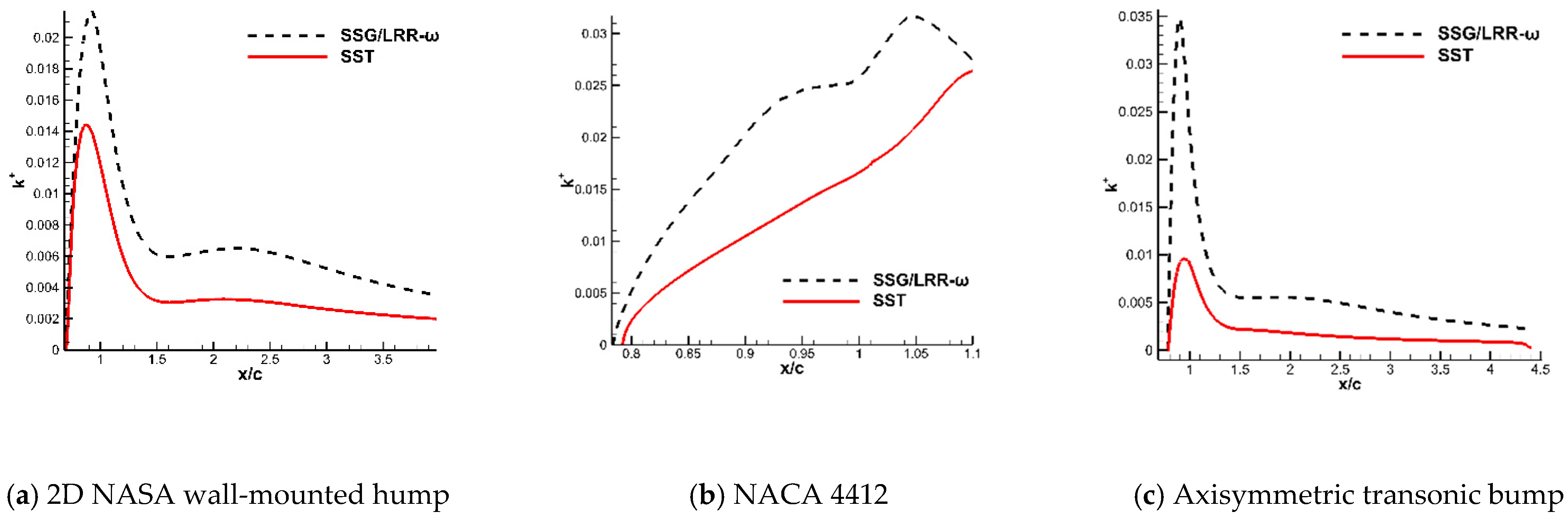
| Exp. Data | SSG/LRR-ω | SST | |
|---|---|---|---|
| Separation onset | 0.665 | 0.654 | 0.654 |
| Error | —— | 1.65% | 1.65% |
| Reattachment point | 1.1 | 1.183 | 1.269 |
| Error | —— | 7.5% | 15.36% |
| Exp. data | SSG/LRR-ω | SST | |
|---|---|---|---|
| Separation onset | 0.7 | 0.67 | 0.647 |
| Error | —— | 4.29% | 7.57% |
| Reattachment point | 1.1 | 1.05 | 1.165 |
| Error | —— | 4.54% | 5.91% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, R.; Li, J.; Zeng, F.; Yan, C. Mechanism and Performance Differences between the SSG/LRR-ω and SST Turbulence Models in Separated Flows. Aerospace 2022, 9, 20. https://doi.org/10.3390/aerospace9010020
Bai R, Li J, Zeng F, Yan C. Mechanism and Performance Differences between the SSG/LRR-ω and SST Turbulence Models in Separated Flows. Aerospace. 2022; 9(1):20. https://doi.org/10.3390/aerospace9010020
Chicago/Turabian StyleBai, Ruijie, Jinping Li, Fanzhi Zeng, and Chao Yan. 2022. "Mechanism and Performance Differences between the SSG/LRR-ω and SST Turbulence Models in Separated Flows" Aerospace 9, no. 1: 20. https://doi.org/10.3390/aerospace9010020
APA StyleBai, R., Li, J., Zeng, F., & Yan, C. (2022). Mechanism and Performance Differences between the SSG/LRR-ω and SST Turbulence Models in Separated Flows. Aerospace, 9(1), 20. https://doi.org/10.3390/aerospace9010020






